安全钳是电梯重要的安全保护装置. 当电梯超速运行时,安全钳将被触发,制动块与导轨间将产生巨大的摩擦力,迫使电梯停止运行. 安全钳能否在规定时间里完成预定功能,关键在于制动块与导轨的接触是否产生足够的摩擦力,有必要开展安全钳制动块与导轨间的接触力学问题研究,建立针对接触面应力和温度场分布的计算方法.
在安全钳的结构和性能方面,Lonkwic[1]研究不同型号的滚柱式安全钳的制动性能,分析了滚柱尺寸、电梯负载和制动延迟等参数对制动性能的影响. 刘磊[2]开展载货电梯瞬时式安全钳的力学分析,由于电梯制动过程产生的冲击载荷极大,作者采用非线性方法计算钳体的塑性形变. 谈伟荣[3]发现安全钳在渐进制动过程中形变量很小,最大应力远小于材料的屈服应力,因此不用考虑钳体的失效问题. Choi等[4]研究低速范围内制动块尺寸对制动性能的影响,发现尺寸较小的制动块更容易产生振动和噪声. Pulecchi等[5]利用数字滤波器精确测量高速电梯制动过程中的加速度,极大降低了振动噪声对测量数据的影响. Ren等[6]在试验研究中测得安全钳的摩擦系数在0.26~0.29之间. 安全钳的制动效果还受到制动块的表面形貌[7-8]、摩擦副的颗粒入侵[9-11]、电梯负载和运行速度[12-13]等因素的影响,应结合电梯型号及参数研究安全钳的性能.
在制动块热效应方面,Wan等[14]基于能量法建立制动系统的动力学模型,发现热效应是影响安全钳摩擦磨损特性的主要因素. Wu等[15]建立安全钳的全耦合热力模型并计算摩擦面的瞬态热,可用于高速电梯的制动仿真. Wang等[16]基于有限元法对制动过程进行热力分析,并结合电梯参数进行制动块寿命预测. Bellini等[17]基于传统的摩擦材料,探究不同温度下材料摩擦系数的变化范围. Wang等[18]研究紧急制动下的制动块摩擦面温度变化和摩擦系数变化曲线,并且通过调整材料组分的比例来提升制动块的摩擦和磨损性能. Rao等[19]通过试验研究发现,随着制动过程中摩擦面温度的上升,摩擦力会减小并且材料的磨损量会降低. Limmer等[20]发现在表面氧化程度不同的情况下,即便摩擦过中的压强与速度的乘积相同,摩擦面的温度和制动性能也不完全相同.
理论研究安全钳制动块与导轨间的接触应力通常使用有限元软件Ansys、Abaqus. 由于安全钳不仅结构复杂,而且存在滚子连接环节,导致使用现有的有限元软件无法在规定的时间内实现精确计算,摩擦面的应力分布往往以均布载荷等效,这显然与实际情况不符. 本研究通过对安全钳的结构和热力学的分析,结合有限元法与赫兹接触公式,建立适用于导轨的热传导方程,进行电梯渐进式楔形安全钳的热力耦合研究,构建计算安全钳制动块与导轨接触应力分布的方法,探究制动块的真实接触应力分布规律,找出影响安全钳制动块应力分布的主要因素.
1. 构建力学模型
1.1. 安全钳的结构及工作原理
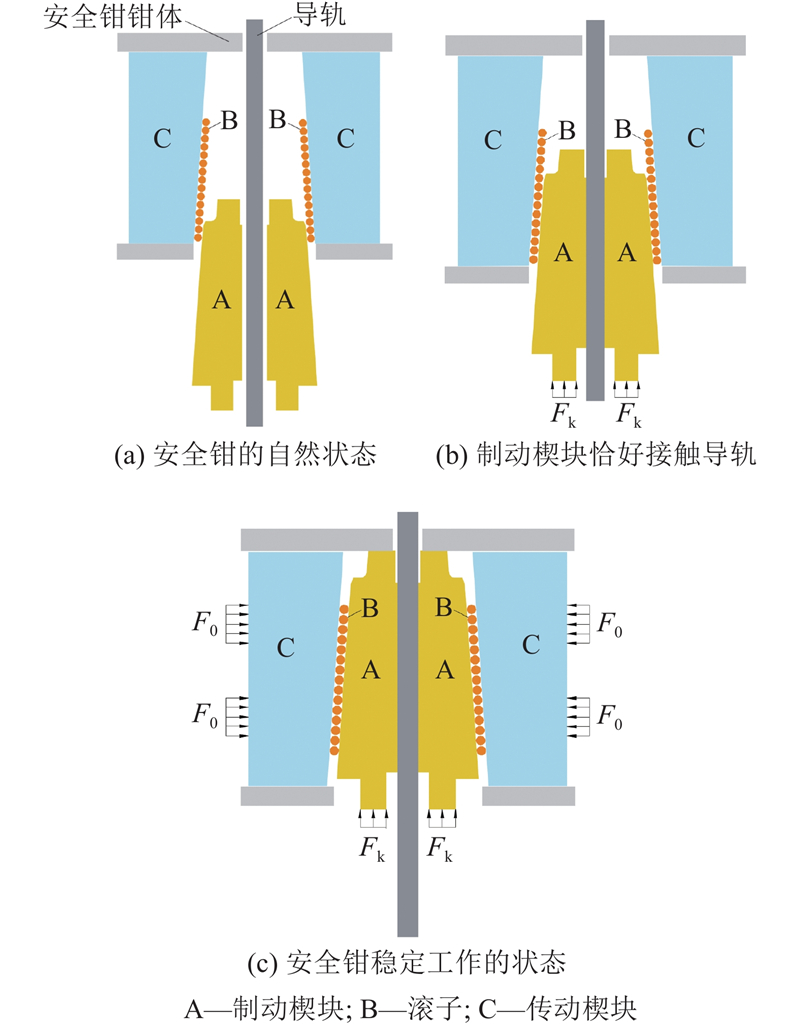
如图1所示为低速载货电梯中楔形渐进式安全钳的结构示意图. 图中,推杆用于触发安全钳工作,在自锁作用下,两侧的弹簧发生形变并产生足够的弹力. 如图2所示为安全钳的工作过程. 在自然状态下,制动楔块(A)自然下垂,滚子位于制动楔块和传动楔块(C)间隙的下方,滚子间通过保持架(图中未画出)维持相对距离. 当电梯超速时,触发推杆产生推力Fk推动制动楔块向上移动,当制动楔块恰好接触导轨时,传动楔块未发生移动,弹簧未产生弹力. 在安全钳稳定工作状态下,制动楔块上端接触安全钳钳体,传动楔块发生位移,弹簧产生弹力F0作用于传动楔块,由于滚子和接触面间存在的摩擦力,滚子上移一定的距离,位于制动楔块和传动楔块间隙的中间位置.
图 1
图 1 楔形渐进式安全钳的结构示意图
Fig.1 Construction schematic of wedge-shaped progressive safety gear
图 2
本研究主要分析安全钳的稳定工作状态,此时制动楔块与导轨间的接触应力分布与传动楔块的受力、滚子的压力分布以及制动楔块自身结构有关. 制动楔块和传动楔块的力学分析,可作为平面应力问题,采用有限元法求解. 由于安全钳的滚子数目较多,采用赫兹接触的解析公式求解滚子的载荷与形变. 安全钳为对称结构,因此只进行安全钳左侧结构分析,并做出如下假设:1)楔块和滚子只发生线弹性形变,不产生塑性形变;2)弹簧对传动楔块施加的弹力在受力面上均匀分布;3)忽略安全钳钳体的形变,将钳体作为刚体.
1.2. 安全钳的热力学分析
1.2.1. 楔块与导轨的形变刚度矩阵
对楔块与导轨进行网格划分,采用六节点三角形单元进行有限元分析,建立面积坐标L1、L2和L3,如图3所示. 结合待定系数α1~α6和β1~β6,单元内任意点的水平和竖直位移U和V描述为
图 3
将单元节点位移U1~ U6、V1~ V6带入式(1)和式(2),分别计算α1~α6和β1~β6,得到单元e中每个节点i的形函数Ni,利用插值法描述单元内任意点的位移:
式中:
式中:
式中,
1.2.2. 滚子的形变刚度矩阵
根据文献[21]中的方程,滚子r的总压缩量Yr和正压力Fr的关系式为
式中:L为滚子长度. 建立滚子的位移阵列
式中:n为滚子总数. 根据虚功原理,滚子的形变能
其中
对
式中:
1.2.3. 安全钳的接触力学分析
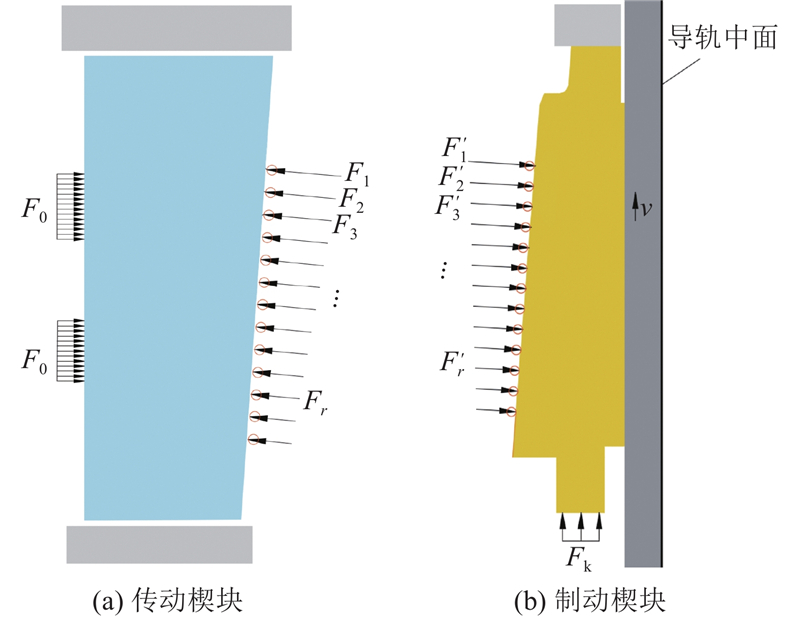
如图4(a)所示,传动楔块的上下边界与钳体接触,在钳体的刚性假设下,考虑楔块与钳体的间隙,上下边界的接触条件即为可分离的刚柔接触. 传动楔块的右侧与滚子接触,取最上端滚子序号r=1,向下依次排列,Fr为对应的滚子压力. 传动楔块的左侧存在线密度为F0的弹簧弹力边界条件,分为上下2个部分,每个部分的分布长度相同. 如图4(b)所示,制动楔块的上侧与钳体接触,为可分离的刚柔接触;右侧与导轨接触,导轨相对制动楔块向上移动,故制动楔块右侧边界的接触条件为存在滑动摩擦力的柔性体接触;制动楔块左侧与滚子接触,
图 4
假定传动楔块初始位置上表面与钳体贴合,则楔块的接触对共分为5类,如表1所示. 表中,w为传动楔块与钳体的总间隙;
表 1 安全钳的接触类型
Tab.1
| 接触对 | 状态 | 约束条件 | 校核条件 |
| 传动楔块上 表面−钳体 | 接触 | ||
| 分离 | |||
| 传动楔块下 表面−钳体 | 接触 | ||
| 分离 | |||
| 制动楔块上 表面−钳体 | 接触 | ||
| 分离 | |||
| 制动楔块右 表面−导轨 | 接触 | ||
| 分离 | |||
| 传动楔块− 滚子−制动楔块 | 接触 | ||
| 分离 |
式(16)要求制动楔块与导轨在接触面的网格节点位置相同. 基于表中的接触条件及式(13)~式(17),计算各类接触的接触势能
式中:
式中:
式中:QC为集成后的接触节点的广义位移阵列,KT为整体的接触切线刚度矩阵.
1.2.4. 安全钳的位移求解
安全钳的总位能
则安全钳总位能
对结构的所有广义位移(X、Y和QC)进行集成后得到结构的总广义位移阵列
微分形式为
根据最小位能原理,基于牛顿-拉夫逊(Newton-Raphson,N-R)方法的表达式为
将式(31)展开后化为
将式(32)写为迭代形式:
式中:n为迭代步数,
1.3. 安全钳的传热分析
摩擦热集中在制动楔块与导轨的接触面,故仅对制动楔块和导轨进行传热分析.
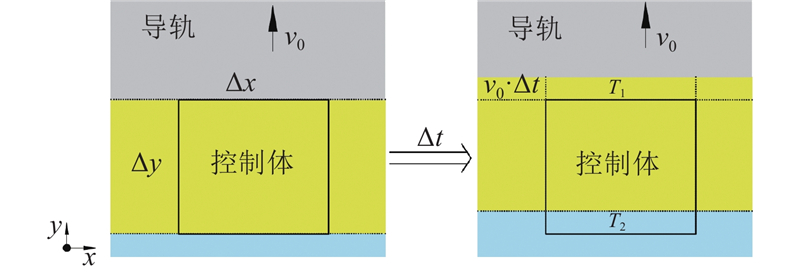
式(34)为二维热传导基本方程,其中ρ为材料密度,c为比热容,t为制动时间,kx、ky分别为水平和竖直方向的热传导系数,Q为内部热源密度. 以制动楔块为参照物,则该楔块的系统与控制体保持一致,导轨以速度v0向上运动,单元控制体如图5所示. 导轨单元控制体的内能变化率还受到质量流量的影响,在
图 5
图 5 制动过程中导轨单元控制体中的内能变化
Fig.5 Internal energy change in control unit of guide rail during braking
安全钳及导轨均为各项同性材料,且无内部热源,故式(34)调整为
式中:kxy为热传导系数,v为相对速度,制动楔块取为0,导轨取为v0. 设定导轨中面为绝热边界条件,制动楔块与导轨的接触面存在热流密度q,其余边界均为自然换热边界. 热流密度由摩擦热的功率决定,定义
采用图3中的单元及对应的网格进行有限元分析,单元内任意点的温度T为
其中T1~T6为对应节点的温度. 基于伽辽金法,单元内的温度方程为
式中:
式中:
1.4. 安全钳的热力耦合求解
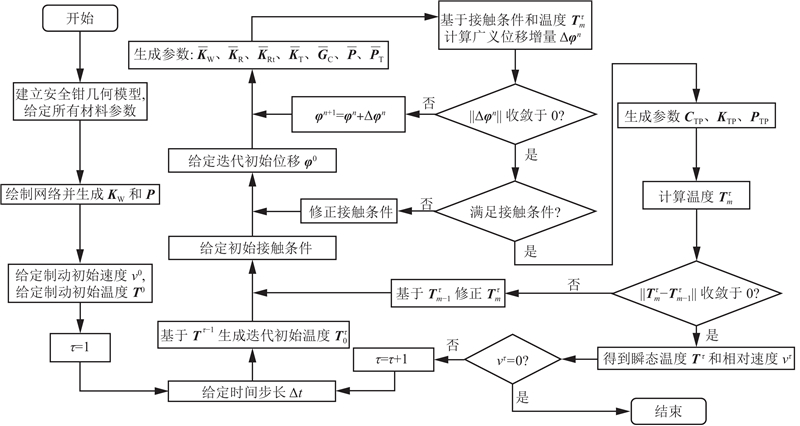
如图6所示,采用弱耦合的形式求解制动过程中的热应力和温度场,即通过热应力分析计算摩擦面的接触应力分布,再由该接触应力计算温度场,二者迭代收敛后得到瞬态的温度场与热应力. 基于时间步长修正楔块与导轨间的相对速度,重复计算瞬态热应力与温度场,直至电梯制动完成.
图 6
图 6 安全钳热力耦合的求解流程
Fig.6 Solution process of thermodynamic coupling of safety gear
2. 算例研究
2.1. 应力和温度场分布规律
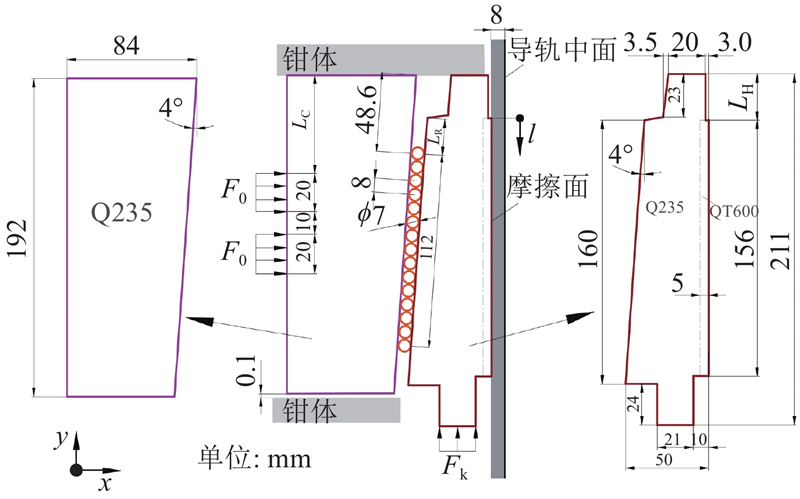
如图7所示为10 t载货电梯楔形渐进式安全钳的几何参数. 图中,传动楔块与钳体间的总间隙为0.1 mm,在安全钳稳定工作时,最上端的滚子到制动楔块左侧上端的距离为LR,理论值为24 mm;制动楔块左侧弹簧到制动楔块上端的距离LC初始值为63 mm,载荷线密度F0=2.5 kN/mm(总压力为100 kN);滚子长度和楔块厚度均为30 mm;制动楔块右侧摩擦面的上端与制动楔块顶端的高度差LH初始值为25 mm;制动楔块底部存在均布的触发推力Fk=2 kN. l为摩擦面上的局部坐标,其原点对应摩擦面的最上端. 制动楔块的主体材料为Q235,对摩擦面进行热处理,得到材料为QT600、厚度为5 mm的摩擦面;导轨与传动楔块的材料均为Q235,滚子材料为GCr15. 材料的性能参数如表2所示,采用线性插值法计算中间温度的材料性能参数. 该电梯的制动初速度为0.63 m/s,制动温变对摩擦系数的影响较小,取制动楔块与导轨间的滑动摩擦系数为0.35.
图 7
表 2 安全钳和导轨的材料参数
Tab.2
| 材料 | E/GPa | µ | α/10−6 | kxy/(W·m−1·℃−1) | c/(J·kg−1·℃−1) |
| Q235(20 ℃) | 211 | 0.30 | 10.6 | 51.6 | 450 |
| Q235(100 ℃) | 207 | 0.30 | 12.2 | 48.9 | 483 |
| QT600(20 ℃) | 169 | 0.27 | 11.1 | 52.2 | 503 |
| QT600(100 ℃) | 166 | 0.27 | 13.2 | 57.2 | 537 |
| GCr15(20 ℃) | 210 | 0.30 | — | — | — |
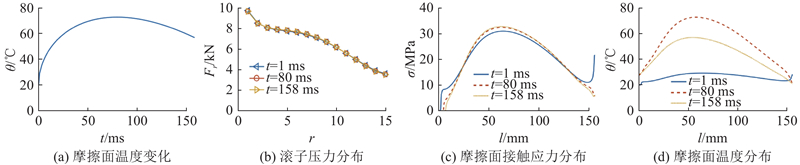
给定环境温度为20℃,使用Matlab求解,分析结果如图8和图9所示. 图8(a)中,
图 8
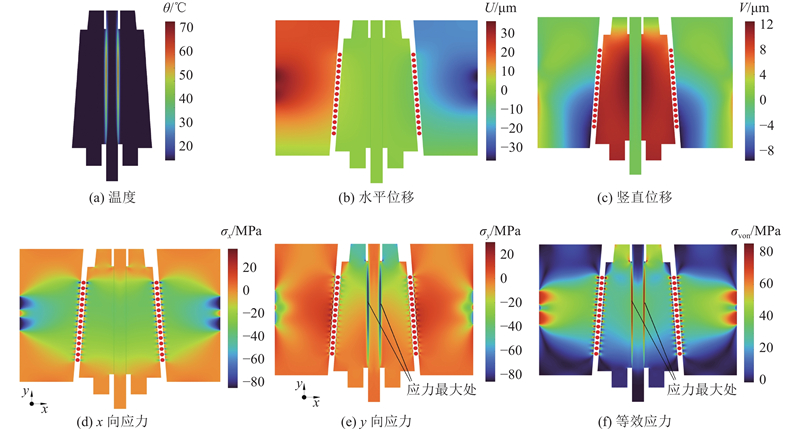
图 9
图 9 制动时间为80 ms时的温度、位移与应力云图
Fig.9 Nephogram of temperature, displacement and stress at braking time of 80 ms
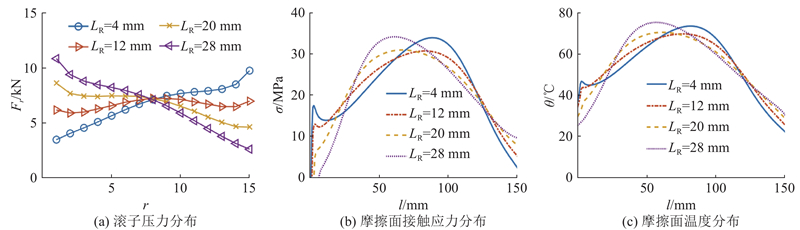
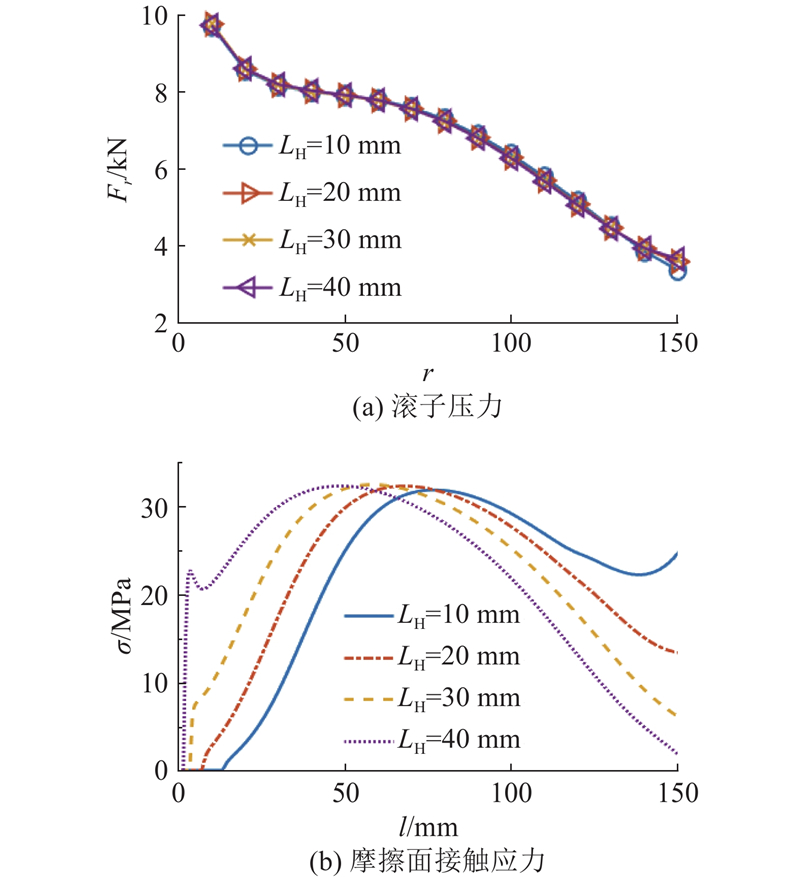
2.2. 滚子位置对应力与温度场分布的影响
图 10
图 10 不同滚子位置下的力与温度分布图
Fig.10 Distribution of force and temperature at different rollers positions
图1所示安全钳中未设计对滚子的限位装置,滚子在工作过程中的实际位置无法预判. 给定电梯总负载为10 000 kg、制动初速度为0.63 m/s,当安全钳完成制动后,制动楔块的实物图如图11所示. 图11(a)中,由于与滚子接触的区域存在应力集中,在安全钳多次工作后,接触面上产生图示压痕,通过压痕的位置可以判断,滚子的实际接触区域靠近制动楔块的上端,结合压痕深度的分布规律可以发现,下方滚子的受力程度大于上方,这与图10(b)中LR=4 mm时的滚子压力分布基本符合. 图11(b)中,下端的磨损量明显小于中上端,这与图10(c)中LR=4 mm时的摩擦面应力分布规律具有一致性. 由图11可以看出,制动楔块在宽度方向上的受力和磨损不均匀,原因是该型号的安全钳在宽度方向上保留较大装配间隙,导致制动楔块在工作时向一侧偏转.
图 11
2.3. 弹簧位置对应力与温度场分布的影响
图 12
图 12 不同弹簧位置下的滚子压力与摩擦面接触应力分布图
Fig.12 Distribution of rollers pressure and friction surface contact stress at different spring positions
2.4. 摩擦面位置对应力与温度场分布的影响
图 13
图 13 不同摩擦面位置的滚子压力与摩擦面接触应力分布图
Fig.13 Distribution of rollers pressure and friction surface contact stress at different friction surface positions
3. 结 论
(1)对楔形渐进式安全钳的结构和工作过程进行热力学分析,通过建立滚子的刚度矩阵和应用接触理论,完成对楔块和导轨形变及应力的精确计算. 相比单一的有限元分析,该方法可以极大地提升计算效率. 针对楔块与导轨间的相对运动,建立适用于控制体的热传导方程,采用伽辽金法进行求解,得到瞬态热的求解公式. 计算结果表明,该方法具有良好的稳定性. 采用弱耦合的求解方式实现对摩擦面接触应力分布的精确计算,研究结果与制动块实验照片的比对结果表明,所建立的计算方法具有可靠性.
(2)通过具体的算例研究,绘制楔块与导轨的温度场、位移分布和应力分布云图,以及滚子的压力分布图和摩擦面的接触应力分布曲线. 研究摩擦面的应力及温度分布曲线发现,制动楔块与导轨接触面的接触应力峰值一般在中间区域,热效应会降低摩擦面两端的接触应力,摩擦面的温度分布及变化规律基本与接触应力的相同. 在通常情况下,传动楔块与钳体的间隙对安全钳应力分布的影响可以忽略. 滚子位置的上移会增大下端的滚子压力,减小上端的滚子压力,使得摩擦面上端的接触应力显著增大. 弹簧位置的下移动会增大下端的滚子压力,同时减小上端的滚子压力,使得摩擦面下端的压力显著增大. 摩擦面位置的变化对滚子压力分布几乎没有影响,但会显著影响摩擦面两端的接触应力,当摩擦面自上而下移动时,两端的接触应力逐渐由上小下大过渡为上大下小,中间段的接触应力没有显著变化.
本研究采用平面应力单元对楔块进行简化,未解释制动块摩擦面在厚度方向上磨损不均匀的现象. 未来将采用三维实体单元对楔块进行数值分析,并结合中厚板理论计算钳体的形变,进一步研究安全钳与导轨间的接触应力在楔块厚度方向上的分布规律,并结合分析结果优化安全钳的结构参数.
参考文献
Influence of friction drive lift gears construction on the length of braking distance
[J].DOI:10.3901/CJME.2015.0108.009 [本文引用: 1]
Size effects of brake pads on stick-slip phenomena
[J].DOI:10.1016/j.triboint.2023.108944 [本文引用: 1]
Digital filtering of acceleration data acquired during the intervention of a lift safety gears
[J].DOI:10.1016/j.measurement.2009.12.004 [本文引用: 1]
Microstructure analysis of elevator brake base
[J].
Brake surface texture exploration and temperature control during braking in the new knee impact test
[J].
Experiment research on emergency stop vibrations of key components in the friction vertical lifting system
[J].
Modeling and simulation of macroscopic friction coefficient of brake pair considering particle flows and interface parameters
[J].DOI:10.1007/s42417-022-00692-9
Study on the influence of three-body particles on the dynamic performance of braking system
[J].DOI:10.1016/j.triboint.2023.109013 [本文引用: 1]
Influence of contact pressure and velocity on the brake behaviour and particulate matter emissions
[J].DOI:10.1016/j.wear.2022.204579 [本文引用: 1]
Experimental evaluation of braking pad materials used for high-speed elevator
[J].DOI:10.1016/j.wear.2021.203872 [本文引用: 1]
Research on the time-varying properties of brake friction (September 2018)
[J].DOI:10.1109/ACCESS.2018.2878776 [本文引用: 1]
Thermo-mechanical modeling and transient analysis of frictional braking of elevator safety gear
[J].DOI:10.1080/01495739.2020.1820921 [本文引用: 1]
Analysis of emergency braking characteristics and prediction of fatigue life for elevator block brake based on thermal-structural coupling
[J].DOI:10.1007/s40430-022-03744-z [本文引用: 1]
Temperature influence on brake pad friction coefficient modelisation
[J].
Preparation of high friction brake shoe material and its tribological behaviors during emergency braking in ultra-deep coal mine hoist
[J].DOI:10.1016/j.wear.2020.203391 [本文引用: 1]
Friction and dry sliding wear properties of compact graphite iron at room temperature and 100 ℃
[J].
Tribo-oxidation of a brake friction couple under varying sliding conditions
[J].DOI:10.1016/j.triboint.2023.108536 [本文引用: 1]