[1]
FRANK T, LIU J, GAT S, et al A machine learning approach to design of aperiodic, clustered-dot halftone screens via direct binary search
[J]. IEEE Transactions on Image Processing , 2022 , 31 : 5498 - 5512
DOI:10.1109/TIP.2022.3196821
[本文引用: 1]
[2]
LAU D L, ARCE G R. Modern digital halftoning [M]. 2nd ed. Boca Raton: CRC Press, 2018.
[本文引用: 1]
[3]
ULICHNEY R A Dithering with blue noise
[J]. Proceedings of the IEEE , 1988 , 76 (1 ): 56 - 79
DOI:10.1109/5.3288
[本文引用: 3]
[4]
KOPF J, COHEN-OR D, DEUSSEN O, et al Recursive Wang tiles for real-time blue noise
[J]. ACM Transactions on Graphics , 2006 , 25 (3 ): 509 - 518
DOI:10.1145/1141911.1141916
[本文引用: 1]
[5]
BAYER B E An optimum method for two level rendition of continuous tone pictures
[J]. IEEE International Conference on Communications , 1973 , 9 (1 ): 26.11 - 26.15
[本文引用: 4]
[6]
YI Y, LI R, YU C, et al Quality evaluation metric for greyscale error diffusion halftone images based on texture and visual characteristics
[J]. Imaging Science Journal , 2017 , 65 (5/6 ): 315 - 326
[本文引用: 1]
[7]
YANG G, JIAO S, LIU J P, et al Error diffusion method with optimized weighting coefficients for binary hologram generation
[J]. Applied Optics , 2019 , 58 (20 ): 5547 - 5555
DOI:10.1364/AO.58.005547
[8]
FUNG Y H, CHAN Y H Tone-dependent error diffusion based on an updated blue-noise model
[J]. Journal of Electronic Imaging , 2016 , 25 (1 ): 013013
DOI:10.1117/1.JEI.25.1.013013
[本文引用: 1]
[9]
CHIZHOV V, GEORGIEV I, MYSZKOWSKI K, et al Perceptual error optimization for Monte Carlo rendering
[J]. ACM Transactions on Graphics , 2022 , 41 (3 ): 1 - 17
[本文引用: 1]
[10]
MAO Y, SARKAR U, BORRELL I, et al Ink drop displacement model-based direct binary search
[J]. IEEE Transactions on Image Processing , 2023 , 32 : 3897 - 3911
DOI:10.1109/TIP.2023.3283924
[本文引用: 1]
[11]
XIA M, WONG T T. Deep inverse halftoning via progressively residual learning [C]// Computer Vision–ACCV 2018 . Perth: Springer, 2019: 523–539.
[本文引用: 1]
[12]
SHAO L, ZHANG E, LI M An efficient convolutional neural network model combined with attention mechanism for inverse halftoning
[J]. Electronics , 2021 , 10 (13 ): 1574
DOI:10.3390/electronics10131574
[13]
JIANG H, MU Y Conditional diffusion process for inverse halftoning
[J]. Advances in Neural Information Processing Systems , 2022 , 35 : 5498 - 5509
[本文引用: 1]
[14]
XIA M, HU W, LIU X, et al. Deep halftoning with reversible binary pattern [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Montreal: IEEE, 2021: 14000–14009.
[本文引用: 7]
[15]
SHAO S, LI Z, ZHANG T, et al. Objects365: a large-scale, high-quality dataset for object detection [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Seoul: IEEE, 2019: 8430–8439.
[本文引用: 1]
[16]
CHOI B, ALLEBACH J P Mimicking DBS halftoning via a deep learning approach
[J]. Electronic Imaging , 2022 , 34 (15 ): 158
[本文引用: 1]
[17]
AGUSTSSON E, TIMOFTE R. NTIRE 2017 challenge on single image super-resolution: dataset and study [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops . Honolulu: IEEE, 2017: 126–135.
[本文引用: 2]
[18]
HUI Z, WANG X, GAO X. Fast and accurate single image super-resolution via information distillation network [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Salt Lake City: IEEE, 2018: 723–731.
[本文引用: 2]
[19]
ZHANG H, WANG P, ZHANG C, et al A comparable study of CNN-based single image super-resolution for space-based imaging sensors
[J]. Sensors , 2019 , 19 (14 ): 3234
DOI:10.3390/s19143234
[本文引用: 2]
[20]
JIU M, PUSTELNIK N A deep primal-dual proximal network for image restoration
[J]. IEEE Journal of Selected Topics in Signal Processing , 2021 , 15 (2 ): 190 - 203
DOI:10.1109/JSTSP.2021.3054506
[本文引用: 3]
[21]
DONG C, LOY C C, TANG X. Accelerating the super-resolution convolutional neural network [C]// Computer Vision–ECCV 2016 . Amsterdam: Springer, 2016: 391–407.
[本文引用: 2]
[22]
MATSUI Y, ITO K, ARAMAKI Y, et al Sketch-based Manga retrieval using Manga109 dataset
[J]. Multimedia Tools and Applications , 2017 , 76 : 21811 - 21838
DOI:10.1007/s11042-016-4020-z
[本文引用: 3]
[23]
HUANG J B, SINGH A, AHUJA N. Single image super-resolution from transformed self-exemplars [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Boston: IEEE, 2015: 5197–5206.
[本文引用: 2]
[24]
OSTROMOUKHOV V. A simple and efficient error-diffusion algorithm [C]// Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques . [S.l.]: ACM, 2001: 567–572.
[本文引用: 3]
[25]
ANALOUI M, ALLEBACH J P. Model-based halftoning using direct binary search [C]// Human Vision, Visual Processing, and Digital Display III . San Jose: [s.n.], 1992: 96–108.
[本文引用: 3]
A machine learning approach to design of aperiodic, clustered-dot halftone screens via direct binary search
1
2022
... 数字半色调是在只能产生二值图像元素的设备上呈现连续调图像错觉的方法. 由于人类视觉系统(human visual system,HVS)的低通滤波特性,半色调图像在足够距离点观测时会被视为连续调图像[1 -2 ] . 半色调图像通常应用于印刷行业[3 ] . 根据网点聚类的方式不同,半色调图像可以分为2种类型:聚类网点和离散网点. 半色调纹理可以分为周期性纹理和非周期性纹理. 给定连续调图像输入,不同的算法生成的半色调图像之间存在差异. 由于人眼感知的低通特性,视觉效果最佳的半色调图像一般具有蓝噪声分布,符合蓝噪声特性的半色调[4 ] 是生成高质量半色调图像的关键. ...
1
... 数字半色调是在只能产生二值图像元素的设备上呈现连续调图像错觉的方法. 由于人类视觉系统(human visual system,HVS)的低通滤波特性,半色调图像在足够距离点观测时会被视为连续调图像[1 -2 ] . 半色调图像通常应用于印刷行业[3 ] . 根据网点聚类的方式不同,半色调图像可以分为2种类型:聚类网点和离散网点. 半色调纹理可以分为周期性纹理和非周期性纹理. 给定连续调图像输入,不同的算法生成的半色调图像之间存在差异. 由于人眼感知的低通特性,视觉效果最佳的半色调图像一般具有蓝噪声分布,符合蓝噪声特性的半色调[4 ] 是生成高质量半色调图像的关键. ...
Dithering with blue noise
3
1988
... 数字半色调是在只能产生二值图像元素的设备上呈现连续调图像错觉的方法. 由于人类视觉系统(human visual system,HVS)的低通滤波特性,半色调图像在足够距离点观测时会被视为连续调图像[1 -2 ] . 半色调图像通常应用于印刷行业[3 ] . 根据网点聚类的方式不同,半色调图像可以分为2种类型:聚类网点和离散网点. 半色调纹理可以分为周期性纹理和非周期性纹理. 给定连续调图像输入,不同的算法生成的半色调图像之间存在差异. 由于人眼感知的低通特性,视觉效果最佳的半色调图像一般具有蓝噪声分布,符合蓝噪声特性的半色调[4 ] 是生成高质量半色调图像的关键. ...
... 在图像处理中,通常用颜色来命名各种类型噪声. 白噪声的功率谱在所有频率上均匀分布;粉红噪声是低频白噪声,其功率谱截至某个高频极限;蓝噪声是高频白噪声,功率谱分布在高频区域,被证明是产生高质量半色调图像的关键[3 ] . 常值灰度图像的蓝噪声半色调具有以下频谱特性[3 ] :1)不含或含有较少低频分量;2)高频区能量分布相对平坦;3)蓝噪声在主频f b 处处于峰值;4)各向异性在所有频率上都低,一般要小于−10 dB. 理想蓝噪声半色调的功率谱如图1 所示,其中f 为频率,P 为功率. ...
... [3 ]:1)不含或含有较少低频分量;2)高频区能量分布相对平坦;3)蓝噪声在主频f b 处处于峰值;4)各向异性在所有频率上都低,一般要小于−10 dB. 理想蓝噪声半色调的功率谱如图1 所示,其中f 为频率,P 为功率. ...
Recursive Wang tiles for real-time blue noise
1
2006
... 数字半色调是在只能产生二值图像元素的设备上呈现连续调图像错觉的方法. 由于人类视觉系统(human visual system,HVS)的低通滤波特性,半色调图像在足够距离点观测时会被视为连续调图像[1 -2 ] . 半色调图像通常应用于印刷行业[3 ] . 根据网点聚类的方式不同,半色调图像可以分为2种类型:聚类网点和离散网点. 半色调纹理可以分为周期性纹理和非周期性纹理. 给定连续调图像输入,不同的算法生成的半色调图像之间存在差异. 由于人眼感知的低通特性,视觉效果最佳的半色调图像一般具有蓝噪声分布,符合蓝噪声特性的半色调[4 ] 是生成高质量半色调图像的关键. ...
An optimum method for two level rendition of continuous tone pictures
4
1973
... 在半色调研究中,生成图像的质量和处理效率是重点. 在传统算法中,基于有序抖动的方法[5 ] 并行性较高,处理速度较快,但生成的半色调图像质量较差. 基于误差扩散的方法[6 -8 ] 较好平衡了图像质量和处理速度,生成的图像质量比有序抖动方法高,但是因需顺序处理难以并行计算,且生成的半色调图像会引入相关伪影. 基于搜索的方法[9 -10 ] 产生的半色调图像质量优于前2种方法,但处理速度缓慢.虽然深度学习在图像处理领域的应用不少,但是它们大多集中在逆半色调方向[11 -13 ] ,半色调处理方向的应用鲜见. 本研究将深度学习模型应用于数字半色调,提出基于残差网络的半色调算法(halftone algorithm based on residual networks,HalfResNet),使得生成的半色调图像在保持较好结构细节的同时提高处理效率. 通过与已有深度半色调方法[14 ] 在VOC数据集[15 ] 上的性能对比实验,验证所提方法的特性. ...
... 将HalfResNet与不同类别的典型算法进行比较,包括Bayer有序抖动算法[5 ] 、Ostromoukhov 误差扩散算法[24 ] 、DBS[25 ] 和RVH[14 ] . 采用峰值信噪比(peak signal-to-noise ratio,PSNR)、结构相似性(structural similarity,SSIM)2项指标比较生成的半色调图像与连续灰度图像间的差异. PSNR是有损变换(如图像压缩、图像修复)中常使用的重构度量. 对于半色调图像,PSNR由图像之间的最大像素值L 和均方误差MSE来定义. 给定具有N 个像素的连续灰度图像和半色调图像,I h 、I s 分别为灰度图像的像素值和半色调图像的像素值, ...
... Quantitative evaluation of halftone algorithms
Tab.1 算法 SSIM PSNR Bayer有序抖动[5 ] 0.098 1 20.174 1 Ostromoukhov误差扩散[24 ] 0.110 0 21.133 3 DBS[25 ] 0.092 4 21.037 0 RVH[14 ] 0.161 5 20.700 8 本研究 0.174 7 20.834 1
如图5 所示为多种算法在“蜗牛形状器官(snail shaped organ)”图片上的半色调效果. 由图可知,传统算法在边缘细节处理效果欠佳,以过度模糊精细纹理细节为代价抑制伪影的出现,所提算法和RVH都很好保留了图像边缘纹理细节,在螺纹处保留了更多的原始图片的纹路信息. 对比RVH,所提算法在边缘细节部分含噪声更少. ...
... Runtime and parameter number comparison for different algorithms
Tab.5 算法 N P /106 t r /msBayer有序抖动[5 ] — 0.40 Ostromoukhov误差扩散[24 ] 38.40×10−5 10.00 DBS[25 ] — 2990.00 RVH[14 ] 37.80 30.06* 本研究 1.22 12.84*
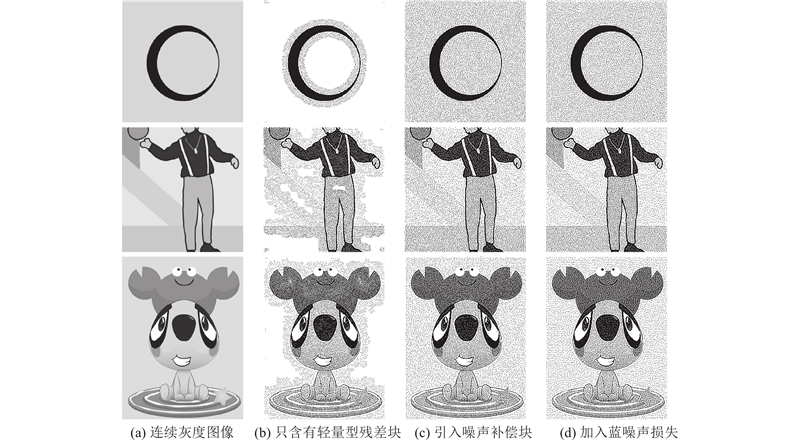
4. 结 语 本研究提出基于轻量残差网络的高效半色调算法. 引入噪声补偿块,解决了CNN平坦性退化问题,在平坦区域产生了出色的抖动效果;将显式的蓝噪声损失引入损失函数,辅助符合人眼感知的蓝噪声特性半色调图像的生成;采用端到端的模型生成半色调图像,通过跳跃连接将浅层特征和深层特征融合. 与RVH模型相比,所提算法的参数量下降了96.77%,处理速度提高了57.28%;在多个数据集上比较不同算法的性能,相比其他典型算法,所提算法具有最佳的SSIM和有竞争力的PSNR,保留了更多的纹理细节. 本研究为半色调图像处理领域带来了显著的性能提升,为实际应用提供了更高质量和效率的解决方案. 所提算法在某些复杂图像场景下的通用性有待进一步验证,未来将在更大规模的数据集上进行测试. ...
Quality evaluation metric for greyscale error diffusion halftone images based on texture and visual characteristics
1
2017
... 在半色调研究中,生成图像的质量和处理效率是重点. 在传统算法中,基于有序抖动的方法[5 ] 并行性较高,处理速度较快,但生成的半色调图像质量较差. 基于误差扩散的方法[6 -8 ] 较好平衡了图像质量和处理速度,生成的图像质量比有序抖动方法高,但是因需顺序处理难以并行计算,且生成的半色调图像会引入相关伪影. 基于搜索的方法[9 -10 ] 产生的半色调图像质量优于前2种方法,但处理速度缓慢.虽然深度学习在图像处理领域的应用不少,但是它们大多集中在逆半色调方向[11 -13 ] ,半色调处理方向的应用鲜见. 本研究将深度学习模型应用于数字半色调,提出基于残差网络的半色调算法(halftone algorithm based on residual networks,HalfResNet),使得生成的半色调图像在保持较好结构细节的同时提高处理效率. 通过与已有深度半色调方法[14 ] 在VOC数据集[15 ] 上的性能对比实验,验证所提方法的特性. ...
Error diffusion method with optimized weighting coefficients for binary hologram generation
0
2019
Tone-dependent error diffusion based on an updated blue-noise model
1
2016
... 在半色调研究中,生成图像的质量和处理效率是重点. 在传统算法中,基于有序抖动的方法[5 ] 并行性较高,处理速度较快,但生成的半色调图像质量较差. 基于误差扩散的方法[6 -8 ] 较好平衡了图像质量和处理速度,生成的图像质量比有序抖动方法高,但是因需顺序处理难以并行计算,且生成的半色调图像会引入相关伪影. 基于搜索的方法[9 -10 ] 产生的半色调图像质量优于前2种方法,但处理速度缓慢.虽然深度学习在图像处理领域的应用不少,但是它们大多集中在逆半色调方向[11 -13 ] ,半色调处理方向的应用鲜见. 本研究将深度学习模型应用于数字半色调,提出基于残差网络的半色调算法(halftone algorithm based on residual networks,HalfResNet),使得生成的半色调图像在保持较好结构细节的同时提高处理效率. 通过与已有深度半色调方法[14 ] 在VOC数据集[15 ] 上的性能对比实验,验证所提方法的特性. ...
Perceptual error optimization for Monte Carlo rendering
1
2022
... 在半色调研究中,生成图像的质量和处理效率是重点. 在传统算法中,基于有序抖动的方法[5 ] 并行性较高,处理速度较快,但生成的半色调图像质量较差. 基于误差扩散的方法[6 -8 ] 较好平衡了图像质量和处理速度,生成的图像质量比有序抖动方法高,但是因需顺序处理难以并行计算,且生成的半色调图像会引入相关伪影. 基于搜索的方法[9 -10 ] 产生的半色调图像质量优于前2种方法,但处理速度缓慢.虽然深度学习在图像处理领域的应用不少,但是它们大多集中在逆半色调方向[11 -13 ] ,半色调处理方向的应用鲜见. 本研究将深度学习模型应用于数字半色调,提出基于残差网络的半色调算法(halftone algorithm based on residual networks,HalfResNet),使得生成的半色调图像在保持较好结构细节的同时提高处理效率. 通过与已有深度半色调方法[14 ] 在VOC数据集[15 ] 上的性能对比实验,验证所提方法的特性. ...
Ink drop displacement model-based direct binary search
1
2023
... 在半色调研究中,生成图像的质量和处理效率是重点. 在传统算法中,基于有序抖动的方法[5 ] 并行性较高,处理速度较快,但生成的半色调图像质量较差. 基于误差扩散的方法[6 -8 ] 较好平衡了图像质量和处理速度,生成的图像质量比有序抖动方法高,但是因需顺序处理难以并行计算,且生成的半色调图像会引入相关伪影. 基于搜索的方法[9 -10 ] 产生的半色调图像质量优于前2种方法,但处理速度缓慢.虽然深度学习在图像处理领域的应用不少,但是它们大多集中在逆半色调方向[11 -13 ] ,半色调处理方向的应用鲜见. 本研究将深度学习模型应用于数字半色调,提出基于残差网络的半色调算法(halftone algorithm based on residual networks,HalfResNet),使得生成的半色调图像在保持较好结构细节的同时提高处理效率. 通过与已有深度半色调方法[14 ] 在VOC数据集[15 ] 上的性能对比实验,验证所提方法的特性. ...
1
... 在半色调研究中,生成图像的质量和处理效率是重点. 在传统算法中,基于有序抖动的方法[5 ] 并行性较高,处理速度较快,但生成的半色调图像质量较差. 基于误差扩散的方法[6 -8 ] 较好平衡了图像质量和处理速度,生成的图像质量比有序抖动方法高,但是因需顺序处理难以并行计算,且生成的半色调图像会引入相关伪影. 基于搜索的方法[9 -10 ] 产生的半色调图像质量优于前2种方法,但处理速度缓慢.虽然深度学习在图像处理领域的应用不少,但是它们大多集中在逆半色调方向[11 -13 ] ,半色调处理方向的应用鲜见. 本研究将深度学习模型应用于数字半色调,提出基于残差网络的半色调算法(halftone algorithm based on residual networks,HalfResNet),使得生成的半色调图像在保持较好结构细节的同时提高处理效率. 通过与已有深度半色调方法[14 ] 在VOC数据集[15 ] 上的性能对比实验,验证所提方法的特性. ...
An efficient convolutional neural network model combined with attention mechanism for inverse halftoning
0
2021
Conditional diffusion process for inverse halftoning
1
2022
... 在半色调研究中,生成图像的质量和处理效率是重点. 在传统算法中,基于有序抖动的方法[5 ] 并行性较高,处理速度较快,但生成的半色调图像质量较差. 基于误差扩散的方法[6 -8 ] 较好平衡了图像质量和处理速度,生成的图像质量比有序抖动方法高,但是因需顺序处理难以并行计算,且生成的半色调图像会引入相关伪影. 基于搜索的方法[9 -10 ] 产生的半色调图像质量优于前2种方法,但处理速度缓慢.虽然深度学习在图像处理领域的应用不少,但是它们大多集中在逆半色调方向[11 -13 ] ,半色调处理方向的应用鲜见. 本研究将深度学习模型应用于数字半色调,提出基于残差网络的半色调算法(halftone algorithm based on residual networks,HalfResNet),使得生成的半色调图像在保持较好结构细节的同时提高处理效率. 通过与已有深度半色调方法[14 ] 在VOC数据集[15 ] 上的性能对比实验,验证所提方法的特性. ...
7
... 在半色调研究中,生成图像的质量和处理效率是重点. 在传统算法中,基于有序抖动的方法[5 ] 并行性较高,处理速度较快,但生成的半色调图像质量较差. 基于误差扩散的方法[6 -8 ] 较好平衡了图像质量和处理速度,生成的图像质量比有序抖动方法高,但是因需顺序处理难以并行计算,且生成的半色调图像会引入相关伪影. 基于搜索的方法[9 -10 ] 产生的半色调图像质量优于前2种方法,但处理速度缓慢.虽然深度学习在图像处理领域的应用不少,但是它们大多集中在逆半色调方向[11 -13 ] ,半色调处理方向的应用鲜见. 本研究将深度学习模型应用于数字半色调,提出基于残差网络的半色调算法(halftone algorithm based on residual networks,HalfResNet),使得生成的半色调图像在保持较好结构细节的同时提高处理效率. 通过与已有深度半色调方法[14 ] 在VOC数据集[15 ] 上的性能对比实验,验证所提方法的特性. ...
... 深度神经网络在半色调领域的应用取得了一定效果. Xia等[14 ] 提出的可逆深度半色调算法引入动态高斯噪声,使CNN能够生成非周期性半色调模式. 该算法模型产生的半色调图具有良好的可恢复性,但没有强烈的蓝噪声特性,而且提出的二阶段训练方案较复杂且不稳定. Choi等[16 ] 采用2种深度生成式模型模拟直接二进制搜索算法(direct binary search algorithm,DBS),该算法生成的半色调图像比DBS生成的噪声更少,也不包含误差扩散算法相关的伪影,但算法非常耗时,无法满足实时需求. 本研究所提算法采用轻量化残差网络,处理速度有大幅提升;为了使CNN模型具有更好的抖动模式,在各层残差模块前配备噪声补偿块;为了加强模型的蓝噪声特性,在损失函数中加入显式蓝噪声损失,生成的半色调图像更加符合蓝噪声特性. ...
... 本研究基于蓝噪声的抖动模式并利用有序抖动过程构造半色调图像提出HalfResNet,相较于可逆半色调模型(reversible halftoning method,RVH)算法[14 ] ,所提算法的参数量及计算量更少,引入噪声补偿块使模型保持较好的抖动模式,避免CNN产生平坦性退化的现象. HVS对低频信号更加敏感,因此半色调图像应含有较少的低频信号. 良好的蓝噪声半色调图像在所有频率上的各向异性应足够低,为了使产生的半色调图更符合蓝噪声特性,在损失函数中设计显式的蓝噪声损失,优化高频区域的各向异性. ...
... 式中:F (∙)为逆半色调模式,采用RVH中的逆半色调模块[14 ] 进行逆半色调重建. ...
... 将HalfResNet与不同类别的典型算法进行比较,包括Bayer有序抖动算法[5 ] 、Ostromoukhov 误差扩散算法[24 ] 、DBS[25 ] 和RVH[14 ] . 采用峰值信噪比(peak signal-to-noise ratio,PSNR)、结构相似性(structural similarity,SSIM)2项指标比较生成的半色调图像与连续灰度图像间的差异. PSNR是有损变换(如图像压缩、图像修复)中常使用的重构度量. 对于半色调图像,PSNR由图像之间的最大像素值L 和均方误差MSE来定义. 给定具有N 个像素的连续灰度图像和半色调图像,I h 、I s 分别为灰度图像的像素值和半色调图像的像素值, ...
... Quantitative evaluation of halftone algorithms
Tab.1 算法 SSIM PSNR Bayer有序抖动[5 ] 0.098 1 20.174 1 Ostromoukhov误差扩散[24 ] 0.110 0 21.133 3 DBS[25 ] 0.092 4 21.037 0 RVH[14 ] 0.161 5 20.700 8 本研究 0.174 7 20.834 1
如图5 所示为多种算法在“蜗牛形状器官(snail shaped organ)”图片上的半色调效果. 由图可知,传统算法在边缘细节处理效果欠佳,以过度模糊精细纹理细节为代价抑制伪影的出现,所提算法和RVH都很好保留了图像边缘纹理细节,在螺纹处保留了更多的原始图片的纹路信息. 对比RVH,所提算法在边缘细节部分含噪声更少. ...
... Runtime and parameter number comparison for different algorithms
Tab.5 算法 N P /106 t r /msBayer有序抖动[5 ] — 0.40 Ostromoukhov误差扩散[24 ] 38.40×10−5 10.00 DBS[25 ] — 2990.00 RVH[14 ] 37.80 30.06* 本研究 1.22 12.84*
4. 结 语 本研究提出基于轻量残差网络的高效半色调算法. 引入噪声补偿块,解决了CNN平坦性退化问题,在平坦区域产生了出色的抖动效果;将显式的蓝噪声损失引入损失函数,辅助符合人眼感知的蓝噪声特性半色调图像的生成;采用端到端的模型生成半色调图像,通过跳跃连接将浅层特征和深层特征融合. 与RVH模型相比,所提算法的参数量下降了96.77%,处理速度提高了57.28%;在多个数据集上比较不同算法的性能,相比其他典型算法,所提算法具有最佳的SSIM和有竞争力的PSNR,保留了更多的纹理细节. 本研究为半色调图像处理领域带来了显著的性能提升,为实际应用提供了更高质量和效率的解决方案. 所提算法在某些复杂图像场景下的通用性有待进一步验证,未来将在更大规模的数据集上进行测试. ...
1
... 在半色调研究中,生成图像的质量和处理效率是重点. 在传统算法中,基于有序抖动的方法[5 ] 并行性较高,处理速度较快,但生成的半色调图像质量较差. 基于误差扩散的方法[6 -8 ] 较好平衡了图像质量和处理速度,生成的图像质量比有序抖动方法高,但是因需顺序处理难以并行计算,且生成的半色调图像会引入相关伪影. 基于搜索的方法[9 -10 ] 产生的半色调图像质量优于前2种方法,但处理速度缓慢.虽然深度学习在图像处理领域的应用不少,但是它们大多集中在逆半色调方向[11 -13 ] ,半色调处理方向的应用鲜见. 本研究将深度学习模型应用于数字半色调,提出基于残差网络的半色调算法(halftone algorithm based on residual networks,HalfResNet),使得生成的半色调图像在保持较好结构细节的同时提高处理效率. 通过与已有深度半色调方法[14 ] 在VOC数据集[15 ] 上的性能对比实验,验证所提方法的特性. ...
Mimicking DBS halftoning via a deep learning approach
1
2022
... 深度神经网络在半色调领域的应用取得了一定效果. Xia等[14 ] 提出的可逆深度半色调算法引入动态高斯噪声,使CNN能够生成非周期性半色调模式. 该算法模型产生的半色调图具有良好的可恢复性,但没有强烈的蓝噪声特性,而且提出的二阶段训练方案较复杂且不稳定. Choi等[16 ] 采用2种深度生成式模型模拟直接二进制搜索算法(direct binary search algorithm,DBS),该算法生成的半色调图像比DBS生成的噪声更少,也不包含误差扩散算法相关的伪影,但算法非常耗时,无法满足实时需求. 本研究所提算法采用轻量化残差网络,处理速度有大幅提升;为了使CNN模型具有更好的抖动模式,在各层残差模块前配备噪声补偿块;为了加强模型的蓝噪声特性,在损失函数中加入显式蓝噪声损失,生成的半色调图像更加符合蓝噪声特性. ...
2
... 训练数据集采用公开的VOC数据集. 数据集中有17 125张彩色图像,随机选取其中的13 758幅图像进行训练,保留其中的3 367幅图像作为测试数据集进行定量评价. 通过裁剪和调整使所有图像大小统一为256×256. 训练式(4)不依赖标签,真实的半色调图像在现实中难以获取,因此损失为计算模型输出和原始连续灰度图像的差异. 为了提高模型泛化能力,收集更多不带任何标签的图片作为模型的训练集. 为了进一步证明模型的泛化能力,在多个公开数据集上进行测试,包括Set5[17 ] ,Set14[18 ] ,T91[19 ] ,BSDS100、BSDS200[20 ] ,General100[21 ] ,Historical、Manga109[22 ] ,Urban100[23 ] 数据集. ...
... Test results of five algorithms in public datasets
Tab.2 数据集 Bayer有序抖动 Ostromoukhov误差扩散 DBS RVH 本研究 SSIM PSNR SSIM PSNR SSIM PSNR SSIM PSNR SSIM PSNR Set5[17 ] 0.0921 19.2703 0.0895 20.0623 0.1002 20.0345 0.1223 18.9258 0.1350 19.0440 Set14[18 ] 0.1102 20.5257 0.1198 21.9181 0.1099 21.8266 0.1660 20.0719 0.1800 20.1359 T91[19 ] 0.0819 17.1405 0.0884 17.6289 0.0768 17.4897 0.1232 16.8595 0.1401 16.9310 BSDS100[20 ] 0.0883 19.5322 0.0937 20.4778 0.0793 20.3055 0.1477 19.9298 0.1611 20.0607 BSDS200[20 ] 0.0753 19.4164 0.0800 20.3194 0.0669 20.1321 0.1267 19.6582 0.1406 19.7947 General100[21 ] 0.0947 19.8076 0.0958 20.6128 0.0916 20.4640 0.1299 19.3996 0.1398 19.4650 Historical[22 ] 0.1510 18.6613 0.1497 19.4255 0.1227 19.1702 0.2298 19.4990 0.2411 19.9650 Manga109[22 ] 0.2478 22.9694 0.2226 23.2956 0.2331 23.2728 0.2543 23.2852 0.2644 23.1815 Urban100[23 ] 0.1443 22.6923 0.1616 23.5567 0.1355 23.3627 0.2141 22.7340 0.2253 22.9097
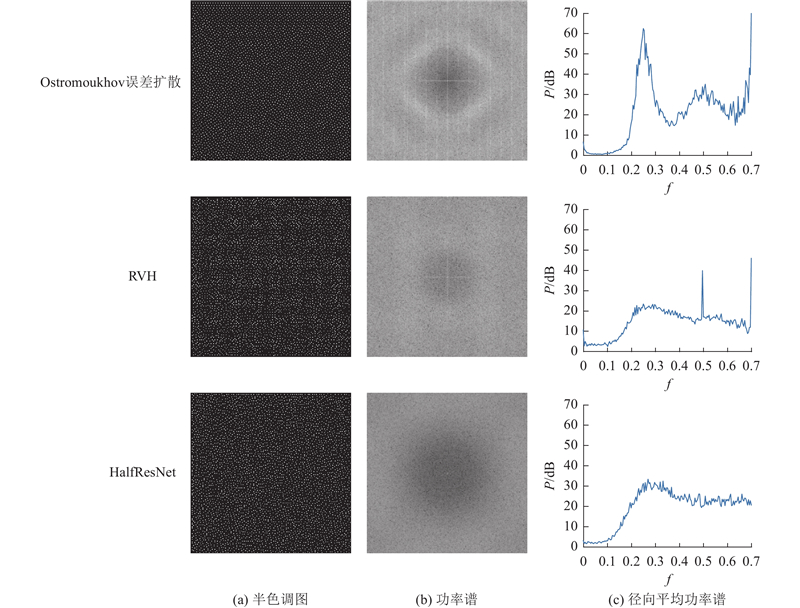
3.4.2. 蓝噪声特性实验 开展半色调方法的蓝噪声特性研究,分析生成的等灰度图像. 对于给定的常值灰度图像,使用不同算法进行半色调处理,计算各个算法生成的半色调图像的功率谱和径向平均功率谱. 傅里叶振幅谱表示频率分量的振幅,从蓝噪声特性可知,半色调图的功率谱含有较少的低频分量,在高频区域能量分布相对平滑. 如图6 所示,3类算法的结果都具有不同程度的蓝噪声特性,含有较少的低频分量;从径向平均功率谱密度可看出,所提算法在高频区域能量分布更加平滑,更符合蓝噪声特性. ...
2
... 训练数据集采用公开的VOC数据集. 数据集中有17 125张彩色图像,随机选取其中的13 758幅图像进行训练,保留其中的3 367幅图像作为测试数据集进行定量评价. 通过裁剪和调整使所有图像大小统一为256×256. 训练式(4)不依赖标签,真实的半色调图像在现实中难以获取,因此损失为计算模型输出和原始连续灰度图像的差异. 为了提高模型泛化能力,收集更多不带任何标签的图片作为模型的训练集. 为了进一步证明模型的泛化能力,在多个公开数据集上进行测试,包括Set5[17 ] ,Set14[18 ] ,T91[19 ] ,BSDS100、BSDS200[20 ] ,General100[21 ] ,Historical、Manga109[22 ] ,Urban100[23 ] 数据集. ...
... Test results of five algorithms in public datasets
Tab.2 数据集 Bayer有序抖动 Ostromoukhov误差扩散 DBS RVH 本研究 SSIM PSNR SSIM PSNR SSIM PSNR SSIM PSNR SSIM PSNR Set5[17 ] 0.0921 19.2703 0.0895 20.0623 0.1002 20.0345 0.1223 18.9258 0.1350 19.0440 Set14[18 ] 0.1102 20.5257 0.1198 21.9181 0.1099 21.8266 0.1660 20.0719 0.1800 20.1359 T91[19 ] 0.0819 17.1405 0.0884 17.6289 0.0768 17.4897 0.1232 16.8595 0.1401 16.9310 BSDS100[20 ] 0.0883 19.5322 0.0937 20.4778 0.0793 20.3055 0.1477 19.9298 0.1611 20.0607 BSDS200[20 ] 0.0753 19.4164 0.0800 20.3194 0.0669 20.1321 0.1267 19.6582 0.1406 19.7947 General100[21 ] 0.0947 19.8076 0.0958 20.6128 0.0916 20.4640 0.1299 19.3996 0.1398 19.4650 Historical[22 ] 0.1510 18.6613 0.1497 19.4255 0.1227 19.1702 0.2298 19.4990 0.2411 19.9650 Manga109[22 ] 0.2478 22.9694 0.2226 23.2956 0.2331 23.2728 0.2543 23.2852 0.2644 23.1815 Urban100[23 ] 0.1443 22.6923 0.1616 23.5567 0.1355 23.3627 0.2141 22.7340 0.2253 22.9097
3.4.2. 蓝噪声特性实验 开展半色调方法的蓝噪声特性研究,分析生成的等灰度图像. 对于给定的常值灰度图像,使用不同算法进行半色调处理,计算各个算法生成的半色调图像的功率谱和径向平均功率谱. 傅里叶振幅谱表示频率分量的振幅,从蓝噪声特性可知,半色调图的功率谱含有较少的低频分量,在高频区域能量分布相对平滑. 如图6 所示,3类算法的结果都具有不同程度的蓝噪声特性,含有较少的低频分量;从径向平均功率谱密度可看出,所提算法在高频区域能量分布更加平滑,更符合蓝噪声特性. ...
A comparable study of CNN-based single image super-resolution for space-based imaging sensors
2
2019
... 训练数据集采用公开的VOC数据集. 数据集中有17 125张彩色图像,随机选取其中的13 758幅图像进行训练,保留其中的3 367幅图像作为测试数据集进行定量评价. 通过裁剪和调整使所有图像大小统一为256×256. 训练式(4)不依赖标签,真实的半色调图像在现实中难以获取,因此损失为计算模型输出和原始连续灰度图像的差异. 为了提高模型泛化能力,收集更多不带任何标签的图片作为模型的训练集. 为了进一步证明模型的泛化能力,在多个公开数据集上进行测试,包括Set5[17 ] ,Set14[18 ] ,T91[19 ] ,BSDS100、BSDS200[20 ] ,General100[21 ] ,Historical、Manga109[22 ] ,Urban100[23 ] 数据集. ...
... Test results of five algorithms in public datasets
Tab.2 数据集 Bayer有序抖动 Ostromoukhov误差扩散 DBS RVH 本研究 SSIM PSNR SSIM PSNR SSIM PSNR SSIM PSNR SSIM PSNR Set5[17 ] 0.0921 19.2703 0.0895 20.0623 0.1002 20.0345 0.1223 18.9258 0.1350 19.0440 Set14[18 ] 0.1102 20.5257 0.1198 21.9181 0.1099 21.8266 0.1660 20.0719 0.1800 20.1359 T91[19 ] 0.0819 17.1405 0.0884 17.6289 0.0768 17.4897 0.1232 16.8595 0.1401 16.9310 BSDS100[20 ] 0.0883 19.5322 0.0937 20.4778 0.0793 20.3055 0.1477 19.9298 0.1611 20.0607 BSDS200[20 ] 0.0753 19.4164 0.0800 20.3194 0.0669 20.1321 0.1267 19.6582 0.1406 19.7947 General100[21 ] 0.0947 19.8076 0.0958 20.6128 0.0916 20.4640 0.1299 19.3996 0.1398 19.4650 Historical[22 ] 0.1510 18.6613 0.1497 19.4255 0.1227 19.1702 0.2298 19.4990 0.2411 19.9650 Manga109[22 ] 0.2478 22.9694 0.2226 23.2956 0.2331 23.2728 0.2543 23.2852 0.2644 23.1815 Urban100[23 ] 0.1443 22.6923 0.1616 23.5567 0.1355 23.3627 0.2141 22.7340 0.2253 22.9097
3.4.2. 蓝噪声特性实验 开展半色调方法的蓝噪声特性研究,分析生成的等灰度图像. 对于给定的常值灰度图像,使用不同算法进行半色调处理,计算各个算法生成的半色调图像的功率谱和径向平均功率谱. 傅里叶振幅谱表示频率分量的振幅,从蓝噪声特性可知,半色调图的功率谱含有较少的低频分量,在高频区域能量分布相对平滑. 如图6 所示,3类算法的结果都具有不同程度的蓝噪声特性,含有较少的低频分量;从径向平均功率谱密度可看出,所提算法在高频区域能量分布更加平滑,更符合蓝噪声特性. ...
A deep primal-dual proximal network for image restoration
3
2021
... 训练数据集采用公开的VOC数据集. 数据集中有17 125张彩色图像,随机选取其中的13 758幅图像进行训练,保留其中的3 367幅图像作为测试数据集进行定量评价. 通过裁剪和调整使所有图像大小统一为256×256. 训练式(4)不依赖标签,真实的半色调图像在现实中难以获取,因此损失为计算模型输出和原始连续灰度图像的差异. 为了提高模型泛化能力,收集更多不带任何标签的图片作为模型的训练集. 为了进一步证明模型的泛化能力,在多个公开数据集上进行测试,包括Set5[17 ] ,Set14[18 ] ,T91[19 ] ,BSDS100、BSDS200[20 ] ,General100[21 ] ,Historical、Manga109[22 ] ,Urban100[23 ] 数据集. ...
... Test results of five algorithms in public datasets
Tab.2 数据集 Bayer有序抖动 Ostromoukhov误差扩散 DBS RVH 本研究 SSIM PSNR SSIM PSNR SSIM PSNR SSIM PSNR SSIM PSNR Set5[17 ] 0.0921 19.2703 0.0895 20.0623 0.1002 20.0345 0.1223 18.9258 0.1350 19.0440 Set14[18 ] 0.1102 20.5257 0.1198 21.9181 0.1099 21.8266 0.1660 20.0719 0.1800 20.1359 T91[19 ] 0.0819 17.1405 0.0884 17.6289 0.0768 17.4897 0.1232 16.8595 0.1401 16.9310 BSDS100[20 ] 0.0883 19.5322 0.0937 20.4778 0.0793 20.3055 0.1477 19.9298 0.1611 20.0607 BSDS200[20 ] 0.0753 19.4164 0.0800 20.3194 0.0669 20.1321 0.1267 19.6582 0.1406 19.7947 General100[21 ] 0.0947 19.8076 0.0958 20.6128 0.0916 20.4640 0.1299 19.3996 0.1398 19.4650 Historical[22 ] 0.1510 18.6613 0.1497 19.4255 0.1227 19.1702 0.2298 19.4990 0.2411 19.9650 Manga109[22 ] 0.2478 22.9694 0.2226 23.2956 0.2331 23.2728 0.2543 23.2852 0.2644 23.1815 Urban100[23 ] 0.1443 22.6923 0.1616 23.5567 0.1355 23.3627 0.2141 22.7340 0.2253 22.9097
3.4.2. 蓝噪声特性实验 开展半色调方法的蓝噪声特性研究,分析生成的等灰度图像. 对于给定的常值灰度图像,使用不同算法进行半色调处理,计算各个算法生成的半色调图像的功率谱和径向平均功率谱. 傅里叶振幅谱表示频率分量的振幅,从蓝噪声特性可知,半色调图的功率谱含有较少的低频分量,在高频区域能量分布相对平滑. 如图6 所示,3类算法的结果都具有不同程度的蓝噪声特性,含有较少的低频分量;从径向平均功率谱密度可看出,所提算法在高频区域能量分布更加平滑,更符合蓝噪声特性. ...
... [
20 ]
0.0753 19.4164 0.0800 20.3194 0.0669 20.1321 0.1267 19.6582 0.1406 19.7947 General100[21 ] 0.0947 19.8076 0.0958 20.6128 0.0916 20.4640 0.1299 19.3996 0.1398 19.4650 Historical[22 ] 0.1510 18.6613 0.1497 19.4255 0.1227 19.1702 0.2298 19.4990 0.2411 19.9650 Manga109[22 ] 0.2478 22.9694 0.2226 23.2956 0.2331 23.2728 0.2543 23.2852 0.2644 23.1815 Urban100[23 ] 0.1443 22.6923 0.1616 23.5567 0.1355 23.3627 0.2141 22.7340 0.2253 22.9097 3.4.2. 蓝噪声特性实验 开展半色调方法的蓝噪声特性研究,分析生成的等灰度图像. 对于给定的常值灰度图像,使用不同算法进行半色调处理,计算各个算法生成的半色调图像的功率谱和径向平均功率谱. 傅里叶振幅谱表示频率分量的振幅,从蓝噪声特性可知,半色调图的功率谱含有较少的低频分量,在高频区域能量分布相对平滑. 如图6 所示,3类算法的结果都具有不同程度的蓝噪声特性,含有较少的低频分量;从径向平均功率谱密度可看出,所提算法在高频区域能量分布更加平滑,更符合蓝噪声特性. ...
2
... 训练数据集采用公开的VOC数据集. 数据集中有17 125张彩色图像,随机选取其中的13 758幅图像进行训练,保留其中的3 367幅图像作为测试数据集进行定量评价. 通过裁剪和调整使所有图像大小统一为256×256. 训练式(4)不依赖标签,真实的半色调图像在现实中难以获取,因此损失为计算模型输出和原始连续灰度图像的差异. 为了提高模型泛化能力,收集更多不带任何标签的图片作为模型的训练集. 为了进一步证明模型的泛化能力,在多个公开数据集上进行测试,包括Set5[17 ] ,Set14[18 ] ,T91[19 ] ,BSDS100、BSDS200[20 ] ,General100[21 ] ,Historical、Manga109[22 ] ,Urban100[23 ] 数据集. ...
... Test results of five algorithms in public datasets
Tab.2 数据集 Bayer有序抖动 Ostromoukhov误差扩散 DBS RVH 本研究 SSIM PSNR SSIM PSNR SSIM PSNR SSIM PSNR SSIM PSNR Set5[17 ] 0.0921 19.2703 0.0895 20.0623 0.1002 20.0345 0.1223 18.9258 0.1350 19.0440 Set14[18 ] 0.1102 20.5257 0.1198 21.9181 0.1099 21.8266 0.1660 20.0719 0.1800 20.1359 T91[19 ] 0.0819 17.1405 0.0884 17.6289 0.0768 17.4897 0.1232 16.8595 0.1401 16.9310 BSDS100[20 ] 0.0883 19.5322 0.0937 20.4778 0.0793 20.3055 0.1477 19.9298 0.1611 20.0607 BSDS200[20 ] 0.0753 19.4164 0.0800 20.3194 0.0669 20.1321 0.1267 19.6582 0.1406 19.7947 General100[21 ] 0.0947 19.8076 0.0958 20.6128 0.0916 20.4640 0.1299 19.3996 0.1398 19.4650 Historical[22 ] 0.1510 18.6613 0.1497 19.4255 0.1227 19.1702 0.2298 19.4990 0.2411 19.9650 Manga109[22 ] 0.2478 22.9694 0.2226 23.2956 0.2331 23.2728 0.2543 23.2852 0.2644 23.1815 Urban100[23 ] 0.1443 22.6923 0.1616 23.5567 0.1355 23.3627 0.2141 22.7340 0.2253 22.9097
3.4.2. 蓝噪声特性实验 开展半色调方法的蓝噪声特性研究,分析生成的等灰度图像. 对于给定的常值灰度图像,使用不同算法进行半色调处理,计算各个算法生成的半色调图像的功率谱和径向平均功率谱. 傅里叶振幅谱表示频率分量的振幅,从蓝噪声特性可知,半色调图的功率谱含有较少的低频分量,在高频区域能量分布相对平滑. 如图6 所示,3类算法的结果都具有不同程度的蓝噪声特性,含有较少的低频分量;从径向平均功率谱密度可看出,所提算法在高频区域能量分布更加平滑,更符合蓝噪声特性. ...
Sketch-based Manga retrieval using Manga109 dataset
3
2017
... 训练数据集采用公开的VOC数据集. 数据集中有17 125张彩色图像,随机选取其中的13 758幅图像进行训练,保留其中的3 367幅图像作为测试数据集进行定量评价. 通过裁剪和调整使所有图像大小统一为256×256. 训练式(4)不依赖标签,真实的半色调图像在现实中难以获取,因此损失为计算模型输出和原始连续灰度图像的差异. 为了提高模型泛化能力,收集更多不带任何标签的图片作为模型的训练集. 为了进一步证明模型的泛化能力,在多个公开数据集上进行测试,包括Set5[17 ] ,Set14[18 ] ,T91[19 ] ,BSDS100、BSDS200[20 ] ,General100[21 ] ,Historical、Manga109[22 ] ,Urban100[23 ] 数据集. ...
... Test results of five algorithms in public datasets
Tab.2 数据集 Bayer有序抖动 Ostromoukhov误差扩散 DBS RVH 本研究 SSIM PSNR SSIM PSNR SSIM PSNR SSIM PSNR SSIM PSNR Set5[17 ] 0.0921 19.2703 0.0895 20.0623 0.1002 20.0345 0.1223 18.9258 0.1350 19.0440 Set14[18 ] 0.1102 20.5257 0.1198 21.9181 0.1099 21.8266 0.1660 20.0719 0.1800 20.1359 T91[19 ] 0.0819 17.1405 0.0884 17.6289 0.0768 17.4897 0.1232 16.8595 0.1401 16.9310 BSDS100[20 ] 0.0883 19.5322 0.0937 20.4778 0.0793 20.3055 0.1477 19.9298 0.1611 20.0607 BSDS200[20 ] 0.0753 19.4164 0.0800 20.3194 0.0669 20.1321 0.1267 19.6582 0.1406 19.7947 General100[21 ] 0.0947 19.8076 0.0958 20.6128 0.0916 20.4640 0.1299 19.3996 0.1398 19.4650 Historical[22 ] 0.1510 18.6613 0.1497 19.4255 0.1227 19.1702 0.2298 19.4990 0.2411 19.9650 Manga109[22 ] 0.2478 22.9694 0.2226 23.2956 0.2331 23.2728 0.2543 23.2852 0.2644 23.1815 Urban100[23 ] 0.1443 22.6923 0.1616 23.5567 0.1355 23.3627 0.2141 22.7340 0.2253 22.9097
3.4.2. 蓝噪声特性实验 开展半色调方法的蓝噪声特性研究,分析生成的等灰度图像. 对于给定的常值灰度图像,使用不同算法进行半色调处理,计算各个算法生成的半色调图像的功率谱和径向平均功率谱. 傅里叶振幅谱表示频率分量的振幅,从蓝噪声特性可知,半色调图的功率谱含有较少的低频分量,在高频区域能量分布相对平滑. 如图6 所示,3类算法的结果都具有不同程度的蓝噪声特性,含有较少的低频分量;从径向平均功率谱密度可看出,所提算法在高频区域能量分布更加平滑,更符合蓝噪声特性. ...
... [
22 ]
0.2478 22.9694 0.2226 23.2956 0.2331 23.2728 0.2543 23.2852 0.2644 23.1815 Urban100[23 ] 0.1443 22.6923 0.1616 23.5567 0.1355 23.3627 0.2141 22.7340 0.2253 22.9097 3.4.2. 蓝噪声特性实验 开展半色调方法的蓝噪声特性研究,分析生成的等灰度图像. 对于给定的常值灰度图像,使用不同算法进行半色调处理,计算各个算法生成的半色调图像的功率谱和径向平均功率谱. 傅里叶振幅谱表示频率分量的振幅,从蓝噪声特性可知,半色调图的功率谱含有较少的低频分量,在高频区域能量分布相对平滑. 如图6 所示,3类算法的结果都具有不同程度的蓝噪声特性,含有较少的低频分量;从径向平均功率谱密度可看出,所提算法在高频区域能量分布更加平滑,更符合蓝噪声特性. ...
2
... 训练数据集采用公开的VOC数据集. 数据集中有17 125张彩色图像,随机选取其中的13 758幅图像进行训练,保留其中的3 367幅图像作为测试数据集进行定量评价. 通过裁剪和调整使所有图像大小统一为256×256. 训练式(4)不依赖标签,真实的半色调图像在现实中难以获取,因此损失为计算模型输出和原始连续灰度图像的差异. 为了提高模型泛化能力,收集更多不带任何标签的图片作为模型的训练集. 为了进一步证明模型的泛化能力,在多个公开数据集上进行测试,包括Set5[17 ] ,Set14[18 ] ,T91[19 ] ,BSDS100、BSDS200[20 ] ,General100[21 ] ,Historical、Manga109[22 ] ,Urban100[23 ] 数据集. ...
... Test results of five algorithms in public datasets
Tab.2 数据集 Bayer有序抖动 Ostromoukhov误差扩散 DBS RVH 本研究 SSIM PSNR SSIM PSNR SSIM PSNR SSIM PSNR SSIM PSNR Set5[17 ] 0.0921 19.2703 0.0895 20.0623 0.1002 20.0345 0.1223 18.9258 0.1350 19.0440 Set14[18 ] 0.1102 20.5257 0.1198 21.9181 0.1099 21.8266 0.1660 20.0719 0.1800 20.1359 T91[19 ] 0.0819 17.1405 0.0884 17.6289 0.0768 17.4897 0.1232 16.8595 0.1401 16.9310 BSDS100[20 ] 0.0883 19.5322 0.0937 20.4778 0.0793 20.3055 0.1477 19.9298 0.1611 20.0607 BSDS200[20 ] 0.0753 19.4164 0.0800 20.3194 0.0669 20.1321 0.1267 19.6582 0.1406 19.7947 General100[21 ] 0.0947 19.8076 0.0958 20.6128 0.0916 20.4640 0.1299 19.3996 0.1398 19.4650 Historical[22 ] 0.1510 18.6613 0.1497 19.4255 0.1227 19.1702 0.2298 19.4990 0.2411 19.9650 Manga109[22 ] 0.2478 22.9694 0.2226 23.2956 0.2331 23.2728 0.2543 23.2852 0.2644 23.1815 Urban100[23 ] 0.1443 22.6923 0.1616 23.5567 0.1355 23.3627 0.2141 22.7340 0.2253 22.9097
3.4.2. 蓝噪声特性实验 开展半色调方法的蓝噪声特性研究,分析生成的等灰度图像. 对于给定的常值灰度图像,使用不同算法进行半色调处理,计算各个算法生成的半色调图像的功率谱和径向平均功率谱. 傅里叶振幅谱表示频率分量的振幅,从蓝噪声特性可知,半色调图的功率谱含有较少的低频分量,在高频区域能量分布相对平滑. 如图6 所示,3类算法的结果都具有不同程度的蓝噪声特性,含有较少的低频分量;从径向平均功率谱密度可看出,所提算法在高频区域能量分布更加平滑,更符合蓝噪声特性. ...
3
... 将HalfResNet与不同类别的典型算法进行比较,包括Bayer有序抖动算法[5 ] 、Ostromoukhov 误差扩散算法[24 ] 、DBS[25 ] 和RVH[14 ] . 采用峰值信噪比(peak signal-to-noise ratio,PSNR)、结构相似性(structural similarity,SSIM)2项指标比较生成的半色调图像与连续灰度图像间的差异. PSNR是有损变换(如图像压缩、图像修复)中常使用的重构度量. 对于半色调图像,PSNR由图像之间的最大像素值L 和均方误差MSE来定义. 给定具有N 个像素的连续灰度图像和半色调图像,I h 、I s 分别为灰度图像的像素值和半色调图像的像素值, ...
... Quantitative evaluation of halftone algorithms
Tab.1 算法 SSIM PSNR Bayer有序抖动[5 ] 0.098 1 20.174 1 Ostromoukhov误差扩散[24 ] 0.110 0 21.133 3 DBS[25 ] 0.092 4 21.037 0 RVH[14 ] 0.161 5 20.700 8 本研究 0.174 7 20.834 1
如图5 所示为多种算法在“蜗牛形状器官(snail shaped organ)”图片上的半色调效果. 由图可知,传统算法在边缘细节处理效果欠佳,以过度模糊精细纹理细节为代价抑制伪影的出现,所提算法和RVH都很好保留了图像边缘纹理细节,在螺纹处保留了更多的原始图片的纹路信息. 对比RVH,所提算法在边缘细节部分含噪声更少. ...
... Runtime and parameter number comparison for different algorithms
Tab.5 算法 N P /106 t r /msBayer有序抖动[5 ] — 0.40 Ostromoukhov误差扩散[24 ] 38.40×10−5 10.00 DBS[25 ] — 2990.00 RVH[14 ] 37.80 30.06* 本研究 1.22 12.84*
4. 结 语 本研究提出基于轻量残差网络的高效半色调算法. 引入噪声补偿块,解决了CNN平坦性退化问题,在平坦区域产生了出色的抖动效果;将显式的蓝噪声损失引入损失函数,辅助符合人眼感知的蓝噪声特性半色调图像的生成;采用端到端的模型生成半色调图像,通过跳跃连接将浅层特征和深层特征融合. 与RVH模型相比,所提算法的参数量下降了96.77%,处理速度提高了57.28%;在多个数据集上比较不同算法的性能,相比其他典型算法,所提算法具有最佳的SSIM和有竞争力的PSNR,保留了更多的纹理细节. 本研究为半色调图像处理领域带来了显著的性能提升,为实际应用提供了更高质量和效率的解决方案. 所提算法在某些复杂图像场景下的通用性有待进一步验证,未来将在更大规模的数据集上进行测试. ...
3
... 将HalfResNet与不同类别的典型算法进行比较,包括Bayer有序抖动算法[5 ] 、Ostromoukhov 误差扩散算法[24 ] 、DBS[25 ] 和RVH[14 ] . 采用峰值信噪比(peak signal-to-noise ratio,PSNR)、结构相似性(structural similarity,SSIM)2项指标比较生成的半色调图像与连续灰度图像间的差异. PSNR是有损变换(如图像压缩、图像修复)中常使用的重构度量. 对于半色调图像,PSNR由图像之间的最大像素值L 和均方误差MSE来定义. 给定具有N 个像素的连续灰度图像和半色调图像,I h 、I s 分别为灰度图像的像素值和半色调图像的像素值, ...
... Quantitative evaluation of halftone algorithms
Tab.1 算法 SSIM PSNR Bayer有序抖动[5 ] 0.098 1 20.174 1 Ostromoukhov误差扩散[24 ] 0.110 0 21.133 3 DBS[25 ] 0.092 4 21.037 0 RVH[14 ] 0.161 5 20.700 8 本研究 0.174 7 20.834 1
如图5 所示为多种算法在“蜗牛形状器官(snail shaped organ)”图片上的半色调效果. 由图可知,传统算法在边缘细节处理效果欠佳,以过度模糊精细纹理细节为代价抑制伪影的出现,所提算法和RVH都很好保留了图像边缘纹理细节,在螺纹处保留了更多的原始图片的纹路信息. 对比RVH,所提算法在边缘细节部分含噪声更少. ...
... Runtime and parameter number comparison for different algorithms
Tab.5 算法 N P /106 t r /msBayer有序抖动[5 ] — 0.40 Ostromoukhov误差扩散[24 ] 38.40×10−5 10.00 DBS[25 ] — 2990.00 RVH[14 ] 37.80 30.06* 本研究 1.22 12.84*
4. 结 语 本研究提出基于轻量残差网络的高效半色调算法. 引入噪声补偿块,解决了CNN平坦性退化问题,在平坦区域产生了出色的抖动效果;将显式的蓝噪声损失引入损失函数,辅助符合人眼感知的蓝噪声特性半色调图像的生成;采用端到端的模型生成半色调图像,通过跳跃连接将浅层特征和深层特征融合. 与RVH模型相比,所提算法的参数量下降了96.77%,处理速度提高了57.28%;在多个数据集上比较不同算法的性能,相比其他典型算法,所提算法具有最佳的SSIM和有竞争力的PSNR,保留了更多的纹理细节. 本研究为半色调图像处理领域带来了显著的性能提升,为实际应用提供了更高质量和效率的解决方案. 所提算法在某些复杂图像场景下的通用性有待进一步验证,未来将在更大规模的数据集上进行测试. ...