高速移动场景包含车对车通信、高速铁路通信,是无线通信技术的重要场景之一. 传统的正交频分复用(orthogonal frequency division multiplexing, OFDM)一直是大多数无线通信系统的波形选择,然而高移动性引起的多普勒频移会导致OFDM调制技术性能下降. 为了解决上述问题,正交时频空(orthogonal time frequency space, OTFS)调制作为新的二维波形调制技术应运而生. 与OFDM仅将信号调制在频域的方式不同,OTFS将信息符号在时延-多普勒域复用[1]. OTFS调制将时频域的时变信道转换为时延-多普勒域的准静态信道,发射符号在时延-多普勒域中经历近乎恒定的信道增益,因此与OFDM相比,OTFS是更具前景的调制技术[2].
类似于OFDM多天线系统,将多输入多输出(multiple-inputs multiple-outputs, MIMO)与OTFS技术结合[5-9]可以进一步提高频谱效率. 广义空间调制(generalized spatial modulation, GSM)被认为是MIMO技术的一个特例,它既继承了MIMO的优点,又避免了MIMO的不足(如天线间同步、信道间干扰以及需要多个射频链),并且GSM可以利用发射天线的空间位置来携带额外的比特,进一步提高系统的频谱效率. 目前已经有部分学者对GSM-OTFS结构做出相关研究,主要关于性能研究[10-12]和信号检测算法设计[13-14] 2方面. Zou等[13]提出基于最小均方误差(minimum mean square error, MMSE)准则的决策反馈检测器. Wang等[14]提出基于广义近似消息传递(generalized approximate message passing,GAMP)的迭代检测器,仿真结果表明,与传统的MMSE检测器相比,所提出的GAMP检测器具有更好的性能.
在享受GSM优点同时,GSM结构给信号检测算法设计引入的难度也不容忽视,消息传递类算法经常被用于解决此类问题. Fan等[15]针对GSM结构基于分层消息传递算法设计了2种检测器,分别为阈值辅助的分层消息传递检测器和概率排序辅助的分层消息传递检测器. 同样是GSM结构,Fan等[16]针对近似消息传递算法设计了基于概率排序的近似消息传递检测器. Wei等[17]研究了近似消息传递(approximate message passing, AMP)算法在多个激活资源(天线或子载波)的索引调制(index modulation, IM)信号检测中的应用. Zhang等[18]提出在期望传播算法框架下的联合信号检测算法,用于具有广义空间调制的上行链路大规模多用户MIMO系统. 期望传播(expectation propagation, EP)和置信传播(belief propagation, BP)算法已经被广泛应用于迭代接收机[19],在此启发下本研究提出混合期望传播和置信传播(hybrid expectation propagation and belief propagation, EP-BP)的联合信号检测方案,用于GSM-OTFS系统的激活天线组合索引检测和星座符号解调.
为了降低和积算法执行消息传递的计算复杂度[20],将离散概率分布近似为多元复高斯概率分布,从而将复杂的和积更新规则转换为均值向量和协方差矩阵的迭代传递. 通过迭代更新发射符号矢量的符号置信度来确定激活天线组合索引和星座符号. 为了进一步降低符号置信度计算须遍历发射符号集合带来的计算复杂度,设计了一种分步的两阶段混合期望传播与置信传播算法TS-EP-BP. 在TS-EP-BP的第1阶段,采用EP-BP算法估计激活天线组合的索引值. 在得到估计索引值之后,发射符号向量中不同激活天线上的星座符号可以看作独立分布,符号置信度的计算次数减少到调制星座的基数.
1. 系统模型
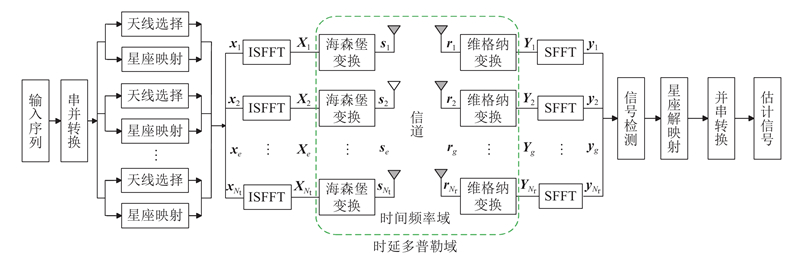
GSM-OTFS的系统模型如图1所示,系统共有
图 1
在GSM-OTFS传输中,输入的比特信息被划分为
激活天线组合索引矩阵在收发端均为已知信息,结合激活天线组合图样和调制星座图集合
综上所述,第
一个GSM符号中共有
在GSM-OTFS系统的发射端,对发射符号
随后,对第
式中:
式中:r(t)表示接收信号矢量,
在接收端进行相对应的逆变换,将第
式中:
式中:
经上述过程后,时延多普勒域上的输入输出关系可以由如下公式表示:
式中:
2. 所提算法
2.1. 混合期望传播和置信传播的EP-BP检测算法
基于式(10)的系统模型,后验概率
式中:
似然函数表达式为
式中:
先验概率的表达式为
式中:
变分推断是常见的计算边缘概率的有效方法,核心思想是选择一个简单的分布
式中:
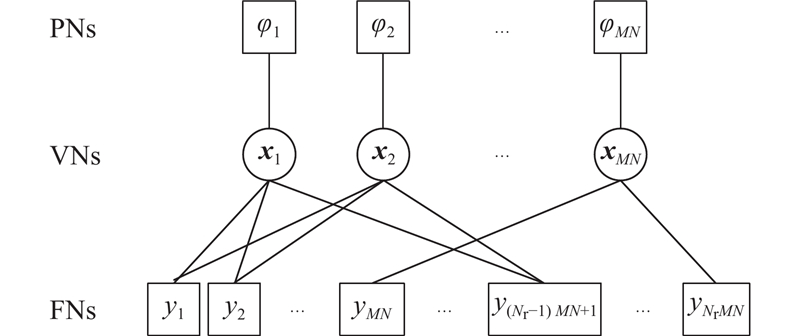
如图2所示给出了GSM-OTFS系统EP-BP因子图[20]示例,其中包含变量节点(variable nodes, VNs)
图 2
令
式中:
接下来以第
式中:
根据(15)、(17)、(18),可得如下消息传递规则:
式(16)中的外部求和涉及到对除
从矢量VN传递到PN的协方差矩阵和均值向量分别计算为
由于发射符号的各个元素相互独立,协方差矩阵为对角矩阵,式(21)和(22)中均值向量
由此复杂的消息传递规则可以由多元复高斯PDF表示为
从矢量VN传递到FN的协方差矩阵和均值向量表达式分别为
由于消息
式中:
式中:
式中:
EP-BP算法的迭代终止原则为
算法1 GSM-OTFS系统EP-BP信号检测算法
1. 输入:
2. 初始化:
3. for
4. for
5.
6.
7.
11. for
12.
13.
14. end for
15. end for
16. for
17. for
20. end for
21. end for
22. for
26. end for
27. 全部检测符号:
28. 终止原则:
29. end for
30. 输出:
2.2. 两阶段TS-EP-BP检测算法
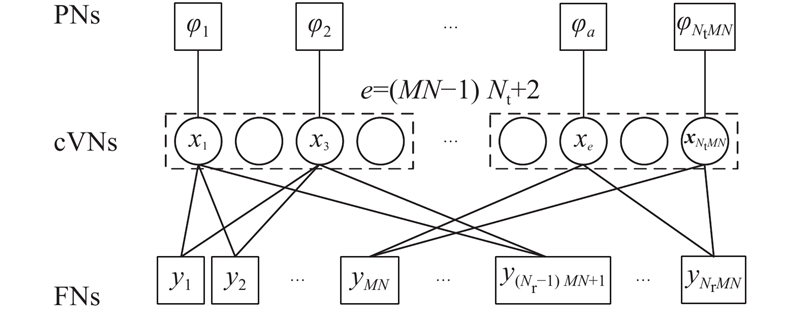
EP-BP算法(式(17))的符号置信度计算须遍历发射符号集合
图 3
基于第1阶段结束时的符号置信度
在TS-EP-BP算法的第2阶段,FN传递到子VN的均值与方差初值设定为
高斯消息
符号置信度
其中,先验概率
此时每个符号置信度的计算次数由
与EP-BP算法类似,TS-EP-BP算法消息传递规则如下:
将其近似为高斯PDF形式,可得
从子VN传递到FN的均值和方差表达式如下:
从FN到子VN的均值和方差表达式如下:
式中:hi,k表示发射符号里第k个子VN符号与接收信号第i个元素之间的相应系数.
根据第
根据式(45)以及激活天线组合索引,可以得到完整的符号估计值
算法2 GSM-OTFS系统TS-EP-BP信号检测算法
1. 输入:
2. for
3. 执行算法1 EP-BP信号检测算法
4. end for
5. 初始化:
6. for
7. for
14. for
17. end for
18. end for
19. for
20. for
23. end for
24. end for
25. for
27. end for
28. 全部检测符号:
29. 终止原则:
30. end for
31. 输出:
2.3. 计算复杂度分析
表 1 算法复杂度总结表
Tab.1
| 算法 | 复数乘法次数 |
| EP-BP | |
| TS- EP-BP | |
| GAMP[14] | |
| MP[21] |
3. 仿真结果分析
为了验证和对比改进后的分阶段TS-EP-BP算法在高速移动场景下的信号检测性能,对GSM-OTFS系统进行性能仿真,收发端各配备4根天线即
表 2 GSM-OTFS系统仿真参数表
Tab.2
| 参数 | 数值 |
| 载波频率/ GHz | 4 |
| 子载波间隔/ kHz | 15 |
| 子载波个数( | 16、32 |
| 时隙数( | 16、32 |
| 调制阶数 | 4-QAM |
| 终端移动速度/ (km·h−1) | 500 |
| 路径数 | 9 |
| 调制脉冲 | 矩形窗 |
| 信道估计 | 理想估计 |
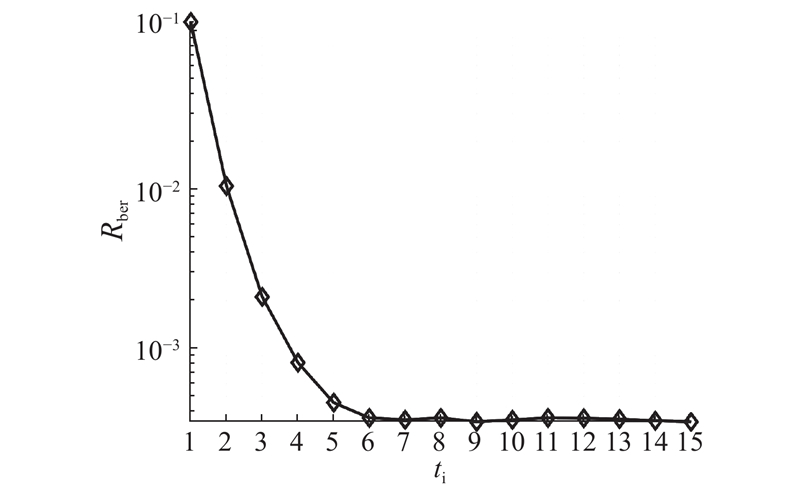
为了证明算法的收敛性,如图4所示给出EP-BP算法的误码率Rber随迭代次数ti变化的曲线. 其中,
图 4
图 4 EP-BP算法的误码率性能与迭代次数关系
Fig.4 Relationship between bit error rate performance and iteration times of EP-BP algorithm
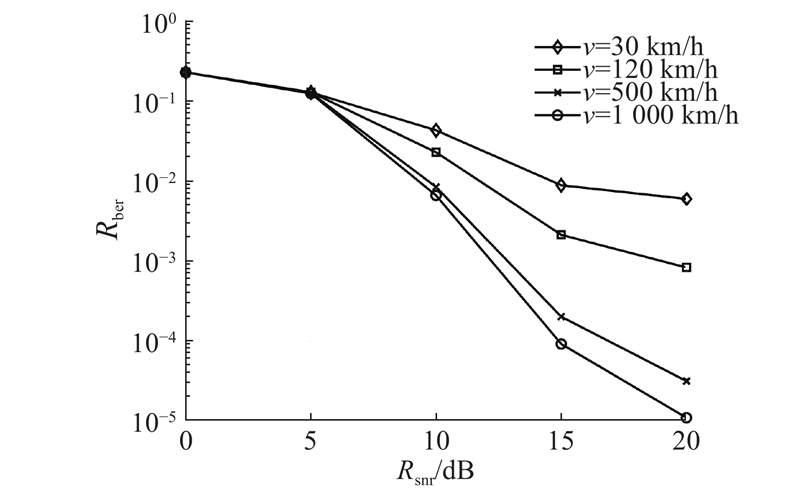
如图5所示给出不同终端移动速度v下GSM-OTFS系统EP-BP检测算法的误码率性能随信噪比Rsnr的变化曲线. 其中,
图 5
图 5 不同终端移动速度下EP-BP算法的误码率性能与信噪比关系
Fig.5 Relationship between bit error rate performance and signal-to-noise ratio of EP-BP algorithm under different UE speeds
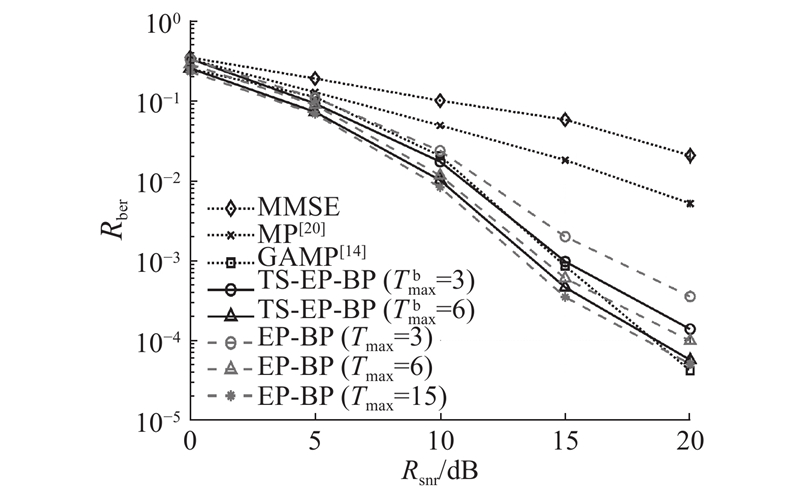
如图6所示给出各算法的误码率性能比较. 其中,
图 6
图 6
Fig.6
Relationship between bit error rate performance and signal-to-noise ratio of different algorithms when
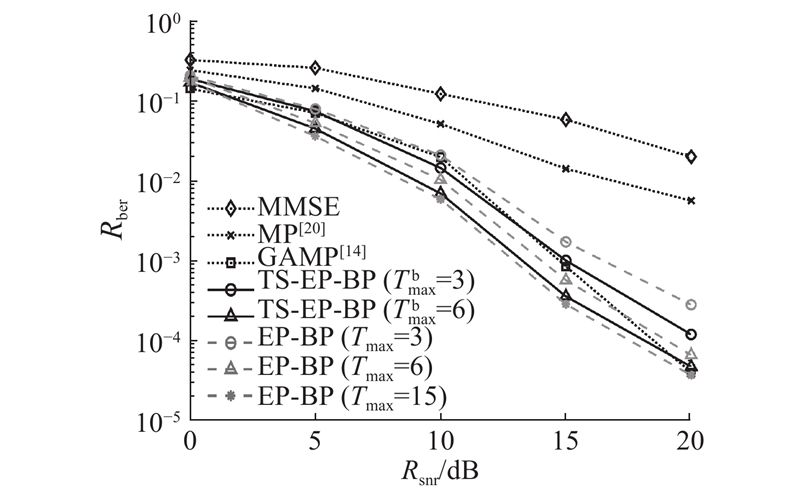
如图7所示为
图 7
图 7
Fig.7
Relationship between bit error rate performance and signal-to-noise ratio of different algorithms when
4. 结 语
针对GSM-OTFS系统提出混合期望传播与置信传播的EP-BP联合信号检测算法,并通过减少迭代中符号置信度计算步骤需要遍历的发射符号集,进一步提出了低复杂度TS-EP-BP算法. 仿真结果表明,TS-EP-BP检测算法能以更低的复杂度取得与EP-BP相近的性能. 另外,所提出的TS-EP-BP算法可以调整第1阶段的迭代次数来实现误码率性能和复杂度之间的灵活权衡. 本研究的GSM模型是以4收4发为例,规模较小,当天线规模提升之后,激活天线组合集的复杂度会指数上升,未来应当关注这一难点,研究适应大规模天线的算法.
参考文献
Practical pulse-shaping waveforms for reduced-cyclic-prefix OTFS
[J].
Channel estimation for orthogonal time frequency space (OTFS) massive MIMO
[J].
Generalized index modulation for MIMO-OTFS transmission
[J].DOI:10.1109/LWC.2023.3250255 [本文引用: 1]
Generalized approximate message passing detector for GSM-OTFS systems
[J].DOI:10.1109/ACCESS.2022.3153703 [本文引用: 5]
Improved layered message passing algorithms for large-scale generalized spatial modulation systems
[J].
Approximate message passing detector based upon probability sorting for large-scale GSM systems
[J].DOI:10.1109/TVT.2019.2928695 [本文引用: 1]
Approximate message passing detector for index modulation with multiple active resources
[J].
Iterative receiver for orthogonal time frequency space with index modulation via structured prior-based hybrid belief and expectation propagation
[J].DOI:10.23919/JCC.2023.01.006 [本文引用: 2]
Factor graphs and the sum-product algorithm
[J].DOI:10.1109/18.910572 [本文引用: 2]
Interference cancellation and iterative detection for orthogonal time frequency space modulation
[J].DOI:10.1109/TWC.2018.2860011 [本文引用: 5]
Products and convolutions of Gaussian probability density functions
[J].