美国睡眠医学会(American Academy of Sleep Medicine, AASM)于2007年发布了最新版的睡眠分期标准. 该标准将睡眠分为5个阶段:觉醒(wakefulness, W)阶段、快速眼动(rapid eye movement, REM)睡眠阶段,以及3个非快速眼动睡眠(nonrapid eye movement, NREM)阶段(NREM1、NREM2、NREM3)[4].
目前,PSG系统被认为是评价睡眠结构的“金标准”[5]. 然而在实际应用中,传统多导睡眠图(polysomnography,PSG)技术采用多电极和多传感器连接身体多部位的数据采集方法,容易干扰睡眠过程,导致测量结果偏离实际情况. 此外,PSG测量过程须在专业实验室中进行,成本昂贵,难以普及. 为了改善舒适性,降低睡眠检测成本,一些研究者尝试基于心电图(electrocardiogram, ECG)信号,通过心率变异性(heart rate variability, HRV)特征分析睡眠过程. HRV特征是指相邻心搏之间的瞬时心率存在微小差异或逐次心跳周期的变化情况[6],反映了交感和副交感神经系统的活动. 目前已有不少针对HRV特征指标的生理可解释性及其随睡眠阶段的变化规律的相关研究[7-16].
在基于单通道ECG信号的睡眠分期任务中,早期研究将睡眠划分为3个阶段(W、REM、NREM). 如Erdenebayar等[8]采用门控循环单元(gated recurrent cell, GRU)模型将睡眠以3个阶段进行分期,实验精度为80.43%. 同时,有部分研究将睡眠划分为4个阶段(W、REM、NREM1/NREM2、NREM3). 例如,Radha等[9]与Fonseca等[10]分别使用长短期记忆(long short-term memory, LSTM)模型与双向长短期记忆网络(bidirectional long short-term memory, BiLSTM)模型对睡眠的4个阶段进行分期,分别取得了77.0%±8.9%与75.9%的实验精度. Geng等[11]通过构建卷积神经网络(convolutional neural network, CNN)分类器取得了91.72%的实验精度. 然而,当前研究通常根据最新的AASM标准将睡眠以5个阶段进行分期处理. 例如,Sun等[12]使用CNN-LSTM架构对5个睡眠阶段进行分期, 实验精度为72.54%. Wang等[13]采用梯度提升决策树(gradient boosting decision tree, GBDT)模型进行睡眠分期,取得了82.02%的实验精度. 同时,Mathunjwa等[14]采用残差网络(residual network, ResNet)模型在睡眠分期研究中取得了77.34%的实验精度. Chakraborty等[15]用随机森林(random forest, RF)模型取得了75.9%的实验精度. 此外,Surantha等[16]采用粒子群优化(particle swarm optimization, PSO)算法结合极限学习机(extreme learning machine, ELM)分类器,在6个阶段、4个阶段、3个阶段睡眠分类中分别取得62.66%、71.52%、76.77%的实验精度.
虽然先前的研究已经在使用HRV特征和不同分类器模型进行睡眠阶段分类方面取得了一些进展,但是睡眠分期研究仍然面临着一系列挑战:首先,采用不同特征和模型的组合形式导致了睡眠分期方法的多样性,然而这并未显著改善其效果. 其次,一些方法在健康受试者中表现良好,但在患者身上效果不佳,缺乏普遍性和稳健性;同时,最先进的睡眠分期方法精度相对较低,难以实际应用.
为了解决上述问题,本研究采用不同睡眠障碍情况患者的整夜睡眠数据作为研究基础,提出基于HRV特征与向量加权平均值(weighted mean of vectors, INFO)优化算法结合ABCLogitBoost模型的自动睡眠分期方法.
1. 自动睡眠分期方法
1.1. 概述
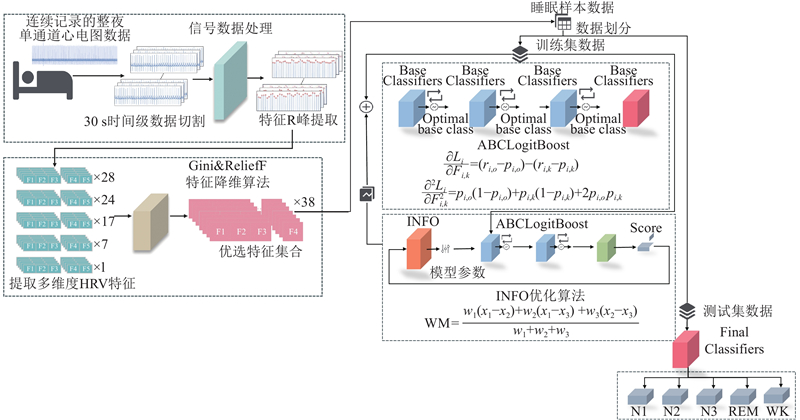
所提出的方法框架如图1所示,主要包含如下3个部分.
图 1
图 1 基于INFO-ABCLogitBoost模型的自动睡眠分期方法总框图
Fig.1 Diagram of automatic sleep stage classification method based on INFO-ABCLogitBoost model
1)通过最大重叠离散小波变换(maximum overlap discrete wavelet transform, MODWT)分解原始心电信号,选择特定频率段进行重构,并提取峰值位置信息以计算一阶偏差构成RRi序列.
2)基于RRi序列,通过数学分析计算,从而多维度计算提取HRV特征. 然后采用Gini指数与ReliefF算法相结合的方式,来去除噪声和冗余特征,从而实现对HRV特征数据的降维.
3)采用INFO-ABCLogitBoost模型对睡眠障碍情况患者整夜睡眠数据进行睡眠分期.
1.2. 预处理
1.2.1. 信号处理
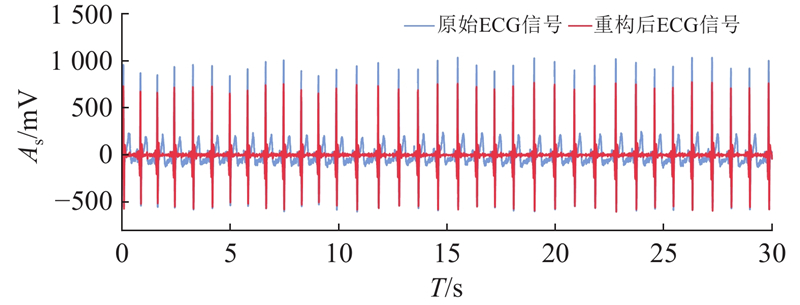
心电信号的特征不仅受个体间差异的影响,而且同一人的心电信号也会随着时间的推移而发生变化,导致出现差异,使其无法仅通过时间函数表示. 同时心电信号在采集过程中常受到大量噪声的干扰,容易导致数据污染,甚至被淹没[17].
图 2
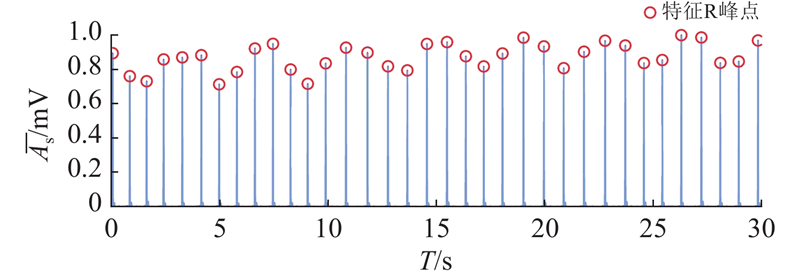
为了精确定位R峰的位置,首先将重构信号进行归一化处理,以确保R峰的振幅范围不会影响后续处理,并保证算法能够适应不同患者在不同条件下的心电信号. 其次,将信号进行半波整流处理,将信号中的负周期数据归零,仅保留正半周期,从而消除负值对信号的影响,以突显正半周期的信息. 接着,将信号进行算术平方操作,以突出信号中R峰高振幅部分. 最后,设定最低峰值高度和峰值之间的距离阈值,实现R峰定位,如图3所示. 图中,
图 3
1.2.2. 信号矫正
为了消除由电极接触问题所引起的随机误差,采用粗大误差分析方法. 首先,对获取的所有R峰的位置进行一阶偏差计算,生成RRi序列,然后计算该序列的平均值. 接着,剔除所有小于RRi序列平均值的0.3倍和大于1.5倍的异常点,并用序列平均值进行补全. 最后,根据拉依达准则剔除异常点[19],并进行均值填充.
式中:xi表示RRi序列中的元素,x表示RRi序列的平均值,
1.2.3. HRV特征处理
首先计算每个特征的Gini指数:
式中:Gini (D)表示数据集D的基尼不纯度,用来衡量数据集中样本的混杂程度;K表示数据集D中的类别数量;pi表示数据集D中第i个类别的样本占比. 通过设置阈值来筛选重要性高的特征,来去除噪声特征.
为了进一步清洗冗余特征,通过ReliefF算法计算每一个特征权重:
式中:dis (a, Ri, Hj)表示样本Ri与Hj在特征a下的距离;m、k分别表示临近样本数与迭代次数;class (Ri)表示样本Ri所属的类别;P (C)表示类别C出现的概率;Mj (C)表示第C类中的第j个临近样本;W(a)由样本间的类别距离与同一类样本内的距离之差决定,值越大说明特征对样本区分能力越强. 通过设置阈值来筛选高权重的特征,可以消除特征冗余.
1.3. ABCLogitBoost模型
1.3.1. 零和约束
ABCLogitBoost模型以多类别逻辑回归为基础,结合零和(sum-to-zero)约束进行建模[22].
式中:L表示单个样本的损失Li之和;N表示样本数量;i表示样本索引;
在该损失函数中,Li以交叉熵的形式度量预测概率pi,k与真实标签ri,k之间的差异. 相较于平方损失之类的常规损失函数,它对错误判别的惩罚更大,从而助于减轻梯度消失问题,提高算法分类性能.
1.3.2. 基类别选择
该模型是一种集成算法,通过集成一系列弱分类器(回归树),并在迭代过程中选择最优基类别,从而实现强分类性能.
式中:
同时,该模型在训练过程中通过采用贪婪策略来提升模型基类别选择的效率. 即在每次迭代中,将每个类别依次作为基类别,并选择使训练中损失最小化的类别作为有效的基类别继续迭代,从而提升整体训练速率.
1.3.3. 搜索策略
为了更好地捕捉类别之间的复杂关系,该模型遍历类别集合,并为每个类别构建基于回归树的模型(除了当前选择的基类别)[23]. 其次,为每棵树节点分配精确的权重,使得模型能够更好地适应不同样本的变化. 这一策略目的是在模型中综合考虑类别关系和样本特征,以提高模型的性能和泛化能力.
式中:v为权值,控制额外加权项对原始得分的影响;J为所有节点的总数;βj,k,m表示每个节点j对应目标类别k与对比类别m的权重,该计算考虑了在当前回归树节点上模型预测与实际值之间的差异,以及每个类别在该节点上的概率分布;
式中:Gi,b,b表示在节点b中不属于类别k的总增益的相反数;qi,k表示在节点b上属于类别k的概率,通过对增益进行指数化及归一化,得到各个类别的概率以评估模型在训练中对不同类别的置信度;
式中:B(m)表示选择在第m次迭代中使损失函数
1.4. INFO优化算法
采用向量加权平均值(INFO)算法解决ABCLogitBoost模型参数的优化问题. 该算法基于加权均值,通过3个核心步骤来更新向量的位置:数据更新、向量组合和局部搜索[24]. 在数据更新阶段采用均值法和收敛加速原理生成新的向量. 在向量组合阶段将已获得的向量与新生成的向量进行组合,从而优化信息拓展与开发能力,以提升整体效能. 最后在局部搜索阶段,利用全局位置和平均值策略来避免信息误导,陷入局部最优解,从而提高开发和搜索性能,达到全局最优.
2. 实验工作
2.1. 数据集描述
表 1 HMC数据集中的各睡眠阶段样本数量统计
Tab.1
| 睡眠阶段 | Ns/个 | Ps/% |
| W | 3 948 | 28.88 |
| REM | 1 877 | 13.73 |
| NREM1 | 1 296 | 09.48 |
| NREM2 | 4 700 | 34.39 |
| NREM3 | 1 847 | 13.51 |
| 总体 | 13 668 | 100.00 |
采用意大利帕尔马Ospedale Maggiore睡眠障碍中心提供的CAP(Cyclic Alternating Pattern)数据库,针对不同睡眠障碍患者人群的睡眠样本数据进行分期实验,以评估模型的泛化能力. 该数据库包含了不同睡眠障碍患者的PSG记录,如夜间额叶癫痫(nocturnal frontal lobe epilepsy, NFLE)、快速眼动期行为障碍(rapid eye movement behavior disorder, RBD)、周期性肢体运动(periodic limb movements, PLM)、睡眠呼吸暂停(sleep disordered breathing, SDB)、失眠(Insomnia)和嗜睡症(Narcolepsy)等. 该记录提供了ECG信号在内的多种生物信号,同时配备了参考睡眠阶段注释. 为了保证数据样本量的平衡性,实验所采用的不同类别的数据片段数量如表2所示. 表中,Nn为记录条数,No pathology表示无病症人群.
表 2 CAP数据集中的各睡眠阶段样本数量统计
Tab.2
| 数据类别 | Nn/条 | Ns/个 |
| No pathology | 5 | 5 114 |
| NFLE | 5 | 5 178 |
| RBD | 5 | 5 596 |
| PLM | 5 | 4 726 |
| SDB | 4 | 2 687 |
| Insomnia | 5 | 5 813 |
| Narcolepsy | 5 | 5 516 |
2.2. 评价指标
为了验证睡眠分类任务中的模型性能,采用精度(accuracy, ACC)、准确率(precision, PRE)、召回率(Recall)、F1(F1-Score)、Kappa作为评价指标. 评价指标表达式如下:
式中:TP为真阳性,表示被正确判断为类别i的样本数;FN为假阴性,表示实际为类别i的样本被判断为其他类别的样本数;FP为假阳性,表示实际不是类别i的样本被判断为类别i的样本数;TN为真阴性,表示被正确判断为非类别i的样本数. 其中,类别i为当前睡觉阶段的类别.
真实的整夜睡眠数据样本,存在数据不均衡问题. 本研究为了更全面、公平地反映模型的整体性能,采用加权平均的PRE与F1评估方法. 其中,权重由当前类别数量与总类别数量的比值确定.
3. 实验结果
3.1. 特征筛选
以HRV特征为基础,并综合考虑RR序列的其他特性,包括时域、频域、非线性域、复杂度指数、庞加莱图几何以及心率碎片指数等,共计77种HRV特征,如表3所示. 表中,n为特征数量.
表 3 睡眠分期任务中所提取的HRV特征统计
Tab.3
| 特征 | n/个 |
| 时域特征 | 28 |
| MeanNN、MedianNN、ModeNN MaxNN、MinNN、MadNN | 6 |
| RMSSD、SDNN、SDSD、CVNN、CVSD、RMSA | 6 |
| SDANN1、SDANN2、SDANN5 SDNNI1、SDNNI2、SDNNI5 | 6 |
| NN20、PNN20、NN50、PNN50 | 4 |
| MeanHR、MinHR、MaxHR、StdHR | 4 |
| TINN、HTI | 2 |
| 频域特征 | 24 |
| LF、HF、MF、TF、VLF、TLF、ULF、Ttlpwr | 8 |
| LFf、HFf、MFf、TFf、TLFf | 5 |
| LFn、HFn、MFn、TLFn | 4 |
| LFHF、MFLF、TLFLF | 3 |
| pHF、pLF | 2 |
| HFmaxf、HFamp | 2 |
| 庞加莱图几何 | 7 |
| SD1、SD2、SD1SD2、S | 4 |
| CVI、CSI、CSI_Modified | 3 |
| 心率碎片指数 | 17 |
| PIP、SI、AI、GI、C1d、C1a、SD1d、SD1a、C2d、C2a SD2d、SD2a、SD2I、Cd、Ca、SDNNd、SDNNa | 17 |
| 复杂度指数 | 1 |
| SampEn | 1 |
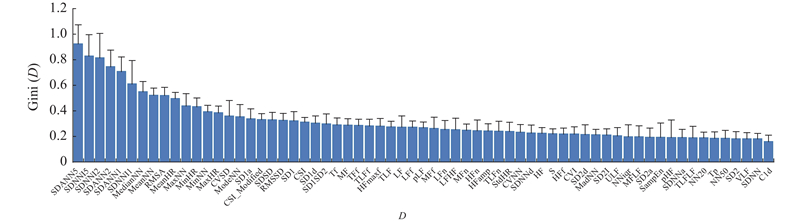
图 4
图 4 根据Gini指数计算的HRV特征的重要性均值与标准差
Fig.4 Mean and standard deviation of importance of HRV features calculated based on Gini index
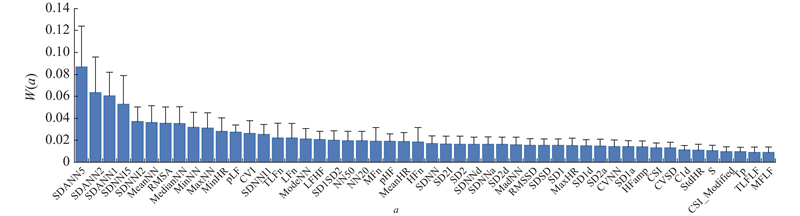
为了进一步消除冗余特征,采用ReliefF算法计算每个特征的权重,并筛选特征权重及其标准差之和大于权重均值(0.013)的特征,以消除潜在的冗余信息. 最终保留的特征及其权重如图5所示. 图中,a表示筛选过的特征名称,W (a)表示根据ReliefF算法所计算的相应特征的权重.
图 5
图 5 根据ReliefF算法计算的HRV特征的权重均值与标准差
Fig.5 Mean and standard deviation of HRV feature weights calculated based on ReliefF algorithm
综合考虑,最终选取38个最具代表性的HRV特征为睡眠分期建模的基础.
为了验证特征筛选的必要性,在本地设备(内存为 16 G,处理器为Intel Core i7-8750H CPU @ 2.20 GHz 2.21 GHz)上将特征筛选后的特征集合通过本研究所提出的分类器进行验证评估,实验结果如表4所示. 表中,t为运行时间. 在共计77个HRV特征基础上,通过Gini指数剔除25个低重要性HRV特征. 基于所保留的52个特征训练的分类器在睡眠分期任务中取得了83.35%的精度,相较采用未降维特征训练的分类器精度(82.43%)提高了0.92个百分点. 同时,运行时间从632.95 min降低到379.06 min,性能提升40.11%. 在此基础上使用ReliefF算法进一步剔除14个低权重特征. 最后含所保留的38个特征的集合使分类器在睡眠分期任务中的精度进一步提升0.32个百分点,且运行时间降低到261.83 min,性能提升30.93%,从而证明了本研究所提出的特征筛选方法能够有效提升分类器鲁棒性和运行效能.
表 4 特征降维实验结果
Tab.4
| 算法 | n/个 | t/min | ACC/% | Kappa/% | F1/% |
| — | 77 | 632.95 | 82.43 | 76.22 | 81.39 |
| Gini | 52 | 379.06 | 83.35 | 77.51 | 82.66 |
| ReliefF | 38 | 261.83 | 83.67 | 77.94 | 82.97 |
3.2. 模型性能评估
为了验证INFO-ABCLogitBoost模型在睡眠阶段分类上的有效性,以主流睡眠分类特征模型作为对照. 同时为了确保实验结果的可靠性,以7∶3的比例将数据集随机划分为训练集和测试集,各模型的性能如表5所示. 其中本研究提出的模型在睡眠分期任务中的ACC、PRE、Kappa和F1分别达到83.67%、82.59%、77.94%和82.97%. 其中模型精度相较于次优的GBDT模型在精度上提升2.94个百分点,较性能较弱的ELM模型在精度上提升17.91个百分点. 同时,相较于睡眠分期任务中主流的神经网络架构(GRU、LSTM、BiLSTM、CNN、CNN-LSTM、ResNet)的精度均值 (71.94%)提升11.73个百分点,较同类别集成模型(XGBoost、Bag、RF、GBDT)的精度均值 (77.99%)提升5.68个百分点. 结果表明,本研究提出的模型架构所取得的预测结果与真实数据标签之间存在高度一致性. 相较于传统的神经网络架构以及同类别集成模型性能有显著提升.
表 5 睡眠分期任务模型性能测试结果
Tab.5
| 方法 | ACC/% | PRE/% | Kappa/% | F1/% |
| ELM | 65.76 | 65.42 | 53.81 | 65.37 |
| SVM | 69.89 | 68.40 | 58.43 | 67.98 |
| GRU | 70.71 | 68.83 | 59.84 | 69.05 |
| LSTM | 70.64 | 68.85 | 59.66 | 68.91 |
| BiLSTM | 71.49 | 69.77 | 61.03 | 70.06 |
| CNN | 72.26 | 71.97 | 62.74 | 72.08 |
| CNN-LSTM | 72.05 | 71.45 | 62.39 | 71.65 |
| ResNet | 73.54 | 73.28 | 64.48 | 73.34 |
| XGBoost | 70.71 | 68.83 | 59.84 | 69.05 |
| Bag | 79.13 | 77.89 | 71.65 | 78.19 |
| RF | 80.37 | 79.10 | 73.38 | 79.45 |
| GBDT | 80.73 | 79.43 | 73.90 | 79.82 |
| 本研究 | 83.67 | 82.59 | 77.94 | 82.97 |
为了进一步验证本模型在睡眠分期任务上性能的优越性,将睡眠各阶段的召回率结果汇总于表6. 可以看出,本研究模型在W阶段精度较高,达到91.49%,同时在NREM2、NREM3、REM这3个阶段精度均高于80.00%,表明本研究所提出的模型对每个类别的分类性能较为均衡,总体精度显著优于其他主流的睡眠分期模型. 由于NREM1阶段在真实睡眠中所占比例较小,NREM1阶段数据量相对较少,从而导致分期精度不高,然而本研究所提出的模型在NREM1阶段精度为29.03%,仍取得了最优分期结果.
表 6 睡眠分期任务中不同睡眠阶段的模型召回率
Tab.6
| 方法 | Recall/% | ||||
| NREM1 | NREM2 | NREM3 | REM | W | |
| ELM | 18.77 | 74.59 | 61.70 | 63.31 | 71.67 |
| SVM | 11.14 | 80.66 | 62.91 | 55.40 | 83.55 |
| GRU | 12.02 | 78.73 | 61.01 | 64.39 | 85.07 |
| LSTM | 12.32 | 78.52 | 61.70 | 61.15 | 86.12 |
| BiLSTM | 14.96 | 77.87 | 64.12 | 65.47 | 85.87 |
| CNN | 25.81 | 76.16 | 72.96 | 67.81 | 82.26 |
| CNN-LSTM | 24.68 | 77.05 | 68.01 | 65.33 | 84.71 |
| ResNet | 26.41 | 77.48 | 71.28 | 70.67 | 84.71 |
| XGBoost | 12.02 | 78.73 | 61.01 | 64.39 | 85.07 |
| Bag | 24.63 | 85.08 | 76.78 | 75.90 | 89.89 |
| RF | 24.93 | 85.87 | 79.38 | 78.78 | 90.53 |
| GBDT | 25.22 | 85.94 | 81.80 | 79.50 | 90.13 |
| 本研究 | 29.03 | 89.08 | 86.31 | 83.27 | 91.49 |
为了验证模型的泛化性能,对CAP数据库中不同睡眠障碍患者人群的睡眠样本数据进行验证评估,实验结果如表7所示. 其中No pathology、RBD、PLM和Insomnia类别数据的实验精度均高于85.00%,而所有类别的平均实验精度达到了83.60%,标准差为4.51%,证明了本研究所提模型具有较好的泛化性能.
表 7 不同类别样本验证结果
Tab.7
| 数据类别 | ACC/% | PRE/% | Kappa/% | F1/% |
| No pathology | 86.78 | 86.28 | 81.10 | 86.19 |
| NFLE | 77.94 | 77.76 | 68.21 | 77.31 |
| RBD | 88.07 | 88.16 | 83.52 | 87.98 |
| PLM | 85.78 | 85.89 | 79.71 | 85.40 |
| SDB | 74.63 | 73.97 | 58.32 | 73.09 |
| Insomnia | 87.98 | 88.09 | 82.46 | 87.72 |
| Narcolepsy | 84.22 | 83.90 | 79.11 | 83.76 |
最后,将本研究与近些年的基于ECG信号进行睡眠分期研究的文献进行比较,数据汇总如表8所示. 本研究基于一组与不同睡眠阶段有强关联的HRV特征集合,提出创新的IFNO-ABCLogitBoost模型架构,以更好地完成睡眠分期任务,在最新公布的HMC数据集上进行验证评估,本研究于5分期实验中取得了83.67%的实验精度,优于其他相关文献实验结果. 证明了本研究所提方法的优越性.
表 8 先进研究与所提出模型的结果对比
Tab.8
4. 结 语
基于ECG信号的HRV特征对睡眠分期开展相关研究. 针对传统睡眠分期方法在处理新的数据集或不同类别数据时泛化性能不足的问题以及特征模型结构不够优化,睡眠分期精度不足的问题,提出基于INFO-ABCLogitBoost方法的睡眠分期方法. 在信号处理中,采用离散小波变换分解原始信号,选择特定频率段进行心电信号重构,从而提取峰值信息以定位R峰,从而构成RRi序列. 在此基础上,提取多维度HRV特征,并通过Gini指数和ReliefF算法筛选不同睡眠阶段的强相关特征. 最后以所提出的INFO-ABCLogitBoost模型和筛选后的HRV特征为基础,对数据样本进行睡眠分期.
在公开数据集上的实验结果表明,所提出的INFO-ABCLogitBoost模型在睡眠分期研究领域展现出卓越的潜力和优越性,相较于主流的基于心率变异性进行睡眠分期的特征模型,其性能更为突出. 因此,这种基于单通道ECG的睡眠分期算法有望应用于家庭和移动场景下,为睡眠疾病的辅助诊断和治疗提供全新、便捷的方案.
在睡眠分期中采用的ECG信号虽然是非侵入式,但在采集睡眠数据样本时依然无法避免传感器与人体的直接接触,这有可能影响真实数据. 为此后续将进一步研究非接触式BCG信号与睡眠分期的映射关系,以实现更准确、可靠的睡眠分期.
参考文献
Circadian rhythms from flies to human
[J].
Impact of lifestyle and technology developments on sleep
[J].
Sleep deficiency and cardiometabolic disease
[J].DOI:10.1016/j.ccm.2022.02.011 [本文引用: 1]
AASM scoring manual updates for 2017 (version 2.4)
[J].DOI:10.5664/jcsm.6576 [本文引用: 1]
Prevalence of positional sleep apnea in patients undergoing polysomnography
[J].DOI:10.1378/chest.128.4.2130 [本文引用: 1]
Heart rate variability (HRV) as a way to understand associations between the autonomic nervous system (ANS) and affective states: a critical review of the literature
[J].
Influence of sleep duration and sex on age-related differences in heart rate variability: findings from program 4 of the HAIE study
[J].
Automatic classification of sleep stage from an ecg signal using a gated-recurrent unit
[J].DOI:10.5391/IJFIS.2020.20.3.181 [本文引用: 2]
Sleep stage classification from heart-rate variability using long short-term memory neural networks
[J].DOI:10.1038/s41598-019-49703-y [本文引用: 2]
Automatic sleep staging using heart rate variability, body movements, and recurrent neural networks in a sleep disordered population
[J].
Convolutional neural network is a good technique for sleep staging based on HRV: a comparative analysis
[J].DOI:10.1016/j.neulet.2022.136550 [本文引用: 2]
Sleep staging from electrocardiography and respiration with deep learning
[J].DOI:10.1093/sleep/zsz306 [本文引用: 2]
Automatic multi-class sleep staging method based on novel hybrid features
[J].DOI:10.1007/s42835-023-01570-4 [本文引用: 2]
Automatic IHR-based sleep stage detection using features of residual neural network
[J].DOI:10.1016/j.bspc.2023.105070 [本文引用: 2]
Sleep stage classification using extreme learning machine and particle swarm optimization for healthcare big data
[J].DOI:10.1186/s40537-020-00387-6 [本文引用: 3]
基于并行架构和时空注意力机制的心电分类方法
[J].
Classification method for electrocardiograph signals based on parallel architecture model and spatial-temporal attention mechanism
[J].
Feature extraction of ECG signal
[J].DOI:10.1080/03091902.2018.1492039 [本文引用: 1]
A fair consensus adjustment mechanism for large-scale group decision making in term of Gini coefficient
[J].
A novel random multi-subspace based ReliefF for feature selection
[J].
INFO: an efficient optimization algorithm based on weighted mean of vectors
[J].DOI:10.1016/j.eswa.2022.116516 [本文引用: 1]