随着各行业的快速发展，消费者的需求更加个性化，企业的生产模式也由传统的大批量生产转为多品种小批量生产. 传统人工物料配送耗时且效率低. 当下的车间物料配送具有多批次、路线复杂的特点. 精益物流追求在正确的时间将正确的物料送往正确的工序，因此要提升车间物料配送的配送效率，确定科学合理的配送顺序至关重要.

物料配送顺序问题属于配送路径规划的一种，其优化算法主要有精确算法和启发式算法. Lanza等^[1]以最小车辆行驶时间为目标，提出混合整数线性规划方法；Ferreira等^[2]将各项成本相加作为目标函数，采用人工藻类算法进行求解；Osaba等^[3]设计渐进离散萤火虫新颖算法；罗亮等^[4]以成本之和最小为目标构建规划模型，并设计改进的蚁群算法求解；Ghannadpour等^[5]考虑车辆数量、顾客满意率、能耗等因素，提出基于进化算法的求解方法；Zhang等^[6]采用基于禁忌搜索和人工蜂群算法的混合方法；Akpinar等^[7]提出能够提高算法多样性的蚁群和邻域搜索的混合算法；Frey等^[8]针对一个客户具有多个交付地点的问题，以配送成本最低为目标，采用混合自适应大邻域搜索算法求解. 整数规划、线性规划和分支定界等精确算法虽然能得到精确解，但计算量随着问题规模增大呈指数增长，因此学者普遍采用改进启发式算法或混合算法向最优解逼近. 上述研究中学者大多求解以路径最短的单目标问题或将多个目标加权为单目标问题，不足在于权重的确定具有主观性.

针对多目标优化问题，诸多学者展开了研究. Kuo等^[9]以供应链总成本最小和碳排放总量最小为目标，采用多目标粒子群优化算法求解两阶段的车辆路径规划问题；Zhu等^[10]结合遗传算法和模拟退火算法求解多目标车间物料配送问题；Wu等^[11]采用改进蚁群算法求解多目标车间配送路径问题；Srivastava等^[12]针对问题特征和每个目标的属性，设计交叉和变异算子,提出基于目标特异性变异算子的快速非支配排序遗传算法(non-dominated sorting genetic algorithm, NSGA-Ⅱ)；Yin等^[13]考虑运输配送过程中产生的能源消耗和碳排放问题，采用基于多因子进化算法的NSGA-Ⅱ算法求解. 上述研究中多目标粒子群算法、改进蚁群算法、NSGA-Ⅱ等方法中，NSGA-Ⅱ采用的遗传操作具有更强的全局搜索能力和更高的计算效率. 但考虑其变异操作是对个体的某段基因进行随机变换，经过变异操作后的新基因和原种群中基因存在重合的可能性，从而可能陷入局部最优. 因此，本研究提出将同样具有遗传操作的差分进化(differential evolution, DE)算法^[14]引入NSGA-Ⅱ中，通过缩放个体的差值确保新的解和原来的几个解都能有一定的距离，确保其搜索能力. 学者对DE算法与多目标优化算法的结合展开相关研究，如Liu等^[15]针对三阶段混合流程车间调度问题，以电力成本和生产率为优化目标，设计双目标DE算法；Stampfli等^[16]采用DE初始化种群、NSGA-Ⅱ 生成帕累托前沿的方式求解多目标优化问题. DE算法因其结构简单、易于实现、收敛速度快、鲁棒性强等特点，已广泛应用于流水车间领域^[17-20].

为了提高启发式算法对搜索空间的探索与开发能力、提高收敛性与算法的进化效率，学者们提出启发式算法和聚类相结合的方法. Gu等^[21]通过距离对客户进行划分聚类；Lo等^[22]提出先聚类后路由的两阶段方法，通过扫频法将顾客聚类；Barletta等^[23]基于客户位置和包裹重量，采用k中值聚类进行分组；Wang等^[24]提出改进的三维 k-means 聚类算法，将客户分配到配送中心. 上述学者采用距离划分、k中值聚类和k均值聚类等方式，其中，距离划分和扫频法的不足之处在于计算量随着问题规模增大呈增长趋势，k中值聚类、k均值聚类缺点在于对初值的设置敏感，不同的初值会产生不同的聚类效果. Rodriguez等^[25]针对这些问题提出新型聚类算法−密度峰值聚类(density peak clustring, DPC)算法. 与距离划分的方式相比，DPC能快速发现任意形状数据集的密度峰值点，并高效进行样本点分配和离群点剔除；相较于k均值聚类算法该算法也较少需要人为干预，目前该算法已在带时间窗的车辆路径规划问题^[26]中应用.

综上所述，本研究针对车间物料配送顺序多目标优化问题，提出融合DPC、NSGA-Ⅱ和DE算法的混合优化算法(INSGA-Ⅱ). 采用DPC初始化种群，缩减问题规模；同时在NSGA-Ⅱ遗传操作阶段采用基于DE的差分进化操作，通过变异向量的差分操作与部分映射交叉加快迭代速度、提高种群多样性，提高车间物料配送的配送效率.

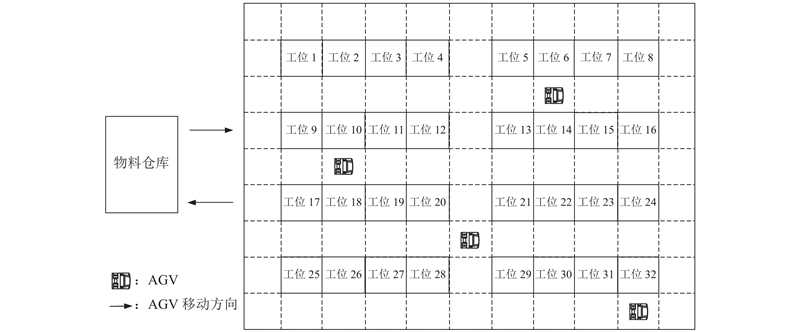
自动导引车(automated guided vehicle, AGV)配送物料的流程可以描述为：物料仓库有n个待配送给工位的物料配送任务，任务开始时所有AGV都从物料仓库出发，按照各自的任务顺序完成配送后再返回物料仓库. 工位点设有相应的时间窗，代表物料理想送达时间，AGV未能在时间窗的规定范围内送达将产生相应的惩罚函数值. 车间布局如图1所示.

本研究旨在缩短AGV配送的总路径长度以及尽可能满足各工位物料在最佳时间段到达. 物料配送车辆运行模式要求如下：物料仓库中的物流工人将工位所需物料放入各AGV中，装载物料的每个AGV按照预定的顺序对其配送任务中的所有工位进行配送，每个AGV在一次配送任务中对多个工位进行配送，且AGV小车的数量满足物料配送的需求.

为了方便模型的建立，对模型做出以下基本假设：1）所研究的物料仓库只有一个，工位需求点有多个；2）工位所需的物料只能由一个AGV配送一次，其他AGV不能重复配送；3）工位所需的物料不会超过AGV的额定车载量；4）AGV的行驶速度不变，且在行驶过程中忽略故障、电量不足带来的问题；5）所有任务的出发点都为物料仓库，当所有配送任务完成时都须返回物料仓库；6）不考虑各工位从AGV上取下其所需物料的时间；7）车间内物料仓库和各工位的位置、点与点之间的距离和时间窗已知.

车间物料配送是车间物流的重要组成部分，不合理的配送路径会影响物料配送的效率，以最小化配送路径为优化目标可以提高车间物料配送效率、降低配送成本；针对传统循环配送准时性差的问题，考虑精益生产模式下各工位所需物料种类多，而生产的中断会导致工人等待、在制品增加和生产效率低等问题，以最小化时间窗惩罚为优化目标可以将物料更加及时地送到工位，确保生产的连续性，从而提高生产效率，因此本研究优化目标为最小化配送路径和最小化时间窗惩罚.

1）最小化配送路径：

(1)$ \min \;Z_1=\sum_{k=1}^K \sum_{i=0}^n \sum_{j=0}^n d_{i j} x_{i j k}. $

式中：k为AGV编号，表示第k辆AGV；K表示AGV的总数；$i$和$j$为待配送物料的工位，n为需要物料配送的工位总数，$i,\;j \in \left\{ {0,\;1,\;2,\; \cdots ,\;n} \right\}$；${d_{ij}}$为工位$i$和$j$之间的曼哈顿距离；${x_{ijk}}$为0或1 (若第k辆AGV在访问工位i后行驶至工位j，则${x_{ijk}} = 1$；若第k辆AGV在访问工位i后不行驶至工位j，则${x_{ijk}} = 0$).

2）最小化时间窗惩罚：

(2)$ \min \;{Z_2} = \alpha \sum\limits_{k = 1}^K {\sum\limits_{i = 1}^n {({t_{i{\mathrm{s}}}} - t_i^k)} } +\beta \sum\limits_{k = 1}^K {\sum\limits_{i = 1}^n {(t_i^k - {t_{i{\mathrm{e}}}})} } . $

式中：$\alpha $为AGV早于时间窗的开始时间到达的惩罚系数，${t_{i{\mathrm{s}}}}$为工位$i$时间窗的开始时间，$t_i^k$为第$k$辆AGV到达工位$i$的时间，$\beta $为AGV晚于时间窗的结束时间到达的惩罚系数，${t_{i{\mathrm{e}}}}$为工位$i$时间窗的结束时间.

(3)$ \sum\limits_{i = 1}^n {{x_{0ik}}} = \sum\limits_{j = 1}^n {{x_{j0k}}} ;\;k \in R. $

(4)$ \sum\limits_{k = 1}^K {\sum\limits_{i = 0}^n {{x_{ijk}}} } = 1;\;{{k}} \in R,\;i \in N,\;{{j}} \in N. $

(5)$ {d_{ij}} = \left| {{x_j} - {x_i}} \right|+\left| {{y_j} - {y_i}} \right|;\;i \in N,\;{{j}} \in N. $

(6)$ \displaystyle\sum\limits_{i = 0}^n {{q_i}} {x_{ijk}} \leqslant {Q_k};\;k \in R. $

(7)$ \alpha < \beta . $

(8)$ \alpha > 0,\;\beta > 0. $

式（3）表示每辆AGV从物料仓库出发，最后返回物料仓库，其中，$0$表示为物料仓库，即AGV的起点，R表示AGV集合，$R=\{1,\;2,\; \cdots ,\;K\} $；式（4）表示各个工位点只能被一辆AGV服务一次，其中，N表示工位点集合，$N = \left\{ {1,\;2,\;3,\; \cdots ,\;n} \right\}$；式（5）表示两工位间的曼哈顿距离，其中，$\left( {{x_i},\;{y_i}} \right)$为工位$i$的位置坐标；式（6）表示每辆AGV从物料仓库出发时的载量不超过其额定车载量，其中，${q_i}$为工位点$i$的所需物料量，${Q_k}$为第$k$辆AGV的额定车载量；式（7）表示物料早于时间窗送达的惩罚值比晚送达的惩罚值要小；式（8）表示2个时间窗的惩罚约束.

针对所研究的车间物料配送顺序优化问题，采用整数编码的编码方式. 在对染色体进行编码时，将一种配送顺序表示为一条染色体. 对待配送物料到达的工位进行编号，将待配送物料的工位编号为1, 2, ···, M，然后根据此编号设计编码. 例如染色体[3, 2, 5, 1, 4, 6]表示的配送顺序为先配送工位3所需的物料，然后配送工位2，最后依次配送其余工位.

通过DPC聚类的方式进行种群的初始化，根据工位的距离属性将所有工位进行分组. 具体过程如下.

1) 输入工位点位置数据集；

2) 计算每个工位点i到其余点的距离，得到距离矩阵D;

3) 计算每个工位点的截断距离范围内的工位点个数，即局部密度${\rho _i}$，表达式如下：

(9)$ {\rho _i} = \sum\limits_{j \ne i} \chi ({S_{ij}} - {S_{\mathrm{c}}}). $

式中：${S_{ij}}$表示i和j工位点间的欧氏距离；${S_{\mathrm{c}}}$为截断距离；设$\varDelta {\text{ = }}{S_{ij}} - {S_{\mathrm{c}}}$，当$\varDelta < 0$时，$\chi (\varDelta ) = 1$，否则$\chi (\varDelta ) = 0$.

4) 计算每个工位点到高于自身局部密度点的最小距离，即相对距离${\delta _i}$，表达式如下：

(10)$ {\delta }_{i}=\left\{\begin{array}{ll}\underset{j}{\mathrm{max}}\;{S}_{ij},&{\rho }_{i}最大;\\ \underset{j:{\rho }_{j} > {\rho }_{i}}{\mathrm{min}}\;{S}_{ij},&其他.\end{array}\right. $

5) 根据每个工位点的局部密度${\rho _i}$与相对距离${\delta _i}$，计算决策值${\theta _i}$，表达式如下：

(11)$ {\theta _i} = {\rho _i}{\delta _i}. $

决策值降序排序后选择前K个作为聚类中心.

6) 遍历聚类中心外各工位点，将其分配至密度比其高的最近距离工位点所在类簇.

聚类后在每个分组内进行初始化，随机生成初始化长度为L的P个染色体，种群初始化过程如图2所示. 该初始化方法可以提高初始种群的多样性，同时将聚类特性嵌入初始种群之中，可以缩减问题规模、加快求解速度.

由Storn和Price提出的DE算法^[14]是基于种群的优化算法，该算法的差分进化操作可以避免遗传算法的变异操作与原先个体的基因可能存在重合的问题. 通过差分的方式生成新的子代，可以在跳出局部最优的同时加快搜索效率.

对于一个具有NP个解向量组成的种群${{\boldsymbol{X}}_G} = \left[ {{{\boldsymbol{X}}_{1,\;G}},\;{{\boldsymbol{X}}_{2,\;G}},\; \cdots ,\;{{\boldsymbol{X}}_{{\mathrm{NP}},\;G}}} \right],\;$其中NP表示种群大小，G表示当前迭代次数. 在第G次迭代中，从种群中随机选择3个个体${{\boldsymbol{X}}_{{\mathrm{r}}1,\;G}}、{{\boldsymbol{X}}_{{\mathrm{r}}2,\;G}}、 {{\boldsymbol{X}}_{{\mathrm{r}}3,\;G}}$生成变异向量，其可通过如下公式计算得到：

(12)$ {{\boldsymbol{V}}_{{\mathrm{I}},\;G}} = {{\boldsymbol{X}}_{{\mathrm{r}}1,\;G}}+F({{\boldsymbol{X}}_{{\mathrm{r}}2,\;G}} - {{\boldsymbol{X}}_{{\mathrm{r}}3,\;G}}). $

式中：$ {{\boldsymbol{X}}_{{\text{r}}2,\;G}} - {{\boldsymbol{X}}_{{\text{r3}},\;G}} $为差分向量；F为变异缩放因子；${\mathrm{r}}1,\;{\mathrm{r}}2,\;{\mathrm{r}}3 \in \left\{ {1,\;2,\; \cdots ,\;{\mathrm{NP}}} \right\}$，且${\mathrm{r}}1 \ne {\mathrm{r}}2 \ne {\mathrm{r}}3$.

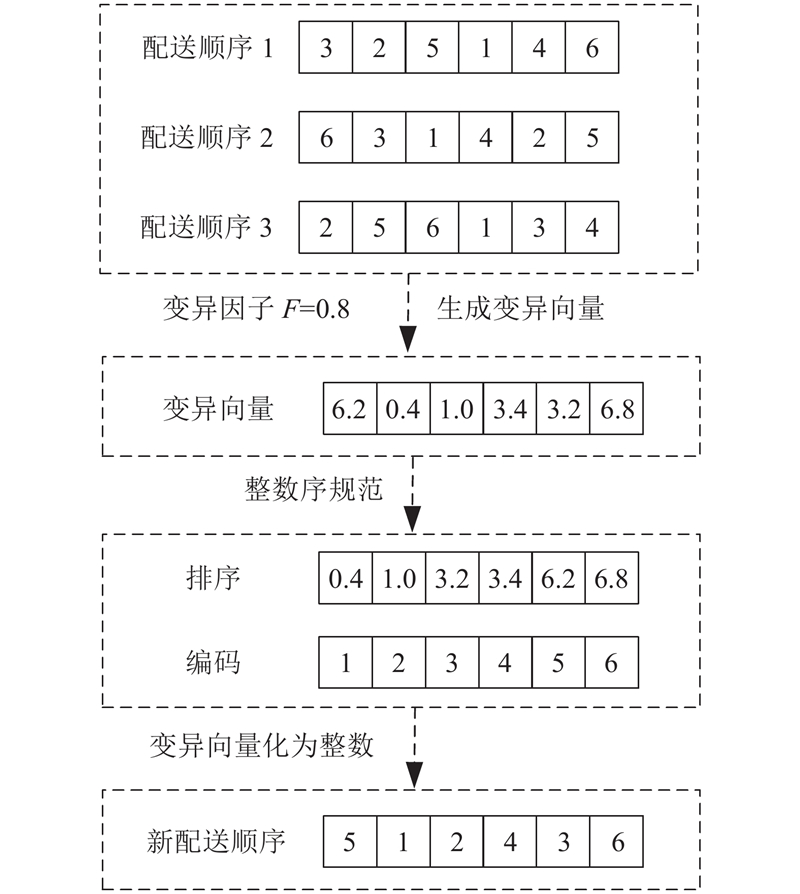
由于本研究的编码为整数编码，须将所得变异向量中的实数全部转化为整数. 因此采用基于整数序规范的方法，将变异向量中的所有实数按照从小到大的顺序排列，最小的实数值编码为1，依此类推直到每个实数都有对应的整数编码. 例如所得变异向量为[6.2, 0.4, 1.0, 3.4, 3.2, 6.8]，按照从小到大的顺序排列为[0.4, 1.0, 3.2, 3.4, 6.2, 6.8]，分别对应工位编号为[1, 2, 3, 4, 5, 6]，则所得变异向量全部转化为整数为序列[5, 1, 2, 4, 3, 6]，变异向量则对应一种新的配送顺序，具体变异过程如图3所示.

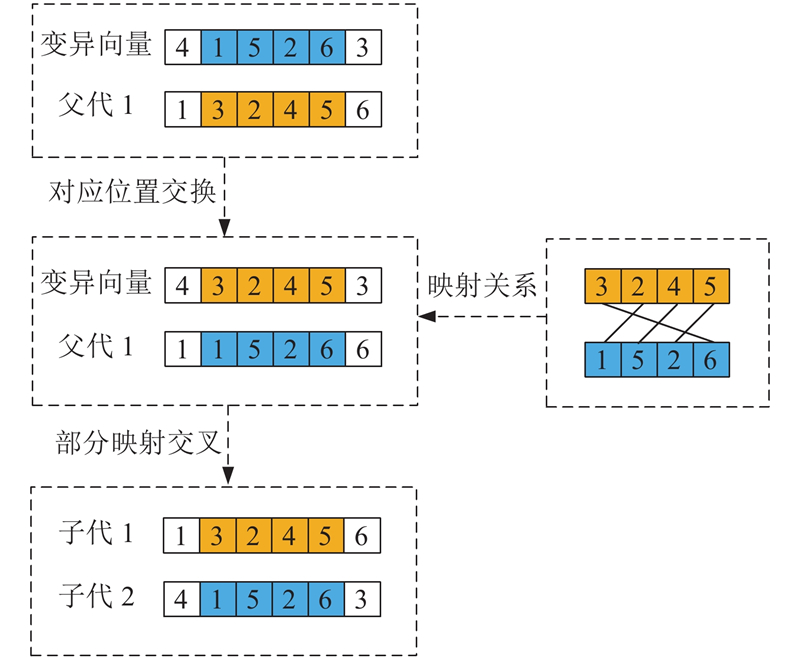
产生一个随机数，若随机数不大于交叉概率CR，则进行交叉. 采用适用于顺序优化问题的部分映射交叉 (partially mapped crossover, PMX) ^[27]. 在变异向量上随机选取起止点作为交叉的起止位置，交换变异向量与父代染色体的对应位置. 根据交换的2组基因建立一个映射关系，保证形成的子代基因无冲突. 为了增加种群多样性，采用错位映射的方式. 例如所得变异向量为[4, 1, 5, 2, 6, 3]，交叉操作后变异向量的冲突基因为4和3. 基于双方基因的错位交叉映射关系修改冲突基因，从而生成2个新子代，即2种新的配送顺序[1, 3, 2, 4, 5, 6]、[4, 1, 5, 2, 6, 3]，交叉过程如图4所示.

1) 初始化种群以及相关参数. 根据2.1节的步骤，采用DPC聚类算法进行种群分组，然后在每个分组内进行初始化，随机生成初始化长度为L的P个染色体. 算法相关参数包括：种群规模NP、迭代次数GEN、变异缩放因子F和交叉概率CR.

2) 根据个体相互之间的支配关系对个体进行非支配排序，划分为不同的非支配等级；得到同一等级中每个个体的拥挤距离，去掉拥挤距离较小的解，提高解集多样性. 若个体$ {P_1} $支配个体$ {P_2} $，则写为$ {P_1} < {P_2} $，支配关系定义如下：

(13)$ {P_1} \leqslant {P_2} ;\; m \in \left\{ {1,\;2,\; \cdots ,\;r} \right\},\;{f_m}({P_1}) < {f_m}({P_2}). $

式中：$ {f_m}({P_1}) $表示个体$ {P_1} $在目标函数$ {f_m} $上的函数值，r为目标函数个数.

支配等级划分须计算个体p的被支配个数以及该个体支配的解的集合，表达式如下：

(14)$ {n_p} = \left| {\left\{ {q \in P\left| {p < q} \right.} \right\}} \right|, $

(15)$ {S_p} = \left\{ {q \in P\left| {q < p} \right.} \right\}. $

式中：$ {n_p} $为个体p的被支配个数，$ {S_p} $为个体p支配的解的集合，q为非p个体，P为包含全部个体的集合. 若$ {n_p} $=0，则将个体p的非支配等级设为1. $ {n_p} $越小，个体p非支配等级越低，个体p越优.

3) 拥挤距离可以用来评估同一级中任一解的相邻解的密集程度，即评估同一级中个体的优劣. 个体的拥挤距离可由同一级相邻个体在各个子目标上的距离差求和得到. 其表达式如下：

(16)$ {\text{dis}}\;[p] = \sum\limits_{m = 1}^r {({\text{dis}}\;[p+1].{f_m} - {\text{dis}}\;[p - 1].{f_m})} . $

式中：$ {\mathrm{dis}}\;[p]$表示个体p的拥挤距离，$ {\mathrm{dis}}[p] \;.\; f_m$表示个体p在目标函数$ f_m$上的函数值.

4) 选择操作. 采用二元锦标赛策略，从种群中随机选择2个个体，将非支配等级较小的个体作为父代，若2个个体拥有相同的非支配等级，则选择拥挤距离较大的个体作为父代.

5) 遗传操作. 按照2.2节的步骤依次进行变异操作和交叉操作，生成子代种群.

6) 合并父代和子代. 合并父代种群和子代种群，对合并后的种群进行非支配排序，再通过精英策略，修剪得到新一代种群.

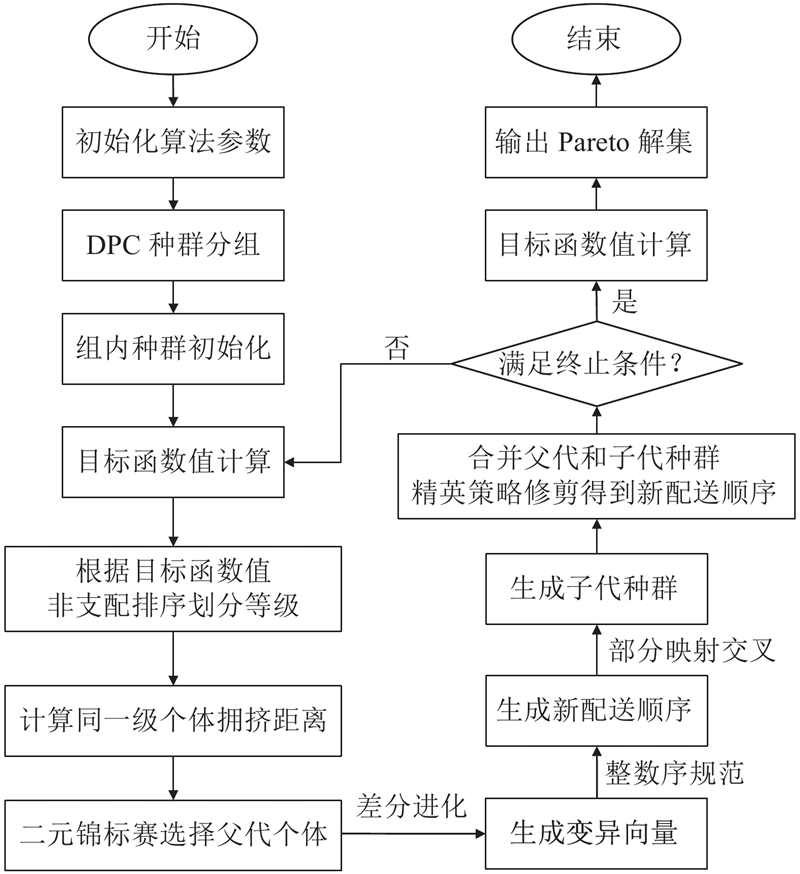
7) 迭代优化. 至此完成一次迭代，判断是否满足迭代终止条件，若满足终止条件则输出Pareto最优解集，否则继续进行迭代, 直到满足算法终止条件. INSGA-Ⅱ算法流程图如图5所示.

算法运行环境为64位Windows 10系统，处理器为Intel(R)Core(TM) i5-7700HQ 2.80 GHz，内存为8 G，编程语言为MATLAB.

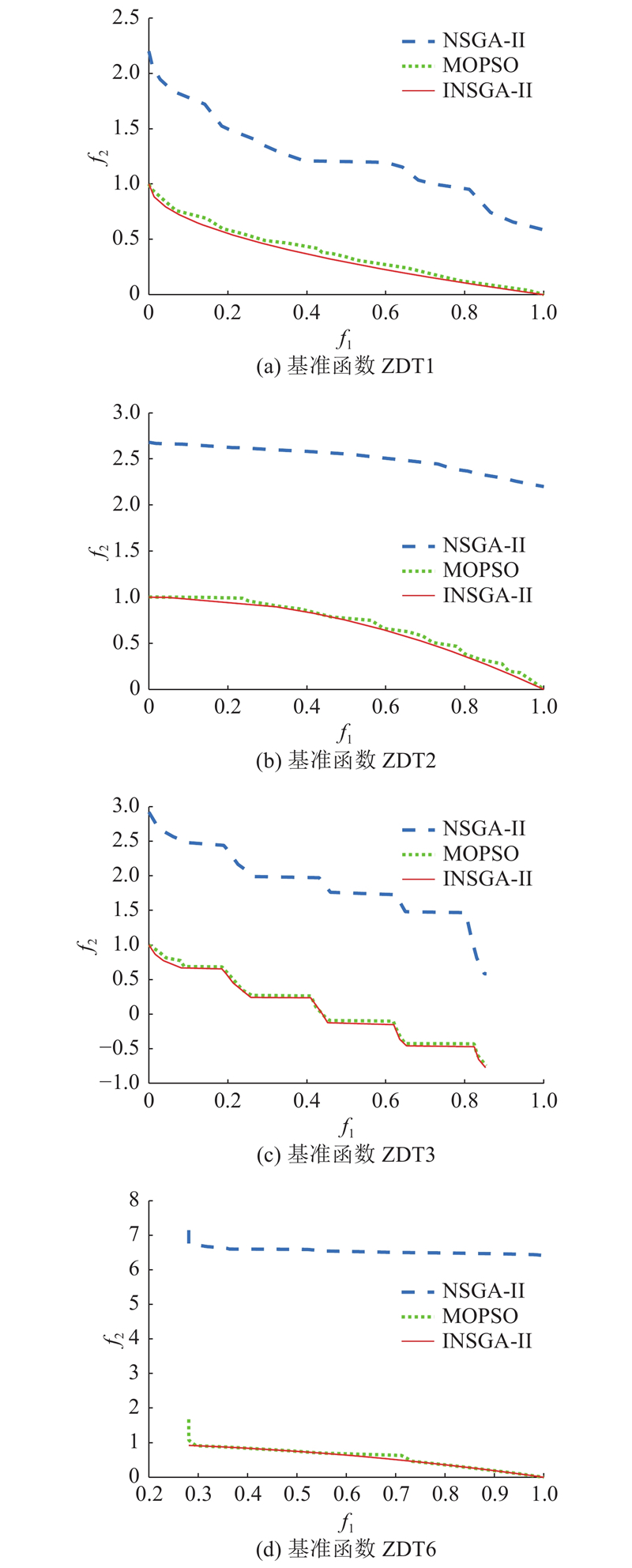
选择不同基准函数ZDT1、ZDT2、ZDT3、ZDT6对算法进行有效性验证. 运用INSGA-Ⅱ对基准函数进行实验，设置种群规模为20、迭代次数为500，并与NSGA-Ⅱ、MOPSO算法进行对比，结果如图6所示.可以看出，在4个基准函数下，INSGA-Ⅱ的2个目标函数的优化结果均优于NSGA-Ⅱ、MOPSO的，且INSGA-Ⅱ的曲线更平滑，符合每个测试函数的理想pareto前沿面.

通过超体积指标(hypervolume，HV)进行算法性能的验证. HV指标是指算法获得的非支配解集与参照点围成的目标空间中区域的体积，在两目标问题中，HV指标计算算法获得的非支配解集与参照点围成的目标空间中区域的面积，HV越大说明算法结果的均匀性和多样性越好. 计算各基准函数下算法结果的HV，如表1所示. 表中，A、B、C分别表示NSGA-Ⅱ、MOPSO、INSGA-Ⅱ结果的HV数值.

从各算法结果的HV可以看出，INSGA-Ⅱ结果均大于NSGA-Ⅱ、MOPSO的，为最优；从增值百分比来看，最低为 0.56%，最高为 32.14%，INSGA-Ⅱ与NSGA-Ⅱ对比的效果更为显著；采用基准函数ZDT1和ZDT3时，INSGA-Ⅱ对比其他算法的效果更佳.

对算法进行求解速度验证，设置种群规模为50、迭代次数为2000，独立运行10次计算平均值，并与NSGA-Ⅱ、MOPSO进行对比，结果如表2所示，表中，t₁~t₄分别为ZDT1、ZDT2、 ZDT3、 ZDT6作为基准函数时的求解时间.

就单次求解时间角度分析，NSGA-Ⅱ最低为10.89 s、MOPSO最低为10.09 s、INSGA-Ⅱ最低为3.40 s；就均值角度分析，NSGA-Ⅱ最低为11.41 s、MOPSO最低为10.87 s、INSGA-Ⅱ最低为3.54 s，差值百分比最低为36.25%，最高为76.45%；就求解时间标准误差角度分析，NSGA-Ⅱ的标准误差范围为(0.15, 1.43)，MOPSO的标准误差范围为(0.17, 0.39)，而INSGA-Ⅱ的标准误差范围为(0.03, 0.18). 综上所述，与NSGA-Ⅱ、MOPSO相比，INSGA-Ⅱ在单次求解时间、时间均值、标准误差和标准误差等方面均为最优.

为了分析算法求解不同规模算例的适应能力，设置不同任务数量分别为25和50. 种群设为20、迭代次数设为1000，算法独立运行10次，计算不同算法结果的差值、减少百分比、均值、标准差和标准误差，结果如表3所示，表中，D、E分别代表NSGA-Ⅱ、INSGA-Ⅱ结果的数值，${Z_1}$、${Z_2}$分别表示总配送行程距离值和总时间窗惩罚值.

INSGA-Ⅱ算法得出的总配送行程距离和总时间窗惩罚均优于NSGA-Ⅱ的. 当任务规模为25时，总配送行程距离的均值减少87.10、减少百分比最高为15.35%、标准差降低30.81%，总时间窗惩罚的均值减少1055.80、减少百分比最高为16.88%、标准差降低37.83%；当任务规模为50时，总配送行程距离均值减少91、减少百分比最高为8.43%、标准差降低23.73%，总时间窗惩罚值均值减少2486、减少百分比最高为11.36%、标准差降低27.29%.

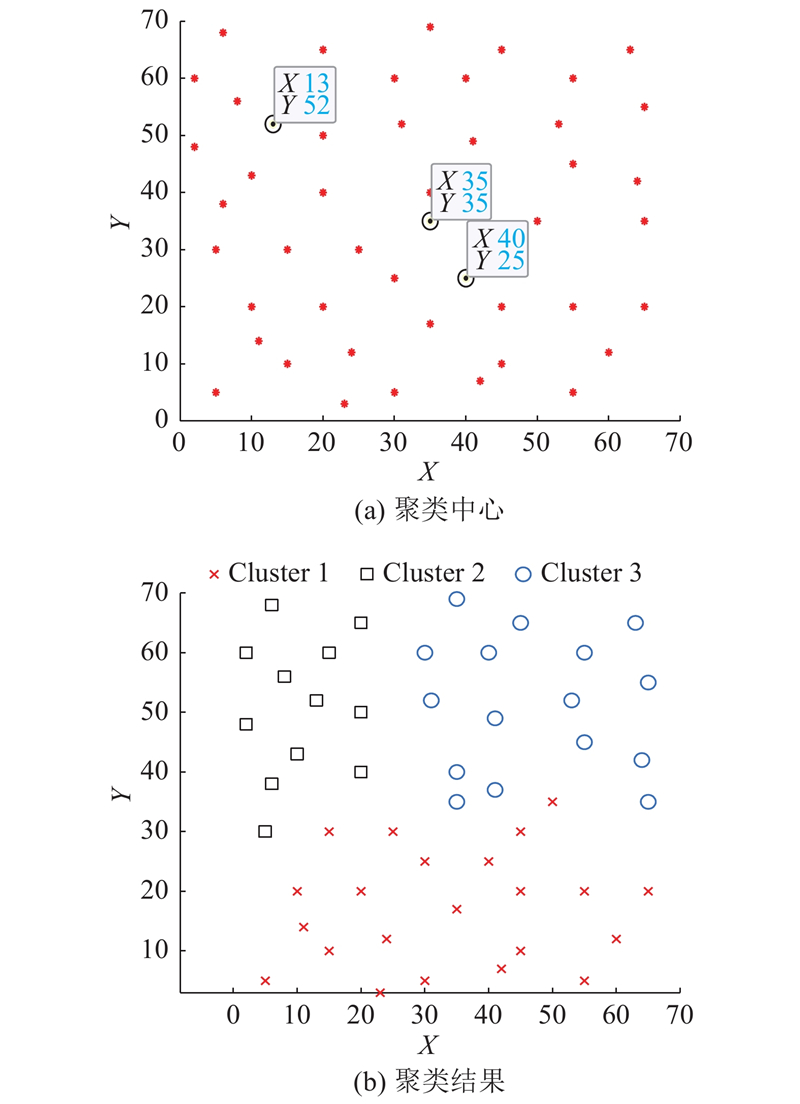
实例数据来源于Solomon测试集R101，聚类中心与聚类结果如图7所示. 3个聚类中心点分别为(40, 25) 、(35, 35) 、(13, 52)，3个聚类中心根据位置相似度将初始种群分为3批.

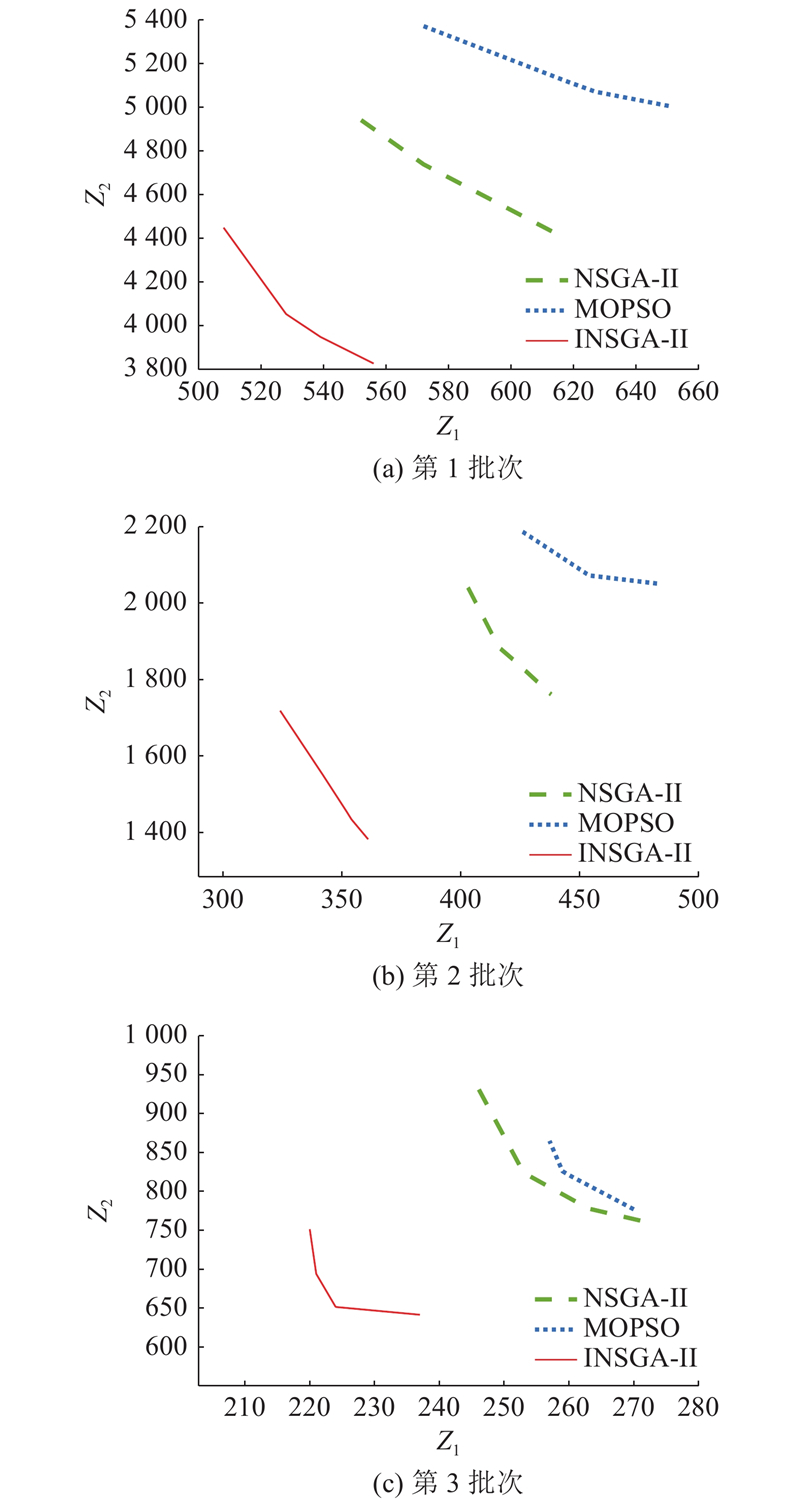
对3个批次物料分别采用NSGA-Ⅱ、MOPSO、INSGA-Ⅱ进行求解，设置种群数为200、迭代次数为1000. 早于时间窗到达的惩罚系数设为0.5，晚于时间窗到达的惩罚系数设为2.0，求解结果如图8所示. 可以看出，INSGA-Ⅱ在3个批次中结果均最优，在求解车间物料配送问题上具有更短的配送路径和更少的时间窗惩罚.

为了避免单次实验结果的误差，将算法独立运行10次，种群数为20、迭代次数为1000，取均值作为对比算法的结果，并计算实验结果的标准差和标准误差，结果如表4所示. 可知，本研究的INSGA-Ⅱ具有更优的解，求得的总行程距离、总时间窗惩罚值均小于其余两算法的，总配送行程距离均值减少范围为11.88% ~26.65%，总时间窗惩罚均值减少范围为20.41%~ 32.5%，标准差与标准误差减少比最高为65.3%，实现了目标函数结果的优化效果.

针对车间物料配送问题，建立以总配送行程距离最短及时间窗惩罚值最小为目标的多目标配送顺序优化数学模型. 针对传统算法计算速度慢的问题，采用DPC算法将大规模问题划分成小规模问题进行求解；同时将DE算法的变异和部分映射交叉操作引入到NSGA-Ⅱ中，通过差分进化操作解决了传统变异操作与原先个体的基因可能存在重合的问题，通过交叉映射的方式增加种群多样性，加快求解速度；最后验证算法的有效性. 结果表明，改进后算法具有更快的求解速度，同时对目标函数的优化效果也更优. 但是，本研究是在不考虑AGV故障和充电情况的假设下展开的，下一步计划考虑故障及充电问题的模型构建以及设计更加高效的求解算法.