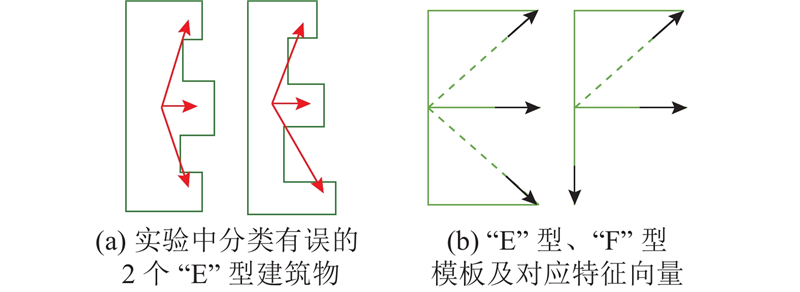
2) 特征向量余弦相似度计算及建筑物类别确定. 将特征向量起点全部移动至原点(0, 0),该操作可以将地图建筑物特征向量同模板库中模板的特征向量置于同一基准. 在此基础上保持模板的特征向量组不动,将建筑物的特征向量组按某一固定角度进行逆时针旋转(本研究采用1度旋转法). 每次旋转后求出建筑物特征向量同模板特征向量的余弦相似度,在旋转一周后,将求得余弦相似度的最大值作为建筑物特征向量同模板特征向量的余弦相似度. 记地图建筑物特征向量组为${\bf{vg}}_1=\left[{\boldsymbol{v}}_1,{\boldsymbol{v}}_2, \cdots,{\boldsymbol{v}}_{{n}} \right] $ ${\boldsymbol{v}}_1,{\boldsymbol{v}}_2, \cdots,{\boldsymbol{v}}_{{n}} $ ${\bf{vg}}_2= \left[{\boldsymbol{v}}'_1,\;{\boldsymbol{v}}'_2,\; \cdots,\right. \left.{\boldsymbol{v}}'_{{n}} \right] $ . 余弦相似度表达式如下:
(2) $ \begin{split} \cos\; \theta=&\dfrac{{\bf{v g}}_1 \cdot {\bf{v g}}_2}{\left\|{\bf{v g}}_1\right\| \times\left\|{\bf{v g}}_2\right\|}=\\& \dfrac{\left[{\boldsymbol{v}}_1, {\boldsymbol{v}}_2, \cdots, {\boldsymbol{v}}_n\right] \cdot\left[{\boldsymbol{v}}_1^{\prime}, {\boldsymbol{v}}_2^{\prime}, \cdots, {\boldsymbol{v}}_n^{\prime}\right]}{\sqrt{\sum_{i=1}^n\left({\boldsymbol{v}}_i\right)^2} \times \sqrt{\sum_{i=1}^n\left({\boldsymbol{v}}_i^{\prime}\right)^2}}.\end{split} $
[2]
晏雄锋, 袁拓, 杨敏, 等 建筑物形状特征分析表达与自适应化简方法
[J]. 测绘学报 , 2022 , 51 (2 ): 269 - 278
DOI:10.11947/j.AGCS.2022.20210302
YAN Xiongfeng, YUAN Tuo, YANG Min, et al An adaptive building simplification approach based on shape analysis and representation
[J]. Acta Geodaetica et Cartographica Sinica , 2022 , 51 (2 ): 269 - 278
DOI:10.11947/j.AGCS.2022.20210302
[3]
刘鹏程, 黄欣, 马宏然, 等 建筑物多边形高精度识别的傅里叶形状描述子神经网络方法
[J]. 测绘学报 , 2022 , 51 (9 ): 1969 - 1976
DOI:10.11947/j.AGCS.2022.20210730
[本文引用: 1]
LIU Pengcheng, HUANG Xin, MA Hongran, et al Fourier descriptor-based neural method for high-precision shape recognition of building polygon
[J]. Acta Geodaetica et Cartographica Sinica , 2022 , 51 (9 ): 1969 - 1976
DOI:10.11947/j.AGCS.2022.20210730
[本文引用: 1]
[4]
RAINSFORD D, MACKANESS W. Template matching in support of generalization of rural buildings [C]// Advances in Spatial Data Handling . Berlin: Springer, 2002: 137−151.
[本文引用: 1]
[5]
WANG Z, LEE D. Building simplification based on pattern recognition and shape analysis [C]∥ Proceedings of the 9th International Symposium on Spatial Data Handling . Beijing: Springer, 2000: 58−72.
[本文引用: 1]
[6]
安晓亚 空间数据几何相似性度量理论方法与应用研究
[J]. 测绘学报 , 2013 , 42 (1 ): 157
[本文引用: 1]
AN Xiaoya Research on theory, methods and applications of geometry similarity measurement for spatial data
[J]. Acta Geodaetica et Cartographica Sinica , 2013 , 42 (1 ): 157
[本文引用: 1]
[7]
刘鹏程. 形状识别在地图综合中的应用研究 [J]. 测绘学报, 2012, 41(2): 1.
[本文引用: 1]
LIU Pengcheng. Applications of shape recognition in map generalization [J]. Acta Geodaetica et Cartographica Sinica , 2021, 41(2): 1.
[本文引用: 1]
[8]
AI T, CHENG X, LIU P, et al A shape analysis and template matching of building features by the Fourier transform method
[J]. Computers, Environment and Urban Systems , 2013 , 41 : 219 - 233
DOI:10.1016/j.compenvurbsys.2013.07.002
[本文引用: 1]
[9]
YAN X, AI T, ZHANG X Template matching and simplification method for building features based on shape cognition
[J]. International Journal of Geo-information , 2017 , 6 (8 ): 1 - 17
[本文引用: 2]
[11]
刘鹏程, 艾廷华, 胡晋山, 等 基于原型模板形状匹配的建筑多边形化简
[J]. 武汉大学学报: 信息科学版 , 2010 , 35 (11 ): 1369 - 1372
[本文引用: 1]
LIU Pengcheng, AI Tinghua, HU Jinshan, et al Building-polygon simplification based on shape matching of prototype template
[J]. Geomatics and Information Science of Wuhan University , 2010 , 35 (11 ): 1369 - 1372
[本文引用: 1]
[12]
晏雄锋, 艾廷华, 杨敏, 等 地图空间形状认知的自编码器深度学习方法
[J]. 测绘学报 , 2021 , 50 (6 ): 757 - 765
DOI:10.11947/j.AGCS.2021.20210046
[本文引用: 1]
YAN Xiongfeng, AI Tinghua, YANG Min, et al Shape cognition in map space using deep auto-encoder learning
[J]. Acta Geodaetica et Cartographica Sinica , 2021 , 50 (6 ): 757 - 765
DOI:10.11947/j.AGCS.2021.20210046
[本文引用: 1]
[13]
杜佳威, 武芳, 行瑞星, 等 几种具有编解码结构的深度学习模型在建筑物综合中的应用与比较
[J]. 武汉大学学报: 信息科学版 , 2022 , 47 (7 ): 1052 - 1062
[本文引用: 1]
DU Jiawei, WU Fang, XING Ruixing, et al Trial and comparison of some encoder decoder based deep learning models for automated generalization of buildings
[J]. Geomatics and Information Science of Wuhan University , 2022 , 47 (7 ): 1052 - 1062
[本文引用: 1]
[14]
马磊. 基于机器学习的建筑物形状化简模型[D]. 兰州: 兰州交通大学, 2018.
[本文引用: 1]
Ma Lei. A simplification model for building shapes based on machine learning [D]. Lanzhou: Lanzhou Jiaotong University, 2018.
[本文引用: 1]
[15]
YAN X, AI T, YANG M, et al Graph convolutional autoencoder model for the shape coding and cognition of buildings in maps
[J]. International Journal of Geographical Information Science , 2021 , 35 (3 ): 490 - 512
DOI:10.1080/13658816.2020.1768260
[本文引用: 3]
[16]
焦洋洋, 刘平芝, 刘爱龙, 等 AlexNet支持下的地图建筑物形状分类方法
[J]. 地球信息科学学报 , 2022 , 24 (12 ): 2333 - 2341
DOI:10.12082/dqxxkx.2022.210396
[本文引用: 1]
JIAO Yangyang, LIU Pingzhi, LIU Ailong, et al Map building shape classification method based on Alexnet
[J]. Journal of Geo-information Science , 2022 , 24 (12 ): 2333 - 2341
DOI:10.12082/dqxxkx.2022.210396
[本文引用: 1]
[17]
于洋洋, 贺康杰, 武芳, 等 面状居民地形状分类的图卷积神经网络方法
[J]. 测绘学报 , 2022 , 51 (11 ): 2390 - 2402
DOI:10.11947/j.AGCS.2022.20210134
[本文引用: 2]
YU Yangyang, HE Kangjie, WU Fang, et al Graph convolution neural network method for shape classification of areal settlements
[J]. Acta Geodaetica et Cartographica Sinica , 2022 , 51 (11 ): 2390 - 2402
DOI:10.11947/j.AGCS.2022.20210134
[本文引用: 2]
[18]
韩晓霞, 崔浩, 孙钰珊 顾及曲线走向及局部面积特征的矢量数据压缩算法
[J]. 北京测绘 , 2017 , (6 ): 6 - 9
[本文引用: 1]
HAN Xiaoxia, CUI Hao, SUN Yushan The algorithm of vector data compression take into consideration of the curve trend and local aera feature
[J]. Beijing Surveying and Mapping , 2017 , (6 ): 6 - 9
[本文引用: 1]
[19]
杜维, 艾廷华, 徐峥 一种组合优化的多边形化简方法
[J]. 武汉大学学报: 信息科学版 , 2004 , (6 ): 548 - 550
[本文引用: 1]
DU Wei, AI Tinghua, XU Zheng A polygon simplification method based on combinatorial optimization
[J]. Geomatics and Information Science of Wuhan University , 2004 , (6 ): 548 - 550
[本文引用: 1]
[21]
顾海燕, 闫利, 李海涛, 等 基于随机森林的地理要素面向对象自动解译方法
[J]. 武汉大学学报: 信息科学版 , 2016 , 41 (2 ): 228 - 234
GU Haiyan, YAN Li, LI Haitao, et al An object-based automatic interpretation method for geographic features based on random forest machine learning
[J]. Geomatics and Information Science of Wuhan University , 2016 , 41 (2 ): 228 - 234
[22]
王猛, 张新长, 王家耀, 等 结合随机森林面向对象的森林资源分类
[J]. 测绘学报 , 2020 , 49 (2 ): 235 - 244
DOI:10.11947/j.AGCS.2020.20190272
[本文引用: 1]
WANG Meng, ZHANG Xinchang, WANG Jiayao, et al Forest resource classification based on random forest and object oriented method
[J]. Acta Geodaetica et Cartographica Sinica , 2020 , 49 (2 ): 235 - 244
DOI:10.11947/j.AGCS.2020.20190272
[本文引用: 1]
[25]
刘鹏程. 形状识别在地图综合中的应用研究[D]. 武汉: 武汉大学, 2009.
[本文引用: 1]
LIU Pengcheng. Applications of shape recognition in map generalization [D]. Wuhan: Wuhan University, 2009.
[本文引用: 1]
[26]
祝国瑞. 地图学[M]. 武汉: 武汉大学出版社, 2003.
[本文引用: 1]
基于形状相似性识别的空间查询
1
2009
... 形状是物体的基本特征之一,是识别物体的有效途径. 地图要素形状的描述和识别是地图空间认知的基本内容[1 -3 ] ,在地图认知、地图制图综合过程及评价、空间要素匹配与查询及城市建设与规划等领域都有重要的应用价值. 地图建筑物形状识别是进行建筑物多边形化简[4 -5 ] 、地图匹配[6 ] 、变化检测等的基础,其形状识别与分类一直是相关领域的研究热点问题[7 ] . ...
基于形状相似性识别的空间查询
1
2009
... 形状是物体的基本特征之一,是识别物体的有效途径. 地图要素形状的描述和识别是地图空间认知的基本内容[1 -3 ] ,在地图认知、地图制图综合过程及评价、空间要素匹配与查询及城市建设与规划等领域都有重要的应用价值. 地图建筑物形状识别是进行建筑物多边形化简[4 -5 ] 、地图匹配[6 ] 、变化检测等的基础,其形状识别与分类一直是相关领域的研究热点问题[7 ] . ...
建筑物形状特征分析表达与自适应化简方法
0
2022
建筑物形状特征分析表达与自适应化简方法
0
2022
建筑物多边形高精度识别的傅里叶形状描述子神经网络方法
1
2022
... 形状是物体的基本特征之一,是识别物体的有效途径. 地图要素形状的描述和识别是地图空间认知的基本内容[1 -3 ] ,在地图认知、地图制图综合过程及评价、空间要素匹配与查询及城市建设与规划等领域都有重要的应用价值. 地图建筑物形状识别是进行建筑物多边形化简[4 -5 ] 、地图匹配[6 ] 、变化检测等的基础,其形状识别与分类一直是相关领域的研究热点问题[7 ] . ...
建筑物多边形高精度识别的傅里叶形状描述子神经网络方法
1
2022
... 形状是物体的基本特征之一,是识别物体的有效途径. 地图要素形状的描述和识别是地图空间认知的基本内容[1 -3 ] ,在地图认知、地图制图综合过程及评价、空间要素匹配与查询及城市建设与规划等领域都有重要的应用价值. 地图建筑物形状识别是进行建筑物多边形化简[4 -5 ] 、地图匹配[6 ] 、变化检测等的基础,其形状识别与分类一直是相关领域的研究热点问题[7 ] . ...
1
... 形状是物体的基本特征之一,是识别物体的有效途径. 地图要素形状的描述和识别是地图空间认知的基本内容[1 -3 ] ,在地图认知、地图制图综合过程及评价、空间要素匹配与查询及城市建设与规划等领域都有重要的应用价值. 地图建筑物形状识别是进行建筑物多边形化简[4 -5 ] 、地图匹配[6 ] 、变化检测等的基础,其形状识别与分类一直是相关领域的研究热点问题[7 ] . ...
1
... 形状是物体的基本特征之一,是识别物体的有效途径. 地图要素形状的描述和识别是地图空间认知的基本内容[1 -3 ] ,在地图认知、地图制图综合过程及评价、空间要素匹配与查询及城市建设与规划等领域都有重要的应用价值. 地图建筑物形状识别是进行建筑物多边形化简[4 -5 ] 、地图匹配[6 ] 、变化检测等的基础,其形状识别与分类一直是相关领域的研究热点问题[7 ] . ...
空间数据几何相似性度量理论方法与应用研究
1
2013
... 形状是物体的基本特征之一,是识别物体的有效途径. 地图要素形状的描述和识别是地图空间认知的基本内容[1 -3 ] ,在地图认知、地图制图综合过程及评价、空间要素匹配与查询及城市建设与规划等领域都有重要的应用价值. 地图建筑物形状识别是进行建筑物多边形化简[4 -5 ] 、地图匹配[6 ] 、变化检测等的基础,其形状识别与分类一直是相关领域的研究热点问题[7 ] . ...
空间数据几何相似性度量理论方法与应用研究
1
2013
... 形状是物体的基本特征之一,是识别物体的有效途径. 地图要素形状的描述和识别是地图空间认知的基本内容[1 -3 ] ,在地图认知、地图制图综合过程及评价、空间要素匹配与查询及城市建设与规划等领域都有重要的应用价值. 地图建筑物形状识别是进行建筑物多边形化简[4 -5 ] 、地图匹配[6 ] 、变化检测等的基础,其形状识别与分类一直是相关领域的研究热点问题[7 ] . ...
1
... 形状是物体的基本特征之一,是识别物体的有效途径. 地图要素形状的描述和识别是地图空间认知的基本内容[1 -3 ] ,在地图认知、地图制图综合过程及评价、空间要素匹配与查询及城市建设与规划等领域都有重要的应用价值. 地图建筑物形状识别是进行建筑物多边形化简[4 -5 ] 、地图匹配[6 ] 、变化检测等的基础,其形状识别与分类一直是相关领域的研究热点问题[7 ] . ...
1
... 形状是物体的基本特征之一,是识别物体的有效途径. 地图要素形状的描述和识别是地图空间认知的基本内容[1 -3 ] ,在地图认知、地图制图综合过程及评价、空间要素匹配与查询及城市建设与规划等领域都有重要的应用价值. 地图建筑物形状识别是进行建筑物多边形化简[4 -5 ] 、地图匹配[6 ] 、变化检测等的基础,其形状识别与分类一直是相关领域的研究热点问题[7 ] . ...
A shape analysis and template matching of building features by the Fourier transform method
1
2013
... 建筑物多为人造要素,表示在地图上通常呈现几种特定的模式. 因此,常用的建筑物形状分类多采用模板匹配方法,如Ai等[8 ] 基于傅里叶变换实现了建筑物形状分析及其形状相似度计算;Yan等[9 ] 采用傅里叶变换计算建筑物和模板的相似度完成模板匹配;晏雄峰等[10 ] 采用转角函数描述建筑物形状,实现建筑物和模板库的匹配;刘鹏程等[11 ] 采用形状数来描述建筑物形状,实现建筑物和模板的匹配. 但传统模板匹配方法存在如下问题:匹配过程中主要通过将建筑物轮廓与模板进行比较,易受到局部特征干扰,通常只在识别直角边较多的建筑物时可以发挥较好效果,对于形状不规则的建筑物识别效果欠佳,导致总体识别精度有限. ...
Template matching and simplification method for building features based on shape cognition
2
2017
... 建筑物多为人造要素,表示在地图上通常呈现几种特定的模式. 因此,常用的建筑物形状分类多采用模板匹配方法,如Ai等[8 ] 基于傅里叶变换实现了建筑物形状分析及其形状相似度计算;Yan等[9 ] 采用傅里叶变换计算建筑物和模板的相似度完成模板匹配;晏雄峰等[10 ] 采用转角函数描述建筑物形状,实现建筑物和模板库的匹配;刘鹏程等[11 ] 采用形状数来描述建筑物形状,实现建筑物和模板的匹配. 但传统模板匹配方法存在如下问题:匹配过程中主要通过将建筑物轮廓与模板进行比较,易受到局部特征干扰,通常只在识别直角边较多的建筑物时可以发挥较好效果,对于形状不规则的建筑物识别效果欠佳,导致总体识别精度有限. ...
... 同时,将本研究方法与文献[9 ]中提到的基于转角函数的方法进行对比,实验依然采用上述的4540 个建筑物数据,实验对比结果如图15 所示. 图中,A 为识别正确率. ...
居民地要素化简的形状识别与模板匹配方法
1
2016
... 建筑物多为人造要素,表示在地图上通常呈现几种特定的模式. 因此,常用的建筑物形状分类多采用模板匹配方法,如Ai等[8 ] 基于傅里叶变换实现了建筑物形状分析及其形状相似度计算;Yan等[9 ] 采用傅里叶变换计算建筑物和模板的相似度完成模板匹配;晏雄峰等[10 ] 采用转角函数描述建筑物形状,实现建筑物和模板库的匹配;刘鹏程等[11 ] 采用形状数来描述建筑物形状,实现建筑物和模板的匹配. 但传统模板匹配方法存在如下问题:匹配过程中主要通过将建筑物轮廓与模板进行比较,易受到局部特征干扰,通常只在识别直角边较多的建筑物时可以发挥较好效果,对于形状不规则的建筑物识别效果欠佳,导致总体识别精度有限. ...
居民地要素化简的形状识别与模板匹配方法
1
2016
... 建筑物多为人造要素,表示在地图上通常呈现几种特定的模式. 因此,常用的建筑物形状分类多采用模板匹配方法,如Ai等[8 ] 基于傅里叶变换实现了建筑物形状分析及其形状相似度计算;Yan等[9 ] 采用傅里叶变换计算建筑物和模板的相似度完成模板匹配;晏雄峰等[10 ] 采用转角函数描述建筑物形状,实现建筑物和模板库的匹配;刘鹏程等[11 ] 采用形状数来描述建筑物形状,实现建筑物和模板的匹配. 但传统模板匹配方法存在如下问题:匹配过程中主要通过将建筑物轮廓与模板进行比较,易受到局部特征干扰,通常只在识别直角边较多的建筑物时可以发挥较好效果,对于形状不规则的建筑物识别效果欠佳,导致总体识别精度有限. ...
基于原型模板形状匹配的建筑多边形化简
1
2010
... 建筑物多为人造要素,表示在地图上通常呈现几种特定的模式. 因此,常用的建筑物形状分类多采用模板匹配方法,如Ai等[8 ] 基于傅里叶变换实现了建筑物形状分析及其形状相似度计算;Yan等[9 ] 采用傅里叶变换计算建筑物和模板的相似度完成模板匹配;晏雄峰等[10 ] 采用转角函数描述建筑物形状,实现建筑物和模板库的匹配;刘鹏程等[11 ] 采用形状数来描述建筑物形状,实现建筑物和模板的匹配. 但传统模板匹配方法存在如下问题:匹配过程中主要通过将建筑物轮廓与模板进行比较,易受到局部特征干扰,通常只在识别直角边较多的建筑物时可以发挥较好效果,对于形状不规则的建筑物识别效果欠佳,导致总体识别精度有限. ...
基于原型模板形状匹配的建筑多边形化简
1
2010
... 建筑物多为人造要素,表示在地图上通常呈现几种特定的模式. 因此,常用的建筑物形状分类多采用模板匹配方法,如Ai等[8 ] 基于傅里叶变换实现了建筑物形状分析及其形状相似度计算;Yan等[9 ] 采用傅里叶变换计算建筑物和模板的相似度完成模板匹配;晏雄峰等[10 ] 采用转角函数描述建筑物形状,实现建筑物和模板库的匹配;刘鹏程等[11 ] 采用形状数来描述建筑物形状,实现建筑物和模板的匹配. 但传统模板匹配方法存在如下问题:匹配过程中主要通过将建筑物轮廓与模板进行比较,易受到局部特征干扰,通常只在识别直角边较多的建筑物时可以发挥较好效果,对于形状不规则的建筑物识别效果欠佳,导致总体识别精度有限. ...
地图空间形状认知的自编码器深度学习方法
1
2021
... 近年来,机器学习及深度学习逐步渗透到地图要素形状识别领域,晏雄峰等[12 ] 提取地图建筑物形状边界的描述特征,通过自编码学习模型对地图建筑物形状进行认知;杜佳威等[13 ] 将地图建筑物综合过程抽象为编码解码过程,并分析对比多种深度学习模型在地图建筑物综合中的应用效果;马磊[14 ] 利用卷积自编码器对建筑物进行编码,并采用模板匹配方法实现建筑物的简化;Yan等[15 ] 将图卷积自编码器引入建筑物形状编码与认知,实现了建筑物形状识别与分类;焦洋洋等[16 ] 提出AlexNet支持下的地图建筑物形状分类方法,将矢量地图中的地图建筑物形状分类问题转化为地图建筑物栅格图像分类问题;于洋洋等[17 ] 借助图卷积神经网络的图数据分类能力,提出基于图卷积神经网络的面状居民地形状分类方法. 这些方法在大量训练样本情况下可以实现比较准确的建筑物形状识别与分类,但对于样本较少的类别,会出现无法准确分类的现象. 同时此类方法的分类结果往往具有不可解释性. ...
地图空间形状认知的自编码器深度学习方法
1
2021
... 近年来,机器学习及深度学习逐步渗透到地图要素形状识别领域,晏雄峰等[12 ] 提取地图建筑物形状边界的描述特征,通过自编码学习模型对地图建筑物形状进行认知;杜佳威等[13 ] 将地图建筑物综合过程抽象为编码解码过程,并分析对比多种深度学习模型在地图建筑物综合中的应用效果;马磊[14 ] 利用卷积自编码器对建筑物进行编码,并采用模板匹配方法实现建筑物的简化;Yan等[15 ] 将图卷积自编码器引入建筑物形状编码与认知,实现了建筑物形状识别与分类;焦洋洋等[16 ] 提出AlexNet支持下的地图建筑物形状分类方法,将矢量地图中的地图建筑物形状分类问题转化为地图建筑物栅格图像分类问题;于洋洋等[17 ] 借助图卷积神经网络的图数据分类能力,提出基于图卷积神经网络的面状居民地形状分类方法. 这些方法在大量训练样本情况下可以实现比较准确的建筑物形状识别与分类,但对于样本较少的类别,会出现无法准确分类的现象. 同时此类方法的分类结果往往具有不可解释性. ...
几种具有编解码结构的深度学习模型在建筑物综合中的应用与比较
1
2022
... 近年来,机器学习及深度学习逐步渗透到地图要素形状识别领域,晏雄峰等[12 ] 提取地图建筑物形状边界的描述特征,通过自编码学习模型对地图建筑物形状进行认知;杜佳威等[13 ] 将地图建筑物综合过程抽象为编码解码过程,并分析对比多种深度学习模型在地图建筑物综合中的应用效果;马磊[14 ] 利用卷积自编码器对建筑物进行编码,并采用模板匹配方法实现建筑物的简化;Yan等[15 ] 将图卷积自编码器引入建筑物形状编码与认知,实现了建筑物形状识别与分类;焦洋洋等[16 ] 提出AlexNet支持下的地图建筑物形状分类方法,将矢量地图中的地图建筑物形状分类问题转化为地图建筑物栅格图像分类问题;于洋洋等[17 ] 借助图卷积神经网络的图数据分类能力,提出基于图卷积神经网络的面状居民地形状分类方法. 这些方法在大量训练样本情况下可以实现比较准确的建筑物形状识别与分类,但对于样本较少的类别,会出现无法准确分类的现象. 同时此类方法的分类结果往往具有不可解释性. ...
几种具有编解码结构的深度学习模型在建筑物综合中的应用与比较
1
2022
... 近年来,机器学习及深度学习逐步渗透到地图要素形状识别领域,晏雄峰等[12 ] 提取地图建筑物形状边界的描述特征,通过自编码学习模型对地图建筑物形状进行认知;杜佳威等[13 ] 将地图建筑物综合过程抽象为编码解码过程,并分析对比多种深度学习模型在地图建筑物综合中的应用效果;马磊[14 ] 利用卷积自编码器对建筑物进行编码,并采用模板匹配方法实现建筑物的简化;Yan等[15 ] 将图卷积自编码器引入建筑物形状编码与认知,实现了建筑物形状识别与分类;焦洋洋等[16 ] 提出AlexNet支持下的地图建筑物形状分类方法,将矢量地图中的地图建筑物形状分类问题转化为地图建筑物栅格图像分类问题;于洋洋等[17 ] 借助图卷积神经网络的图数据分类能力,提出基于图卷积神经网络的面状居民地形状分类方法. 这些方法在大量训练样本情况下可以实现比较准确的建筑物形状识别与分类,但对于样本较少的类别,会出现无法准确分类的现象. 同时此类方法的分类结果往往具有不可解释性. ...
1
... 近年来,机器学习及深度学习逐步渗透到地图要素形状识别领域,晏雄峰等[12 ] 提取地图建筑物形状边界的描述特征,通过自编码学习模型对地图建筑物形状进行认知;杜佳威等[13 ] 将地图建筑物综合过程抽象为编码解码过程,并分析对比多种深度学习模型在地图建筑物综合中的应用效果;马磊[14 ] 利用卷积自编码器对建筑物进行编码,并采用模板匹配方法实现建筑物的简化;Yan等[15 ] 将图卷积自编码器引入建筑物形状编码与认知,实现了建筑物形状识别与分类;焦洋洋等[16 ] 提出AlexNet支持下的地图建筑物形状分类方法,将矢量地图中的地图建筑物形状分类问题转化为地图建筑物栅格图像分类问题;于洋洋等[17 ] 借助图卷积神经网络的图数据分类能力,提出基于图卷积神经网络的面状居民地形状分类方法. 这些方法在大量训练样本情况下可以实现比较准确的建筑物形状识别与分类,但对于样本较少的类别,会出现无法准确分类的现象. 同时此类方法的分类结果往往具有不可解释性. ...
1
... 近年来,机器学习及深度学习逐步渗透到地图要素形状识别领域,晏雄峰等[12 ] 提取地图建筑物形状边界的描述特征,通过自编码学习模型对地图建筑物形状进行认知;杜佳威等[13 ] 将地图建筑物综合过程抽象为编码解码过程,并分析对比多种深度学习模型在地图建筑物综合中的应用效果;马磊[14 ] 利用卷积自编码器对建筑物进行编码,并采用模板匹配方法实现建筑物的简化;Yan等[15 ] 将图卷积自编码器引入建筑物形状编码与认知,实现了建筑物形状识别与分类;焦洋洋等[16 ] 提出AlexNet支持下的地图建筑物形状分类方法,将矢量地图中的地图建筑物形状分类问题转化为地图建筑物栅格图像分类问题;于洋洋等[17 ] 借助图卷积神经网络的图数据分类能力,提出基于图卷积神经网络的面状居民地形状分类方法. 这些方法在大量训练样本情况下可以实现比较准确的建筑物形状识别与分类,但对于样本较少的类别,会出现无法准确分类的现象. 同时此类方法的分类结果往往具有不可解释性. ...
Graph convolutional autoencoder model for the shape coding and cognition of buildings in maps
3
2021
... 近年来,机器学习及深度学习逐步渗透到地图要素形状识别领域,晏雄峰等[12 ] 提取地图建筑物形状边界的描述特征,通过自编码学习模型对地图建筑物形状进行认知;杜佳威等[13 ] 将地图建筑物综合过程抽象为编码解码过程,并分析对比多种深度学习模型在地图建筑物综合中的应用效果;马磊[14 ] 利用卷积自编码器对建筑物进行编码,并采用模板匹配方法实现建筑物的简化;Yan等[15 ] 将图卷积自编码器引入建筑物形状编码与认知,实现了建筑物形状识别与分类;焦洋洋等[16 ] 提出AlexNet支持下的地图建筑物形状分类方法,将矢量地图中的地图建筑物形状分类问题转化为地图建筑物栅格图像分类问题;于洋洋等[17 ] 借助图卷积神经网络的图数据分类能力,提出基于图卷积神经网络的面状居民地形状分类方法. 这些方法在大量训练样本情况下可以实现比较准确的建筑物形状识别与分类,但对于样本较少的类别,会出现无法准确分类的现象. 同时此类方法的分类结果往往具有不可解释性. ...
... 本次实验的数据源选取自文献[15 ]中开源的建筑物样本数据以及兰州市的OSM数据,共计4540 个建筑物数据,包括开源数据中的H型、Z型、矩形、T型、C型、L型、F型、E型、Y型建筑物数据各500个,兰州市OSM数据中的π型和十字型建筑物数据各20个,部分实验数据如图9 所示. ...
... 随着深度学习及其相关技术的快速发展,已有文献已经将深度学习引入建筑物模式识别领域,例如,Yan等[15 -17 ] 利用图卷积神经网络较好地实现了建筑物模式识别与形状分类. 但是,截止目前,传统方法相比较深度学习,仍然具有对数据量要求较低且可解释性较强的优势. 进一步的研究重点在于如何将传统方法中涉及到的视觉认知和知识经验人类智能与人工智能相耦合,实现优势互补,构建以知识为引导、数据为驱动的更加全面、智能、可解释且符合人类认知的形状分类模型. ...
AlexNet支持下的地图建筑物形状分类方法
1
2022
... 近年来,机器学习及深度学习逐步渗透到地图要素形状识别领域,晏雄峰等[12 ] 提取地图建筑物形状边界的描述特征,通过自编码学习模型对地图建筑物形状进行认知;杜佳威等[13 ] 将地图建筑物综合过程抽象为编码解码过程,并分析对比多种深度学习模型在地图建筑物综合中的应用效果;马磊[14 ] 利用卷积自编码器对建筑物进行编码,并采用模板匹配方法实现建筑物的简化;Yan等[15 ] 将图卷积自编码器引入建筑物形状编码与认知,实现了建筑物形状识别与分类;焦洋洋等[16 ] 提出AlexNet支持下的地图建筑物形状分类方法,将矢量地图中的地图建筑物形状分类问题转化为地图建筑物栅格图像分类问题;于洋洋等[17 ] 借助图卷积神经网络的图数据分类能力,提出基于图卷积神经网络的面状居民地形状分类方法. 这些方法在大量训练样本情况下可以实现比较准确的建筑物形状识别与分类,但对于样本较少的类别,会出现无法准确分类的现象. 同时此类方法的分类结果往往具有不可解释性. ...
AlexNet支持下的地图建筑物形状分类方法
1
2022
... 近年来,机器学习及深度学习逐步渗透到地图要素形状识别领域,晏雄峰等[12 ] 提取地图建筑物形状边界的描述特征,通过自编码学习模型对地图建筑物形状进行认知;杜佳威等[13 ] 将地图建筑物综合过程抽象为编码解码过程,并分析对比多种深度学习模型在地图建筑物综合中的应用效果;马磊[14 ] 利用卷积自编码器对建筑物进行编码,并采用模板匹配方法实现建筑物的简化;Yan等[15 ] 将图卷积自编码器引入建筑物形状编码与认知,实现了建筑物形状识别与分类;焦洋洋等[16 ] 提出AlexNet支持下的地图建筑物形状分类方法,将矢量地图中的地图建筑物形状分类问题转化为地图建筑物栅格图像分类问题;于洋洋等[17 ] 借助图卷积神经网络的图数据分类能力,提出基于图卷积神经网络的面状居民地形状分类方法. 这些方法在大量训练样本情况下可以实现比较准确的建筑物形状识别与分类,但对于样本较少的类别,会出现无法准确分类的现象. 同时此类方法的分类结果往往具有不可解释性. ...
面状居民地形状分类的图卷积神经网络方法
2
2022
... 近年来,机器学习及深度学习逐步渗透到地图要素形状识别领域,晏雄峰等[12 ] 提取地图建筑物形状边界的描述特征,通过自编码学习模型对地图建筑物形状进行认知;杜佳威等[13 ] 将地图建筑物综合过程抽象为编码解码过程,并分析对比多种深度学习模型在地图建筑物综合中的应用效果;马磊[14 ] 利用卷积自编码器对建筑物进行编码,并采用模板匹配方法实现建筑物的简化;Yan等[15 ] 将图卷积自编码器引入建筑物形状编码与认知,实现了建筑物形状识别与分类;焦洋洋等[16 ] 提出AlexNet支持下的地图建筑物形状分类方法,将矢量地图中的地图建筑物形状分类问题转化为地图建筑物栅格图像分类问题;于洋洋等[17 ] 借助图卷积神经网络的图数据分类能力,提出基于图卷积神经网络的面状居民地形状分类方法. 这些方法在大量训练样本情况下可以实现比较准确的建筑物形状识别与分类,但对于样本较少的类别,会出现无法准确分类的现象. 同时此类方法的分类结果往往具有不可解释性. ...
... 随着深度学习及其相关技术的快速发展,已有文献已经将深度学习引入建筑物模式识别领域,例如,Yan等[15 -17 ] 利用图卷积神经网络较好地实现了建筑物模式识别与形状分类. 但是,截止目前,传统方法相比较深度学习,仍然具有对数据量要求较低且可解释性较强的优势. 进一步的研究重点在于如何将传统方法中涉及到的视觉认知和知识经验人类智能与人工智能相耦合,实现优势互补,构建以知识为引导、数据为驱动的更加全面、智能、可解释且符合人类认知的形状分类模型. ...
面状居民地形状分类的图卷积神经网络方法
2
2022
... 近年来,机器学习及深度学习逐步渗透到地图要素形状识别领域,晏雄峰等[12 ] 提取地图建筑物形状边界的描述特征,通过自编码学习模型对地图建筑物形状进行认知;杜佳威等[13 ] 将地图建筑物综合过程抽象为编码解码过程,并分析对比多种深度学习模型在地图建筑物综合中的应用效果;马磊[14 ] 利用卷积自编码器对建筑物进行编码,并采用模板匹配方法实现建筑物的简化;Yan等[15 ] 将图卷积自编码器引入建筑物形状编码与认知,实现了建筑物形状识别与分类;焦洋洋等[16 ] 提出AlexNet支持下的地图建筑物形状分类方法,将矢量地图中的地图建筑物形状分类问题转化为地图建筑物栅格图像分类问题;于洋洋等[17 ] 借助图卷积神经网络的图数据分类能力,提出基于图卷积神经网络的面状居民地形状分类方法. 这些方法在大量训练样本情况下可以实现比较准确的建筑物形状识别与分类,但对于样本较少的类别,会出现无法准确分类的现象. 同时此类方法的分类结果往往具有不可解释性. ...
... 随着深度学习及其相关技术的快速发展,已有文献已经将深度学习引入建筑物模式识别领域,例如,Yan等[15 -17 ] 利用图卷积神经网络较好地实现了建筑物模式识别与形状分类. 但是,截止目前,传统方法相比较深度学习,仍然具有对数据量要求较低且可解释性较强的优势. 进一步的研究重点在于如何将传统方法中涉及到的视觉认知和知识经验人类智能与人工智能相耦合,实现优势互补,构建以知识为引导、数据为驱动的更加全面、智能、可解释且符合人类认知的形状分类模型. ...
顾及曲线走向及局部面积特征的矢量数据压缩算法
1
2017
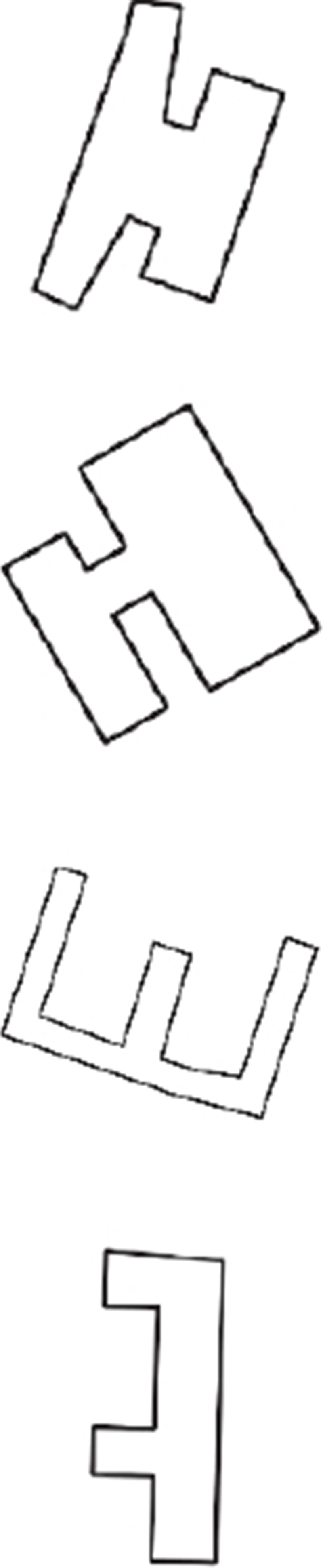
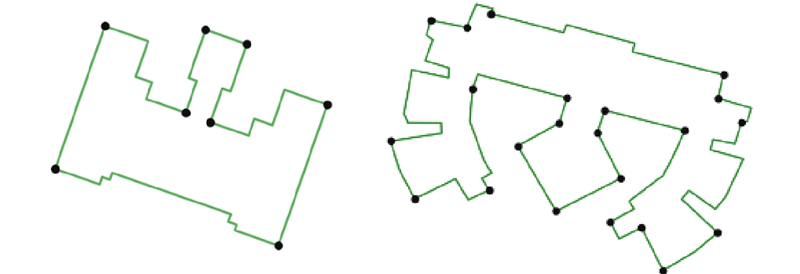
... 地图建筑物中用于概括曲线基本形状的点被称为特征点[18 ] . 如图1 所示,这些特征点能够捕捉到地图建筑物的关键形状特征,从而使人们更容易理解地图建筑物的整体形状和结构[19 ] ,它不仅是构建地图建筑物最小二乘模板的必要数据,还具有突出地图建筑物主要形状特征、降低数据处理和存储复杂性等功能. ...
顾及曲线走向及局部面积特征的矢量数据压缩算法
1
2017
... 地图建筑物中用于概括曲线基本形状的点被称为特征点[18 ] . 如图1 所示,这些特征点能够捕捉到地图建筑物的关键形状特征,从而使人们更容易理解地图建筑物的整体形状和结构[19 ] ,它不仅是构建地图建筑物最小二乘模板的必要数据,还具有突出地图建筑物主要形状特征、降低数据处理和存储复杂性等功能. ...
一种组合优化的多边形化简方法
1
2004
... 地图建筑物中用于概括曲线基本形状的点被称为特征点[18 ] . 如图1 所示,这些特征点能够捕捉到地图建筑物的关键形状特征,从而使人们更容易理解地图建筑物的整体形状和结构[19 ] ,它不仅是构建地图建筑物最小二乘模板的必要数据,还具有突出地图建筑物主要形状特征、降低数据处理和存储复杂性等功能. ...
一种组合优化的多边形化简方法
1
2004
... 地图建筑物中用于概括曲线基本形状的点被称为特征点[18 ] . 如图1 所示,这些特征点能够捕捉到地图建筑物的关键形状特征,从而使人们更容易理解地图建筑物的整体形状和结构[19 ] ,它不仅是构建地图建筑物最小二乘模板的必要数据,还具有突出地图建筑物主要形状特征、降低数据处理和存储复杂性等功能. ...
Random forest
1
2001
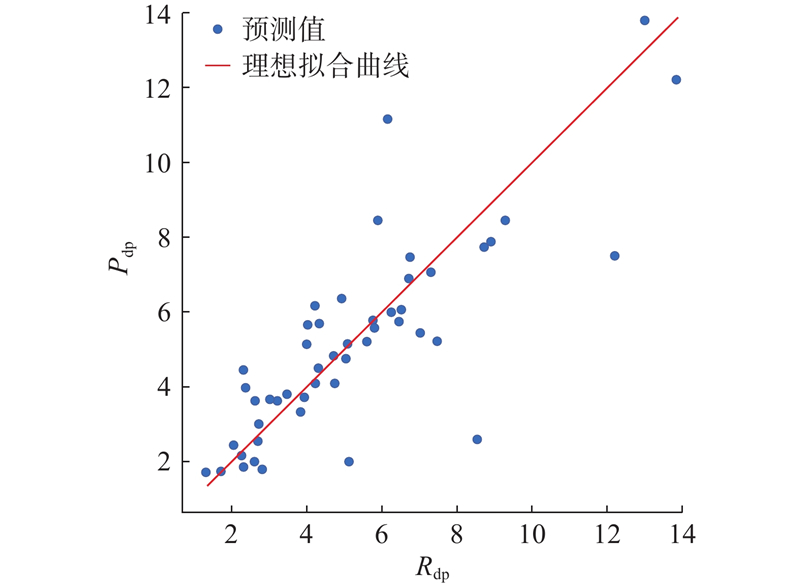
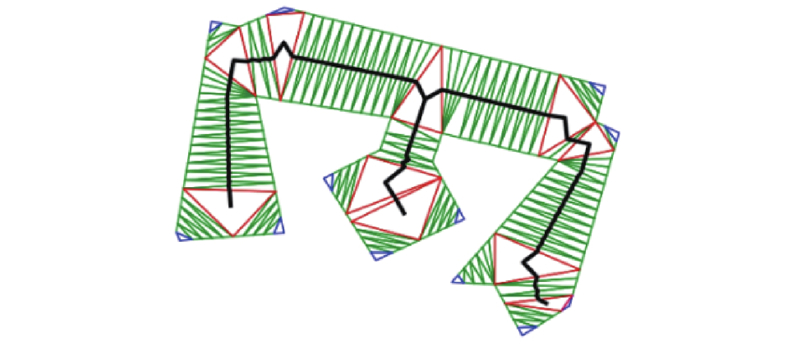
... 在基于道格拉斯-普克算法提取建筑物特征点时,恰当的阈值设置直接决定了特征点选取以及最小二乘模板构建的合理性. 随机森林(random forest,RF)是由数据驱动的非参数分类方法,无须预先设定函数形式,通过给定样本进行学习训练,形成分类规则,无需分类的先验知识. 其具有分析复杂地理信息系统分类特征的能力,对于噪声数据具有较好的鲁棒性,具有较快的学习速度,相比同类算法具有较高的准确性[20 -22 ] ,近年来,RF已被成功应用到滑坡制图、变化检测、地表覆盖分类等领域. 为了得到更加客观合理的阈值,本研究将RF引入道格拉斯-普克算法,以期为最小二乘模板构建提供更好的支持. 首先,选择不同类别、不同大小、不同化简复杂度的典型代表性建筑物194个;其次,分别计算平均边长、边长中位数、最大边长、最小边长、边数量5类特征,利用Python对样本数据进行随机森林建模. 其中最小叶子数设为1,决策树数目设为100,训练集占总数据75%,测试集占25%. 如图2 所示给出了随机森林方法预测DP算法阈值与实际阈值的关系散点图. 图中,R dp 为实际DP阈值, P dp 为预测DP阈值. 图中样本大部分聚集于1∶1线周围,有较高拟合度,均方误差(mean squared error)为2.37,决定系数(R-squared)为0.67. 须说明的是,对于一个建筑物特征点提取而言,道格拉斯-普克算法的最佳阈值通常是一个区间,而不是一个准确的数值,计算发现95.83%的预测值被包含在道格拉斯-普克算法阈值区间内,可以较为准确地提取建筑物特征点. ...
基于随机森林的地理要素面向对象自动解译方法
0
2016
基于随机森林的地理要素面向对象自动解译方法
0
2016
结合随机森林面向对象的森林资源分类
1
2020
... 在基于道格拉斯-普克算法提取建筑物特征点时,恰当的阈值设置直接决定了特征点选取以及最小二乘模板构建的合理性. 随机森林(random forest,RF)是由数据驱动的非参数分类方法,无须预先设定函数形式,通过给定样本进行学习训练,形成分类规则,无需分类的先验知识. 其具有分析复杂地理信息系统分类特征的能力,对于噪声数据具有较好的鲁棒性,具有较快的学习速度,相比同类算法具有较高的准确性[20 -22 ] ,近年来,RF已被成功应用到滑坡制图、变化检测、地表覆盖分类等领域. 为了得到更加客观合理的阈值,本研究将RF引入道格拉斯-普克算法,以期为最小二乘模板构建提供更好的支持. 首先,选择不同类别、不同大小、不同化简复杂度的典型代表性建筑物194个;其次,分别计算平均边长、边长中位数、最大边长、最小边长、边数量5类特征,利用Python对样本数据进行随机森林建模. 其中最小叶子数设为1,决策树数目设为100,训练集占总数据75%,测试集占25%. 如图2 所示给出了随机森林方法预测DP算法阈值与实际阈值的关系散点图. 图中,R dp 为实际DP阈值, P dp 为预测DP阈值. 图中样本大部分聚集于1∶1线周围,有较高拟合度,均方误差(mean squared error)为2.37,决定系数(R-squared)为0.67. 须说明的是,对于一个建筑物特征点提取而言,道格拉斯-普克算法的最佳阈值通常是一个区间,而不是一个准确的数值,计算发现95.83%的预测值被包含在道格拉斯-普克算法阈值区间内,可以较为准确地提取建筑物特征点. ...
结合随机森林面向对象的森林资源分类
1
2020
... 在基于道格拉斯-普克算法提取建筑物特征点时,恰当的阈值设置直接决定了特征点选取以及最小二乘模板构建的合理性. 随机森林(random forest,RF)是由数据驱动的非参数分类方法,无须预先设定函数形式,通过给定样本进行学习训练,形成分类规则,无需分类的先验知识. 其具有分析复杂地理信息系统分类特征的能力,对于噪声数据具有较好的鲁棒性,具有较快的学习速度,相比同类算法具有较高的准确性[20 -22 ] ,近年来,RF已被成功应用到滑坡制图、变化检测、地表覆盖分类等领域. 为了得到更加客观合理的阈值,本研究将RF引入道格拉斯-普克算法,以期为最小二乘模板构建提供更好的支持. 首先,选择不同类别、不同大小、不同化简复杂度的典型代表性建筑物194个;其次,分别计算平均边长、边长中位数、最大边长、最小边长、边数量5类特征,利用Python对样本数据进行随机森林建模. 其中最小叶子数设为1,决策树数目设为100,训练集占总数据75%,测试集占25%. 如图2 所示给出了随机森林方法预测DP算法阈值与实际阈值的关系散点图. 图中,R dp 为实际DP阈值, P dp 为预测DP阈值. 图中样本大部分聚集于1∶1线周围,有较高拟合度,均方误差(mean squared error)为2.37,决定系数(R-squared)为0.67. 须说明的是,对于一个建筑物特征点提取而言,道格拉斯-普克算法的最佳阈值通常是一个区间,而不是一个准确的数值,计算发现95.83%的预测值被包含在道格拉斯-普克算法阈值区间内,可以较为准确地提取建筑物特征点. ...
基于最小二乘的建筑物多边形的化简与直角化
1
2008
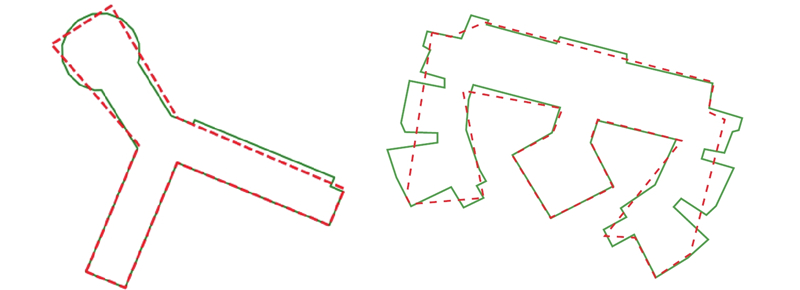
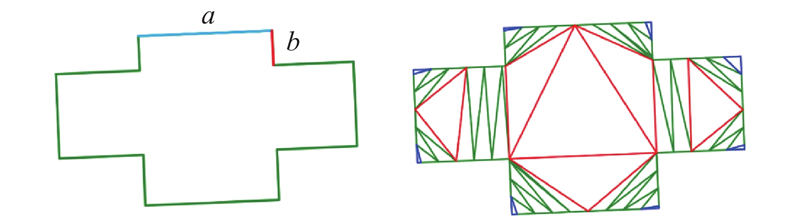
... 在建筑物多边形拟合中,最小二乘估计理论可以应用于构建最佳的拟合曲线或曲面,使其与观测数据的误差最小化. 通过最小二乘法,对建筑物多边形中各特征点之间的点进行拟合,得到一条线段,然后延长各拟合线段,构成的封闭多边形就是地图建筑物的最小二乘模板[23 ] . 构成的最小二乘模板不仅能够平衡表面的细小凹凸,同时保持了建筑物的形状和面积特征,如图3 所示. 图中,绿色实线多边形为地图建筑物,红色虚线多边形为最小二乘模板. ...
基于最小二乘的建筑物多边形的化简与直角化
1
2008
... 在建筑物多边形拟合中,最小二乘估计理论可以应用于构建最佳的拟合曲线或曲面,使其与观测数据的误差最小化. 通过最小二乘法,对建筑物多边形中各特征点之间的点进行拟合,得到一条线段,然后延长各拟合线段,构成的封闭多边形就是地图建筑物的最小二乘模板[23 ] . 构成的最小二乘模板不仅能够平衡表面的细小凹凸,同时保持了建筑物的形状和面积特征,如图3 所示. 图中,绿色实线多边形为地图建筑物,红色虚线多边形为最小二乘模板. ...
基于约束Delaunay结构的街道中轴线提取及网络模型建立
1
2000
... 构成最小二乘模板中轮廓边的点数量过少,直接构建Delaunay三角网往往会破坏Delaunay的最邻近性质,产生众多的狭长三角型. 为此,首先对地图建筑物最小二乘模板的轮廓边进行加密处理. 由于不同的加密程度对构网结构具有较为明显的影响,参考文献[24 ]中采用的加密方法. ...
基于约束Delaunay结构的街道中轴线提取及网络模型建立
1
2000
... 构成最小二乘模板中轮廓边的点数量过少,直接构建Delaunay三角网往往会破坏Delaunay的最邻近性质,产生众多的狭长三角型. 为此,首先对地图建筑物最小二乘模板的轮廓边进行加密处理. 由于不同的加密程度对构网结构具有较为明显的影响,参考文献[24 ]中采用的加密方法. ...
1
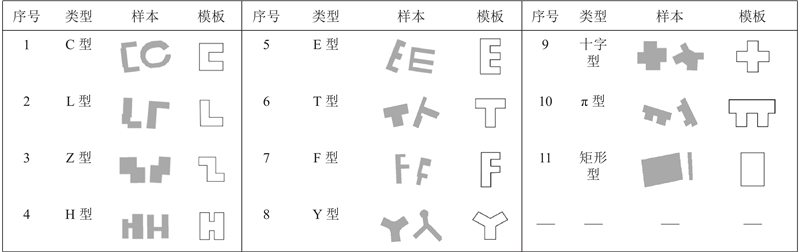
... 建筑物是根据设计师预先制定的设计方案修建的,往往具有特定的几何特征、规范的结构模式. 对应的建筑物多边形在地图上往往表现出正交化、对称性、区域性和模式化的特点[25 ] . 按照地图认知理论,人类对空间的认知是以心象地图的形式驻留在人的记忆中,人们在通过感知途径获取空间环境信息后,在头脑中经过抽象思维加工处理成关于认知环境的抽象替代物[26 ] . 结合认知心理学的原型匹配模式,认为人们会将这种心象地图匹配到几种常见的相对稳定的模式上. 在长期认知经验积累的基础上,通过对常见建筑物形状进行抽象和提炼,就能得到可以代表建筑物形状的模板库,本研究在综合建筑学中建筑形态分类及已有文献模板的基础上,遵循以下3种原则设计制作了建筑物分类模板. ...
1
... 建筑物是根据设计师预先制定的设计方案修建的,往往具有特定的几何特征、规范的结构模式. 对应的建筑物多边形在地图上往往表现出正交化、对称性、区域性和模式化的特点[25 ] . 按照地图认知理论,人类对空间的认知是以心象地图的形式驻留在人的记忆中,人们在通过感知途径获取空间环境信息后,在头脑中经过抽象思维加工处理成关于认知环境的抽象替代物[26 ] . 结合认知心理学的原型匹配模式,认为人们会将这种心象地图匹配到几种常见的相对稳定的模式上. 在长期认知经验积累的基础上,通过对常见建筑物形状进行抽象和提炼,就能得到可以代表建筑物形状的模板库,本研究在综合建筑学中建筑形态分类及已有文献模板的基础上,遵循以下3种原则设计制作了建筑物分类模板. ...
1
... 建筑物是根据设计师预先制定的设计方案修建的,往往具有特定的几何特征、规范的结构模式. 对应的建筑物多边形在地图上往往表现出正交化、对称性、区域性和模式化的特点[25 ] . 按照地图认知理论,人类对空间的认知是以心象地图的形式驻留在人的记忆中,人们在通过感知途径获取空间环境信息后,在头脑中经过抽象思维加工处理成关于认知环境的抽象替代物[26 ] . 结合认知心理学的原型匹配模式,认为人们会将这种心象地图匹配到几种常见的相对稳定的模式上. 在长期认知经验积累的基础上,通过对常见建筑物形状进行抽象和提炼,就能得到可以代表建筑物形状的模板库,本研究在综合建筑学中建筑形态分类及已有文献模板的基础上,遵循以下3种原则设计制作了建筑物分类模板. ...