准确掌握居民出行信息是交通规划、交通需求管理决策的重要基础. 一般而言，居民在一日出行中倾向于从居住地出发，经过一系列停留活动后返回居住地，将这一过程中的多次出行串接起来，就构成出行链^[1]. 相较于传统基于单次出行的分析，基于出行链的分析能够更全面地反映前后出行的时间、空间和方式的关联性，更真实地描绘居民出行行为的特征，因此成为近年来研究出行行为的热点^[2].

手机信令数据中蕴含着地理位置信息，能够有效描述居民的出行轨迹路径^[3]和出行起讫点(origin and destination, OD)^[4-5]，进一步应用于分析城市人口职住分布^[6]、识别出行方式^[7]、客流特征分析^[8]等，较详实地刻画城市居民出行行为. 现有研究大多关注单次出行的某一要素，如出行OD，较少对出行链整体进行挖掘，割裂了出行链中前后出行间起讫点、路径各要素间的关联性.

在出行链分析领域，Chen等^[9]提出基于信令数据和地图服务的出行方式推导框架，将出行轨迹切分为不同的出行方式段，构建出行链. Bonnetain等^[10]提出TRANSIT框架来区分手机用户的移动和静止，利用人类移动的重复性大规模地重建移动轨迹. Martin等^[11]基于交通规划中使用的人类移动性标准数据模型构建Trackintel框架，涵盖了出行分析的整个生命周期. 尽管以上研究已经进行了一定的探索，但对于出行链中的各要素如何构建和连接，仍存在一定的模糊.

停留点识别是基于轨迹数据的出行分析中关键的基础性步骤. 目前算法主要可以分为密度聚类算法^[12-13]和基于规则的算法（增长聚类算法）^[14–16]. Jiang等^[12,17]引入可变参数和参数优化的概念，通过动态调整时空参数来提高算法的适用性. 近年来，出现了结合手机信令与其他多源数据进行分析的方法，如结合其他交通数据^[18]、交通调查数据^[19]和地理信息数据^[20–22]等. 综上所述，可变参数和外部地理信息的引入已被证明能够提升基于手机信令数据的出行停留点识别，但一些关键问题仍有待研究，例如如何优化设置可变参数、如何融合多源数据以提升识别精度等.

在手机信令轨迹数据获取方面，现有研究大多通过从通信运营商处获取信令数据^[13,23-24]，缺乏对应的居民真实出行信息，难以验证出行链识别算法的准确性.

为了提高基于手机信令数据的出行链识别精度，本文通过数据同步采集实验获取手机信令数据和对应的真实出行信息，在停留点识别中引入比兴趣点（POI）数据维度更高的兴趣面（area of interest, AOI）和基站位置数据，提出可变参数滑动窗口的停留点识别方法. 构建出行链识别框架，该框架通过贝叶斯优化方法来优化模型，以获得最佳参数. 这一研究有效地提升了出行链的识别精度，为进一步分析交通需求提供了准确的基础数据，支撑城市尺度的出行行为建模和交通规划.

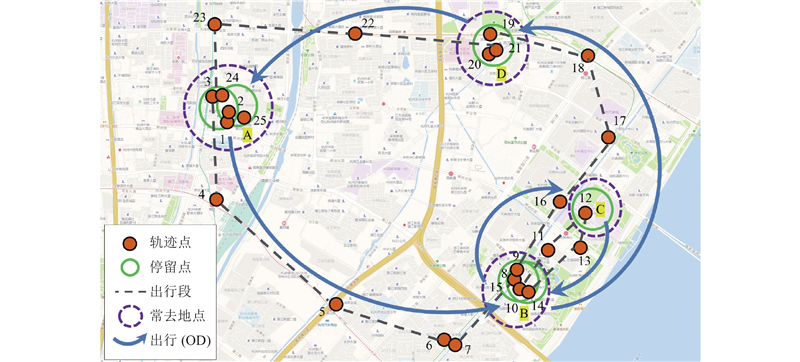
定义手机信令数据条件下的出行相关概念如下. 如图1所示，轨迹点表示每个手机信令的地理坐标采样点，一个轨迹点对应一条信令数据. 停留点指的是用户在一定空间范围内停留超过一定时间的地点，它是由一个或多个相邻轨迹点聚集形成的，D和T分别为停留点判别的空间和时间阈值. 停留主要包括工作、购物、用餐等“活动”过程.

常去地点由停留点聚类形成，表示用户经常去的位置. 参数e为停留点聚类的邻域半径参数.

出行段指的是2个连续停留点之间所有出行轨迹点组成的路径，所有未被划归到停留点的轨迹点均被划归到出行段中. 参数g为出行段内连续轨迹点间允许的最大时间间隔，用于识别短暂的等待和换乘行为，若相邻2个轨迹点的时间间隔超过这个阈值参数，则出行段将会在此处切分. 一般认为每个出行段只对应一种出行方式.

出行（OD）指的是为了某种目的，从一个停留点到另一个停留点的移动，一次“出行”可能由一个或多个不同方式的“出行段”组成. 由于针对的是城市交通，在某些封闭或半封闭区域（如大学校园、工业园区、公园景点等）的内部道路上的移动，不算作一次出行. 对行程时间小于最短持续时间阈值u的出行进行删除处理.

由此，将出行链定义为从居住地出发，经过一系列单一目的的出行和停留，返回居住地的链路集合.

为了便于理解，结合图1对出行相关概念进行阐述. 图1中显示某用户一天的典型出行过程，早上从居住地（A点）出发乘坐地铁到公司（B点）上班，中午到餐厅（C点）用餐（停留30 min）后返回公司，下午下班后从公司（B点）乘坐地铁到购物中心（D点）购物（停留50 min）后返回居住地. 在该场景中，产生信令轨迹点1~25，停留点依次为A1、B1、C、B2、D、A2，出行段依次为3~8、10~12、12~14、15~19、21~24，停留点聚类得到A、B、C、D 4个地点，出行（OD）依次为A-B、B-C、C-B、B-D、D-A，出行链为A-B-C-B-D-A.

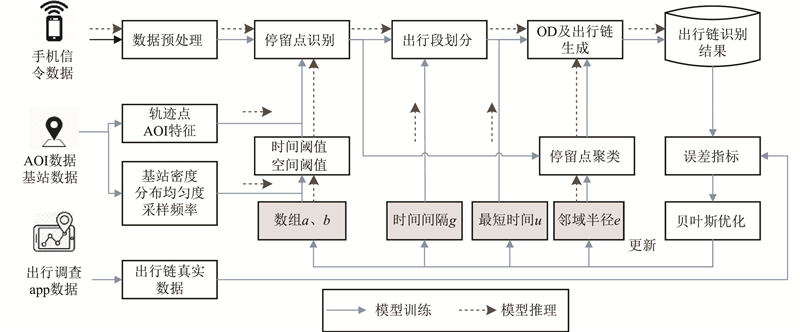
算法框架如图2所示. 1）通过数据同步采集实验获取手机信令数据及对应的出行GPS数据，要求出行者对出行轨迹进行标注，获取真实的出行标签. 2）手机信令数据预处理，对重复数据、漂移数据进行清洗. 3）可变参数滑动窗口的停留点识别方法，其中引入了比POI数据维度更高的AOI信息和环境变量，如每个轨迹点的周围基站分布密度、均匀度和采样频率等特征，这些变量决定停留点识别中的时空阈值. 4）判别出行段，基于DBSCAN方法对停留点进行聚类，形成出行OD及出行链. 在模型训练阶段，将基于采集的真实出行数据与识别结果进行对比，利用贝叶斯优化方法对模型参数进行优化，优化目标包含起讫点识别误差、多识别率、准确率等多个性能度量指标.

手机信令数据可能会因为通信扰动或基站连接原因产生异常数据，如重复数据、漂移数据和乒乓切换数据. 现有的部分研究针对这些异常的噪声数据提出了特定的处理方法，包括卡尔曼滤波^[23]、规则过滤器^[25].

对同一用户同一时刻的多条信令数据仅保留一条. 对于漂移数据，采用距离速度阈值法进行识别，即根据连续3个轨迹点的采样间隔距离和速度（采样间隔距离除以采样间隔时间）的相对关系，判断中间点是否为漂移数据. 假设A、B、C为连续3个轨迹点，若AB间距离和BC间距离均大于阈值，而AC间距离小于阈值，则判定B点为漂移数据，删去B点. 同理可以使用速度判定方法. 参考文献[24,26]的取值，漂移数据处理设置距离阈值为3 000 m，速度阈值为100 km/h. 对于乒乓切换数据，采用规则法识别乒乓切换数据并删除. 在经过预处理后，信令数据总数量减少了约3%.

停留点是指从轨迹数据中识别出行者在较小空间区域内停留了较长时间的轨迹点集合. 可变参数滑动窗口的停留点识别方法的基本思想如下：由每个轨迹点的环境变量（包括周围基站分布和采样频率）计算获得对应的时空阈值，使得时空阈值能够动态调整，以此可变的时空阈值参数来设置滑动窗口. 通过滑动窗口选取在时间和空间上都临近的轨迹点进行聚集，利用各轨迹点所在的AOI辅助判断，实现个体停留点的识别.

停留点识别算法的具体流程如下. 1）对轨迹点根据记录时间进行排序，计算每个轨迹点的环境变量. 2）根据环境变量，计算每点对应的空间阈值D和时间阈值T（可变参数）. 3）逐个检查连续2个轨迹点之间的时间间隔，如果大于最大停留时间阈值$ {{{T}}_{{\text{ms}}}} $（可设为24 h），则两轨迹点的时间间隔太长，无法判断两点间的出行状态，打断两点，它们无法形成停留点. 4）以初始点作为基准点$ {{\boldsymbol{x}}_s} $，依次遍历后续轨迹点作为点$ {{\boldsymbol{x}}_i} $，计算$ {{\boldsymbol{x}}_s} $和$ {{\boldsymbol{x}}_i} $两点间的距离和时间间隔，与空间阈值D和时间阈值T进行比较. 考虑两点所在的AOI，若满足相应条件，则认为点$ {{\boldsymbol{x}}_i} $处发生移动，并更新其为基准点$ {{\boldsymbol{x}}_s} $（以当前$ {{\boldsymbol{x}}_i} $点作为新$ {{\boldsymbol{x}}_s} $点）. 在遍历的过程中，合并$ {{\boldsymbol{x}}_s} $和$ {{\boldsymbol{x}}_i} $之间的所有轨迹点（即$ {{\boldsymbol{x}}_s} $−$ {{\boldsymbol{x}}_{i - 1}} $），形成停留点. 从新的基准点$ {{\boldsymbol{x}}_s} $开始，重复上述过程. 5）当遍历到最后时，不会发生新的移动，若此时持续时间满足要求，则将剩余的轨迹点汇总为最后一个停留点. 该算法通过以上步骤遍历每个个体的轨迹点，识别停留点，构建个体的停留点序列. 具体的步骤细节如图3所示.

时间阈值和空间阈值是判断出行者是否停留的2个关键参数. 考虑这些阈值的设定依据和背后影响机理，而非简单地依赖于固定值或研究者的经验. 一般而言，出行者在停留或者静止时不会因基站切换产生手机信令或者产生的信令位置相同或临近，当出行者移动时，由于手机连接的基站发生切换，产生相应的手机信令记录. 切换动作的发生与2个因素密切相关：一是基站的分布，二是手机用户的移动速度. 每个基站本身的覆盖范围影响时空阈值. 在基站密度较高，分布较均匀的情况下，单个基站的服务半径和空间阈值较小；当用户的移动速度较大时，信令采样频率会增加，此时用户更有可能处于出行状态，设置较小的时间阈值. 相反条件时同理.

提出定性假设，即识别停留点时的T、D与轨迹点及所在环境的一些特征有关，具体如下.

1）基站密度为与每个轨迹点距离小于400 m的基站数量$ {m_1} $.

2）基站方向分布均匀度为与每个轨迹点距离小于400 m的基站相对分布方向的方差$ {m_2} $.

基于Zar等^[27-28]提出的关于角度及方向数据方差的计算方法，将与每个轨迹点距离小于400 m的所有基站按其相对于轨迹点的方位，分布到以轨迹点为圆心的单位圆上，如图4（a）所示. 每个基站相对轨迹点的方向可以视作单位向量$ {\boldsymbol{z}} $，其与x轴的夹角为$\theta $，则向量$ z $的坐标为$ {(}\cos \theta ,\sin \theta ) $. 利用某轨迹点附近所有基站的单位向量$ {{\boldsymbol{z}}_1}, $ $ {{\boldsymbol{z}}_2} , \cdots , {{\boldsymbol{z}}_n} $表示对应的角度$ {\theta _1} ,$ $ {\theta _2} , \cdots , {\theta _n} $，则$ {\theta _1}, $ $ {\theta _2} , \cdots , {\theta _n} $的平均方向$ \overline \theta $是$ {{\boldsymbol{z}}_1}, $ $ {{\boldsymbol{z}}_2} , \cdots , {{\boldsymbol{z}}_n} $的平均向量$ \overline {\boldsymbol{z}} $所指的方向. 设平均向量$ \overline {\boldsymbol{z}} $的坐标为$(\overline C ,\overline S )$，则

(1)$ \overline C = \frac{1}{n}\sum\limits_{j = 1}^n {\cos {\theta _j}} , $

(2)$ \overline S = \frac{1}{n}\sum\limits_{j = 1}^n {\sin {\theta _j}} . $

平均向量$ \overline {\boldsymbol{z}} $的长度$ \overline R $为

(3)$ \overline R = \sqrt {{{\overline C }^2}+{{\overline S }^2}} . $

$ \overline R $的取值为0~1.0，它能够反映数据的离散程度，如图4（b）所示. 具体来说，若$ {\theta _1} $,$ {\theta _2} , \cdots , {\theta _n} $都聚集在一起，则$ \overline R $接近于1，反之则接近于0. $ \overline R $越小，数据越分散，分布越均匀.

(4)$ {m_2} = 1 - \overline R . $

使用$ {m_2} $作为方差来衡量基站分布的均匀度，则离散性（均匀度）与方差是正相关的.

3）采样频率为每个轨迹点前15 min和后15 min的采样数量（$ {m_3} $，$ {m_4} $）.

为了使时空阈值能够随环境变量的变化而动态调整，给出线性关系的假设：

(5)$ D = {a_0}+{a_1} {m_1}+{a_2} {m_2}+{a_3} {m_3}+{a_4} {m_4} , $

(6)$ T = {b_0}+{b_1} {m_1}+{b_2} {m_2}+{b_3} {m_3}+{b_4} {m_4} . $

式中：特征数组[$ {m_1} ,\; {m_2} ,\; {m_3} ,\; {m_4} $]为自变量，阈值D和T为因变量；[$ {a_0} ,\; {a_1} ,\; {a_2} ,\; {a_3} ,\; {a_4} $]（即数组a）和[$ {b_0} $,$ {b_1} $,$ {b_2} $,$ {b_3} $,$ {b_4} $]（即数组b）中的元素都是待确定的系数参数，这10个数值被作为模型参数.

AOI（area of interest）即兴趣面，比POI（point of interest）多一项区域边界信息，主要用于在地图中表达区域状的地理实体，如一个居民小区、一所学校或一个景区等. 通过百度地图API方式共获取到杭州市AOI数据一万多条，分布示意图如图5所示.

轨迹点的AOI信息主要用于帮助判断是否形成新的停留点，根据1节的出行链定义可知，若只在同一个AOI区域内移动，则不被视为一次新的出行，处在停留过程中. 根据2.2节的内容和图3可知，$ {{\boldsymbol{x}}_s} $和$ {{\boldsymbol{x}}_i} $ 2个轨迹点所在的AOI不同是$ {{\boldsymbol{x}}_s} $~$ {{\boldsymbol{x}}_{i - 1}} $间所有点形成新停留点的必要不充分条件. 换言之，即使$ {{\boldsymbol{x}}_s} $与$ {{\boldsymbol{x}}_i} $的时间间隔和空间间隔都满足停留点判别条件，若两点的AOI相同，也不会被识别为新的停留点. 此时$ {{\boldsymbol{x}}_i} $需要继续往后遍历，直到满足时空条件且两点的AOI不同为止. 由于不同的AOI区域存在重叠的情况，一个轨迹点可能对应多个AOI. 为了解决该问题，匹配原则是进行一对一匹配，优先匹配到面积较大、级别较高的AOI.

停留点是一个或多个连续地被识别为停留状态的轨迹点的质心. 对于用户多次停留的同一地点，由于每次停留时连接基站不同，不同的停留点坐标间略有偏差，具体如图1所示. 为了解决该问题，使用DBSCAN方法对识别的停留点进行空间聚类，形成“常去地点”，即将空间上临近的停留点按不同用户聚类形成“簇”. 在该算法中，设置邻域半径参数e，并将聚类的最小停留点数量设置为1，这样多次停留的有偏移的停留点会聚合为一个，单次停留点会保留.

在停留点识别后，所有未被识别为停留状态的轨迹点均被划归为出行状态，由2个连续停留点之间所有出行轨迹点组成的路径将被划分为出行段. 为了切分出连续的出行轨迹，需要识别短暂的等待和换乘行为. 若某2个连续出行轨迹点的时间间隔大于g，则原先的出行段将在此处中断，形成2个新的出行段.

一个出行段至少包含2个轨迹点，确定出行段的起终点时间和坐标时存在以下多种情况. 如图6（a）所示，若出行段前面是一个停留点，则出行段的起点时间为出行段第一个轨迹点的采样时间，起点坐标为前一个停留点的最后一个轨迹点的坐标. 如图6（b）所示，若出行段前面是另一个出行段，则出行段的起点时间和坐标与该出行段第一个轨迹点的采样时间和坐标一致. 类似地，如图6（c）、（d）所示，若出行段后面是一个停留点，则出行段的终点时间和坐标为后一个停留点的第一个轨迹点的采样时间和坐标；反之，则出行段的终点时间和坐标与该出行段最后一个轨迹点的采样时间和坐标一致.

2个停留点之间的所有出行段可以合并为1次出行（OD），它可能包含一个或多个出行段. 出行的起止时间分别为该出行的第1个出行段的起点时间和最后1个出行段的终点时间，出行的O点和D点坐标分别为两端停留点的坐标. 少部分出行两端或其中一端没有停留点的，O点和D点坐标分别为第1个出行段起点和最后1个出行段终点的坐标.

在部分往返的真实出行中，因在目的地停留时间较短而未识别出停留点，较典型的为“去车站接送人”场景，导致识别的出行的起、终点位置相同. 根据出行定义，此类出行应该被划分为2次出行而不是1次. 针对这种情况，对O、D点位置相同的出行进行拆分. 具体如下：筛选出O点和D点在同一常去地点且中间有至少2个出行段的出行，找到每个出行中D点离O点最远的出行段. 由此将1次出行拆分为2次出行：第1次为原O点到离O点最远的出行段的终点，第2次为离原O点最远的出行段的下一个出行段的起点到原D点.

对于持续时间较短的出行，设置出行时间阈值u，删掉持续时间小于阈值的出行OD. 将原本属于该出行的轨迹点划归到前一个停留点中，该过程相当于间接处理掉了一些噪声数据.

如图7所示为某用户某天完整的原始信令数据和经过模型处理后获得的出行链信息示意图，共识别到3个停留点、2个出行段、2个常去地点及2次出行OD. 其中，第1、第3个停留点被聚类到同一个常去地点中，2次出行OD各包含一个出行段. 如表1所示为整理后的基本出行链信息.

在获得真实出行轨迹和标注信息的前提下，可以进行模型参数的优化. 确定8个性能度量指标作为优化目标，总体上可以分为以下2个方面. 1）识别率指标，用于评估真实出行是否被识别或识别错误. 2）误差指标，用于评估识别结果与真实出行在时间空间上的一致性.

识别率各项指标的计算公式如下.

1） 查准率

(7)$ P = {{{N_{{\mathrm{y}}}}} \mathord{\left/ {\vphantom {{{N_{y}}} {{N_{r}}}}} \right. } {{N_{{\mathrm{r}}}}}} . $

2）查全率

(8)$ R = {{{N_{{\mathrm{y}}}}} \mathord{\left/ {\vphantom {{{N_{y}}} {{N_{{all}}}}}} \right. } {{N_{{{\mathrm{all}}}}}}} . $

3）正确率

(9)$ A = 1 - {{\left( {{N_{{\mathrm{c}}}}+{N_{{\mathrm{u}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{N_{c}}+{N_{u}}} \right)} {{N_{{all}}}}}} \right. } {{N_{{{\mathrm{all}}}}}}} . $

4）多识别率

(10)$ M = {{\left( {{N_{{\mathrm{s}}}}+{N_{{\mathrm{m}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{N_{s}}+{N_{m}}} \right)} {{N_{{all}}}}}} \right. } {{N_{{{\mathrm{all}}}}}}} . $

式中：$ {N_{{\mathrm{all}}}} $为用户标注的出行次数，$ {N_{\mathrm{r}}} $为模型识别得到的出行次数，$ {N_{{\mathrm{y}}}} $为模型识别结果与真实标注出行在时间上产生交集且一一对应的出行次数，$ {N_{{\mathrm{c}}}} $为实际中为一次出行但被模型识别为多次出行的出行个数，$ {N_{{\mathrm{s}}}} $为实际中多次出行但被模型识别为一次出行的出行个数，$ {N_{{\mathrm{m}}}} $为被模型识别为出行但实际不存在的出行个数，$ {N_{{\mathrm{u}}}} $为实际存在出行但未被模型识别出的出行个数.

使用模型识别结果与真实标注在时间上产生交集且一一对应的出行对，即$ {N_{{\mathrm{y}}}} $的所有出行对作为样本. 计算所有出行对的起点平均距离误差$ \Delta {{{D}}_{\text{o}}} $、终点平均距离误差$ \Delta {{{D}}_{\text{d}}} $、起点平均时间误差$ \Delta {{{T}}_{\text{o}}} $、终点平均时间误差$ \Delta {{{T}}_{\text{d}}} $，将此4项作为误差评价指标.

在优化参数上，模型中共有13个参数需要确定. 具体来说，有10个系数参数（[$ {a_0} $,$ {a_1} $,$ {a_2} $,$ {a_3} $,$ {a_4} $]、[$ {b_0} $,$ {b_1} $,$ {b_2} $,$ {b_3} $,$ {b_4} $]）以及3个阈值参数（出行段内轨迹点的最大时间间隔g 、聚类的邻域半径e、出行的最短持续时间u）. 根据各项性能度量指标构建损失函数，以最小化损失函数为目标，对模型进行多目标优化，获得模型的最优参数.

当构建损失函数时，考虑各项指标的归一化，即将各项指标的变化范围控制在同一尺度下. 将多目标优化的目标函数即损失函数Y定义为

(11)$ Y =\; \alpha (\Delta {{{D}}_{\text{o}}}+\Delta {{{D}}_{\text{d}}})+\beta (\Delta {{{T}}_{\text{o}}}+\Delta {{{T}}_{\text{d}}})+ \\ \gamma ({{{M}} - {{A}})} . $

式中：$ \alpha 、\beta 、\gamma $为待定的归一化系数.

损失函数对各参数的导数是未知的，因此无法使用梯度下降的方法求最优解. 贝叶斯优化（Bayesian optimization）适用于解决计算成本昂贵的黑盒优化问题，利用贝叶斯定理来指导搜索以找到目标函数的最小值或最大值，在每次迭代的时候，利用之前观测到的历史信息（先验知识）进行下一次优化. 采用贝叶斯优化中的TPE（tree-structured Parzen estimator）方法^[29-30]求解损失函数的最小值，得到最优参数. TPE是非参数化的概率密度估计方法，用于在高维空间中进行贝叶斯优化，优势在于能够自适应地选择新的候选参数组合，更新核密度估计器来引导搜索，可以快速收敛到具有良好性能的参数组合，提高贝叶斯优化的效率.

由于贝叶斯优化的结果有一定的随机性，每次优化的结果可能都略有不同，不一定能达到全局最优，需要进行多轮优化，选择其中较好的结果. 将此优化得到的最优参数输入，可得最终的出行链识别模型.

使用的“手机信令数据”指的是用户设备在与基站进行通信时所产生的日志数据，存储于运营商通信系统数据库，如表2所示，每行记录包含用户编号（user_id）、与基站通信时的时刻（time）、与手机通信的基站的经纬度坐标（longitude、latitude）等基本数据字段. 同一用户id的不同记录集合即该用户的轨迹点集，通过从数据集中提取以个体为单位的轨迹点序列，形成了轨迹信息.

使用的手机信令数据采集时间为2022年10月31日至11月27日，共获取到31位用户的共7.3 万条手机信令位置数据，平均每人每天产生85 条信令数据. 如图8所示为某用户某次出行的手机信令轨迹和同时收集到的GPS轨迹.

对所有手机信令数据的采样间隔时间$ \Delta t $和间隔距离$ \Delta d $进行统计，数据采样间隔时间的平均值为1 009 s，中位数为81 s；采样间隔距离的平均值为474 m，中位数为326 m. 将手机信令数据的经纬度坐标与相应用户和时间的GPS坐标进行比较，统计出手机信令数据的定位误差平均值约为240 m，中位数约为190 m.

对比分析手机信令数据与出行者的实际出行状态及GPS数据，可以得到手机信令数据相对于GPS数据的特点如下.

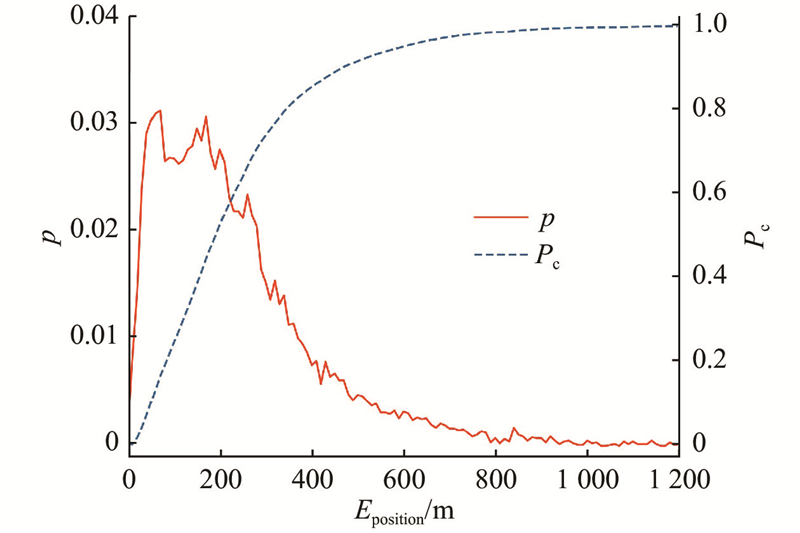
1）位置不确定性. 手机信令数据通常使用通信基站位置作为用户位置坐标，由于基站的空间分布差异较大，定位误差$ {E_{{{\mathrm{position}}}}} $大多为数十米至数百米，其分布如图9所示. 图中，p为概率密度，P_c为累积概率.

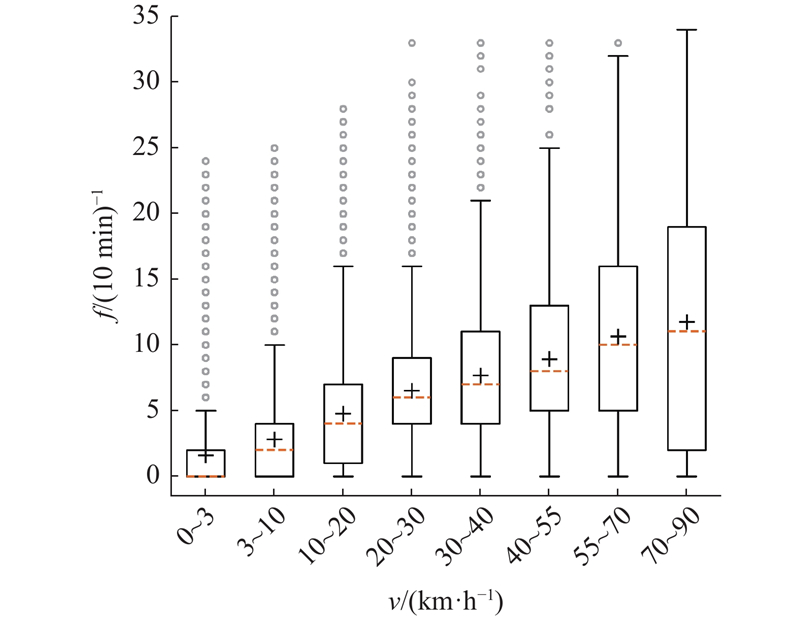
2）采样间隔的不均匀性. 手机信令数据是由移动通信网络在为手机用户提供通信服务时产生的，包括打电话、上网及移动过程中的基站切换等. 用户在出行中产生连续的基站切换，此时采样间隔较短，速度越快采样频率越高. 在静止驻留时，可能在较长时间内不产生基站切换，采样频率较低. 手机信令数据的采样频率f与实际移动速度v的关系如图10所示.

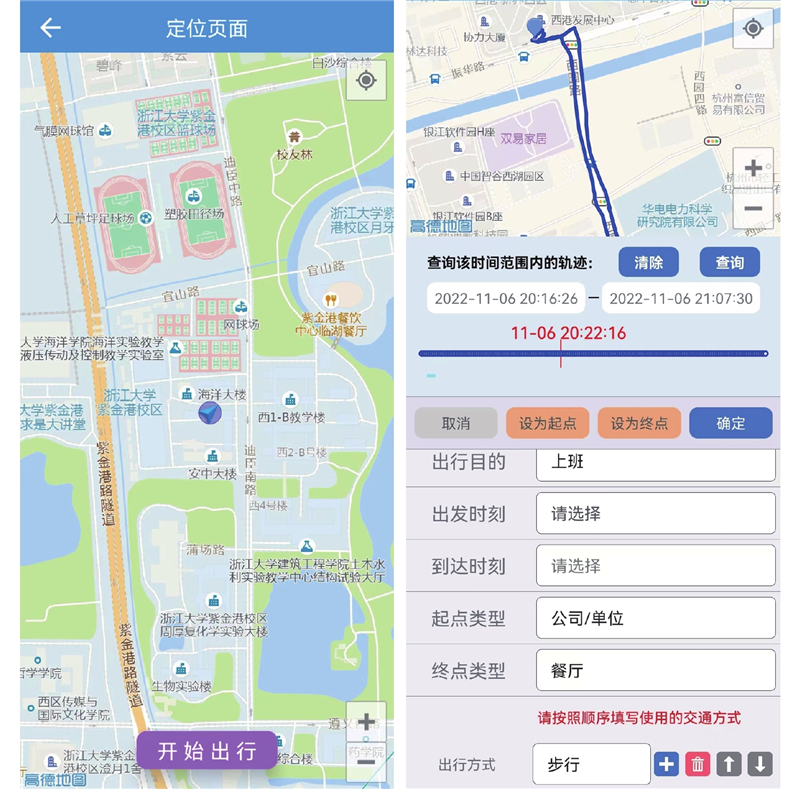
为了更加精准地对提出的方法进行参数优化和结果验证，开发了一款名为Check·Track的APP，用于出行调查的GPS轨迹收集和出行标注，以此配合从运营商处获取的对应手机信令数据. APP的页面如图11所示，用户点击“开始出行”即可开始记录GPS轨迹，轨迹数据的采样频率为5 s/次. 在当天的GPS数据记录完成后，用户需要手动在APP中划分出行，标注每次出行的起止时刻、起终点类型、出行目的和出行方式等信息.

2022年11月，组织37名志愿者使用该APP进行2~4周不等的连续出行调查和轨迹记录，累计472 （人×天）的出行数据. 从运营商处获取这些志愿者对应的手机信令数据. 将调查得到的出行OD标注数据，与GPS、信令数据进行核对，筛选出29名用户的737 次准确出行OD作为真实标签，累计276 （人×天）的出行数据. 这些数据对应31 994 条手机信令数据. 真实的出行标注数据如表3所示.

将收集的出行OD标注作为真实标签，采用贝叶斯优化方法对模型进行参数优化. 在该过程中，采用网格搜索（grid search）方法对贝叶斯优化的超参数进行选取，得到最优参数组合为初始观测值60个，计算集合函数考虑样本数80个. 经过多次优化实验，损失函数停止减小时的迭代次数为600~1400，故最终设置最大迭代次数为1 500. 定义参数空间，即13个参数的取值范围，如表4所示，其中$ {a_0} $、$ {b_0} $的默认取值分别为500 m、30 min^[14-15]. 计算所有采集的信令数据轨迹点的环境变量[$ {m_1}, $ $ {m_2}, $ $ {m_3}, $ $ {m_4} $]，统计得到各中位数分别为[34, 0.644, 6, 6]，将对应系数数组[$ {a_1}, $ $ {a_2}, $ $ {a_3}, $ $ {a_4} $]和[$ {b_1}, $ $ {b_2}, $ $ {b_3}, $ $ {b_4} $]中各值的正、负边界设置为与各中位数相乘后，能够使$ {a_0} $和$ {b_0} $的默认值变化幅度为5%的数值.

在各参数的取值范围内进行随机取值，运行本文模型500 次，统计各项性能指标组合的变化，以75%分位数与25%分位数的差作为变化幅度. 分别赋予3个指标组合25%、25%、50%的权重，计算得到对应的归一化系数，如表5所示. 将多目标优化的目标函数即损失函数Y定义为

(12)$ {Y = }\frac{{\Delta {D_{\mathrm{o}}}+\Delta {D_{\mathrm{d}}}}}{{1\;570}}+\frac{{\Delta {T_{\mathrm{o}}}+\Delta {T_{\mathrm{d}}}}}{{32}}+{{{M}} - {{A}}} . $

经过5轮优化，每次得到的Y和各项参数如表4所示. 对比各个优化结果的系数参数和损失函数，可以确定停留点识别时的D和T分别与部分环境变量具有相关性. 具体来讲，D与轨迹点周围的基站密度和基站方向分布均匀度负相关，T与采样频率负相关. 经过比较，优化结果5得到的损失函数最小，因此选择优化结果5的参数值作为最优参数，将最优参数输入到模型中，可得最终模型.

由于出行链是由识别的出行OD连接而成的，出行OD的识别指标能够反映出行链的识别效果，以识别的出行OD为基本比较单元构建指标，可以间接地反映出停留点、出行段及出行链的整体识别质量. 评价指标为2.6节所述的8个性能度量指标，对比方法分别是Marra’s Heuristic算法^[16]、Trackintel方法^[11]及本文框架下的固定时空阈值法. Marra’s Heuristic算法是启发式停留点识别算法，在本研究中增加了形成出行的步骤. 由于本研究的算法存在优化模型参数的过程，类似于机器学习中的“训练”，为了综合比较，将性能对比分为最优性能和泛化性能两部分，如表6所示. 最优性能指使用100%的数据优化模型参数，直接比较优化后的性能. 泛化性能指用60%的数据优化模型参数，使用剩余40%的数据运行并比较性能.

从表6可以看出，本文算法在除了泛化性能中的起点和终点平均距离误差（$ \Delta {{{D}}_{\text{o}}} $和$ \Delta {{{D}}_{\text{d}}} $）之外的所有性能指标上均优于另外2个算法. 对于$ \Delta {{{D}}_{\text{o}}} $和$ \Delta {{{D}}_{\text{d}}} $2项指标，略差于Trackintel算法的原因主要是本研究算法较大地提升了4个识别率指标，更多地识别了与真实标注对应的出行. 对于部分Trackintel算法未能识别出的真实出行，它们所对应的手机信令数据本身可能有较大的误差，而这部分真实出行在本研究算法中被成功识别，导致整体平均误差略微增大. 相对于固定阈值算法，采用贝叶斯优化后的可变参数算法在各项指标上都有全方位的提升，证明了可变参数滑动窗口及贝叶斯优化步骤的有效性. 总的来说，本研究算法在通过手机信令数据辨识出行链，特别是识别出行OD的准确性方面，优于对比方法.

为了验证模型的稳定性，采用五折交叉验证方法估计模型的泛化能力. 将276 （人×天）的出行OD和对应的信令数据随机划分为5个相同大小的子集. 依次选择其中1份作为测试集，其余4份用于训练，重复5次，每次实验中都计算各项评价指标，分别计算训练和测试的平均结果. 如表7所示，当使用不同的样本进行优化时，部分参数几乎不发生变化，如$ {a_0} $、$ {b_0} $. 部分参数的数值产生一定的变化，如$ {b_3} $、g、e等，但变化幅度在可接受范围内，不影响每次优化的有效性. 样本量越大，则随机性越小，优化结果的可信度越高. 与平均训练结果相比，平均测试结果的部分指标略有劣化，各项指标的变化率为1%~8%，总体较稳定，因此可以认为该算法具有较好的稳定性. 该实验说明基于部分样例数据标定的参数可以在一定程度上适用于其他个体.

（1）针对手机信令数据时空特性的分析表明，手机信令数据的定位存在时空不确定性，即位置不确定性和采样间隔不均匀性，且采样频率与实际移动速度相关. 采样间隔时间和间隔距离的中位数分别为81 s和326 m. 将手机信令数据的经纬度坐标与真实GPS坐标对比可知，手机信令数据的平均定位误差为240 m.

（2）本研究的贡献主要在于提出的基于手机信令数据的出行链识别框架，在传统时空阈值识别停留点方法的基础上，考虑轨迹点所在AOI和周围基站密度、均匀度等环境变量对时空阈值参数的影响，提出可变参数滑动窗口的出行停留点识别方法. 采用贝叶斯多目标优化得到出行链模型的最佳参数，实现时空阈值的动态调整，提升模型的识别精度和泛化性能. 基于开发的出行轨迹记录APP采集的数据与从运营商处获取的手机信令数据对比实验结果表明，本文方法在泛化性能和最优性能两方面均能够有效地降低模型的误差，提升识别率. 识别率比其他最新的算法有3%~26%的改进，尤其多识别率显著降低. 五折交叉验证结果证明了算法的良好泛化性能.

（3）提出的环境变量对停留点时空阈值的影响基于简单的线性关系假设，函数关系的形式需要进一步的探究. 此外，可以直接使用本文中的参数标定结果，也可以遵循该方法进行更大规模的出行轨迹和标签收集实验，便于应用到城市规模的手机信令数据分析上，刻画城市尺度的交通出行需求. 在未来的研究中，可以基于识别的出行链进一步判断居住和工作地点，计算城市规模的通勤OD矩阵和路径，分析城市出行的瓶颈，研究降低通勤时耗的策略. 另外，可以基于历史轨迹推演人口整体的迁移态势，如预测交通拥堵及群体性聚集事件，便于实施智能管控.