[1]
金鑫, 庄建军, 徐子恒 轻量化YOLOv5s网络车底危险物识别算法
[J]. 浙江大学学报: 工学版 , 2023 , 57 (8 ): 1516 - 1526
[本文引用: 1]
JIN Xin, ZHUANG Jianjun, XU Ziheng Lightweight YOLOv5s network-based algorithm for identifying hazardous objects under vehicles
[J]. Journal of Zhejiang University: Engineering Science , 2023 , 57 (8 ): 1516 - 1526
[本文引用: 1]
[2]
熊帆, 陈田, 卞佰成, 等 基于卷积循环神经网络的芯片表面字符识别
[J]. 浙江大学学报: 工学版 , 2023 , 57 (5 ): 948 - 956
[本文引用: 1]
XIONG Fan, CHEN Tian, BIAN Baicheng, et al Chip surface character recognition based on convolutional recurrent neural network
[J]. Journal of Zhejiang University: Engineering Science , 2023 , 57 (5 ): 948 - 956
[本文引用: 1]
[3]
刘春娟, 乔泽, 闫浩文, 等 基于多尺度互注意力的遥感图像语义分割网络
[J]. 浙江大学学报: 工学版 , 2023 , 57 (7 ): 1335 - 1344
[本文引用: 1]
LIU Chunjuan, QIAO Ze, YAN Haowen, et al Semantic segmentation network for remote sensing image based on multi-scale mutual attention
[J]. Journal of Zhejiang University: Engineering Science , 2023 , 57 (7 ): 1335 - 1344
[本文引用: 1]
[4]
杨长春, 叶赞挺, 刘半藤, 等 基于多源信息融合的医学图像分割方法
[J]. 浙江大学学报: 工学版 , 2023 , 57 (2 ): 226 - 234
[本文引用: 1]
YANG Changchun, YE Zanting, LIU Banteng, et al Medical image segmentation method based on multi-source information fusion
[J]. Journal of Zhejiang University: Engineering Science , 2023 , 57 (2 ): 226 - 234
[本文引用: 1]
[5]
宋秀兰, 董兆航, 单杭冠, 等 基于时空融合的多头注意力车辆轨迹预测
[J]. 浙江大学学报: 工学版 , 2023 , 57 (8 ): 1636 - 1643
[本文引用: 1]
SONG Xiulan, DONG Zhaohang, SHAN Hangguan, et al Vehicle trajectory prediction based on temporal-spatial multi-head attention mechanism
[J]. Journal of Zhejiang University: Engineering Science , 2023 , 57 (8 ): 1636 - 1643
[本文引用: 1]
[6]
SZEGEDY C, ZAREMBA W, SUTSKEVER I, et al. Intriguing properties of neural networks [C]// 2nd International Conference on Learning Representations. Banff: [s. n. ], 2014.
[本文引用: 1]
[7]
MADRY A, MAKELOV A, SCHMIDT L, et al. Towards deep learning models resistant to adversarial attacks [C]// International Conference on Learning Representations. Vancouver: [s. n.], 2018.
[本文引用: 5]
[8]
WANG Y, MA X, BAILEY J, et al. On the convergence and robustness of adversarial training [C]// International Conference on Machine Learning . Long Beach: International Machine Learning Society, 2019: 6586-6595.
[本文引用: 1]
[9]
GOODFELLOW J, SHLENS J, SZEGEDY C. Explaining and harnessing adversarial examples [C]// International Conference on Learning Representation . San Diego: [s. n.], 2015.
[本文引用: 3]
[10]
WONG E, RICE L, KOLTER J. Z. Fast is better than free: revisiting adversarial training [C]// International Conference on Learning Representations . Addis Ababa, Ethiopia: [s. n.], 2020.
[本文引用: 9]
[11]
ANDRIUSHCHENKO M, FLAMMARION N. Understanding and improving fast adversarial training [C]// Neural Information Processing Systems . [S. l. ]: Curran Associates, Inc, 2020: 16048-16059.
[本文引用: 10]
[12]
KIM H, LEE W, LEE J. Understanding catastrophic overfitting in single-step adversarial training [C]// Proceedings of the AAAI Conference on Artificial Intelligence . Vancouver: AAAI Press, 2021: 8119-8127.
[本文引用: 19]
[13]
SHAFAHI A, NAJIBI M, GHIASI A, et al. Adversarial training for free! [C]// Neural Information Processing Systems . Vancouver: Curran Associates, Inc. , 2019: 3353-3364.
[本文引用: 1]
[14]
SRIRAMANAN G, ADDEPALLI S, BABURAJ A, et al. Towards efficient and effective adversarial training [C]// Neural Information Processing Systems . [S. l. ]: Curran Associates, Inc. , 2021: 11821-11833.
[本文引用: 1]
[15]
IOFFE S, SZEGEDY C. Batch normalization: accelerating deep network training by reducing internal covariate shift [C]// International Conference on Machine Learning . Lille: MIT Press, 2015: 448-456.
[本文引用: 1]
[16]
AGARAP F. Deep learning using rectified linear units (ReLU) [EB/OL]. [2023-06-20]. https://arxiv.org/abs/1803.08375.
[本文引用: 1]
[17]
MIYATO T, KATAOKA T, KOYAMAM M, et al. Spectral normalization for generative adversarial networks [C]// International Conference on Learning Representations . Vancouver: [s. n. ], 2018.
[本文引用: 1]
[18]
WANG H, WU X, HUANG Z, et al. High-frequency component helps explain the generalization of convolutional neural networks [C]// IEEE Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 8681–8691.
[本文引用: 1]
[19]
AHMED N, NATARAJAN T, RAO K R. Discrete cosine transform
[J]. IEEE Transactions on Computers , 1974 , 23 (1 ): 90 - 93
[本文引用: 1]
[20]
SELVARAJU R. R. COGSWELL M, DAS A, et al. Grad-CAM: visual explanations from deep networks via gradient-based localization [C]// IEEE International Conference on Computer Vision. Venice: IEEE, 2017: 618-626.
[本文引用: 1]
[21]
KRIZHEVSKY A, HINTON G. Learning multiple layers of features from tiny images [D]. Toronto: University of Toronto, 2009.
[本文引用: 2]
[22]
CARLINI N, WAGNER D. A. Towards evaluating the robustness of neural networks [C]// IEEE Symposium on Security and Privacy . San Jose: IEEE, 2017: 39–57.
[本文引用: 1]
[23]
REBUFFI S A, GOWAL S, CALIAN D A, et al. Fixing data augmentation to improve adversarial robustness [EB/OL]. [2023-06-20]. https://arxiv.org/abs/2103.01946.
[本文引用: 1]
[24]
HO J, JAIN A, ABBEEL P. Denoising diffusion probabilistic models [C]// Advances in Neural Information Processing Systems . [S. l. ]: Curran Associates, Inc. , 2020: 6840-6851.
[本文引用: 1]
[25]
ZAGORUYKO S, KOMODAKIS N. Wide residual networks [C]// Proceedings of the British Machine Vision Conference . York: BMVA Press, 2016: 87.1-87.12.
[本文引用: 1]
[26]
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition [C]// IEEE Conference on Computer Vision and Pattern Recognition . Las Vegas: IEEE Computer Society, 2016: 770–778.
[本文引用: 1]
[27]
HE K, ZHANG X, REN S, et al. Identity mappings in deep residual networks [C]// European Conference on Computer Vision . Amsterdam: Springer Verlag, 2016: 630–645.
[本文引用: 1]
[28]
QIAN N On the momentum term in gradient descent learning algorithms
[J]. Neural Networks , 1999 , 12 (1 ): 145 - 151
DOI:10.1016/S0893-6080(98)00116-6
[本文引用: 1]
轻量化YOLOv5s网络车底危险物识别算法
1
2023
... 深度神经网络在图像识别[1 -2 ] 、图像分割[3 -4 ] 、自动驾驶[5 ] 等诸多方面取得了显著的进展. 随着深度神经网络模型的不断发展,安全性与鲁棒性问题日益凸显. Szegedy等[6 ] 发现深度神经网络容易受到微小的对抗性扰动影响,这些扰动是专门设计的,旨在欺骗模型使其误分类. 为了应对这一问题,防御算法不断涌现,其中对抗训练(adversarial training, AT)[7 ] 是常用的方法,通过在训练过程中引入对抗样本,提高系统的鲁棒性. 对抗训练可被视为极大极小的优化问题[8 ] . 该优化问题的内部目标为最大化损失函数以生成对抗样本,外部目标是最小化对抗性损失. 常见的对抗训练方法可以分为多步对抗训练和快速对抗训练. 多步对抗训练一般采用近似求解的方法,常用的方法为投影梯度下降(project gradient descent, PGD)[7 ] ,然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
轻量化YOLOv5s网络车底危险物识别算法
1
2023
... 深度神经网络在图像识别[1 -2 ] 、图像分割[3 -4 ] 、自动驾驶[5 ] 等诸多方面取得了显著的进展. 随着深度神经网络模型的不断发展,安全性与鲁棒性问题日益凸显. Szegedy等[6 ] 发现深度神经网络容易受到微小的对抗性扰动影响,这些扰动是专门设计的,旨在欺骗模型使其误分类. 为了应对这一问题,防御算法不断涌现,其中对抗训练(adversarial training, AT)[7 ] 是常用的方法,通过在训练过程中引入对抗样本,提高系统的鲁棒性. 对抗训练可被视为极大极小的优化问题[8 ] . 该优化问题的内部目标为最大化损失函数以生成对抗样本,外部目标是最小化对抗性损失. 常见的对抗训练方法可以分为多步对抗训练和快速对抗训练. 多步对抗训练一般采用近似求解的方法,常用的方法为投影梯度下降(project gradient descent, PGD)[7 ] ,然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
基于卷积循环神经网络的芯片表面字符识别
1
2023
... 深度神经网络在图像识别[1 -2 ] 、图像分割[3 -4 ] 、自动驾驶[5 ] 等诸多方面取得了显著的进展. 随着深度神经网络模型的不断发展,安全性与鲁棒性问题日益凸显. Szegedy等[6 ] 发现深度神经网络容易受到微小的对抗性扰动影响,这些扰动是专门设计的,旨在欺骗模型使其误分类. 为了应对这一问题,防御算法不断涌现,其中对抗训练(adversarial training, AT)[7 ] 是常用的方法,通过在训练过程中引入对抗样本,提高系统的鲁棒性. 对抗训练可被视为极大极小的优化问题[8 ] . 该优化问题的内部目标为最大化损失函数以生成对抗样本,外部目标是最小化对抗性损失. 常见的对抗训练方法可以分为多步对抗训练和快速对抗训练. 多步对抗训练一般采用近似求解的方法,常用的方法为投影梯度下降(project gradient descent, PGD)[7 ] ,然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
基于卷积循环神经网络的芯片表面字符识别
1
2023
... 深度神经网络在图像识别[1 -2 ] 、图像分割[3 -4 ] 、自动驾驶[5 ] 等诸多方面取得了显著的进展. 随着深度神经网络模型的不断发展,安全性与鲁棒性问题日益凸显. Szegedy等[6 ] 发现深度神经网络容易受到微小的对抗性扰动影响,这些扰动是专门设计的,旨在欺骗模型使其误分类. 为了应对这一问题,防御算法不断涌现,其中对抗训练(adversarial training, AT)[7 ] 是常用的方法,通过在训练过程中引入对抗样本,提高系统的鲁棒性. 对抗训练可被视为极大极小的优化问题[8 ] . 该优化问题的内部目标为最大化损失函数以生成对抗样本,外部目标是最小化对抗性损失. 常见的对抗训练方法可以分为多步对抗训练和快速对抗训练. 多步对抗训练一般采用近似求解的方法,常用的方法为投影梯度下降(project gradient descent, PGD)[7 ] ,然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
基于多尺度互注意力的遥感图像语义分割网络
1
2023
... 深度神经网络在图像识别[1 -2 ] 、图像分割[3 -4 ] 、自动驾驶[5 ] 等诸多方面取得了显著的进展. 随着深度神经网络模型的不断发展,安全性与鲁棒性问题日益凸显. Szegedy等[6 ] 发现深度神经网络容易受到微小的对抗性扰动影响,这些扰动是专门设计的,旨在欺骗模型使其误分类. 为了应对这一问题,防御算法不断涌现,其中对抗训练(adversarial training, AT)[7 ] 是常用的方法,通过在训练过程中引入对抗样本,提高系统的鲁棒性. 对抗训练可被视为极大极小的优化问题[8 ] . 该优化问题的内部目标为最大化损失函数以生成对抗样本,外部目标是最小化对抗性损失. 常见的对抗训练方法可以分为多步对抗训练和快速对抗训练. 多步对抗训练一般采用近似求解的方法,常用的方法为投影梯度下降(project gradient descent, PGD)[7 ] ,然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
基于多尺度互注意力的遥感图像语义分割网络
1
2023
... 深度神经网络在图像识别[1 -2 ] 、图像分割[3 -4 ] 、自动驾驶[5 ] 等诸多方面取得了显著的进展. 随着深度神经网络模型的不断发展,安全性与鲁棒性问题日益凸显. Szegedy等[6 ] 发现深度神经网络容易受到微小的对抗性扰动影响,这些扰动是专门设计的,旨在欺骗模型使其误分类. 为了应对这一问题,防御算法不断涌现,其中对抗训练(adversarial training, AT)[7 ] 是常用的方法,通过在训练过程中引入对抗样本,提高系统的鲁棒性. 对抗训练可被视为极大极小的优化问题[8 ] . 该优化问题的内部目标为最大化损失函数以生成对抗样本,外部目标是最小化对抗性损失. 常见的对抗训练方法可以分为多步对抗训练和快速对抗训练. 多步对抗训练一般采用近似求解的方法,常用的方法为投影梯度下降(project gradient descent, PGD)[7 ] ,然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
基于多源信息融合的医学图像分割方法
1
2023
... 深度神经网络在图像识别[1 -2 ] 、图像分割[3 -4 ] 、自动驾驶[5 ] 等诸多方面取得了显著的进展. 随着深度神经网络模型的不断发展,安全性与鲁棒性问题日益凸显. Szegedy等[6 ] 发现深度神经网络容易受到微小的对抗性扰动影响,这些扰动是专门设计的,旨在欺骗模型使其误分类. 为了应对这一问题,防御算法不断涌现,其中对抗训练(adversarial training, AT)[7 ] 是常用的方法,通过在训练过程中引入对抗样本,提高系统的鲁棒性. 对抗训练可被视为极大极小的优化问题[8 ] . 该优化问题的内部目标为最大化损失函数以生成对抗样本,外部目标是最小化对抗性损失. 常见的对抗训练方法可以分为多步对抗训练和快速对抗训练. 多步对抗训练一般采用近似求解的方法,常用的方法为投影梯度下降(project gradient descent, PGD)[7 ] ,然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
基于多源信息融合的医学图像分割方法
1
2023
... 深度神经网络在图像识别[1 -2 ] 、图像分割[3 -4 ] 、自动驾驶[5 ] 等诸多方面取得了显著的进展. 随着深度神经网络模型的不断发展,安全性与鲁棒性问题日益凸显. Szegedy等[6 ] 发现深度神经网络容易受到微小的对抗性扰动影响,这些扰动是专门设计的,旨在欺骗模型使其误分类. 为了应对这一问题,防御算法不断涌现,其中对抗训练(adversarial training, AT)[7 ] 是常用的方法,通过在训练过程中引入对抗样本,提高系统的鲁棒性. 对抗训练可被视为极大极小的优化问题[8 ] . 该优化问题的内部目标为最大化损失函数以生成对抗样本,外部目标是最小化对抗性损失. 常见的对抗训练方法可以分为多步对抗训练和快速对抗训练. 多步对抗训练一般采用近似求解的方法,常用的方法为投影梯度下降(project gradient descent, PGD)[7 ] ,然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
基于时空融合的多头注意力车辆轨迹预测
1
2023
... 深度神经网络在图像识别[1 -2 ] 、图像分割[3 -4 ] 、自动驾驶[5 ] 等诸多方面取得了显著的进展. 随着深度神经网络模型的不断发展,安全性与鲁棒性问题日益凸显. Szegedy等[6 ] 发现深度神经网络容易受到微小的对抗性扰动影响,这些扰动是专门设计的,旨在欺骗模型使其误分类. 为了应对这一问题,防御算法不断涌现,其中对抗训练(adversarial training, AT)[7 ] 是常用的方法,通过在训练过程中引入对抗样本,提高系统的鲁棒性. 对抗训练可被视为极大极小的优化问题[8 ] . 该优化问题的内部目标为最大化损失函数以生成对抗样本,外部目标是最小化对抗性损失. 常见的对抗训练方法可以分为多步对抗训练和快速对抗训练. 多步对抗训练一般采用近似求解的方法,常用的方法为投影梯度下降(project gradient descent, PGD)[7 ] ,然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
基于时空融合的多头注意力车辆轨迹预测
1
2023
... 深度神经网络在图像识别[1 -2 ] 、图像分割[3 -4 ] 、自动驾驶[5 ] 等诸多方面取得了显著的进展. 随着深度神经网络模型的不断发展,安全性与鲁棒性问题日益凸显. Szegedy等[6 ] 发现深度神经网络容易受到微小的对抗性扰动影响,这些扰动是专门设计的,旨在欺骗模型使其误分类. 为了应对这一问题,防御算法不断涌现,其中对抗训练(adversarial training, AT)[7 ] 是常用的方法,通过在训练过程中引入对抗样本,提高系统的鲁棒性. 对抗训练可被视为极大极小的优化问题[8 ] . 该优化问题的内部目标为最大化损失函数以生成对抗样本,外部目标是最小化对抗性损失. 常见的对抗训练方法可以分为多步对抗训练和快速对抗训练. 多步对抗训练一般采用近似求解的方法,常用的方法为投影梯度下降(project gradient descent, PGD)[7 ] ,然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
1
... 深度神经网络在图像识别[1 -2 ] 、图像分割[3 -4 ] 、自动驾驶[5 ] 等诸多方面取得了显著的进展. 随着深度神经网络模型的不断发展,安全性与鲁棒性问题日益凸显. Szegedy等[6 ] 发现深度神经网络容易受到微小的对抗性扰动影响,这些扰动是专门设计的,旨在欺骗模型使其误分类. 为了应对这一问题,防御算法不断涌现,其中对抗训练(adversarial training, AT)[7 ] 是常用的方法,通过在训练过程中引入对抗样本,提高系统的鲁棒性. 对抗训练可被视为极大极小的优化问题[8 ] . 该优化问题的内部目标为最大化损失函数以生成对抗样本,外部目标是最小化对抗性损失. 常见的对抗训练方法可以分为多步对抗训练和快速对抗训练. 多步对抗训练一般采用近似求解的方法,常用的方法为投影梯度下降(project gradient descent, PGD)[7 ] ,然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
5
... 深度神经网络在图像识别[1 -2 ] 、图像分割[3 -4 ] 、自动驾驶[5 ] 等诸多方面取得了显著的进展. 随着深度神经网络模型的不断发展,安全性与鲁棒性问题日益凸显. Szegedy等[6 ] 发现深度神经网络容易受到微小的对抗性扰动影响,这些扰动是专门设计的,旨在欺骗模型使其误分类. 为了应对这一问题,防御算法不断涌现,其中对抗训练(adversarial training, AT)[7 ] 是常用的方法,通过在训练过程中引入对抗样本,提高系统的鲁棒性. 对抗训练可被视为极大极小的优化问题[8 ] . 该优化问题的内部目标为最大化损失函数以生成对抗样本,外部目标是最小化对抗性损失. 常见的对抗训练方法可以分为多步对抗训练和快速对抗训练. 多步对抗训练一般采用近似求解的方法,常用的方法为投影梯度下降(project gradient descent, PGD)[7 ] ,然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
... [7 ],然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
... 为了评估本文方法的有效性,在CIFAR-10[21 ] 、CIFAR-100[21 ] 数据集上进行广泛的测试. 运用FGSM[9 ] 、PGD-10[7 ] 、PGD-20[7 ] 、PGD-50[7 ] 、C&W[22 ] 5种算法对训练好的模型进行攻击,将实验结果与其他先进方法进行对比分析. ...
... [7 ]、PGD-50[7 ] 、C&W[22 ] 5种算法对训练好的模型进行攻击,将实验结果与其他先进方法进行对比分析. ...
... [7 ]、C&W[22 ] 5种算法对训练好的模型进行攻击,将实验结果与其他先进方法进行对比分析. ...
1
... 深度神经网络在图像识别[1 -2 ] 、图像分割[3 -4 ] 、自动驾驶[5 ] 等诸多方面取得了显著的进展. 随着深度神经网络模型的不断发展,安全性与鲁棒性问题日益凸显. Szegedy等[6 ] 发现深度神经网络容易受到微小的对抗性扰动影响,这些扰动是专门设计的,旨在欺骗模型使其误分类. 为了应对这一问题,防御算法不断涌现,其中对抗训练(adversarial training, AT)[7 ] 是常用的方法,通过在训练过程中引入对抗样本,提高系统的鲁棒性. 对抗训练可被视为极大极小的优化问题[8 ] . 该优化问题的内部目标为最大化损失函数以生成对抗样本,外部目标是最小化对抗性损失. 常见的对抗训练方法可以分为多步对抗训练和快速对抗训练. 多步对抗训练一般采用近似求解的方法,常用的方法为投影梯度下降(project gradient descent, PGD)[7 ] ,然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
3
... 深度神经网络在图像识别[1 -2 ] 、图像分割[3 -4 ] 、自动驾驶[5 ] 等诸多方面取得了显著的进展. 随着深度神经网络模型的不断发展,安全性与鲁棒性问题日益凸显. Szegedy等[6 ] 发现深度神经网络容易受到微小的对抗性扰动影响,这些扰动是专门设计的,旨在欺骗模型使其误分类. 为了应对这一问题,防御算法不断涌现,其中对抗训练(adversarial training, AT)[7 ] 是常用的方法,通过在训练过程中引入对抗样本,提高系统的鲁棒性. 对抗训练可被视为极大极小的优化问题[8 ] . 该优化问题的内部目标为最大化损失函数以生成对抗样本,外部目标是最小化对抗性损失. 常见的对抗训练方法可以分为多步对抗训练和快速对抗训练. 多步对抗训练一般采用近似求解的方法,常用的方法为投影梯度下降(project gradient descent, PGD)[7 ] ,然而该方法需要进行多次梯度运算,计算成本较高. 相对而言,基于快速梯度符号方法(fast gradient sign method, FGSM)[9 ] 的快速对抗训练在提高系统鲁棒性方面虽不如多步对抗训练,但计算成本较低. ...
... 在快速对抗训练方法中,通常采用基于FGSM[9 ] 的对抗训练,生成的对抗扰动可以表示为 ...
... 为了评估本文方法的有效性,在CIFAR-10[21 ] 、CIFAR-100[21 ] 数据集上进行广泛的测试. 运用FGSM[9 ] 、PGD-10[7 ] 、PGD-20[7 ] 、PGD-50[7 ] 、C&W[22 ] 5种算法对训练好的模型进行攻击,将实验结果与其他先进方法进行对比分析. ...
9
... 针对上述问题,研究人员开始探索如何运用快速对抗训练来提升系统鲁棒性. 其中,初始化方法成为研究热点. Wong等[10 ] 针对快速对抗训练的过拟合问题提出FGSM-RS模型,结合快速对抗训练与随机初始化,缓解了对抗训练中的过拟合问题. 在此基础上,Andriushchenko等[11 ] 提出正则化的方法,称为FGSM-GA,以应对过拟合问题. Kim等[12 ] 提出FGSM-CKPT模型,通过调整图像尺寸来抑制过拟合. Shafahi等[13 ] 提出Free-AT模型,训练成本几乎与自然训练相当. Sriramanan等[14 ] 使用核范数来优化对抗样本的生成,提出NuAT模型. ...
... 为了评估提出方法的可行性,选取一些先进方法进行对比,包括FGSM-RS[10 ] 、FGSM-GA[11 ] 、FGSM-CKPT[12 ] 、Free-AT[12 ] 等方法. 在对比实验中,按照原文中的设置进行训练,选取各方法在相应数据集上的最优结果作为评价指标. ...
... Test robustness on CIFAR-10 database using ResNet18
% Tab.1 方法 模型 P clean P robust PGD-10 PGD-20 PGD-50 C&W Auto-Attack FGSM-RS[10 ] 最好 73.81 42.31 41.55 41.26 39.84 37.07 FGSM-RS[10 ] 最后 83.82 0.09 0.04 0.02 0.00 0.00 FGSM-CKPT[12 ] 最好 90.29 41.96 39.84 39.15 41.13 37.15 FGSM-CKPT[12 ] 最后 90.29 41.96 39.84 39.15 41.13 37.15 FGSM-GA[11 ] 最好 83.96 49.23 47.57 46.89 47.46 43.45 FGSM-GA[11 ] 最后 84.43 48.67 46.66 46.08 46.75 42.63 Free-AT[12 ] 最好 80.38 47.10 45.85 45.62 44.42 42.17 Free-AT[12 ] 最后 80.75 45.82 44.82 44.48 43.73 41.17 本文方法 最好 83.30 51.86 50.61 50.15 49.65 46.42 本文方法 最后 83.76 51.55 50.16 49.84 49.68 46.21
图 5 在不同攻击方式下ResNet18在CIFAR-10上的鲁棒精度对比 ...
... [
10 ]
最后 83.82 0.09 0.04 0.02 0.00 0.00 FGSM-CKPT[12 ] 最好 90.29 41.96 39.84 39.15 41.13 37.15 FGSM-CKPT[12 ] 最后 90.29 41.96 39.84 39.15 41.13 37.15 FGSM-GA[11 ] 最好 83.96 49.23 47.57 46.89 47.46 43.45 FGSM-GA[11 ] 最后 84.43 48.67 46.66 46.08 46.75 42.63 Free-AT[12 ] 最好 80.38 47.10 45.85 45.62 44.42 42.17 Free-AT[12 ] 最后 80.75 45.82 44.82 44.48 43.73 41.17 本文方法 最好 83.30 51.86 50.61 50.15 49.65 46.42 本文方法 最后 83.76 51.55 50.16 49.84 49.68 46.21 图 5 在不同攻击方式下ResNet18在CIFAR-10上的鲁棒精度对比 ...
... Test robustness on CIFAR-10 database using WideResNet34-10
% Tab.2 方法 P clean P robust PGD-10 PGD-20 PGD-50 C&W Auto-Attack FGSM-RS[10 ] 74.29 41.24 40.21 39.98 39.27 36.40 FGSM-CKPT[12 ] 91.84 44.70 42.72 42.22 42.25 40.46 FGSM-GA[11 ] 81.80 48.20 47.97 46.60 46.87 45.19 Free-AT[12 ] 81.83 49.07 48.17 47.83 47.25 44.77 本文方法 83.54 51.05 49.66 49.21 49.06 44.76
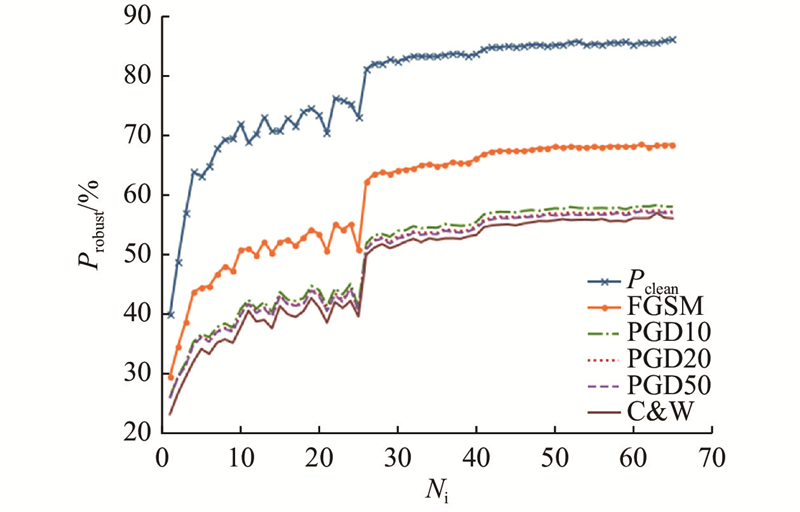
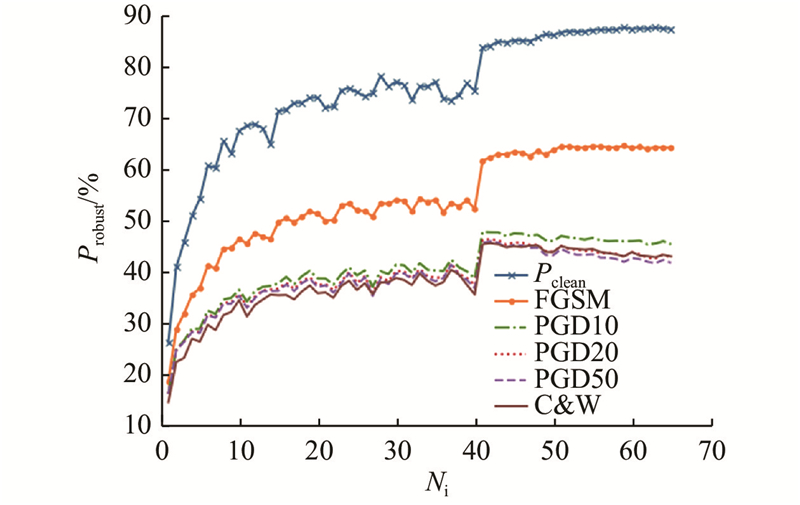
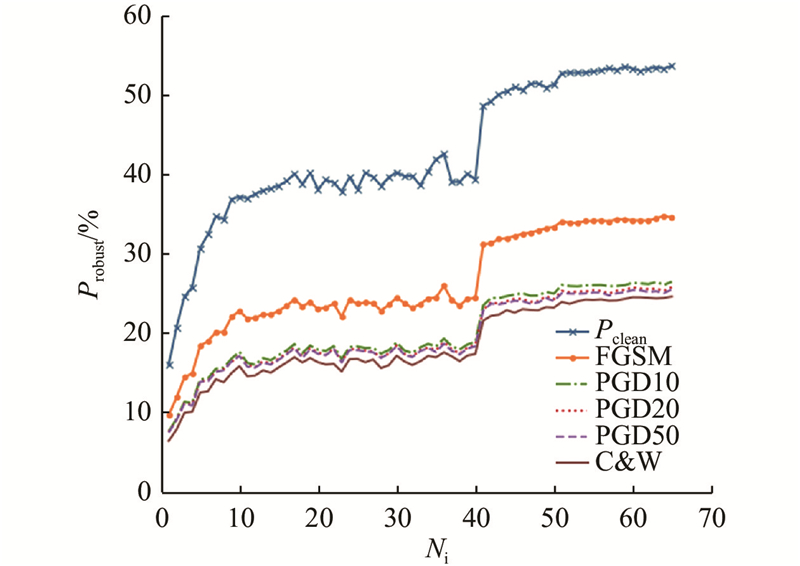
为了研究本文方法在不同攻击下的表现,对训练过程中该方法的鲁棒精度变化趋势进行可视化,如图6 所示. 图中,$N_{\mathrm{i}} $ 图6 可以看出,在整个训练过程中,鲁棒精度稳步提升,当调整学习速率时有显著提升,未出现过拟合现象,说明该方法可以有效解决快速对抗训练中的灾难性过拟合问题,证明了提出方法的有效性. 为了验证该现象具有普适性,在PreActNet18框架下绘制了该方法在面对不同攻击时鲁棒精度的变化趋势,如图7 所示. 在不同的网络架构下,鲁棒精度的变化趋势与更复杂的网络WideResNet34-10框架下的趋势保持一致,表明所提方法具有普适性和有效性. ...
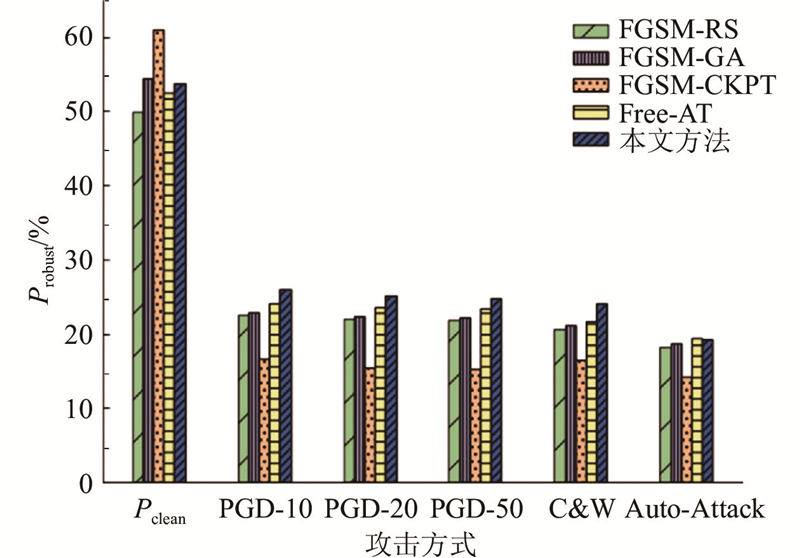
... 在ResNet18框架下,将所提出的方法与其他先进算法进行比较,比较结果如表3 所示. 在更复杂的数据集上,本文方法展现出了优越的性能. 在PGD-20攻击下,所提方法的鲁棒性比Free-AT[12 ] 提高了1.7%. 在C&W攻击下,比FGSM-RS[10 ] 提高了3.52%. 在Auto-Attack攻击下与Free-AT[12 ] 表现相当,均取得了19%以上的鲁棒性,具体的对比结果如图8 所示. ...
... Test robustness on CIFAR-100 database using ResNet18
% Tab.3 方法 模型 P clean P robust PGD-10 PGD-20 PGD-50 C&W Auto-Attack FGSM-RS[10 ] 最好 49.85 22.47 22.01 21.82 20.55 18.29 FGSM-RS[10 ] 最后 60.55 0.25 0.19 0.25 0.00 0.00 FGSM-CKPT[12 ] 最好 60.93 16.58 15.47 15.19 16.40 14.17 FGSM-CKPT[12 ] 最后 60.93 16.69 15.61 15.24 16.60 14.34 FGSM-GA[11 ] 最好 54.35 22.93 22.36 22.20 21.20 18.80 FGSM-GA[11 ] 最后 55.10 20.04 19.13 18.84 18.96 16.45 Free-AT[12 ] 最好 52.49 24.07 23.52 23.36 21.66 19.47 Free-AT[12 ] 最后 52.63 22.86 22.32 22.16 20.68 18.57 本文方法 最好 53.77 25.92 25.22 24.82 24.07 19.28 本文方法 最后 54.08 25.91 25.00 24.67 23.82 19.16
图 8 在不同攻击方式下ResNet18在CIFAR-100上的鲁棒精度对比 ...
... [
10 ]
最后 60.55 0.25 0.19 0.25 0.00 0.00 FGSM-CKPT[12 ] 最好 60.93 16.58 15.47 15.19 16.40 14.17 FGSM-CKPT[12 ] 最后 60.93 16.69 15.61 15.24 16.60 14.34 FGSM-GA[11 ] 最好 54.35 22.93 22.36 22.20 21.20 18.80 FGSM-GA[11 ] 最后 55.10 20.04 19.13 18.84 18.96 16.45 Free-AT[12 ] 最好 52.49 24.07 23.52 23.36 21.66 19.47 Free-AT[12 ] 最后 52.63 22.86 22.32 22.16 20.68 18.57 本文方法 最好 53.77 25.92 25.22 24.82 24.07 19.28 本文方法 最后 54.08 25.91 25.00 24.67 23.82 19.16 图 8 在不同攻击方式下ResNet18在CIFAR-100上的鲁棒精度对比 ...
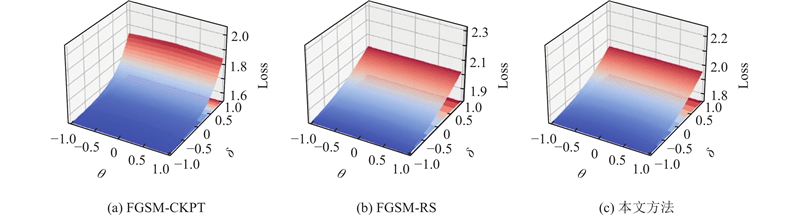
... CIFAR-10和CIFAR-100数据集上的结果验证了所提出方法的有效性. 为了评估该方法的稳健性,将该方法与FGSM-CKPT[12 ] 、FGSM-RS[10 ] 方法的损失景观图进行对比. 图10 中,$ \theta $ 图10 所示,沿对抗方向和随机方向绘制空间变化的交叉熵损失. 与FGSM-CKPT相比,本文提出的方法更加线性,与FGSM-RS相比在线性度上未有明显差距,但具有更小的损失,这表明所提出的方法能够更好地拟合数据. 总之,使用该方法生成的对抗扰动可以更好地保持目标模型的局部线性性质. 利用所提出的方法,可以提高快速对抗训练模型的鲁棒性. ...
10
... 针对上述问题,研究人员开始探索如何运用快速对抗训练来提升系统鲁棒性. 其中,初始化方法成为研究热点. Wong等[10 ] 针对快速对抗训练的过拟合问题提出FGSM-RS模型,结合快速对抗训练与随机初始化,缓解了对抗训练中的过拟合问题. 在此基础上,Andriushchenko等[11 ] 提出正则化的方法,称为FGSM-GA,以应对过拟合问题. Kim等[12 ] 提出FGSM-CKPT模型,通过调整图像尺寸来抑制过拟合. Shafahi等[13 ] 提出Free-AT模型,训练成本几乎与自然训练相当. Sriramanan等[14 ] 使用核范数来优化对抗样本的生成,提出NuAT模型. ...
... 为了评估提出方法的可行性,选取一些先进方法进行对比,包括FGSM-RS[10 ] 、FGSM-GA[11 ] 、FGSM-CKPT[12 ] 、Free-AT[12 ] 等方法. 在对比实验中,按照原文中的设置进行训练,选取各方法在相应数据集上的最优结果作为评价指标. ...
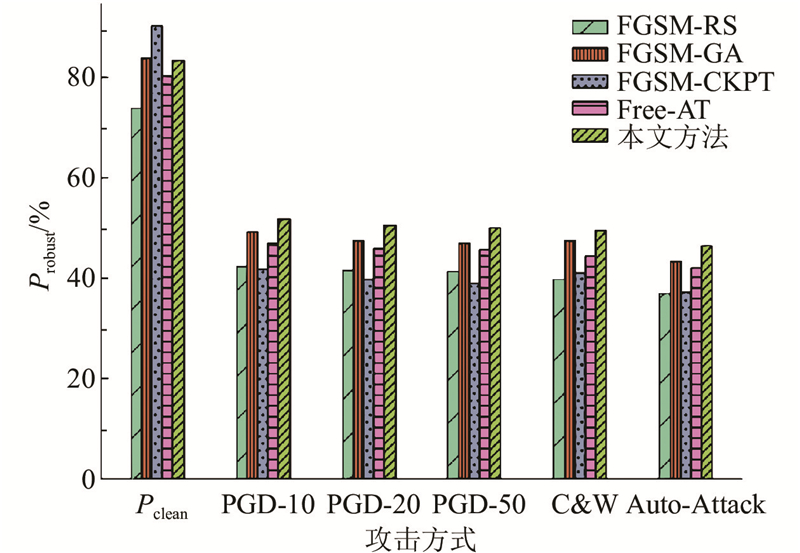
... 在以ResNet18作为目标网络的实验中,将所提出的方法与其他先进算法进行对比,比较结果如表1 所示. 选取在训练过程中表现最佳的模型,与最后一个模型分别进行对比. 表中,P clean 为干净精度,P robust 为鲁棒精度. 从表1 可知,所提出的方法在不同攻击方式下均取得了最优的鲁棒精度. 虽然所提出方法的干净精度未达到最优,但表现出良好的性能,实现了鲁棒精度和干净精度之间的平衡. 例如在PGD-10攻击下,所提出方法的鲁棒精度比FGSM-GA[11 ] 方法高2.63%. 在C&W攻击下,相较于Free-AT[12 ] ,本文方法提高了5.23%的性能. 在Auto-Attack攻击下,本文方法的鲁棒精度达到46.42%,比FGSM-CKPT[12 ] 方法高9.27%. 为了说明本文方法的优越性,将对比结果进行可视化,如图5 所示. 可知,提出方法的性能较现有的一些方法具有显著的优势. 这主要是由于在对抗样本生成环节中引入了随机谱变换. ...
... Test robustness on CIFAR-10 database using ResNet18
% Tab.1 方法 模型 P clean P robust PGD-10 PGD-20 PGD-50 C&W Auto-Attack FGSM-RS[10 ] 最好 73.81 42.31 41.55 41.26 39.84 37.07 FGSM-RS[10 ] 最后 83.82 0.09 0.04 0.02 0.00 0.00 FGSM-CKPT[12 ] 最好 90.29 41.96 39.84 39.15 41.13 37.15 FGSM-CKPT[12 ] 最后 90.29 41.96 39.84 39.15 41.13 37.15 FGSM-GA[11 ] 最好 83.96 49.23 47.57 46.89 47.46 43.45 FGSM-GA[11 ] 最后 84.43 48.67 46.66 46.08 46.75 42.63 Free-AT[12 ] 最好 80.38 47.10 45.85 45.62 44.42 42.17 Free-AT[12 ] 最后 80.75 45.82 44.82 44.48 43.73 41.17 本文方法 最好 83.30 51.86 50.61 50.15 49.65 46.42 本文方法 最后 83.76 51.55 50.16 49.84 49.68 46.21
图 5 在不同攻击方式下ResNet18在CIFAR-10上的鲁棒精度对比 ...
... [
11 ]
最后 84.43 48.67 46.66 46.08 46.75 42.63 Free-AT[12 ] 最好 80.38 47.10 45.85 45.62 44.42 42.17 Free-AT[12 ] 最后 80.75 45.82 44.82 44.48 43.73 41.17 本文方法 最好 83.30 51.86 50.61 50.15 49.65 46.42 本文方法 最后 83.76 51.55 50.16 49.84 49.68 46.21 图 5 在不同攻击方式下ResNet18在CIFAR-10上的鲁棒精度对比 ...
... 在同样的参数设置下,将目标网络更换为网络结构更复杂的WideResNet34-10. 如表2 所示为该框架下所提出的方法与其他方法的对比结果. 在不同的攻击方式下,本文方法展现出了更优的性能. 在PGD-10的攻击下,相比Free-AT[12 ] ,本文方法的鲁棒性提高了1.98%. 在C&W攻击下,本文方法的鲁棒精度比FGSM-GA[11 ] 方法高2.19%. 在更具挑战性的Auto-Attack攻击下,与FGSM-GA[11 ] 相比,鲁棒精度均达到45%左右. ...
... [11 ]相比,鲁棒精度均达到45%左右. ...
... Test robustness on CIFAR-10 database using WideResNet34-10
% Tab.2 方法 P clean P robust PGD-10 PGD-20 PGD-50 C&W Auto-Attack FGSM-RS[10 ] 74.29 41.24 40.21 39.98 39.27 36.40 FGSM-CKPT[12 ] 91.84 44.70 42.72 42.22 42.25 40.46 FGSM-GA[11 ] 81.80 48.20 47.97 46.60 46.87 45.19 Free-AT[12 ] 81.83 49.07 48.17 47.83 47.25 44.77 本文方法 83.54 51.05 49.66 49.21 49.06 44.76
为了研究本文方法在不同攻击下的表现,对训练过程中该方法的鲁棒精度变化趋势进行可视化,如图6 所示. 图中,$N_{\mathrm{i}} $ 图6 可以看出,在整个训练过程中,鲁棒精度稳步提升,当调整学习速率时有显著提升,未出现过拟合现象,说明该方法可以有效解决快速对抗训练中的灾难性过拟合问题,证明了提出方法的有效性. 为了验证该现象具有普适性,在PreActNet18框架下绘制了该方法在面对不同攻击时鲁棒精度的变化趋势,如图7 所示. 在不同的网络架构下,鲁棒精度的变化趋势与更复杂的网络WideResNet34-10框架下的趋势保持一致,表明所提方法具有普适性和有效性. ...
... Test robustness on CIFAR-100 database using ResNet18
% Tab.3 方法 模型 P clean P robust PGD-10 PGD-20 PGD-50 C&W Auto-Attack FGSM-RS[10 ] 最好 49.85 22.47 22.01 21.82 20.55 18.29 FGSM-RS[10 ] 最后 60.55 0.25 0.19 0.25 0.00 0.00 FGSM-CKPT[12 ] 最好 60.93 16.58 15.47 15.19 16.40 14.17 FGSM-CKPT[12 ] 最后 60.93 16.69 15.61 15.24 16.60 14.34 FGSM-GA[11 ] 最好 54.35 22.93 22.36 22.20 21.20 18.80 FGSM-GA[11 ] 最后 55.10 20.04 19.13 18.84 18.96 16.45 Free-AT[12 ] 最好 52.49 24.07 23.52 23.36 21.66 19.47 Free-AT[12 ] 最后 52.63 22.86 22.32 22.16 20.68 18.57 本文方法 最好 53.77 25.92 25.22 24.82 24.07 19.28 本文方法 最后 54.08 25.91 25.00 24.67 23.82 19.16
图 8 在不同攻击方式下ResNet18在CIFAR-100上的鲁棒精度对比 ...
... [
11 ]
最后 55.10 20.04 19.13 18.84 18.96 16.45 Free-AT[12 ] 最好 52.49 24.07 23.52 23.36 21.66 19.47 Free-AT[12 ] 最后 52.63 22.86 22.32 22.16 20.68 18.57 本文方法 最好 53.77 25.92 25.22 24.82 24.07 19.28 本文方法 最后 54.08 25.91 25.00 24.67 23.82 19.16 图 8 在不同攻击方式下ResNet18在CIFAR-100上的鲁棒精度对比 ...
19
... 针对上述问题,研究人员开始探索如何运用快速对抗训练来提升系统鲁棒性. 其中,初始化方法成为研究热点. Wong等[10 ] 针对快速对抗训练的过拟合问题提出FGSM-RS模型,结合快速对抗训练与随机初始化,缓解了对抗训练中的过拟合问题. 在此基础上,Andriushchenko等[11 ] 提出正则化的方法,称为FGSM-GA,以应对过拟合问题. Kim等[12 ] 提出FGSM-CKPT模型,通过调整图像尺寸来抑制过拟合. Shafahi等[13 ] 提出Free-AT模型,训练成本几乎与自然训练相当. Sriramanan等[14 ] 使用核范数来优化对抗样本的生成,提出NuAT模型. ...
... 为了评估提出方法的可行性,选取一些先进方法进行对比,包括FGSM-RS[10 ] 、FGSM-GA[11 ] 、FGSM-CKPT[12 ] 、Free-AT[12 ] 等方法. 在对比实验中,按照原文中的设置进行训练,选取各方法在相应数据集上的最优结果作为评价指标. ...
... [12 ]等方法. 在对比实验中,按照原文中的设置进行训练,选取各方法在相应数据集上的最优结果作为评价指标. ...
... 在以ResNet18作为目标网络的实验中,将所提出的方法与其他先进算法进行对比,比较结果如表1 所示. 选取在训练过程中表现最佳的模型,与最后一个模型分别进行对比. 表中,P clean 为干净精度,P robust 为鲁棒精度. 从表1 可知,所提出的方法在不同攻击方式下均取得了最优的鲁棒精度. 虽然所提出方法的干净精度未达到最优,但表现出良好的性能,实现了鲁棒精度和干净精度之间的平衡. 例如在PGD-10攻击下,所提出方法的鲁棒精度比FGSM-GA[11 ] 方法高2.63%. 在C&W攻击下,相较于Free-AT[12 ] ,本文方法提高了5.23%的性能. 在Auto-Attack攻击下,本文方法的鲁棒精度达到46.42%,比FGSM-CKPT[12 ] 方法高9.27%. 为了说明本文方法的优越性,将对比结果进行可视化,如图5 所示. 可知,提出方法的性能较现有的一些方法具有显著的优势. 这主要是由于在对抗样本生成环节中引入了随机谱变换. ...
... [12 ]方法高9.27%. 为了说明本文方法的优越性,将对比结果进行可视化,如图5 所示. 可知,提出方法的性能较现有的一些方法具有显著的优势. 这主要是由于在对抗样本生成环节中引入了随机谱变换. ...
... Test robustness on CIFAR-10 database using ResNet18
% Tab.1 方法 模型 P clean P robust PGD-10 PGD-20 PGD-50 C&W Auto-Attack FGSM-RS[10 ] 最好 73.81 42.31 41.55 41.26 39.84 37.07 FGSM-RS[10 ] 最后 83.82 0.09 0.04 0.02 0.00 0.00 FGSM-CKPT[12 ] 最好 90.29 41.96 39.84 39.15 41.13 37.15 FGSM-CKPT[12 ] 最后 90.29 41.96 39.84 39.15 41.13 37.15 FGSM-GA[11 ] 最好 83.96 49.23 47.57 46.89 47.46 43.45 FGSM-GA[11 ] 最后 84.43 48.67 46.66 46.08 46.75 42.63 Free-AT[12 ] 最好 80.38 47.10 45.85 45.62 44.42 42.17 Free-AT[12 ] 最后 80.75 45.82 44.82 44.48 43.73 41.17 本文方法 最好 83.30 51.86 50.61 50.15 49.65 46.42 本文方法 最后 83.76 51.55 50.16 49.84 49.68 46.21
图 5 在不同攻击方式下ResNet18在CIFAR-10上的鲁棒精度对比 ...
... [
12 ]
最后 90.29 41.96 39.84 39.15 41.13 37.15 FGSM-GA[11 ] 最好 83.96 49.23 47.57 46.89 47.46 43.45 FGSM-GA[11 ] 最后 84.43 48.67 46.66 46.08 46.75 42.63 Free-AT[12 ] 最好 80.38 47.10 45.85 45.62 44.42 42.17 Free-AT[12 ] 最后 80.75 45.82 44.82 44.48 43.73 41.17 本文方法 最好 83.30 51.86 50.61 50.15 49.65 46.42 本文方法 最后 83.76 51.55 50.16 49.84 49.68 46.21 图 5 在不同攻击方式下ResNet18在CIFAR-10上的鲁棒精度对比 ...
... [
12 ]
最好 80.38 47.10 45.85 45.62 44.42 42.17 Free-AT[12 ] 最后 80.75 45.82 44.82 44.48 43.73 41.17 本文方法 最好 83.30 51.86 50.61 50.15 49.65 46.42 本文方法 最后 83.76 51.55 50.16 49.84 49.68 46.21 图 5 在不同攻击方式下ResNet18在CIFAR-10上的鲁棒精度对比 ...
... [
12 ]
最后 80.75 45.82 44.82 44.48 43.73 41.17 本文方法 最好 83.30 51.86 50.61 50.15 49.65 46.42 本文方法 最后 83.76 51.55 50.16 49.84 49.68 46.21 图 5 在不同攻击方式下ResNet18在CIFAR-10上的鲁棒精度对比 ...
... 在同样的参数设置下,将目标网络更换为网络结构更复杂的WideResNet34-10. 如表2 所示为该框架下所提出的方法与其他方法的对比结果. 在不同的攻击方式下,本文方法展现出了更优的性能. 在PGD-10的攻击下,相比Free-AT[12 ] ,本文方法的鲁棒性提高了1.98%. 在C&W攻击下,本文方法的鲁棒精度比FGSM-GA[11 ] 方法高2.19%. 在更具挑战性的Auto-Attack攻击下,与FGSM-GA[11 ] 相比,鲁棒精度均达到45%左右. ...
... Test robustness on CIFAR-10 database using WideResNet34-10
% Tab.2 方法 P clean P robust PGD-10 PGD-20 PGD-50 C&W Auto-Attack FGSM-RS[10 ] 74.29 41.24 40.21 39.98 39.27 36.40 FGSM-CKPT[12 ] 91.84 44.70 42.72 42.22 42.25 40.46 FGSM-GA[11 ] 81.80 48.20 47.97 46.60 46.87 45.19 Free-AT[12 ] 81.83 49.07 48.17 47.83 47.25 44.77 本文方法 83.54 51.05 49.66 49.21 49.06 44.76
为了研究本文方法在不同攻击下的表现,对训练过程中该方法的鲁棒精度变化趋势进行可视化,如图6 所示. 图中,$N_{\mathrm{i}} $ 图6 可以看出,在整个训练过程中,鲁棒精度稳步提升,当调整学习速率时有显著提升,未出现过拟合现象,说明该方法可以有效解决快速对抗训练中的灾难性过拟合问题,证明了提出方法的有效性. 为了验证该现象具有普适性,在PreActNet18框架下绘制了该方法在面对不同攻击时鲁棒精度的变化趋势,如图7 所示. 在不同的网络架构下,鲁棒精度的变化趋势与更复杂的网络WideResNet34-10框架下的趋势保持一致,表明所提方法具有普适性和有效性. ...
... [
12 ]
81.83 49.07 48.17 47.83 47.25 44.77 本文方法 83.54 51.05 49.66 49.21 49.06 44.76 为了研究本文方法在不同攻击下的表现,对训练过程中该方法的鲁棒精度变化趋势进行可视化,如图6 所示. 图中,$N_{\mathrm{i}} $ 图6 可以看出,在整个训练过程中,鲁棒精度稳步提升,当调整学习速率时有显著提升,未出现过拟合现象,说明该方法可以有效解决快速对抗训练中的灾难性过拟合问题,证明了提出方法的有效性. 为了验证该现象具有普适性,在PreActNet18框架下绘制了该方法在面对不同攻击时鲁棒精度的变化趋势,如图7 所示. 在不同的网络架构下,鲁棒精度的变化趋势与更复杂的网络WideResNet34-10框架下的趋势保持一致,表明所提方法具有普适性和有效性. ...
... 在ResNet18框架下,将所提出的方法与其他先进算法进行比较,比较结果如表3 所示. 在更复杂的数据集上,本文方法展现出了优越的性能. 在PGD-20攻击下,所提方法的鲁棒性比Free-AT[12 ] 提高了1.7%. 在C&W攻击下,比FGSM-RS[10 ] 提高了3.52%. 在Auto-Attack攻击下与Free-AT[12 ] 表现相当,均取得了19%以上的鲁棒性,具体的对比结果如图8 所示. ...
... [12 ]表现相当,均取得了19%以上的鲁棒性,具体的对比结果如图8 所示. ...
... Test robustness on CIFAR-100 database using ResNet18
% Tab.3 方法 模型 P clean P robust PGD-10 PGD-20 PGD-50 C&W Auto-Attack FGSM-RS[10 ] 最好 49.85 22.47 22.01 21.82 20.55 18.29 FGSM-RS[10 ] 最后 60.55 0.25 0.19 0.25 0.00 0.00 FGSM-CKPT[12 ] 最好 60.93 16.58 15.47 15.19 16.40 14.17 FGSM-CKPT[12 ] 最后 60.93 16.69 15.61 15.24 16.60 14.34 FGSM-GA[11 ] 最好 54.35 22.93 22.36 22.20 21.20 18.80 FGSM-GA[11 ] 最后 55.10 20.04 19.13 18.84 18.96 16.45 Free-AT[12 ] 最好 52.49 24.07 23.52 23.36 21.66 19.47 Free-AT[12 ] 最后 52.63 22.86 22.32 22.16 20.68 18.57 本文方法 最好 53.77 25.92 25.22 24.82 24.07 19.28 本文方法 最后 54.08 25.91 25.00 24.67 23.82 19.16
图 8 在不同攻击方式下ResNet18在CIFAR-100上的鲁棒精度对比 ...
... [
12 ]
最后 60.93 16.69 15.61 15.24 16.60 14.34 FGSM-GA[11 ] 最好 54.35 22.93 22.36 22.20 21.20 18.80 FGSM-GA[11 ] 最后 55.10 20.04 19.13 18.84 18.96 16.45 Free-AT[12 ] 最好 52.49 24.07 23.52 23.36 21.66 19.47 Free-AT[12 ] 最后 52.63 22.86 22.32 22.16 20.68 18.57 本文方法 最好 53.77 25.92 25.22 24.82 24.07 19.28 本文方法 最后 54.08 25.91 25.00 24.67 23.82 19.16 图 8 在不同攻击方式下ResNet18在CIFAR-100上的鲁棒精度对比 ...
... [
12 ]
最好 52.49 24.07 23.52 23.36 21.66 19.47 Free-AT[12 ] 最后 52.63 22.86 22.32 22.16 20.68 18.57 本文方法 最好 53.77 25.92 25.22 24.82 24.07 19.28 本文方法 最后 54.08 25.91 25.00 24.67 23.82 19.16 图 8 在不同攻击方式下ResNet18在CIFAR-100上的鲁棒精度对比 ...
... [
12 ]
最后 52.63 22.86 22.32 22.16 20.68 18.57 本文方法 最好 53.77 25.92 25.22 24.82 24.07 19.28 本文方法 最后 54.08 25.91 25.00 24.67 23.82 19.16 图 8 在不同攻击方式下ResNet18在CIFAR-100上的鲁棒精度对比 ...
... CIFAR-10和CIFAR-100数据集上的结果验证了所提出方法的有效性. 为了评估该方法的稳健性,将该方法与FGSM-CKPT[12 ] 、FGSM-RS[10 ] 方法的损失景观图进行对比. 图10 中,$ \theta $ 图10 所示,沿对抗方向和随机方向绘制空间变化的交叉熵损失. 与FGSM-CKPT相比,本文提出的方法更加线性,与FGSM-RS相比在线性度上未有明显差距,但具有更小的损失,这表明所提出的方法能够更好地拟合数据. 总之,使用该方法生成的对抗扰动可以更好地保持目标模型的局部线性性质. 利用所提出的方法,可以提高快速对抗训练模型的鲁棒性. ...
1
... 针对上述问题,研究人员开始探索如何运用快速对抗训练来提升系统鲁棒性. 其中,初始化方法成为研究热点. Wong等[10 ] 针对快速对抗训练的过拟合问题提出FGSM-RS模型,结合快速对抗训练与随机初始化,缓解了对抗训练中的过拟合问题. 在此基础上,Andriushchenko等[11 ] 提出正则化的方法,称为FGSM-GA,以应对过拟合问题. Kim等[12 ] 提出FGSM-CKPT模型,通过调整图像尺寸来抑制过拟合. Shafahi等[13 ] 提出Free-AT模型,训练成本几乎与自然训练相当. Sriramanan等[14 ] 使用核范数来优化对抗样本的生成,提出NuAT模型. ...
1
... 针对上述问题,研究人员开始探索如何运用快速对抗训练来提升系统鲁棒性. 其中,初始化方法成为研究热点. Wong等[10 ] 针对快速对抗训练的过拟合问题提出FGSM-RS模型,结合快速对抗训练与随机初始化,缓解了对抗训练中的过拟合问题. 在此基础上,Andriushchenko等[11 ] 提出正则化的方法,称为FGSM-GA,以应对过拟合问题. Kim等[12 ] 提出FGSM-CKPT模型,通过调整图像尺寸来抑制过拟合. Shafahi等[13 ] 提出Free-AT模型,训练成本几乎与自然训练相当. Sriramanan等[14 ] 使用核范数来优化对抗样本的生成,提出NuAT模型. ...
1
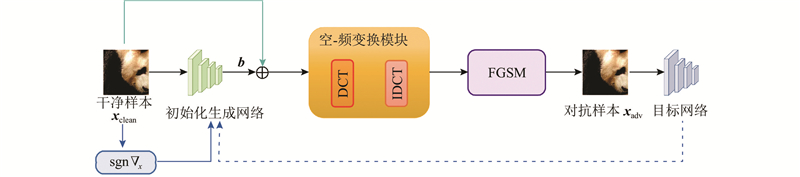
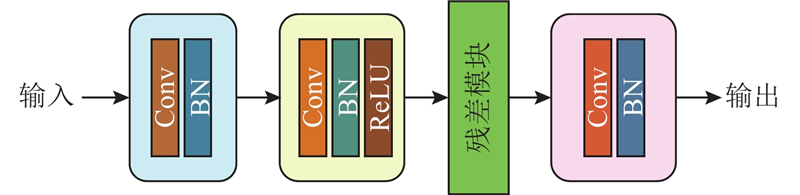
... 样本初始化生成模块的输入为干净样本及样本的梯度信息,输出为样本的初始化信息. 生成的对抗初始化信息将被用于对抗样本生成模块,参与对抗样本的生成. 为了兼顾网络的运行效率和性能,选择轻量级生成网络作为初始化生成器. 生成网络的结构包含4层,其中第1层和第4层是单一的卷积层和归一化层[15 ] ,第2层由卷积层、归一化层和激活函数组成,激活函数采用ReLU[16 ] ,第3层采用残差模块[17 ] . 在网络设计中,不同层次采用不同的卷积和滤波器设置. 这种设置可以帮助网络更好地学习特定的特征和信息,以生成更好的对抗性初始化. 使用批量归一化层和ReLU激活函数提高训练的稳定性和收敛性,批量归一化层有助于防止梯度消失和爆炸的问题. ReLU激活函数引入非线性,以便网络可以更好地捕捉图像中的特征. 提出的生成网络生成了与每个样本相关的初始化,这意味着每个输入样本都有与其对应的对抗性初始化,而不是使用随机初始化. 这不仅有利于解决灾难性过拟合问题,而且可以提高对抗性训练的效果. 具体的初始化生成网络架构如图2 所示. ...
1
... 样本初始化生成模块的输入为干净样本及样本的梯度信息,输出为样本的初始化信息. 生成的对抗初始化信息将被用于对抗样本生成模块,参与对抗样本的生成. 为了兼顾网络的运行效率和性能,选择轻量级生成网络作为初始化生成器. 生成网络的结构包含4层,其中第1层和第4层是单一的卷积层和归一化层[15 ] ,第2层由卷积层、归一化层和激活函数组成,激活函数采用ReLU[16 ] ,第3层采用残差模块[17 ] . 在网络设计中,不同层次采用不同的卷积和滤波器设置. 这种设置可以帮助网络更好地学习特定的特征和信息,以生成更好的对抗性初始化. 使用批量归一化层和ReLU激活函数提高训练的稳定性和收敛性,批量归一化层有助于防止梯度消失和爆炸的问题. ReLU激活函数引入非线性,以便网络可以更好地捕捉图像中的特征. 提出的生成网络生成了与每个样本相关的初始化,这意味着每个输入样本都有与其对应的对抗性初始化,而不是使用随机初始化. 这不仅有利于解决灾难性过拟合问题,而且可以提高对抗性训练的效果. 具体的初始化生成网络架构如图2 所示. ...
1
... 样本初始化生成模块的输入为干净样本及样本的梯度信息,输出为样本的初始化信息. 生成的对抗初始化信息将被用于对抗样本生成模块,参与对抗样本的生成. 为了兼顾网络的运行效率和性能,选择轻量级生成网络作为初始化生成器. 生成网络的结构包含4层,其中第1层和第4层是单一的卷积层和归一化层[15 ] ,第2层由卷积层、归一化层和激活函数组成,激活函数采用ReLU[16 ] ,第3层采用残差模块[17 ] . 在网络设计中,不同层次采用不同的卷积和滤波器设置. 这种设置可以帮助网络更好地学习特定的特征和信息,以生成更好的对抗性初始化. 使用批量归一化层和ReLU激活函数提高训练的稳定性和收敛性,批量归一化层有助于防止梯度消失和爆炸的问题. ReLU激活函数引入非线性,以便网络可以更好地捕捉图像中的特征. 提出的生成网络生成了与每个样本相关的初始化,这意味着每个输入样本都有与其对应的对抗性初始化,而不是使用随机初始化. 这不仅有利于解决灾难性过拟合问题,而且可以提高对抗性训练的效果. 具体的初始化生成网络架构如图2 所示. ...
1
... Wang等[18 ] 的研究表明,模型在做出决策时会根据输入图像的不同频率分量进行判别. 本文绘制频谱显著性特征图,如图3 所示,不同模型对不同频率分量的兴趣通常会因模型而异. 频谱显著性图被视为模型损失函数相对于输入图像的频谱的梯度,具体的绘制方法可以描述如下. ...
R. Discrete cosine transform
1
1974
... 式中:$D( \cdot )$ [19 ] ,${{\boldsymbol{A}}}$ ${{\boldsymbol{A}}}{{{\boldsymbol{A}}}^{{\mathrm{T}}}}$ ${\boldsymbol{x}}_{\boldsymbol{b}} $ ${\boldsymbol{x}} $ . 一幅图像经过DCT变换后,其主要能量集中在频谱的低频部分,图像的细节信息分布在中高频部分. ...
1
... 将随机谱变换直接应用于整个图像,在保证提高系统鲁棒性的前提下,提高模型的迁移性,增强模型的泛化能力. 为了说明随机谱变换的有效性,应用Grad-cam[20 ] 来生成整块DCT的热力图和随机谱变换的热力图,具体的频谱图与热力图对比如图4 所示. 图中,$ C_{\mathrm{M}} $ 图4 可以看出,与整块DCT相比,利用提出的随机谱变换生成的热力图更能匹配出有效区域. 为了保证该模块的效果,在实际应用中可以进行$N$
2
... 为了评估本文方法的有效性,在CIFAR-10[21 ] 、CIFAR-100[21 ] 数据集上进行广泛的测试. 运用FGSM[9 ] 、PGD-10[7 ] 、PGD-20[7 ] 、PGD-50[7 ] 、C&W[22 ] 5种算法对训练好的模型进行攻击,将实验结果与其他先进方法进行对比分析. ...
... [21 ]数据集上进行广泛的测试. 运用FGSM[9 ] 、PGD-10[7 ] 、PGD-20[7 ] 、PGD-50[7 ] 、C&W[22 ] 5种算法对训练好的模型进行攻击,将实验结果与其他先进方法进行对比分析. ...
1
... 为了评估本文方法的有效性,在CIFAR-10[21 ] 、CIFAR-100[21 ] 数据集上进行广泛的测试. 运用FGSM[9 ] 、PGD-10[7 ] 、PGD-20[7 ] 、PGD-50[7 ] 、C&W[22 ] 5种算法对训练好的模型进行攻击,将实验结果与其他先进方法进行对比分析. ...
1
... 在数据集处理方面,使用文献[23 ]的环境设置及其提供的Pytorch实现细节,选取1MDDPM[24 ] 生成的数据集作为实验数据集. ...
1
... 在数据集处理方面,使用文献[23 ]的环境设置及其提供的Pytorch实现细节,选取1MDDPM[24 ] 生成的数据集作为实验数据集. ...
1
... 在具体的实验中,选取WideResNet34-10[25 ] 、ResNet18[26 ] 和PreActResNet18[27 ] 作为目标网络,对CIFAR-10和CIFAR-100进行测试. 在训练过程中,将WideResNet34-10作为目标网络时进行了25次训练,将ResNet18和PreActResNet18作为目标网络时训练65次. 将初始学习速率设置为0.1,采用SGD[28 ] 进行优化并设置权重衰减系数为5×10−4 . 在初始化生成网络和目标网络更新方面,每隔20次训练就更新一次初始化生成网络. 实验将算法的干净精度和鲁棒精度作为主要的评价指标,干净精度是指模型在正常情况下的准确率,鲁棒精度(即分类对抗样本的准确率)是指模型在受到攻击的情况下抵抗对抗样本的能力. ...
1
... 在具体的实验中,选取WideResNet34-10[25 ] 、ResNet18[26 ] 和PreActResNet18[27 ] 作为目标网络,对CIFAR-10和CIFAR-100进行测试. 在训练过程中,将WideResNet34-10作为目标网络时进行了25次训练,将ResNet18和PreActResNet18作为目标网络时训练65次. 将初始学习速率设置为0.1,采用SGD[28 ] 进行优化并设置权重衰减系数为5×10−4 . 在初始化生成网络和目标网络更新方面,每隔20次训练就更新一次初始化生成网络. 实验将算法的干净精度和鲁棒精度作为主要的评价指标,干净精度是指模型在正常情况下的准确率,鲁棒精度(即分类对抗样本的准确率)是指模型在受到攻击的情况下抵抗对抗样本的能力. ...
1
... 在具体的实验中,选取WideResNet34-10[25 ] 、ResNet18[26 ] 和PreActResNet18[27 ] 作为目标网络,对CIFAR-10和CIFAR-100进行测试. 在训练过程中,将WideResNet34-10作为目标网络时进行了25次训练,将ResNet18和PreActResNet18作为目标网络时训练65次. 将初始学习速率设置为0.1,采用SGD[28 ] 进行优化并设置权重衰减系数为5×10−4 . 在初始化生成网络和目标网络更新方面,每隔20次训练就更新一次初始化生成网络. 实验将算法的干净精度和鲁棒精度作为主要的评价指标,干净精度是指模型在正常情况下的准确率,鲁棒精度(即分类对抗样本的准确率)是指模型在受到攻击的情况下抵抗对抗样本的能力. ...
On the momentum term in gradient descent learning algorithms
1
1999
... 在具体的实验中,选取WideResNet34-10[25 ] 、ResNet18[26 ] 和PreActResNet18[27 ] 作为目标网络,对CIFAR-10和CIFAR-100进行测试. 在训练过程中,将WideResNet34-10作为目标网络时进行了25次训练,将ResNet18和PreActResNet18作为目标网络时训练65次. 将初始学习速率设置为0.1,采用SGD[28 ] 进行优化并设置权重衰减系数为5×10−4 . 在初始化生成网络和目标网络更新方面,每隔20次训练就更新一次初始化生成网络. 实验将算法的干净精度和鲁棒精度作为主要的评价指标,干净精度是指模型在正常情况下的准确率,鲁棒精度(即分类对抗样本的准确率)是指模型在受到攻击的情况下抵抗对抗样本的能力. ...