接运公交的早期研究多集中于接运模式. Calabrò等^[1]讨论多对一接运模式，设计优化的接运路线将不同出发地的乘客送至同一目的地. Yang等^[2-3]采用多对多模式来寻找最优的接运公交线网，以满足不同出发地对应不同目的地的乘客需求. 许多学者针对接运公交路线优化模型与算法开展了研究，Zermasli等^[4-5]构建的接驳公交路线优化模型采用遗传算法求解；Taplin等^[6]将接驳公交路线与乘客步行距离问题统一考虑，采用遗传算法求解接驳公交路线优化模型. 由于传统的遗传算法收敛速度较慢且容易陷入局部最优解，高明瑶等^[7]提出基于改进粒子群算法的接运公交路线优化算法；Lee等^[8]以乘客总行程时间最短和车辆成本最小为目标，通过模拟退火算法得到满意路径；Badia等^[9]利用数值分析方法，分别讨论固定接驳与门到门接驳的服务方案；Dou等^[10]研究接驳公交的时刻表问题，建立混合整数非线性规划（mixed integer non-linear programming，MINLP）模型最小化乘客成本和公交运营成本，用混合人工蜂群算法求解该模型. 文献[4]~[10]中采用的算法适用多类问题，但要多次迭代，极易得出局部最优解. 郭戎格等^[11]以运营总收益最大化为目标，设计新的自适应大邻域搜索算法，通过算例验证算法的有效性. 孙倩等^[12]以系统总成本最小为目标建立数学模型，提出遗传算法和邻域搜索相结合的启发式算法，使用该算法求解模型；该算法融合了遗传算法的全局搜索优势和邻域搜索的局部搜索能力. 为了追求全局最优，避免出现将多目标累加最小或最大设置为最优结果的情况，刘晓佳等^[13]围绕接运公交线网和运营方案优化，提出考虑客流弹性需求的双层规划模型，设计双层遗传算法进行模型求解. 少量学者在接驳路线优化问题中考虑了土地类型、出行需求^[14]、环境因素^[15]等其他因素对公交线路的影响. 此外，付康林等^[16]从出行者角度出发研究考虑换乘时间需求的接驳公交运行路径与调度的协调优化；郑亚晶等^[17]以换乘人数最大化为目标构建优化模型，研究了城市轨道交通末班车衔接方案优化问题；王顺等^[18]对多个换乘站进行协调设计，构建了接运公交多换乘站协同运行的优化模型.

周边公交线路优化研究大多针对单一地铁站点，连续的多个地铁站点采用纵向割裂成若干小段的方式对单地铁站的优化结果进行简单叠加，达不到系统的整体最优. 现有研究虽然能够兼顾公交运营企业和乘客的利益，但接运线路协调优化方式大多围绕对接运公交时刻表的优化^[19-20]，公交接运线路优化模型缺少对站点换乘因素的考虑. 起点−终点（origin-destination，OD）需求点间的客流换乘方案和乘客出行时间成本随接运公交线网方案的变化而变化，本研究构建地铁接运公交线路双层规划模型，其中上层模型兼顾公交运营企业与乘客双方利益，下层模型为客流分配模型；基于改进遗传算法设计构建模型的求解算法.

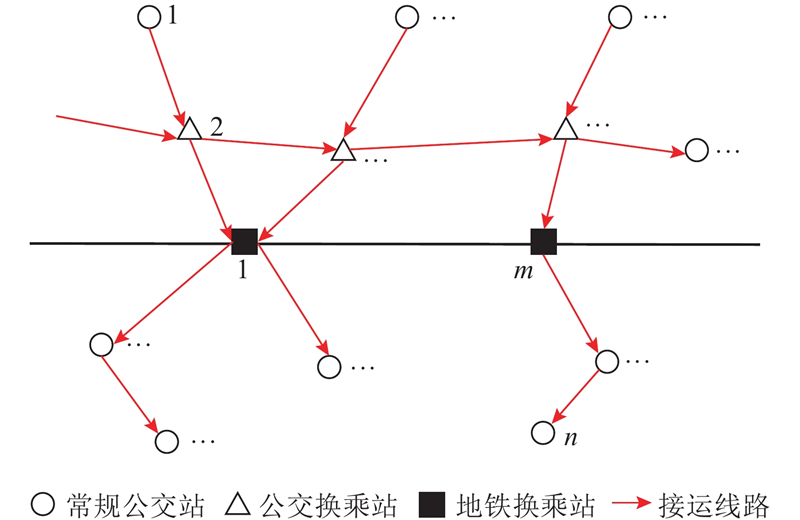
地铁与公交的接运模式为将公交线路站点的乘客运送到地铁站点，将地铁出站乘客疏散到各自目的地. 接运线路优化设计问题以车辆路径问题为基础，须考虑地铁接运站点、公交站点、客流需求与站点换乘等因素. 设路网中存在m个地铁站点、n个公交站点，有s条接运公交线路，每条线路最大客流运输能力为Q_max，每个换乘站点的通行能力为C，线路开行频率为f，路网中每2个站点间由第s条公交线路服务的客流需求为$ q_{ij}^s $，每个换乘站所在接运公交线路数量为R_bus. 本研究在满足$ q_{ij}^s $≤Q_max、R_bus≤C/f的条件下，求最优接运线路方案，使得公交运营成本及乘客出行成本之和最小.

接运公交线路示意如图1所示. 为了方便建模求解，进行如下假设：1）每条接运公交线路最多服务$ \theta $个地铁站；2）接运公交在路线上的每个公交站点都停靠，不跨站；3）接运公交与地铁的行驶速度已知；4）所有出行者对费用和时间有相同的理解，均以最短路为标准选择路径，无其他选择.

接运公交线路的布置须兼顾乘客和公交运营者的利益，以保证出行者使用公共交通的积极性和公交运营公司的经济效益. 在公交运营方面，主要考虑接运公交车辆的运营成本，包括燃油费用、人工费用、折旧费用等，与各接运线路运行里程正相关，计算式为

(1)$ {c_{\mathrm{b}}} = {{{c}}_0}\sum\limits_{i \in {\text{V}}} {\sum\limits_{j \in {\text{V}}} {{d_{ij}} x_{ij}^s} } . $

式中：c_b为公交运营成本；c₀为接运公交单位距离内的运营成本；$ {d_{ij}} $为从站点i到j的实际距离；$ x_{{{ij}}}^s $为决策变量，如果i，j在线路s上，则值为1，否则为0；V为所有节点的集合. 在乘客方面，主要考虑乘客全程的广义出行费用，包括所有乘客的乘车时间成本和换乘时间成本. 乘客的出行时间包括直接出行不进行换乘的时间$T_{ij}^1 $和出行并换乘的时间$T_{ij}^2 $，计算式分别为

(2)$ T_{ij}^1 = \sum\limits_{m \in B \cup T} {\sum\limits_{n \in B \cup T} {\frac{{{d_{mn}}}}{{{v_{{\text{bus}}}}}}} } y_{mn}^{ij} x_{ij}^s. $

(3)$ \begin{split} T_{ij}^2 =& \sum\limits_{m \in B \cup T} {\sum\limits_{n \in B \cup T} {\frac{{{d_{mn}}}}{{{v_{mn}}}}} } y_{mn}^{ij} \left( {1 - x_{ij}^s} \right)+\\&\sum\limits_{a \in T} {{t^a} z_{ij}^a} +\sum\limits_{b \in B} {{t^b} z_{ij}^b} .\end{split} $

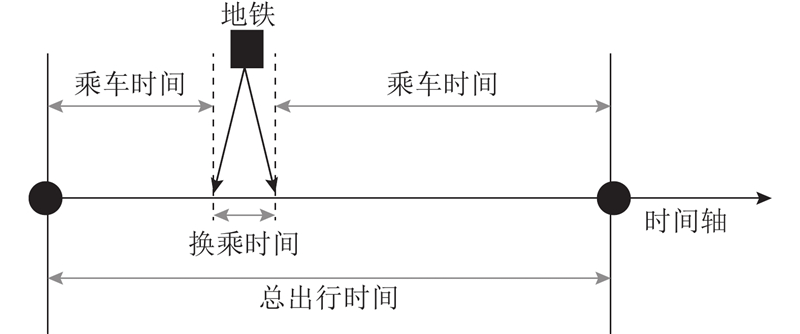
乘客的总出行时间为

(4)$ {T_{ij}} = T_{ij}^1+T_{ij}^2. $

式中：v_bus为公交车的行驶速度；$ y_{mn}^{ij} $为决策变量，如果m、n所在路段在i、j所在路径上，则值为1，否则为0；t^a为在站点a的换乘时间；$ z_{ij}^a $为决策变量，如果从i到j在站点a存在换乘，则值为1，否则为0；a、b均为换乘站点；B为公交站点的集合；T为地铁站点的集合. 如图2所示为出行时间示意图. 如图3所示，相较于直达及一次换乘，换乘多次通常会使乘客疲劳、厌倦，考虑到乘客舒适度，利用惩罚函数增加多次换乘的成本，达到对换乘2次及以上行为的惩罚，表达式为

(5)$ {P_{ij}} = \left\{ \begin{array}{*{20}{l}} 0 ,& {n_{ij}} \leqslant 1; \\ r {t^a} {n_{ij}} ,& {n_{ij}} > 1. \\ \end{array} \right. $

(6)$ {c_{\mathrm{p}}} = {{{c}}_1}\sum\limits_{i \in {{B}} \cup {{T}}} {\sum\limits_{j \in {{B}} \cup {{T}}} {{q_{{{ij}}}} \left( {{T_{{{ij}}}}+{P_{{{ij}}}}} \right)} } \delta _{{{ij}}}^{l,\eta }. $

式中：$ {P_{ij}} $为从点i出发到点j换乘次数过多的惩罚函数；$ {n_{ij}} $为从点i出发到点j换乘次数；r为换乘次数过多惩罚系数^[21]；c_p为乘客总出行成本；c₁为乘客单位时间内的出行成本；q_ij为从i到j的客流量；$\delta _{ij}^{l,\eta }$为决策变量，如果路段l在i，j间的第$ \eta $条路径上，则值为1，否则为0. 通过地铁接运公交系统的费用分析，以公交车辆运营成本及乘客出行成本之和最小为优化目标，建立上层规划模型目标函数为

(7)$ \begin{split} \min c_{\mathrm{z}} = &{{{c}}_0}\sum\limits_{i \in B \cup T} {\sum\limits_{j \in B \cup T} {{d_{ij}} x_{ij}^s} } +{{{c}}_1}\sum\limits_{i \in B \cup T} \sum\limits_{j \in B \cup T} {q_{ij}} \times \\&\left( {{T_{ij}}+{P_{ij}}} \right) \delta _{ij}^{l,\eta }.\end{split} $

共设置接运线路完整性约束和路径合理性约束2个约束条件. 1)接运线路的完整性约束代表接运公交在路网上行驶的基本规则，确保每条接运公交线路最多服务$ \theta $个地铁站，约束条件表达式为

(8)$ \sum\limits_{i \in B} {\sum\limits_{j \in T} {x_{ij}^s} } \leqslant \theta ;\;\;\;\; s \in S. $

式中：S为公交线路的集合.

2）路径合理性约束：接运线路的站点数量过多会增加绕行距离和行驶时间，过少会影响线路输送的客运量，为此设置约束条件表达式：

(9)$ \sum\limits_{i \in V} {y_i^s} \leqslant {{{N}}_{\max }};\;\;\;\; s \in S. $

式中：$ y_i^s $为决策变量，如果站点i在线路s上，则值为1，否则为0；N_max为最大站点数. 每条接运线路所经过的站点数量须满足式(9). 如图4所示，任何一条接运线路必须保证不构成回路，即满足约束条件表达式：

(10)$ 0 \leqslant \sum\limits_{i \in V - \left\{ {O{\text{,}}D} \right\}} {x_{ik}^s} +\sum\limits_{i \in V - \left\{ {O{\text{,}}D} \right\}} {x_{ki}^s} \leqslant 1;\;\;\; k \in V - \left\{ {O{\text{,}}D} \right\}. $

式中：k为站点索引，O为起点站的集合，D为终点站的集合. 对于任一接运线路上的起终点和中间节点应满足以下约束：

(11)$ {\displaystyle \sum _{i\in V\left(i\ne k\right)}{x}_{ik}^{s}}=0\text{，}{\displaystyle \sum _{j\in V\left(k\ne j\right)}{x}_{kj}^{s}}=1\text{；} k\in O. $

(12)$ {\displaystyle \sum _{i\in V\left(i\ne k\right)}{x}_{ik}^{s}}=1\text{，}{\displaystyle \sum _{j\in V\left(k\ne j\right)}{x}_{kj}^{s}}=0\text{；} k\in D. $

(13)$ {\displaystyle \sum _{i\in V\left(i\ne k\right)}{x}_{ik}^{s}}={\displaystyle \sum _{j\in V\left(k\ne j\right)}{x}_{kj}^{s}}=1\text{；} k\in V-\left\{O\text{,}D\right\}. $

式(11)针对起点，确保不存在进入起点的路径，由起点发出的路径存在且只有一条. 式(12)针对终点，确保终点只进不出. 式(13)针对中间站点，如果线路s经过站点k，则s进入站点k和由站点k出发的路径均存在且只有一条.

下层规划是基于系统最优原理（SO）的交通分配模型. 分配问题应满足的条件只有交通流量守恒条件，即OD间各条路径上的客流总量应等于OD客流量：

(14)$ \sum\limits_\eta {F_\eta ^{ij}} = {q_{ij}};\;\;\; i \in O, j \in D. $

(15)$ F_\eta ^{ij} \geqslant 0. $

式中：$F_\eta ^{ij}$为出发地为i、目的地为j之间第$ \eta $条路径上的客流量. $F_\eta ^{ij}$与路段交通量$ {x_l} $的关系式为

(16)$ {x_l} = \sum\limits_{i,j} {\sum\limits_\eta {F_\eta ^{ij} \delta _{ij}^{l,\eta }} } ;\;\;\;\; l \in L. $

式中：L为路网中路段的集合. 下层规划模型的目标函数为系统中的总阻抗取最小值：

(17)$ \min W(x) = \sum\limits_l {{x_l}} {t_l}. $

式中：$ {t_l} $为路段l的阻抗函数.

共设置线路容量约束和站点换乘约束2个约束条件. 1) 线路容量约束条件式为

(18)$ \sum\limits_{i \in V} {{q_{ij}} x_{ij}^s+{q_{ij}} \left( {1 - x_{ij}^s} \right) z_{ij}^a} \leqslant Q ;\;\;\; j \in V, a \in T, s \in S. $

(19)$ \sum\limits_{i \in V} {\sum\limits_{j \in V} {{q_{ij}} x_{ij}^s} } \leqslant {Q_{\max }} ;\;\;\;\; s \in S. $

式中：Q为单个节点容量. 本研究不进行发车间隔优化，因此没有考虑班次的影响，班次仅用于计算公交的最大运输能力，为定值. 式(18)确保接运公交车到达每个节点的容量不超过限制. 式(19)是对接运公交线路运能的约束，确保每小时线路上的乘客人数不超过每辆公交车的最大载客量与每小时发车数的乘积，如图5所示.

2) 站点换乘约束. 换乘行为不可避免，存在于公交与公交之间及公交与地铁之间. 在模型求解过程中要针对不同的路线方案进行搜索筛选，某2个站点间的乘客换乘行为会随着路线方案的不同而发生改变，从而影响乘客的出行成本.

(20)$ \left.\begin{split}& {y}_{ma}^{ij}={y}_{an}^{ij}=1;\;\;\; m, n\in B \cup T, a\in T.\\& {x}_{ij}^{s}=0;\;\; i,j\in B\cup T, s\in S,\\ & \Rightarrow {\displaystyle \sum _{s\in S}{y}_{i}^{s}}\leqslant {{R}}_{\text{bus}}\text{，} i\in T.\end{split}\right\} $

(21)$ \left.\begin{split}& y_{mb}^{ij} = y_{bn}^{ij} = 1;\;\;\; m,n \in B, b \in B. \\ & x_{ij}^s = 0;\;\;\; i,j \in B \cup T, s \in S. \\ & \Rightarrow \sum\limits_{s \in S} {y_i^s} \geqslant 2,\;\;\; i \in B. \end{split}\right\} $

(22)$ {t^a} = {t_{\text{w}}}+\frac{1}{{2{f_{{\text{sub}}}}}}. $

(23)$ {t^b} = \frac{1}{{2{f_{{\text{bus}}}}}}. $

式中：t_w为公交换乘地铁所需步行时间，f_sub为地铁的开行频率，f_bus为接运公交的开行频率，R_bus为每个地铁站能通过的最大接运公交线路条数. 式(20)定义a为从i到j所在路径上的公交-地铁间的地铁换乘站，确保地铁换乘站数量不超过每个地铁站能通过的最大接运公交线路条数. 式(21)定义b为从i到j所在路径上的公交-公交间的公交换乘站，确保公交换乘站在公交线路上. 式(22)、式(23)分别定义公交-地铁、公交-公交的换乘时间.

(24)$ C = N{C^{'}}, $

(25)$ {C^{'}} = \frac{{3\;600}}{{{t_{\text{c}}}+{t_{\text{d}}}}}, $

(26)$ {{{R}}_{{\text{bus}}}} \leqslant {{{C_i}}}/{{{f_i}}}\,\,. $

式中：N为换乘站点实际泊位数，C^'为单个泊位的通行能力，C为换乘站点的通行能力，t_c为公交从关门到驶离站点重新汇入车流的时间，t_d为平均停靠时间. 式(24)、式(25)计算公交换乘站点的通行能力，式(26)表示公交换乘站点服务的公交线路能力.

模型采取自然数编码，研究对象有m个地铁站点，s条接运线路，n个公交站点. 染色体编码分为3段：第一段为每条线路经过的地铁站编号，第二段为每条线路所经过的公交站点的数量，第三段为按次序经过的公交站点编号. 染色体编码长度为2×s+n，解向量表示为[rai₁, rai₂, ···, rai_s; Num₁, Num₂, ···, Num_s; i₁, i₂, ···, i_n].

遗传算法的适应度衡量个体在优化过程中优劣程度，本研究利用目标函数构造适应度评价函数，采用精英保留策略和轮盘赌方式进行优秀个体选择. 由于算法迭代初期优良个体较少，采用动态精英保留策略，在算法迭代初期保留较少的种群数量，到了算法后期，个体达到最优或接近最优，此时保留数量增加. 这样既在初期保留了种群多样性，又在后期避免了个体被破坏，加快了算法的收敛速度. 动态精英保留策略的主要步骤：计算种群所有个体适应度值并按照从大到小依次排序；确定当前保留优秀个体数量，计算式为

(27)$ \varphi =\left\{ {\begin{array}{*{20}{l}}{ \Bigg\lceil{\alpha }^{{2{\mathrm{Gen}}}/{{\mathrm{Ge}}{{\mathrm{n}}}_{\text{max}}}} \beta \Bigg\rceil\text{，} }&{ {\mathrm{Gen}}\text{ < }{{\mathrm{Ge}}{{\mathrm{n}}}_{\text{max}}}/{\text{2}}; }\\{ \alpha \beta \text{，} }&{ {\mathrm{Gen}}\geqslant {{\mathrm{Ge}}{{\mathrm{n}}}_{\text{max}}}/{2}. }\end{array}} \right.$

式中：$\lceil\cdot\rceil $为向上取整，$\alpha $为种群个体数量，$\beta $为优秀个体占总个体的比例，Gen为当前迭代次数；剩余个体则按照轮盘赌的方式进行选择.

采用多点交叉的方式，设置交叉概率为0.6，交叉算子设计如下. 1)分别在2个父代染色体的3段编码染色体中随机选择3个位置进行基因交换，产生2个子代染色体. 2)对子代染色体进行验证并进行编码矫正. 对于第二段编码染色体，若交叉后的公交站点总数与实际站点总数不符，则进行增减；对于第三段编码染色体，若交叉后产生重复的站点，则将重复的站点删除，补位未出现的站点.变异方法采用基本位变异，为了增强全局搜索能力，设置概率为0.1进行变异操作. 分别在3段编码染色体中选择3个变异位，将3个发生变异的位置进行随机交换，得到新的染色体. 此时，接运路线中的站点顺序发生变化，即接运线路问题的解已获更新.

遗传算法的局部搜索能力不足，虽然能够以一定的概率找到最优解，但要消耗大量时间. 为了扩大搜索算法的搜索空间，本研究在遗传操作之后加入邻域搜索算法，通过将遗传算法与邻域搜索算法结合的方式来提高解的质量与求解速度. 设计两点交换法：从路径间或路径内随机选择2个点，如果交换有效，则交换2个点在路径中的位置. 该算法设计简单，无需复杂的参数设置，加快了遗传算法寻优的速度.

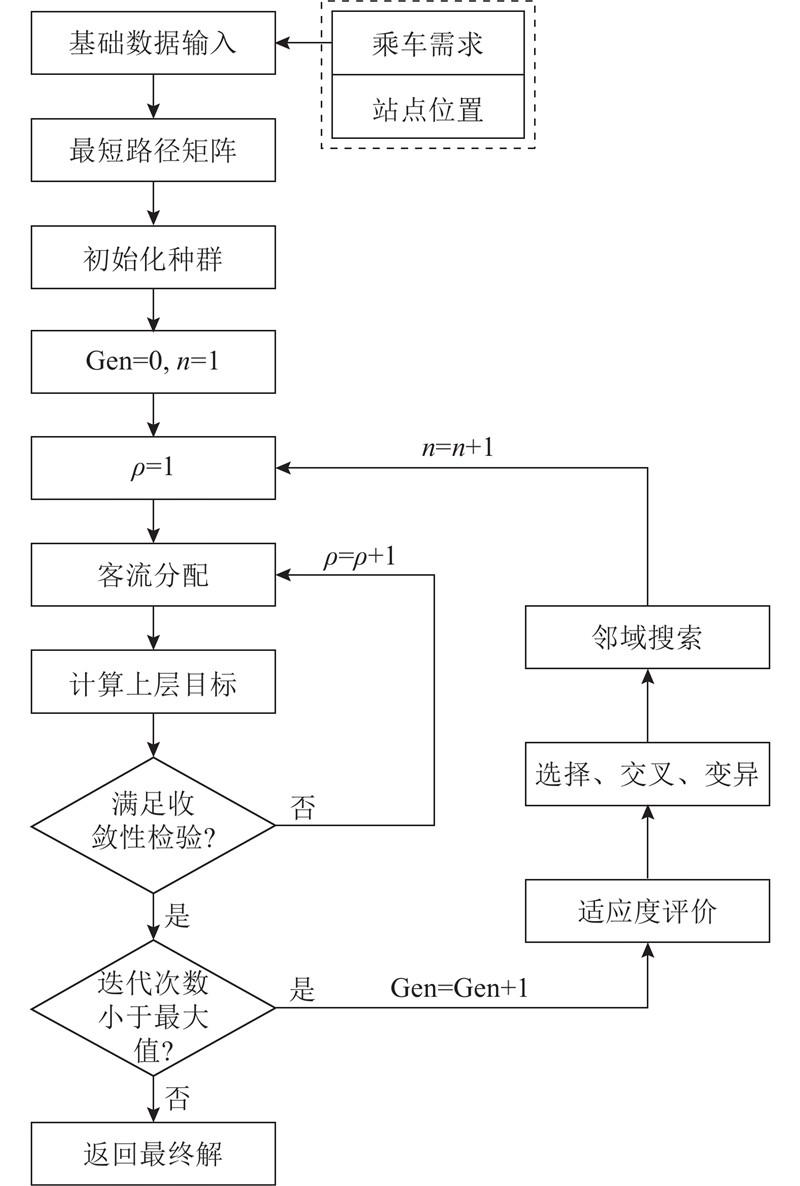
采用改进的遗传算法求解上层模型，采用Frank-Wolfe算法求解下层客流分配模型，将上、下层模型的求解算法组合，得到双层接运公交线路优化模型的求解算法. 如图6所示为双层接运公交线路优化模型的求解流程图，具体步骤如下.

1）设置种群规模和最大进化代数，对如乘车需求、站点位置的相关模型参数进行初始化.

2）令上层模型迭代次数Gen=0，令混合算法总迭代次数为1，生成初始种群.

3）求解下层模型. 采用全有全无分配法进行1次流量分配，得到各个路段的交通流量，令下层模型迭代次数ρ＝１；更新各个路段的时间阻抗，计算OD间最短路径；寻找下一步迭代方向；按照更新后的时间阻抗再利用全有全无分配法进行1次流量分配，得到附加流量；确定最优迭代步长；确定新的迭代起点.

4）进行收敛性检验，若满足收敛性检验，则得到平衡解，转到步骤5），否则更新下层模型迭代次数ρ，令ρ＝ρ+1，转到步骤3）；将得到的结果代入阻抗模型，求得每个路段的时间值并反馈到上层目标函数中.

5）检查是否迭代到最大次数，若没有达到，则Gen=Gen+1，进行步骤6）；若达到，则算法停止返回最优解.

6）对种群进行适应度评价，执行选择、交叉、变异操作，生成子代种群.

7）遗传操作完成后，进行新生成的染色体邻域搜索，调整新染色体. 迭代次数n=n+1，转到步骤3）.

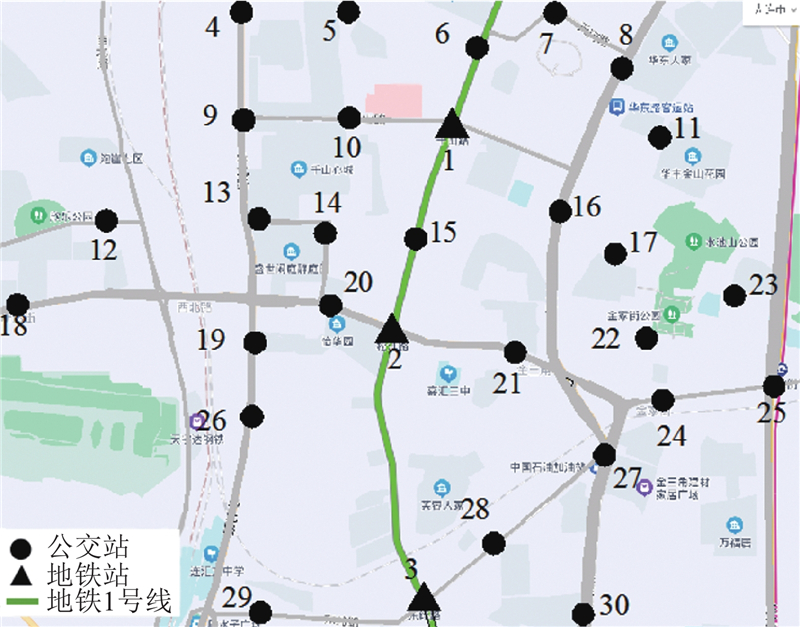
整条地铁线路较长，且沿线公交站点数量较多，为了便于计算和说明模型的设计思路，选取大连地铁1号线3个地铁站及沿线27个公交站作为案例研究对象. 通过调查，获得此区域内各站点位置如图7所示. 采用抽样问卷调查的方法获取客流OD数据：在每个公交站点安排1名调查员，对候车乘客进行随机抽样问卷调查，调查时间为高峰2 h，调查内容为出行者的起终点，记录2 h的候车总人数，得到抽样率；整理全部问卷，汇总乘客需求均在本案例区域内的问卷，得到样本OD数据；依据调查抽样率进行样本扩算，得到总体客流OD数据. 根据大连市公交及地铁现有运行标准，公交运行速度为25 km/h，地铁运行速度为80 km/h，接运公交单位距离的成本系数c₀=25元/km. 根据2018年大连市薪资水平报告，乘客单位时间内的出行成本系数c₁=26元/h. 接运公交和地铁的发车间隔为定值，分别为6、7 min. 接运公交最大载客量为80人. 换乘次数过多惩罚系数设置为1.18.

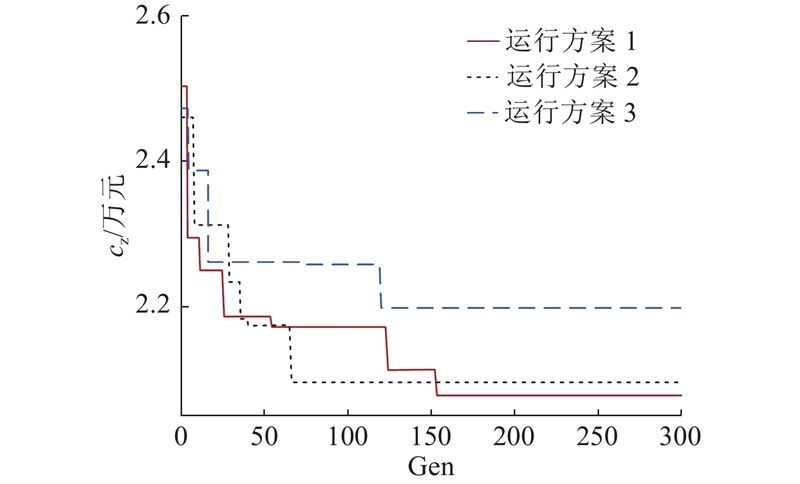
如图8所示，借助Matlab对改进的遗传算法编程，选择初始种群规模为50，经过300代进化，适应度函数趋于稳定得到最终结果，经过3次运行得到适应度函数（改进的遗传算法求解得到的是近似最优解，因此3次运算后的结果会有所不同）. 可以看出，目标函数在迭代160次后趋于稳定，运行方案1的系统总成本c_z=20 716.9元，运行方案2的c_z=20 940.3元，运行方案3的c_z=21 935.2元，其中最优系统总费用为20 716.9 元，最优接运路线如图9所示. 为了验证求解精度，利用Matlab编程枚举法得系统全局最优解的总费用为20 386.1元. 改进的遗传算法与枚举法求解得到的接运线路优化结果如表1所示；2种算法运算性能的比较如表2所示. 表中，t_op为运行时间，ơ为相对误差. 由表2可知，尽管枚举法能够得到全局最优解，但在相同的计算规模下，改进的遗传算法的运算时间远远小于枚举法. 可以预见，随着路网规模及需求扩大至城市级，枚举法的运算时效性显著变差，且无法满足大规模求解的需要. 在计算精度方面，改进的遗传算法多次运行的结果波动不大，与全局最优解的系统总费用的最小误差为1.6%，在合理范围内.

在现状路网中，共有5条既有公交线路经过所选公交站点，分别为805路、612路、9路、45路、1022路，其中45路及1022路为非接运公交. 针对接运线路优化方案及同等需求条件下的既有公交路线方案，进行客流、公交运营成本和乘客出行成本的对比分析与讨论，如表3所示，其中q为客流需求，$ {\overline c_{\mathrm{p}}} $为人均出行成本. 由表可知，就本案例区域整体性能而言，在公交载客人数方面，优化前载客人数为2 760人，优化后为3 563人. 优化后的载客量较优化前提升了29%，虽然公交运营成本增加，但是人均运营成本基本不变，说明优化方案能够充分提高接运公交载客量，保障乘客的出行需求与公交运营者的利益. 在系统人均出行成本方面，优化后乘客出行的人均出行成本降低了13%，说明优化方案能够保障出行者的利益. 由最优接运方案和既有非接运线路可知，在优化调整后的5条接运线路方案中，线路3可以弥补静慧街站点所在的45路公交与松江路路所在的地铁1号线的直接有效衔接；1022路公交所经站点区域与地铁1号线无接驳关系，优化后的线路1和线路5则可以弥补此区域的接驳空白. 由此可以说明，设计优化接运线路可以更全面地覆盖各地的出行需求. 综上所述，与既有的公交线路相比，本研究建立的接运公交优化模型能够更好满足较多乘客的出行需求，充分提高接运公交系统整体运营效率.

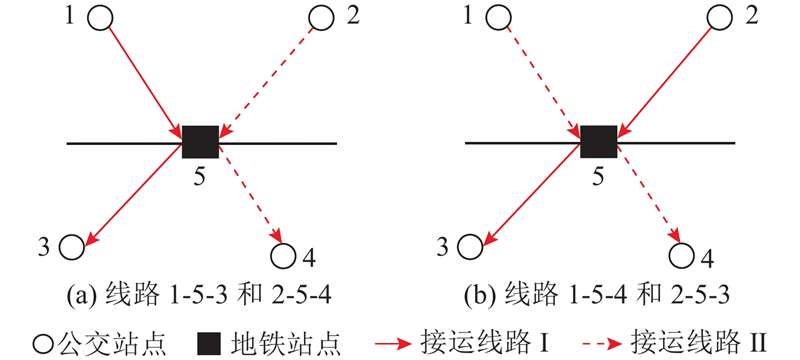
现有研究基本针对单一地铁站点周边的公交站进行路径优化. 当面对整条地铁线路的多个站点时，现有做法是将全线按地铁站纵向割裂，对每个地铁站及其周边公交站进行优化，再将优化方案简单叠加，形成总体方案. 本研究对多个地铁站与周边公交站进行系统建模全局优化，模型的系统性具有一定优势. 例如，当OD点对1、2间的客流需求较大，其他OD点对间客流较小时，若采用传统方法，将形成如图10(a)所示的方案. 此时，自点1出发至点2的大量乘客要经过公交-地铁-公交的复杂过程，出行成本显著增加. 若按本研究构建的模型求解，将得到如图10(b)所示的方案. 尽管此时公交线路长度有所增加，但考虑到不同OD点对间的客流比重不同，模型将优先照顾客流需求大的OD点对，以此权衡总体出行成本（ 即自点1出发至点2的大量乘客可公交一站直达）. 由此也印证了多个局部最优方案的简单加和无法达到系统全局最优的结论.

在进行接运公交线路优化求解时，须不断生成不同的可行解并计算比较目标函数值，过程中不同OD点对间的客流出行及换乘方案随不同可行解的变化而变化，致使乘客出行成本变化. 在进行某次路径搜索时得到如图11 (a)所示的接运方案，此时自点1至点3的乘客可以直接乘接运公交线路I抵达目的地，出行时间成本为该公交线路自点1至点3的行程时间. 重新搜索路径后生成如图11(b)所示的接运方案，此时该股客流的出行成本将变成线路II自点1至点5的时间、换乘时间以及线路I自点5至点3的时间之和. 如须换乘地铁或存在多次换乘的情况，时间成本的变化将更为复杂. 本研究在模型优化过程中综合考虑了上述情况，具有一定的进步性.

构建地铁接运公交线路优化模型，从系统最优的角度对多个地铁站点及其周边公交站进行整体优化，求出接运公交线网的全局近似最优解，体现了系统性；求解算法在搜索路线方案时，考虑乘客站点换乘方案变更导致的出行时间成本变化，体现了动态性；模型约束条件中考虑了多次换乘成本惩罚，兼顾了公交运营企业与乘客双方利益，体现了公平性. 与既有公交线网相比，求解得到的接运公交线网优化方案在提升载客率，降低人均出行成本与提高系统整体运营效率方面优势明显，但公交运营成本略有增加. 虽然受调查资源与研究条件所限，案例分析所选区域较小，没有扩展到整条地铁线路，但是本研究在理论建模与算法设计方面所得的一般性规律仍可为同类研究借鉴. 本研究以动态需求-动态线路为基础构建模型，客流需求即为动态需求，优化方案随OD变化而变化，但路网为已知路网，未进行动态路网下的优化研究. 计划在后续研究中逐步克服案例对象体量偏小以及动态路网的问题，进一步完善大规模动态路网下的接运公交线路优化.