浙江大学学报(工学版)

浙江大学学报(工学版), 2024, 58(10): 2119-2127 doi: 10.3785/j.issn.1008-973X.2024.10.016

土木工程、交通工程

基于机器学习算法的块石形状分类及土石混合体数值模拟

曾海英,, 叶沛楠, 金华辉, 刘京雨, 岑夺丰,

1. 玉环市农业农村和水利局，浙江 台州 317600

2. 浙江广川工程咨询有限公司，浙江 杭州 310020

3. 河北工业大学 土木与交通学院，天津 300401

4. 宁波大学 岩石力学研究所，浙江 宁波 315211

Rock block shape classification and numerical simulation of soil-rock mixture based on machine learning algorithms

ZENG Haiying,, YE Peinan, JIN Huahui, LIU Jingyu, CEN Duofeng,

1. Yuhuan Agriculture and Water Conservancy Bureau, Taizhou 317600, China

2. Zhejiang Guangchuan Engineering Consultation Limited Company, Hangzhou 310020, China

3. School of Civil and Transportation Engineering, Hebei University of Technology, Tianjin 300401, China

4. Institute of Rock Mechanics, Ningbo University, Ningbo 315211, China

通讯作者: 岑夺丰，男，副研究员，硕导. orcid.org/0000-0001-5959-4200. E-mail：cdfschool@126.com

收稿日期: 2023-08-8  

Received: 2023-08-8  

作者简介 About authors

曾海英（1977—），男，高级工程师，从事水利工程运行管理和安全监测研究.orcid.org/0009-0008-5082-2172.E-mail：617660521@qq.com , E-mail：617660521@qq.com

摘要

现有块石形状特征的数值模型或过于简化块石形状或未进行块石形状的频率统计，为此基于主成分分析算法（PCA）和K均值聚类算法，提出新的建模方法. 利用Matlab对土石混合体断面照片进行数字图像处理，得到块石轮廓样本；对块石轮廓进行形心原点化、长轴水平化、最大极径归一化等标准化处理，得到标准化后的块石轮廓向量. 分别采用PCA和K均值聚类算法对块石轮廓向量进行降维和聚类，对得到的分类块石形状进行频率统计. 建立考虑块石形状分类及频率、颗粒级配、块石倾角的土石混合体随机模型，进行双轴压缩数值模拟，分析塑性应变和应力-应变曲线特征. 在较高含石量和较大块石粒径情况下比较模型的变形和抗压强度，考虑块石形状的土石混合体模型与传统含多边形块石的土石混合体模型差异明显.

关键词： 土石混合体 ; 块石形状 ; 主成分分析算法(PCA) ; K均值聚类算法

Abstract

Existing numerical models of rock block shape characteristics either oversimplified the block shapes or did not carry out the statistics of the block shapes. A new modeling method was proposed based on the principal component analysis algorithm (PCA) and K-means clustering algorithm. Matlab programs were used to digitally process the cross-section photos of the soil-rock mixture to obtain the contour samples of rock blocks, and the standardization processings of rock block contour such as moving the centroid to the origin, rotating the long-axis to the horizontal-axis, and normalizing the polar radius were performed to obtain standardized silhouette vectors of rock blocks. The PCA was used to reduce the dimension of the contour vector of the rock blocks, and the K-means clustering algorithm was used to cluster the contour vector after the dimension reduction. The shapes of the rock blocks were classified and the frequencies of various types of rock blocks were counted. A random model of soil-rock mixture considering the shape classification and frequency, grain composition, and inclination was established. The biaxial compression numerical simulation was carried out, and the characteristics of the plastic strain and the stress-strain curves were analyzed. The models of the deformation and compression strength of the soil-rock mixture considering the rock block shape are significantly different from those of the traditional soil-rock mixture models with polygonal rock blocks, under the conditions of higher rock content and larger rock block size.

Keywords： soil-rock mixture ; rock block shape ; principal component analysis algorithm(PCA) ; K-means clustering algorithm

PDF (3047KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

曾海英, 叶沛楠, 金华辉, 刘京雨, 岑夺丰. 基于机器学习算法的块石形状分类及土石混合体数值模拟. 浙江大学学报(工学版)[J], 2024, 58(10): 2119-2127 doi:10.3785/j.issn.1008-973X.2024.10.016

ZENG Haiying, YE Peinan, JIN Huahui, LIU Jingyu, CEN Duofeng. Rock block shape classification and numerical simulation of soil-rock mixture based on machine learning algorithms. Journal of Zhejiang University(Engineering Science)[J], 2024, 58(10): 2119-2127 doi:10.3785/j.issn.1008-973X.2024.10.016

土石混合体是普遍存在的天然地质体（如崩积物、残积物、洪积物），也是岩土工程中常用的人工填料，广泛应用于基础工程、道路工程以及水利工程. 土石混合体由粒径较大、强度较高的块石和强度相对较弱的细粒土体组成，其物理力学性质具有不均质性、非线性、非连续性的复杂特点，是工程项目设计和建设必须解决的难题[1]. 已有学者针对土石混合体力学性质开展了大量室内试验和一些原位试验[1-7]. 一方面，室内试验一般采用重组的试样，不宜包含超大粒径块石，此外，尺寸效应使得实际工程尺度土石混合体的结构特征很难被再现. 另一方面，原位试验操作困难，边界条件不清晰，常采用重物堆载或千斤顶加载，加载精度难以保证.

数值模拟技术已成为研究土石混合体力学性质的有力手段[5-11]，而如何建立更加符合实际土石混合体结构特征的模型成为数值模拟的关键问题. 油新华[8]采用规则几何体（圆形、正多边形）随机生成块石，宋来忠等[9]采用随机凸多边形构建块石. 这种人为自定义的规则多边形和随机多边形显然与实际块石的复杂形状不符. 为此，一些学者建立了基于真实土石混合体结构的数值模型，即根据某个土石混合体断面照片提取复制出同样的块石结构建立模型. 例如，Xu等[10]采用数字图像处理技术提取照片中块石，据此生成了土石混合体细观结构模型. 这种根据实际断面构建的模型只能代表局部个例，不具有统计学意义，不符合数值模型的随机性要求. Zhang等[12-16]采用机器学习的方法来生成岩土颗粒，提高了模型的合理性. 为了建立更加科学有效的数值模型，有学者尝试对大量块石图像样本进行处理、统计，建立块石形状数据库，据此生成考虑块石形状真实性又具有统计学意义的随机数值模型[11]. 以上块石建模方法未对块石形状进行分类，建模时只是随机选择数据库块石，缺乏对块石形状特征的统一归纳整理. 实际上，同一土石混合体内的块石形状一般是多样的，且各类型块石具有一定的频率（占比），数值建模时应考虑这种频率来随机生成块石.

土石混合体的模型构建经历了从规则和不规则图形代替块石，到考虑块石真实形状，再到块石真实形状及统计意义均考虑的发展过程. 现有方法过于简化块石形状或未进行统计学分类，为了进一步考虑块石形状分类及其频率，本研究将机器学习领域常用的主成分分析算法（principal component analysis algorithm，PCA）和K均值（K-means）聚类算法[17]引入块石形状分类，避免采用单个形状参数无法有效区分形状类别的问题，充分利用土石混合体的细观结构特征在宏观层面的统计规律，建立考虑块石形状分类的二维土石混合体随机模型，提高土石混合体建模方法的科学性.

1. 块石形状分类方法

1.1. 块石形状提取及标准化处理

利用数字图像处理技术[18]获取块石样本信息，采用Matlab处理某机场建设工程采集的土石混合体断面照片，获得只具有块石轮廓信息的几何图形[19]如图1所示. 设定块石轮廓由一系列像素点组成，将这些点视为在二维平面直角坐标系下的坐标集合. 如图2所示，以提取的块石轮廓像素点的所有横、纵坐标的平均值为中心点的横、纵坐标，绕此中心每隔1°取一个坐标点（可以取更小角度来提高精度），将每个块石图形都转换成360个坐标点组成的数据点集，实现从图形到数据的转换.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   块石轮廓提取

Fig.1   Contour extraction of rock blocks


图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   块石轮廓点坐标的采集

Fig.2   Collection of coordinates of rock block contour points


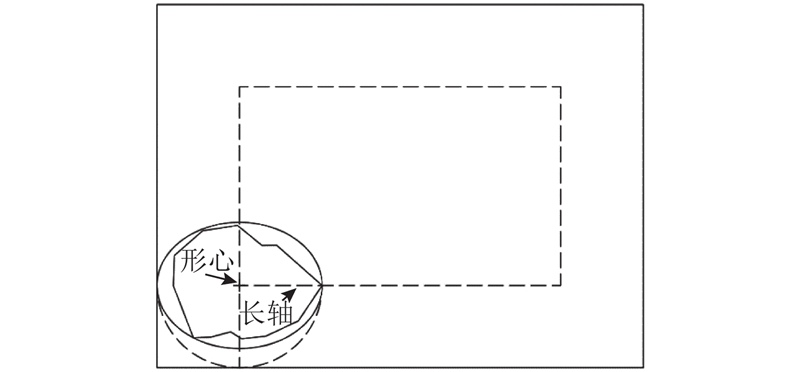
采集的块石的形心位置、大小、长轴-水平方向夹角和块石较尖锐侧朝向都存在差异，在块石形状分类之前须对上述因素进行标准化处理，即将块石处理成如图3所示的标准化状态，具体处理方法如下. 1）形心原点化处理：先取块石边缘轮廓点的所有横、纵坐标的平均值为中心点，再将每个块石分解成360个以中心点为共同顶点的小三角形，根据几何图形分割法的形心公式，求出准确的形心，

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   块石标准化处理后的示意图

Fig.3   Schematic diagram of rock block after standardized processing


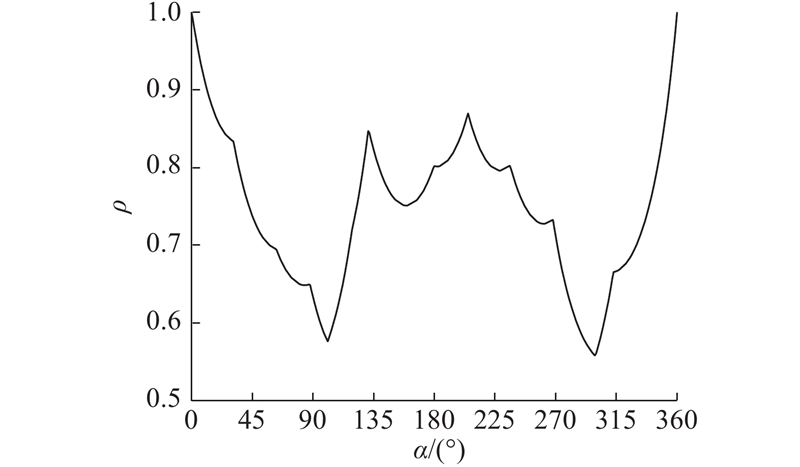
$ {x_{\mathrm{c}}} = \frac{1}{A}{{\displaystyle\sum {{A_i}{x_i}} }} ,\;{y_{\mathrm{c}}} = \frac{1}{A} {{\displaystyle\sum {{A_i}{y_i}} }}.$
(1)

式中：xi、yi分别为每个小三角形的形心横、纵坐标(i=1,2,···,360)，Ai为与xi、yi对应的小三角形面积，A为块石的总面积，xc、yc分别为整个块石形心的横、纵坐标. 将每个块石轮廓坐标都减去形心坐标，得到新的轮廓坐标点集合(xi', yi')，实现块石的平移，使形心移至坐标系原点. 2）最大极径归一化处理（无量纲化处理）：以形心为极点，将块石最大极径（长轴方向）除以自身值，且其余极径均除以最大极径，使得所有块石的最大极径保持一致，便于在同一尺度下进行分析. 3）长轴水平化处理：求出块石长轴（朝上为正方向）与x轴正方向旋转角，顺时针旋转块石，使其长轴旋转至位于水平位置. 4）较尖锐侧朝向统一化处理：经过步骤3）的处理，块石边缘轮廓较尖锐侧可能会朝向x轴正方向，也可能会朝向x轴负方向，影响图形相似判断的准确率，为此以形心为对称轴将较尖锐侧朝向x轴负方向的块石轮廓进行轴对称变换，统一调整为较尖锐侧朝向x轴正方向. 标准化之后的块石轮廓坐标点集以及各点极径ρ，如图4所示，其中α为各点对应的角度. 将每个块石轮廓表示为 m条（m=360）极径组成的向量x=[x1，x2，···，xm]，称为块石轮廓向量. 从土石混合体断面中提取并进行标准化处理的45个块石样本如图5所示.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   标准化处理后的块石极径

Fig.4   Polar radius of rock block after standardized processing


图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   标准化处理后的块石样本

Fig.5   Rock block samples after standardized processing


1.2. 块石轮廓向量PCA降维

在采用K-means聚类算法进行块石形状分类前须进行块石轮廓向量降维. PCA是通过降维来得到能反映大部分原始变量关系的新的综合变量（即主成分）的分析算法. 降维目的是消除数据冗余，便于研究各个数据的距离关系，使得变换后的维度两两正交. PCA降维对轮廓形状影响小，能够保留块石轮廓数据的大部分原始特征，用于块石轮廓向量的降维原理[17]如下. 设μ为向量x均值，通过线性变换将向量x变成新的向量 y=[y1，y2，···，yn]，具体为

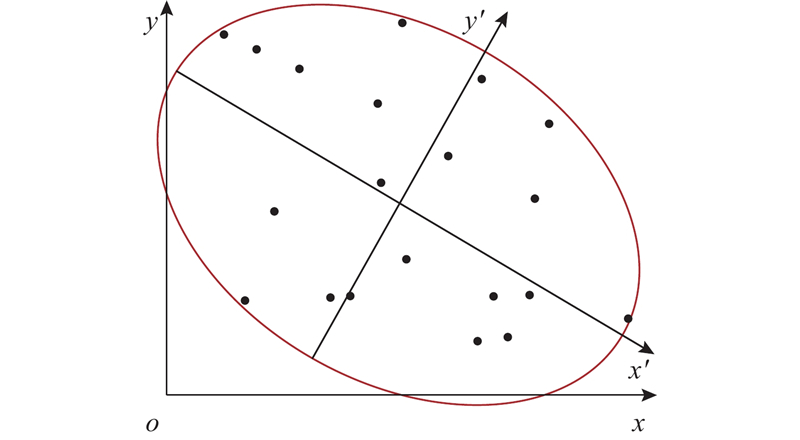
$ \left.\begin{array}{c}{y}_{1}={\mu }_{11}{x}_{1}+{\mu }_{12}{x}_{2}+\cdots+ {\mu }_{1m}{x}_{m},\\ {y}_{2}={\mu }_{21}{x}_{1}+{\mu }_{22}{x}_{2}+\cdots+ {\mu }_{2m}{x}_{m},\\ \vdots \\{y}_{n}={\mu }_{n1}{x}_{1}+{\mu }_{n2}{x}_{2}+\cdots+ {\mu }_{nm}{x}_{m}.\end{array}\right\} $
(2)

系数μij的确定原则：1）μi12+μi22+···+μim2=1；i=1，2，···，m. 2）yi与yj（i≠j；i，j=1，2，···，n）线性无关. 3）yn为与yj（j=1，2，···，n−1）不相关的xi（i=1，2，···，m）所有线性组合中方差最大者. 新变量y1，y2，···，yn称为原始的块石轮廓变量x1，x2，···，xn的第1、第2、···、第n主成分，通常选择前面最大的几个主成分来反映原始块石轮廓向量的距离关系. 如图6所示，散点表示二维（x、y）向量，将散点分布看做近似呈椭圆形（三维则呈椭球形）分布，找出椭圆的长轴x′、短轴（次长轴）y′，将原数据投影到x′、y′轴上，则数据在x′轴坐标就是第1主成分，在y′轴坐标是第2主成分（均等于0）. 为了降低数据冗余，将数据距离关系可视化，通常将高维度数据降至二维或者三维. 如图7所示，通过Matlab的drtoolbox数据降维工具箱实现将包含m维的块石轮廓向量降低到二维，图中每个点对应1个块石，这些数据可反映原始块石轮廓向量的距离关系.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   二维向量降至一维向量的示意图

Fig.6   Schematic diagram of reducing two-dimensional vector to one-dimensional vector


图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   降至二维的块石轮廓向量分布

Fig.7   Vector distribution of rock block contour reduced to two-dimensional


1.3. 块石轮廓向量K均值聚类

K-means是无监督机器学习聚类算法，将距离作为相似性的评价指标，本研究采取欧几里得距离[17]，定义式为

$ d(x,y) = \sqrt {\sum\limits_{i = 1}^n {{{({x_i} - {y_i})}^2}} } . $
(3)

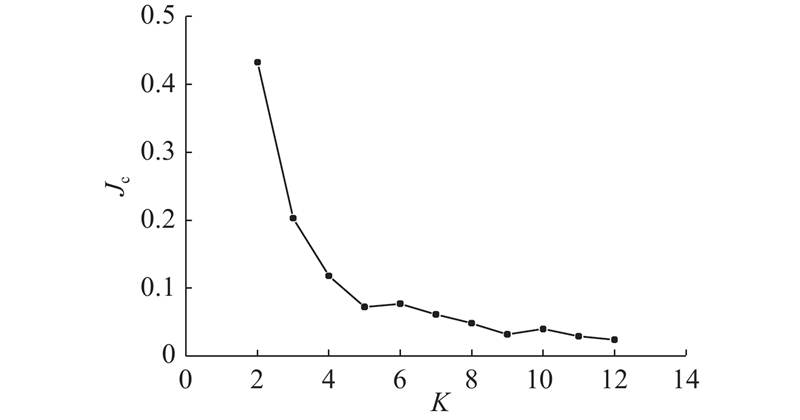
式中：xi、yi分别为子集合中不同的数据点，n为xi、yi数据的维度. K-means聚类算法执行步骤：1）在降维后的块石轮廓集合中选择尽可能远的K个随机初始点，称为聚类中心μj（j=1,2,···,K）；2）计算块石轮廓集合内的样本点与聚类中心的距离，按照集合内部点的距离尽可能近，与其他集合点的距离尽可能远的原则，把样本点分配到不同的子集合nj内，通过不断地改变聚类中心，直至误差平方和Jc最小，计算式为

$\left. \begin{array}{l}{J_{\mathrm{c}}} = {\displaystyle\sum\limits_{j = 1}^K {\displaystyle\sum\limits_{k = 1}^{{n_j}} {\left\| {{{\boldsymbol{x}}_k} - {{\boldsymbol{\mu}} _j}} \right\|^2} } } ;\\{{\boldsymbol{\mu}} _j} = \dfrac{1}{{{n_j}}}\displaystyle\sum\limits_{j = 1}^{{n_j}} {{{\boldsymbol{x}}_j}} ;\;j = 1,2, \cdots ,K .\end{array}\right\}$
(4)

式中：K为聚类总数，nj为子集合的元素个数，xk为子集合nj里的样本. K-means聚类是以Jc达到最小值为目的，Jc的值越小，代表子集内块石元素差异越小，类别越多. 如图8所示，对于有一定区分度的数据，在K达到某个临界值之前Jc减小幅度很大，达到该临界点之后减小缓慢，此临界值为最优聚类数（肘部法则），作为最终的聚类数量. 由图7可知，本研究中K=5，被虚线框住的块石为同一类别；图左下方的2个点与其他各类相距较远，不宜与其他点归为一类（通常为奇异块石）. 图7体现了PCA降维过程数据可视化的意义，即在程序自动化实现聚类的基础上，辅以对数据的直观观察，以便寻得局部块石数据与整体之间的关系.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   聚类数量与误差平方和的关系

Fig.8   Relationship between number of clusters and sum of squared errors


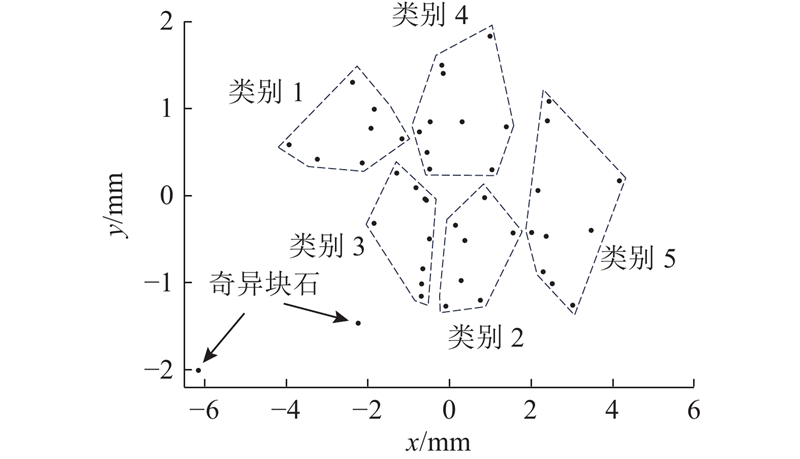
1.4. 块石形状分类结果分析

通过PCA降维和K-means聚类得到标准化后的块石形状分类如表1所示，其中rrb为块石的频率（占比）. 可以看出，同类别的块石具有大概相似的形状特征，第1类和第2类相对扁平，第3类和第4类稍圆润，第5类最圆. 本研究所提分类方法是综合性的方法，用单一的某个形状特征参数去衡量形状分类效果，会出现个别块石看似与组内其他块石有所区别的情况. 如表2所示，各组块石的长短轴比μb总体上相近，个别略有差异. 所提方法避免了单个形状参数无法有效区分形状类别的问题.

表 1   块石形状分类结果

Tab.1  Classification result of rock block shapes

类别rrb/%块石形状
116.3
216.3
320.8
423.3
523.3

新窗口打开| 下载CSV


表 2   块石的长短轴比

Tab.2  Ratio of long and short axes of rock blocks

类别μb
11.582.302.081.921.701.722.32———
21.971.711.661.861.901.871.95———
31.621.221.351.151.691.591.391.421.14—
41.571.591.361.411.781.011.381.411.771.59
51.101.091.321.191.071.331.321.161.211.35

新窗口打开| 下载CSV


2. 考虑块石形状的土石混合体数值模拟

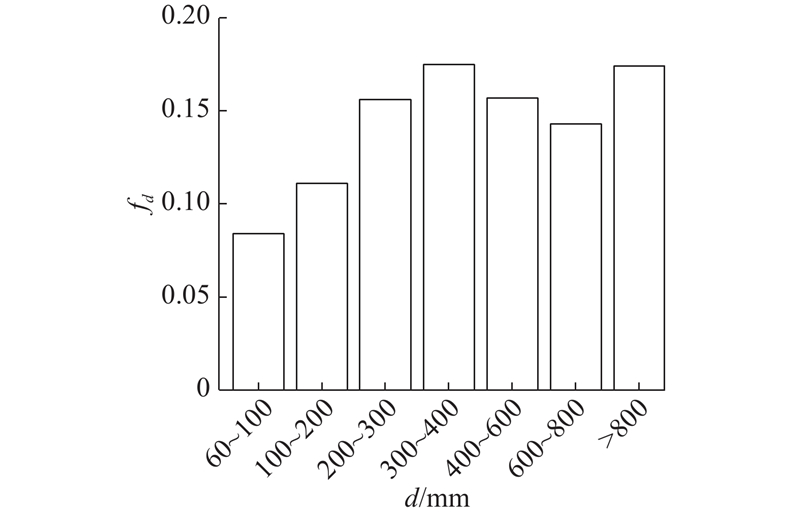
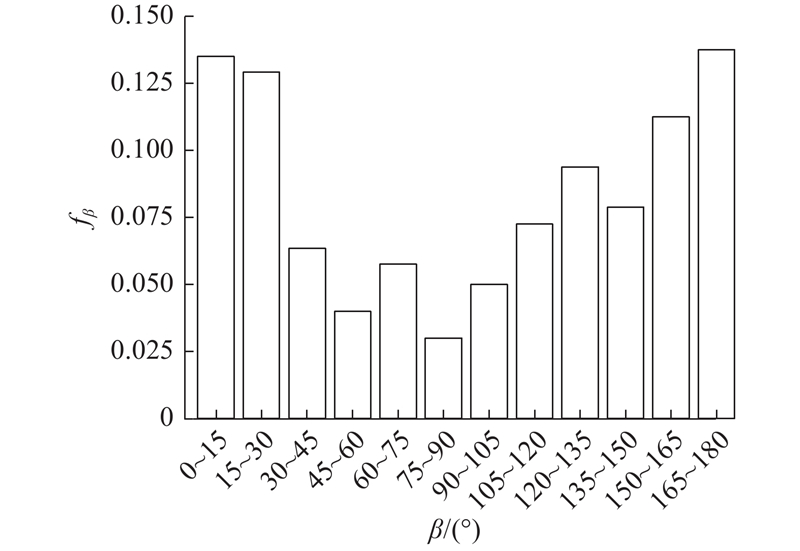
2.1. 块石分布特征统计

科学的土石混合体数值建模应考虑基本的块石分布特征[1,18,20]，如块石粒径分布（级配）、块石定向性（块石倾角分布）. 1）根据Medley[21]所提方法确定土石混合体的土-石阈值dthr，

$ \mathit{d} _{ \mathrm{thr}} \leqslant\mathrm{ 0.05} \mathit{L} _{ \mathrm{c}} \mathrm{.} $
(5)

其中Lc为土石混合体的工程特征尺度，取为研究的断面尺度. 将长轴小于dthr的小块石视为土体，本研究设定dthr=60 mm. 2）分别统计如图9所示的所研究断面土石混合体[5]的块石粒径d的频率fd分布，如图10所示的长轴方向与水平方向逆时针夹角β的频率fβ分布（块石倾角），定义为定向性. 3）根据块石分布特征统计结果、块石形状分类结果及其频率建立数值模型.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   块石粒径频率直方图

Fig.9   Histogram of rock block size frequency


图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   块石倾角频率直方图

Fig.10   Histogram of rock block inclination angle


2.2. 考虑块石形状分类及分布特征的建模方法

为了建立土石混合体的细观结构模型，采用随机模拟方法并考虑块石的形状因素. 土石混合体细观结构模型的生成须考虑3个关键问题：块石粒度分布、块石形状选取和块石放置区域生成.

2.2.1. 块石的粒度分布

1)设定模拟形状的控制区域为矩形区域，范围为（Xmin, Xmax）×（Ymin, Ymax）. 2)确定土石混合体的含石率s（块石总面积与模型区域面积之比），求出块石总面积：

$ {S_{\mathrm{R}}} = ({X_{\max }} - {X_{\min }}) ({Y_{\max }} - {Y_{\min }}) s. $
(6)

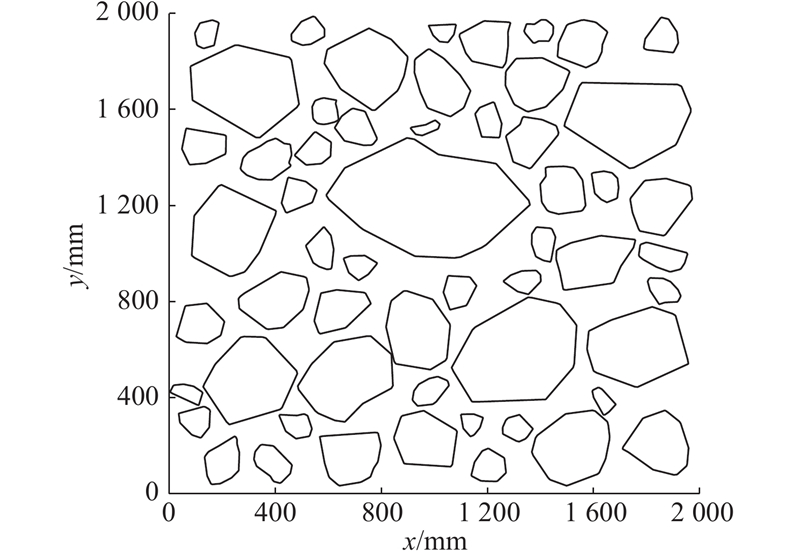
3)由图9可知，块石根据粒径的不同共分为7个不同的粒组n，每个粒组的频率为${f_{d_n}} $，以此求出模拟区域的各个粒组块石的面积：

$ {S_n} = {f_{d_n}} {S_{\mathrm{R}}}. $
(7)

4)求出各个粒组块石的数量Qn. 为了便于生成块石放置区域，利用表2列出的块石长短轴比，以椭圆作为包裹块石的“外壳”，生成符合级配要求的椭圆集. 椭圆集采取先放大后循环累加再缩小还原的方法生成，该方法比单纯累加法效率高. 以[60,100]的粒组为例，步骤如下：（a）将本粒组最小值扩大a（令a=1.1）倍，粒组范围为[66,100]，每个椭圆的长轴 am = rand×(100−66)+66，其中rand为0~1的随机数，结合长短轴比，求出每次生成的小椭圆面积SEm. （b）循环累加SEm，求出总面积$S_{\mathrm{E}}' $. 若$S_{\mathrm{E}}' \in $[Sn, a2Sn]，则说明生成椭圆的长轴满足要求，且长轴放大系数为$\sqrt {S_{\mathrm{E}}'/{S_n}} $，记录每个am和m，否则将$ {\mathrm{S}}_{\mathrm{E}m}'$清零，重新生成SEm. （c）将得到的每个椭圆的长轴am除以长轴放大系数，得到符合级配要求的长轴$a_m' $. 块石面积小于椭圆面积，须根据椭圆与块石的面积比将$a_m' $进行放大.

2.2.2. 块石形状的选取

由块石形状分类方法可得表1，单个随机块石的选取原则须遵循表1所述的形状分类及其频率，方法如下. 1)根据椭圆数量m和不同形状块石的频率（可根据m适当扩大块石样本数量重新聚类），求出每个形状类别的个数mK. 2)根据m和mK随机从块石形状数据库中选取对应类别的块石，将块石长轴乘以$a_m' $进行放大，求出放大后的块石面积之和Sr. 3) 求出各个随机块石的长轴：

$ {a_{\mathrm{r}}} = {a'_{m}} \sqrt {{S_n}/{S_{\mathrm{r}}}} . $
(8)

2.2.3. 块石放置区域的生成

随机块石放置区域的生成问题包括1）块石-边界的相交检测，2）块石-块石的相交检测. 处理随机结构模型块石-块石的相交检测问题最基础的算法是将块石轮廓的每条边都与其他块石的每条边进行相交判断，但该算法的效率低下. 徐文杰等[20]采用将包裹块石的椭圆简化为4段圆弧的方法进行相交判断；喻江武等[22]采用AABB包围盒相交检测法，通过先全局后局部的相交判定来进行相交判断.

如图11所示，块石的形心在虚线矩形内随机生成，即可保证块石不会超出边界. 虚线矩形区域随机点的计算式为

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   块石-边界位置关系示意图

Fig.11   Schematic diagram of position relationship between rock blocks and boundary


$ \left. \begin{gathered} {x_{\mathrm{p}}} = {a_{\mathrm{r}}}+({X_{\max }} - {X_{\min }} - 2{a_{\mathrm{r}}}) {\mathrm{rand}}, \\ {y_{\mathrm{p}}} = {a_{\mathrm{r}}}+({Y_{\max }} - {Y_{\min }} - 2{a_{\mathrm{r}}}) {\mathrm{rand}}. \\ \end{gathered} \right\} $
(9)

式中：xp、yp为虚线矩形区域的横、纵坐标， Xmin、 Ymin、Xmax、Ymax分别为最外侧实线矩形区域斜的左下、右上两点的横、纵坐标.

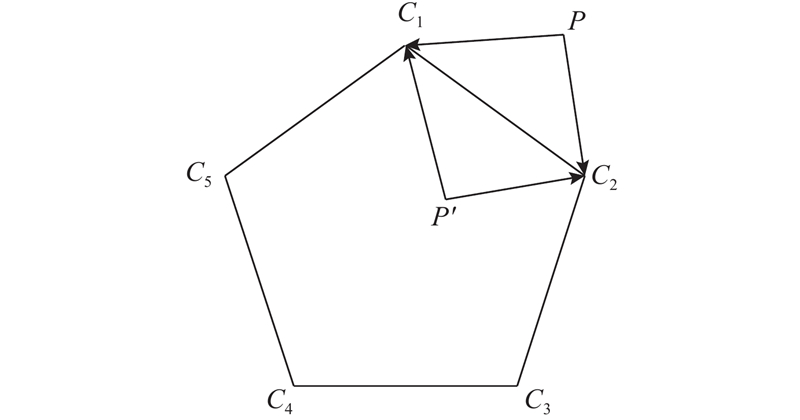
Matlab的内置函数inpolygon能够判断点与多边形位置关系. 如图12所示，设点P(x, y)，多边形由点$\left\{ {{C_1},{C_2}, \cdots, \left. {{C_n}} \right\}} \right.$ 组成且呈顺时针或逆时针排列，计算P与相邻Ci、Ci+1组成向量的叉积PCi×PCi+1. 若所有的叉积符号均相同，则说明点P在多边形内；为0，说明点在多边形上；符号有正有负，说明点在多边形外部. 将要放置椭圆的所有轮廓点与已经生成椭圆的轮廓点进行位置判断，若每个点都在已生成椭圆外部，则说明椭圆放置成功，否则重新进行放置. 由于椭圆的粒径不同，在放置过程中，尺寸大的面积大，为此在投放之前，先按照尺寸大小进行排序，保证尺寸大的椭圆能够被先投放，以提高椭圆的放置效率. 如图13所示，将Matlab模型坐标导入自动计算机辅助设计软件AutoCAD中，用Abaqus的草图导入功能得到如图14所示的土石混合体，细观有限元计算模型.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   点与多边形位置关系示意图

Fig.12   Schematic diagram of position relationship between points and polygons


图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   土石混合体模拟断面

Fig.13   Simulation section of soil-rock mixture


图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   Abaqus模型网格图

Fig.14   Mesh image of Abaqus model


2.3. 有限元数值模型的生成与模拟

建立土石混合体细观结构模型，其土、石物理力学参数（密度ρm、弹性模量E、泊松比υ、内摩擦角φ、黏聚力c）如表3所示. 块石与土体部分分别建模再装配. 本构模型采用摩尔-库伦模型，土区域的网格单元采用CPE4R单元，块石区域的网格单元采用CPE3单元. 对模型的底部边界设置水平和垂直约束，先施加围压σ3=100 kPa进行固结，再在上边界采用位移控制施加竖向应力σ1进行压缩.

表 3   模型中土、块石的物理力学参数

Tab.3  Physical and mechanical parameters of soil and rock block in models

材料ρm/（g·cm−3）E/MPaυφ/（°）c/kPa
块石2.601 1000.2361 125
土体1.90500.32042

新窗口打开| 下载CSV


2.4. 计算结果分析

对不同含石率和级配的模型进行双轴压缩数值实验，将本研究所提方法构建的模型与使用简单多边形进行建模的对应模型进行对比. 试样尺寸均为2 m×2 m，简单多边形与本研究所建模型的块石数量、位置、尺寸和倾向等参数均相同，仅轮廓形状特征不同.

2.4.1. 含石率对土石混合体力学行为的影响

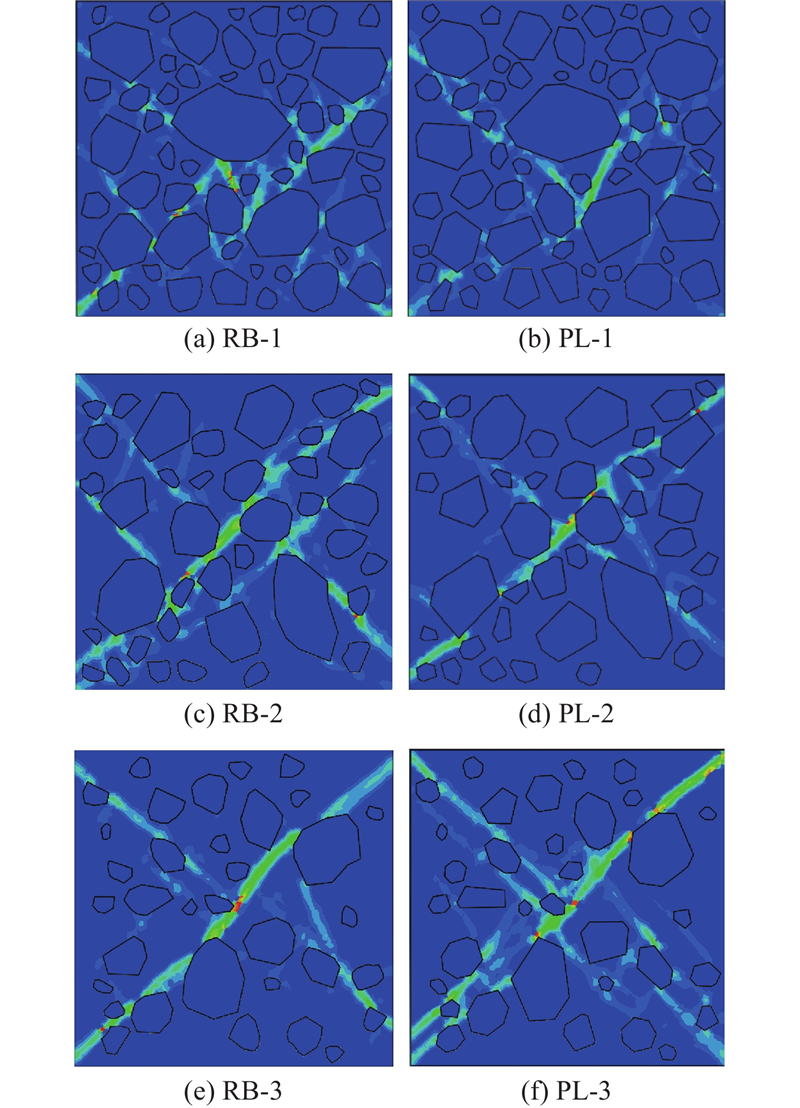
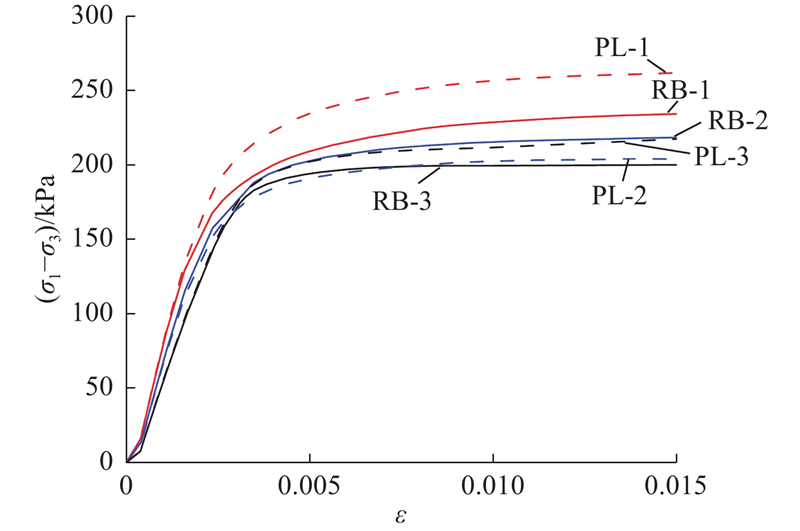
如图15所示为3种含石率（s=65%，50%，35%）的模拟试件（编号分别为RB-1、RB-2，RB-3）与随机凸多边形形状的模拟试件（编号分别为PL-1、PL-2，PL-3）的塑性应变云图对比. 可以看出，当含石率s=35%时，土石混合体模型的整体剪切破碎带，与均质土体的X形剪切带较为类似[23]，随着含石率提高，块石阻碍剪切带发育，剪切带形状逐渐变得不规则，且受土石混合体内部大块石的影响增大. 当含石率s=35%时，考虑块石形状对剪切破碎带的影响明显小于含石率s=65%的情况. 如图16所示为试件的应力（σ1−σ3）-应变ε曲线. 可以看出，含石率s=50%、35%的试件应力-应变曲线差异较小，抗压强度变化不大，但RB-1与PL-1（当s=65%时的2种试件）抗压强度变化较大. 由此可知，在对含石率较高尤其是含有大粒径块石的模型进行数值模拟时，应当尽可能建立形状更加细致的模型，不可以简单的凸多边形代替.

图 15

新窗口打开| 下载原图ZIP| 生成PPT

图 15   不同含石率的试件塑性应变云图

Fig.15   Plastic strain maps of specimens with different rock block contents


图 16

新窗口打开| 下载原图ZIP| 生成PPT

图 16   不同含石率的试件偏应力-轴向应变曲线

Fig.16   Deviatoric stress and axial strain curves of specimens with different rock block contents


2.4.2. 粒度分布对土石混合体力学行为的影响

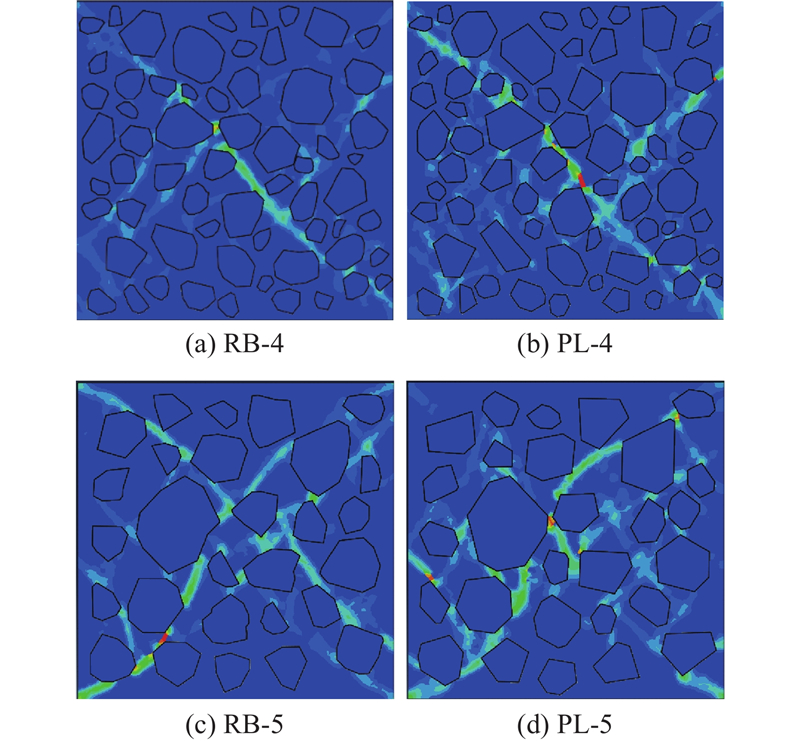
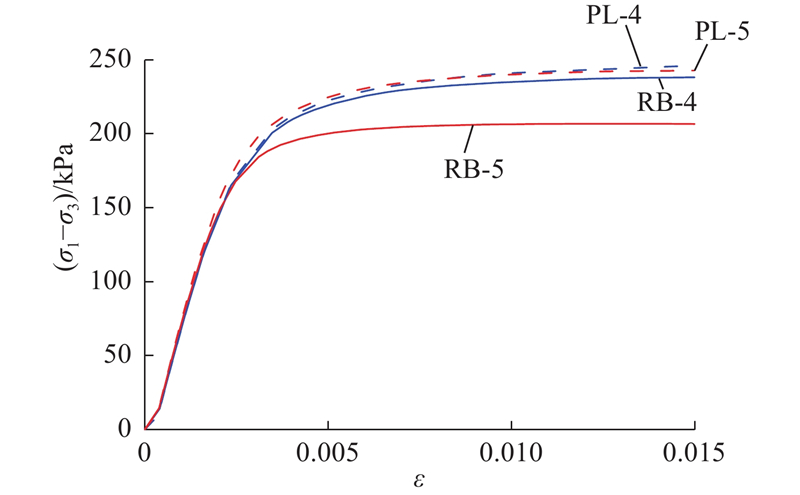
如图17所示为2种级配（级配Ⅰ、级配Ⅱ）的模拟试件（编号分别为RB-4、RB-5）与随机凸多边形形状的模拟试件（编号分别为PL-4、PL-5）的塑性应变云图对比，试件的含石率均为55%. 图中，级配1的粒径范围为60~400 mm，代表中、小块石；级配2的粒径范围为300~800 mm，代表大块石. 可以看出，在由中小块石组成的土石混合体模型中，块石形状的选取对剪切破碎带的影响小于由大块石组成的土石混合体模型. 由如图18所示的应力-应变曲线可以看出，形状特征对中小块石组成的土石混合体模型力学性质的影响小于由大块石组成模型的. 原因是部分大粒径块石对整体剪切破碎带的形状影响较大，对于中小块石来说，形状效应不明显，土石混合体力学性质取决于各块石的整体作用. 因此，在以大块石为主体的土石混合体模型中，应当考虑到块石形状特征的影响，建立更加细致的土石混合体模型.

图 17

新窗口打开| 下载原图ZIP| 生成PPT

图 17   不同块石粒径级配的试件塑性应变云图

Fig.17   Plastic strain maps of specimens with different rock block size gradations


图 18

新窗口打开| 下载原图ZIP| 生成PPT

图 18   不同块石粒径级配的试件偏应力-轴向应变曲线

Fig.18   Deviatoric stress and axial strain curves of specimens with different rock block size gradations


3. 结　语

本研究1）提出块石形心原点化、长轴水平化，最大极径归一化等一系列标准化处理方法，定义了标准化后的块石轮廓向量；2）提出采用PCA对块石轮廓向量进行降维，采用K-means聚类算法对降维后轮廓向量进行聚类的块石形状分类方法，避免了采用单个形状参数无法有效区分形状类别的问题；4）提出考虑块石形状分类及频率、颗粒级配、块石倾角的土石混合体数值建模方法，提高了土石混合体数值模拟的科学性. 在较高含石量和较大粒径情况下比较模型的变形和抗压强度，考虑块石形状的土石混合体模型与传统含多边形块石的土石混合体模型差异明显，表明了考虑块石形状的必要性. 本研究以数值模拟的方式给出考虑块石形状及分类的建模方法并证明考虑块石形状的重要性，但采用何种数值方法并非文章的重点；本研究开展的二维块石形状分析方法可拓展至三维空间使用.

参考文献

徐文杰, 张海洋

土石混合体研究现状及发展趋势

[J]. 水利水电科技进展, 2013, 33 (1): 80- 88

[本文引用: 3]

XU Wenjie, ZHANG Haiyang

Research status and development trend of soil-rock mixture

[J]. Advances in Science and Technology of Water Resources, 2013, 33 (1): 80- 88

[本文引用: 3]

胡峰, 李志清, 胡瑞林, 等

基于大型直剪试验的土石混合体剪切带变形特征试验研究

[J]. 岩石力学与工程学报, 2018, 37 (3): 766- 778

HU Feng, LI Zhiqing, HU Ruilin, et al

Research on the deformation characteristics of shear band of soil-rock mixture based on large scale direct shear test

[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37 (3): 766- 778

XU W, XU Q, HU R

Study on the shear strength of soil-rock mixture by large scale direct shear test

[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48 (8): 1235- 1247

DOI:10.1016/j.ijrmms.2011.09.018     

李晓, 廖秋林, 赫建明, 等

土石混合体力学特性的原位试验研究

[J]. 岩石力学与工程学报, 2007, 26 (12): 2377- 2384

DOI:10.3321/j.issn:1000-6915.2007.12.001     

LI Xiao, LIAO Qiulin, HE Jianming, et al

Study on in-situ tests of mechanical characteristics on soil-rock aggregate

[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26 (12): 2377- 2384

DOI:10.3321/j.issn:1000-6915.2007.12.001     

CEN D, HUANG D, REN F

Shear deformation and strength of the interphase between the soil-rock mixture and the benched bedrock slope surface

[J]. Acta Geotechnica, 2017, 12 (2): 391- 413

DOI:10.1007/s11440-016-0468-2      [本文引用: 2]

涂义亮, 刘新荣, 任青阳, 等

含石量和颗粒破碎对土石混合料强度的影响研究

[J]. 岩土力学, 2020, 41 (12): 3919- 3928

TU Yiliang, LIU Xinrong, REN Qingyang, et al

Effects of rock contents and particle breakage on strength characteristics of soil-rock aggregate

[J]. Rock and Soil Mechanics, 2020, 41 (12): 3919- 3928

涂义亮, 李军, 柴贺军, 等

剪切作用下土石混合料的颗粒破碎演化规律

[J]. 铁道工程学报, 2022, 39 (3): 19- 25

DOI:10.3969/j.issn.1006-2106.2022.03.004      [本文引用: 1]

TU Yiliang, LI Jun, CHAI Hejun, et al

Evolution of particle breakage of soil-rock mixture under shearing

[J]. Journal of Railway Engineering Society, 2022, 39 (3): 19- 25

DOI:10.3969/j.issn.1006-2106.2022.03.004      [本文引用: 1]

油新华. 土石混合体的随机结构模型及其应用研究[D]. 北京: 北方交通大学, 2001.

[本文引用: 1]

YOU Xinhua. Stochastic structural model of the earth-rock aggregate and its application [D]. Beijing: Northern Jiaotong University, 2001.

[本文引用: 1]

宋来忠, 沈涛, 彭刚, 等

土石混合体二维细观结构的模拟方法研究

[J]. 岩石力学与工程学报, 2014, 33 (7): 1488- 1495

[本文引用: 1]

SONG Laizhong, SHEN Tao, PENG Gang, et al

Two dimensional mesoscale simulation of soil-rock mixture

[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33 (7): 1488- 1495

[本文引用: 1]

XU W, YUE Z, HU R

Study on the mesostructure and mesomechanical characteristics of the soil-rock mixture using digital image processing based finite element method

[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45 (5): 749- 762

DOI:10.1016/j.ijrmms.2007.09.003      [本文引用: 1]

赵鑫曜, 陈建功, 张海权, 等

基于块石形状数据库的土石混合体模型随机生成方法

[J]. 岩土力学, 2018, 39 (12): 4691- 4697

[本文引用: 2]

ZHAO Xinyao, CHEN Jiangong, ZHANG Haiquan, et al

Random generation of soil-rock mixture models by rock shape database using digital imaging technology

[J]. Rock and Soil Mechanics, 2018, 39 (12): 4691- 4697

[本文引用: 2]

ZHANG W, HAN L, WANG Z, et al

Generation of 3D geotechnical particles using random angular bend algorithm

[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2023, 47 (8): 1313- 1330

DOI:10.1002/nag.3515      [本文引用: 1]

WANG Z, THOMAS B, ZHANG W, et al

A novel random angular bend (RAB) algorithm and DEM modeling of thermal cracking responses of sandstone

[J]. Geomechanics for Energy and the Environment, 2022, 32: 100335

DOI:10.1016/j.gete.2022.100335     

PHOON K, ZHANG W

Future of machine learning in geotechnics

[J]. Georisk, 2023, 17 (1): 7- 22

ZHANG W, GU X, TANG L, et al

Application of machine learning, deep learning and optimization algorithms in geoengineering and geoscience: comprehensive review and future challenge

[J]. Gondwana Research, 2022, 109: 1- 17

DOI:10.1016/j.gr.2022.03.015     

ZHANG W, LI H, LI Y, et al

Application of deep learning algorithms in geotechnical engineering: a short critical review

[J]. Artificial Intelligence Review, 2021, 54: 5633- 5673

DOI:10.1007/s10462-021-09967-1      [本文引用: 1]

崔丹丹. K-means聚类算法的研究与改进[D]. 合肥: 安徽大学, 2012.

[本文引用: 3]

CUI Dandan. Research and improvement of the K-means clustering algorithm [D]. Hefei: Anhui University, 2012.

[本文引用: 3]

徐文杰, 王玉杰, 陈祖煜, 等. 基于数字图像技术的土石混合体边坡稳定性分析[J]. 岩土力学, 2008, 28(增1): 341−346.

[本文引用: 2]

XU Wenjie, WANG Yujie, CHEN Zuyu, et al. Stability analysis of soil-rock mixed slope based on digital image technology [J]. Rock and Soil Mechanics , 2008, 28(Suppl. 1): 341–346.

[本文引用: 2]

马昊, 黄达, 肖衡林, 等

江北机场高填方夯后碎块石土剪切力学性质研究

[J]. 水文地质工程地质, 2019, 46 (3): 88- 94

[本文引用: 1]

MA Hao, HUANG Da, XIAO Henglin, et al

A study of the shear mechanical properties of high-filled gravel-block soil after dynamic compaction near the Jiangbei airport

[J]. Hydrogeology and Engineering Geology, 2019, 46 (3): 88- 94

[本文引用: 1]

徐文杰, 胡瑞林, 岳中崎

土-石混合体随机细观结构生成系统的研发及其细观结构力学数值试验研究

[J]. 岩石力学与工程学报, 2009, 28 (8): 1652- 1665

DOI:10.3321/j.issn:1000-6915.2009.08.017      [本文引用: 2]

XU Wenjie, HU Ruilin, YUE Z Q

Development of random mesostructure generating system of soil-rock mixture and study of its mesostructural mechanics based on numerical test

[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28 (8): 1652- 1665

DOI:10.3321/j.issn:1000-6915.2009.08.017      [本文引用: 2]

MEDLEY E W. The engineering characterization of mélanges and similar block-in-matrix rocks (bimrocks) [D]. Berkeley: University of California at Berkeley, 1994.

[本文引用: 1]

喻江武, 苟志龙, 雷瑜, 等

基于傅里叶逆变换的土石混合体模型生成研究

[J]. 水利水电技术, 2019, 50 (4): 7- 15

[本文引用: 1]

YU Jiangwu, GOU Zhilong, LEI Yu, et al

Inverse Fourier transform-based study on generating model of soil-rock mixture

[J]. Water Resources and Hydropower Engineering, 2019, 50 (4): 7- 15

[本文引用: 1]

丁巍, 楚锡华, 常江芳

横观各向同性岩土材料的应变局部化分析

[J]. 地震工程学报, 2017, 39 (3): 481- 487

DOI:10.3969/j.issn.1000-0844.2017.03.0481      [本文引用: 1]

DING Wei, CHU Xihua, CHANG Jiangfang

Numerical analysis of strain localization for transversely isotropic geomaterials

[J]. China Earthquake Engineering Journal, 2017, 39 (3): 481- 487

DOI:10.3969/j.issn.1000-0844.2017.03.0481      [本文引用: 1]

/

〈 〉