超大型土工离心机是用来揭示岩土体大时空演变、地质过程演变重现的重要实验装备. 土工离心机载重量越大、重力加速度越大，获得实验结果的时间越短，因此大型化是其发展趋势^[1-4]. 截至2020年，世界上装机容量最大的土工离心机是由法国Actidyn公司制造的WES土工离心机，其最大装机容量达到1 200g·t^[5-7]. 为了推进中国土工离心机的大型化，浙江大学进行了重力加速度为1 500g、装机容量为2 200g·t超大型土工离心机的研制^[5].

装备大型化的技术难点之一是离心机风阻功率随着重力加速度的增加呈现二次方的同步增加，导致机室温度快速升高，影响机器与传感器的正常运行^[8-9]. 温升控制在离心加速度较低时相对容易，原因是风阻功率较小，能量密度流不高，散热快. 当离心加速度超过1 500g时，风阻功率可达5 MW，每平方毫米的能量密度流超过瓦级，散热系数如此高的材料很少，温升问题突出，温升控制变得困难. 可以从2个方向思考温升控制问题：1）将机室内的热量导出. 常用方法是在机室开通风口，当设备运行时，机室内的热空气在通风口被置换为冷空气^[6,10-13]. 该方法能够有效降低机室温度，但当机室内气体达到稳态后，气体随流速度与总动能维持恒定，流速较高的气体在空气置换时逸出，导致总动能下降，新进入的冷空气须重新加速到稳态速度，增加了不必要的功率损耗. 考虑到较大的机室侧壁面积是空气摩擦产热的主要原因，也有方法通过在侧壁安装液冷夹套并通入制冷剂来导出侧壁热量^[5,14-15]. 2）降低风阻功率，减少产热来源. 风阻功率与离心机转子结构、机室结构、空气密度、转子转速等有关^[4,7,14,16]. 在离心机几何结构尺寸、操作工况一定的情况下，风阻功率主要与气体的密度有关，气体密度越低，风阻功率越小. 由于影响气体密度的主要因素是介质物性、温度和压力，且受限于机室温控的要求，降低机室真空度成为温升控制常用手段. 空气密度随着机室内压力的降低而降低，使得风阻功率线性下降，实现温控目标^[17-18]. 真空机室带来3个问题：1）实验环境改变使常压下进行的环境实验变得困难；2）离心机设备的运行环境改变造成润滑系统和传动系统密封困难；3）转子的热量难以传导到机室壁面.

本研究采用氦气置换空气的方法，以期从源头降低风阻功率，减少温升；利用超重力离心模拟与实验装置（centrifugal hypergravity and interdisciplinary experiment facility，CHIEF）的缩比模型验证氦气置换实现温控的有效性^[19].

稳定运转的土工离心机总驱动功率由风阻功率和固有功率组成，其中固有功率包括机械传动系统的摩擦功率、电动机的损耗功率. 总驱动功率将全部转化为热量，如果土工离心机置于密闭的环境中，则热量将被气体介质、机室壁面、测量设备等吸收，使得机室内温度升高. 风阻功率为抵消转子上的空气阻力消耗的功率，该功率产自机室，大型土工离心机的风阻功率在总功率中的占比超过85%^[20]，是造成机室内温度升高的主要原因. 土工离心机风阻功率$ {P}_{\mathrm{w}} $的计算式^[4,7,16]为

(1)$ {P}_{\mathrm{w}}=0.5\rho C{\left(1-\alpha \right)}^{2}{r}^{3}{\omega }^{3}S . $

式中：$ \rho $为气体密度；$ S $为迎风面面积；$ C $为转子的阻力系数，与转子的几何形状有关；$ \alpha $为气体随流比，表示转子周围空气与转子的相对速度；$ r $为转子的转动半径；$ \omega $为转子的角速度. 对于特定设备，$ r $、$ C $为定值，当转速确定时，$ \omega $为定值，在氦气和空气工况下，风阻功率的主要区别在于气体密度和气体随流比. 由式（1）可知，风阻功率与气体密度成正比，在室温条件下，空气密度为1.16 kg/m³，氦气密度为0.1 698 kg/m³. 氦气置换空气后，风阻功率将显著降低，从源头上抑制了机室内热量的产生，实现机室内温度的控制，在温控过程中降低了能源消耗.

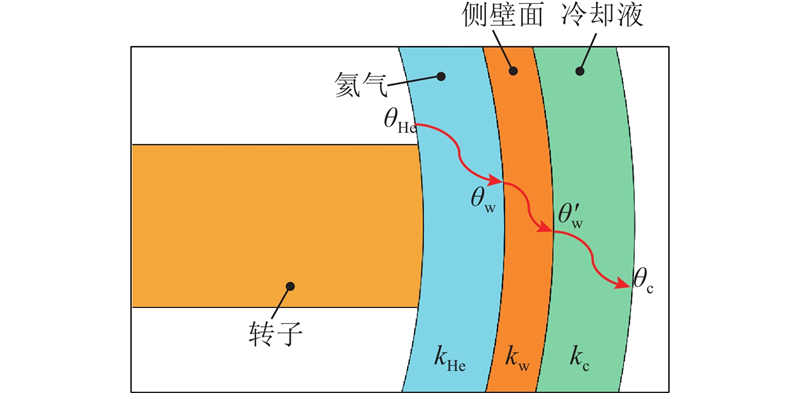
土工离心机巨大的离心作用使机室内的绝大部分气体被甩到机室侧壁面，形成高压、高密度的圆环，为此将离心机室内的旋转气体的运动视为环形气体沿壁面旋转. 参照圆管对流进行传热计算，如图1所示为土工离心机壁面的传热模型，机室侧壁面安装有冷却装置，其中$ {k}_{\mathrm{g}} $、$ {k}_{\mathrm{w}} $、$ {k}_{\mathrm{c}} $分别为气体侧、机室侧壁面、冷却液的传热系数，$ \theta _{\mathrm{g}} $为气体侧的温度，$ \theta _{\mathrm{w}} $为机室侧壁面内侧的温度，$ \theta _{\mathrm{c}} $为冷却液的温度. 机室内的气体在矩形截面的环形槽道中流动，在气体与壁面的摩擦作用下，槽道中的气体沿半径方向上的速度逐渐降低. 槽道范围内，气体的速度波动范围约在0~25%^[14,21-22]，为了简化计算，假设槽道中的气体以气体整体的平均速度流动，则气体的传热系数计算式^[23]为

(2)$ {k}_{\mathrm{g}}=Nu\cdot \lambda \cdot {d}_{{\mathrm{e}}}^{-1} . $

式中：$ \lambda $为导热系数；$ {d}_{{\mathrm{e}}} $为当量直径，$ {d}_{{\mathrm{e}}}=4{A}_{c}/L $，$ {A}_{{\mathrm{c}}} $为槽道的流动面积，$ L $湿周长度；$ Nu $为努赛尔数，管槽内湍流强制对流的努赛尔数计算式为

(3)$ Nu=0.023{Re}^{0.8}{Pr}^{0.33} . $

式中：雷诺数$ Re=u{d}_{{\mathrm{e}}}\rho /\mu $，其中气体的旋转速度$ u=\alpha r\omega $，$ \mu $为动力黏度；普朗特数$ Pr=\mu {c}_{p}/\lambda $，其中$ {c}_{p} $为比定压热容. 将式（3）代入式（2）可以得到

(4)$ {k}_{\mathrm{g}}=0.023{u}^{0.8}{d}_{{\mathrm{e}}}^{-0.2}{\mu }^{-0.47}{{c}_{p}}^{0.33}{\lambda }^{0.67}{\rho }^{0.8} . $

氦气置换空气后，物性参数发生了变化，两者的物性参数如表1所示. 由于氦气置换空气后机室内的密度大幅降低，转子转动过程中受到的压差阻力将显著下降，气体与摩擦产生的热量也大幅降低，有效地抑制了热量的产生. 氦气的比定压热容是空气的5.17倍，这意味着，在相同的产热量下，氦气的温升必然更低. 此外，氦气的导热系数提高至原来的5.86倍，通过置换后系统的换热能力得到大幅提升. 结合式(4)可知，置换后系统的传热系数增大，热量更容易导出. 设氦气下的传热系数为$ {k}_{\mathrm{H}\mathrm{e}} $，空气下的传热系数为$ {k}_{\mathrm{a}\mathrm{i}\mathrm{r}} $，假设氦气置换后$ \alpha $不变，由式(4)得到：$ {k}_{\mathrm{H}\mathrm{e}} $/$ {k}_{\mathrm{a}\mathrm{i}\mathrm{r}} $=1.15，可以看出，氦气置换后，传热系数提高了15%，将有利于气体侧热量的导出.

为了提出更具有针对性的温控方案，郑传祥等^[18]根据热量的产生原因将土工离心机中的热源分成2个热源：高速转子与气体的摩擦产热（第一热源）、高速随流气体与机室侧壁面的摩擦产热（第二热源）. 第一热源的热量传递路径为气体—侧壁面—冷却液，第二热源的路径为侧壁面—冷却液，2条路径的热量都通过冷却液的流动将热量导出. 根据热量的传递路径，得到第一热源的传热系数为

(5)$ {K}_{1}={\left(\frac{1}{{k}_{\mathrm{g}}}+\frac{1}{{k}_{\mathrm{w}}}+\frac{1}{{k}_{\mathrm{c}}}\right)}^{-1} . $

气体侧的温度与相对半径近似呈线性关系^[15]，因此假设环形槽道内气体的温度均匀变化，通过计算得到第一热源的热流量为

(6)$ {{\varPhi }}_{1}={K}_{1} \left(\theta _{\mathrm{g}}-\theta _{\mathrm{c}}\right) A . $

若已知冷却液进口温度$ \theta _{\mathrm{i}\mathrm{n}} $、出口温度$ \theta _{\mathrm{o}\mathrm{u}\mathrm{t}} $，冷却液的总热流量的计算式为

(7)$ {\varPhi }={c}_{p}{q}_{m}\left(\theta _{\mathrm{o}\mathrm{u}\mathrm{t}}-\theta _{\mathrm{i}\mathrm{n}}\right) . $

式中：$ {q}_{m}=\rho {q}_{V} $为质量流量，其中$ {q}_{V} $为体积流量. 第二热源的热流量计算式为

(8)$ {\mathrm{\varPhi }}_{2}=\mathrm{\varPhi }-{\mathrm{\varPhi }}_{1} . $

上述方法在实验中须测得靠近转子的气体侧温度、冷却液进出口温度、冷却液的温度和体积流量，由此计算出设备的总热量以及第一热源和第二热源的热量.

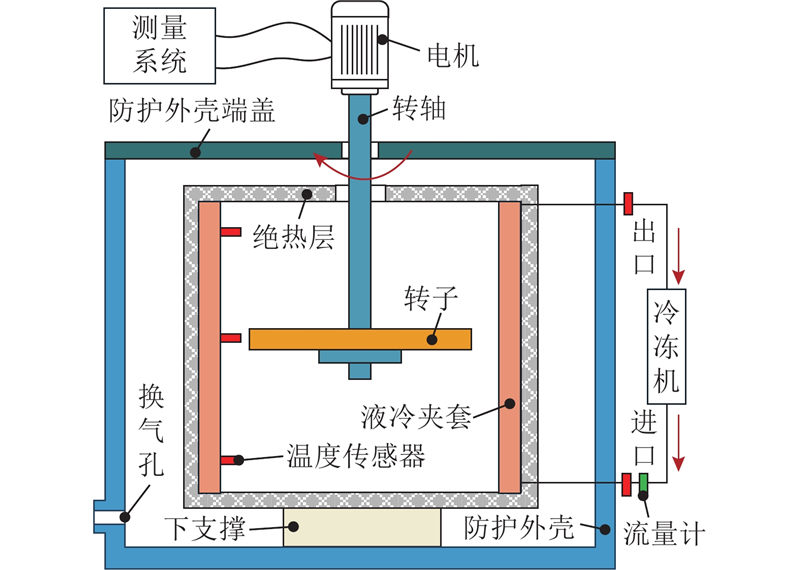
CHIEF高速机的最大离心加速度为1 500g，转子最大线速度为291 m/s，以机室直径1∶20的比例建造缩比模型实验装置，实验原理如图2所示. 如图3所示为缩比模型实验系统的实物图，螺旋形的液冷夹套与绝热层构成机室，机室直径为0.600 m，液冷夹套的外径为0.700 m；夹套中通有冷却液，冷却液由带恒温控制的冷冻机控制，冷却液为质量分数为40%的乙二醇溶液，温度设定为−15 ℃；转子通过螺栓连接的方式固定在转轴上，转轴由电机驱动，转子外径为0.470 m，高度为0.034 m. 上述机室结构放置在防护装置中以保证实验的安全性；电机与测量系统相连，系统测得电机的输入电压、电流、转速，由此计算出电机的输入功率、输入力矩. 在靠近转子端面的同心柱面上、中、下分别布置温度传感器（共3个温度传感器）以测量气体侧的温度$ \theta _{\mathrm{g}} $，在冷却液的进、出口分别布置温度传感器以测量冷却液进出口温度$ \theta _{\mathrm{i}\mathrm{n}} $、$ \theta _{\mathrm{o}\mathrm{u}\mathrm{t}} $；由于难以在冷却液中单独布置温度传感器，$ \theta _{\mathrm{c}} $近似取为进出口温度的平均值；在冷却液的进口处安装体积流量计测量$ {q}_{m} $. 传感器的导线通过密封系统连接到对应的仪表. 在装置防护外壳外侧设有换气孔，实现机室内气体的置换.

准确获得风阻功率须排除系统固有功率的影响，如图4所示设置实验装置测定风阻功率，实验过程如下. 1）不安装转子测量系统的总驱动功率，将该功率视为设备的固有功率；2）安装转子进行相关实验，测得实验工况下的总驱动功率，功率减去固有功率得到风阻功率.

将机室内的最高温度控制在（40±5） ℃是CHIEF原型机温控设计的一大难点. 为了探究氦气置换后的温控效果，设计2组实验. 根据CHIEF的运行工况，确定转子的线速度分别为158、214、291 m/s.

第一组实验：以线速度158 m/s为基准进行空气工况和氦气工况实验，测定各工况下的风阻功率和机室内温度的变化，对比氦气置换前后的减阻降温效果. 在进行空气工况实验时，将装置的换气孔堵住，开启冷冻机，启动电机，使转子末端的线速度达到158 m/s并保持该转速稳定运行，每隔1 min记录电机的电压、电流，温度传感器和流量计的数值，待所有数值均稳定后，停止实验. 与空气工况不同之处，氦气工况须先通过换气孔将机室内抽真空到1 Pa（绝对压力），再将氦气缓慢通入机室内，直到机室内压力稳定在常压0.1 MPa（表压），完成氦气的置换，之后再开启冷冻机，启动电机，进行实验.

第二组实验：分别以214、291 m/s为基准进行氦气工况的实验，测定不同转速下的风阻功率与机室内温度的变化，以验证氦气置换实现CHIEF温控的可行性.

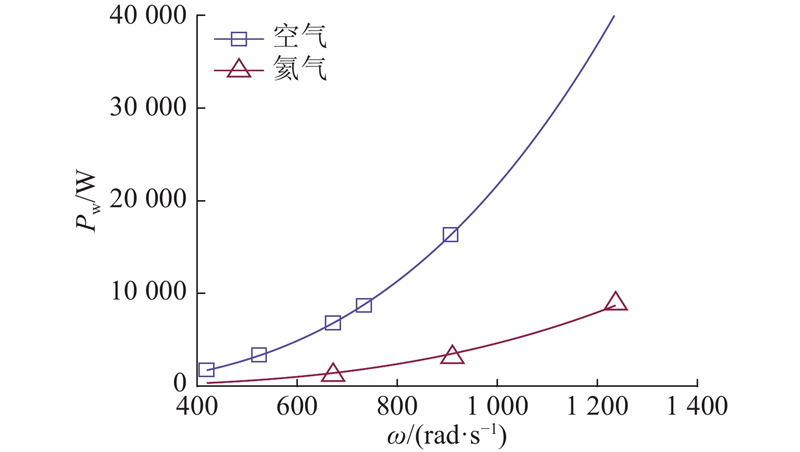
第一组实验测得空气工况下风阻功率为6 825.1 W；氦气工况下风阻功率为1 200.1 W，为空气工况下的17.6%，略大于2种气体的密度之比. 由式(1)推测，气体置换后，随流比$ \alpha $也会受到影响，但远小于密度变化带来的影响. 王永志等^[12]通过分析2台土工离心机实验数据发现，式(1)可简化成幂函数的形式，简化计算式为

(9)$ {P}_{\mathrm{w}}=k{\omega }^{p} . $

式中：$ k $、$ p $为常量. 式（9）将与设备结构有关的$ C $、$ r $和$ \alpha $的常数部分以及机室气体介质密度$ \rho $的影响综合到系数$ k $中，与设备转速有关的影响综合到系数$ p $中，即随流比$ \alpha $与$ \omega $有关的部分. 令式(1)中的$ {\left(1-\alpha \right)}^{2}={k}^{{''}}{\omega }^{q} $，$ {k}^{{''}} $为随流比对风阻功率影响的常数部分，$ {\omega }^{q} $为与转速有关的部分，可以得到

(10)$ \alpha =1-\sqrt{{k}^{{''}}{\omega }^{q}} . $

结合前述分析，为了描述气体介质变化后对风阻功率特性的影响，将式(9)变化为

(11)$ {P}_{{\mathrm{w}}}={k}^{{'}}{k}^{{''}}\rho {\omega }^{3+q} . $

式中：$ {k}^{{'}}=C{r}^{3}{S}^{2}/2 $为与设备结构有关的常数；$ {k}^{{'}}{k}^{{''}}=k/\rho $，即将密度的影响分离出来. $ \omega $的幂次包含转子自身旋转特性带来的幂次3和气体介质变化后引入的幂次$ q $. 氦气实验测量得到3个不同线速度下的风阻功率（线速度分别为158、214、291 m/s，对应角速度$ \omega $=671.6、910.2、1 236.7 rad/s），为了与空气下的风阻工况进行对比，单独测定空气工况下设备在不同角速度下的风阻功率. 通过式(11)分别对氦气和空气工况下的风阻功率进行拟合，拟合结果如图5所示. 可以看出，空气工况下风阻功率随着$ \omega $的增大而急剧增大；相较而言，氦气工况下风阻功率随$ \omega $的变化趋势较为平缓.

如表2所示为不同工况下风阻功率拟合曲线的参数. $ {R}^{2} $均接近于1，说明该拟合曲线的特性能较好地反映实验数据的特征；$ q $均为负值，由式(10)可知，$ q $的数值越小，$ \alpha $越大，随流空气速度越大，转子与空气的相对速度就越小，从而气体流速产生的压差阻力就越小. 表2中氦气的$ q $值大于空气的$ q $值，说明氦气置换后，气体的随流比减小，使得风阻功率有上升的趋势；结合图5可知，随流比的变化带来的影响很小，整体趋势上空气工况下的风阻功率随角速度的变化率远大于氦气工况下的结果. $ k $反映空气和氦气密度带来的影响，氦气下的该数值比空气下小一个量级，说明气体密度是造成风阻功率呈现这一变化趋势的关键因素.

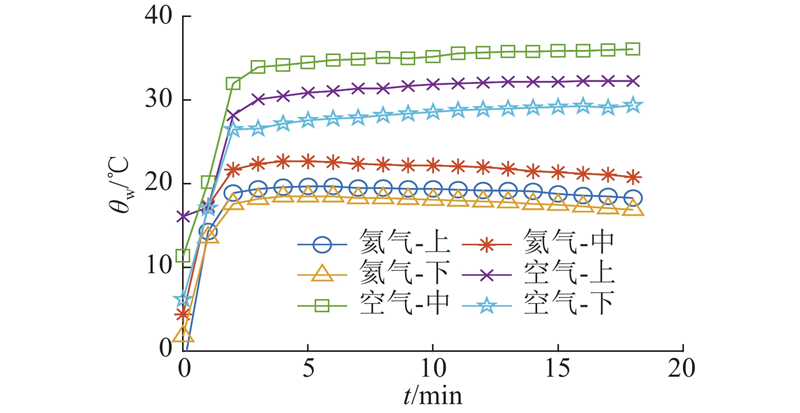
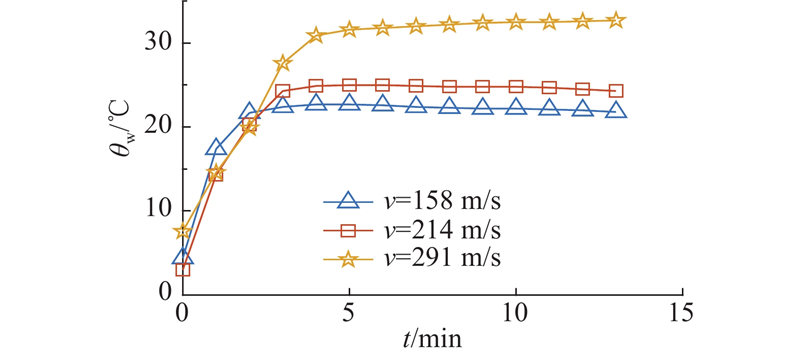
如图6所示为第一组实验中线速度为158 m/s时氦气和空气工况下近壁面的温度，其中“上”、“中”、“下”分别表示靠近机室上壁面、转子、下壁面的温度传感器测得的数值. 固有功率的一部分热量经转轴传导入机室内，也会造成侧壁面温度的升高，由于该部分热量较小，本实验忽略转轴上的热量. 可以看出，无论是氦气工况还是空气工况，靠近转子附近的空气温度最高，机室上下壁面的温度相对较低. 原因是转子高速旋转与周围的气体摩擦产生热量，使气体温度升高，同时机室内气体受到转子的切割，向转子上下空间流动，使得热量向上下壁面传递，传递过程中气体的动能不断耗散，温度略有下降. 在空气工况下，气体的最高温度为36.6 ℃，若线速度进一步提高，将很快超过限定的（40±5）℃. 氦气置换后，机室内的最高温度仅为22.7 ℃，相比空气工况下降低了13.9 ℃，说明氦气置换能够有效降低机室内的温度，温控的效果明显.

如图7所示为第二组实验中氦气工况下不同线速度时机室内转子附近的温度变化. 可以看出，随着线速度的增大，机室内的温度逐渐升高，当线速度达到291 m/s时，机室内最高温度为32.9 ℃，小于目标温度（40±5） ℃. 在该线速度的空气工况下，机室温度将超过56.4 ℃，若要使得温度不超过45 ℃，须使机室的真空度低于20 kPa^[5]，这样的真空度一方面会对实验环境产生很大的影响，另一方面也增加了密封的难度. 相比于空气工况，氦气工况下更容易实现（40±5） ℃的温控要求，同时降低了对实验环境和密封性的要求.

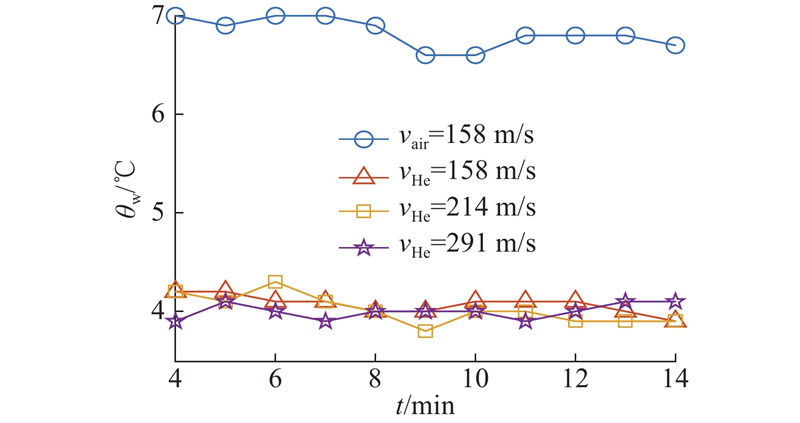
除了温度，温控的另一目标是希望机室内的温度变化均匀，以保证岩土试样环境温度的相对恒定. 为了评估温度的变化，计算2组实验各工况下机室内的最大温差 $ \mathrm{\Delta } \theta _{\mathrm{w}} $，结果如图8所示. 由图可知，氦气工况下的最大温差在3.9~4.3 ℃波动，不同转速下最大温差基本接近，说明对于特定的气体，最大温差几乎与转速无关. 还可以看出，空气下的最大温差在6.8 ℃附近波动，比氦气工况下的温差高出65.8%，说明氦气置换后能够有效减少机室内温度的波动，有利于实现恒定的室温条件.

氦气置换后能够大幅度降低风阻、降低机室内的温度，风阻功率与机室内的最高温度随转速增大而增大，因此在设计温控系统时，只需确保最高转速下的温控目标能够实现. 开展氦气工况最高线速度下（291 m/s）的传热过程分析，将分析结果应用于CHIEF原型机的计算.

1）氦气侧传热系数$ {k}_{\mathrm{H}\mathrm{e}} $. 机室内的氦气随着离心机转臂高速旋转，氦气的旋转速度为$ u=\alpha r\omega $，取$ C $=2.1^[24]，由式(1)、(9)~(11)计算得到$ \alpha $=0.5005. 由式(2)~(4)计算得到$ {k}_{\mathrm{H}\mathrm{e}} $=344.9834 W/(m²·K).

2）机室侧壁面传热系数$ {k}_{\mathrm{w}} $. 将机室侧壁面视为单层圆筒壁，其传热系数为

(12)$ {k}_{\mathrm{w}}=\frac{2{\text{π}}\lambda h}{\mathrm{l}\mathrm{n}\;({d}_{3}/{d}_{2})} . $

式中：$ h $=0.6 m为机室高度；$ {d}_{3} $为圆筒壁外径，$ {d}_{3}={d}_{2}+2\delta $，其中$ \delta $=0.003 m为壁厚. 机室侧壁为不锈钢材料，$ \lambda $=16 W/(m·K)，由式（12）得到$ {k}_{\mathrm{w}} $= 6 061.9 672 W/(m²·K).

3）冷却液侧的传热系数$ {k}_{\mathrm{c}} $. 实验测得冷却液进口处温度为−14 ℃，出口处温度为−2.1 ℃，$ \theta _{c} $取为冷却液进出口的平均温度，即−8.05 ℃（264.95 K），取该温度为定性温度，$ \lambda $= 0.3728 W/(m·K)，$ {c}_{p} $= 3 359 J/(kg·K)，$ \mu $=1.0150×10⁻² Pa·s，$ \rho $=1 070 kg/m³. 流量计测得冷却液的体积流量为0.7853 m³/h，流速为0.1206 m/s，计算得到$ Re $=609.9858. 对于螺旋管道中流动的液体，当$ Re $<2 100 时传热系数的计算式^[25]为

(13)$ {k}_{\mathrm{c}}=1.86{\left[Re\cdot Pr\left({{d}_{{\mathrm{e}}}}/{L}\right)\right]}^{0.33}{V}_{{\mathrm{is}}}^{0.14} . $

式中：$ {V}_{{\mathrm{is}}} $为流体在主体温度下的黏度和壁温下的黏度之比，计算中忽略壁温的阻力，取$ {V}_{{\mathrm{is}}}=1 $；$ L $=19.4644 m为螺旋管的长度. 由式（13）计算得到$ {k}_{\mathrm{c}} $=60.2349 W/(m²·K). 由式（5）计算得到第一热源的综合传热系数$ {K}_{1} $=50.8509 W/(m²·K).

由式(5)~(8)计算得第一热源的热流量为2 355.1 W，第二热源的热流量为6 974.5 W，总热流量为9 329.6 W. 第二热源的热流量占总热量的75%，第一热源和第二热源热流量之比为1∶2.96，说明气体与机室侧壁面的摩擦产热是设备热量的主要来源. 液冷夹套外侧包覆有绝热层，因此将液冷夹套的总热流量视为风阻功率，由式(7)计算得到的风阻功率为8 905.7 W，与$ {\varPhi } $的值非常接近，误差为4.543%，验证了液冷夹套测量结果的准确性，绝热层并非理想绝热材料以及部分摩擦功率通过转轴传递至机室内是产生误差的可能原因.

CHIEF中功率最高的为高速机，该设备的机室直径为9 m，高度为3.5 m，机室侧壁面厚度为0.008 m. 转臂直径为8.3 m，转子高度为0.8 m，转子线速度为291 m/s. 在空气常温常压下该设备的风阻功率最高将达到5 MW^[5]，根据前述分析，氦气置换后风阻功率将降低至常温工况的17.6%，则氦气置换后风阻功率将降至880 kW. 采用与缩比模型相同的温控方案进行温控计算，可以得到$ {k}_{\mathrm{H}\mathrm{e}} $=245.9867 W/(m²·K)，$ {k}_{\mathrm{w}} $=198096.2143 W/(m²·K). 根据第一热源和第二热源的产热功率之比，计算得到第一热源产热功率为223 kW. 由于要求机室内最高温度低于40 ℃，以该温度为氦气侧的临界温度，即$ \theta _{\mathrm{H}\mathrm{e}} $=40 ℃，取$ \theta _{\mathrm{c}} $=5 ℃，由式(5)计算得到第一热源的综合传热系数$ {K}_{1} $=64.3838 W/(m²·K)，因此只要综合传热系数大于该值即可实现所需温控，由式(5)、(6)反算得到$ {k}_{\mathrm{c}}> $87.2482 W/(m²·K)即可. 保持液冷夹套的槽道尺寸不变，通过计算发现，当Re=2 100时，$ {k}_{\mathrm{c}} $=24.0490 W/(m²·K)，k_c≤87.2482 W/(m²·K)，因此液冷夹套在层流工况时已满足不了温控的要求，此时须增加冷却液的流速. 通过计算，当冷却液流速大于0.410 m/s时，$ Re $=2 320，此时$ {k}_{\mathrm{c}} $的计算式^[25]为

(14)$ \begin{split} {k}_{\mathrm{c}}= & 0.027{Re}^{0.8}{Pr}^{0.33} \left({V}_{{\mathrm{is}}}^{0.14}\left[1+3.5\left({{d}_{{\mathrm{e}}}}/{{d}_{\mathrm{c}}}\right)\right]\right) \phi \left({\mathrm{\lambda }}/{{d}_{{\mathrm{e}}}}\right) .\end{split} $

式中：$ {d}_{\mathrm{c}} $为液冷夹套的中径；$ \phi $为修正系数，须依据不同的雷诺数进行插值，取$ \phi $=0.456，得到$ {k}_{\mathrm{c}} $=195.3453 W/(m²·K) >87.2482 W/(m²·K)，对应的氦气侧最高温度为25.7 ℃<40 ℃，因此温控可实现.

基于全文的综合分析，氦气置换技术是实现温控目标的有效手段，尤其适用于必须在常压下进行的实验工况. 抽真空系统是离心机温控的基本方式，真空系统能够满足氦气置换后机室的密闭性要求，因此无需更改设备的技术方案，只要预留氦气置换的接口. 应该指出氦气的使用成本较高. 据测算，在长时间（> 3.5 d）运行工况中，氦气置换的经济效益优于真空抽取. 因此，在实际应用中，应根据工况需求和经济性来选择是否采用氦气置换技术.

本研究通过理论分析和实验测试验证了所提方法的有效性：用氦气置换空气不但大幅降低了风阻功率，而且大大提升了转子的散热效果. 该方法为大型土工离心机常压下实现温控提供了新的思路，研究所得结论如下. 1）氦气置换空气后，风阻功率降低了82.4%，气体密度降低是造成风阻功率骤降的主要原因. 2）氦气置换空气后，机室内的最高温度从56.4 ℃降至32.9 ℃，说明氦气置换能够有效降低机室内的温度，实现温控要求. 3）机室内的最大温差与转速无关，与气体介质有关，氦气置换后，最大温差从6.8 ℃降至4.1 ℃；由于氦气的导热系数高，氦气置换后机室内的温度更为稳定. 4）高速转子与氦气的摩擦产热形成的第一热源和随流气体与侧壁面摩擦产热形成的第二热源产热功率之比为1∶2.96，说明第二热源是造成机室温度升高的主要原因. 5）传热模型分析结果表明，CHIEF的最高温度能够控制在25.7 ℃，不超过（40±5） ℃的温控目标，满足设备在常压工况下稳定运行的要求. 为了将该方法应用到原型机中，下一步将在1∶3和1∶1的缩比模型上进行验证，探究放大过程中的温升规律.

致谢　　本研究课题得到浙江大学超重力离心实验中心、浙江海骆航空科技有限公司的大力支持，在此表示衷心感谢.