浙江大学学报(工学版)

浙江大学学报(工学版), 2024, 58(10): 2069-2075 doi: 10.3785/j.issn.1008-973X.2024.10.010

机械工程、能源工程

基于连续小波卷积神经网络的轴承智能故障诊断方法

耿志强,, 陈威, 马波, 韩永明,

1. 北京化工大学 信息科学与技术学院，北京 100029

2. 智能过程系统工程教育部工程研究中心，北京 100029

3. 北京化工大学 机电工程学院，北京 100029

Bearing intelligent fault diagnosis method based on continuous wavelet convolutional neural network

GENG Zhiqiang,, CHEN Wei, MA Bo, HAN Yongming,

1. College of Information Science and Technology, Beijing University of Chemical Technology, Beijing 100029, China

2. Engineering Research Center of Intelligent Process Systems Engineering, Ministry of Education, Beijing 100029, China

3. College of Mechanical and Electrical Engineering, Beijing University of Chemical Technology, Beijing 100029, China

通讯作者: 韩永明，男，教授. orcid.org/0000-0003-3209-725X. E-mail：hanym@mail.buct.edu.cn

收稿日期: 2024-01-14  

基金资助: 国家自然科学基金资助项目（62373035, 62273025）.

Received: 2024-01-14  

Fund supported: 国家自然科学基金资助项目（62373035,62273025）.

作者简介 About authors

耿志强（1973—），男，教授，博导，从事智能建模与故障诊断研究.orcid.org/0000-0003-0647-3792.E-mail：gengzhiqiang@mail.buct.edu.cn , E-mail：gengzhiqiang@mail.buct.edu.cn

摘要

传统故障诊断方法存在特征提取有限和故障检测不准确的问题，为此提出新的轴承智能故障诊断方法. 构建连续小波卷积层取代卷积神经网络(CNN)中的初始卷积层，用于提取轴承数据的初级特征；使用增强ACON激活函数处理提取的振动信号；设计新的计算空间，提高CNN的整体自适应性. 在凯斯西储大学轴承数据集上开展滚动轴承故障诊断方法对比实验. 结果表明，与传统基于CNN、快速傅里叶变换-CNN、长短时记忆-CNN故障诊断方法相比，所提方法的故障诊断精度分别提高了7.45、4.46和1.53个百分点，CNN的收敛速度更快. 在不同工况的泛化任务中，所提方法的平均准确率为99.64%，准确性和泛化能力良好.

关键词： 卷积神经网络(CNN) ; 连续小波 ; 自适应激活函数 ; 轴承 ; 故障诊断

Abstract

A new bearing intelligent fault diagnosis method was proposed, aiming at the problems of limited feature extraction and inaccurate fault detection in traditional fault diagnosis methods. A continuous wavelet convolutional layer was constructed to replace the initial convolutional layer in the convolutional neural network (CNN) for extracting the primary features of the bearing data. The enhanced ACON activation function was used to process the extracted vibration signals. A new computational space was designed to improve the overall adaptivity of CNN. Comparative experiments of rolling bearing fault diagnosis methods based on the Case Western Reserve University bearing dataset were carried out. Experimental results showed that the fault diagnosis accuracy of the proposed method was improved by 7.45, 4.46 and 1.53 percentage points, respectively, and the convergence speed of CNN was faster compared with the traditional fault diagnosis methods based on CNN, the fast Fourier transform with CNN, the long short-term memory with CNN. In the generalization task for different working conditions, the proposed method had an average accuracy of 99.64%, demonstrating superior accuracy and generalisability.

Keywords： convolutional neural network (CNN) ; continuous wavelet ; adaptive activation function ; bearing ; fault diagnosis

PDF (1052KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

耿志强, 陈威, 马波, 韩永明. 基于连续小波卷积神经网络的轴承智能故障诊断方法. 浙江大学学报(工学版)[J], 2024, 58(10): 2069-2075 doi:10.3785/j.issn.1008-973X.2024.10.010

GENG Zhiqiang, CHEN Wei, MA Bo, HAN Yongming. Bearing intelligent fault diagnosis method based on continuous wavelet convolutional neural network. Journal of Zhejiang University(Engineering Science)[J], 2024, 58(10): 2069-2075 doi:10.3785/j.issn.1008-973X.2024.10.010

轴承故障通常由磨损、润滑不足、材料疲劳或过载引起，易造成设备停机、生产损失，是潜在的安全隐患[1]. 精确、及时地检测轴承故障对于确保设备可靠性、提高维护效率和保障安全至关重要[2]. 随着物联网、大数据分析和机器学习等技术的兴起，轴承智能故障诊断为设备健康监测和预测性维护提供了新途径. 滚动轴承性能监控已进入大数据时代[3]，依赖经验准则和阈值的传统故障诊断方法可能无法精确检测和诊断潜伏和萌芽故障，如何从大数据中提取有价值的信息并进行有效分析也是故障诊断须面临挑战.

故障诊断方法[4]主要分为传统信号处理、机器学习和深度学习. 传统信号处理常用的技术有小波变换[5]和傅立叶变换[6]；机器学习的常用方法有支持向量机[7](support sector machine, SVM)和极限学习机[8](extreme learning machine, ELM)；包括卷积神经网络[9](convolutional neural network, CNN)和长短期记忆[10]( long short-term memory, LSTM)在内的深度学习方法越来越受欢迎. 传统的信号处理方法计算简单、易于理解和实现，特定类型的故障诊断性能良好. 针对经验小波变换（empirical wavelet transform, EWT）在划分数据边界时的不准确性，Xu等[11]提出新颖的频谱分割方法. 为了解决EWT无法检测滚动轴承故障的问题，Huang等[12]提出频相空间EWT (frequency phase space EWT， FPSEWT). 为了解决轴承早期故障特征难提取和避免应用变异模态分解（variational mode decomposition, VMD）时出现的过度分解的问题，Li等[13]提出基于VMD-短期傅里叶变换(short time Fourier transform，FRFT)的滚动轴承诊断方法VMD-FRFT. Xu等[11-13]所提方法须进行人工选择和提取特征，处理复杂的故障模式时不够灵活，而且严重依赖工程师的经验和领域知识. Zhang等[14]提出基于贝叶斯的轴承故障诊断方法，旨在增强轴承数据独立性，提高故障诊断的准确性. Ye等[15]基于VMD、多尺度置换熵和基于粒子群优化的支持向量机，提出能够提高诊断准确率的轴承故障诊断方法. Ma等[16]提出的滚动轴承综合故障诊断方法优化了VMD和ELM，能够从轴承振动信号中更有效地提取特征信息. 机器学习方法在处理小数据样本时若遇过拟合问题，须进行人工设计和特征方向选择. 深度学习可以从原始数据中学习和提取更高层次的特征，而无需人工干预，能够比传统信号处理方法更好地处理复杂的数据模式和故障特征. CNN因良好的特征提取能力在滚动轴承故障诊断领域得到广泛应用. Xu等[17]提出的基于迁移CNN (transfer CNN, TCNN)框架的在线故障诊断方法，能够利用源领域学到的知识有效解决目标领域中的问题. Yang等[18]将由对抗神经网络创建的故障信号二维灰度图像与二维CNN结合，完成了小样本轴承的故障诊断. Wang等[19]建议使用对称点图案(symmetrized dot pattern, SDP)图解轴承状况，采用基于挤压和激励的CNN (squeeze-and-excitation-enabled CNN, SE-CNN)模型自动提取数据特征. Mao等[20]将原始振动信号转换为二维频率和平方包络谱，这些信号与红外热图像相结合后输入用于跨域变速箱诊断的网络.

在实际工业中，轴承的工作条件可能不同，而且振动信号经常包含噪声，导致网络处理信号能力下降，使得网络诊断效果欠佳. CNN与信号处理方法结合的特定轴承故障诊断方法常用却难以准确地提取轴承的故障特征. 为了提高CNN的泛化能力和特征提取能力，本研究提出基于连续小波CNN的轴承智能故障诊断方法CWCNN. 该方法基于传统的端到端诊断模型，将具有物理意义的小波卷积层作为CNN的首层，以增强模型的可解释性和通用性. 为了提高小波函数在振动数据中的定位精度，本研究改进原始小波函数提出新的时频定位函数. 在凯斯西储大学（CWRU）轴承数据集[21]上开展所提方法与传统故障诊断方法的对比分析实验，验证所提方法的有效性.

1. 相关理论和模型改进

1.1. 卷积神经网络模型

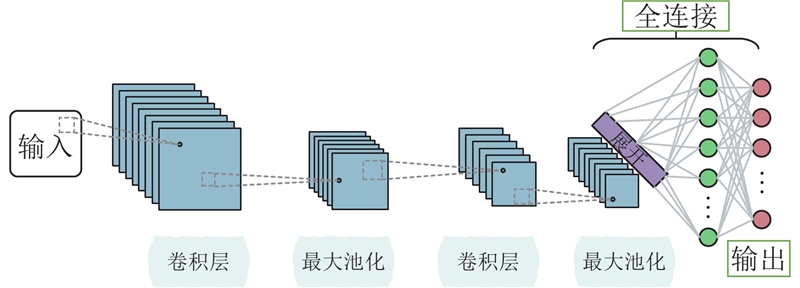
CNN的自适应特征提取能力强大，它的网络结构分为卷积层、激活层、池化层，特征提取过程具有权重共享和空间不变的特性. 经典的CNN模型主要有LeNet-5、AlexNet、GoogleNet、ResNet等. AlexNet因其出色的分类精度、并行计算和多层次特征提取能力成为较早应用于实践的深度神经网络. 本研究优化了用于训练轴承故障数据集的AlexNet，CNN的结构如图1所示. 以振动信号作为输入，由卷积层和池化层提取故障特征；使用 Softmax 分类器识别故障；交叉熵为损失函数，表达式为

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   卷积神经网络的结构

Fig.1   Structure of convolutional neural network


$ L = \; - \sum\limits_x {f\left( x \right)\lg g(x)} . $
(1)

式中：f(x)为样本 x 的真实分类结果，g(x)为样本 x 的输出分类结果. 通过反向传播来更新权重和偏差，使损失函数最小化，满足模型的设计要求.

1.2. ACON激活函数及改进

Ma等[22]提出ACON激活函数，用于确定是否激活神经元. ACON的原理：考虑具有n个值的标准最大值函数 max (x1, ···, xn)，该函数近似为

$ {{{{S}}}_\beta }\left( {{x_1}, \cdots ,{x_n}} \right) = {{\displaystyle\sum\limits_{i = 1}^n {{x_i}{\text{exp (}}\beta {x_i}{\text{)}}} }}\Bigg/{{\displaystyle\sum\limits_{i = 1}^n {{\text{exp (}}\beta {x_i}{\text{)}}} }}. $
(2)

式中：Sβ为近似最大值函数；xi 为输入；n 为数据集中的样本数；β 为切换因子： 当 β→0, Sβ→平均值时，近似函数为线性；当 β→∞, Sβ→最大时，近似函数为非线性. 设 η1(x) = p1x、η2(x) = p2x，式（2）转化为

$ \begin{split} {{{{S}}}_\beta }\left( {{\eta _1}\left( x \right),{\eta _2}\left( x \right)} \right) = \left( {{p_1} - {p_2}} \right)x \cdot \sigma \left( {\beta \left( {{p_1} - {p_2}} \right)x} \right)+{p_2}x. \end{split} $
(3)

当 p1=1、p2=0 时，激活函数是神经网络中常用的ReLU. 在本研究中，ACON激活函数由式（3）得出，定义输入为一维振动信号. 利用通道权重建立具有多个通道的一维自适应函数，计算式为

$ {\beta _{\text{a}}} = \sigma {{\boldsymbol{X}}_1}{{\boldsymbol{X}}_2}\sum\limits_{w = 1}^H {{x_{c,w}}} . $
(4)

式中：βa为数据空间中的自适应函数，它根据输入数据选择激活函数；σ 为Sigmoid函数；c 、 w 为空间维度；X1=Rc×c/r, X2=Rc/r×c, r 为比例因子. 本研究构建适合振动信号的ACON激活函数替代ReLU，增强了所提方法的学习和泛化能力.

1.3. 小波核

Morlet小波是常用于信号处理和时频分析的小波函数，表达式为

$ \psi (t) = {{\text{π }}^{ - {1}/{4}}}{\text{exp (}}{\mathrm{j}}{\omega _{\text{0}}}t)\;{\mathrm{exp}}\left( - {{{t^2}}}/{2}\right). $
(5)

式中：ω0为频率参数，用于控制小波在频域中的中心频率；t为时间. 为了改善小波核在振动数据中的定位精度，增加调节形状的参数，使得小波函数能够更好地适应不同频率的信号. 引入调节参数m来改进小波函数的时频局部化能力. 改进后的Morlet小波函数表达式为

$ {\psi _{{\text{im}}}}(t,\;m \;) = {{\text{π }}^{ - {1}/{4}}}\;{\text{exp (}}{\mathrm{j}}{\omega _{\text{0}}}t)\;{\mathrm{exp}}\left( - {{{t^2}}}/({{2{m ^2}}})\right){\text{.}}\; $
(6)

其中m的数值大小对于Morlet小波函数的频率和时域分辨率有重要影响. 通常情况下，数值较小的m能够提高时域分辨率，但会降低频率分辨率；数值较大的m能够产生更好的频率分辨率，但时域分辨率会降低. CNN中的卷积运算与小波函数类似，可以表示为信号处理中2个向量的内积. 同样基于内积，连续小波变换的表达式为

$ {\text{CW}}{{\text{T}}_f}(u,s) = \frac{1}{{\sqrt s }}\int x (t){\psi ^ * }\left( {\frac{{t - u}}{s}} \right){\text{d}}t. $
(7)

式中：s为与频率成反比的尺度参数；u为平移参数，控制小波函数在时间轴上的移动；x(t)为输入信号；$ {\psi }^{*}(\cdot ) $为小波函数的复共轭. s可以使信号膨胀或压缩，当s数值相对较小时，信号收缩得更多，从而生成更详细的结果图. 结合式（6）和式（7），改进后的小波函数为

$ {\text{CW}}{{\text{T}}_f}\left( {u,s} \right) = \frac{1}{{\sqrt s }}\int x \left( t \right){\psi _{{\text{im}}}}^ * \left( {\frac{{t - u}}{s}} \right){\text{d}}t. $
(8)

1.4. 基于连续小波卷积神经网络的轴承智能故障诊断方法

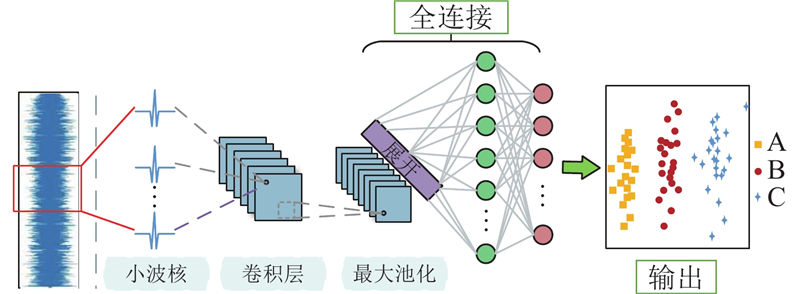
现实中诊断方法须自适应应对不同类型的诊断任务，特征提取能力要求高. 为此，将CNN的第一层改为小波核，并用改进的ACON激活函数代替ReLU. 第一层卷积层在CNN中负责提取基本特征（如边缘、纹理的低级特征）. 小波核在时频域上有比传统信号处理方法更好的局部化性质，更适合于对信号进行初步的特征提取和局部分析. 使用小波核替代全部的卷积层会增加计算复杂度和模型复杂度，将小波核仅用于第一层在一定程度上降低模型的复杂度和计算开销. 振动信号通常涉及非平稳特性，而小波变换在处理非平稳信号时具有优势，在初始阶段使用小波核可以更好地处理这些非平稳信号的初步表示. 因此，将Morlet小波核作为CNN的第一层卷积层能够更好地提取信号的初级特征. CWCNN可用于故障诊断的自适应提取和泛化，该方法训练振动信号的过程如图2所示. CWCNN在不同运行条件下的滚动轴承故障诊断步骤如下. 1）通过测试平台获取振动信号并进行分段；2）初始化模型参数，如学习率等；3）输入数据，小波核提取初始特征信息；4）计算损失参数，根据损失更新网络参数；5）重复训练达到迭代次数.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   连续小波卷积神经网络训练振动信号的过程

Fig.2   Continuous wavelet convolutional neural network training process for vibrating signals


2. 实验验证

2.1. 实验平台及参数介绍

实验环境为Python 3.8，采用Tensorflow 2.3.0深度学习框架搭建模型. CWCNN的详细参数如表1所示，其中NK为核数目. CWCNN加入了批量归一化层以提高网络训练的稳定性. 在训练过程中，使用Adam梯度下降算法对参数进行自适应优化，学习率设定为0.001. 丢失率设定为0.5，在训练过程中随机剔除一半参数，以避免网络过度拟合. 设置批量大小为32，迭代轮次epoch为50，损失函数采用交叉熵损失函数. 对比实验中的其他故障诊断方法如CNN、快速傅里叶变换-CNN[23](fast Fourier transform with CNN，FFT-CNN), 长短时记忆-CNN[24](long short-term memory with CNN，LSTM-CNN)的超参数设置和CWCNN的基本一致. 结果表明，当设置m= 0.5 时，可以获得最佳的模型定位性能.

表 1   连续小波卷积神经网络的结构参数

Tab.1  Structure parameters of continuous wavelet convolutional neural network

网络层核大小NK输出大小
输入层——1×1024
连续小波——16×128
最大池化64×1×23216×64
卷积层64×1×33232×64
最大池化64×1×23232×32
卷积层64×1×36464×32
最大池化1×26464×16
全连接100—1×100
输出层10—10

新窗口打开| 下载CSV


2.2. 数据集说明

使用CWRU公开的实验数据集作为训练和测试实验数据，轴承测试台如图3所示. 该数据集通常用于诊断轴承故障和比较不同算法的性能. 选取信号的频率为12 kHz、负载为0.7457 kW. 轴承故障为3个类别：内圈、外圈和滚动体故障. 结合正常数据共有 10 个分类供验证.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   轴承试验台[21]

Fig.3   Bearing test bench[21]


2.3. 数据预处理

在CWRU轴承数据集中，以12 kHz的采样频率计算，每种故障情况有120 000个采样点，采样选取120个样本，正常状态的样本有300个. 正常与故障样本的数量差距明显，会对网络识别准确性产生负面影响，数据集中的样本量不足以满足网络训练和验证的要求容易在训练过程中出现过拟合. 数据增强可以有效地缓解模型的过拟合程度，增加模型对新数据样本的适应度. 为了解决数据量不平衡的问题，采用随机抽取的数据增强方法进行样本抽样；使用宽度为1 024的窗口按一定步长平移，每次平移都会对窗口中的所有数据点进行采样. 每个信号段都会与后一个信号段重叠以便有效利用原始信号中的信息并改进数据集. 实验中训练集和测试集的比例为4∶1，确保划分的合理性. 如表2 所示为CWRU轴承数据集，其中SF为故障长度，ntr为训练样本数，nte为测试样本数. 工况A、B、C的负载分别为0.7457、1.4914、2.2371 kW.

表 2   凯斯西储大学轴承数据集

Tab.2  Case Western Reserve University bearing dataset

故障位置标签SF/mmA工况B工况C工况
ntrntentrntentrnte
正常0—400100400100400100
外圈10.18400100400100400100
20.36400100400100400100
30.53400100400100400100
内圈40.18400100400100400100
50.36400100400100400100
60.53400100400100400100
70.18400100400100400100
80.36400100400100400100
滚动90.53400100400100400100

新窗口打开| 下载CSV


2.4. 模型诊断性能实验

CWRU轴承数据集不含有噪声，为了使实验数据贴合实际，在对比实验中加入高斯白噪声以模拟实际信号. 当使用小波内核代替第一层卷积并在数据集上进行训练和测试时，将实验结果与第一层卷积不变时的结果进行比较，结果如图4 、图5所示. 图中，Acc为诊断的准确率. 可以看出，使用小波核代替第一层卷积的模型不管在训练精度还是测试精度上都比没有使用小波核的精度高很多.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

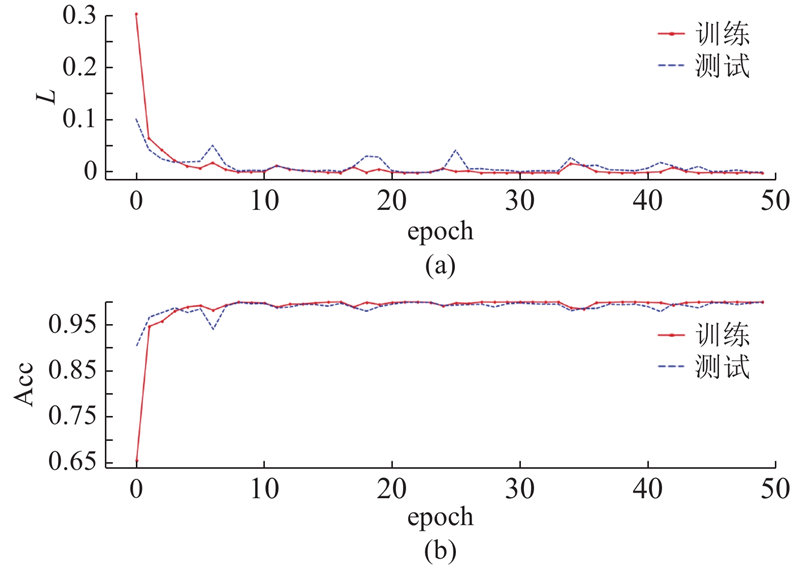
图 4   添加小波核后的轴承故障诊断实验结果

Fig.4   Experimental results of bearing fault diagnosis after adding wavelet kernel


图 5

新窗口打开| 下载原图ZIP| 生成PPT

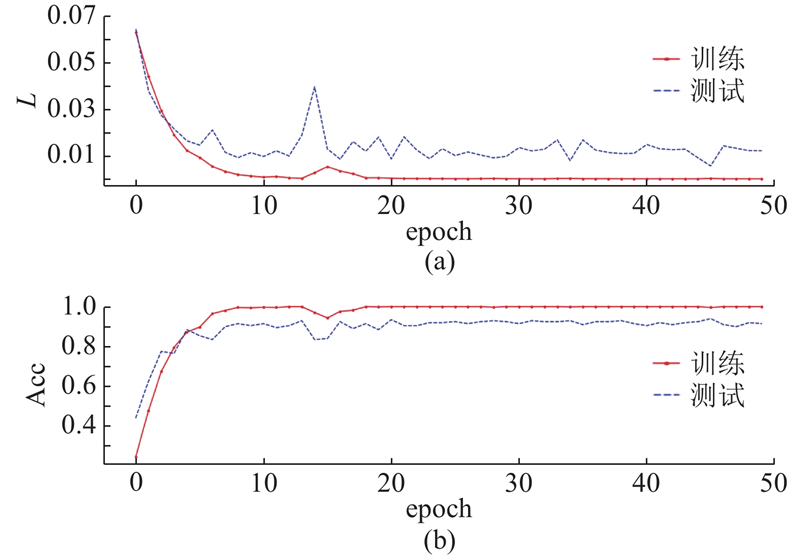
图 5   未添加小波核的轴承故障诊断实验结果

Fig.5   Experimental results of bearing fault diagnosis without adding wavelet kernel


小波核不仅提高模型的诊断精度，还大大缩短了训练模型的时间，收敛速度大大提升. 为了证实CWCNN在故障诊断方面的功效，对比不同方法的轴承故障诊断结果，如表3所示，其中tc为平均计算时间，采用随机抽样技术处理数据集，最终的准确度是10次训练的平均值，以平衡方法的影响. CWCNN的故障诊断准确率为 99.87%，与传统CNN相比提高了7.45个百分点，与FFT-CNN相比提高了4.46个百分点，与LSTM-CNN相比提高了1.53个百分点. 与其他模型相比，平均评估持续时间明显缩短.

表 3   不同方法的轴承故障诊断结果对比

Tab.3  Comparison of bearing fault diagnosis results for different methods

方法Acc/%tc/ms
CNN92.4217.36
FFT-CNN95.4111.56
LSTM-CNN98.3414.32
CWCNN99.878.63

新窗口打开| 下载CSV


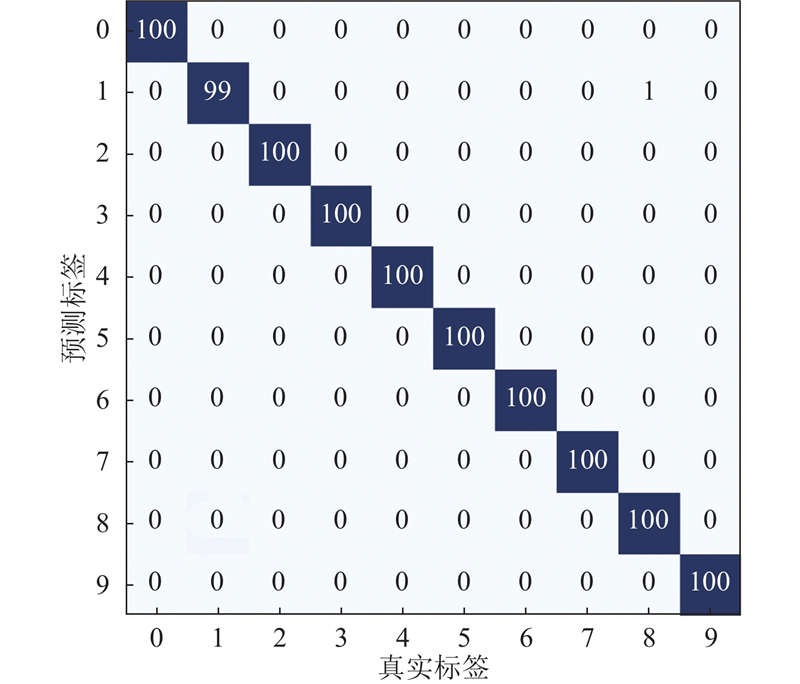
测试集的混淆矩阵如图6所示. 可以看出，10种类型的故障，每种100个样本，只有1个样本分类出现错误. 具体来说，1个外圈中度缺陷样本（标签 1）被误分类为滚动体中度缺陷（标签 8）. 该结果表明，CWCNN在检测不同故障方面的分类准确性良好.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   测试集轴承故障分类结果的混淆矩阵

Fig.6   Confusion matrix for test set bearing fault classification results


2.5. 变工况下模型的泛化性分析

在现实工业世界中，为了应对不同的工作条件，轴承载荷不可避免地会发生变化. 在多变的工作条件下，模型良好的诊断性能对确保安全运行至关重要. 从CWRU轴承数据集中选取3组不同负载、采样频率一致的数据，验证CWCNN在不同条件下的有效性和泛化能力. CWCNN在滚动轴承故障诊断领域的有效性通过变工况准确率测试验证. 对宽卷积-CNN (wide convolution kernels with CNN，WKCNN)[25]、GhostCNN[26]、多分支深度可分离-CNN[27] (multi branch depth seperable with CNN，MBDS-CNN)、ILeNet-5[28]及CWCNN在变工况下进行实验，各实验分别取10次结果的平均值，以减小误差，结果如表4所示，其中a-b表示将数据集a作为模型的训练集，数据集b作为模型诊断结果使用的测试集，其余同理. CWCNN在变工况下的平均准确度为99.64%，均高于其他对比方法，与WKCNN相比提高0.87个百分点，比GhostCNN提高2.39个百分点，比MBDS-CNN提高0.93个百分点，比ILeNet-5提高1.32个百分点. 结果表明，在不同的工况之下，CWCNN具有非常优异的分类精度以及泛化性能.

表 4   不同方法在变工况下的诊断准确率

Tab.4  Diagnostic accuracy of different methods under variable operating conditions

方法Acc/%
a-ba-cb-ab-cc-ac-b
CWCNN99.8299.6599.7099.5399.5599.58
WKCNN99.3298.1599.4297.7199.1498.85
GhostCNN97.1696.8997.1897.8997.1497.26
MBDS-CNN99.1497.4299.1498.4298.8599.28
ILeNet-598.5696.8698.9598.2998.8598.43

新窗口打开| 下载CSV


3. 结　语

本研究提出基于连续小波CNN的轴承智能故障诊断方法，通过将ACON激活函数替代ReLU的方式增强方法的适应性. 实验结果表明，所提方法在轴承智能诊断准确性和稳定性方面比传统故障诊断方法更具优势. 采用小波核卷积可以解决传统神经网络参数数量多、收敛速度慢、计算复杂等问题；改进后的小波函数提高了振动数据分析模型的精度和时频分辨率，使模型能够更好地捕捉振动信号的瞬态特征. 所提方法具有比其他CNN方法更强的自适应特征提取能力，在使用相同轴承数据集的情况下，所提方法的准确率为99.87%，高于传统CNN、FFT-CNN以及LSTM-CNN. 相较于传统CNN、FFT-CNN以及LSTM-CNN，所提方法的平均评估持续时间明显缩短. 加入构造的ACON激活函数增强网络的泛化能力，在变工况的泛化任务中表现优良，所提方法的平均准确度为99.64%，高于WKCNN、GhostCNN、MBDS-CNN 、ILeNet-5. 后续研究将考虑使用不同频率或不同类别的振动信号进行跨域故障诊断实验，实现不同领域的轴承故障诊断.

参考文献

RANDALL R B, ANTONI J

Rolling element bearing diagnostics: a tutorial

[J]. Mechanical Systems and Signal Processing, 2011, 25 (2): 485- 520

DOI:10.1016/j.ymssp.2010.07.017      [本文引用: 1]

沈保明, 陈保家, 赵春华, 等

深度学习在机械设备故障预测与健康管理中的研究综述

[J]. 机床与液压, 2021, 49 (19): 162- 171

DOI:10.3969/j.issn.1001-3881.2021.19.033      [本文引用: 1]

SHEN Baoming, CHEN Baojia, ZHAO Chunhua, et al

Review on the research of deep learning in mechanical equipment fault prognostics and health management

[J]. Machine Tool and Hydraulics, 2021, 49 (19): 162- 171

DOI:10.3969/j.issn.1001-3881.2021.19.033      [本文引用: 1]

JUNG H, PARK M

A study of big data-based machine learning techniques for wheel and bearing fault diagnosis

[J]. Journal of the Korea Academia-Industrial Cooperation Society, 2018, 19 (1): 75- 84

[本文引用: 1]

LEI Y, YANG B, JIANG X, et al

Applications of machine learning to machine fault diagnosis: a review and roadmap

[J]. Mechanical Systems and Signal Processing, 2020, 138: 106587

DOI:10.1016/j.ymssp.2019.106587      [本文引用: 1]

温竹鹏, 陈捷, 刘连华, 等

基于小波变换和优化CNN的风电齿轮箱故障诊断

[J]. 浙江大学学报: 工学版, 2022, 56 (6): 1212- 1219

[本文引用: 1]

WEN Zhupeng, CHEN Jie, LIU Lianhua, et al

Fault diagnosis of wind power gearbox based on wavelet transform and improved CNN

[J]. Journal of Zhejiang University: Engineering Science, 2022, 56 (6): 1212- 1219

[本文引用: 1]

BURRIEL-VALENCIA J, PUCHE-PANADERO R, MARTINEZ-ROMAN J, et al

Short-frequency Fourier transform for fault diagnosis of induction machines working in transient regime

[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66 (3): 432- 440

DOI:10.1109/TIM.2016.2647458      [本文引用: 1]

YIN Z, HOU J

Recent advances on SVM based fault diagnosis and process monitoring in complicated industrial processes

[J]. Neurocomputing, 2016, 174: 643- 650

DOI:10.1016/j.neucom.2015.09.081      [本文引用: 1]

YAN K, JI Z, LU H, et al

Fast and accurate classification of time series data using extended ELM: application in fault diagnosis of air handling units

[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 49 (7): 1349- 1356

[本文引用: 1]

金列俊, 詹建明, 陈俊华, 等

基于一维卷积神经网络的钻杆故障诊断

[J]. 浙江大学学报: 工学版, 2020, 54 (3): 467- 474

[本文引用: 1]

JIN Liejun, ZHAN Jianming, CHEN Junhua, et al

Drill pipe fault diagnosis method based on one-dimensional convolutional neural network

[J]. Journal of Zhejiang University: Engineering Science, 2020, 54 (3): 467- 474

[本文引用: 1]

ZHAO H, SUN S, JIN B

Sequential fault diagnosis based on LSTM neural network

[J]. IEEE Access, 2018, 6: 12929- 12939

DOI:10.1109/ACCESS.2018.2794765      [本文引用: 1]

XU Y, DENG Y, ZHAO J, et al

A novel rolling bearing fault diagnosis method based on empirical wavelet transform and spectral trend

[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 69 (6): 2891- 2904

[本文引用: 2]

HUANG X, WEN G, LIANG L, et al

Frequency phase space empirical wavelet transform for rolling bearings fault diagnosis

[J]. IEEE Access, 2019, 7: 86306- 86318

DOI:10.1109/ACCESS.2019.2922248      [本文引用: 1]

LI X, MA Z, KANG D, et al

Fault diagnosis for rolling bearing based on VMD-FRFT

[J]. Measurement, 2020, 155: 107554

DOI:10.1016/j.measurement.2020.107554      [本文引用: 2]

ZHANG N, WU L, YANG J, et al

Naive bayes bearing fault diagnosis based on enhanced independence of data

[J]. Sensors, 2018, 18 (2): 463

DOI:10.3390/s18020463      [本文引用: 1]

YE M, YAN X, JIA M

Rolling bearing fault diagnosis based on VMD-MPE and PSO-SVM

[J]. Entropy, 2021, 23 (6): 762

DOI:10.3390/e23060762      [本文引用: 1]

MA J, YU S, CHENG W

Composite fault diagnosis of rolling bearing based on chaotic honey badger algorithm optimizing VMD and ELM

[J]. Machines, 2022, 10 (6): 469

DOI:10.3390/machines10060469      [本文引用: 1]

XU G, LIU M, JIANG Z, et al

Online fault diagnosis method based on transfer convolutional neural networks

[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 69 (2): 509- 520

[本文引用: 1]

YANG J, LIU J, XIE J, et al

Conditional GAN and 2-D CNN for bearing fault diagnosis with small samples

[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 3525712

[本文引用: 1]

WANG H, XU J, YAN R, et al

A new intelligent bearing fault diagnosis method using SDP representation and SE-CNN

[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 69 (5): 2377- 2389

[本文引用: 1]

MAO G, ZHANG Z, QIAO B, et al

Fusion domain-adaptation CNN driven by images and vibration signals for fault diagnosis of gearbox cross-working conditions

[J]. Entropy, 2022, 24 (1): 119

DOI:10.3390/e24010119      [本文引用: 1]

NEUPANE D, SEOK J

Bearing fault detection and diagnosis using Case Western Reserve University dataset with deep learning approaches: a review

[J]. IEEE Access, 2020, 8: 93155- 93178

[本文引用: 3]

MA N, ZHANG X, LIU M, et al. Activate or not: learning customized activation [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Nashville: IEEE, 2021: 8032–8042.

[本文引用: 1]

尹文哲, 夏虹, 彭彬森, 等

基于FFT和CNN的滚动轴承故障诊断方法

[J]. 应用科技, 2021, 48 (6): 97- 101

DOI:10.11991/yykj.202101004      [本文引用: 1]

YIN Wenzhe, XIA Hong, PENG Binsen, et al

A fault diagnosis method of rolling bearing based on FFT and CNN

[J]. Applied Science and Technology, 2021, 48 (6): 97- 101

DOI:10.11991/yykj.202101004      [本文引用: 1]

GAO Y, PING G, LI L. An end-to-end model based on CNN-LSTM for industrial fault diagnosis and prognosis [C]// 2018 International Conference on Network Infrastructure and Digital Content . Guiyang: IEEE, 2018: 274–278.

[本文引用: 1]

黄海

基于WKCNN的风电机组轴承声信号故障诊断研究

[J]. 电子技术与软件工程, 2023, (2): 97- 100

[本文引用: 1]

HUANG Hai

Fault diagnosis of wind turbine bearing acoustic signal based on WKCNN

[J]. Electronic Technology and Software Engineering, 2023, (2): 97- 100

[本文引用: 1]

HAN K, WANG Y, TIAN Q, et al. GhostCNN: more features from cheap operations [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 1580–1589.

[本文引用: 1]

刘恒畅, 姚德臣, 杨建伟, 等

基于多分支深度可分离卷积神经网络的滚动轴承故障诊断研究

[J]. 振动与冲击, 2021, 40 (10): 95- 102

[本文引用: 1]

LIU Hengchang, YAO Dechen, YANG Jianwei, et al

Fault diagnosis of rolling bearings based on a multi branch depth separable convolutional neural network

[J]. Journal of Vibration and Shock, 2021, 40 (10): 95- 102

[本文引用: 1]

WANG Z, XU G, WANG J, et al. Cross-domain fault diagnosis with one-dimensional convolutional neural network [C]// 2020 IEEE 16th International Conference on Automation Science and Engineering . Hong Kong: IEEE, 2020: 494–499.

[本文引用: 1]

/

〈 〉