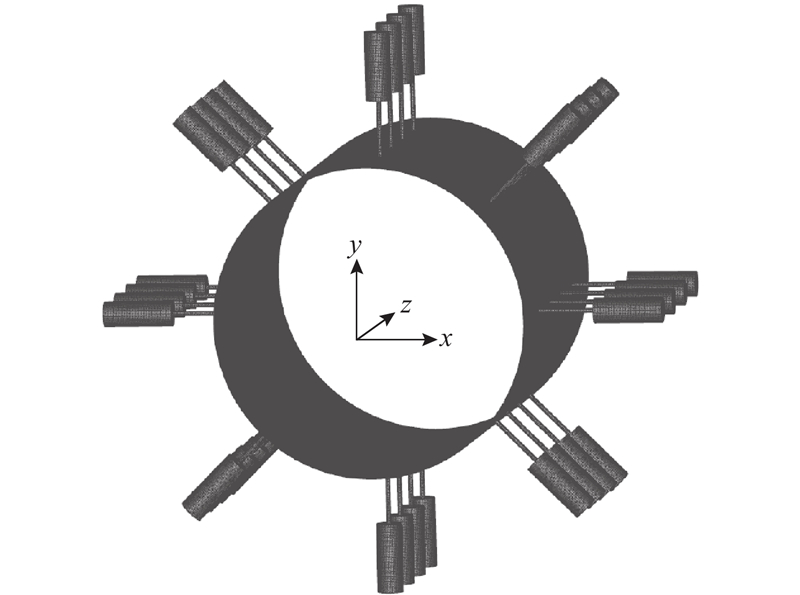
氢燃料电池汽车几乎无污染排放、燃料来源广泛、充能快速,被称为绿色新型环保汽车. 空气压缩机作为燃料电池阴极气体供应系统的重要部件,向电堆提供高压空气作为反应原料,有无油、高效、小型化的要求[1].
空气箔片轴承是当前的主流选择,因其在高速下的功率损耗较低,相关的空气回路也相对简单. Daejong[6]利用高速旋转试验台测试2种不同的多瓦箔片轴承的性能以及对相应轴系进行转子动力学分析,选取测试中性能最优的轴承提出单级空压机设计;Zhang等[7] 针对120 kW氢燃料电池系统,设计22 kW离心式空压机及配套的箔片式轴承,搭建相应的试验台对空压机以及轴承性能进行测试验证;张雯等[8]针对野外战车应急发电机组的氢燃料电池空压机提出设计空气动压箔片轴承-转子系统的方法,并对相应转子系统进行实验测试;冯凯等[9]建立气体箔片轴承刚度预测模型,搭建刚度测试试验台验证模型的有效性;王伟等[10]将自主研发设计的鼓泡型箔片全动压气体轴承在微型透平膨胀机上进行试验研究;靳彩妍等[11]对箔片轴承的动态特性进行研究,并对其支承的两级空压机轴系进行转子动力学分析. 然而,箔轴承的启动扭矩高,整体尺寸和重量大[12]. 在建立有效的空气压力支撑之前,箔轴承必须达到最小“起飞”转速,在压缩机的启停与低速运转过程中会产生磨损.
为了解决这一问题,本研究提出适用于氢燃料电池汽车车载高速离心空压机的新型三楔气体轴承. 不管是在启停、变速还是稳定高速运转阶段,该轴承都能在仅利用车载空压机内部气路的前提下,为车载空压机转子提供有效、稳定的支承. 在对该轴承进行性能研究的过程中,为了求解其非线性气膜力,提出由自编的用户自定义函数(user-defined functions, UDF)动网格程序为基础的计算流体力学(computational fluid dynamics, CFD)计算方法,能在轴颈中心移动的过程中不断更新计算模型的网格,保证瞬态计算中的模型网格质量. 应用该方法研究三楔气体轴承在不同的偏心率和转速下的流场特性、动静压耦合效应,以及静、动态参数的变化,深入解析三楔动压气体轴承的工作机理和性能优势.
1. 三楔气体轴承流场建模
1.1. 流场结构
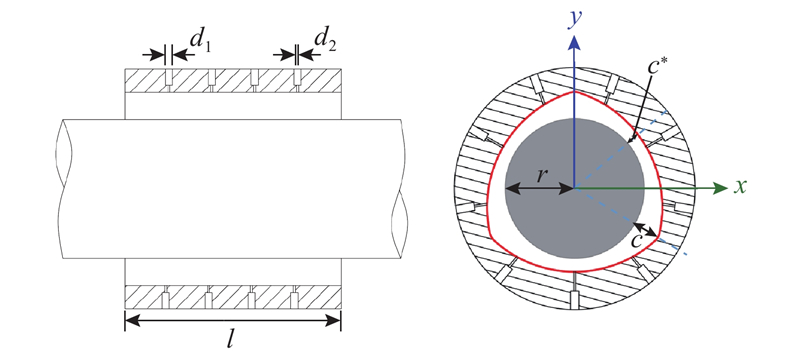
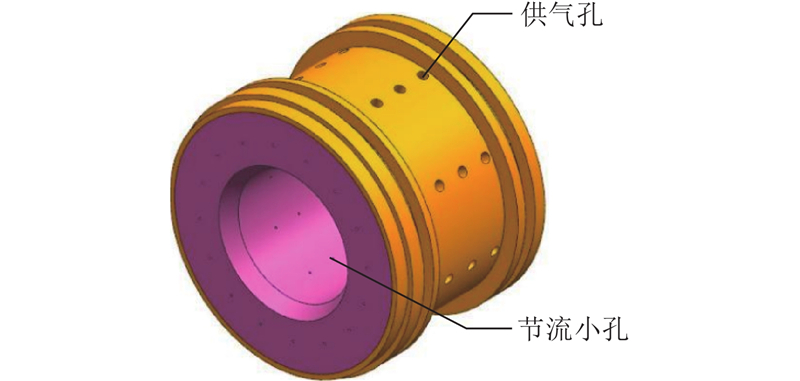
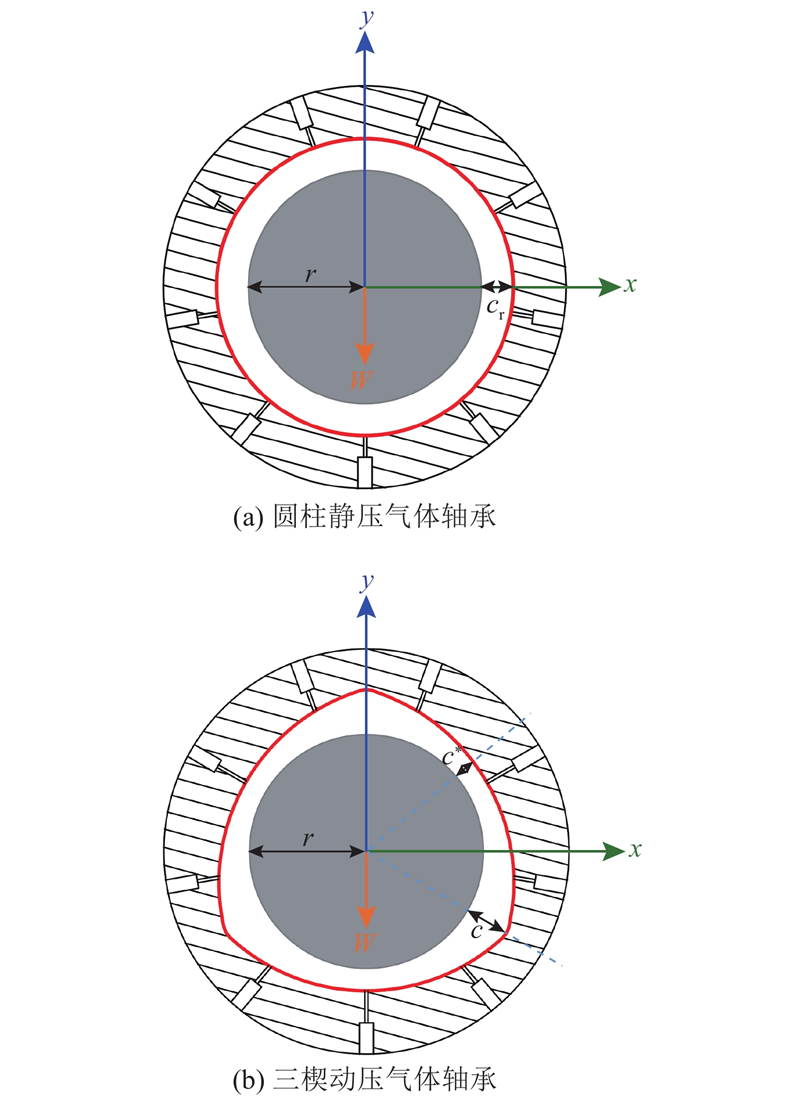
图 1
图 1 三楔气体轴承及其流场结构示意图
Fig.1 Structural diagram of three-wedge gas bearing and its flow field
当轴高速旋转时,气膜中的高压气体就会跟随轴颈以一定的速度通过厚度变化的楔形间隙. 随着间隙大小的变化,气膜流场中会出现收敛和发散的结构. 由于流体黏度的存在,通过收敛楔的流体会在运动法向上产生一个对转子的支持力. 这种现象被称为动压效应[14],而楔槽的存在加强了动压效应的形成.
在高速离心空压机启停过程中,外部气源气体通过微孔产生节流作用后,进入三楔轴承的润滑间隙,形成高压气膜支撑转子,使轴承呈现出静压气体轴承的特性,包括稳定性强、承载力大和刚度大等. 在转速变化的过程中,由于转子始终处于悬浮状态,有效避免了轴与轴承之间的摩擦. 当转子在恒定的高速下运行时,由于气膜收敛楔的存在,动压效应将取代静压效应起主导作用,能在提高轴承工作性能的同时降低系统的功耗[15].
总体而言,该轴承在燃料电池车载高速空压机的使用工况下,既可以实现在压缩机启停、变速时无磨损,又能在压缩机高速运转时,在有限的供气压力下表现出优良的承载力与稳定性,兼具了静压和动压气体轴承的优点.
1.2. 几何建模
本研究的三楔气体轴承几何参数如表1所示.
表 1 三楔气体轴承参数
Tab.1
| 物理量 | 变量符号 | 数值 |
| 供气孔直径 | dl/mm | 2.0 |
| 节流孔直径 | d2/mm | 0.35 |
| 平均气膜间隙 | 0.02 | |
| 轴承半径 | r/mm | 12.5 |
| 轴承长度 | l/mm | 34.5 |
1.3. 网格划分和无关性验证
图 2
利用CFD分析的前处理软件GAMBIT创建包括气膜、供气孔和节流孔在内的气体轴承流场的计算模型,然后将其划分为结构化的六面体单元. 为了选择最合适的网格密度,选择气膜的最大压力pmax和轴承承载力Fc为参数进行网格无关性分析. 如表2所示为不同网格数N的计算模型在相同条件下(偏心率ε = 0.5、转速n = 100 000 r/min)的模拟结果比较. 表中,
表 2 网格无关性验证
Tab.2
| N/104 | pmax / Pa | ΔDP / % | Fc / N | ΔDF / % |
| 42 | 4.145 | 124.7 | 4.954 | |
| 85 | 2.617 | 128.3 | 2.210 | |
| 114 | 0.810 | 130.1 | 0.838 | |
| 180 | 0.119 | 130.9 | 0.229 | |
| 250 | 参考值 | 131.2 | 参考值 |
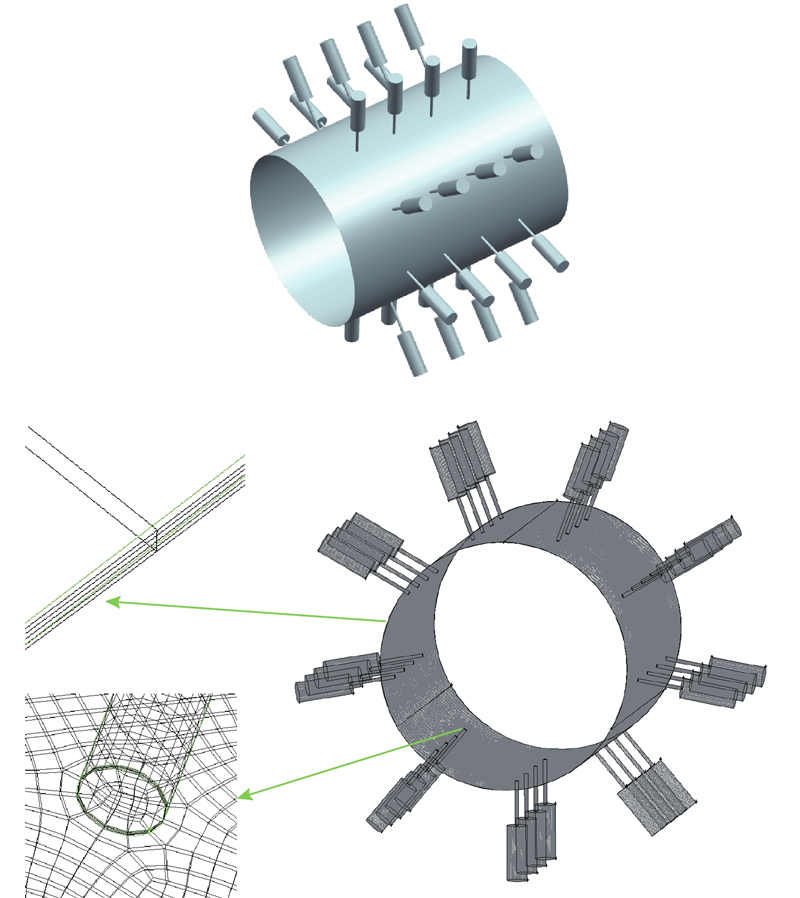
图 3
图 3 三楔气体轴承流场建模和网格划分
Fig.3 Modeling and meshing of three-wedge gas bearing fluid field
由于气体轴承在空间的3个方向上存在较大的尺寸差异(气膜厚度在几十微米以内),为了得到合理的网格长宽比,在保证计算量合理的前提下能高效收敛至与实际情况最接近的模拟计算结果,对计算模型气膜厚度方向的网格层数进行手动调整. 在压力和速度分布变化更显著的孔口区域周围对网格也进行了细化.
1.3.1. Fluent计算方法
1.3.2. 边界条件和瞬态计算设置
在Fluent软件中对该网格模型进行模拟计算时,采用三维的压力基(pressure-based)隐式求解器PISO进行瞬态计算的求解. 流场计算使用进口、出口和壁面3个边界条件. 1)气体轴承的供气孔为压力进口边界条件,在计算中提供进口总压力;2)气体轴承两侧面端为压力出口边界条件,根据实际情况,压力设置为环境大气压力;3)气膜的内表面设置为随轴旋转的移动壁面,剩余边界设置为固定壁面,壁面之间不发生相对滑动.
1.3.3. 动网格的动态参数求解法
为了计算轴颈径向位移的过程中轴承气膜力的变化,流场的计算模型及其网格须随着轴颈中心的运动进行相应的变化和更新. 气体轴承的流场计算模型在空间的3个方向上尺寸的尺度存在较大差异,且在瞬态计算过程中轴位移的方向和大小在每个时间步都不固定。因此,在使用Fluent自带的3种动网格方法时,可能会出现网格质量下降、网格变形率大甚至负体积网格等问题,难以获得准确的计算结果.
为了避免网格变形,保证瞬态计算的进行,提出基于结构化网格的动网格移动方法. 该方法利用C语言编写了计算每个时间步中网格节点坐标的程序,并通过UDF接口将该动态网格函数加载到Fluent中. 在瞬态计算过程中,当轴颈中心发生移动时,程序将根据轴颈中心的位置计算出所有网格节点的新坐标,并将节点更新至相应位置[21].
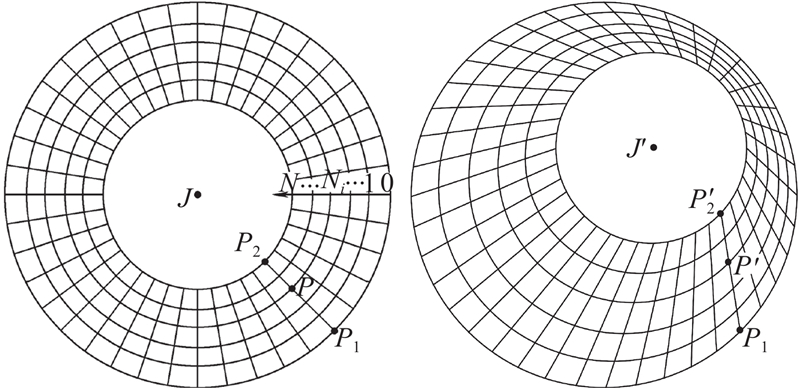
当气体轴承流场模型采用全结构化网格划分后,取流场计算模型轴承面上的任意节点P1,其沿网格线投影到轴表面上的节点为P2. 当轴心移动时,在轴承壁面上的节点P1保持不动,而轴颈表面的节点P2移动到
当轴心移动时,在所有计算模型的节点中,轴颈上节点(如P2)的位移距离最大,离轴心越远的节点位移越小. 对于P1和P2的连接网格线上的任意节点P,其坐标可以计算如下:
式中:Ni为节点P所在的径向网格层数,N为径向网格的总层数. 如图4所示,径向网格层数的编号从轴承表面(编号为0)开始到轴颈表面(编号为N).
图 4
可以看出,在配备该动网格程序后,在网格更新的过程中,网格节点的总数量及节点之间的拓扑关系保持不变. 即使经过多次的网格更新后,网格质量依旧良好. 该方法可以保证轴颈中心运动时,流场计算模型网格单元的光滑性和规律性,有效避免单元体积为负的情况. 如此,在轴颈扰动的瞬态计算过程中,可以通过网格更新后的模型求解得到轴颈在不同位置时的气膜力与轴承参数.
1.4. 基于动网格的刚度阻尼计算方法
刚度和阻尼系数反映了轴颈处于静平衡位置时,在外部载荷和小扰动的作用下,轴承气膜力与轴颈中心位移、速度变化的关系. 两者直接影响转子-轴承系统的稳定性、临界转速、谐响应等动态特性[22].
1.4.1. 理论计算方法
当气体轴承的轴颈中心处于静平衡位置时,在外界的位移或速度扰动下,轴颈受到的气膜力就会发生变化. 该气膜力的变化与外界扰动(位移或速度变化)呈非线性关系,但当扰动为微小量的情况下,为了简化分析可以将其视为线性关系. 因此,当轴在静平衡位置附近发生小扰动时,气膜力
式中:
图 5
1.4.2. 动网格CFD瞬态模拟求解方法
当轴颈匀速运动时,表示气膜力的方程(式(3))可以简化,气膜力的变化量
轴承刚度即可使用CFD模拟分析进行计算. 当轴颈沿x方向匀速移动时,沿y方向的位移
为了计算阻尼系数,须再进行一次轴颈位移相同,但时间步长不同的瞬态模拟分析. 由于时间步长的改变,在此次分析中,轴颈会进行相同位移和方向的运动,但速度与前次模拟中不同. 根据式(5),当
该方法已在微孔静压气体轴承的研究中进行过使用. 相应的实验验证表明,该方法能对轴承的非线性气膜力及动态参数进行瞬态模拟计算,且能比传统的稳态计算方法更准确地预测转子-轴承系统的临界转速[23].
2. 三楔气体轴承仿真结果分析
由1.1节中的理论分析可以看出,动静压耦合效应的直接决定因素是流场中气膜的收敛楔结构和气体随转子的转动. 因此本研究主要关注不同轴颈偏心率和转子转速下三楔气体轴承的性能参数变化.
在直接利用车载压缩机气路进行供气的前提下,气体轴承供气压力最高为0.25 MPa,因此,后续研究均在该条件下进行.
2.1. 轴承流场压力分布
图 6
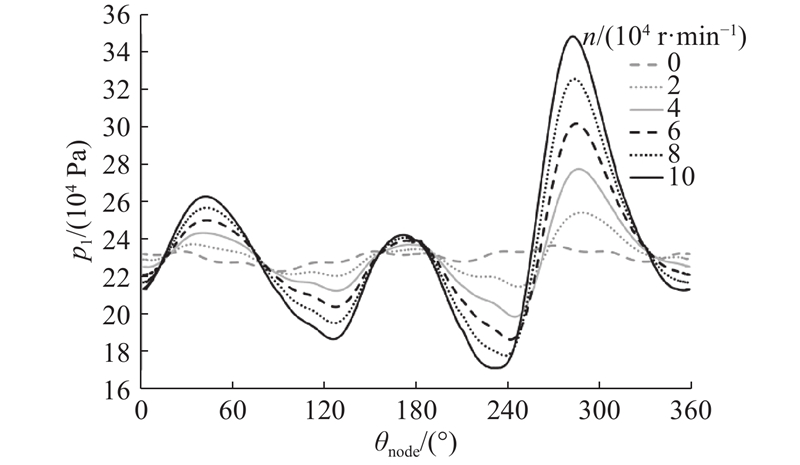
图 6 不同转速下的气膜周向压力分布
Fig.6 Circumferential pressure distribution of gas bearing fluid film under different rotational speeds
由图6可以看出,当转速为零时,轴承几乎没有受到动压效应的作用,几个小型的压力峰值代表了进气孔带来的静压节流作用,各进气孔之间的压力不同则是气膜厚度不同带来的流场静压力变化. 此时气膜压力关于高压中心对称分布,且最大压力不超过供气压力0.25 MPa. 随着转速升高,动静压耦合效应增强,可以明显观察到流场最大压力的上升. 在轴承转速增加至100 000 r/min的过程中,气膜压力峰值由
图 7
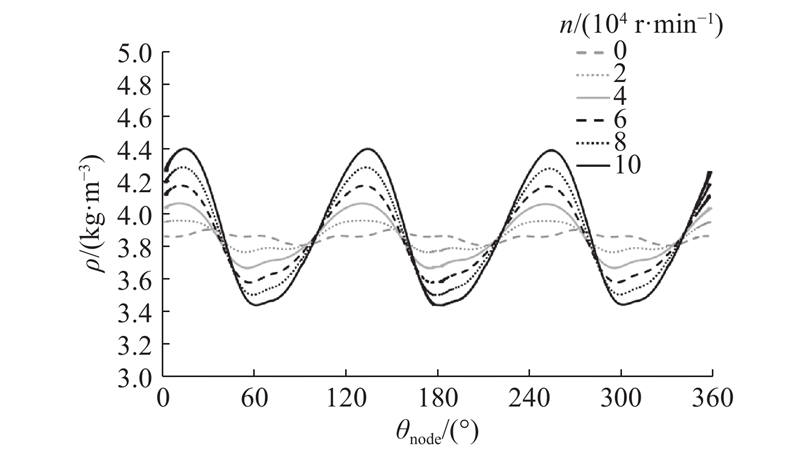
图 7 不同转速下气膜周向密度分布
Fig.7 Circumferential density distribution of gas bearing fluid film under different rotational speeds
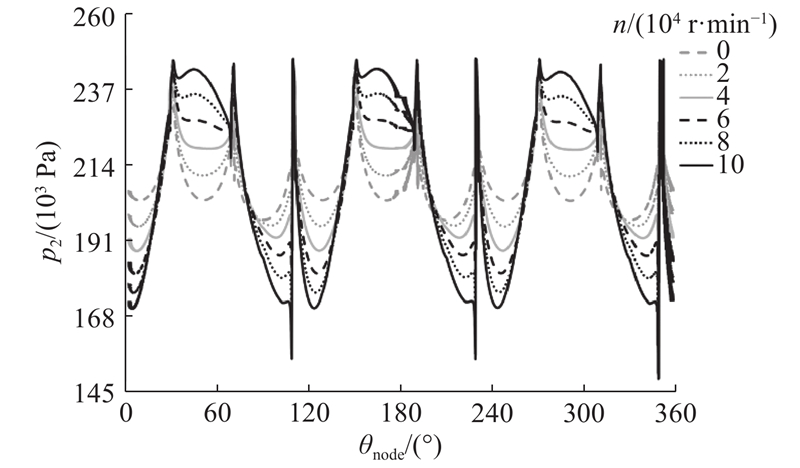
如图8所示为不同转速下流场节流孔附近的周向压力p2分布. 由于轴承微孔带来的节流静压效应,气体在节流孔处达到压力峰值. 在气体流出节流孔并进入楔形间隙的过程中,压力由峰值逐渐减小. 转速越高,节流孔周围由轴承楔形效应带来的动压现象表现得越强.
图 8
图 8 不同转速下节流孔区域周向压力分布
Fig.8 Circumferential pressure distribution around gas bearing orifices under different rotational speeds
从气膜的平铺压力云图(见图9)可以更直观地看到,在低转速下,压力峰值出现在节流孔和3个楔槽的中心处. 随着转速增加,轴颈中心的静平衡位置开始变化,高压区中心从楔槽中心逐渐偏移. 此时,随着楔形间隙内的气体与转子一起高速旋转,气体的可压缩性增大并能提供更高的气膜压力,可观察到云图中的压力峰值从
图 9
图 9 不同转速下的气膜压力云图
Fig.9 Gas film pressure nephogram under different rotational speeds
2.2. 轴承动态参数分析研究
图 10
图 10 偏心率为0.3时的气膜周向压力分布
Fig.10 Circumferential pressure distribution of gas bearing fluid film under eccentricity of 0.3
由于外加载荷方向的动态参数是轴承性能主要关注的研究对象,因此后文中轴承动态参数的主刚度、阻尼方向为yy,交叉刚度、阻尼方向为xy.
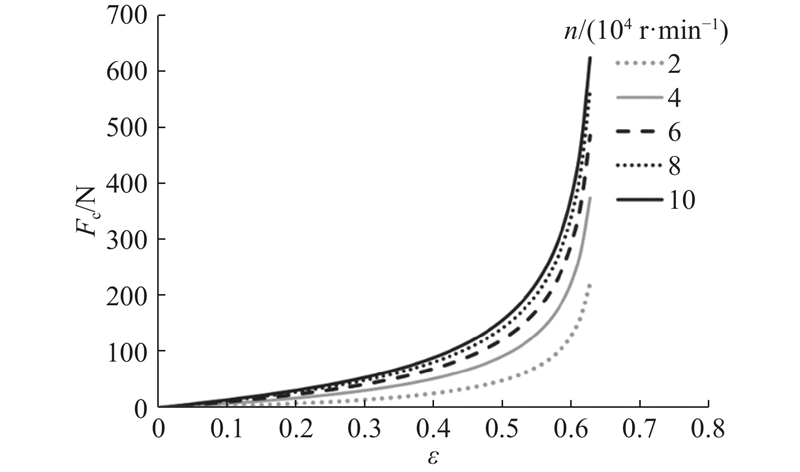
如图11所示为不同转速和偏心率下的轴承承载力. 三楔气体轴承的承载力Fc随偏心率ε和转速n的上升而增加. 其中,承载力关于转速线性增大,而关于偏心率呈指数式快速增大,特别是在偏心率大于0.4以及转速大于40 000 r/min之后.
图 11
图 11 不同转速和偏心率下的轴承承载力
Fig.11 Bearing capacity of gas bearing under different rotational speeds and eccentricities
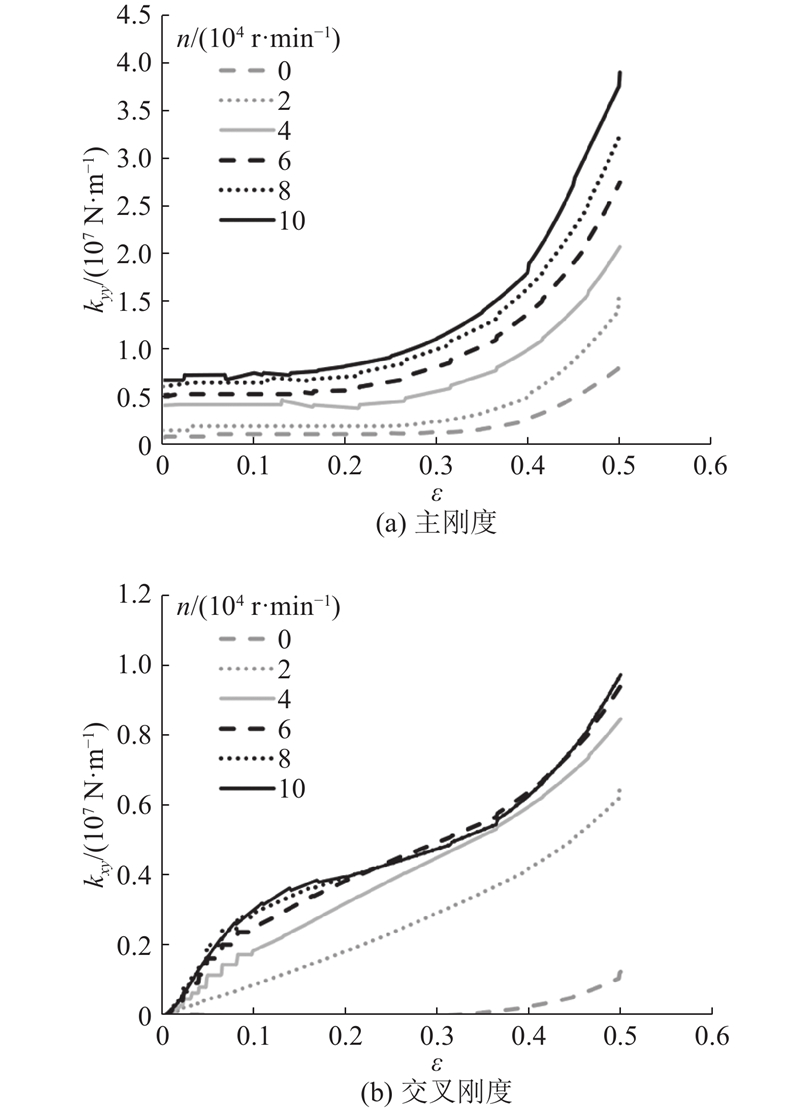
不同偏心率和转速对轴承动态系数的影响如图12所示. 随着偏心率和转速的增加,动压效应变强,主刚度kyy、交叉刚度kxy系数均有增大的趋势,且在偏心率大于0.4后变化更显著. 在大于40 000 r/min的高转速下,交叉刚度系数受转速影响较小,变化趋势相近.
图 12
图 12 不同转速和偏心率下的轴承刚度系数
Fig.12 Stiffness coefficients of gas bearing under different rotational speeds and eccentricities
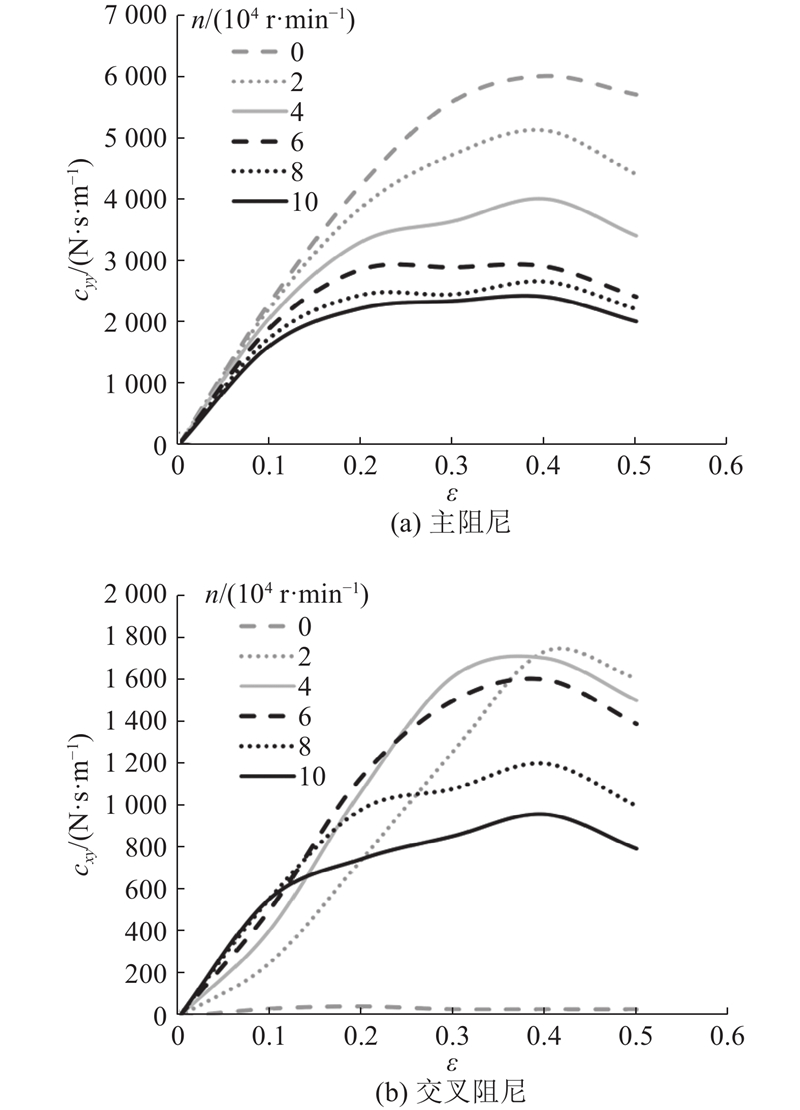
阻尼系数表征了气膜力随速度的变化率,气膜阻尼的存在对旋涡能量消耗有影响,是抑制旋涡运动的一个因素. 如图13所示为不同转速和偏心率下的轴承阻尼系数. 可以看出,随着转速的增加,转子更容易克服气膜力进行运动,阻尼系数有减小的趋势. 随着偏心率的增大,动压效应增强,导致转子必须施加更多的功来克服气膜力. 因此可看到在偏心率ε< 0.4时,随着偏心率的升高,轴承阻尼系数有增大的趋势,轴承对涡动的抑制加强,转子系统运行更稳定. 但在偏心率大于0.4后,阻尼的主系数cyy与交叉系数cxy均表现出下降的趋势. 说明偏心率的持续增加导致了轴承气膜过薄,无法再提供有效支承.
图 13
图 13 不同转速和偏心率下的轴承阻尼系数
Fig.13 Damping coefficients of gas bearing under different rotational speeds and eccentricities
2.3. 与圆柱气体轴承的性能对比
图 14
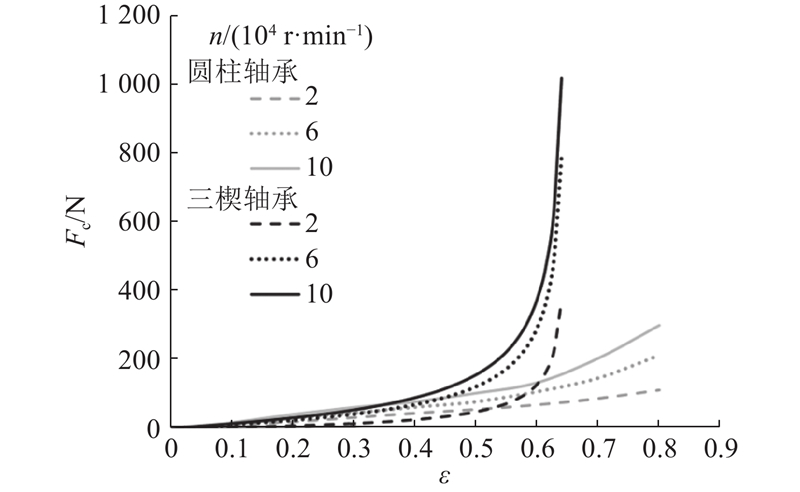
如图15所示为不同供气压力下,2种轴承在不同转速和偏心率下的轴承承载力对比. 可以看出,三楔轴承与圆柱轴承的承载力Fc随偏心率的增加均呈整体上升的趋势. 在低转速(小于60 000 r/min)与小偏心率(ε<0.4)范围内,三楔轴承与圆柱轴承能达到相似的支承效果. 但在偏心率ε>0.4之后,通过分析曲线斜率可知,三楔轴承承载力的增加速度远超圆柱轴承的,这主要是由于三楔轴承动压效应的增强趋势远大于圆柱轴承的. 这种偏心率达到某个数值之后,承载力会出现非线性陡增的现象,这是动压结构的轴承特有的属性.
图 15
图 15 不同转速和偏心率下三楔与圆柱气体轴承承载力对比
Fig.15 Comparison of load capacity between three-wedge and cylindrical gas bearings under different rotational speeds and eccentricities
从对轴承承载力和动态参数的理论研究中可以看出,轴承的实际工作性能与轴颈中心的静平衡位置密切相关. 为了确定三楔轴承在指定供气压力下能否代替传统的圆柱轴承,须研究2种轴承在实际工况下的平衡位置,并对比相应位置处的动态性能.
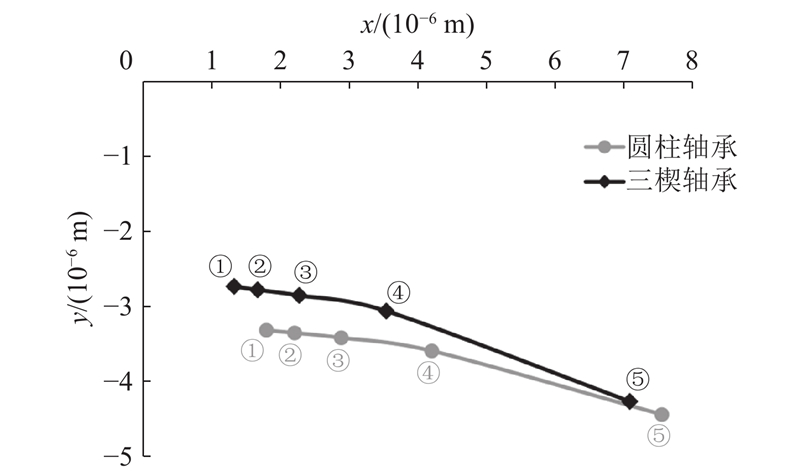
图 16
图 16 不同转速下三楔与圆柱气体轴承在车载空压机转子上的静平衡位置对比
Fig.16 Comparison of static equilibrium positions between three-wedge and cylindrical gas bearings on FCV compressor rotors under different rotational speeds
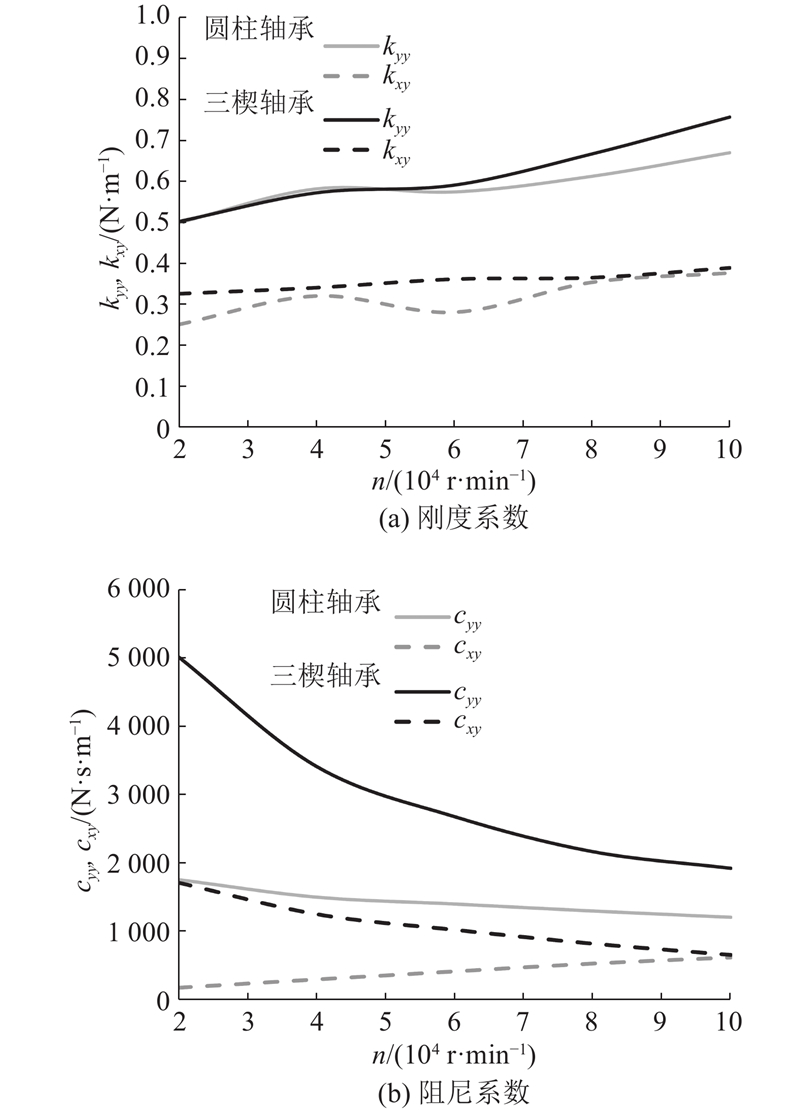
图 17
图 17 不同转速下三楔与圆柱气体轴承在车载空压机转子上的动态参数对比
Fig.17 Comparison of hydrodynamic characteristics between three-wedge and cylindrical gas bearings on compressor rotors in fuel cell vehicle under different rotational speeds
3. 结 论
提出适用于氢燃料电池汽车车载高速离心空压机的新型三楔气体轴承,以克服传统的静压圆柱轴承需要额外供气的缺点. 经由对三楔轴承的动、静压特性分析可知,此类轴承能在车载压缩机启停、变速、稳定运行中始终表现出良好的支承特性. 主要内容如下:
(1)提出基于自编UDF动网格程序的CFD瞬态模拟方法,用以计算轴颈在任意偏心位置时的轴承非线性气膜力. 使用该方法研究三楔气体轴承的流场特性、动静压耦合效应以及静、动态参数的变化,并与圆柱气体轴承的各项参数对比.
(2)气体黏性和压缩性均会影响三楔气体轴承的动静压耦合效应强度. 三楔轴承流场中气体的黏性力和小孔节流的静压效应在转子系统低转速(小于20 000 r/min)时起主导作用;当转速较高(大于20 000 r/min)时,气体的压缩性变化对轴承流场动静压耦合效应强度的影响逐渐增大,动压效应占主导地位.
(3)将传统使用的0.50 MPa供气压力下的圆柱气体轴承与使用车载空压机内部气路的0.25 MPa供气压力下的三楔气体轴承进行性能对比. 结果表明,相较于圆柱轴承,动压效应对三楔轴承特性的增益更显著.
通过对2类轴承实际使用中静平衡位置及相应位置的动态参数计算,可以观察到三楔轴承在低转速与下能表现出与传统圆柱轴承相似的静压效应,而当转速升高时,三楔轴承的动静压耦合特征能使其在更低的供气压力下表现出良好的支承特性和稳定性. 较传统的圆柱轴承,三楔气体轴承因其无须外接气源的优点,能降低燃料电池汽车系统内气体回路的复杂度,同时其也能适应车载空压机需要频繁启停、变速的工作环境.
本研究已经取得了初步的成果,在后续工作中,可设计加工氢燃料电池汽车车载空压机样机,通过实验与理论分析相结合的方式,进一步证明三楔动压气体轴承设计的有效性,以及仅使用空压机内部气路为轴承供气这一研究方向的合理性.
参考文献
氢燃料电池汽车发动机关键技术研究现状及趋势展望
[J].DOI:10.3969/j.issn.2095-1469.2022.04.05 [本文引用: 1]
Research and development trends of key technologies of hydrogen fuel cell engines
[J].DOI:10.3969/j.issn.2095-1469.2022.04.05 [本文引用: 1]
Improved empirical parameters design method for centrifugal compressor in PEM fuel cell vehicle application
[J].
Foil bearing technology for high speed single stage air compressors for fuel cell applications
[J].
Design and key technology of oil-free centrifugal air compressor for hydrogen fuel cell
[J].DOI:10.30941/CESTEMS.2022.00003 [本文引用: 1]
氢燃料电池空压机动压箔片轴承设计与试验
[J].DOI:10.11809/bqzbgcxb2022.04.028 [本文引用: 1]
Design and test of aerodynamic foil bearings for hydrogen fuel cell air compressors
[J].DOI:10.11809/bqzbgcxb2022.04.028 [本文引用: 1]
径向气体箔片轴承高速重载测试及实验台搭建
[J].
Test of high speed and heavy load gas foil bearing and set up of test rig
[J].
高速透平机械全金属鼓泡箔片动压气体轴承稳定性研究
[J].
Stability analysis for fully hydrodynamic gas-lubricated protuberant foil bearings in high speed turbomachinery
[J].
空气轴承支撑的燃料电池离心空压机转子动力学分析
[J].
Calculation and analysis of air bearing centrifugal compressor rotor dynamics for fuel cells
[J].
空气动压箔片轴承启停性能的实验研究
[J].DOI:10.3969/j.issn.0254-0150.2011.07.013 [本文引用: 1]
Experimental study on the start-stop characteristic of foil air bearing
[J].DOI:10.3969/j.issn.0254-0150.2011.07.013 [本文引用: 1]
基于RNG k-
DOI:10.3969/j.issn.2096-5419.2023.01.004
Numerical simulation of hydraulic characteristics of spillway based on RNG k-
DOI:10.3969/j.issn.2096-5419.2023.01.004
阳升观台阶溢洪道水流数值模拟研究
[J].
Numerical simulation of the water flow in the stepped spillway of Yangshengguan reservoir
[J].
A new method for studying the 3D transient flow of misaligned journal bearings in flexible rotor-bearing systems
[J].
Unbalance and resonance elimination with active bearings on general rotors
[J].
The dynamic pressure effect of gas microbearings under high rotational speed
[J].