粉砂质泥岩具有水理性强、易开裂、强度低、变形大的特点,在我国南方湿热地区高速公路路堑边坡广泛分布. 在季节性降雨作用下,岩石反复经受干湿循环作用,岩体内部裂隙动态萌生、扩展及贯通,造成岩石力学性能劣化,极易诱发边坡失稳破坏,严重威胁高速公路的长期运营安全. 因此,研究干湿循环条件下粉砂质泥岩强度劣化规律与微观损伤机理,对维护其边坡稳定具有重要工程意义.
目前,已有学者针对干湿循环作用下岩石的力学特性开展了大量研究[1-3]. Zhang等[4-5]对干湿循环作用下砂岩力学性能开展系统研究,发现弹性模量在第一次饱水之后降幅较大;王维等[6]认为水岩循环对变质砂岩各力学参数的敏感度表现为黏聚力˃弹性模量˃内摩擦角˃单轴抗压强度;Chen等[7]发现岩石水岩循环损伤主要由内部裂隙的萌生与扩展引起. 以上研究表明干湿循环作用可显著诱发岩体损伤和变形,但南方湿热地区降雨具有明显的周期性,不同干湿循环路径对岩石力学性能势必产生不同的干湿劣化效应. 此外,现阶段开展的岩石力学试验多考虑高围压应力状态,而降雨条件下软岩边坡失稳模式多为浅层渐进失稳,滑坡体厚度一般小于5 m[8],其滑坡面处的自重应力约为114.6 kPa,目前有关低围压下不同干湿循环路径参数(如循环幅度)对岩石力学参数损伤的研究还鲜有报道.
在岩石本构模型方面,为了评估干湿循环作用下岩石的损伤程度,众多学者基于试验结果构建了岩石损伤本构模型. 统计损伤本构模型可以精确描述岩石损伤演化过程中裂隙的随机分布特性,因而被广泛采用. 曹文贵等[9]基于D-P准则提出岩石微元强度服从正态分布的概念,建立了岩石损伤本构模型;Lin等[10]认为准脆性岩石基元体各向同性强度服从对数正态分布,定义了准脆性岩石力学损伤变量,并建立了冻融损伤本构模型;王辉等[11]基于大理岩微元强度服从Weibull分布,建立了单轴应力状态下岩石损伤本构模型,经与试验数据对比分析,发现弹性阶段契合程度较高,而塑性阶段拟合效果不理想. 上述基于岩石微元强度服从概率分布建立的统计损伤本构模型为研究岩石损伤演化过程提供了有益参考,但少有涉及不同干湿循环路径下的岩石损伤本构模型,难以定量描述不同循环路径下粉砂质泥岩的损伤演化特征.
本研究开展不同循环路径下粉砂质泥岩低围压三轴压缩试验,分析其力学特性演化规律和破坏模式,结合扫描电镜(scanning electron microscopy,SEM)试验,揭示不同干湿循环路径下粉砂质泥岩强度劣化机制;构建考虑干湿循环路径作用的岩石统计损伤本构模型,为粉砂质泥岩边坡变形分析及灾变防控提供理论依据.
1. 试验概况
1.1. 试验材料与试样制备
试验所用粉砂质泥岩取自湖南省浏阳市某路堑边坡,边坡岩体层理特征明显. 为了避免层理特征对试验结果产生影响,选取层理不明显(微层理)的粉砂质泥岩进行取样,采集后蜡封运抵试验室,严格按照国际岩石力学学会试验规程[12],将粉砂质泥岩钻芯、切割、打磨成Ф50 mm×100 mm圆柱形岩样. X射线衍射分析表明粉砂质泥岩主要矿物成分为石英(质量分数为42.87%)、蒙脱石(29.58%)、伊利石(9.64%)、长石(7.75%)和绿泥石(8.17%);X-射线荧光光谱结果表明,粉砂质泥岩的化学成分主要为SiO2(68.01%)、Al2O3(19.74%). 依据《公路工程岩石试验规程》(JTG
表 1 粉砂质泥岩物理力学性能
Tab.1
| 物理力学指标 | 取值 |
| 颗粒密度/(g·cm−3) | 2.73 |
| 毛体积干密度/( g·cm−3) | 2.30 |
| 孔隙率/% | 15.80 |
| 水的质量分数/% | 11.78 |
| 吸水率/% | 14.34 |
| 饱和吸水率/% | 15.10 |
| 抗压强度/MPa | 18.02 |
| 变形模量/GPa | 35.35 |
| 黏聚力/MPa | 9.50 |
| 内摩擦角/(°) | 6.91 |
1.2. 试样筛选
图 1
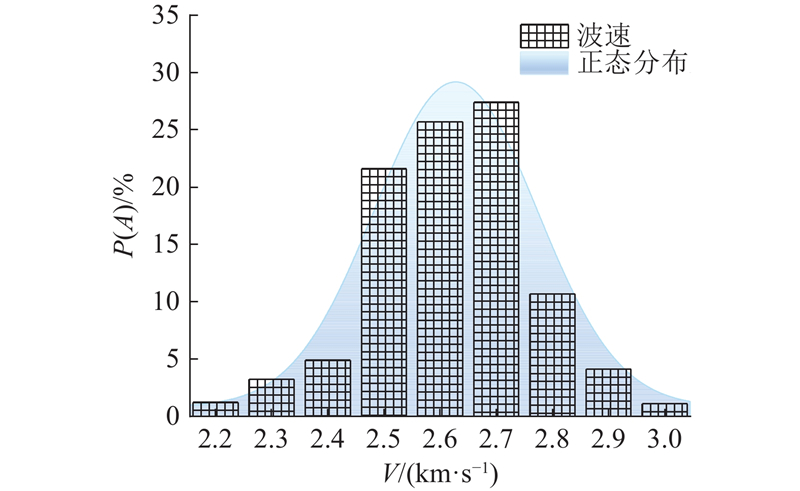
图 1 粉砂质泥岩纵波波速分布
Fig.1 Longitudinal wave velocity distribution of silty mudstone
1.3. 试验方案
1.3.1. 干湿循环试验
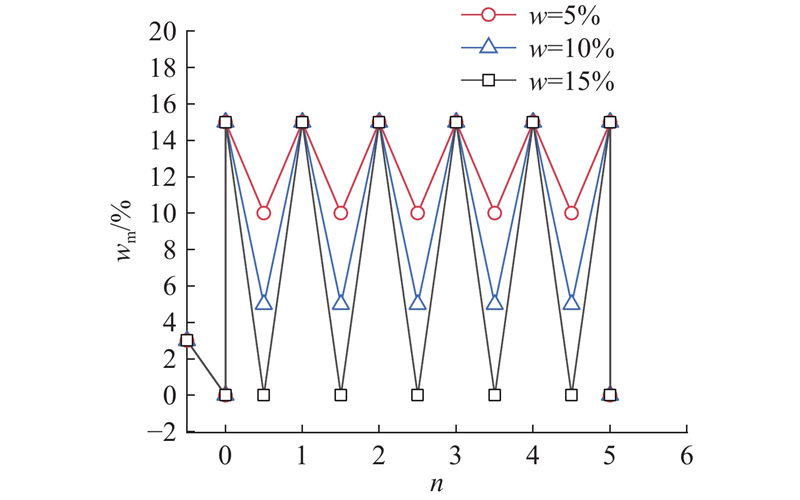
干湿循环路径:粉砂质泥岩的饱和水的质量分数wm为15.1%,故选择水的质量分数为15%作为每组循环路径水的质量分数的上限,通过调整水的质量分数的下限实现对循环幅度的控制. 考虑到南方湿热地区周期性降雨以及雨后不同高温时长对粉砂质泥岩边坡的影响,设定5%、10%和15%这3种干湿循环幅度. 在每种循环幅度下分别进行循环次数n为0、5、10和20的干湿循环试验,设置3个平行岩样. 以5次循环为例,其干湿循环路径如图2所示.
图 2
干湿循环试验分为饱和与干燥2个过程. 1)饱和:在岩样端部放置滤纸和透水石,采用三轴饱和器将其固定,放入盛满去离子水的真空饱和桶中抽真空饱和,直至岩样饱和度达到96%~98%. 2)干燥:将饱和岩样放入70 ℃烘箱中干燥,当岩样质量达到目标水的质量分数(即每种循环路径对应的水的质量分数的下限)时即停止干燥. 已知干燥岩样质量,可由如下公式计算得到目标水的质量分数下的岩样质量:
式中:wT为岩样目标水的质量分数,ma为目标水的质量分数下的岩样质量,m0为干燥岩样质量. 通过实时测量饱和与干燥过程中岩样的质量可以实现对循环幅度的有效控制. 在岩样达到目标循环次数后,将其置于70 ℃烘箱中干燥48 h,取完全干燥的岩样开展三轴压缩试验.
1.3.2. 三轴压缩试验
式中:t、D分别为橡皮膜厚度和内径,εm为橡皮膜环向拉伸应变,Em为橡皮膜弹性模量.
三轴压缩试验:本试验分为30组,共需90块岩样. 在使用WDW-100万能材料试验机开展低围压三轴压缩试验时,先将轴向应力加载至目标轴压(10、30、90 kPa)后清零数据,再以0.1 mm/min的速率加载至岩样破坏,使用coolpixp510相机记录岩样破坏形态.
1.3.3. SEM试验
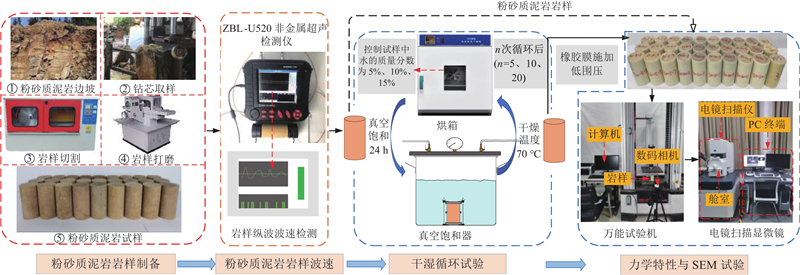
采用ZEISS高分辨电子扫描显微镜EVO10,最大分辨率为3 nm,加速电压为0.2~30.0 kV,10 V步进可调,最大探针电流为5 μA. 为了探究不同干湿循环路径下粉砂质泥岩孔隙与裂隙演化规律,在岩样破裂面处切取5 mm×5 mm×3 mm块状SEM样品置于70 ℃烘箱中干燥,采用喷金仪对干燥样品表面喷金后,置于电镜微观扫描仪舱室中抽真空处理,以加速电压为10 kV,放大倍数为2.0 kX进行扫描电镜试验. 试验设备及流程如图3所示.
图 3
图 3 不同干湿循环路径下的粉砂质泥岩试验流程图
Fig.3 Experimental flow chart of silty mudstone under different drying-wetting cycle paths
2. 结果与分析
2.1. 应力-应变曲线
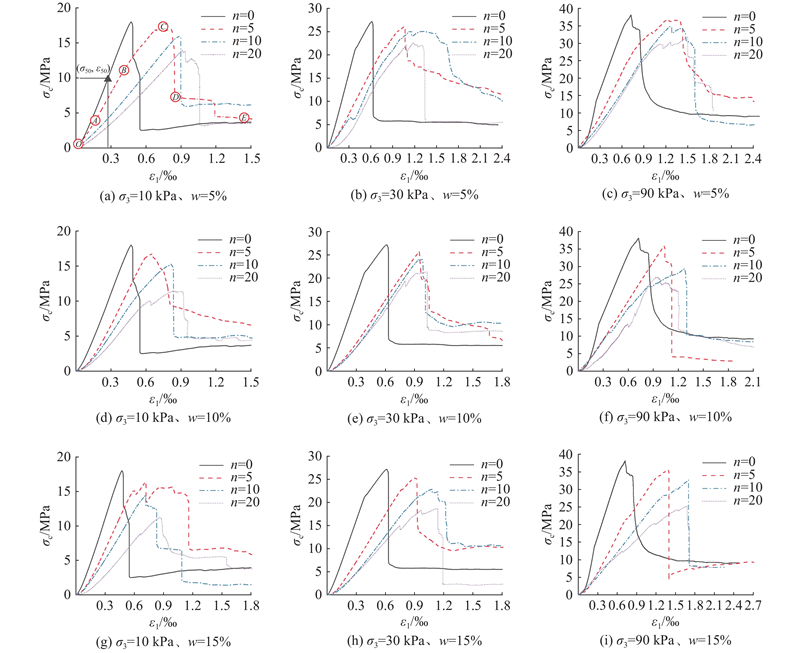
不同干湿循次数n与不同循环幅度w下粉砂质泥岩应力-应变曲线如图4所示.
图 4
图 4 不同干湿循环路径下粉砂质泥岩应力-应变曲线
Fig.4 Stress-strain curves of silty mudstone under different drying-wetting cycle paths
如图4(a)所示,以围压10 kPa、干湿循环次数5次、循环幅度5%为例,分析可知,岩样应力应变曲线可以分为5个阶段:(I)裂隙压密阶段(OA),此阶段岩样轴向应力随应变快速增长,应力-应变曲线呈非线性上凹式;(II)弹性变形阶段(AB),此阶段随轴向应力增大应变能的储存呈线性增长,以0.5倍峰值强度
在相同围压下,随干湿循环次数或循环幅度增加,岩样内部空隙和微裂纹不断扩展,应力-应变曲线压密阶段与塑性屈服阶段延长,弹性阶段应变能增长速度逐渐减弱,峰值强度逐渐降低,峰值应变逐渐增大,残余强度变化规律不明显;在相同干湿循环路径下,随围压增加,岩石峰值强度、变形模量和残余强度增大.
采用如下公式对不同干湿循环路径下粉砂质泥岩力学参数进行定量分析:
式中:S(n,w)与T(n,w)为循环幅度为w、循环次数为n时的岩样力学参数劣化率和力学参数,T0为岩样未经循环处理的力学参数.
2.2. 变形模量和峰值强度
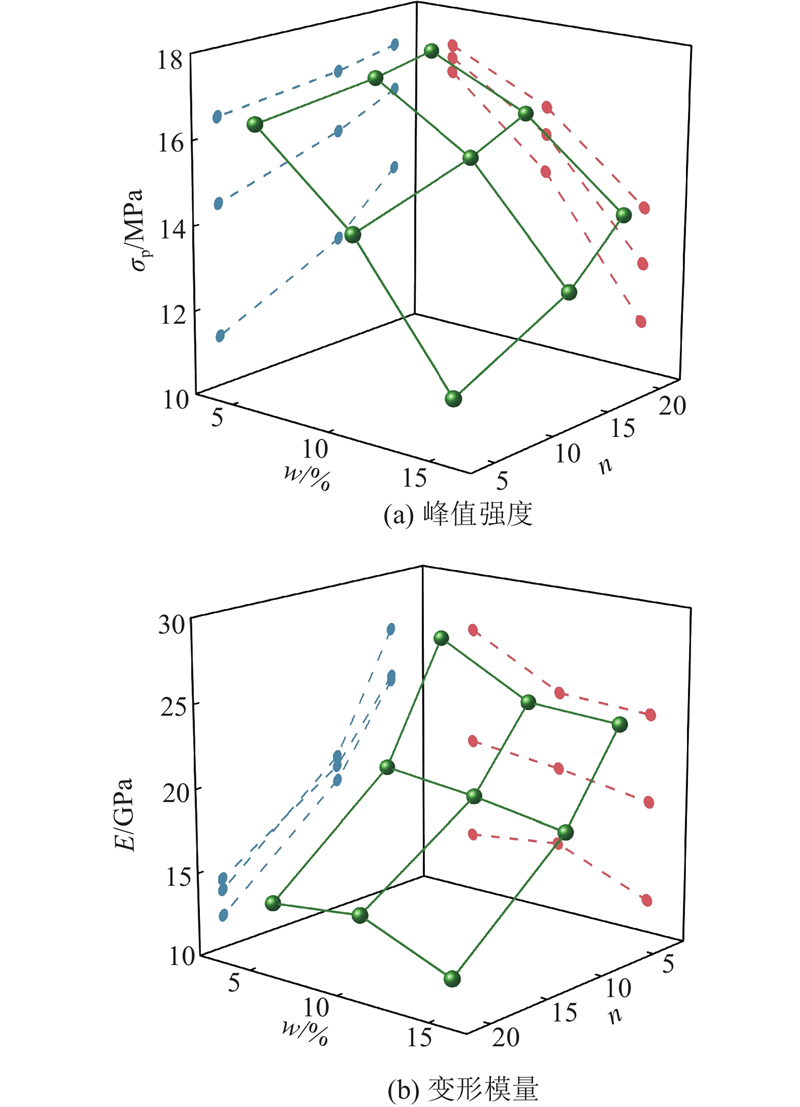
以10 kPa围压为例,定量分析粉砂质泥岩变形模量E和峰值强度σp随不同干湿循环路径的变化关系,如图5所示. 可以看出,循环幅度为5%、10%和15%的岩样经过10次循环后,变形模量分别下降43.86%、45.21%和48.30%,峰值强度降低11.54%、15.16%和20.25%;循环幅度为5%的岩样经过5、10和20次干湿循环后,变形模量分别降低25.53%、43.86%和62.02%,峰值强度分别降低5.54%、11.54%和24.79%. 表明干湿循环次数对岩样变形模量的劣化程度显著高于峰值强度的. 这与类似岩石干湿循环试验结果一致[6,17]. 这是因为随着干湿循环次数的增加,岩样内部裂纹持续扩展、贯通,结构逐渐变得松散,岩石峰值强度不断降低. 在相同应力水平下,循环次数多的岩样产生更大的轴向应变,变形模量显著减小. 随着循环幅度增加,压实黄土峰值强度劣化42.48%~65.95%[18],劣化程度远高于粉砂质泥岩. 这是因为,岩石致密性高于土体,循环幅度越大,土体内部颗粒受水流冲击,破碎越显著.
图 5
图 5 不同干湿循环路径下粉砂质泥岩峰值强度与变形模量
Fig.5 Peak strength and deformation modulus of silty mudstone under different drying-wetting cycle paths
通过Poly 2D拟合,可以得到10 、30 、90 kPa围压下岩样变形模量E(n,w)1、E(n,w)2和E(n,w)3与干湿循环次数和循环幅度间的函数表达式:
其拟合优度均超过0.98.
2.3. 抗剪强度指标
不同干湿循环路径下粉砂质泥岩抗剪强度指标如图6所示. 循环幅度为5%的岩样经过5、10和20次循环后,黏聚力c分别下降21.15%、25.36%和43.01%,内摩擦角
图 6
图 6 不同干湿循环路径下粉砂质泥岩抗剪强度指标
Fig.6 Shear strength index of silty mudstone under different drying-wetting cycle paths
采用Origin内置的非线性曲面拟合模型(Stirling与Log3P1)拟合得到考虑干湿循环次数和循环幅度共同作用下的内摩擦角
2.4. 粉砂质泥岩破坏形态
对岩样破坏形态进行统计分析,可知,岩样破坏形态包括顶锥和剪切2种基本破坏形态以及顶锥-劈裂与剪切-顶锥2种过渡破坏形态,根据围压σ3选取不同干湿路径下岩样典型破坏形态进行分析,如图7所示.当围压为10 kPa时,岩样破坏面由端部斜向延伸至内部,形成锥形滑裂面,呈顶锥-劈裂破坏;当围压为30 kPa时,以顶锥-劈裂破坏和剪切破坏为主,当围压为90 kPa时,岩样均为剪切破坏,剪切面存在明显的摩擦痕迹.可以看出,围压、干湿循环次数和循环幅度对粉砂质泥岩损伤演化具有重要影响,其中,围压主要控制岩样的破坏形态、循环次数与循环幅度,从而影响岩石裂隙发展. 当围压为10 kPa时,岩样裂隙面剪切应力小于抗剪强度,剪切裂纹难以扩展,而张拉裂纹则易达到应力极值而扩展,发生顶锥-劈裂破坏. 随着干湿循环次数的增加,岩石在溶蚀与潜蚀作用下,内部孔隙与微裂隙不断扩展,颗粒粒间接触边缘的锯齿状或不规则状趋向变成圆滑状,岩样黏聚力和内摩擦角下降,此时,剪切裂纹比张拉裂纹更容易扩展,岩样逐渐由以顶锥-劈裂破坏为主向以剪切破坏为主过渡. 与类似试验结果[21]一致,在相同循环次数下,随着循环幅度的增加,岩石溶蚀与潜蚀作用更加显著;当围压 为90 kPa时,岩样侧向变形被大幅限制,三轴压缩过程中产生的拉应力不足以使岩样发生顶锥-劈裂破坏,于是沿斜截面发生剪切破坏.
图 7
图 7 不同干湿循环路径下粉砂质泥岩破坏形态
Fig.7 Failure modes of silty mudstone under different drying-wetting cycle paths
2.5. 粉砂质泥岩强度劣化机制
图 8
图 8 不同干湿循环路径下粉砂质泥岩微观结构图
Fig.8 Microstructure of silty mudstone under different wet-dry cycle paths
上述现象原因为,随干湿循环次数增加,组成粉砂质泥岩的矿物与水溶液发生潜蚀、溶蚀反应,结合力相对较强的离子(H+)可置换出岩样矿物中相应离子(Ca2+、K+、Na+),使岩样局部矿物成份发生改变. 例如,长石类矿物较易与水溶液发生相关化学反应,生成膨胀性黏土矿物高岭石[22]. 随循环幅度增大,岩样增湿和干燥状态下水的质量分数之差越大. 岩样潜蚀、溶蚀作用更加显著,加快了岩样力学性能损伤演化进程与边坡变形破坏程度. 蒙脱石、伊利石以及新生成的高岭石等膨胀性矿物浸水或干燥时,无法同步吸水或失水,导致岩样内外产生应力差[3],极易在岩样裂纹和裂隙尖端区域出现应力集中现象,当膨胀应力大于岩样抗拉强度时,尖端区域裂隙逐渐扩展,为水岩物理化学作用提供更多接触面. 随干湿循环次数增加,岩样反复受“干缩-湿胀”扰动,内部微裂隙不断扩展,孔隙率不断增大;随循环幅度增加,岩样吸水或失水速率增大,内外产生的应力差随之增大,在相同循环次数下,裂隙扩展更显著. 此外,绿泥石具有吸水软化性较强以及水岩循环后极易破坏的特征[23],是导致岩样力学性能劣化的重要原因.
在实际边坡工程中,周期性降雨对边坡稳定性存在不利影响,且在周期性降雨时,岩体中水的质量分数变化幅度越大,边坡稳定性的不利影响越显著.
3. 考虑干湿循环路径的粉砂质泥岩损伤本构模型构建
采用正态分布损伤方法来分析粉砂质泥岩的力学特征,采用干湿循环损伤变量确定不同干湿循环路径对岩石力学特性的影响;利用干湿循环和荷载的耦合损伤效应来定义岩石总损伤变量,然后基于修正D-P强度准则构建考虑干湿循环路径的岩石损伤本构模型.
3.1. 干湿循环损伤变量的选择
研究发现,在定义岩石损伤变量方面,一般采用弹性模量、孔隙率、纵波波速等参数变化来表征. 试验结果表明,粉砂质泥岩变形模量随干湿循环次数或循环幅度增加而降低,且变形模量便于获取和分析,故选择变形模量表征不同干湿循环路径下粉砂质泥岩损伤变量:
式中:
3.2. 受荷损伤变量的确定
在荷载作用下,粉砂质泥岩受荷损伤主要由岩石局部微元体的不均匀性和破坏效应引起. 因此,以对数正态分布定义准脆性岩石受荷损伤变量:
式中:
3.3. 干湿循环与荷载共同作用下岩石总损伤变量的确定
干湿循环与荷载耦合作用对岩石造成的损伤不是干湿循环和荷载分别单独作用造成的损伤简单相加,而是干湿循环与荷载耦合而成的整体效应. 设岩石在2种状态下的损伤用缺陷材料的体积表示,即缺陷材料占材料总体积的比率,设未损伤岩石、干湿循环损伤岩石和干湿循环与荷载耦合作用损伤后岩石的有效体积分别为V0、V1和V2,则有
联立式(8)、(9)可得不同干湿循环路径与荷载共同作用下岩石总损伤变量[24]:
将式(6)、(7)代入式(10)可得岩石在干湿与荷载共同作用下的总损伤变量:
式中:
3.4. 基于D-P强度准则确定岩石微元强度
Drucker-Prager准则(D-P准则)克服了Mohr-Coulomb准则(M-C准则)中不能考虑中间主应力的难题,相对于M-C准则而言,D-P准则更适合岩石类材料. 因此,基于D-P强度准则建立考虑干湿循环次数n与循环幅度w的岩石微元强度p:
式中:σ*为有效压力,
基于广义胡克定律、Lemaitre应变等效理论[25]以及三轴压缩条件下围压相等的原则,可以得到
式中:v为泊松比.
将I1和J2用名义应力可以表示为
式中:ε1为低围压三轴压缩过程中粉砂质泥岩的应变.
将式(15)、(16)代入式(12)确定荷载作用下岩石微元强度p:
3.5. 考虑干湿循环路径的岩石损伤本构模型
将微元强度式(16)代入式(10)得到考虑干湿循环路径的岩石总损伤演化:
将式(18)代入式(14)可得考虑干湿循环路径的岩石损伤本构模型:
3.6. 本构模型参数确定
岩石损伤本构模型参数r0和m0可根据应力-应变曲线峰值点
1)当
式(19)两端对ε求导,得到
将式(14)代入(20)并化简,得到
式(14)变形,可以得到
通过式(22)可以看出,当试验中任意一条应力-应变曲线的变形模量和峰值强度点确定后,均可通过式(22)计算得到一个函数
3.7. 粉砂质泥岩损伤本构模型验证
将三轴试验数据代入式(21)、(23)~(25),求得考虑干湿循环路径的岩石损伤本构模型参数值,如表2所示.
表 2 不同干湿循环路径作用下粉砂质泥岩损伤模型参数
Tab.2
| w/% | n | m0 | r0 | w/% | n | m0 | r0 | |||
| 10 | — | 0 | 30 | 10 | 5 | |||||
| 30 | — | 0 | 30 | 10 | 10 | |||||
| 90 | — | 0 | 30 | 10 | 20 | |||||
| 10 | 5 | 5 | 90 | 10 | 5 | |||||
| 10 | 5 | 10 | 90 | 10 | 10 | |||||
| 10 | 5 | 20 | 90 | 10 | 20 | |||||
| 30 | 5 | 5 | 10 | 15 | 5 | |||||
| 30 | 5 | 10 | 10 | 15 | 10 | |||||
| 30 | 5 | 20 | 10 | 15 | 20 | |||||
| 90 | 5 | 5 | 30 | 15 | 5 | |||||
| 90 | 5 | 10 | 30 | 15 | 10 | |||||
| 90 | 5 | 20 | 30 | 15 | 20 | |||||
| 10 | 10 | 5 | 90 | 15 | 5 | |||||
| 10 | 10 | 10 | 90 | 15 | 10 | |||||
| 10 | 10 | 20 | 90 | 15 | 20 |
为了验证该损伤本构模型正确性,将该模型理论曲线与试验数据进行对比,结果如图9所示. 图中,σc为低围压三轴压缩过程中粉砂质泥岩的抗压强度. 当应力-应变曲线由弹性阶段进入应变软化阶段后,偏应力增速逐渐减缓,达到峰值强度后迅速降低. 随干湿循环次数或循环幅度增加,岩样峰值强度和变形模量均降低,峰值应变逐渐增大;在相同干湿循环路径下,随围压的增加岩样峰值强度、变形模量和峰值应变均增加. 可以看出,基于胡克定律、修正D-P强度准则和Lemaitre应变等效假设理论建立的损伤本构模型,能准确地描述粉砂质泥岩弹性阶段与应变软化阶段的变形特征,揭示岩石随干湿循环次数和循环幅度的损伤演化规律. 基于不同干湿循环路径的粉砂质泥岩理论峰值强度与围压,通过M-C强度准则计算有效抗剪强度指标,为边坡安全系数Fs的计算提供数据支撑,而边坡安全系数Fs是评价边坡稳定性的重要指标. 因此,本研究所建立的粉砂质泥岩损伤本构模型,为周期性降雨条件下粉砂质泥岩边坡与路堤稳定性分析提供依据,对湿热地区岩土体工程建设具有指导意义.
图 9
图 9 不同干湿循环路径下粉砂质泥岩试验曲线和理论曲线
Fig.9 Experimental and theoretical curves of silty mudstone under different drying-wetting cycle paths
4. 结 论
(1)随围压降低、循环次数与循环幅度增大,粉砂质泥岩力学参数损伤程度越高,表现出明显的干湿劣化效应. 在不同围压、循环次数与循环幅度下,粉砂质泥岩变形模量、峰值强度、黏聚力和内摩擦角分别下降21.13%~66.39%、3.69%~37.84%、21.15%~46.42%和13.76%~31.73%.
(2)三轴压缩下岩样破坏具有脆性特征. 当围压低于90 kPa时,岩样主要为以剪切破坏形式为主的顶锥-劈裂破坏,随干湿循环次数或循环幅度的增加,逐渐向以剪切破坏为主过渡;当围压为90 kPa时,岩样均为剪切破坏.
(3)所建立的不同循环路径下的岩石损伤本构模型理论曲线与粉砂质泥岩三轴压缩试验曲线较吻合,能有效反映岩石变形特性和损伤演化规律.
本研究针对粉砂质泥岩力学特性与损伤本构模型开展研究,但仍存在不足之处. 例如,基于胡克定律建立的损伤本构模型,认为岩样受压便进入弹性阶段,忽略了压密阶段岩样内部孔隙与裂隙的影响,导致实验数据与理论曲线之间存在一定偏差. 对此,后续作者将基于有效介质理论,将岩石变形分为孔隙和骨架2个部分,构建考虑孔隙压密阶段特征的粉砂质泥岩损伤本构模型.
参考文献
Effect of dry-wet cycling on the mechanical properties of rocks: a laboratory-scale experimental study
[J].DOI:10.3390/pr6100199 [本文引用: 2]
Combined effects of salt, cyclic wetting and drying cycles on the physical and mechanical properties of sandstone
[J].DOI:10.1016/j.enggeo.2018.11.009
水–岩作用下红层软岩力学特性劣化规律研究
[J].
Mechanical properties deteriorating change rule research of red-layer soft rock under water-rock interaction
[J].
Quantification and acoustic emission characteristics of sandstone damage evolution under dry-wet cycles
[J].DOI:10.1016/j.jobe.2022.103996 [本文引用: 1]
Investigation on mechanical and AE characteristics of yellow sandstone undergoing wetting-drying cycles
[J].
水岩循环作用下变质砂岩力学参数劣化试验研究
[J].
Experimental study on deteriorating characteristics of metamorphic sandstone mechanical parameters under the effect of wetting-drying cycles
[J].
Strength weakening and energy mechanism of rocks subjected to wet-dry cycles
[J].DOI:10.1007/s10706-019-00881-6 [本文引用: 1]
低应力与覆水环境下单裂隙粉砂质泥岩渗流特性
[J].
Seepage characteristics of single-fractured silty mudstone under low stress and overlying water environment
[J].
岩石破裂过程的统计损伤模拟研究
[J].
Study on simulation of statistical damage in the full process of rock failure
[J].
A damage constitutive model of rock subjected to freeze-thaw cycles based on lognormal distribution
[J].
考虑干湿循环的大理岩统计损伤本构模型
[J].
Statistical damage constitutive model of marble considering dry-wet cycle
[J].
Yielding of clays in states wetter than critical
[J].DOI:10.1680/geot.1963.13.3.211 [本文引用: 1]
Seepage characteristics of a fractured silty mudstone under different confining pressures and temperatures
[J].DOI:10.1007/s11771-020-4419-6 [本文引用: 1]
干湿循环下宁明粉砂岩宏微观损伤劣化规律
[J].
Macro/micro damage degradation law of Ningming siltstone under dry-wet cycles
[J].
干湿循环作用下压实黄土三轴剪切特性试验研究
[J].
Experimental study on triaxial shear characteristics of compacted loess under drying and wetting cycles
[J].
干湿循环作用下砂岩细观损伤演化及宏观劣化研究
[J].
Meso damage evolution characteristics and macro degradation of sandstone under wetting-drying cycles
[J].
大理岩干湿循环力学特性试验研究
[J].
Experimental study on mechanical properties of marble under hydraulic weathering coupling
[J].
砂岩力学特性对干湿循环效应响应规律的试验研究
[J].
Mechanical properties response of sandstone to cyclic drying-wetting effect
[J].
鄂西北页岩饱水软化微观机制与力学特性研究
[J].
Softening micro-mechanism and mechanical properties of water-saturated shale in Northwestern Hubei
[J].
Statistical damage model of altered granite under dry-wet cycles
[J].DOI:10.3390/sym11010041 [本文引用: 1]
Thermo-mechanical coupling damage constitutive model of rock based on the Hoek-Brown strength criterion
[J].DOI:10.1177/1056789517726838 [本文引用: 1]