采用多分类模型来构建拓扑生成器,由[1, 0, 0]、[0, 1, 0]和[0, 0, 1]分别表示类别为0、1和2的材料. 将其解码器的最后一层输出传递给Softmax层,并基于多分类交叉熵计算与输入数据的重建损失. 为了有效表征拓扑结构,并且学习数据的潜在分布,将编码维度设置为8,以储存相关信息. 整个模型在包含30万组样本的拓扑数据集上进行训练,并使用Adam优化器[31 ] 最小化损失函数,训练过程如图3 (a)所示. 图中,S 为迭代步,KLD为KL散度提取解码器作为拓扑生成器,从标准正态空间中采样z t ~$ {{N}}$ ( 0 , 1 .0 ),可以合成与训练数据类似的拓扑结构. 另外,不同于拓扑生成器,材料生成器采用回归模型进行构建,使用均方误差计算重建损失. 材料生成器目标不在于合成新的数据,而是在潜在空间中利用2个连续变量{z m1 , z m2 }来表征材料参数,获取材料参数的潜在信息. 在材料数据库上同样使用Adam优化器对其进行训练,直至满足误差要求,如图3 (b)所示.
[1]
KUSHWAHA M S, HALEVI P, DOBRZYNSKI L, et al Acoustic band structure of periodic elastic composites
[J]. Physical Review Letters , 1993 , 71 (13 ): 2022 - 2025
DOI:10.1103/PhysRevLett.71.2022
[本文引用: 1]
[3]
唐豪, 陈晓斌, 唐孟雄, 等 基于复频散曲线特征的周期结构高铁路基减振研究
[J]. 岩土工程学报 , 2021 , 43 (12 ): 2169 - 2179
DOI:10.11779/CJGE202112003
[本文引用: 1]
TANG Hao, CHENG Xiaobing, TANG Mengxiong, et al Vibration reduction of high-speed railway subgrade with periodic structures based on complex dispersion curves
[J]. Chinese Journal of Geotechnical Engineering , 2021 , 43 (12 ): 2169 - 2179
DOI:10.11779/CJGE202112003
[本文引用: 1]
[4]
CHENG Z, SHI Z, MO Y Complex dispersion relations and evanescent waves in periodic beams via the extended differential quadrature method
[J]. Composite Structures , 2018 , 187 : 122 - 136
DOI:10.1016/j.compstruct.2017.12.037
[5]
DEASI R, GUHA A, SESHU P Modelling and simulation of active and passive seat suspensions for vibration attenuation of vehicle occupants
[J]. International Journal of Dynamics and Control , 2021 , 9 (4 ): 1423 - 1443
DOI:10.1007/s40435-021-00788-2
[本文引用: 1]
[6]
LI X, CHENG S, YANG H, et al Optimization of vibration characteristics and directional propagation of plane waves in branching ligament structures of wind models
[J]. Results in Physics , 2023 , 47 : 106345
DOI:10.1016/j.rinp.2023.106345
[本文引用: 1]
[7]
LI X, CHENG S, YANG H, et al Bandgap tuning and in-plane wave propagation of chiral and anti-chiral hybrid metamaterials with assembled six oscillators
[J]. Physica A , 2023 , 615 : 128600
DOI:10.1016/j.physa.2023.128600
[8]
XIAO L, CAO Z, LU H, et al Controllable and scalable gradient-driven optimization design for two-dimensional metamaterials based on deep learning
[J]. Composite Structures , 2024 , 337 : 118072
DOI:10.1016/j.compstruct.2024.118072
[本文引用: 1]
[10]
YI G, YOUN B A comprehensive survey on topology optimization of phononic crystals
[J]. Structural and Multidisciplinary Optimization , 2016 , 54 (5 ): 1315 - 1344
DOI:10.1007/s00158-016-1520-4
[本文引用: 5]
[11]
熊远皓, 李凤明, 张传增 周期结构振动带隙特性优化研究进展
[J]. 哈尔滨工程大学学报 , 2022 , 43 (9 ): 1229 - 1240
XIONG Yuanhao, LI Fengming, ZHANG Chuanzeng Research progress on the optimization of vibration band-gap characteristics for periodic structures
[J]. Journal of Harbin Engineering University , 2022 , 43 (9 ): 1229 - 1240
[12]
WANG X, WAN S, ZHOU P, et al Topology optimization of periodic pile barriers and its application in vibration reduction for plane waves
[J]. Soil Dynamics and Earthquake Engineering , 2022 , 153 : 107119
DOI:10.1016/j.soildyn.2021.107119
[本文引用: 1]
[13]
ZHOU P, WAN S, WANG X, et al Topology optimization of the periodic pile barrier with initial stresses arranged in rectangular and equilateral triangular lattices
[J]. Structures , 2023 , 51 : 628 - 639
DOI:10.1016/j.istruc.2023.03.013
[本文引用: 1]
[15]
贾宇翔, 王甲富, 陈维, 等 基于智能算法的超材料快速优化设计方法研究进展
[J]. 雷达学报 , 2021 , 10 (2 ): 220 - 239
DOI:10.12000/JR21027
[本文引用: 1]
JIA Yuxiang, WANG Jiafu, CHEN Wei, et al Research progress on rapid optimization design methods of metamaterials based on intelligent algorithms
[J]. Journal of Radars , 2021 , 10 (2 ): 220 - 239
DOI:10.12000/JR21027
[本文引用: 1]
[16]
JIN Y, HE L, WEN Z, et al Intelligent on-demand design of phononic metamaterials
[J]. Nanophotonics , 2022 , 11 (3 ): 439 - 460
DOI:10.1515/nanoph-2021-0639
[本文引用: 1]
[17]
LI X, NING S, LIU Z, et al Designing phononic crystal with anticipated band gap through a deep learning based data-driven method
[J]. Computer Methods in Applied Mechanics and Engineering , 2020 , 361 : 112737
DOI:10.1016/j.cma.2019.112737
[本文引用: 1]
[18]
GURBUZ C, KRONOWETTER F, DIETZ C, et al Generative adversarial networks for the design of acoustic metamaterials
[J]. The Journal of the Acoustical Society of America , 2021 , 149 (2 ): 1162 - 1174
DOI:10.1121/10.0003501
[本文引用: 1]
[19]
曹蕾蕾, 朱旺, 武建华, 等 基于人工神经网络的声子晶体逆向设计
[J]. 力学学报 , 2021 , 53 (7 ): 1992 - 1998
DOI:10.6052/0459-1879-21-142
[本文引用: 2]
CAO Leilei, ZHU Wang, WU Jianhua, et al Inverse design of phononic crystals by artificial neural networks
[J]. Chinese Journal of Theoretical and Applied Mechanics , 2021 , 53 (7 ): 1992 - 1998
DOI:10.6052/0459-1879-21-142
[本文引用: 2]
[21]
LIU C, YU G Inverse design of locally resonant metabarrier by deep learning with a rule-based topology dataset
[J]. Computer Methods in Applied Mechanics and Engineering , 2022 , 394 : 114925
DOI:10.1016/j.cma.2022.114925
[23]
LIU D, TAN Y, KHORAM E, et al Training deep neural networks for the inverse design of nanophotonic structures
[J]. ACS Photonics , 2018 , 5 (4 ): 1365 - 1369
DOI:10.1021/acsphotonics.7b01377
[本文引用: 1]
[24]
ABUEIDDA D W, ALMASRI M, AMMOURAH R, et al Prediction and optimization of mechanical properties of composites using convolutional neural networks
[J]. Composite Structures , 2019 , 227 : 111264
DOI:10.1016/j.compstruct.2019.111264
[本文引用: 1]
[25]
CUI X, WANG S, HU S A method for optimal design of automotive body assembly using multi-material construction
[J]. Materials and Design , 2008 , 29 (2 ): 381 - 387
DOI:10.1016/j.matdes.2007.01.024
[本文引用: 1]
[26]
XIAO L, CAO Z, LU H, et al Optimal design of one-dimensional elastic metamaterials through deep convolutional neural network and genetic algorithm
[J]. Structures , 2023 , 57 : 105349
DOI:10.1016/j.istruc.2023.105349
[本文引用: 1]
[27]
石志飞, 程志宝, 向宏军. 周期结构理论及其在隔震减振中的应用[M]. 北京: 科学出版社, 2017: 270−276.
[本文引用: 2]
[28]
CAMLEY R, DJAFARIROUHANI B, DOBRZYNSKI L, et al Transverse elastic-waves in periodically layered infinite, semi-infinite, and slab media
[J]. Journal of Vacuum Science and Technology B, Woodbury: Amer Inst Physics , 1983 , 1 (2 ): 371 - 375
DOI:10.1116/1.582559
[本文引用: 1]
[29]
LUO C, NING S, LIU Z, et al Interactive inverse design of layered phononic crystals based on reinforcement learning
[J]. Extreme Mechanics Letters , 2020 , 36 : 100651
DOI:10.1016/j.eml.2020.100651
[本文引用: 1]
[30]
KINGMA D P, WELLING M. Auto-encoding variational bayes [EB/OL]. (2013-12-20) [2023-9-13]. https://doi.org/10.48550/arXiv.1312.6114.
[本文引用: 1]
[31]
KINGMA D P, BA J. Adam: a method for stochastic optimization [EB/OL]. (2014-12-22) [2023-9-13]. https://doi.org/10.48550/arXiv.1412.6980.
[本文引用: 1]
[32]
BAYDIN A G, PEARLMUTTER B A, RADUL A A. Automatic differentiation in machine learning: a survey [EB/OL]. (2015-2-20) [2023-9-13]. https://doi.org/10.48550/arXiv.1502.05767.
[本文引用: 1]
[33]
ABADI M, BARHAM P, CHEN J, et al. TensorFlow: a system for large-scale machine learning [EB/OL]. (2016-5-24) [2023-9-13]. https://doi.org/10.48550/arXiv.1605.08695.
[本文引用: 1]
[34]
GUO T, LIU Y, HAN C An overview of stochastic quasi-newton methods for large-scale machine learning
[J]. Journal of the Operations Research Society of China , 2023 , 10 : 245 - 275
[本文引用: 2]
[35]
RAKSHIT S, ANANTHASURESH G K Simultaneous material selection and geometry design of statically determinate trusses using continuous optimization
[J]. Structural and Multidisciplinary Optimization , 2007 , 35 (1 ): 55 - 68
DOI:10.1007/s00158-007-0116-4
[本文引用: 1]
Acoustic band structure of periodic elastic composites
1
1993
... 弹性超材料是一类人工构筑的周期性复合材料,具有自然界不存在的超常物理特性. 通过合理的设计,可以实现在波长(布拉格散射机制[1 ] )和亚波长(局域共振[2 ] )尺度下对弹性波的调控和控制. 弹性超材料最主要的特征是在一定频率范围内,弹性波的传播受到抑制和阻隔,这个频率范围被称为带隙(band gap, BG). 由于这一现象,弹性波超材料被广泛运用于噪声和振动控制中 [3 -5 ] . 通过调整拓扑结构和材料参数,可以定制和优化弹性超材料的带隙特性. 许多学者设计出大量有趣的超材料拓扑结构,通过结构优化实现对带隙的调谐以获得更好的减振降噪能力,引起了广泛的关注[6 -8 ] . 其中,一维弹性超材料如周期屏障和基础[9 ] ,被安装在建筑物附近或底部,降低交通荷载所引起的低频环境振动,从而减少对环境的负面影响. 因此,根据特定的环境减振需求设计定制弹性超材料具有重要的理论意义和工程应用价值. ...
Locally resonant sonic materials
1
2000
... 弹性超材料是一类人工构筑的周期性复合材料,具有自然界不存在的超常物理特性. 通过合理的设计,可以实现在波长(布拉格散射机制[1 ] )和亚波长(局域共振[2 ] )尺度下对弹性波的调控和控制. 弹性超材料最主要的特征是在一定频率范围内,弹性波的传播受到抑制和阻隔,这个频率范围被称为带隙(band gap, BG). 由于这一现象,弹性波超材料被广泛运用于噪声和振动控制中 [3 -5 ] . 通过调整拓扑结构和材料参数,可以定制和优化弹性超材料的带隙特性. 许多学者设计出大量有趣的超材料拓扑结构,通过结构优化实现对带隙的调谐以获得更好的减振降噪能力,引起了广泛的关注[6 -8 ] . 其中,一维弹性超材料如周期屏障和基础[9 ] ,被安装在建筑物附近或底部,降低交通荷载所引起的低频环境振动,从而减少对环境的负面影响. 因此,根据特定的环境减振需求设计定制弹性超材料具有重要的理论意义和工程应用价值. ...
基于复频散曲线特征的周期结构高铁路基减振研究
1
2021
... 弹性超材料是一类人工构筑的周期性复合材料,具有自然界不存在的超常物理特性. 通过合理的设计,可以实现在波长(布拉格散射机制[1 ] )和亚波长(局域共振[2 ] )尺度下对弹性波的调控和控制. 弹性超材料最主要的特征是在一定频率范围内,弹性波的传播受到抑制和阻隔,这个频率范围被称为带隙(band gap, BG). 由于这一现象,弹性波超材料被广泛运用于噪声和振动控制中 [3 -5 ] . 通过调整拓扑结构和材料参数,可以定制和优化弹性超材料的带隙特性. 许多学者设计出大量有趣的超材料拓扑结构,通过结构优化实现对带隙的调谐以获得更好的减振降噪能力,引起了广泛的关注[6 -8 ] . 其中,一维弹性超材料如周期屏障和基础[9 ] ,被安装在建筑物附近或底部,降低交通荷载所引起的低频环境振动,从而减少对环境的负面影响. 因此,根据特定的环境减振需求设计定制弹性超材料具有重要的理论意义和工程应用价值. ...
基于复频散曲线特征的周期结构高铁路基减振研究
1
2021
... 弹性超材料是一类人工构筑的周期性复合材料,具有自然界不存在的超常物理特性. 通过合理的设计,可以实现在波长(布拉格散射机制[1 ] )和亚波长(局域共振[2 ] )尺度下对弹性波的调控和控制. 弹性超材料最主要的特征是在一定频率范围内,弹性波的传播受到抑制和阻隔,这个频率范围被称为带隙(band gap, BG). 由于这一现象,弹性波超材料被广泛运用于噪声和振动控制中 [3 -5 ] . 通过调整拓扑结构和材料参数,可以定制和优化弹性超材料的带隙特性. 许多学者设计出大量有趣的超材料拓扑结构,通过结构优化实现对带隙的调谐以获得更好的减振降噪能力,引起了广泛的关注[6 -8 ] . 其中,一维弹性超材料如周期屏障和基础[9 ] ,被安装在建筑物附近或底部,降低交通荷载所引起的低频环境振动,从而减少对环境的负面影响. 因此,根据特定的环境减振需求设计定制弹性超材料具有重要的理论意义和工程应用价值. ...
Complex dispersion relations and evanescent waves in periodic beams via the extended differential quadrature method
0
2018
Modelling and simulation of active and passive seat suspensions for vibration attenuation of vehicle occupants
1
2021
... 弹性超材料是一类人工构筑的周期性复合材料,具有自然界不存在的超常物理特性. 通过合理的设计,可以实现在波长(布拉格散射机制[1 ] )和亚波长(局域共振[2 ] )尺度下对弹性波的调控和控制. 弹性超材料最主要的特征是在一定频率范围内,弹性波的传播受到抑制和阻隔,这个频率范围被称为带隙(band gap, BG). 由于这一现象,弹性波超材料被广泛运用于噪声和振动控制中 [3 -5 ] . 通过调整拓扑结构和材料参数,可以定制和优化弹性超材料的带隙特性. 许多学者设计出大量有趣的超材料拓扑结构,通过结构优化实现对带隙的调谐以获得更好的减振降噪能力,引起了广泛的关注[6 -8 ] . 其中,一维弹性超材料如周期屏障和基础[9 ] ,被安装在建筑物附近或底部,降低交通荷载所引起的低频环境振动,从而减少对环境的负面影响. 因此,根据特定的环境减振需求设计定制弹性超材料具有重要的理论意义和工程应用价值. ...
Optimization of vibration characteristics and directional propagation of plane waves in branching ligament structures of wind models
1
2023
... 弹性超材料是一类人工构筑的周期性复合材料,具有自然界不存在的超常物理特性. 通过合理的设计,可以实现在波长(布拉格散射机制[1 ] )和亚波长(局域共振[2 ] )尺度下对弹性波的调控和控制. 弹性超材料最主要的特征是在一定频率范围内,弹性波的传播受到抑制和阻隔,这个频率范围被称为带隙(band gap, BG). 由于这一现象,弹性波超材料被广泛运用于噪声和振动控制中 [3 -5 ] . 通过调整拓扑结构和材料参数,可以定制和优化弹性超材料的带隙特性. 许多学者设计出大量有趣的超材料拓扑结构,通过结构优化实现对带隙的调谐以获得更好的减振降噪能力,引起了广泛的关注[6 -8 ] . 其中,一维弹性超材料如周期屏障和基础[9 ] ,被安装在建筑物附近或底部,降低交通荷载所引起的低频环境振动,从而减少对环境的负面影响. 因此,根据特定的环境减振需求设计定制弹性超材料具有重要的理论意义和工程应用价值. ...
Bandgap tuning and in-plane wave propagation of chiral and anti-chiral hybrid metamaterials with assembled six oscillators
0
2023
Controllable and scalable gradient-driven optimization design for two-dimensional metamaterials based on deep learning
1
2024
... 弹性超材料是一类人工构筑的周期性复合材料,具有自然界不存在的超常物理特性. 通过合理的设计,可以实现在波长(布拉格散射机制[1 ] )和亚波长(局域共振[2 ] )尺度下对弹性波的调控和控制. 弹性超材料最主要的特征是在一定频率范围内,弹性波的传播受到抑制和阻隔,这个频率范围被称为带隙(band gap, BG). 由于这一现象,弹性波超材料被广泛运用于噪声和振动控制中 [3 -5 ] . 通过调整拓扑结构和材料参数,可以定制和优化弹性超材料的带隙特性. 许多学者设计出大量有趣的超材料拓扑结构,通过结构优化实现对带隙的调谐以获得更好的减振降噪能力,引起了广泛的关注[6 -8 ] . 其中,一维弹性超材料如周期屏障和基础[9 ] ,被安装在建筑物附近或底部,降低交通荷载所引起的低频环境振动,从而减少对环境的负面影响. 因此,根据特定的环境减振需求设计定制弹性超材料具有重要的理论意义和工程应用价值. ...
有覆层土体中部分埋入式表面波屏障
1
2020
... 弹性超材料是一类人工构筑的周期性复合材料,具有自然界不存在的超常物理特性. 通过合理的设计,可以实现在波长(布拉格散射机制[1 ] )和亚波长(局域共振[2 ] )尺度下对弹性波的调控和控制. 弹性超材料最主要的特征是在一定频率范围内,弹性波的传播受到抑制和阻隔,这个频率范围被称为带隙(band gap, BG). 由于这一现象,弹性波超材料被广泛运用于噪声和振动控制中 [3 -5 ] . 通过调整拓扑结构和材料参数,可以定制和优化弹性超材料的带隙特性. 许多学者设计出大量有趣的超材料拓扑结构,通过结构优化实现对带隙的调谐以获得更好的减振降噪能力,引起了广泛的关注[6 -8 ] . 其中,一维弹性超材料如周期屏障和基础[9 ] ,被安装在建筑物附近或底部,降低交通荷载所引起的低频环境振动,从而减少对环境的负面影响. 因此,根据特定的环境减振需求设计定制弹性超材料具有重要的理论意义和工程应用价值. ...
有覆层土体中部分埋入式表面波屏障
1
2020
... 弹性超材料是一类人工构筑的周期性复合材料,具有自然界不存在的超常物理特性. 通过合理的设计,可以实现在波长(布拉格散射机制[1 ] )和亚波长(局域共振[2 ] )尺度下对弹性波的调控和控制. 弹性超材料最主要的特征是在一定频率范围内,弹性波的传播受到抑制和阻隔,这个频率范围被称为带隙(band gap, BG). 由于这一现象,弹性波超材料被广泛运用于噪声和振动控制中 [3 -5 ] . 通过调整拓扑结构和材料参数,可以定制和优化弹性超材料的带隙特性. 许多学者设计出大量有趣的超材料拓扑结构,通过结构优化实现对带隙的调谐以获得更好的减振降噪能力,引起了广泛的关注[6 -8 ] . 其中,一维弹性超材料如周期屏障和基础[9 ] ,被安装在建筑物附近或底部,降低交通荷载所引起的低频环境振动,从而减少对环境的负面影响. 因此,根据特定的环境减振需求设计定制弹性超材料具有重要的理论意义和工程应用价值. ...
A comprehensive survey on topology optimization of phononic crystals
5
2016
... 以往研究普遍采用参数分析法,调整参数以匹配特定需求,这完全依赖于研究者的经验,须反复对参数进行调整. 近十几年,拓扑优化方法作为典型设计方法被广泛运用,包括基于梯度的优化算法和无梯度的进化算法[10 -13 ] ,可以在设计过程中提供理论指导并节省了大量计算成本. 然而,这些方法依赖复杂的数值计算提供准确的预测,求解效率低且耗时[14 ] . 随着人工智能领域的快速发展,深度学习和结构设计的结合有效解决了上述设计方法过程繁琐、速度慢的问题,展现出高效、准确、智能的特点[15 -16 ] . Li等[17 ] 训练自动编码器和多层感知器,建立从带隙分布到拓扑图像的潜义向量的映射关系,实现二维声子晶体的逆向设计. Gurbuz等[18 ] 基于生成式对抗神经网络实现了二维声学超材料的快速设计. 曹蕾蕾等[19 ] 基于逻辑回归和多任务学习的深度学习模型设计一维声子晶体. Liu等[20 -22 ] 通过建立一个预训练的结构解码器和一个目标带隙编码器,组装形成设计模型,系统地研究了一维、二维布拉格超屏障以及局域共振超屏障的设计方法. ...
... 以上研究展示了深度学习在超材料设计中的适用性和高效性. 这些研究通过各种巧妙方式建立目标带隙到设计结构的“端到端”映射关系,将设计时间压缩至秒级水平[23 ] . 然而,这些权重确定的映射关系无法表征寻优的迭代过程,局限于指定带隙区间的设计中,无法扩展到其他的设计场景,如约束条件下的带隙最大化设计[10 ] . 因此,与遗传算法结合深度学习模型评估目标函数的迭代方法相比,其灵活性和通用性较差[24 -26 ] . 尽管遗传算法(genetic algorithm, GA)能够在设计空间中进行迭代优化,但是其本质上属于随机搜索,设计效率较低,同时忽略了深度学习模型中所蕴含的梯度信息. 而这些信息可以被更高效的梯度优化算法加以利用,实现更快的设计速度. 此外,工程设计过程通常须在优化结构的同时选择合适的材料. 当前研究往往将材料参数视为连续变量进行设计[20 ] ,但所设计的材料在真实世界可能并不存在,不具有实用性,目前鲜有研究者关注材料参数的离散性. 因此,亟须进一步探索新颖的超材料设计方法,以解决上述问题. ...
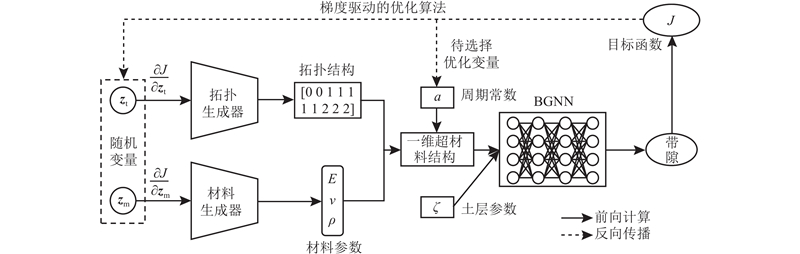
... 采用TensorFlow框架[33 ] ,利用tf.GradientTape API实现梯度信息获取. 在设计过程中,z t 、z m 作为设计变量,目标是找到最佳的材料参数和拓扑结构. 通过创建梯度带上下文,记录设计网络的前向计算过程,能够自动计算出目标函数相对于设计变量的梯度. 这些梯度信息可以被梯度优化算法有效利用,能够按照目标函数梯度下降的方向高效搜索设计空间[10 ] . Adam和BFGS算法[34 ] 是优化领域中常用的2种优化算法,具有极高的优化效率. 因此,本研究结合Adam算法与BFGS算法根据梯度信息迭代优化设计变量以最小化目标函数J ,其中Adam算法作为BFGS算法的暖启动,可以避免陷入局部最优. 整个优化设计过程如图6 所示,这种综合利用自动微分和优化算法的方法,能够在极短的时间内实现最佳设计. ...
... 指定带隙区间设计和约束条件下带隙宽度最大化是2种常见的超材料结构设计场景[10 ] . 然而,大多数研究都集中在根据地基环境振动频率进行指定带隙区间设计,但地铁系统可能会面临未来老化或地基变化的情况. 因此,对超材料结构在特定范围内进行带隙宽度最大化优化,可以使隔振结构在未来适应潜在的振动频率变化或新的振动需求,而无须重新布置新结构,这具有重要的工程意义. 为此,首先展示给定周期常数的约束条件下(a =0.5 m)低频一阶带隙宽度最大化设计,其目标函数定义如下: ...
... 本研究所用设计方法的平均时间约为4.5 s. 为了展示所提设计框架的优越性能,对比遗传算法分别结合数值计算[10 ] 和深度学习模型[25 ] 评估目标函数在工况3上的设计效率. 通过遗传算法在橡胶数据库和拓扑结构空间中进行随机搜索,找到最优结构和材料,结果如表3 所示. 其中,遗传算法所得到的最优结构与本研究方法得出的结果一致,均实现了108.9 Hz的带隙宽度,证明了本研究方法的可靠性. 其中,遗传算法结合传递矩阵法所用设计时间为7.8 h,设计低效耗时. 带隙神经网络的引入将评估时间减少了2个数量级,显著缩短了设计时间. 相较于遗传算法的随机搜索,本研究所提方法利用目标函数对设计变量的梯度信息,在梯度下降的方向上迭代更新解,从而进一步提高了设计效率,实现了更快的设计速度,达到了“端到端”设计模型的速度[20 ] . ...
Topology optimization of periodic pile barriers and its application in vibration reduction for plane waves
1
2022
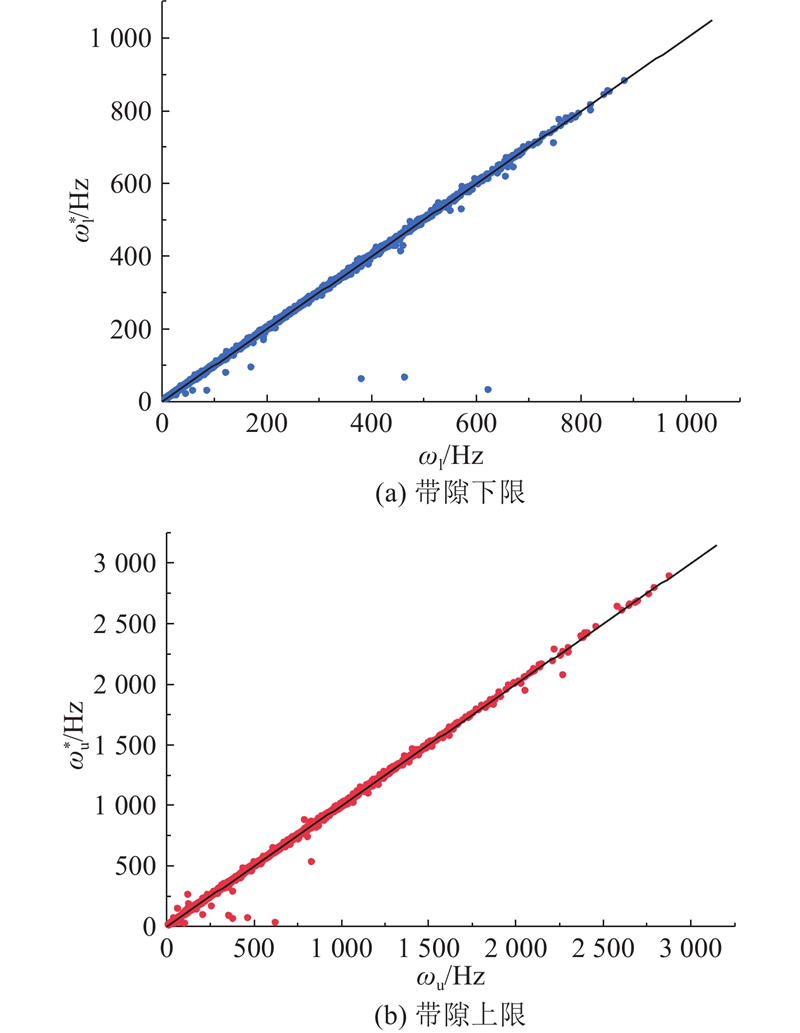
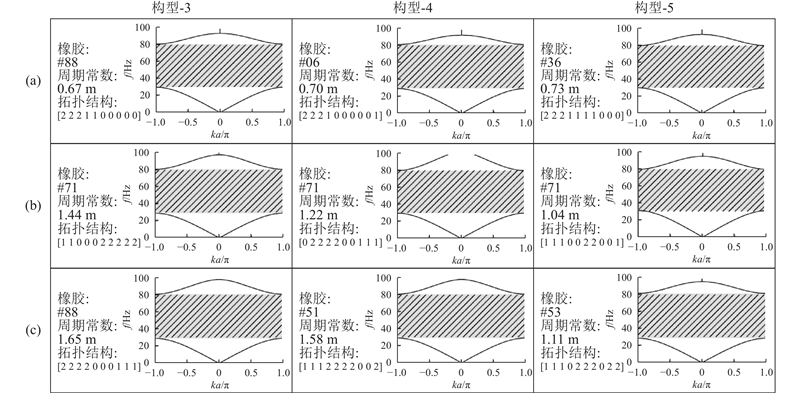
... 式中:$\omega _1^* $ $\omega _{\mathrm{u}}^* $ [12 ] 的研究,地铁引起的环境振动的主频率范围为30~80 Hz. 因此将目标带隙上下限分别设置为80、30 Hz. 为了实现指定带隙的精确设计,将周期常数也视为连续的设计变量. 如图9 所示,展示了在表4 中的3种不同场地条件下(软土、中硬土和硬土)设计所得到的结果,并考虑了不同的拓扑构型,其中,曲线为频散曲线,灰色区域和阴影区域分别代表所设计弹性超材料的实际带隙范围和设计带隙范围. 可以发现,这些设计结构的目标带隙和实际带隙上下限基本一致,并且设计材料都收敛到材料库中的真实材料,证明了所提方法的可靠性. 随着土层逐渐变硬,场地内弹性波的传播速度增大,导致波长变长. 因而隔振结构所需尺寸逐渐增大,这一现象在设计结果中得以体现. 另外,在图9 (b)中,3种构型在优化过程中均选择了#71橡胶作为最优材料. 可以观察到,随着结构分层数量的增加,周期常数也在逐渐降低. 具体而言,构型-5的周期常数相较于构型-3降低了约30%. 然而,结构内部土的体积分数随层数的增多在不断减少,从构型-3的50%减少至构型-5的20%. 这意味着构型-5在工程造价上的增加,但在土地资源紧张的情况下,它可能更具吸引力. 因此,构型的选择须综合考虑工程成本和土地资源. ...
Topology optimization of the periodic pile barrier with initial stresses arranged in rectangular and equilateral triangular lattices
1
2023
... 以往研究普遍采用参数分析法,调整参数以匹配特定需求,这完全依赖于研究者的经验,须反复对参数进行调整. 近十几年,拓扑优化方法作为典型设计方法被广泛运用,包括基于梯度的优化算法和无梯度的进化算法[10 -13 ] ,可以在设计过程中提供理论指导并节省了大量计算成本. 然而,这些方法依赖复杂的数值计算提供准确的预测,求解效率低且耗时[14 ] . 随着人工智能领域的快速发展,深度学习和结构设计的结合有效解决了上述设计方法过程繁琐、速度慢的问题,展现出高效、准确、智能的特点[15 -16 ] . Li等[17 ] 训练自动编码器和多层感知器,建立从带隙分布到拓扑图像的潜义向量的映射关系,实现二维声子晶体的逆向设计. Gurbuz等[18 ] 基于生成式对抗神经网络实现了二维声学超材料的快速设计. 曹蕾蕾等[19 ] 基于逻辑回归和多任务学习的深度学习模型设计一维声子晶体. Liu等[20 -22 ] 通过建立一个预训练的结构解码器和一个目标带隙编码器,组装形成设计模型,系统地研究了一维、二维布拉格超屏障以及局域共振超屏障的设计方法. ...
Generative model for the inverse design of metasurfaces
1
2018
... 以往研究普遍采用参数分析法,调整参数以匹配特定需求,这完全依赖于研究者的经验,须反复对参数进行调整. 近十几年,拓扑优化方法作为典型设计方法被广泛运用,包括基于梯度的优化算法和无梯度的进化算法[10 -13 ] ,可以在设计过程中提供理论指导并节省了大量计算成本. 然而,这些方法依赖复杂的数值计算提供准确的预测,求解效率低且耗时[14 ] . 随着人工智能领域的快速发展,深度学习和结构设计的结合有效解决了上述设计方法过程繁琐、速度慢的问题,展现出高效、准确、智能的特点[15 -16 ] . Li等[17 ] 训练自动编码器和多层感知器,建立从带隙分布到拓扑图像的潜义向量的映射关系,实现二维声子晶体的逆向设计. Gurbuz等[18 ] 基于生成式对抗神经网络实现了二维声学超材料的快速设计. 曹蕾蕾等[19 ] 基于逻辑回归和多任务学习的深度学习模型设计一维声子晶体. Liu等[20 -22 ] 通过建立一个预训练的结构解码器和一个目标带隙编码器,组装形成设计模型,系统地研究了一维、二维布拉格超屏障以及局域共振超屏障的设计方法. ...
基于智能算法的超材料快速优化设计方法研究进展
1
2021
... 以往研究普遍采用参数分析法,调整参数以匹配特定需求,这完全依赖于研究者的经验,须反复对参数进行调整. 近十几年,拓扑优化方法作为典型设计方法被广泛运用,包括基于梯度的优化算法和无梯度的进化算法[10 -13 ] ,可以在设计过程中提供理论指导并节省了大量计算成本. 然而,这些方法依赖复杂的数值计算提供准确的预测,求解效率低且耗时[14 ] . 随着人工智能领域的快速发展,深度学习和结构设计的结合有效解决了上述设计方法过程繁琐、速度慢的问题,展现出高效、准确、智能的特点[15 -16 ] . Li等[17 ] 训练自动编码器和多层感知器,建立从带隙分布到拓扑图像的潜义向量的映射关系,实现二维声子晶体的逆向设计. Gurbuz等[18 ] 基于生成式对抗神经网络实现了二维声学超材料的快速设计. 曹蕾蕾等[19 ] 基于逻辑回归和多任务学习的深度学习模型设计一维声子晶体. Liu等[20 -22 ] 通过建立一个预训练的结构解码器和一个目标带隙编码器,组装形成设计模型,系统地研究了一维、二维布拉格超屏障以及局域共振超屏障的设计方法. ...
基于智能算法的超材料快速优化设计方法研究进展
1
2021
... 以往研究普遍采用参数分析法,调整参数以匹配特定需求,这完全依赖于研究者的经验,须反复对参数进行调整. 近十几年,拓扑优化方法作为典型设计方法被广泛运用,包括基于梯度的优化算法和无梯度的进化算法[10 -13 ] ,可以在设计过程中提供理论指导并节省了大量计算成本. 然而,这些方法依赖复杂的数值计算提供准确的预测,求解效率低且耗时[14 ] . 随着人工智能领域的快速发展,深度学习和结构设计的结合有效解决了上述设计方法过程繁琐、速度慢的问题,展现出高效、准确、智能的特点[15 -16 ] . Li等[17 ] 训练自动编码器和多层感知器,建立从带隙分布到拓扑图像的潜义向量的映射关系,实现二维声子晶体的逆向设计. Gurbuz等[18 ] 基于生成式对抗神经网络实现了二维声学超材料的快速设计. 曹蕾蕾等[19 ] 基于逻辑回归和多任务学习的深度学习模型设计一维声子晶体. Liu等[20 -22 ] 通过建立一个预训练的结构解码器和一个目标带隙编码器,组装形成设计模型,系统地研究了一维、二维布拉格超屏障以及局域共振超屏障的设计方法. ...
Intelligent on-demand design of phononic metamaterials
1
2022
... 以往研究普遍采用参数分析法,调整参数以匹配特定需求,这完全依赖于研究者的经验,须反复对参数进行调整. 近十几年,拓扑优化方法作为典型设计方法被广泛运用,包括基于梯度的优化算法和无梯度的进化算法[10 -13 ] ,可以在设计过程中提供理论指导并节省了大量计算成本. 然而,这些方法依赖复杂的数值计算提供准确的预测,求解效率低且耗时[14 ] . 随着人工智能领域的快速发展,深度学习和结构设计的结合有效解决了上述设计方法过程繁琐、速度慢的问题,展现出高效、准确、智能的特点[15 -16 ] . Li等[17 ] 训练自动编码器和多层感知器,建立从带隙分布到拓扑图像的潜义向量的映射关系,实现二维声子晶体的逆向设计. Gurbuz等[18 ] 基于生成式对抗神经网络实现了二维声学超材料的快速设计. 曹蕾蕾等[19 ] 基于逻辑回归和多任务学习的深度学习模型设计一维声子晶体. Liu等[20 -22 ] 通过建立一个预训练的结构解码器和一个目标带隙编码器,组装形成设计模型,系统地研究了一维、二维布拉格超屏障以及局域共振超屏障的设计方法. ...
Designing phononic crystal with anticipated band gap through a deep learning based data-driven method
1
2020
... 以往研究普遍采用参数分析法,调整参数以匹配特定需求,这完全依赖于研究者的经验,须反复对参数进行调整. 近十几年,拓扑优化方法作为典型设计方法被广泛运用,包括基于梯度的优化算法和无梯度的进化算法[10 -13 ] ,可以在设计过程中提供理论指导并节省了大量计算成本. 然而,这些方法依赖复杂的数值计算提供准确的预测,求解效率低且耗时[14 ] . 随着人工智能领域的快速发展,深度学习和结构设计的结合有效解决了上述设计方法过程繁琐、速度慢的问题,展现出高效、准确、智能的特点[15 -16 ] . Li等[17 ] 训练自动编码器和多层感知器,建立从带隙分布到拓扑图像的潜义向量的映射关系,实现二维声子晶体的逆向设计. Gurbuz等[18 ] 基于生成式对抗神经网络实现了二维声学超材料的快速设计. 曹蕾蕾等[19 ] 基于逻辑回归和多任务学习的深度学习模型设计一维声子晶体. Liu等[20 -22 ] 通过建立一个预训练的结构解码器和一个目标带隙编码器,组装形成设计模型,系统地研究了一维、二维布拉格超屏障以及局域共振超屏障的设计方法. ...
Generative adversarial networks for the design of acoustic metamaterials
1
2021
... 以往研究普遍采用参数分析法,调整参数以匹配特定需求,这完全依赖于研究者的经验,须反复对参数进行调整. 近十几年,拓扑优化方法作为典型设计方法被广泛运用,包括基于梯度的优化算法和无梯度的进化算法[10 -13 ] ,可以在设计过程中提供理论指导并节省了大量计算成本. 然而,这些方法依赖复杂的数值计算提供准确的预测,求解效率低且耗时[14 ] . 随着人工智能领域的快速发展,深度学习和结构设计的结合有效解决了上述设计方法过程繁琐、速度慢的问题,展现出高效、准确、智能的特点[15 -16 ] . Li等[17 ] 训练自动编码器和多层感知器,建立从带隙分布到拓扑图像的潜义向量的映射关系,实现二维声子晶体的逆向设计. Gurbuz等[18 ] 基于生成式对抗神经网络实现了二维声学超材料的快速设计. 曹蕾蕾等[19 ] 基于逻辑回归和多任务学习的深度学习模型设计一维声子晶体. Liu等[20 -22 ] 通过建立一个预训练的结构解码器和一个目标带隙编码器,组装形成设计模型,系统地研究了一维、二维布拉格超屏障以及局域共振超屏障的设计方法. ...
基于人工神经网络的声子晶体逆向设计
2
2021
... 以往研究普遍采用参数分析法,调整参数以匹配特定需求,这完全依赖于研究者的经验,须反复对参数进行调整. 近十几年,拓扑优化方法作为典型设计方法被广泛运用,包括基于梯度的优化算法和无梯度的进化算法[10 -13 ] ,可以在设计过程中提供理论指导并节省了大量计算成本. 然而,这些方法依赖复杂的数值计算提供准确的预测,求解效率低且耗时[14 ] . 随着人工智能领域的快速发展,深度学习和结构设计的结合有效解决了上述设计方法过程繁琐、速度慢的问题,展现出高效、准确、智能的特点[15 -16 ] . Li等[17 ] 训练自动编码器和多层感知器,建立从带隙分布到拓扑图像的潜义向量的映射关系,实现二维声子晶体的逆向设计. Gurbuz等[18 ] 基于生成式对抗神经网络实现了二维声学超材料的快速设计. 曹蕾蕾等[19 ] 基于逻辑回归和多任务学习的深度学习模型设计一维声子晶体. Liu等[20 -22 ] 通过建立一个预训练的结构解码器和一个目标带隙编码器,组装形成设计模型,系统地研究了一维、二维布拉格超屏障以及局域共振超屏障的设计方法. ...
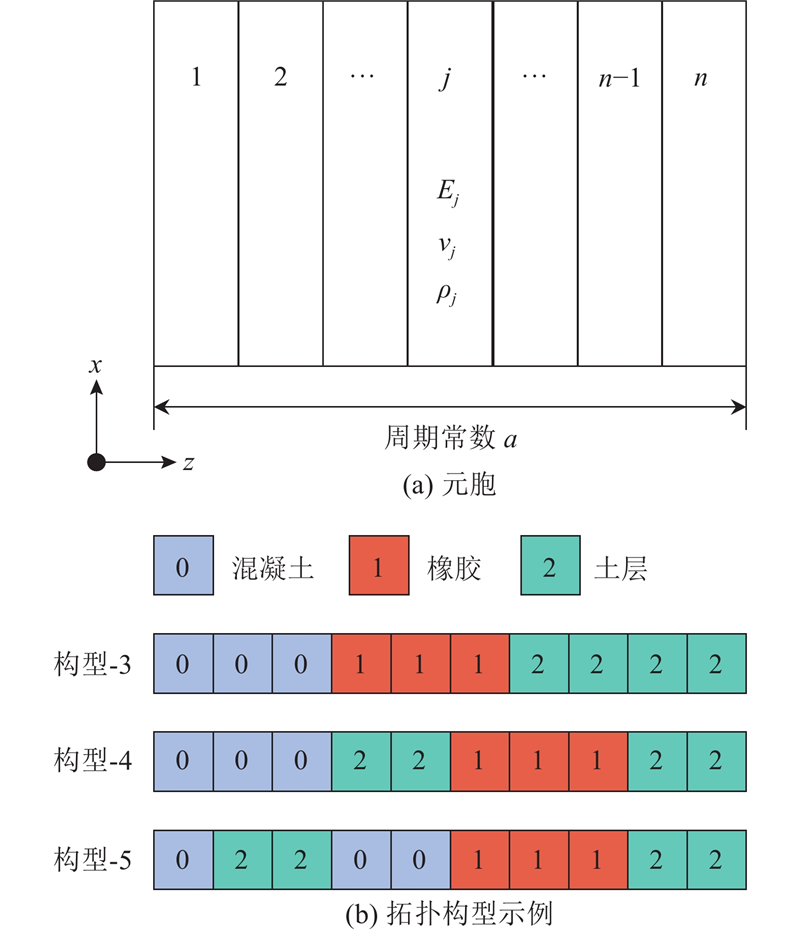
... 考虑将混凝土、橡胶和原位土组成的弹性超材料埋置在地基中,用于隔绝地基中传递的环境振动. 构建3组数据集以训练后续的VAE和BGNN. 首先,为了使设计结构具有丰富的多样性,参考文献[19 ]将周期常数为a 的元胞沿着周期方向离散成10等份,通过填入混凝土、橡胶和原位土形成不同的拓扑结构,并以0、1、2进行数字化表示. 为了简化,仅考虑如图1 (b)所示的3类不同拓扑构型,其中构型后的数字表示元胞的结构层数. 通过随机程序产生大量元胞结构,作为拓扑数据集以训练拓扑生成器. 另外,收集5种常用混凝土和100种工程橡胶的材料参数,构建材料数据库(部分数据如表1 所示),用于训练材料生成器. 这一类模型属于无监督学习,无需标签数据. 最后,采用训练好的拓扑构型和材料生成器生成大量的样本,并进行随机组合形成超材料结构. 采用传递矩阵法计算相应的频散曲线,提取一阶带隙上下限作为标签,作为物理数据集为BGNN的训练和测试提供样本. ...
基于人工神经网络的声子晶体逆向设计
2
2021
... 以往研究普遍采用参数分析法,调整参数以匹配特定需求,这完全依赖于研究者的经验,须反复对参数进行调整. 近十几年,拓扑优化方法作为典型设计方法被广泛运用,包括基于梯度的优化算法和无梯度的进化算法[10 -13 ] ,可以在设计过程中提供理论指导并节省了大量计算成本. 然而,这些方法依赖复杂的数值计算提供准确的预测,求解效率低且耗时[14 ] . 随着人工智能领域的快速发展,深度学习和结构设计的结合有效解决了上述设计方法过程繁琐、速度慢的问题,展现出高效、准确、智能的特点[15 -16 ] . Li等[17 ] 训练自动编码器和多层感知器,建立从带隙分布到拓扑图像的潜义向量的映射关系,实现二维声子晶体的逆向设计. Gurbuz等[18 ] 基于生成式对抗神经网络实现了二维声学超材料的快速设计. 曹蕾蕾等[19 ] 基于逻辑回归和多任务学习的深度学习模型设计一维声子晶体. Liu等[20 -22 ] 通过建立一个预训练的结构解码器和一个目标带隙编码器,组装形成设计模型,系统地研究了一维、二维布拉格超屏障以及局域共振超屏障的设计方法. ...
... 考虑将混凝土、橡胶和原位土组成的弹性超材料埋置在地基中,用于隔绝地基中传递的环境振动. 构建3组数据集以训练后续的VAE和BGNN. 首先,为了使设计结构具有丰富的多样性,参考文献[19 ]将周期常数为a 的元胞沿着周期方向离散成10等份,通过填入混凝土、橡胶和原位土形成不同的拓扑结构,并以0、1、2进行数字化表示. 为了简化,仅考虑如图1 (b)所示的3类不同拓扑构型,其中构型后的数字表示元胞的结构层数. 通过随机程序产生大量元胞结构,作为拓扑数据集以训练拓扑生成器. 另外,收集5种常用混凝土和100种工程橡胶的材料参数,构建材料数据库(部分数据如表1 所示),用于训练材料生成器. 这一类模型属于无监督学习,无需标签数据. 最后,采用训练好的拓扑构型和材料生成器生成大量的样本,并进行随机组合形成超材料结构. 采用传递矩阵法计算相应的频散曲线,提取一阶带隙上下限作为标签,作为物理数据集为BGNN的训练和测试提供样本. ...
Intelligent design of engineered metabarrier based on deep learning
3
2022
... 以往研究普遍采用参数分析法,调整参数以匹配特定需求,这完全依赖于研究者的经验,须反复对参数进行调整. 近十几年,拓扑优化方法作为典型设计方法被广泛运用,包括基于梯度的优化算法和无梯度的进化算法[10 -13 ] ,可以在设计过程中提供理论指导并节省了大量计算成本. 然而,这些方法依赖复杂的数值计算提供准确的预测,求解效率低且耗时[14 ] . 随着人工智能领域的快速发展,深度学习和结构设计的结合有效解决了上述设计方法过程繁琐、速度慢的问题,展现出高效、准确、智能的特点[15 -16 ] . Li等[17 ] 训练自动编码器和多层感知器,建立从带隙分布到拓扑图像的潜义向量的映射关系,实现二维声子晶体的逆向设计. Gurbuz等[18 ] 基于生成式对抗神经网络实现了二维声学超材料的快速设计. 曹蕾蕾等[19 ] 基于逻辑回归和多任务学习的深度学习模型设计一维声子晶体. Liu等[20 -22 ] 通过建立一个预训练的结构解码器和一个目标带隙编码器,组装形成设计模型,系统地研究了一维、二维布拉格超屏障以及局域共振超屏障的设计方法. ...
... 以上研究展示了深度学习在超材料设计中的适用性和高效性. 这些研究通过各种巧妙方式建立目标带隙到设计结构的“端到端”映射关系,将设计时间压缩至秒级水平[23 ] . 然而,这些权重确定的映射关系无法表征寻优的迭代过程,局限于指定带隙区间的设计中,无法扩展到其他的设计场景,如约束条件下的带隙最大化设计[10 ] . 因此,与遗传算法结合深度学习模型评估目标函数的迭代方法相比,其灵活性和通用性较差[24 -26 ] . 尽管遗传算法(genetic algorithm, GA)能够在设计空间中进行迭代优化,但是其本质上属于随机搜索,设计效率较低,同时忽略了深度学习模型中所蕴含的梯度信息. 而这些信息可以被更高效的梯度优化算法加以利用,实现更快的设计速度. 此外,工程设计过程通常须在优化结构的同时选择合适的材料. 当前研究往往将材料参数视为连续变量进行设计[20 ] ,但所设计的材料在真实世界可能并不存在,不具有实用性,目前鲜有研究者关注材料参数的离散性. 因此,亟须进一步探索新颖的超材料设计方法,以解决上述问题. ...
... 本研究所用设计方法的平均时间约为4.5 s. 为了展示所提设计框架的优越性能,对比遗传算法分别结合数值计算[10 ] 和深度学习模型[25 ] 评估目标函数在工况3上的设计效率. 通过遗传算法在橡胶数据库和拓扑结构空间中进行随机搜索,找到最优结构和材料,结果如表3 所示. 其中,遗传算法所得到的最优结构与本研究方法得出的结果一致,均实现了108.9 Hz的带隙宽度,证明了本研究方法的可靠性. 其中,遗传算法结合传递矩阵法所用设计时间为7.8 h,设计低效耗时. 带隙神经网络的引入将评估时间减少了2个数量级,显著缩短了设计时间. 相较于遗传算法的随机搜索,本研究所提方法利用目标函数对设计变量的梯度信息,在梯度下降的方向上迭代更新解,从而进一步提高了设计效率,实现了更快的设计速度,达到了“端到端”设计模型的速度[20 ] . ...
Inverse design of locally resonant metabarrier by deep learning with a rule-based topology dataset
0
2022
Deep learning-based topology design of periodic barrier for full-mode waves
1
2022
... 以往研究普遍采用参数分析法,调整参数以匹配特定需求,这完全依赖于研究者的经验,须反复对参数进行调整. 近十几年,拓扑优化方法作为典型设计方法被广泛运用,包括基于梯度的优化算法和无梯度的进化算法[10 -13 ] ,可以在设计过程中提供理论指导并节省了大量计算成本. 然而,这些方法依赖复杂的数值计算提供准确的预测,求解效率低且耗时[14 ] . 随着人工智能领域的快速发展,深度学习和结构设计的结合有效解决了上述设计方法过程繁琐、速度慢的问题,展现出高效、准确、智能的特点[15 -16 ] . Li等[17 ] 训练自动编码器和多层感知器,建立从带隙分布到拓扑图像的潜义向量的映射关系,实现二维声子晶体的逆向设计. Gurbuz等[18 ] 基于生成式对抗神经网络实现了二维声学超材料的快速设计. 曹蕾蕾等[19 ] 基于逻辑回归和多任务学习的深度学习模型设计一维声子晶体. Liu等[20 -22 ] 通过建立一个预训练的结构解码器和一个目标带隙编码器,组装形成设计模型,系统地研究了一维、二维布拉格超屏障以及局域共振超屏障的设计方法. ...
Training deep neural networks for the inverse design of nanophotonic structures
1
2018
... 以上研究展示了深度学习在超材料设计中的适用性和高效性. 这些研究通过各种巧妙方式建立目标带隙到设计结构的“端到端”映射关系,将设计时间压缩至秒级水平[23 ] . 然而,这些权重确定的映射关系无法表征寻优的迭代过程,局限于指定带隙区间的设计中,无法扩展到其他的设计场景,如约束条件下的带隙最大化设计[10 ] . 因此,与遗传算法结合深度学习模型评估目标函数的迭代方法相比,其灵活性和通用性较差[24 -26 ] . 尽管遗传算法(genetic algorithm, GA)能够在设计空间中进行迭代优化,但是其本质上属于随机搜索,设计效率较低,同时忽略了深度学习模型中所蕴含的梯度信息. 而这些信息可以被更高效的梯度优化算法加以利用,实现更快的设计速度. 此外,工程设计过程通常须在优化结构的同时选择合适的材料. 当前研究往往将材料参数视为连续变量进行设计[20 ] ,但所设计的材料在真实世界可能并不存在,不具有实用性,目前鲜有研究者关注材料参数的离散性. 因此,亟须进一步探索新颖的超材料设计方法,以解决上述问题. ...
Prediction and optimization of mechanical properties of composites using convolutional neural networks
1
2019
... 以上研究展示了深度学习在超材料设计中的适用性和高效性. 这些研究通过各种巧妙方式建立目标带隙到设计结构的“端到端”映射关系,将设计时间压缩至秒级水平[23 ] . 然而,这些权重确定的映射关系无法表征寻优的迭代过程,局限于指定带隙区间的设计中,无法扩展到其他的设计场景,如约束条件下的带隙最大化设计[10 ] . 因此,与遗传算法结合深度学习模型评估目标函数的迭代方法相比,其灵活性和通用性较差[24 -26 ] . 尽管遗传算法(genetic algorithm, GA)能够在设计空间中进行迭代优化,但是其本质上属于随机搜索,设计效率较低,同时忽略了深度学习模型中所蕴含的梯度信息. 而这些信息可以被更高效的梯度优化算法加以利用,实现更快的设计速度. 此外,工程设计过程通常须在优化结构的同时选择合适的材料. 当前研究往往将材料参数视为连续变量进行设计[20 ] ,但所设计的材料在真实世界可能并不存在,不具有实用性,目前鲜有研究者关注材料参数的离散性. 因此,亟须进一步探索新颖的超材料设计方法,以解决上述问题. ...
A method for optimal design of automotive body assembly using multi-material construction
1
2008
... 本研究所用设计方法的平均时间约为4.5 s. 为了展示所提设计框架的优越性能,对比遗传算法分别结合数值计算[10 ] 和深度学习模型[25 ] 评估目标函数在工况3上的设计效率. 通过遗传算法在橡胶数据库和拓扑结构空间中进行随机搜索,找到最优结构和材料,结果如表3 所示. 其中,遗传算法所得到的最优结构与本研究方法得出的结果一致,均实现了108.9 Hz的带隙宽度,证明了本研究方法的可靠性. 其中,遗传算法结合传递矩阵法所用设计时间为7.8 h,设计低效耗时. 带隙神经网络的引入将评估时间减少了2个数量级,显著缩短了设计时间. 相较于遗传算法的随机搜索,本研究所提方法利用目标函数对设计变量的梯度信息,在梯度下降的方向上迭代更新解,从而进一步提高了设计效率,实现了更快的设计速度,达到了“端到端”设计模型的速度[20 ] . ...
Optimal design of one-dimensional elastic metamaterials through deep convolutional neural network and genetic algorithm
1
2023
... 以上研究展示了深度学习在超材料设计中的适用性和高效性. 这些研究通过各种巧妙方式建立目标带隙到设计结构的“端到端”映射关系,将设计时间压缩至秒级水平[23 ] . 然而,这些权重确定的映射关系无法表征寻优的迭代过程,局限于指定带隙区间的设计中,无法扩展到其他的设计场景,如约束条件下的带隙最大化设计[10 ] . 因此,与遗传算法结合深度学习模型评估目标函数的迭代方法相比,其灵活性和通用性较差[24 -26 ] . 尽管遗传算法(genetic algorithm, GA)能够在设计空间中进行迭代优化,但是其本质上属于随机搜索,设计效率较低,同时忽略了深度学习模型中所蕴含的梯度信息. 而这些信息可以被更高效的梯度优化算法加以利用,实现更快的设计速度. 此外,工程设计过程通常须在优化结构的同时选择合适的材料. 当前研究往往将材料参数视为连续变量进行设计[20 ] ,但所设计的材料在真实世界可能并不存在,不具有实用性,目前鲜有研究者关注材料参数的离散性. 因此,亟须进一步探索新颖的超材料设计方法,以解决上述问题. ...
2
... 如图1 (a)所示,一维弹性超材料是由沿某个方向周期性分布的元胞组成的. 假定每层材料在x-y 平面上无限大,并且每层材料都是各向同性的均质弹性材料,E j ν j ρ j j 层材料的弹性模量、泊松比和密度. 对于在结构中沿着z 方向传播的P波,其控制方程表达式[27 ] 如下: ...
... 式中:ω u 和ω l 分别代表一阶带隙的上下限;ω thre 为带隙上限的限值,在本研究中设置为150 Hz;C 为宽带和低频2个目标之间的平衡因子,取C =10000 . 由于混凝土材料参数对带隙影响较小[27 ] ,采用C30混凝土;地基土参数为E s = 50 MPa, ρ s = 1800 kg/m3 , ν s = 0.35. 此外,为了比较材料和结构同步优化与单独优化性能,设置了以下3组工况: ...
Transverse elastic-waves in periodically layered infinite, semi-infinite, and slab media
1
1983
... 式中:a 为周期常数;k 为波数,k =ω/c . 采用传递矩阵法(transfer matrix method, TMM)[28 ] 求解式(2)、(3),将其转化为特征方程进行求解,表达式如下: ...
Interactive inverse design of layered phononic crystals based on reinforcement learning
1
2020
... 式中:T T T n T n− 1···T 1 ,I T j 29 ],其表达式为 ...
1
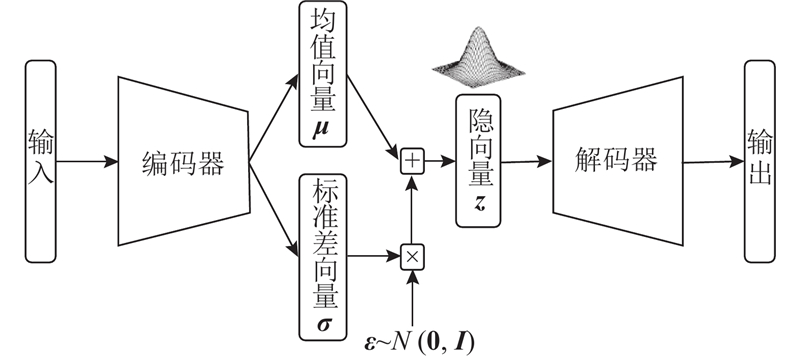
... 变分自动编码器(VAE)是一种生成模型[30 ] ,用于学习数据的潜在表示和生成新的样本. 它在自编码器降维重建的基础上引入了概率推断的思想,可以学习数据分布的潜在结构. 如图2 所示,它假设潜在空间中的数据服从高斯分布,并利用编码器将输入数据映射到潜在空间中的均值和方差参数. 然后,从这个潜在空间中的分布中随机采样得到编码. 解码器将这个编码映射回原始数据空间,生成重建的样本. 其损失函数可以表示为 ...
1
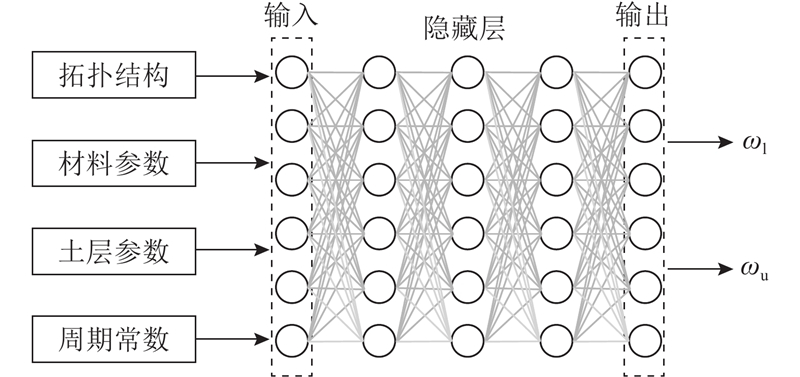
... 采用多分类模型来构建拓扑生成器,由[1, 0, 0]、[0, 1, 0]和[0, 0, 1]分别表示类别为0、1和2的材料. 将其解码器的最后一层输出传递给Softmax层,并基于多分类交叉熵计算与输入数据的重建损失. 为了有效表征拓扑结构,并且学习数据的潜在分布,将编码维度设置为8,以储存相关信息. 整个模型在包含30万组样本的拓扑数据集上进行训练,并使用Adam优化器[31 ] 最小化损失函数,训练过程如图3 (a)所示. 图中,S 为迭代步,KLD为KL散度提取解码器作为拓扑生成器,从标准正态空间中采样z t ~$ {{N}}$ ( 0 , 1 .0 ),可以合成与训练数据类似的拓扑结构. 另外,不同于拓扑生成器,材料生成器采用回归模型进行构建,使用均方误差计算重建损失. 材料生成器目标不在于合成新的数据,而是在潜在空间中利用2个连续变量{z m1 , z m2 }来表征材料参数,获取材料参数的潜在信息. 在材料数据库上同样使用Adam优化器对其进行训练,直至满足误差要求,如图3 (b)所示. ...
1
... 式中:G t 、G m 和F 分别表示拓扑结构生成器、材料生成器和BGNN的映射函数,z t 、z m 分别为拓扑结构和材料参数的潜义变量. 整个设计网络通过神经元之间连接和激活函数的非线性变换,将输入有效地转化为输出. 这意味着它具有可微性,在可微分的编程框架中通过自动微分技术[32 ] 能够计算目标函数对设计变量变化的灵敏度. 例如,目标函数J 对于设计变量z t 的微分可以表示为 ...
1
... 采用TensorFlow框架[33 ] ,利用tf.GradientTape API实现梯度信息获取. 在设计过程中,z t 、z m 作为设计变量,目标是找到最佳的材料参数和拓扑结构. 通过创建梯度带上下文,记录设计网络的前向计算过程,能够自动计算出目标函数相对于设计变量的梯度. 这些梯度信息可以被梯度优化算法有效利用,能够按照目标函数梯度下降的方向高效搜索设计空间[10 ] . Adam和BFGS算法[34 ] 是优化领域中常用的2种优化算法,具有极高的优化效率. 因此,本研究结合Adam算法与BFGS算法根据梯度信息迭代优化设计变量以最小化目标函数J ,其中Adam算法作为BFGS算法的暖启动,可以避免陷入局部最优. 整个优化设计过程如图6 所示,这种综合利用自动微分和优化算法的方法,能够在极短的时间内实现最佳设计. ...
An overview of stochastic quasi-newton methods for large-scale machine learning
2
2023
... 采用TensorFlow框架[33 ] ,利用tf.GradientTape API实现梯度信息获取. 在设计过程中,z t 、z m 作为设计变量,目标是找到最佳的材料参数和拓扑结构. 通过创建梯度带上下文,记录设计网络的前向计算过程,能够自动计算出目标函数相对于设计变量的梯度. 这些梯度信息可以被梯度优化算法有效利用,能够按照目标函数梯度下降的方向高效搜索设计空间[10 ] . Adam和BFGS算法[34 ] 是优化领域中常用的2种优化算法,具有极高的优化效率. 因此,本研究结合Adam算法与BFGS算法根据梯度信息迭代优化设计变量以最小化目标函数J ,其中Adam算法作为BFGS算法的暖启动,可以避免陷入局部最优. 整个优化设计过程如图6 所示,这种综合利用自动微分和优化算法的方法,能够在极短的时间内实现最佳设计. ...
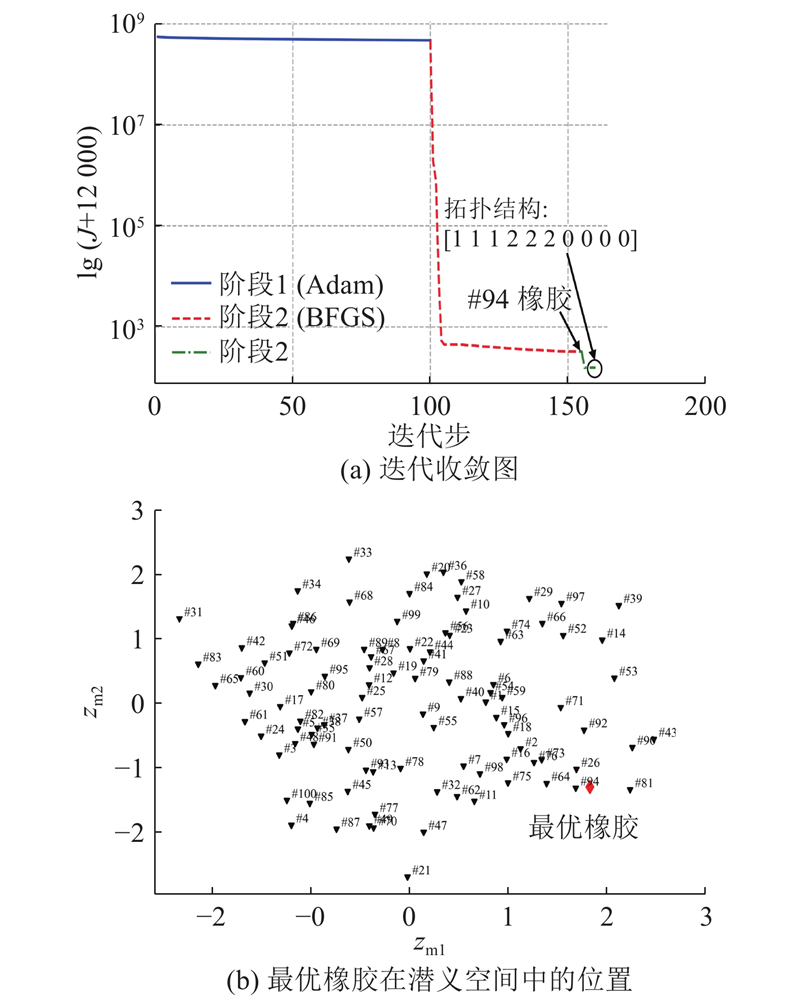
... 上述3种工况的优化结果如表3 所示. 表中,t d 为设计时间. 其中,工况1的带隙宽度为86.1 Hz,这是由于尚未对拓扑结构进行优化,材料分布不合理,导致其带隙宽度最小. 在工况2中,基于工况1的优化基础,对拓扑结构进行优化,使带隙宽度增加至91.1 Hz,性能略有提升. 在工况3中,同时对材料参数和拓扑结构进行优化,实现了最佳的优化性能,带隙宽度达到108.9 Hz. 工况3选择的橡胶材料与工况1并不同,因此通过同步优化拓扑结构和材料选择,能够有效产生最优解. 如图8 (a)所示,展示了工况3的迭代收敛图. 在迭代的过程中,采用Adam优化算法进行起始优化,为 BFGS算法提供良好的起始点,加速收敛并降低局部优化的可能性[34 ] . 其中,第1阶段优化后的橡胶材料参数在潜义空间{z m1 , z m2 }中的位置如图8 (b)所示. 可以看到,所优化的橡胶材料参数并不属于材料库中的任意材料,无法直接应用在实际工程中. 因此在第2阶段中,通过协同优化策略在材料库中选择置信度最高的#94橡胶作为最优材料,而后对拓扑结构进行进一步的微调,最终获得可行的最优方案. ...
Simultaneous material selection and geometry design of statically determinate trusses using continuous optimization
1
2007
... 梯度优化方法难以处理离散的设计变量,常用的方式是对材料和结构参数进行单独优化[35 ] . 然而,由于结构和材料的相互影响,难以找到最优解,设计效率较低. 为此,本研究提出拓扑结构和材料参数协同优化策略,以实现材料和结构的同步优化. 具体而言,将设计流程分为2个阶段,如图7 所示.图中,$ \Delta {\boldsymbol{z}} $ z z m 进行表征,使得梯度优化算法可以处理材料参数. 因此,在阶段1中采用优化算法在设计网络上对拓扑结构和材料参数2组潜义变量同时进行优化,直至迭代过程收敛,得到最佳材料潜义向量${\boldsymbol{z}}_{\mathrm{m}}^* $ . 为了使得优化材料能够收敛为材料库中的真实材料,定义了材料库中各真实材料的置信度以供选择,其表达式如下: ...