室内空间安全评估是在建筑的设计阶段对基础设施进行安全分析和优化, 可以避免事后高昂的额外成本. 紧急情况下的人群疏散, 不仅依赖于人群内在的自组织、外界的安全引导, 还与物理场景中的室内建筑布局有关. 在危险发生时, 室内布局的不合理性将加剧人群对安全逃生路线的选择困难度, 同时还会引发人群拥挤现象. 在设计阶段前期,建筑设计单位对室内空间布局进行安全评估, 可以极大提升建筑空间的人群应对危险的能力; 在设计阶段后期,建筑设计单位对该空间和其中的安全设施(如灭火器、防火门)进行人群仿真模拟, 可以进一步帮助人群对危险进行提前预防.
在室内建筑空间的建模任务中,布局合理性评估是一个十分重要的环节. 一般室内仿真仅仅针对一个较小的室内空间进行建模, 构建有限数量的出口进行人群观察[1]. 然而, 真实世界中的建筑在水平平面结构和垂直层级结构上都有一定的复杂性. 对单一室内空间进行人群仿真无法反映出人群疏散的真实情况, 也无法对整体建筑布局提出优化, 更无法在整体建筑上对人群疏散的合理性和安全性提出有效建议,如最优疏散路径. 现有的室内空间安全性评估方法主要考虑路线上的危险源和动态规划路线. 本研究考虑路线选择多样性、通行率因素,使得模型能够定位疏散时的拥堵节点,并确认拥堵程度. 因此, 通过对室内空间进行建模, 并在此基础上进行合理性评估, 对人群疏散和未知危险的预防至关重要. 本研究提出室内空间安全性评估方法, 从室内空间的布局合理性入手, 在建筑的初期就对其进行合理性评估, 以增加建筑的容错性.
本研究的贡献可归纳如下:1)提出面向自组织人群的建筑安全评估方法,从空间布局角度, 在建筑设计阶段提升建筑的安全性;2)提出安全疏散路线选择算法, 对单元空间的风险、通行率进行评估,获得安全通行路线;3)实现面向建筑物水平平面结构和垂直层级结构的计算机语言抽象和表达.
1. 相关工作
1.1. 人群建模方法
传统的人群仿真模型有社会力模型(social force model ,SFM) [2]、速度障碍模型(velocity obstacle,VM) [3]和元胞自动机模型(cellular automata,CA). 3种模型自提出后, 一直是人群仿真领域的研究热点. Wu等[4]提出基于行为异质性社会力模型的人群疏散建模;Makmul[5]研究烟雾扩散对行人运动影响的社会力模型;Snape等[6]提出混合反速度障碍模型;Gonon等[7]研究了加速障碍这一概念,通过线性约束来接近其边界,并在模拟的双向人群流动中进行评估. Wang等[8] 将模糊逻辑与经典元胞自动机模型相结合,建立新的进化推理模型.
1.2. 室内空间安全性评估及相关工作
1.3. 空间建模方法
CityGML(geography markup language)[15]是基于OGC(open geospatial consortium)[16]标准的城市建模语言, 主要用于城市建模和地理定位服务. Konde等[17]根据目前CityGML 3.0的建议, 提出室内LoD0的多个变体, 讨论了CityGML中楼层平面图的建模. Li等[18]在CityGML基础上定义了IndoorGML, 用于表示室内建筑空间模型. Diakité等[19]在此基础上进行了细分: 可通行空间单元、不可通行空间单元和导航图. Alattas等[20]联合使用IndoorGML和土地管理领域模型, 根据建筑物的类型和空间功能创建室内空间用户与空间的关系. Kim等[21]提出用于室内空间分区的多阶段框架, 每个阶段都可以根据目标应用程序来灵活调整, 该框架的主要特征之一是参数化约束.
1.4. 室内安全评估和人群仿真系统及相关工作
2. 建筑安全评估总体架构
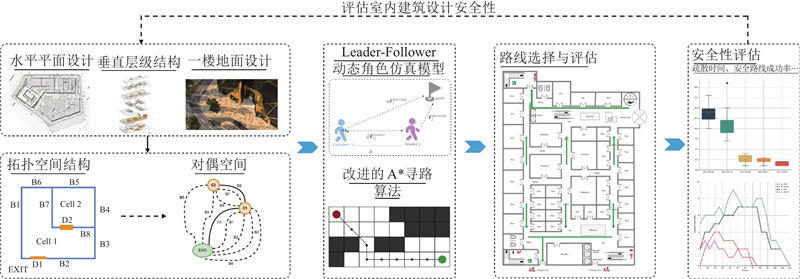
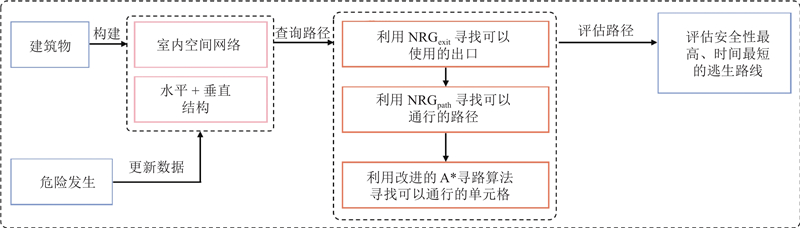
在相关室内安全设计研究的基础上, 本研究首先设计了新的室内网络模型, 利用室内建筑的位置和连接关系将建筑空间抽象为立体的网络图, 可以清晰描述室内建筑的水平平面结构和垂直层级结构. 然后,将室内拓扑空间结构映射到对偶空间, 实现室内建筑元素节点化, 用于人群仿真安全出口和安全逃生路线的查找. 接着,利用改进的A*算法寻找安全逃生路线; 通过定义安全单元空间,进一步筛选安全逃生路线. 最后,进行紧急情况下的人群仿真, 分析室内空间结构的不合理性, 并提出相应的改进方法. 本研究的安全评估整体流程图如图1所示.
图 1
实验分别在单层引发火灾,观察并记录人群逃生情况. 通过分析人群对安全逃生路线的选择情况、安全逃生路线的平均逃生时间情况、单条逃生路线上各个节点的时间占比和拥堵情况,可以得出水平平面结构中不合理的建筑节点. 比如在实验结果中,R12→D116路径中d102拥堵系数为10,这使得疏散效率降低,可以认为d102是不合理的节点. 研究发现,研究发现通过对不合理的建筑节点进行适当的调整,可以改善节点和整体布局,减少拥堵情况并提高路线选择弹性,较好地改善疏散效率.
3. 多层建筑物的空间表示
基于IndoorGML室内空间建模方法, 设计建筑场景下建筑物体的语义和几何表示;构建对象之间的连接关系;利用Poincaré对偶性将室内空间转换为拓扑空间中的节点关联图(node-relation graph, NRG), 建立室内空间的网络关系. 这样,通过对室内建筑进行多级抽象, 建立起各个建筑之间的关联关系, 并使用UML进行表示.
3.1. 室内空间安全性评估及相关工作
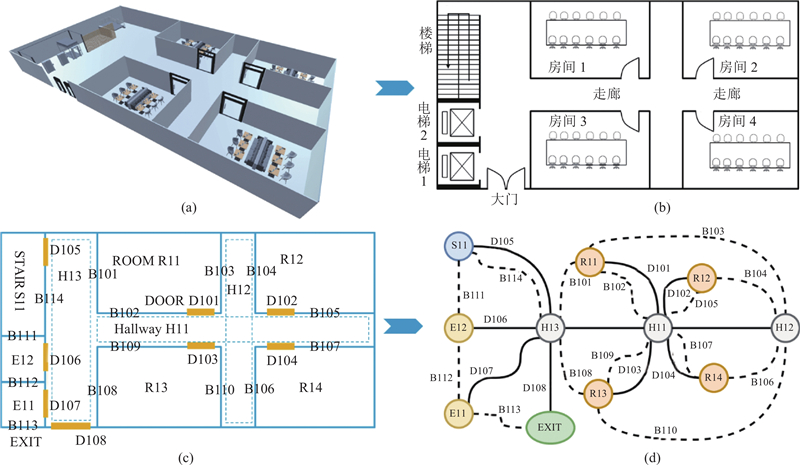
图 2
图 2 室内空间结构映射到对偶空间的过程
Fig.2 Process of mapping indoor space structure to dual space
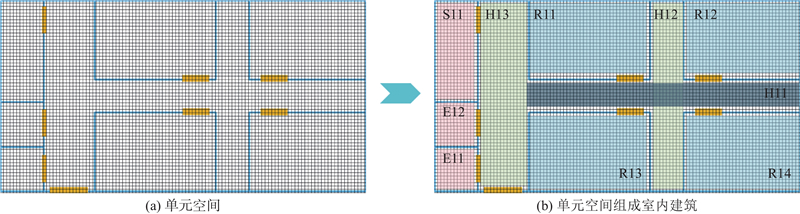
图 3
图 3 单元空间分割并组合为室内建筑区域的过程
Fig.3 Process of dividing and combining unit spaces into indoor building areas
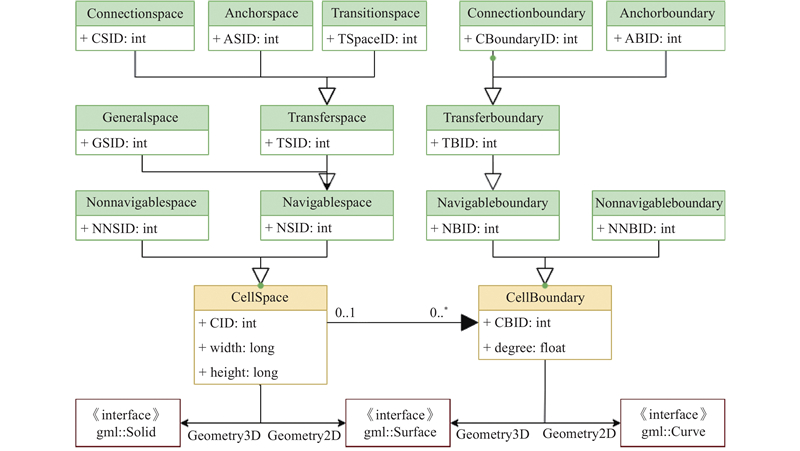
IndoorGML标准定义了建筑对象的几何关系、语义关系和连接关系, 抽象的UML类图如图4所示. CellSpace是最重要的基类, 表示单元空间, 它包含了基础的几何属性和位置信息, 以及附加信息(如语义解释、分类). 该标准对CellSpace和CellBoundary进行了属性补充, 以满足紧急情况下室内导航的需求. 其中, 单元空间CellSpace除了包含宽、高、面积等基础属性外, 还包含单元空间风险阈值、单元空间通行率这些内容.
图 4
3.2. 水平平面结构和垂直层级结构
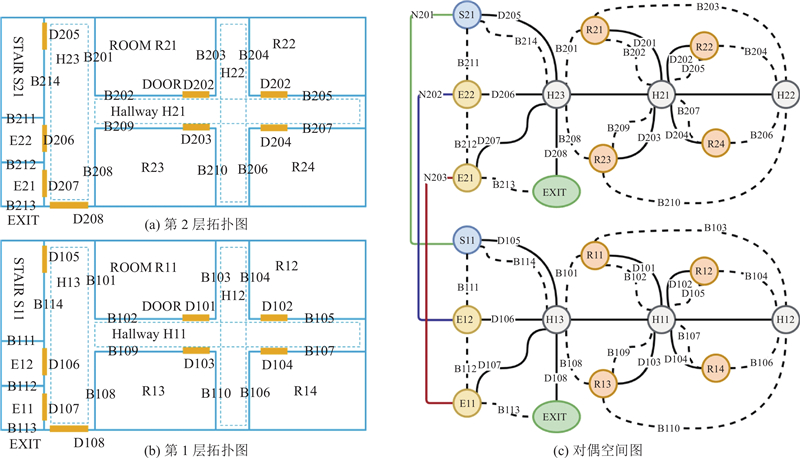
从建筑的水平平面结构和垂直层级结构2个层次, 分析室内建筑对人群疏散的影响. 对于大型商场、博览会, 楼层层级不高, 在发生危险时, 室内平面结构构成主要因素;对于高层居民楼, 垂直层级结构对人群逃生的影响程度更高. 室内平面空间结构如图2所示.
在垂直层级结构中除了涉及平面结构以外, 还存在电梯、自动扶梯、楼梯等连接平面的设施. 如图5(a)、5(b)所示分别表示2层平面图(见图2(a))所构成的拓扑图;将其映射到对偶空间后,结果如图5(c)所示. 电梯
图 5
3.3. 平面结构范围划分和自动融合
设计同时考虑室内网络模型中危害和时间因素的疏散路线选择算法(见图6), 可获得最优疏散路线, 能够使居住者远离危险, 并以最快的疏散时间到达安全区域. 将室内空间进行范围划分, 构建出口节点关联图
图 6
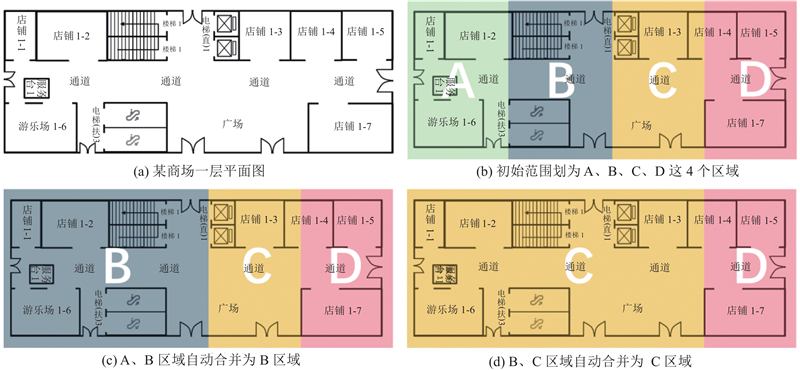
对于多出口的平面建筑结构,人群一般会选择离自己最近的安全出口. 因此 在场景构建时,进行了初始范围划分(见图7), 将整体平面结构划分为
图 7
图 7 平面结构范围划分和自动融合过程
Fig.7 Planar structure range division and automatic fusion process
除了
图 8
4. 安全疏散路线选择算法
在生成对应的
式中:
个体
式中:
个体
式中:
单元空间的风险与该空间距离危险源的距离,以及与危险的相关特性有关(如发生火灾时, 与空间的一氧化碳、二氧化碳和氧气的浓度有关). 本研究将单元空间的危险性
式中:
除了单元空间的危险阈值外, 走廊、室内广场通道之类空间的通行率也是影响群体逃生的重要因素. 室内空间的通行率与其宽度有关, 建筑在垂直方向上的通行宽度、不可通行宽度和通行率,定义分别如下:
式中:
一般的,个体
式中:
当式(8)成立且式(3)成立(风险低于人类所能承受的风险阈值)时, 表示该空间可以通行. 在考虑室内空间的危险阈值和可通行区域的通行率后, 个体
据此,本研究将个体的安全逃生路线定义为
最后, 本研究通过
图 9
5. 实验与对比分析
5.1. 获取路线与路线选择
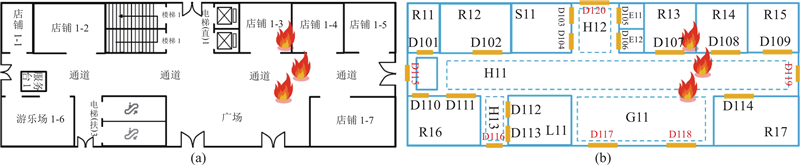
图 10
图 10 水平平面结构单条逃生路径的火灾源位置图
Fig.10 Locations of fire with a single escape route in a horizontal plane structure
如表1所示,统计所有的逃生路线以及选择每条路线的人数. 表中,NuSe表示选择这条路线的人数. 可以看出,人数差异较明显. 不失一般性,选取R12、R13、R14这3个室内空间以及H11中间大走廊进行分析. 4个区域的逃生路线统计如表2所示. 表中,MAXRT表示可行单条逃生路线上危险程度最高的节点的风险,AvT表示该路线的平均逃生时间. 其中,危险程度表示某条路线对逃生人群的危险程度,如果该路线危险程度超过
表 1 逃生路线选择人数对比表
Tab.1
| 逃生路线 | NuSe | 逃生路线 | NuSe | |
| E11-d105-H12-d120 | 12 | R12-d102-H11-d115 | 11 | |
| E12-d106-H12-d120 | 11 | R12-d102-H11-g11-G11-d117 | 1 | |
| E12-d106-H12-h12-H11-h13-H13-d116 | 1 | R12-d102-H11-h13-H13-d116 | 10 | |
| G11-d117 | 10 | R13-d107-H11-d119 | 16 | |
| G11-d118 | 5 | R13-d107-H11-g11-G11-d117 | 1 | |
| H11-d115 | 3 | R13-d107-H11-h12-H12-d120 | 2 | |
| H11-d119 | 2 | R14-d108-H11-d119 | 27 | |
| H11-g11-G11-d117 | 5 | R14-d108-H11-g11-G11-d117 | 1 | |
| H11-g11-G11-d118 | 3 | R14-d108-H11-h12-H12-d120 | 1 | |
| H11-h12-H12-d120 | 4 | R14-d108-H11-h13-H13-d116 | 2 | |
| H11-h13-H13-d116 | 12 | R15-d109-H11-d119 | 15 | |
| H12-d120 | 19 | R15-d109-H11-h13-H13-d116 | 1 | |
| H13-d116 | 9 | R16-d111-H11-d115 | 14 | |
| H13-h13-H11-d115 | 5 | R16-d111-H11-h13-H13-d116 | 10 | |
| H13-h13-H11-d119 | 2 | R17-d114-H11-d119 | 17 | |
| L11-d113-H13-d116 | 12 | R17-d114-H11-g11-G11-d118 | 1 | |
| L11-d113-H13-h13-H11-d115 | 8 | R17-d114-H11-h13-H13-d116 | 1 | |
| R11-d101-H11-d115 | 16 | S11-d103-H12-d120 | 25 | |
| R11-d101-H11-h13-H13-d116 | 5 | 总计:37条路径 | 300 |
表 2 R12、R13、R14房间逃生路线、危险程度和平均逃生时间表
Tab.2
| 开始房间 | 逃生路线 | MAXRT | AvT/s |
| R12 | R12-d102-H11-d115 | 0.02 | 28.51 |
| R12-d102-H11-g11-G11-d117 | 0.56 | 35.94 | |
| R12-d102-H11-h13-H13-d116 | 0 | 26.68 | |
| R12-d102-H11-d115 (Dijkstra) | 0.02 | 21.35 | |
| R13 | R13-d107-H11-d119 | 0 | 35.12 |
| R13-d107-H11-g11-G11-d117 | 0.33 | 25.13 | |
| R13-d107-H11-h12-H12-d120 | 0.41 | 31.53 | |
| R13-d107-H11-h12-H12-d120 (Dijkstra) | 0.41 | 20.30 | |
| R14 | R14-d108-H11-d119 | 0 | 25.57 |
| R14-d108-H11-g11-G11-d117 | 0.46 | 35.40 | |
| R14-d108-H11-h12-H12-d120 | 0.55 | 42.14 | |
| R14-d108-H11-h13-H13-d116 | 0.42 | 34.57 | |
| R14-d108-H11-d119 (Dijkstra) | 0 | 7.46 | |
| H11 | H11-d115 | 0.49 | 27.44 |
| H11-d119 | 0.50 | 46.52 | |
| H11-g11-G11-d117 | 0.45 | 21.27 | |
| H11-g11-G11-d118 | 0.48 | 16.54 | |
| H11-h12-H12-d120 | 0.33 | 26.69 | |
| H11-h13-H13-d116 | 0.31 | 21.06 | |
| H11-d115 (Dijkstra) | 0.49 | 13.88 | |
| H11-d119 (Dijkstra) | 0.50 | 10.10 | |
| H11-h12-H12-d120 (Dijkstra) | 0.33 | 5.86 |
结合图10(b), R13和R14这2个房间虽然都在火灾附近,但出现危险程度为0的逃生路线. 本研究主要考虑火灾大小和逃生距离,当火灾较大时即使很远也有一定危险,这是绝对危险;逃生距离越远,逃生时间可能越长,发生危险的概率也越大,这是相对危险,绝对危险和相对危险共同影响危险程度的大小. 在本次实验中火灾大小设置较小,所以可能出现危险程度为0的路线,但一般情况下每个房间的逃生路线中只能有一条危险程度为0的路线.
走廊H11是特殊节点,在疏散仿真中人群初始位置可以设在此处. 在表2中可以发现H11可以往所有出口进行疏散,这是由于H11较长,且与每个房间连通. 由于H11的特性,可以观察到,离火灾较近的出口D119所需要的平均逃生时间大于其他出口,其中包括空间上位于D119相对一侧的D115. 另外上下两侧出口的逃生时间普遍低于左右两侧出口的逃生时间,这主要和逃生距离有一定关系.
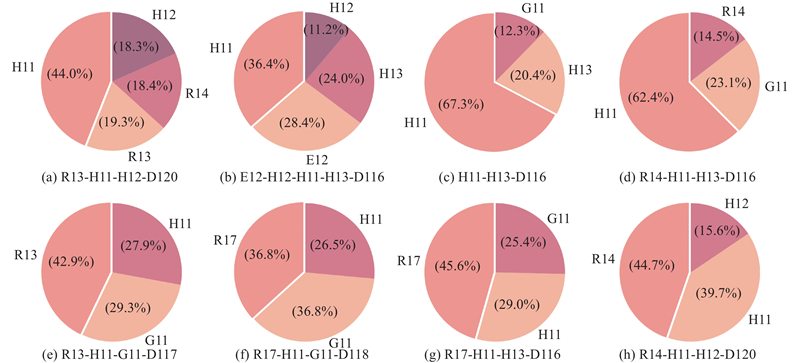
逃生路径各节点平均疏散时间占比如图11所示. 可以看出,占逃生时间比例最大的往往是前2个区域节点,如图11(a)~(d)所示. H11节点是时间占比最大的,主要原因是H11整体大小远大于其他节点,在此处花费时间都较长. 在图11(e)~(h)中,时间占比最大的是该路径的起始节点,主要由于疏散刚启动时人群分布较为分散,会从四面八方汇集于门口,导致在门口处出现拥堵. 随着仿真的进行,人群会逐渐稳定,呈排队状从出口逃离,拥堵现象明显减缓. 在灾害较为稳定时,该规律也是符合客观事实的. 时间占比高的节点是重点观察的对象, 这些节点就是影响人群逃生效率的关键节点, 它们可能是危险程度较高、可通行的人数过小或设计不合理导致的.
图 11
图 11 逃生路径各节点平均疏散时间占比
Fig.11 Average evacuation time proportion of each node on escape path
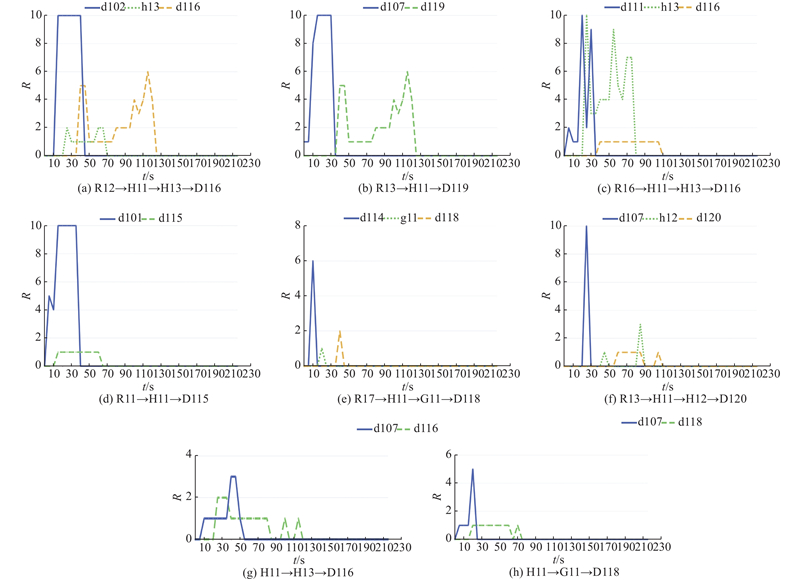
单条逃生路径各节点的拥堵指数随时间的变化如图12所示,每个子图的图注表示了特定的逃生路线. 拥堵指数R是比较人群通过房间(即逃出对应的门)的总时间与单人通畅经过对应的门的时间而获得的. 观察图12(a), 节点R12在
图 12
图 12 单条逃生路径各节点的拥堵指数随时间的变化
Fig.12 Variation of congestion index of each node of a single escape route with time
为了改善拥堵情况,算法须找到不合理的节点并进行修改. 例如图12(a)中R12房间虽然远离火灾,但房间较大且门宽度较小,使得人群更容易聚集于门口. d102门口正对H13,大量人群会在此处交汇让d102更加拥堵,因此,可以增加门宽,使得人群更容易离开d102来到更宽阔的H11;略微改变门位置使得交叉口错开,可以减少疏散时的人流量汇聚,避免混乱和拥堵. 同理对于R13,也可以增加门宽,来减少拥堵情况.
5.2. 路径选择算法对比与分析
对比本研究所提出的安全疏散路线选择算法和基于IndoorGML室内空间建模的 Dijkstra算法,以分析本研究路线选择算法的优势. 在表2中, 黑体部分表示从房间R12、R13、R14和走廊H11出发执行Dijkstra算法所获得的路线. 可以发现,在R12和R14房间中分别选择R12-d102-H11-d115和R14-d108-H11-d119路线,这2条路线实际长度较短,逃生速度快. 在R12和R14房间分别执行本研究的安全疏散路线选择算法,也将选择上述2条路线. 这2条路线具有最小的MAXRT值和AvT值(见表2),且选择的人数较多(见表1),是较符合疏散预期的. 在R13房间中Dijkstra算法选择R13-d107-H11-h12-H12-d120路线,与本研究算法发生冲突. Dijkstra算法选择了最危险的路线,而不是较为安全的R14-d108-H11-d119. 在H11中也可以发现,Dijkstra只考虑距离因素,而不考虑危险程度. 例如H11-d119是很危险的,在安全选择算法中仅有2人选择. 最安全的且选择人数最多的路线H11-h13-H13-d116反而没有被Dijkstra考虑. 证明Dijkstra不能直接用于有危险区域的路径规划,而本研究所提出的安全疏散路径选择算法更合适.
单纯的Dijkstra算法只会给同一个房间内的人同一个路径(走廊H11在使用Dijkstra时进行了分区),这使得在该条路径的人数始终只增不减,在通过较为狭窄的通道时会造成拥堵. 与此相对的,本研究疏散算法会给每个人多个的可行路线,减轻拥堵情况,也更符合真实情况.
5.3. 优化方案结果对比与分析
通过移除H11的前台并拓宽R12连接H11的门d102可以较大改善拥堵情况. 关于d115的疏散路线平均逃生时间te的对比结果如表3所示. 可以看出,在移除前台后,绝大部分以d115为出口的疏散路线的逃生时间都减少了.
表 3 d115疏散路线平均逃生时间表的对比
Tab.3
| 逃生路线 | te/s | |
| 优化前 | 优化后 | |
| H11-d115 | 27.44 | 26.26 |
| H13-h13-H11-d115 | 30.13 | 25.85 |
| L11-d113-H13-h13-H11-d115 | 35.63 | 34.55 |
| R11-d101-H11-d115 | 15.20 | 16.39 |
| R12-d102-H11-d115 | 28.51 | 25.40 |
| R16-d111-H11-d115 | 23.56 | 17.84 |
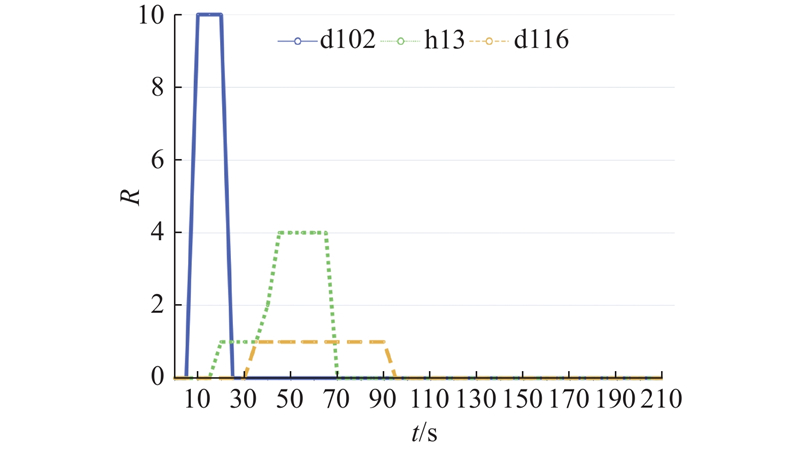
优化后的R12→H11→H13→D116路径的拥堵指数曲线如图13所示. 在
图 13
图 13 优化后的R12→H11→H13→D116路径拥堵指数随时间的变化
Fig.13 Path congestion index variation of optimized R12→H11→H13→D116 over time
6. 结 语
提出室内空间安全性评估方法, 从空间布局角度, 为人群仿真安全提供了有效的扩展和新的维度. 对建筑的水平平面结构和垂直层级结构进行计算机语言抽象和表达, 提出了安全疏散路线选择算法. 在此基础上, 进一步提出室内空间安全性评估算法. 通过对每条路线危险阈值、通行率分析, 并对单条逃生路径关键节点、单个出口逃生关键节点进行分析, 找出室内建筑不合理节点并提出优化方案. 通过模拟场景仿真实验, 证明了评估算法的有效性.
室内空间建模具有一定的复杂性, 并且还原真实空间非常耗时, 当前场景构建还需要人工建模, 后续研究考虑使用图片或视频自动扫描建模. 未来计划考虑建模拥堵下个体的路径选择与建筑结构的关系,以评估这些关系对应急疏散的作用,从而调节建筑结构来达到更安全的疏散.
参考文献
Evacuation assistants: an extended model for determining effective locations and optimal numbers
[J].DOI:10.1016/j.physa.2011.11.051 [本文引用: 1]
Social force model for pedestrian dynamics
[J].DOI:10.1103/PhysRevE.51.4282 [本文引用: 1]
Reciprocal n-body collision avoidance
[J].
Modeling crowd evacuation via behavioral heterogeneity-based social force model
[J].DOI:10.1109/TITS.2022.3232999 [本文引用: 1]
A social force model for pedestrians’ movements affected by smoke spreading
[J].
The hybrid reciprocal velocity obstacle
[J].DOI:10.1109/TRO.2011.2120810 [本文引用: 1]
Robots’ motion planning in human crowds by acceleration obstacles
[J].DOI:10.1109/LRA.2022.3199818 [本文引用: 1]
Research on an improved cellular automata model
[J].DOI:10.4028/www.scientific.net/AMM.160.109 [本文引用: 1]
Assessment of building security cost determinants effects
[J].
Methodological approach to risk assessment in building security
[J].
Fuzzy-based escape route fire-vulnerability assessment model for indoor built environment
[J].
Escape route typology
[J].DOI:10.4028/www.scientific.net/AMM.820.402 [本文引用: 1]
Numerical study of the effect of gender composition and partitioning boards on evacuation in a two-line transfer transit rail subway station
[J].DOI:10.1177/1420326X221079215 [本文引用: 1]
Fire hazard assessment with indoor spaces for evacuation route selection in building fire scenarios
[J].
Open-source tool for transforming citygml levels of detail
[J].DOI:10.3390/en14248250 [本文引用: 1]
Floor plans in citygml
[J].
Indoorgml: a standard for indoor spatial modeling
[J].
About the subdivision of indoor spaces in indoorgml
[J].
Supporting indoor navigation using access rights to spaces based on combined use of indoorgml and ladm models
[J].DOI:10.3390/ijgi6120384 [本文引用: 1]
A flexible framework for covering and partitioning problems in indoor spaces
[J].DOI:10.3390/ijgi9110618 [本文引用: 1]
Hybrid long-range collision avoidance for crowd simulation
[J].
Generating pedestrian trajectories consistent with the fundamental diagram based on physiological and psychological factors
[J].DOI:10.1371/journal.pone.0117856 [本文引用: 1]
Ped-air: a simulator for loading, unloading, and evacuating aircraft
[J].DOI:10.1016/j.trpro.2014.09.052 [本文引用: 1]
Real-time evacuation route selection methodology for complex buildings
[J].DOI:10.1016/j.firesaf.2017.04.011 [本文引用: 1]
An evaluation model for analyzing robustness and spatial closeness of 3d indoor evacuation networks
[J].DOI:10.3390/ijgi10050331 [本文引用: 1]
Evacusafe: a real-time model for building evacuation based on dijkstra’s algorithm
[J].DOI:10.1016/j.jobe.2020.101687 [本文引用: 1]