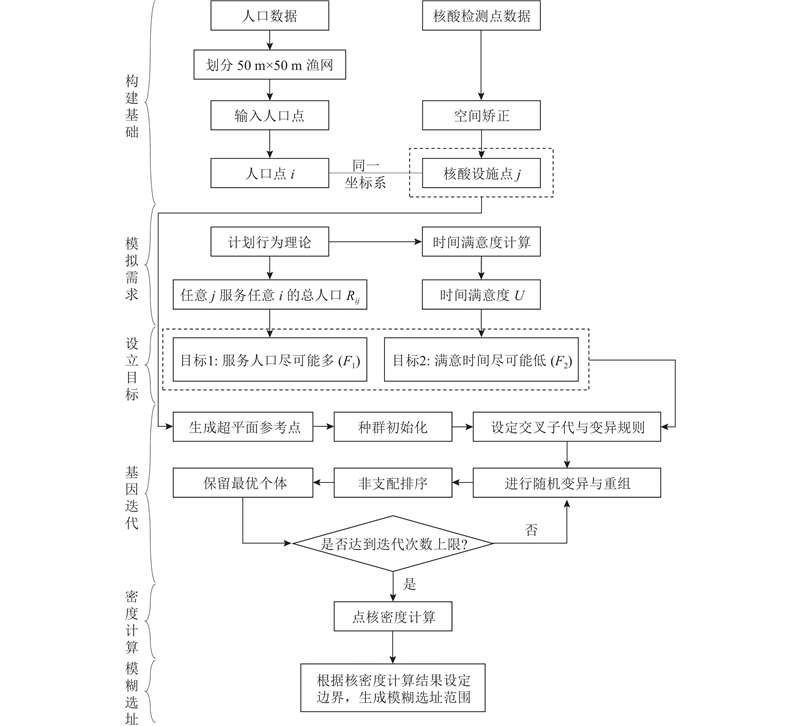
基于$ {N}_{{\mathrm{g}}} $ $ {N}_{1} $ $ {N}_{2} $ $ {F}_{1} $ $ {F}_{2} $ $ {N}_{{\mathrm{g}}}+{N}_{1}+{N}_{2} $ $ {F}_{1} $ $ {F}_{2} $ $ {f} $ $ {f} $ $ {n}_{f} $ [27 ] 的研究方法,针对归一化后的目标函数$ {F}_{1} $ $ {F}_{2} $ $ {F}_{1}\in \left[0,1.0\right],{F}_{2}\in \left[\mathrm{0,1.0}\right] $ $ {n}_{f} $ $ \left({F}_{1},{F}_{2}\right) $ $ \mathrm{\mu } $ $ {n}_{f} $ $ \mathrm{\mu } $ $ {n}_{f} $
[1]
赵汗青. 中国现代城市公共安全管理研究[D]. 长春: 东北师范大学, 2012.
[本文引用: 1]
ZHAO Hanqing. Study of China's modern city public safety management [D]. Changchun: Northeast Normal University, 2012.
[本文引用: 1]
[2]
陈美华, 张明亮, 王延飞 面向国家安全体系和能力现代化建设的应急情报工作研究
[J]. 情报科学 , 2023 , 41 (7 ): 2 - 7
[本文引用: 1]
CHEN Meihua, ZHANG Mingliang, WANG Yanfei Emergency information work for modernization of national security system and capacity
[J]. Information Science , 2023 , 41 (7 ): 2 - 7
[本文引用: 1]
[3]
WAN S, CHEN Z, DONG J Bi-objective trapezoidal fuzzy mixed integer linear program-based distribution center location decision for large-scale emergencies
[J]. Applied Soft Computing , 2021 , 110 : 107757
DOI:10.1016/j.asoc.2021.107757
[本文引用: 1]
[4]
WAN S, CHEN Z, DONG J An efficiency-based interactive dynamic technique with interval-valued hesitant fuzzy constraint cone for rescue route planning
[J]. Expert Systems with Applications , 2023 , 231 : 120648
DOI:10.1016/j.eswa.2023.120648
[本文引用: 1]
[5]
WANG J, WU X, WANG R, et al Review of associations between built environment characteristics and severe acute respiratory syndrome coronavirus 2 infection risk
[J]. International Journal of Environmental Research and Public Health , 2021 , 18 (14 ): 7561
DOI:10.3390/ijerph18147561
[本文引用: 1]
[6]
World Health Organization. WHO director-general's opening remarks at the media briefing on COVID-19 - 11 March 2020 [EB/OL]. (2020-03-11) [2023-07-14]. https://www.who.int/director-general/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19---11-march-2020.
[本文引用: 1]
[7]
王阳 基层治理的社会基础: 对地域性社会团结的再认识: 基于重大公共卫生事件应急治理的分析
[J]. 求实 , 2023 , (1 ): 55 - 65
[本文引用: 1]
WANG Yang Social basis of primary-level governance: re-understanding regional social solidarity based on the analysis of major public health emergency management
[J]. Truth Seeking , 2023 , (1 ): 55 - 65
[本文引用: 1]
[8]
张腾飞, 苏桂武, 齐文华, 等 民众灾害意识国内研究现状与趋势: 基于科学计量学和文献内容分析的联合诊断
[J]. 地震学报 , 2023 , 45 (1 ): 142 - 166
ZHANG Tengfei, SU Guiwu, QI Wenhua, et al Development and future directions of the disaster awareness research in China: an integrated identification coupling scientometric method and literature content analysis
[J]. Acta Seismologica Sinica , 2023 , 45 (1 ): 142 - 166
[9]
张璇 新冠疫情下的基层社区治理能力现代化研究
[J]. 上海市社会主义学院学报 , 2020 , (5 ): 9 - 15
[本文引用: 1]
ZHANG Xuan A study on the modernization of grass roots community governance ability under the COVID-19
[J]. Journal of Shanghai Institute of Socialism , 2020 , (5 ): 9 - 15
[本文引用: 1]
[10]
毛成蕊 城市现代化治理背景下城市运行“一网统管”研究与实践: 以襄阳市为例
[J]. 襄阳职业技术学院学报 , 2023 , 22 (3 ): 24 - 27
[本文引用: 1]
MAO Chengrui Research and practice of “one integrated platform” in urban operation under the background of urban modernization governance
[J]. Journal of Xiangyang Polytechnic , 2023 , 22 (3 ): 24 - 27
[本文引用: 1]
[11]
江海凤, 毛申宇, 黄光梅, 等 “横向协同 纵向贯通”机制在医院感染防控网格化督查的应用
[J]. 现代医院 , 2023 , 23 (4 ): 493 - 496
DOI:10.3969/j.issn.1671-332X.2023.04.001
JIANG Haifeng, MAO Shenyu, HUANG Guangmei, et al The application and practice of grid supervision of nosocomial infection prevention and control based on the mechanism of horizontal collaboration and vertical linkage
[J]. Modern Hospitals , 2023 , 23 (4 ): 493 - 496
DOI:10.3969/j.issn.1671-332X.2023.04.001
[12]
邵献平, 袁漫兮, 冯婧, 等 韧性社区数字治理的协同机制探析
[J]. 武汉理工大学学报: 社会科学版 , 2023 , 36 (2 ): 65 - 72
[本文引用: 1]
SHAO Xianping, YUAN Manxi, FENG Jing, et al Collaborative mechanism of digital governance in urban communities from the perspective of resilience
[J]. Wuhan University of Technology: Social Science Edition , 2023 , 36 (2 ): 65 - 72
[本文引用: 1]
[13]
王远飞, 张超 GIS和引力多边形方法在公共设施服务域研究中的应用: 以上海浦东新区综合医院为例
[J]. 经济地理 , 2005 , (6 ): 800 - 803
[本文引用: 1]
WANG Yuanfei, ZHANG Chao GIS and gravity polygon based service area analysis of public facility: case study of hospitals in Pudong New Area
[J]. Economic Geography , 2005 , (6 ): 800 - 803
[本文引用: 1]
[14]
刘钊, 郭苏强, 金慧华, 等 基于GIS的两步移动搜寻法在北京市就医空间可达性评价中的应用
[J]. 测绘科学 , 2007 , 32 (1 ): 61 - 63
DOI:10.3771/j.issn.1009-2307.2007.01.023
[本文引用: 1]
LIU Zhao, GUO Suqiang, JIN Huihua, et al Application of the GIS-based two-step floating catchment area method in measurement of spatial accessibility to hospitals in Beijing
[J]. Science of Surveying and Mapping , 2007 , 32 (1 ): 61 - 63
DOI:10.3771/j.issn.1009-2307.2007.01.023
[本文引用: 1]
[15]
程明骏, 朱云辰 , 岑沛立, 等. 基于个人选择偏好的城市医疗资源配置分析[J]. 浙江大学学报: 工学版, 2021, 55(11): 2194−2206.
[本文引用: 1]
CHENG Mingjun, ZHU Yunchen, CEN Peili, et al. Allocation of urban medical resources based on personal choice preference [J]. Journal of Zhejiang University: Engineering Science , 2021, 55(11): 2194−2206.
[本文引用: 1]
[16]
CHEN Z, WAN S, DONG J An efficiency-based interval type-2 fuzzy multi-criteria group decision making for makeshift hospital selection
[J]. Applied Soft Computing , 2022 , 115 : 108243
DOI:10.1016/j.asoc.2021.108243
[本文引用: 1]
[17]
CHEN Z, WAN S, DONG J An integrated interval-valued intuitionistic fuzzy technique for resumption risk assessment amid COVID-19 prevention
[J]. Information Sciences , 2023 , 619 : 695 - 721
DOI:10.1016/j.ins.2022.11.028
[本文引用: 1]
[18]
WAN S, YAN J, DONG J Personalized individual semantics based consensus reaching process for large-scale group decision making with probabilistic linguistic preference relations and application to COVID-19 surveillance
[J]. Expert Systems with Applications , 2022 , 191 : 116328
DOI:10.1016/j.eswa.2021.116328
[本文引用: 1]
[19]
BAKER J E. Reducing bias and inefficiency in the selection algorithm [C]// Proceedings of the 2nd International Conference on Genetic Algorithms . Hillsdale: L. Erlbaum Associates Inc. , 1987: 14−21.
[本文引用: 1]
[20]
SRINIVAS N, DEB K Multiobjective optimization using nondominated sorting in genetic algorithms
[J]. Evolutionary Computation , 1994 , 2 (3 ): 221 - 248
DOI:10.1162/evco.1994.2.3.221
[本文引用: 1]
[21]
DEB K, PRATAP A, AGARWAL S, et al A fast and elitist multiobjective genetic algorithm: NSGA-II
[J]. IEEE Transactions on Evolutionary Computation , 2002 , 6 (2 ): 182 - 197
DOI:10.1109/4235.996017
[本文引用: 1]
[22]
DEB K, JAIN H An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: solving problems with box constraints
[J]. IEEE Transactions on Evolutionary Computation , 2014 , 18 (4 ): 577 - 601
DOI:10.1109/TEVC.2013.2281535
[本文引用: 1]
[23]
SHAVARANI S Multi-level facility location-allocation problem for post-disaster humanitarian relief distribution
[J]. Journal of Humanitarian Logistics and Supply Chain Management , 2019 , 9 (1 ): .70 - 81
DOI:10.1108/JHLSCM-05-2018-0036
[本文引用: 1]
[24]
LIU J, LI Y, LI Y, er al Location optimization of emergency medical facilities for public health emergencies in megacities based on genetic algorithm
[J]. Journal of Modelling in Management , 2019 , 14 (2 ): 476 - 494
DOI:10.1108/JM2-07-2018-0092
[本文引用: 1]
[25]
李晓辉, 高铎, 杨晰, 等. 不同支配关系的NSGA-III算法在机器人制造单元调度问题中的应用[J]. 计算机系统应用, 2022, 31(2): 279−284.
[本文引用: 1]
LI Xiaohui, GAO Duo, YANG Xi, et al. Application of NSGA-III algorithm based on different dominance relations in robotic cell scheduling problem [J]. Computer Systems and Applications , 2023, 31(2): 279−284.
[本文引用: 1]
[26]
ZAHO Q, DING J, LI J, et al Network-based structure optimization method of the anti-aircraft system
[J]. Journal of Systems Engineering and Electronics , 2023 , 34 (2 ): 374 - 395
DOI:10.23919/JSEE.2023.000019
[本文引用: 1]
[27]
TIAN Y, XIANG X, ZHANG X, et al. Sampling reference points on the pareto fronts of benchmark multi-objective optimization problems [C]// IEEE Congress on Evolutionary Computation . Rio de Janeiro: IEEE Computational Intelligence Society, 2018: 2677−2684.
[本文引用: 1]
[28]
周俊. 城市火灾消防规划支持方法研究[D]. 武汉: 武汉大学, 2011.
[本文引用: 1]
ZHOU Jun. Research on methodology for planning support urban fire protection planning [D]. Wuhan: Wuhan University, 2011.
[本文引用: 1]
[29]
缪遇虹. 低影响开发设施的选址布局优化方法研究[D]. 北京: 北京建筑大学, 2020.
[本文引用: 1]
MIU Yuhong. Method study on location and layout optimization of low impact development facilities [D]. Beijing: Beijing University of Civil Engineering and Architecture, 2020.
[本文引用: 1]
[30]
贾冲, 冯慧芳, 杨振娟 基于出租车GPS轨迹和POI数据的商业选址推荐
[J]. 计算机与现代化 , 2020 , (2 ): 21 - 25
JIA Chong, FENG Huifang, YANG Zhenjuan A commercial site recommendation algorithm based on taxi GPS trajectory and POI data
[J]. Computer and Modernization , 2020 , (2 ): 21 - 25
[31]
刘思君, 靖常峰, 杜明义, 等 GIS多准则的城市垃圾楼空间布局优化选址
[J]. 测绘科学 , 2018 , 43 (8 ): 45 - 49
[本文引用: 1]
LIU Sijun, JING Changfeng, DU Mingyi, et al Spatial layout optimization and location of urban garbage buildings based on GIS-multicriteria
[J]. Science of Surveying and Mapping , 2018 , 43 (8 ): 45 - 49
[本文引用: 1]
[32]
王威, 朱峻佚, 费智涛, 等 国土空间韧性规划建设整体框架与发展路径研究
[J]. 中国工程科学 , 2023 , 25 (3 ): 209 - 218
DOI:10.15302/J-SSCAE-2023.03.017
[本文引用: 1]
WANG Wei, ZHU Junyi, FEI Zhitao, et al Overall framework and development path of national land space resilience planning and construction
[J]. Strategic Study of CAE , 2023 , 25 (3 ): 209 - 218
DOI:10.15302/J-SSCAE-2023.03.017
[本文引用: 1]
1
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
1
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
面向国家安全体系和能力现代化建设的应急情报工作研究
1
2023
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
面向国家安全体系和能力现代化建设的应急情报工作研究
1
2023
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
Bi-objective trapezoidal fuzzy mixed integer linear program-based distribution center location decision for large-scale emergencies
1
2021
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
An efficiency-based interactive dynamic technique with interval-valued hesitant fuzzy constraint cone for rescue route planning
1
2023
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
Review of associations between built environment characteristics and severe acute respiratory syndrome coronavirus 2 infection risk
1
2021
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
1
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
基层治理的社会基础: 对地域性社会团结的再认识: 基于重大公共卫生事件应急治理的分析
1
2023
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
基层治理的社会基础: 对地域性社会团结的再认识: 基于重大公共卫生事件应急治理的分析
1
2023
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
民众灾害意识国内研究现状与趋势: 基于科学计量学和文献内容分析的联合诊断
0
2023
民众灾害意识国内研究现状与趋势: 基于科学计量学和文献内容分析的联合诊断
0
2023
新冠疫情下的基层社区治理能力现代化研究
1
2020
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
新冠疫情下的基层社区治理能力现代化研究
1
2020
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
城市现代化治理背景下城市运行“一网统管”研究与实践: 以襄阳市为例
1
2023
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
城市现代化治理背景下城市运行“一网统管”研究与实践: 以襄阳市为例
1
2023
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
“横向协同 纵向贯通”机制在医院感染防控网格化督查的应用
0
2023
“横向协同 纵向贯通”机制在医院感染防控网格化督查的应用
0
2023
韧性社区数字治理的协同机制探析
1
2023
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
韧性社区数字治理的协同机制探析
1
2023
... 社会公共安全事件分为以下几大类型:自然灾害、事故灾难、公共卫生事件以及社会安全事件[1 ] . 陈美华等[2 ] 认为,所有社会公共安全事件都具有突发性、紧急性特征,须以“大安全大应急框架”应对这类事件所突然产生的大量社会需求. Wan等[3 -4 ] 以汶川地震这一自然灾害事件为切入点,研究事件发生时最佳应急物流与救援路线生成模型. 自2019年新冠肺炎爆发以来,疫情已扩散到全球大部分国家[5 ] ;2020年1月30日,世界卫生组织正式宣布此次新冠疫情为“公共卫生紧急事件” [6 ] . 在新冠疫情扩散与抵御过程中,世界各地都在医疗体系、社会资源运转上尝试多种实践方式,中国将社会基层组织力量放在抗击疫情的核心位置[7 -9 ] . 毛成蕊等[10 -12 ] 认为,浙江省网格化治理模式为防止疫情扩散起到了重要作用. 新冠疫情防疫基层工作,为中国应急管理研究提供了大量实践经验. ...
GIS和引力多边形方法在公共设施服务域研究中的应用: 以上海浦东新区综合医院为例
1
2005
... 以城市空间为切入点的新冠疫情相关理论研究主要在于医疗相关设施选址方面. 如王远飞等[13 -14 ] 基于GIS对上海与北京的综合医疗服务能力进行现状评价分析;程明骏等[15 ] 基于高斯两步移动搜索法(Gaussian 2-step floating catchment area, Ga2SFCA)与计划行为理论对杭州市主城区公共医疗资源空间的分配情况进行分级评价; Chen等[16 -17 ] 分别采用基于效率的多标准群决策方法TrIT2F-BWM-DEA与基于集成区间值的直觉模糊技术IVIF-DBWM-SPA,从遏制新冠疫情传播的角度出发,分别对临时医院选址决策与疫情恢复风险评估提供有效理论支撑;Wan等[18 ] 从高校新冠疫情监测方案入手,构建基于语义偏好模型的大规模群体决策共识达成模型LSGDM,帮助相关部门制定新冠疫情监测计划. 已有相关研究,大多是以设施可达性与空间分布合理性为基础,分析评价当前医疗事件现状及人流现状,预测未来走向,确定合理设施选址,注重从客观角度来分析研究应急公共事件;而由于应急设施主要面向对象为应急事件中的“人”,之前研究大多采用Ga2SFCA、神经网络算法的空间地理数学模型分析人的行动范围,未考虑其随机性与非理性. ...
GIS和引力多边形方法在公共设施服务域研究中的应用: 以上海浦东新区综合医院为例
1
2005
... 以城市空间为切入点的新冠疫情相关理论研究主要在于医疗相关设施选址方面. 如王远飞等[13 -14 ] 基于GIS对上海与北京的综合医疗服务能力进行现状评价分析;程明骏等[15 ] 基于高斯两步移动搜索法(Gaussian 2-step floating catchment area, Ga2SFCA)与计划行为理论对杭州市主城区公共医疗资源空间的分配情况进行分级评价; Chen等[16 -17 ] 分别采用基于效率的多标准群决策方法TrIT2F-BWM-DEA与基于集成区间值的直觉模糊技术IVIF-DBWM-SPA,从遏制新冠疫情传播的角度出发,分别对临时医院选址决策与疫情恢复风险评估提供有效理论支撑;Wan等[18 ] 从高校新冠疫情监测方案入手,构建基于语义偏好模型的大规模群体决策共识达成模型LSGDM,帮助相关部门制定新冠疫情监测计划. 已有相关研究,大多是以设施可达性与空间分布合理性为基础,分析评价当前医疗事件现状及人流现状,预测未来走向,确定合理设施选址,注重从客观角度来分析研究应急公共事件;而由于应急设施主要面向对象为应急事件中的“人”,之前研究大多采用Ga2SFCA、神经网络算法的空间地理数学模型分析人的行动范围,未考虑其随机性与非理性. ...
基于GIS的两步移动搜寻法在北京市就医空间可达性评价中的应用
1
2007
... 以城市空间为切入点的新冠疫情相关理论研究主要在于医疗相关设施选址方面. 如王远飞等[13 -14 ] 基于GIS对上海与北京的综合医疗服务能力进行现状评价分析;程明骏等[15 ] 基于高斯两步移动搜索法(Gaussian 2-step floating catchment area, Ga2SFCA)与计划行为理论对杭州市主城区公共医疗资源空间的分配情况进行分级评价; Chen等[16 -17 ] 分别采用基于效率的多标准群决策方法TrIT2F-BWM-DEA与基于集成区间值的直觉模糊技术IVIF-DBWM-SPA,从遏制新冠疫情传播的角度出发,分别对临时医院选址决策与疫情恢复风险评估提供有效理论支撑;Wan等[18 ] 从高校新冠疫情监测方案入手,构建基于语义偏好模型的大规模群体决策共识达成模型LSGDM,帮助相关部门制定新冠疫情监测计划. 已有相关研究,大多是以设施可达性与空间分布合理性为基础,分析评价当前医疗事件现状及人流现状,预测未来走向,确定合理设施选址,注重从客观角度来分析研究应急公共事件;而由于应急设施主要面向对象为应急事件中的“人”,之前研究大多采用Ga2SFCA、神经网络算法的空间地理数学模型分析人的行动范围,未考虑其随机性与非理性. ...
基于GIS的两步移动搜寻法在北京市就医空间可达性评价中的应用
1
2007
... 以城市空间为切入点的新冠疫情相关理论研究主要在于医疗相关设施选址方面. 如王远飞等[13 -14 ] 基于GIS对上海与北京的综合医疗服务能力进行现状评价分析;程明骏等[15 ] 基于高斯两步移动搜索法(Gaussian 2-step floating catchment area, Ga2SFCA)与计划行为理论对杭州市主城区公共医疗资源空间的分配情况进行分级评价; Chen等[16 -17 ] 分别采用基于效率的多标准群决策方法TrIT2F-BWM-DEA与基于集成区间值的直觉模糊技术IVIF-DBWM-SPA,从遏制新冠疫情传播的角度出发,分别对临时医院选址决策与疫情恢复风险评估提供有效理论支撑;Wan等[18 ] 从高校新冠疫情监测方案入手,构建基于语义偏好模型的大规模群体决策共识达成模型LSGDM,帮助相关部门制定新冠疫情监测计划. 已有相关研究,大多是以设施可达性与空间分布合理性为基础,分析评价当前医疗事件现状及人流现状,预测未来走向,确定合理设施选址,注重从客观角度来分析研究应急公共事件;而由于应急设施主要面向对象为应急事件中的“人”,之前研究大多采用Ga2SFCA、神经网络算法的空间地理数学模型分析人的行动范围,未考虑其随机性与非理性. ...
1
... 以城市空间为切入点的新冠疫情相关理论研究主要在于医疗相关设施选址方面. 如王远飞等[13 -14 ] 基于GIS对上海与北京的综合医疗服务能力进行现状评价分析;程明骏等[15 ] 基于高斯两步移动搜索法(Gaussian 2-step floating catchment area, Ga2SFCA)与计划行为理论对杭州市主城区公共医疗资源空间的分配情况进行分级评价; Chen等[16 -17 ] 分别采用基于效率的多标准群决策方法TrIT2F-BWM-DEA与基于集成区间值的直觉模糊技术IVIF-DBWM-SPA,从遏制新冠疫情传播的角度出发,分别对临时医院选址决策与疫情恢复风险评估提供有效理论支撑;Wan等[18 ] 从高校新冠疫情监测方案入手,构建基于语义偏好模型的大规模群体决策共识达成模型LSGDM,帮助相关部门制定新冠疫情监测计划. 已有相关研究,大多是以设施可达性与空间分布合理性为基础,分析评价当前医疗事件现状及人流现状,预测未来走向,确定合理设施选址,注重从客观角度来分析研究应急公共事件;而由于应急设施主要面向对象为应急事件中的“人”,之前研究大多采用Ga2SFCA、神经网络算法的空间地理数学模型分析人的行动范围,未考虑其随机性与非理性. ...
1
... 以城市空间为切入点的新冠疫情相关理论研究主要在于医疗相关设施选址方面. 如王远飞等[13 -14 ] 基于GIS对上海与北京的综合医疗服务能力进行现状评价分析;程明骏等[15 ] 基于高斯两步移动搜索法(Gaussian 2-step floating catchment area, Ga2SFCA)与计划行为理论对杭州市主城区公共医疗资源空间的分配情况进行分级评价; Chen等[16 -17 ] 分别采用基于效率的多标准群决策方法TrIT2F-BWM-DEA与基于集成区间值的直觉模糊技术IVIF-DBWM-SPA,从遏制新冠疫情传播的角度出发,分别对临时医院选址决策与疫情恢复风险评估提供有效理论支撑;Wan等[18 ] 从高校新冠疫情监测方案入手,构建基于语义偏好模型的大规模群体决策共识达成模型LSGDM,帮助相关部门制定新冠疫情监测计划. 已有相关研究,大多是以设施可达性与空间分布合理性为基础,分析评价当前医疗事件现状及人流现状,预测未来走向,确定合理设施选址,注重从客观角度来分析研究应急公共事件;而由于应急设施主要面向对象为应急事件中的“人”,之前研究大多采用Ga2SFCA、神经网络算法的空间地理数学模型分析人的行动范围,未考虑其随机性与非理性. ...
An efficiency-based interval type-2 fuzzy multi-criteria group decision making for makeshift hospital selection
1
2022
... 以城市空间为切入点的新冠疫情相关理论研究主要在于医疗相关设施选址方面. 如王远飞等[13 -14 ] 基于GIS对上海与北京的综合医疗服务能力进行现状评价分析;程明骏等[15 ] 基于高斯两步移动搜索法(Gaussian 2-step floating catchment area, Ga2SFCA)与计划行为理论对杭州市主城区公共医疗资源空间的分配情况进行分级评价; Chen等[16 -17 ] 分别采用基于效率的多标准群决策方法TrIT2F-BWM-DEA与基于集成区间值的直觉模糊技术IVIF-DBWM-SPA,从遏制新冠疫情传播的角度出发,分别对临时医院选址决策与疫情恢复风险评估提供有效理论支撑;Wan等[18 ] 从高校新冠疫情监测方案入手,构建基于语义偏好模型的大规模群体决策共识达成模型LSGDM,帮助相关部门制定新冠疫情监测计划. 已有相关研究,大多是以设施可达性与空间分布合理性为基础,分析评价当前医疗事件现状及人流现状,预测未来走向,确定合理设施选址,注重从客观角度来分析研究应急公共事件;而由于应急设施主要面向对象为应急事件中的“人”,之前研究大多采用Ga2SFCA、神经网络算法的空间地理数学模型分析人的行动范围,未考虑其随机性与非理性. ...
An integrated interval-valued intuitionistic fuzzy technique for resumption risk assessment amid COVID-19 prevention
1
2023
... 以城市空间为切入点的新冠疫情相关理论研究主要在于医疗相关设施选址方面. 如王远飞等[13 -14 ] 基于GIS对上海与北京的综合医疗服务能力进行现状评价分析;程明骏等[15 ] 基于高斯两步移动搜索法(Gaussian 2-step floating catchment area, Ga2SFCA)与计划行为理论对杭州市主城区公共医疗资源空间的分配情况进行分级评价; Chen等[16 -17 ] 分别采用基于效率的多标准群决策方法TrIT2F-BWM-DEA与基于集成区间值的直觉模糊技术IVIF-DBWM-SPA,从遏制新冠疫情传播的角度出发,分别对临时医院选址决策与疫情恢复风险评估提供有效理论支撑;Wan等[18 ] 从高校新冠疫情监测方案入手,构建基于语义偏好模型的大规模群体决策共识达成模型LSGDM,帮助相关部门制定新冠疫情监测计划. 已有相关研究,大多是以设施可达性与空间分布合理性为基础,分析评价当前医疗事件现状及人流现状,预测未来走向,确定合理设施选址,注重从客观角度来分析研究应急公共事件;而由于应急设施主要面向对象为应急事件中的“人”,之前研究大多采用Ga2SFCA、神经网络算法的空间地理数学模型分析人的行动范围,未考虑其随机性与非理性. ...
Personalized individual semantics based consensus reaching process for large-scale group decision making with probabilistic linguistic preference relations and application to COVID-19 surveillance
1
2022
... 以城市空间为切入点的新冠疫情相关理论研究主要在于医疗相关设施选址方面. 如王远飞等[13 -14 ] 基于GIS对上海与北京的综合医疗服务能力进行现状评价分析;程明骏等[15 ] 基于高斯两步移动搜索法(Gaussian 2-step floating catchment area, Ga2SFCA)与计划行为理论对杭州市主城区公共医疗资源空间的分配情况进行分级评价; Chen等[16 -17 ] 分别采用基于效率的多标准群决策方法TrIT2F-BWM-DEA与基于集成区间值的直觉模糊技术IVIF-DBWM-SPA,从遏制新冠疫情传播的角度出发,分别对临时医院选址决策与疫情恢复风险评估提供有效理论支撑;Wan等[18 ] 从高校新冠疫情监测方案入手,构建基于语义偏好模型的大规模群体决策共识达成模型LSGDM,帮助相关部门制定新冠疫情监测计划. 已有相关研究,大多是以设施可达性与空间分布合理性为基础,分析评价当前医疗事件现状及人流现状,预测未来走向,确定合理设施选址,注重从客观角度来分析研究应急公共事件;而由于应急设施主要面向对象为应急事件中的“人”,之前研究大多采用Ga2SFCA、神经网络算法的空间地理数学模型分析人的行动范围,未考虑其随机性与非理性. ...
1
... Baker等[19 -20 ] 基于帕累托最优理论,提出非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA)便是接近自然选择,并带有随机性的算法;在此基础上,Deb等[21 -22 ] 提出NSGA2与NSGA3,大大提升了计算轻便度与因子兼顾能力. 遗传算法在城市公共设施方面的研究较广泛,Shavarani[23 ] 以混合遗传算法为基础,针对无人机在灾后救援行动中响应速度与对应充电站分布的问题,提出无人机救援分配策略与充电设施拓扑分布结构;Liu等[24 ] 采用NSGA2,确定广州市公共卫生紧急情况下的应急医疗设施选址优化问题,并建立对应的选址模型. 李晓辉等[25 ] 采用NSGA3来优化机器人制造单元调度问题;Zhao等[26 ] 在防空系统优化中采用NSGA3,提升了防空系统在作战中的生存能力与准确性. 目前尚无基于NSGA3的城市应急设施问题研究. ...
Multiobjective optimization using nondominated sorting in genetic algorithms
1
1994
... Baker等[19 -20 ] 基于帕累托最优理论,提出非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA)便是接近自然选择,并带有随机性的算法;在此基础上,Deb等[21 -22 ] 提出NSGA2与NSGA3,大大提升了计算轻便度与因子兼顾能力. 遗传算法在城市公共设施方面的研究较广泛,Shavarani[23 ] 以混合遗传算法为基础,针对无人机在灾后救援行动中响应速度与对应充电站分布的问题,提出无人机救援分配策略与充电设施拓扑分布结构;Liu等[24 ] 采用NSGA2,确定广州市公共卫生紧急情况下的应急医疗设施选址优化问题,并建立对应的选址模型. 李晓辉等[25 ] 采用NSGA3来优化机器人制造单元调度问题;Zhao等[26 ] 在防空系统优化中采用NSGA3,提升了防空系统在作战中的生存能力与准确性. 目前尚无基于NSGA3的城市应急设施问题研究. ...
A fast and elitist multiobjective genetic algorithm: NSGA-II
1
2002
... Baker等[19 -20 ] 基于帕累托最优理论,提出非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA)便是接近自然选择,并带有随机性的算法;在此基础上,Deb等[21 -22 ] 提出NSGA2与NSGA3,大大提升了计算轻便度与因子兼顾能力. 遗传算法在城市公共设施方面的研究较广泛,Shavarani[23 ] 以混合遗传算法为基础,针对无人机在灾后救援行动中响应速度与对应充电站分布的问题,提出无人机救援分配策略与充电设施拓扑分布结构;Liu等[24 ] 采用NSGA2,确定广州市公共卫生紧急情况下的应急医疗设施选址优化问题,并建立对应的选址模型. 李晓辉等[25 ] 采用NSGA3来优化机器人制造单元调度问题;Zhao等[26 ] 在防空系统优化中采用NSGA3,提升了防空系统在作战中的生存能力与准确性. 目前尚无基于NSGA3的城市应急设施问题研究. ...
An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: solving problems with box constraints
1
2014
... Baker等[19 -20 ] 基于帕累托最优理论,提出非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA)便是接近自然选择,并带有随机性的算法;在此基础上,Deb等[21 -22 ] 提出NSGA2与NSGA3,大大提升了计算轻便度与因子兼顾能力. 遗传算法在城市公共设施方面的研究较广泛,Shavarani[23 ] 以混合遗传算法为基础,针对无人机在灾后救援行动中响应速度与对应充电站分布的问题,提出无人机救援分配策略与充电设施拓扑分布结构;Liu等[24 ] 采用NSGA2,确定广州市公共卫生紧急情况下的应急医疗设施选址优化问题,并建立对应的选址模型. 李晓辉等[25 ] 采用NSGA3来优化机器人制造单元调度问题;Zhao等[26 ] 在防空系统优化中采用NSGA3,提升了防空系统在作战中的生存能力与准确性. 目前尚无基于NSGA3的城市应急设施问题研究. ...
Multi-level facility location-allocation problem for post-disaster humanitarian relief distribution
1
2019
... Baker等[19 -20 ] 基于帕累托最优理论,提出非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA)便是接近自然选择,并带有随机性的算法;在此基础上,Deb等[21 -22 ] 提出NSGA2与NSGA3,大大提升了计算轻便度与因子兼顾能力. 遗传算法在城市公共设施方面的研究较广泛,Shavarani[23 ] 以混合遗传算法为基础,针对无人机在灾后救援行动中响应速度与对应充电站分布的问题,提出无人机救援分配策略与充电设施拓扑分布结构;Liu等[24 ] 采用NSGA2,确定广州市公共卫生紧急情况下的应急医疗设施选址优化问题,并建立对应的选址模型. 李晓辉等[25 ] 采用NSGA3来优化机器人制造单元调度问题;Zhao等[26 ] 在防空系统优化中采用NSGA3,提升了防空系统在作战中的生存能力与准确性. 目前尚无基于NSGA3的城市应急设施问题研究. ...
Location optimization of emergency medical facilities for public health emergencies in megacities based on genetic algorithm
1
2019
... Baker等[19 -20 ] 基于帕累托最优理论,提出非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA)便是接近自然选择,并带有随机性的算法;在此基础上,Deb等[21 -22 ] 提出NSGA2与NSGA3,大大提升了计算轻便度与因子兼顾能力. 遗传算法在城市公共设施方面的研究较广泛,Shavarani[23 ] 以混合遗传算法为基础,针对无人机在灾后救援行动中响应速度与对应充电站分布的问题,提出无人机救援分配策略与充电设施拓扑分布结构;Liu等[24 ] 采用NSGA2,确定广州市公共卫生紧急情况下的应急医疗设施选址优化问题,并建立对应的选址模型. 李晓辉等[25 ] 采用NSGA3来优化机器人制造单元调度问题;Zhao等[26 ] 在防空系统优化中采用NSGA3,提升了防空系统在作战中的生存能力与准确性. 目前尚无基于NSGA3的城市应急设施问题研究. ...
1
... Baker等[19 -20 ] 基于帕累托最优理论,提出非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA)便是接近自然选择,并带有随机性的算法;在此基础上,Deb等[21 -22 ] 提出NSGA2与NSGA3,大大提升了计算轻便度与因子兼顾能力. 遗传算法在城市公共设施方面的研究较广泛,Shavarani[23 ] 以混合遗传算法为基础,针对无人机在灾后救援行动中响应速度与对应充电站分布的问题,提出无人机救援分配策略与充电设施拓扑分布结构;Liu等[24 ] 采用NSGA2,确定广州市公共卫生紧急情况下的应急医疗设施选址优化问题,并建立对应的选址模型. 李晓辉等[25 ] 采用NSGA3来优化机器人制造单元调度问题;Zhao等[26 ] 在防空系统优化中采用NSGA3,提升了防空系统在作战中的生存能力与准确性. 目前尚无基于NSGA3的城市应急设施问题研究. ...
1
... Baker等[19 -20 ] 基于帕累托最优理论,提出非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA)便是接近自然选择,并带有随机性的算法;在此基础上,Deb等[21 -22 ] 提出NSGA2与NSGA3,大大提升了计算轻便度与因子兼顾能力. 遗传算法在城市公共设施方面的研究较广泛,Shavarani[23 ] 以混合遗传算法为基础,针对无人机在灾后救援行动中响应速度与对应充电站分布的问题,提出无人机救援分配策略与充电设施拓扑分布结构;Liu等[24 ] 采用NSGA2,确定广州市公共卫生紧急情况下的应急医疗设施选址优化问题,并建立对应的选址模型. 李晓辉等[25 ] 采用NSGA3来优化机器人制造单元调度问题;Zhao等[26 ] 在防空系统优化中采用NSGA3,提升了防空系统在作战中的生存能力与准确性. 目前尚无基于NSGA3的城市应急设施问题研究. ...
Network-based structure optimization method of the anti-aircraft system
1
2023
... Baker等[19 -20 ] 基于帕累托最优理论,提出非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA)便是接近自然选择,并带有随机性的算法;在此基础上,Deb等[21 -22 ] 提出NSGA2与NSGA3,大大提升了计算轻便度与因子兼顾能力. 遗传算法在城市公共设施方面的研究较广泛,Shavarani[23 ] 以混合遗传算法为基础,针对无人机在灾后救援行动中响应速度与对应充电站分布的问题,提出无人机救援分配策略与充电设施拓扑分布结构;Liu等[24 ] 采用NSGA2,确定广州市公共卫生紧急情况下的应急医疗设施选址优化问题,并建立对应的选址模型. 李晓辉等[25 ] 采用NSGA3来优化机器人制造单元调度问题;Zhao等[26 ] 在防空系统优化中采用NSGA3,提升了防空系统在作战中的生存能力与准确性. 目前尚无基于NSGA3的城市应急设施问题研究. ...
1
... 基于$ {N}_{{\mathrm{g}}} $ $ {N}_{1} $ $ {N}_{2} $ $ {F}_{1} $ $ {F}_{2} $ $ {N}_{{\mathrm{g}}}+{N}_{1}+{N}_{2} $ $ {F}_{1} $ $ {F}_{2} $ $ {f} $ $ {f} $ $ {n}_{f} $ [27 ] 的研究方法,针对归一化后的目标函数$ {F}_{1} $ $ {F}_{2} $ $ {F}_{1}\in \left[0,1.0\right],{F}_{2}\in \left[\mathrm{0,1.0}\right] $ $ {n}_{f} $ $ \left({F}_{1},{F}_{2}\right) $ $ \mathrm{\mu } $ $ {n}_{f} $ $ \mathrm{\mu } $ $ {n}_{f} $
1
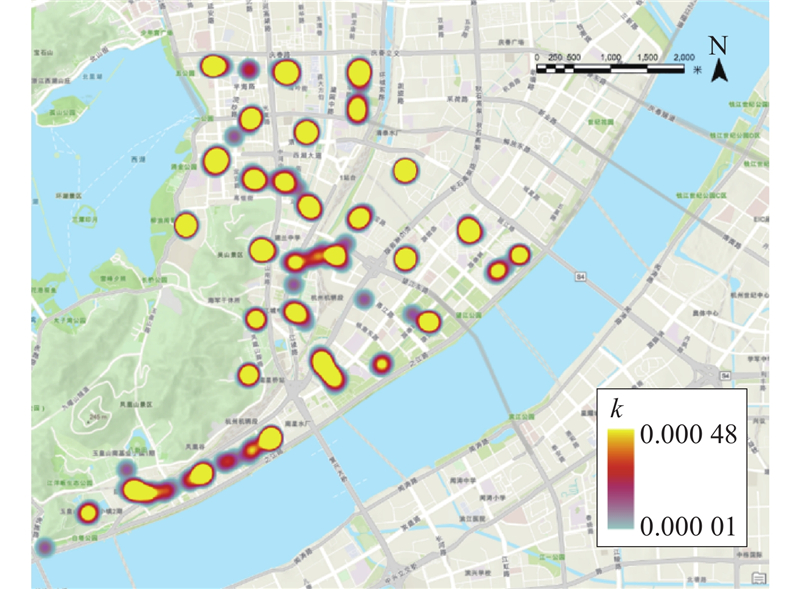
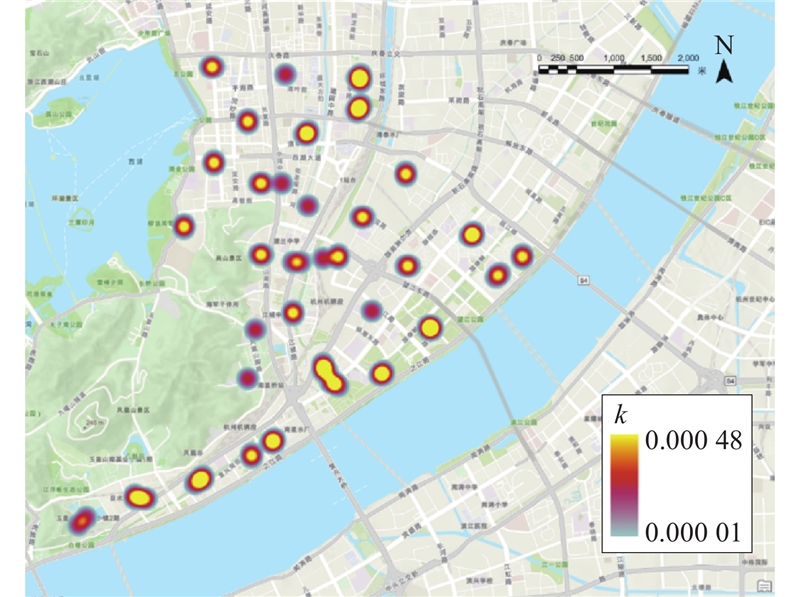
... 基于上城区人口点与核酸设施点数据,基于周俊[28 ] 关于灾害应急研究的成果,以“5 min应急响应时间、15 min应急疏散时间”为基础,设定人们的出行意愿在15 min生活圈范围内(即式(2)中,取$ z $ 图3 ),进行模糊选址范围的判定分析. 将50 000 次迭代生成的设施点分布结果与现实中202 个设施点分布情况,分别代入到目标函数$ {F}_{1} $ $ {F}_{2} $ $ {F}_{1} $ $ {F}_{1}=0.996\;7 $ F 1 =1.0000 ,即做到了上城区内的服务人口全覆盖. 因此,主要的优化目标在目标函数$ {F}_{2} $ 0.5796 优化到了0.6423 ,平均到达设施点的步行所花时间则从292.44 s优化到了264.62 s,总体优化27.82 s,优化幅度为9.51%. 在ArcGIS Pro进行点核密度分析时,将搜索半径设为100 m,进行圆形范围内的领域搜索,生成图3 ,由该结果可以得出,上城区共有32 个连片的“点聚集区”(每一个连片的黄色部分与红色部分即代表点聚集区). ...
1
... 基于上城区人口点与核酸设施点数据,基于周俊[28 ] 关于灾害应急研究的成果,以“5 min应急响应时间、15 min应急疏散时间”为基础,设定人们的出行意愿在15 min生活圈范围内(即式(2)中,取$ z $ 图3 ),进行模糊选址范围的判定分析. 将50 000 次迭代生成的设施点分布结果与现实中202 个设施点分布情况,分别代入到目标函数$ {F}_{1} $ $ {F}_{2} $ $ {F}_{1} $ $ {F}_{1}=0.996\;7 $ F 1 =1.0000 ,即做到了上城区内的服务人口全覆盖. 因此,主要的优化目标在目标函数$ {F}_{2} $ 0.5796 优化到了0.6423 ,平均到达设施点的步行所花时间则从292.44 s优化到了264.62 s,总体优化27.82 s,优化幅度为9.51%. 在ArcGIS Pro进行点核密度分析时,将搜索半径设为100 m,进行圆形范围内的领域搜索,生成图3 ,由该结果可以得出,上城区共有32 个连片的“点聚集区”(每一个连片的黄色部分与红色部分即代表点聚集区). ...
1
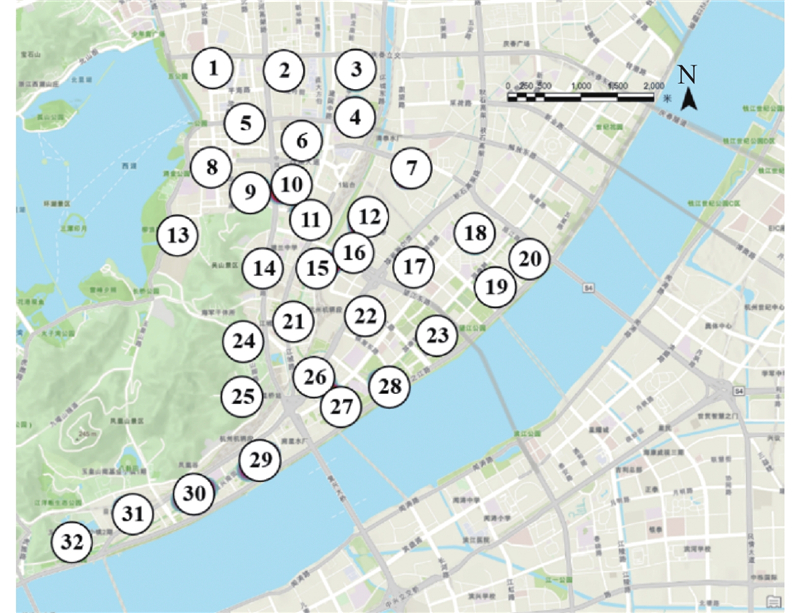
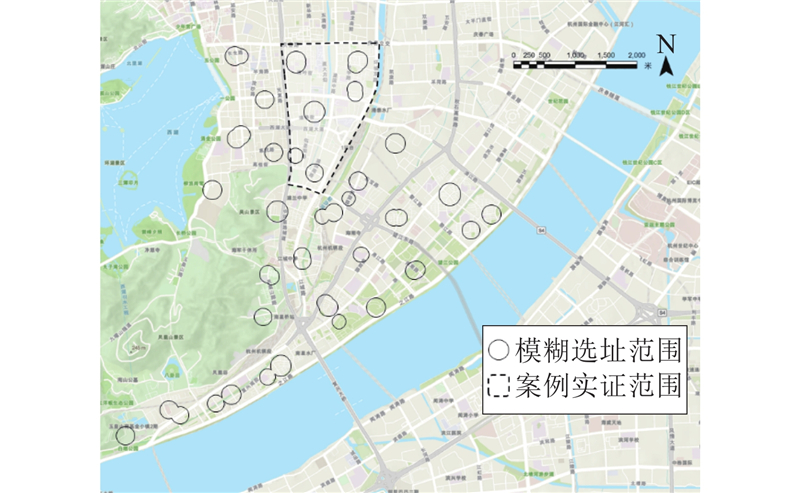
... 在“小集聚-大分散”空间规律的基础上,提出面向城市规划复杂系统的模糊选址方法. 在如图3 所示的核密度分析结果基础上,将点核密度分析结果大于等于0.00001 的区域作为边界,生成围合区域(见图8 ). 模糊选址在本研究的空间意义是,在图8 的线框所构成的点聚集区内,任意位置皆可以作为对应应急事件所需设施的建设点,并且在同一点聚集区内的任意选点,都不会对该区域服务范围内人口点进行核酸检测活动的时间效能产生变化. 由表1 统计结果及研究计算结果可得,32 个点聚集区能够涵盖上城区所有人口点的核酸检测活动需求,并且在这样的分布情况下,任意人口点到往设施点的耗时都在215.5516 ~319.1667 s,虽然全区域最大极差为103.6151 s,但在各个点聚集区内部的最大极差则为9.8221 s,故而在各个点聚集区内,不同设施点选址方案对于该区域服务能力的影响程度不大. 在以往以缪遇虹等[29 -31 ] 为代表的城市设施选址研究中,选址研究成果往往具有精确坐标,虽然这类结果具有较强的落地性与精确性,但是城市作为一个复杂巨系统,并不能完全保证这一精确计算结果实际可用,留有余地的模糊选址方案能让规划人员在施行方案设计时,更充分地考虑实际规划条件,并且扩大了设施点备选规模,保证选址结果的可用性. ...
1
... 在“小集聚-大分散”空间规律的基础上,提出面向城市规划复杂系统的模糊选址方法. 在如图3 所示的核密度分析结果基础上,将点核密度分析结果大于等于0.00001 的区域作为边界,生成围合区域(见图8 ). 模糊选址在本研究的空间意义是,在图8 的线框所构成的点聚集区内,任意位置皆可以作为对应应急事件所需设施的建设点,并且在同一点聚集区内的任意选点,都不会对该区域服务范围内人口点进行核酸检测活动的时间效能产生变化. 由表1 统计结果及研究计算结果可得,32 个点聚集区能够涵盖上城区所有人口点的核酸检测活动需求,并且在这样的分布情况下,任意人口点到往设施点的耗时都在215.5516 ~319.1667 s,虽然全区域最大极差为103.6151 s,但在各个点聚集区内部的最大极差则为9.8221 s,故而在各个点聚集区内,不同设施点选址方案对于该区域服务能力的影响程度不大. 在以往以缪遇虹等[29 -31 ] 为代表的城市设施选址研究中,选址研究成果往往具有精确坐标,虽然这类结果具有较强的落地性与精确性,但是城市作为一个复杂巨系统,并不能完全保证这一精确计算结果实际可用,留有余地的模糊选址方案能让规划人员在施行方案设计时,更充分地考虑实际规划条件,并且扩大了设施点备选规模,保证选址结果的可用性. ...
基于出租车GPS轨迹和POI数据的商业选址推荐
0
2020
基于出租车GPS轨迹和POI数据的商业选址推荐
0
2020
GIS多准则的城市垃圾楼空间布局优化选址
1
2018
... 在“小集聚-大分散”空间规律的基础上,提出面向城市规划复杂系统的模糊选址方法. 在如图3 所示的核密度分析结果基础上,将点核密度分析结果大于等于0.00001 的区域作为边界,生成围合区域(见图8 ). 模糊选址在本研究的空间意义是,在图8 的线框所构成的点聚集区内,任意位置皆可以作为对应应急事件所需设施的建设点,并且在同一点聚集区内的任意选点,都不会对该区域服务范围内人口点进行核酸检测活动的时间效能产生变化. 由表1 统计结果及研究计算结果可得,32 个点聚集区能够涵盖上城区所有人口点的核酸检测活动需求,并且在这样的分布情况下,任意人口点到往设施点的耗时都在215.5516 ~319.1667 s,虽然全区域最大极差为103.6151 s,但在各个点聚集区内部的最大极差则为9.8221 s,故而在各个点聚集区内,不同设施点选址方案对于该区域服务能力的影响程度不大. 在以往以缪遇虹等[29 -31 ] 为代表的城市设施选址研究中,选址研究成果往往具有精确坐标,虽然这类结果具有较强的落地性与精确性,但是城市作为一个复杂巨系统,并不能完全保证这一精确计算结果实际可用,留有余地的模糊选址方案能让规划人员在施行方案设计时,更充分地考虑实际规划条件,并且扩大了设施点备选规模,保证选址结果的可用性. ...
GIS多准则的城市垃圾楼空间布局优化选址
1
2018
... 在“小集聚-大分散”空间规律的基础上,提出面向城市规划复杂系统的模糊选址方法. 在如图3 所示的核密度分析结果基础上,将点核密度分析结果大于等于0.00001 的区域作为边界,生成围合区域(见图8 ). 模糊选址在本研究的空间意义是,在图8 的线框所构成的点聚集区内,任意位置皆可以作为对应应急事件所需设施的建设点,并且在同一点聚集区内的任意选点,都不会对该区域服务范围内人口点进行核酸检测活动的时间效能产生变化. 由表1 统计结果及研究计算结果可得,32 个点聚集区能够涵盖上城区所有人口点的核酸检测活动需求,并且在这样的分布情况下,任意人口点到往设施点的耗时都在215.5516 ~319.1667 s,虽然全区域最大极差为103.6151 s,但在各个点聚集区内部的最大极差则为9.8221 s,故而在各个点聚集区内,不同设施点选址方案对于该区域服务能力的影响程度不大. 在以往以缪遇虹等[29 -31 ] 为代表的城市设施选址研究中,选址研究成果往往具有精确坐标,虽然这类结果具有较强的落地性与精确性,但是城市作为一个复杂巨系统,并不能完全保证这一精确计算结果实际可用,留有余地的模糊选址方案能让规划人员在施行方案设计时,更充分地考虑实际规划条件,并且扩大了设施点备选规模,保证选址结果的可用性. ...
国土空间韧性规划建设整体框架与发展路径研究
1
2023
... 以核酸检测为代表的公共卫生事件,实际上是公共应急场景的一个子集. 王威等[32 ] 认为,当前的国土空间规划体系,仍缺少对应急事件相关资源配置的全方位考虑. 因此,在现今的城市规划过程中,须应对可能发生的应急管理事件作出合理规划,即“城市应急空间规划”. 而在城市应急事件中,所涉及到的应急事件大多为单一目的行为过程,因此本研究提出的方法论可以修改对应参数(如人群特征、目标函数)后进行针对设施布点的科学建议. ...
国土空间韧性规划建设整体框架与发展路径研究
1
2023
... 以核酸检测为代表的公共卫生事件,实际上是公共应急场景的一个子集. 王威等[32 ] 认为,当前的国土空间规划体系,仍缺少对应急事件相关资源配置的全方位考虑. 因此,在现今的城市规划过程中,须应对可能发生的应急管理事件作出合理规划,即“城市应急空间规划”. 而在城市应急事件中,所涉及到的应急事件大多为单一目的行为过程,因此本研究提出的方法论可以修改对应参数(如人群特征、目标函数)后进行针对设施布点的科学建议. ...