[1]
LI Z, GUAN S, JIN X, et al. Complex evolutional pattern learning for temporal knowledge graph reasoning [C]// Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 2: Short Papers) . Dublin: ACL, 2022: 290-296.
[本文引用: 1]
[2]
CHEN Z, ZHAO X, LIAO J, et al Temporal knowledge graph question answering via subgraph reasoning
[J]. Knowledge-Based Systems , 2022 , 251 : 109134
DOI:10.1016/j.knosys.2022.109134
[本文引用: 1]
[3]
LONG J, CHEN Z, HE W, et al An integrated framework of deep learning and knowledge graph for prediction of stock price trend: an application in Chinese stock exchange market
[J]. Applied Soft Computing , 2020 , 91 : 106205
DOI:10.1016/j.asoc.2020.106205
[本文引用: 1]
[4]
GARCIA-DURAN A, DUMANČIĆ S, NIEPERT M. Learning sequence encoders for temporal knowledge graph completion [C]// Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing . Brussel: ACL, 2018: 4816-4821.
[本文引用: 5]
[5]
LEBLAY J, CHEKOL M W. Deriving validity time in knowledge graph [C]// Companion Proceedings of the Web Conference . Lyon: ACM, 2018: 1771-1776.
[本文引用: 2]
[6]
LEETARU K, SCHRODT P A. Gdelt: global data on events, location, and tone, 1979–2012 [C]// ISA Annual Convention . San Francisco: Citeseer, 2013: 1-49.
[本文引用: 1]
[7]
KIM H A, D’ORAZIO V, BRANDT P T, et al UTDEventData: an r package to access political event data
[J]. Journal of Open Source Software , 2019 , 4 (36 ): 1322
DOI:10.21105/joss.01322
[本文引用: 1]
[8]
WANG Q, MAO Z, WANG B, et al Knowledge graph embedding: a survey of approaches and applications
[J]. IEEE Transactions on Knowledge and Data Engineering , 2017 , 29 (12 ): 2724 - 2743
DOI:10.1109/TKDE.2017.2754499
[本文引用: 1]
[9]
BORDES A, USUNIER N, GARCIA-DURAN A, et al Translating embeddings for modeling multi-relational data
[J]. Advances in Neural Information Processing Systems , 2013 , 26 : 2787 - 2795
[本文引用: 1]
[10]
WANG Z, ZHANG J, FENG J, et al. Knowledge graph embedding by translating on hyperplanes [C]// Proceedings of the AAAI Conference on Artificial Intelligence . Québec: AAAI, 2014: 752-786.
[本文引用: 1]
[11]
LIN Y, LIU Z, SUN M, et al. Learning entity and relation embeddings for knowledge graph completion [C]// Proceedings of the AAAI conference on Artificial Intelligence . Texas: AAAI, 2015: 762-816.
[本文引用: 1]
[12]
TROUILLON T, DANCE C R, GAUSSIER É, et al Knowledge graph completion via complex tensor factorization
[J]. The Journal of Machine Learning Research , 2017 , 18 (1 ): 4735 - 4772
[本文引用: 1]
[13]
NICKEL M, TRESP V, KRIEGEL H P. A three-way model for collective learning on multi-relational data [C]// Proceedings of the 28th International Conference on International Conference on Machine Learning . [S. l. ]: IEEE, 2011: 809-816.
[本文引用: 1]
[14]
YANG B, YIH S W, HE X, et al. Embedding entities and relations for learning and inference in knowledge bases [C]// Proceedings of the International Conference on Learning Representations . San Diego: IEEE, 2015.
[本文引用: 1]
[15]
TROUILLON T, DANCE C R, GAUSSIER É, et al Knowledge graph completion via complex tensor factorization
[J]. Journal of Machine Learning Research , 2017 , 18 (130 ): 1 - 38
[本文引用: 1]
[16]
DETTMERS T, MINERVINI P, STENETORP P, et al. Convolutional 2d knowledge graph embeddings [C]// Proceedings of the AAAI Conference on Artificial Intelligence . New Orleans: AAAI, 2018: 612-618.
[本文引用: 1]
[17]
NGUYEN T D, NGUYEN D Q, PHUNG D, et al. A novel embedding model for knowledge base completion based on convolutional neural network [C]// Proceedings of NAACL-HLT . New Orleans: ACL, 2018: 327-333.
[本文引用: 1]
[18]
SCHLICHTKRULL M, KIPF T N, BLOEM P, et al. Modeling relational data with graph convolutional networks [C]// The Semantic Web: 15th International Conference, ESWC 2018. Heraklion: Springer, 2018: 593-607.
[本文引用: 1]
[19]
VASHISHTH S, SANYAL S, NITIN V, et al. Composition-based multi-relational graph convolutional networks [C]// International Conference on Learning Representations . New Orleans: IEEE, 2019.
[本文引用: 1]
[20]
JIANG T, LIU T, GE T, et al. Encoding temporal information for time-aware link prediction [C]// Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing . Texas: ACL, 2016: 2350-2354.
[本文引用: 1]
[21]
GARCIA-DURAN A, DUMANČIĆ S, NIEPERT M. Learning sequence encoders for temporal knowledge graph completion [C]// Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing . Brussels: ACL, 2018: 4816-4821.
[本文引用: 1]
[22]
DASGUPTA S S, RAY S N, TALUKDAR P P. HyTE: hyperplane-based temporally aware knowledge graph embedding [C]// Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing . Brussels: ACL, 2018: 2001-2011.
[本文引用: 1]
[23]
XU C, NAYYERI M, ALKHOURY F, et al. Temporal knowledge graph embedding model based on additive time series decomposition [C]// International Semantic Web Conference . [S. l. ]: IEEE, 2020.
[本文引用: 1]
[24]
LEBLAY J, CHEKOL M W. Deriving validity time in knowledge graph [C]// Companion Proceedings of the Web Conference . Lyon: WWW, 2018: 1771-1776.
[本文引用: 1]
[25]
LACROIX T, OBOZINSKI G, USUNIER N. Tensor decompositions for temporal knowledge base completion [C]// International Conference on Learning Representations . New Orleans: IEEE, 2019.
[本文引用: 3]
[27]
GAO Y, FENG L, KAN Z, et al. Modeling precursors for temporal knowledge graph reasoning via auto-encoder structure [C]// Proceedings of the 31st International Joint Conference on Artificial Intelligence . Vienna: ACM, 2022: 23-29.
[本文引用: 5]
[28]
YU Y, SI X, HU C, et al A review of recurrent neural networks: LSTM cells and network architectures
[J]. Neural Computation , 2019 , 31 (7 ): 1235 - 1270
DOI:10.1162/neco_a_01199
[本文引用: 1]
[29]
HAN Z, ZHANG G, MA Y, et al. Time-dependent entity embedding is not all you need: a re-evaluation of temporal knowledge graph completion models under a unified framework [C]// Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing . Punta Cana: ACL, 2021: 8104-8118.
[本文引用: 3]
[30]
DAI Y, WANG S, XIONG N N, et al A survey on knowledge graph embedding: approaches, applications and benchmarks
[J]. Electronics , 2020 , 9 (5 ): 750
DOI:10.3390/electronics9050750
[本文引用: 1]
[31]
LEBLAY J, CHEKOL M W, LIU X, et al. Towards temporal knowledge graph embeddings with arbitrary time precision [C]// Proceedings of the 29th ACM International Conference on Information and Knowledge Management. [S. l.]: ACM, 2020: 685-694.
[本文引用: 1]
[32]
KAZEMI S M, POOLE D Simple embedding for link prediction in knowledge graphs
[J]. Advances in Neural Information Processing Systems , 2018 , 31 (3 ): 4289 - 4300
[本文引用: 1]
[33]
GOEL R, KAZEMI S M, BRUBAKER M, et al. Diachronic embedding for temporal knowledge graph completion [C]// Proceedings of the AAAI Conference on Artificial Intelligence . New York: AAAI, 2020, 34(4): 3988-3995.
[本文引用: 10]
[34]
XU C, NAYYERI M, ALKHOURY F, et al. TeRo: a time-aware knowledge graph embedding via temporal rotation [C]// Proceedings of the 28th International Conference on Computational Linguistics . Barcelona: ACL, 2020: 1583-1593.
[本文引用: 3]
[35]
JIN W, QU M, JIN X, et al. Recurrent event network: autoregressive structure inference over temporal knowledge graphs [C]// Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing . [S. l. ]: ACL, 2020: 6669-6683.
[本文引用: 1]
[36]
LI Z, JIN X, LI W, et al. Temporal knowledge graph reasoning based on evolutional representation learning [C]// Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval . [S. l. ]: ACM, 2021: 408-417.
[本文引用: 1]
[37]
SHAO P, ZHANG D, YANG G, et al Tucker decomposition-based temporal knowledge graph completion
[J]. Knowledge-Based Systems , 2022 , 238 : 107841
DOI:10.1016/j.knosys.2021.107841
[本文引用: 4]
1
... 传统的知识图谱仅关注实体之间的静态关系,然而在实际应用中,知识图谱往往包含了时间信息,以表示2个实体之间的关系在特定时间内成立. 为了对时序知识进行感知推理,引入时序知识图谱(temporal knowledge graph,TKG). TKG以四元组(s ,r , o , t )的形式表示事实,描述该事实在时间t 内有效,其中s (subject)和o (object)表示实体,r (relation)表示边类型即关系,t (timestamp)表示时间戳,例如(Joe Biden, inauguration, Chief Executive, 2021). 此外,时间信息可以广泛应用于多个领域的下游任务中,如历史事件的推理[1 ] 、问答系统[2 ] 、金融预测[3 ] 等. 在时序知识图谱表示学习中,实体和关系之间的时间信息常常以嵌入的形式进行表示,嵌入是将时间信息编码成连续向量的技术,可以将时间维度纳入知识图谱中的实体和关系表示中,以便于模型进行时间感知的推理. 时序嵌入方式包括时序内嵌的三元组[4 ] 及时间独立的四元组[5 ] . 随着时间信息的重要性日益凸显,知识图谱的时间感知推理成为知识图谱研究领域的热门研究方向. ...
Temporal knowledge graph question answering via subgraph reasoning
1
2022
... 传统的知识图谱仅关注实体之间的静态关系,然而在实际应用中,知识图谱往往包含了时间信息,以表示2个实体之间的关系在特定时间内成立. 为了对时序知识进行感知推理,引入时序知识图谱(temporal knowledge graph,TKG). TKG以四元组(s ,r , o , t )的形式表示事实,描述该事实在时间t 内有效,其中s (subject)和o (object)表示实体,r (relation)表示边类型即关系,t (timestamp)表示时间戳,例如(Joe Biden, inauguration, Chief Executive, 2021). 此外,时间信息可以广泛应用于多个领域的下游任务中,如历史事件的推理[1 ] 、问答系统[2 ] 、金融预测[3 ] 等. 在时序知识图谱表示学习中,实体和关系之间的时间信息常常以嵌入的形式进行表示,嵌入是将时间信息编码成连续向量的技术,可以将时间维度纳入知识图谱中的实体和关系表示中,以便于模型进行时间感知的推理. 时序嵌入方式包括时序内嵌的三元组[4 ] 及时间独立的四元组[5 ] . 随着时间信息的重要性日益凸显,知识图谱的时间感知推理成为知识图谱研究领域的热门研究方向. ...
An integrated framework of deep learning and knowledge graph for prediction of stock price trend: an application in Chinese stock exchange market
1
2020
... 传统的知识图谱仅关注实体之间的静态关系,然而在实际应用中,知识图谱往往包含了时间信息,以表示2个实体之间的关系在特定时间内成立. 为了对时序知识进行感知推理,引入时序知识图谱(temporal knowledge graph,TKG). TKG以四元组(s ,r , o , t )的形式表示事实,描述该事实在时间t 内有效,其中s (subject)和o (object)表示实体,r (relation)表示边类型即关系,t (timestamp)表示时间戳,例如(Joe Biden, inauguration, Chief Executive, 2021). 此外,时间信息可以广泛应用于多个领域的下游任务中,如历史事件的推理[1 ] 、问答系统[2 ] 、金融预测[3 ] 等. 在时序知识图谱表示学习中,实体和关系之间的时间信息常常以嵌入的形式进行表示,嵌入是将时间信息编码成连续向量的技术,可以将时间维度纳入知识图谱中的实体和关系表示中,以便于模型进行时间感知的推理. 时序嵌入方式包括时序内嵌的三元组[4 ] 及时间独立的四元组[5 ] . 随着时间信息的重要性日益凸显,知识图谱的时间感知推理成为知识图谱研究领域的热门研究方向. ...
5
... 传统的知识图谱仅关注实体之间的静态关系,然而在实际应用中,知识图谱往往包含了时间信息,以表示2个实体之间的关系在特定时间内成立. 为了对时序知识进行感知推理,引入时序知识图谱(temporal knowledge graph,TKG). TKG以四元组(s ,r , o , t )的形式表示事实,描述该事实在时间t 内有效,其中s (subject)和o (object)表示实体,r (relation)表示边类型即关系,t (timestamp)表示时间戳,例如(Joe Biden, inauguration, Chief Executive, 2021). 此外,时间信息可以广泛应用于多个领域的下游任务中,如历史事件的推理[1 ] 、问答系统[2 ] 、金融预测[3 ] 等. 在时序知识图谱表示学习中,实体和关系之间的时间信息常常以嵌入的形式进行表示,嵌入是将时间信息编码成连续向量的技术,可以将时间维度纳入知识图谱中的实体和关系表示中,以便于模型进行时间感知的推理. 时序嵌入方式包括时序内嵌的三元组[4 ] 及时间独立的四元组[5 ] . 随着时间信息的重要性日益凸显,知识图谱的时间感知推理成为知识图谱研究领域的热门研究方向. ...
... 受文献[4 ,5 ]的启发,在进行时间信息内嵌的同时,对时间信息进行了独立表示. 本节将详细描述提出的TAC方法. ...
... 为了更方便地处理实际应用中的格式化时间(如2023-06-16),受文献[4 ]的启发,对时间戳进行特殊处理. 对于给定的(可能是缺失的)时间戳,将其分解为表2 所示时间标记组成的序列. 表中, k y: n 中k 表示年份的一位取值,y为年份标记,n 为索引值;i m: n 中i 表示月份的一位取值,m为月份标记,n 为索引值;j d: n 中j 表示天的一位取值,d为天的标记,n 为索引值. 例如对于2014-12-01的时间戳,年份2014表示为2y:2,0y:0,1y:1,4y:4. 对于月份与日的标记,本文与文献[4 ]不同,考虑将月份拆分用2个索引值标记,例如对于12月将其拆分为1m:11和2m:12,对于25日将其拆解为2d:22和5d:25,以此类推. ...
... 为索引值. 例如对于2014-12-01的时间戳,年份2014表示为2y:2,0y:0,1y:1,4y:4. 对于月份与日的标记,本文与文献[4 ]不同,考虑将月份拆分用2个索引值标记,例如对于12月将其拆分为1m:11和2m:12,对于25日将其拆解为2d:22和5d:25,以此类推. ...
... 综合危机预警系统(ICEWS)是当前公开的最大动态知识库之一,收集了来自社交媒体和新闻媒体的政治事件信息. 198个国家从1995年到2018年为该数据集贡献了超过1 700万次政治事件. Garcia-Duran等[4 ] 将ICEWS划分为多个子数据集,其中ICEWS14记录了2014年1月到12月的政治事件,时间非常紧密. ICEWS05-15记录了从2005年1月至2015年12月近10年的政治事件,时间跨度相对较长. GDELT数据集记录全球范围内发生的政治事件,它记录了从1969 年至今的新闻,代表政治领袖、组织和国家等实体一个月内不同类型的事件. 其中ICEWS05-15、ICEWS14、ICEWS11-14、GDELT数据集都是每24 h记录一次. 数据集中包含实体关系和时间统计信息,具体可以参考表3 . ...
2
... 传统的知识图谱仅关注实体之间的静态关系,然而在实际应用中,知识图谱往往包含了时间信息,以表示2个实体之间的关系在特定时间内成立. 为了对时序知识进行感知推理,引入时序知识图谱(temporal knowledge graph,TKG). TKG以四元组(s ,r , o , t )的形式表示事实,描述该事实在时间t 内有效,其中s (subject)和o (object)表示实体,r (relation)表示边类型即关系,t (timestamp)表示时间戳,例如(Joe Biden, inauguration, Chief Executive, 2021). 此外,时间信息可以广泛应用于多个领域的下游任务中,如历史事件的推理[1 ] 、问答系统[2 ] 、金融预测[3 ] 等. 在时序知识图谱表示学习中,实体和关系之间的时间信息常常以嵌入的形式进行表示,嵌入是将时间信息编码成连续向量的技术,可以将时间维度纳入知识图谱中的实体和关系表示中,以便于模型进行时间感知的推理. 时序嵌入方式包括时序内嵌的三元组[4 ] 及时间独立的四元组[5 ] . 随着时间信息的重要性日益凸显,知识图谱的时间感知推理成为知识图谱研究领域的热门研究方向. ...
... 受文献[4 ,5 ]的启发,在进行时间信息内嵌的同时,对时间信息进行了独立表示. 本节将详细描述提出的TAC方法. ...
1
... 在实际应用中,事实性知识和过程性知识往往伴有实时更新的特性,目前,不少知识库都包含时间标记,如全球事件、语言和语调数据库(global database of events, language, and tone,GDELT)[6 ] 、综合危机预警系统(integrated crisis early warning system,ICEWS)[7 ] . 在时序知识图谱中,合理地利用时间信息可以提升知识图谱表示学习的质量,引出知识图谱补全任务,通过给定的已知信息预测主语(?, r , o , t )或宾语(s , r , ?, t ). 为了完成时序知识图谱补全的任务,时序知识图谱嵌入[8 ] (temporal knowledge graph embedding,TKGE)技术应运而生. 结合时间信息与实体和关系嵌入向量,对推导出的新事实进行评分,从而学习到新的实体关系,以达到增强知识图谱完备性的目的;因此,时序知识图谱嵌入的相关研究具有巨大的应用潜力. ...
UTDEventData: an r package to access political event data
1
2019
... 在实际应用中,事实性知识和过程性知识往往伴有实时更新的特性,目前,不少知识库都包含时间标记,如全球事件、语言和语调数据库(global database of events, language, and tone,GDELT)[6 ] 、综合危机预警系统(integrated crisis early warning system,ICEWS)[7 ] . 在时序知识图谱中,合理地利用时间信息可以提升知识图谱表示学习的质量,引出知识图谱补全任务,通过给定的已知信息预测主语(?, r , o , t )或宾语(s , r , ?, t ). 为了完成时序知识图谱补全的任务,时序知识图谱嵌入[8 ] (temporal knowledge graph embedding,TKGE)技术应运而生. 结合时间信息与实体和关系嵌入向量,对推导出的新事实进行评分,从而学习到新的实体关系,以达到增强知识图谱完备性的目的;因此,时序知识图谱嵌入的相关研究具有巨大的应用潜力. ...
Knowledge graph embedding: a survey of approaches and applications
1
2017
... 在实际应用中,事实性知识和过程性知识往往伴有实时更新的特性,目前,不少知识库都包含时间标记,如全球事件、语言和语调数据库(global database of events, language, and tone,GDELT)[6 ] 、综合危机预警系统(integrated crisis early warning system,ICEWS)[7 ] . 在时序知识图谱中,合理地利用时间信息可以提升知识图谱表示学习的质量,引出知识图谱补全任务,通过给定的已知信息预测主语(?, r , o , t )或宾语(s , r , ?, t ). 为了完成时序知识图谱补全的任务,时序知识图谱嵌入[8 ] (temporal knowledge graph embedding,TKGE)技术应运而生. 结合时间信息与实体和关系嵌入向量,对推导出的新事实进行评分,从而学习到新的实体关系,以达到增强知识图谱完备性的目的;因此,时序知识图谱嵌入的相关研究具有巨大的应用潜力. ...
Translating embeddings for modeling multi-relational data
1
2013
... Bordes等[9 ] 提出的TransE是第一个基于翻译距离的加法模型,将关系建模为头实体到尾实体的翻译,尽管它简单高效,但是不能很好地处理复杂关系. 为了解决该问题,Wang等[10 ] 提出TransH,该模型将关系建模为超平面,对实体进行平移操作,通过实体在关系平面上的映射,能够处理一对多、多对多、多对一的复杂关系. TransH将实体和关系放到了同一向量空间,不能区分实体和关系的语义. Lin等[11 ] 提出TransR模型,它将关系建模为实体空间到关系空间的投影矩阵,不仅考虑关系的多样性,而且考虑实体的多样性. TransR模型计算复杂,忽略头实体、尾实体不同的类型和属性. TransD[12 ] 模型在TransR的基础上,将投影矩阵进一步分解为2个向量的乘积. ...
1
... Bordes等[9 ] 提出的TransE是第一个基于翻译距离的加法模型,将关系建模为头实体到尾实体的翻译,尽管它简单高效,但是不能很好地处理复杂关系. 为了解决该问题,Wang等[10 ] 提出TransH,该模型将关系建模为超平面,对实体进行平移操作,通过实体在关系平面上的映射,能够处理一对多、多对多、多对一的复杂关系. TransH将实体和关系放到了同一向量空间,不能区分实体和关系的语义. Lin等[11 ] 提出TransR模型,它将关系建模为实体空间到关系空间的投影矩阵,不仅考虑关系的多样性,而且考虑实体的多样性. TransR模型计算复杂,忽略头实体、尾实体不同的类型和属性. TransD[12 ] 模型在TransR的基础上,将投影矩阵进一步分解为2个向量的乘积. ...
1
... Bordes等[9 ] 提出的TransE是第一个基于翻译距离的加法模型,将关系建模为头实体到尾实体的翻译,尽管它简单高效,但是不能很好地处理复杂关系. 为了解决该问题,Wang等[10 ] 提出TransH,该模型将关系建模为超平面,对实体进行平移操作,通过实体在关系平面上的映射,能够处理一对多、多对多、多对一的复杂关系. TransH将实体和关系放到了同一向量空间,不能区分实体和关系的语义. Lin等[11 ] 提出TransR模型,它将关系建模为实体空间到关系空间的投影矩阵,不仅考虑关系的多样性,而且考虑实体的多样性. TransR模型计算复杂,忽略头实体、尾实体不同的类型和属性. TransD[12 ] 模型在TransR的基础上,将投影矩阵进一步分解为2个向量的乘积. ...
Knowledge graph completion via complex tensor factorization
1
2017
... Bordes等[9 ] 提出的TransE是第一个基于翻译距离的加法模型,将关系建模为头实体到尾实体的翻译,尽管它简单高效,但是不能很好地处理复杂关系. 为了解决该问题,Wang等[10 ] 提出TransH,该模型将关系建模为超平面,对实体进行平移操作,通过实体在关系平面上的映射,能够处理一对多、多对多、多对一的复杂关系. TransH将实体和关系放到了同一向量空间,不能区分实体和关系的语义. Lin等[11 ] 提出TransR模型,它将关系建模为实体空间到关系空间的投影矩阵,不仅考虑关系的多样性,而且考虑实体的多样性. TransR模型计算复杂,忽略头实体、尾实体不同的类型和属性. TransD[12 ] 模型在TransR的基础上,将投影矩阵进一步分解为2个向量的乘积. ...
1
... 乘法模型是根据相似性的评分函数来评价三元组的可信度,其中Nickel等[13 ] 提出的RESCAL模型是张量分解模型,它在各种规范关系学习任务中表现良好,缺点是包含的参数过多,容易导致模型的过拟合. 为了解决上述问题,Yang等[14 ] 提出DistMult,它将关系矩阵限制为对角矩阵,减少了模型的参数量,降低了模型过拟合的可能性. DistMult模型的评分函数具有对称性质,不能建模非对称关系. Trouillon等[15 ] 提出ComplEx,它将实体与关系嵌入到复数空间中,由于复数向量乘法的不对称性,ComplEx可以很好地建模非对称关系. ...
1
... 乘法模型是根据相似性的评分函数来评价三元组的可信度,其中Nickel等[13 ] 提出的RESCAL模型是张量分解模型,它在各种规范关系学习任务中表现良好,缺点是包含的参数过多,容易导致模型的过拟合. 为了解决上述问题,Yang等[14 ] 提出DistMult,它将关系矩阵限制为对角矩阵,减少了模型的参数量,降低了模型过拟合的可能性. DistMult模型的评分函数具有对称性质,不能建模非对称关系. Trouillon等[15 ] 提出ComplEx,它将实体与关系嵌入到复数空间中,由于复数向量乘法的不对称性,ComplEx可以很好地建模非对称关系. ...
Knowledge graph completion via complex tensor factorization
1
2017
... 乘法模型是根据相似性的评分函数来评价三元组的可信度,其中Nickel等[13 ] 提出的RESCAL模型是张量分解模型,它在各种规范关系学习任务中表现良好,缺点是包含的参数过多,容易导致模型的过拟合. 为了解决上述问题,Yang等[14 ] 提出DistMult,它将关系矩阵限制为对角矩阵,减少了模型的参数量,降低了模型过拟合的可能性. DistMult模型的评分函数具有对称性质,不能建模非对称关系. Trouillon等[15 ] 提出ComplEx,它将实体与关系嵌入到复数空间中,由于复数向量乘法的不对称性,ComplEx可以很好地建模非对称关系. ...
1
... 神经网络模型具有强大的特征捕获能力,它可以通过非线性变换将输入数据的特征分布从原始空间转换到另一个特征空间,并自动学习特征表示. Dettmers等[16 ] 提出利用二维卷积进行知识图谱嵌入的模型ConvE. 随后,出现了各种利用神经网络进行知识图谱嵌入的工作. Nguyen等[17 ] 认为ConvE只考虑了主语向量e s e r e s e r e o [18 ] 提出R-GCN,引入权值共享和系数约束的方法,采用图卷积神经网络解决知识图谱关系型数据的补全任务,包括链接预测和实体分类. CompGCN[19 ] 设计实体和关系的组合表示算子,在邻居聚合过程中允许各种实体和关系的交互,通过同样的聚合函数完成不同关系类型的邻居实体聚合,具有参数少但灵活的特点. ...
1
... 神经网络模型具有强大的特征捕获能力,它可以通过非线性变换将输入数据的特征分布从原始空间转换到另一个特征空间,并自动学习特征表示. Dettmers等[16 ] 提出利用二维卷积进行知识图谱嵌入的模型ConvE. 随后,出现了各种利用神经网络进行知识图谱嵌入的工作. Nguyen等[17 ] 认为ConvE只考虑了主语向量e s e r e s e r e o [18 ] 提出R-GCN,引入权值共享和系数约束的方法,采用图卷积神经网络解决知识图谱关系型数据的补全任务,包括链接预测和实体分类. CompGCN[19 ] 设计实体和关系的组合表示算子,在邻居聚合过程中允许各种实体和关系的交互,通过同样的聚合函数完成不同关系类型的邻居实体聚合,具有参数少但灵活的特点. ...
1
... 神经网络模型具有强大的特征捕获能力,它可以通过非线性变换将输入数据的特征分布从原始空间转换到另一个特征空间,并自动学习特征表示. Dettmers等[16 ] 提出利用二维卷积进行知识图谱嵌入的模型ConvE. 随后,出现了各种利用神经网络进行知识图谱嵌入的工作. Nguyen等[17 ] 认为ConvE只考虑了主语向量e s e r e s e r e o [18 ] 提出R-GCN,引入权值共享和系数约束的方法,采用图卷积神经网络解决知识图谱关系型数据的补全任务,包括链接预测和实体分类. CompGCN[19 ] 设计实体和关系的组合表示算子,在邻居聚合过程中允许各种实体和关系的交互,通过同样的聚合函数完成不同关系类型的邻居实体聚合,具有参数少但灵活的特点. ...
1
... 神经网络模型具有强大的特征捕获能力,它可以通过非线性变换将输入数据的特征分布从原始空间转换到另一个特征空间,并自动学习特征表示. Dettmers等[16 ] 提出利用二维卷积进行知识图谱嵌入的模型ConvE. 随后,出现了各种利用神经网络进行知识图谱嵌入的工作. Nguyen等[17 ] 认为ConvE只考虑了主语向量e s e r e s e r e o [18 ] 提出R-GCN,引入权值共享和系数约束的方法,采用图卷积神经网络解决知识图谱关系型数据的补全任务,包括链接预测和实体分类. CompGCN[19 ] 设计实体和关系的组合表示算子,在邻居聚合过程中允许各种实体和关系的交互,通过同样的聚合函数完成不同关系类型的邻居实体聚合,具有参数少但灵活的特点. ...
1
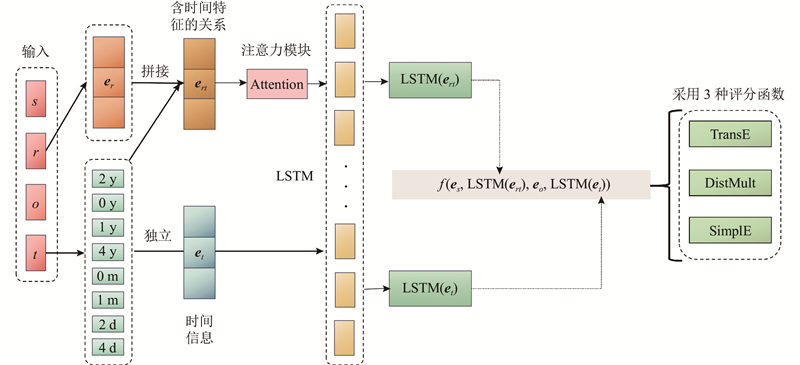
... 时间内嵌的嵌入方法是把时间信息的特征内嵌到实体或关系中,使得实体或关系在建模中含有时间特征. 本质上是将四元组降维成含有时间信息的三元组,使用传统的静态知识图谱嵌入方法开展链接预测任务. t-TransE[20 ] 是最早利用时间信息的嵌入模型之一,尤其是时间敏感事实中关系的时间顺序会影响时序知识推理. 如果r i r j e i r i r j r i r j g (r i r j r i M r j 1 ,其中M r i [21 ] 分别是TransE和DistMult的扩展,其中时间戳向量通过与关系向量进行拼接,得到更好的关系向量表示,然后输入到LSTM并获得它的最终输出,用于表示降维后三元组中的关系. 采用TransE的评分方式,具有以下评分函数:f (s, r, o, t ) = ||e s e rt e o 1/2 . 采用DistMult的评分方式,具有以下评分函数:f (s, r, o, t ) = (e s $ \circ $ e o e rt T . 其中e s e o e rt $ \circ $ [22 ] 方法将主语、关系和宾语的嵌入向量投影到特定于时间戳的超平面中,对投影的嵌入应用TransE的评分函数:f (s, r, o, t ) = ||P t e s P t e r P t e o P t v t 上的实体或关系v [23 ] 通过使用加性时间序列分解,将时间信息合并到实体或关系表示中. 每个实体或关系在一个时间步嵌入的平均值显示了当前的预期位置,而它的协方差(在时间上是固定的)表示它的时间不确定性. 综上所述,时序信息内嵌方法已被证明可以取得较好的结果. ...
1
... 时间内嵌的嵌入方法是把时间信息的特征内嵌到实体或关系中,使得实体或关系在建模中含有时间特征. 本质上是将四元组降维成含有时间信息的三元组,使用传统的静态知识图谱嵌入方法开展链接预测任务. t-TransE[20 ] 是最早利用时间信息的嵌入模型之一,尤其是时间敏感事实中关系的时间顺序会影响时序知识推理. 如果r i r j e i r i r j r i r j g (r i r j r i M r j 1 ,其中M r i [21 ] 分别是TransE和DistMult的扩展,其中时间戳向量通过与关系向量进行拼接,得到更好的关系向量表示,然后输入到LSTM并获得它的最终输出,用于表示降维后三元组中的关系. 采用TransE的评分方式,具有以下评分函数:f (s, r, o, t ) = ||e s e rt e o 1/2 . 采用DistMult的评分方式,具有以下评分函数:f (s, r, o, t ) = (e s $ \circ $ e o e rt T . 其中e s e o e rt $ \circ $ [22 ] 方法将主语、关系和宾语的嵌入向量投影到特定于时间戳的超平面中,对投影的嵌入应用TransE的评分函数:f (s, r, o, t ) = ||P t e s P t e r P t e o P t v t 上的实体或关系v [23 ] 通过使用加性时间序列分解,将时间信息合并到实体或关系表示中. 每个实体或关系在一个时间步嵌入的平均值显示了当前的预期位置,而它的协方差(在时间上是固定的)表示它的时间不确定性. 综上所述,时序信息内嵌方法已被证明可以取得较好的结果. ...
1
... 时间内嵌的嵌入方法是把时间信息的特征内嵌到实体或关系中,使得实体或关系在建模中含有时间特征. 本质上是将四元组降维成含有时间信息的三元组,使用传统的静态知识图谱嵌入方法开展链接预测任务. t-TransE[20 ] 是最早利用时间信息的嵌入模型之一,尤其是时间敏感事实中关系的时间顺序会影响时序知识推理. 如果r i r j e i r i r j r i r j g (r i r j r i M r j 1 ,其中M r i [21 ] 分别是TransE和DistMult的扩展,其中时间戳向量通过与关系向量进行拼接,得到更好的关系向量表示,然后输入到LSTM并获得它的最终输出,用于表示降维后三元组中的关系. 采用TransE的评分方式,具有以下评分函数:f (s, r, o, t ) = ||e s e rt e o 1/2 . 采用DistMult的评分方式,具有以下评分函数:f (s, r, o, t ) = (e s $ \circ $ e o e rt T . 其中e s e o e rt $ \circ $ [22 ] 方法将主语、关系和宾语的嵌入向量投影到特定于时间戳的超平面中,对投影的嵌入应用TransE的评分函数:f (s, r, o, t ) = ||P t e s P t e r P t e o P t v t 上的实体或关系v [23 ] 通过使用加性时间序列分解,将时间信息合并到实体或关系表示中. 每个实体或关系在一个时间步嵌入的平均值显示了当前的预期位置,而它的协方差(在时间上是固定的)表示它的时间不确定性. 综上所述,时序信息内嵌方法已被证明可以取得较好的结果. ...
1
... 时间内嵌的嵌入方法是把时间信息的特征内嵌到实体或关系中,使得实体或关系在建模中含有时间特征. 本质上是将四元组降维成含有时间信息的三元组,使用传统的静态知识图谱嵌入方法开展链接预测任务. t-TransE[20 ] 是最早利用时间信息的嵌入模型之一,尤其是时间敏感事实中关系的时间顺序会影响时序知识推理. 如果r i r j e i r i r j r i r j g (r i r j r i M r j 1 ,其中M r i [21 ] 分别是TransE和DistMult的扩展,其中时间戳向量通过与关系向量进行拼接,得到更好的关系向量表示,然后输入到LSTM并获得它的最终输出,用于表示降维后三元组中的关系. 采用TransE的评分方式,具有以下评分函数:f (s, r, o, t ) = ||e s e rt e o 1/2 . 采用DistMult的评分方式,具有以下评分函数:f (s, r, o, t ) = (e s $ \circ $ e o e rt T . 其中e s e o e rt $ \circ $ [22 ] 方法将主语、关系和宾语的嵌入向量投影到特定于时间戳的超平面中,对投影的嵌入应用TransE的评分函数:f (s, r, o, t ) = ||P t e s P t e r P t e o P t v t 上的实体或关系v [23 ] 通过使用加性时间序列分解,将时间信息合并到实体或关系表示中. 每个实体或关系在一个时间步嵌入的平均值显示了当前的预期位置,而它的协方差(在时间上是固定的)表示它的时间不确定性. 综上所述,时序信息内嵌方法已被证明可以取得较好的结果. ...
1
... 时间独立嵌入方法是学习四元组(e s e r e o e t [24 ] 模型,该模型将时间戳嵌入单独表示,时间信息、实体和关系表示在相同的向量空间中. TTransE具有较好的可解释性,能够处理多关系的情况,即同一实体对应多个不同的关系,对于链式关系的效果较好,但对于反义关系和对称关系的处理效果较差. TTransE存在过拟合的问题,当知识图谱数据量较小时,模型容易受到噪声的影响,导致效果不佳,评分函数为f (s, r, o, t ) = ||e s e r e t e o 1/2 . TComplEx[25 ] 添加了时间戳嵌入,调制多线性点积. 时间戳可以用于等效的调制主语、谓词或对象,评分函数为f (s, r, o, t ) = Re(<e s w r e o w t w [25 ] 提出的另一种引入非时间组件的知识图谱表示学习方法,即只允许嵌入组件的一小部分γ 在时间上被调制,从而将嵌入向量分解为时间相关的向量和非时间相关的向量2个部分,这种分解称为TNTComplEx[25 ] . 这几个模型将时间信息作为独立的向量进行处理. ...
3
... 时间独立嵌入方法是学习四元组(e s e r e o e t [24 ] 模型,该模型将时间戳嵌入单独表示,时间信息、实体和关系表示在相同的向量空间中. TTransE具有较好的可解释性,能够处理多关系的情况,即同一实体对应多个不同的关系,对于链式关系的效果较好,但对于反义关系和对称关系的处理效果较差. TTransE存在过拟合的问题,当知识图谱数据量较小时,模型容易受到噪声的影响,导致效果不佳,评分函数为f (s, r, o, t ) = ||e s e r e t e o 1/2 . TComplEx[25 ] 添加了时间戳嵌入,调制多线性点积. 时间戳可以用于等效的调制主语、谓词或对象,评分函数为f (s, r, o, t ) = Re(<e s w r e o w t w [25 ] 提出的另一种引入非时间组件的知识图谱表示学习方法,即只允许嵌入组件的一小部分γ 在时间上被调制,从而将嵌入向量分解为时间相关的向量和非时间相关的向量2个部分,这种分解称为TNTComplEx[25 ] . 这几个模型将时间信息作为独立的向量进行处理. ...
... [25 ]提出的另一种引入非时间组件的知识图谱表示学习方法,即只允许嵌入组件的一小部分γ 在时间上被调制,从而将嵌入向量分解为时间相关的向量和非时间相关的向量2个部分,这种分解称为TNTComplEx[25 ] . 这几个模型将时间信息作为独立的向量进行处理. ...
... [25 ]. 这几个模型将时间信息作为独立的向量进行处理. ...
基于时序感知LR的动态知识图谱补全方法
1
2022
... 如表1 所示为现有的知识图谱补全方法在相似性理论和知识维度建模方面的差异[26 ] . 表中,$ \circ $ $* $ Ω W w f 为非线性函数,σ 为sigmoid激活函数,ConvTransE为评分函数,H t D KL 为基于KL散度的对称相似度度量,P r ,t P e ,t
基于时序感知LR的动态知识图谱补全方法
1
2022
... 如表1 所示为现有的知识图谱补全方法在相似性理论和知识维度建模方面的差异[26 ] . 表中,$ \circ $ $* $ Ω W w f 为非线性函数,σ 为sigmoid激活函数,ConvTransE为评分函数,H t D KL 为基于KL散度的对称相似度度量,P r ,t P e ,t
5
... Comparison of approaches for knowledge graph completion
Tab.1 补全方法 适用知识库 建模维度 时间特征 时间维度融合 相似性评价函数 TransE 三元组 s,r,o × × $ f\left( {s,r,o} \right) = \left\| {{{\boldsymbol{e}}_s}+{{\boldsymbol{e}}_r} - {{\boldsymbol{e}}_o}} \right\| $ DistMult 三元组 s,r,o × × $ f\left( {s,r,o} \right) = \left\langle {{{\boldsymbol{e}}_s},{{\boldsymbol{e}}_r},{{\boldsymbol{e}}_o}} \right\rangle $ ComplEx 三元组 s,r,o × × $ f\left( {s,r,o} \right) = {{\mathrm{Re}}} \left( {\langle {{\boldsymbol{e}}_s},{{\boldsymbol{w}}_r},{{\boldsymbol{e}}_o}\rangle } \right) $ ConvE 三元组 s,r,o × × $ f\left( {s,r,o} \right) = f({\mathrm{vec}}(f([{{\boldsymbol{\bar e}}_s};{{\boldsymbol{\bar r}}_r}] * {\boldsymbol{\varOmega}})){{\boldsymbol{W}}}){{\boldsymbol{e}}_o} $ ConvKB 三元组 s,r,o × × $ f\left( {s,r,o} \right) = {\text{concat}}(f([{{\boldsymbol{e}}_s},{{\boldsymbol{e}}_r},{{\boldsymbol{e}}_o}] * {\boldsymbol{\varOmega}} )) \cdot {\boldsymbol{w}} $ HyTE 四元组 s,r,o √ √ $ f\left( {s,r,o,t} \right) = \left\| {{P_t}({{\boldsymbol{e}}_s})+{P_t}({{\boldsymbol{e}}_r}) - {P_t}({{\boldsymbol{e}}_o})} \right\| $ TA-TransE 四元组 s,r,o √ √ $ f\left( {s,r,o,t} \right) = \left\| {{{\boldsymbol{e}}_s}+{{\boldsymbol{e}}_{{r_{{\mathrm{seq}}}}}} - {{\boldsymbol{e}}_o}} \right\| $ TA-DistMult 四元组 s,r,o √ √ $ f\left( {s,r,o,t} \right) = ({{\boldsymbol{e}}_s} \circ {{\boldsymbol{e}}_o}){{\boldsymbol{e}}_{{r_{{\mathrm{seq}}}}}}^{\text{T}} $ ST-ConvKB 四元组 s,r,o √ √ $ f\left( {s,r,o,t} \right) = {\text{concat}}(f([{{\boldsymbol{e}}_{{s_t}}},{{\boldsymbol{e}}_r},{{\boldsymbol{e}}_{{o_t}}}] * {\boldsymbol{\varOmega}} )) \cdot {\boldsymbol{w}} $ TTransE 四元组 s,r,o,t √ × $ f\left( {s,r,o,t} \right) = \left\| {{{\boldsymbol{e}}_s}+{{\boldsymbol{e}}_r}+{{\boldsymbol{e}}_t} - {{\boldsymbol{e}}_o}} \right\| $ TComplEx 四元组 s,r,o,t √ × $ f\left( {s,r,o,t} \right) = {{\mathrm{Re}}} (\langle {{\boldsymbol{e}}_s},{{\boldsymbol{w}}_r},{{\boldsymbol{e}}_o},{{\boldsymbol{w}}_t}\rangle ) $ RE-GCN[27 ] 四元组 s,r,o √ √ $ \vec p(o|s,r,{{\boldsymbol{H}}_t},{R_t}) = \sigma ({{\boldsymbol{H}}_t}{\text{ConvTransE}}({{\boldsymbol{e}}_{{s_t}}},{{\boldsymbol{e}}_{{r_t}}})) $ ATiSE 四元组 s,r,o √ √ $ f\left( {s,r,o,t} \right) = {D_{{\mathrm{KL}}}}({{\boldsymbol{P}}_{r,t}},{{\boldsymbol{P}}_{e,t}}) $ TeRo 四元组 s,r,o √ √ $ f\left( {s,r,o,t} \right) = ||{{\boldsymbol{e}}_{{s_t}}}+{{\boldsymbol{e}}_r} - \overline {{{\boldsymbol{e}}_{ot}}} || $
综上所述,尽管静态知识图谱嵌入模型具有较好的推理能力,但对如今实时更新的知识库而言,静态知识图谱对时序信息不敏感,不能很好地建模时序关系,推理时序知识. 为了更好地表示学习动态知识图谱,时序知识图谱嵌入的研究是未来的趋势. 时间内嵌与时间独立的时序知识图谱嵌入方法没有充分利用时间信息,补全性能有待进一步的加强. 亟需新的时序信息嵌入方法来提升时序知识图谱嵌入模型的补全性能. 为此,本文提出TAC方法,解决上述问题. ...
... 本文将提出的TAC方法模型与几种经典的静态知识图谱嵌入[30 ] 模型和动态知识图谱嵌入[31 ] 模型进行比较. 其中,TransE、DistMult、SimplE[32 ] 被选为静态嵌入对比模型,这些传统经典的模型在实验中被广泛使用. HyTE、TTransE、TA-DistMult、DE-SimplE[33 ] 、ATiSE、TeRo[34 ] 、RE-Net[35 ] 、RE-GCN[36 ] 、rGalT[27 ] 、TNTcomplEx、TuckERT[37 ] 被选为动态嵌入对比模型,这些模型在处理时序知识图谱补全任务上都取得了较先进的结果,且一些经典的动态嵌入模型在时序链接预测实验中作为对比模型被广泛使用. ...
... Link prediction results of different embedding methods in ICEWS14 and ICEWS05-15
% Tab.4 模型 ICEWS14 ICEWS05-15 GDELT MRR H@1 H@3 H@10 MRR H@1 H@3 H@10 MRR H@1 H@3 H@10 TransE[33 ] 28.0 9.4 — 63.7 29.4 9.0 — 66.3 11.3 0.0 15.8 31.2 DistMult[33 ] 43.9 32.3 — 67.2 45.6 33.7 — 69.1 19.6 11.7 20.8 34.8 SimplE[33 ] 45.8 34.1 51.6 68.7 47.8 35.9 53.9 70.8 20.6 12.4 22.0 36.6 TTransE[33 ] 25.5 7.4 — 60.1 27.1 8.4 — 61.6 11.5 0.0 16.0 31.8 HyTE[33 ] 29.7 10.8 41.6 65.5 31.6 11.6 44.5 68.1 11.8 0.0 16.5 32.6 TA-DistMult[33 ] 47.7 36.3 — 68.6 47.4 34.6 — 72.8 20.6 12.4 21.9 36.5 DE-TransE[33 ] 32.6 12.4 46.7 68.6 31.4 10.8 45.3 68.5 12.6 0.0 18.1 35.0 DE-DistMult[33 ] 50.1 39.2 56.9 70.8 48.4 36.6 54.6 71.8 21.3 13.0 22.8 37.6 DE-SimplE[33 ] 52.6 41.8 59.2 72.5 51.3 39.2 57.8 74.8 23.0 14.1 24.8 40.3 ATiSE[34 ] 55.0 43.6 62.9 75.0 51.9 37.8 60.6 79.4 — — — — TeRo[34 ] 56.2 46.8 62.1 73.2 58.6 46.9 66.8 79.5 — — — — RE-Net[27 ] 36.3 26.7 41.0 54.2 36.7 26.1 41.6 56.8 19.4 11.9 20.5 33.7 RE-GCN[27 ] 37.4 27.4 41.7 57.0 38.0 27.0 43.3 58.9 19.0 11.8 20.3 33.0 rGalT[27 ] 38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8
表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
... [
27 ]
37.4 27.4 41.7 57.0 38.0 27.0 43.3 58.9 19.0 11.8 20.3 33.0 rGalT[27 ] 38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8 表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
... [
27 ]
38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8 表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
A review of recurrent neural networks: LSTM cells and network architectures
1
2019
... 考虑将实体s 和o 的嵌入映射到低维向量空间中,表示为e s e o e r e t e rt e rt = [e r e t e rt e rta e rta e rt = e rta +e rt e rt [28 ] 的网络结构比RNN复杂,从微观上看,LSTM引入了细胞状态,使用输入门、遗忘门、输出门3种门来保持和控制信息,使得LSTM既能够处理短时依赖问题,又能够处理长时依赖问题. 本文将优化后的关系向量表示e rt e rt e t e t 图1 所示为时间序列组合的嵌入方式,其中LSTM的公式如下. ...
3
... 使用Han等[29 ] 提出的最佳模型配置为参考,采用Adam优化器最小化损失函数,对基于加法模型的TAC_TransE采用边际损失函数: ...
... 根据文献[29 ]的研究,采用Adam优化器来训练本文的模型. 对于翻译距离(TransE)的评分,本文采用Marginloss损失函数;对于双线性(DistMult和SimplE)的评分,本文采用BCE损失函数. 根据验证集上的MRR结果,通过早停法来选择最优的超参数. 将最大迭代轮数设置为3 000. 对于ICEWS的2个数据集,将批量大小选择设为{256,512,1 024};对于GDELT,采用{128,256,512,1 024,2 048}中的批量大小,采用{100,200,300,400,500}中的嵌入维数d 及{0.000 1,0.000 3,0.001,0.003}中的学习率l r . ...
... 表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
A survey on knowledge graph embedding: approaches, applications and benchmarks
1
2020
... 本文将提出的TAC方法模型与几种经典的静态知识图谱嵌入[30 ] 模型和动态知识图谱嵌入[31 ] 模型进行比较. 其中,TransE、DistMult、SimplE[32 ] 被选为静态嵌入对比模型,这些传统经典的模型在实验中被广泛使用. HyTE、TTransE、TA-DistMult、DE-SimplE[33 ] 、ATiSE、TeRo[34 ] 、RE-Net[35 ] 、RE-GCN[36 ] 、rGalT[27 ] 、TNTcomplEx、TuckERT[37 ] 被选为动态嵌入对比模型,这些模型在处理时序知识图谱补全任务上都取得了较先进的结果,且一些经典的动态嵌入模型在时序链接预测实验中作为对比模型被广泛使用. ...
1
... 本文将提出的TAC方法模型与几种经典的静态知识图谱嵌入[30 ] 模型和动态知识图谱嵌入[31 ] 模型进行比较. 其中,TransE、DistMult、SimplE[32 ] 被选为静态嵌入对比模型,这些传统经典的模型在实验中被广泛使用. HyTE、TTransE、TA-DistMult、DE-SimplE[33 ] 、ATiSE、TeRo[34 ] 、RE-Net[35 ] 、RE-GCN[36 ] 、rGalT[27 ] 、TNTcomplEx、TuckERT[37 ] 被选为动态嵌入对比模型,这些模型在处理时序知识图谱补全任务上都取得了较先进的结果,且一些经典的动态嵌入模型在时序链接预测实验中作为对比模型被广泛使用. ...
Simple embedding for link prediction in knowledge graphs
1
2018
... 本文将提出的TAC方法模型与几种经典的静态知识图谱嵌入[30 ] 模型和动态知识图谱嵌入[31 ] 模型进行比较. 其中,TransE、DistMult、SimplE[32 ] 被选为静态嵌入对比模型,这些传统经典的模型在实验中被广泛使用. HyTE、TTransE、TA-DistMult、DE-SimplE[33 ] 、ATiSE、TeRo[34 ] 、RE-Net[35 ] 、RE-GCN[36 ] 、rGalT[27 ] 、TNTcomplEx、TuckERT[37 ] 被选为动态嵌入对比模型,这些模型在处理时序知识图谱补全任务上都取得了较先进的结果,且一些经典的动态嵌入模型在时序链接预测实验中作为对比模型被广泛使用. ...
10
... 本文将提出的TAC方法模型与几种经典的静态知识图谱嵌入[30 ] 模型和动态知识图谱嵌入[31 ] 模型进行比较. 其中,TransE、DistMult、SimplE[32 ] 被选为静态嵌入对比模型,这些传统经典的模型在实验中被广泛使用. HyTE、TTransE、TA-DistMult、DE-SimplE[33 ] 、ATiSE、TeRo[34 ] 、RE-Net[35 ] 、RE-GCN[36 ] 、rGalT[27 ] 、TNTcomplEx、TuckERT[37 ] 被选为动态嵌入对比模型,这些模型在处理时序知识图谱补全任务上都取得了较先进的结果,且一些经典的动态嵌入模型在时序链接预测实验中作为对比模型被广泛使用. ...
... Link prediction results of different embedding methods in ICEWS14 and ICEWS05-15
% Tab.4 模型 ICEWS14 ICEWS05-15 GDELT MRR H@1 H@3 H@10 MRR H@1 H@3 H@10 MRR H@1 H@3 H@10 TransE[33 ] 28.0 9.4 — 63.7 29.4 9.0 — 66.3 11.3 0.0 15.8 31.2 DistMult[33 ] 43.9 32.3 — 67.2 45.6 33.7 — 69.1 19.6 11.7 20.8 34.8 SimplE[33 ] 45.8 34.1 51.6 68.7 47.8 35.9 53.9 70.8 20.6 12.4 22.0 36.6 TTransE[33 ] 25.5 7.4 — 60.1 27.1 8.4 — 61.6 11.5 0.0 16.0 31.8 HyTE[33 ] 29.7 10.8 41.6 65.5 31.6 11.6 44.5 68.1 11.8 0.0 16.5 32.6 TA-DistMult[33 ] 47.7 36.3 — 68.6 47.4 34.6 — 72.8 20.6 12.4 21.9 36.5 DE-TransE[33 ] 32.6 12.4 46.7 68.6 31.4 10.8 45.3 68.5 12.6 0.0 18.1 35.0 DE-DistMult[33 ] 50.1 39.2 56.9 70.8 48.4 36.6 54.6 71.8 21.3 13.0 22.8 37.6 DE-SimplE[33 ] 52.6 41.8 59.2 72.5 51.3 39.2 57.8 74.8 23.0 14.1 24.8 40.3 ATiSE[34 ] 55.0 43.6 62.9 75.0 51.9 37.8 60.6 79.4 — — — — TeRo[34 ] 56.2 46.8 62.1 73.2 58.6 46.9 66.8 79.5 — — — — RE-Net[27 ] 36.3 26.7 41.0 54.2 36.7 26.1 41.6 56.8 19.4 11.9 20.5 33.7 RE-GCN[27 ] 37.4 27.4 41.7 57.0 38.0 27.0 43.3 58.9 19.0 11.8 20.3 33.0 rGalT[27 ] 38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8
表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
... [
33 ]
43.9 32.3 — 67.2 45.6 33.7 — 69.1 19.6 11.7 20.8 34.8 SimplE[33 ] 45.8 34.1 51.6 68.7 47.8 35.9 53.9 70.8 20.6 12.4 22.0 36.6 TTransE[33 ] 25.5 7.4 — 60.1 27.1 8.4 — 61.6 11.5 0.0 16.0 31.8 HyTE[33 ] 29.7 10.8 41.6 65.5 31.6 11.6 44.5 68.1 11.8 0.0 16.5 32.6 TA-DistMult[33 ] 47.7 36.3 — 68.6 47.4 34.6 — 72.8 20.6 12.4 21.9 36.5 DE-TransE[33 ] 32.6 12.4 46.7 68.6 31.4 10.8 45.3 68.5 12.6 0.0 18.1 35.0 DE-DistMult[33 ] 50.1 39.2 56.9 70.8 48.4 36.6 54.6 71.8 21.3 13.0 22.8 37.6 DE-SimplE[33 ] 52.6 41.8 59.2 72.5 51.3 39.2 57.8 74.8 23.0 14.1 24.8 40.3 ATiSE[34 ] 55.0 43.6 62.9 75.0 51.9 37.8 60.6 79.4 — — — — TeRo[34 ] 56.2 46.8 62.1 73.2 58.6 46.9 66.8 79.5 — — — — RE-Net[27 ] 36.3 26.7 41.0 54.2 36.7 26.1 41.6 56.8 19.4 11.9 20.5 33.7 RE-GCN[27 ] 37.4 27.4 41.7 57.0 38.0 27.0 43.3 58.9 19.0 11.8 20.3 33.0 rGalT[27 ] 38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8 表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
... [
33 ]
45.8 34.1 51.6 68.7 47.8 35.9 53.9 70.8 20.6 12.4 22.0 36.6 TTransE[33 ] 25.5 7.4 — 60.1 27.1 8.4 — 61.6 11.5 0.0 16.0 31.8 HyTE[33 ] 29.7 10.8 41.6 65.5 31.6 11.6 44.5 68.1 11.8 0.0 16.5 32.6 TA-DistMult[33 ] 47.7 36.3 — 68.6 47.4 34.6 — 72.8 20.6 12.4 21.9 36.5 DE-TransE[33 ] 32.6 12.4 46.7 68.6 31.4 10.8 45.3 68.5 12.6 0.0 18.1 35.0 DE-DistMult[33 ] 50.1 39.2 56.9 70.8 48.4 36.6 54.6 71.8 21.3 13.0 22.8 37.6 DE-SimplE[33 ] 52.6 41.8 59.2 72.5 51.3 39.2 57.8 74.8 23.0 14.1 24.8 40.3 ATiSE[34 ] 55.0 43.6 62.9 75.0 51.9 37.8 60.6 79.4 — — — — TeRo[34 ] 56.2 46.8 62.1 73.2 58.6 46.9 66.8 79.5 — — — — RE-Net[27 ] 36.3 26.7 41.0 54.2 36.7 26.1 41.6 56.8 19.4 11.9 20.5 33.7 RE-GCN[27 ] 37.4 27.4 41.7 57.0 38.0 27.0 43.3 58.9 19.0 11.8 20.3 33.0 rGalT[27 ] 38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8 表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
... [
33 ]
25.5 7.4 — 60.1 27.1 8.4 — 61.6 11.5 0.0 16.0 31.8 HyTE[33 ] 29.7 10.8 41.6 65.5 31.6 11.6 44.5 68.1 11.8 0.0 16.5 32.6 TA-DistMult[33 ] 47.7 36.3 — 68.6 47.4 34.6 — 72.8 20.6 12.4 21.9 36.5 DE-TransE[33 ] 32.6 12.4 46.7 68.6 31.4 10.8 45.3 68.5 12.6 0.0 18.1 35.0 DE-DistMult[33 ] 50.1 39.2 56.9 70.8 48.4 36.6 54.6 71.8 21.3 13.0 22.8 37.6 DE-SimplE[33 ] 52.6 41.8 59.2 72.5 51.3 39.2 57.8 74.8 23.0 14.1 24.8 40.3 ATiSE[34 ] 55.0 43.6 62.9 75.0 51.9 37.8 60.6 79.4 — — — — TeRo[34 ] 56.2 46.8 62.1 73.2 58.6 46.9 66.8 79.5 — — — — RE-Net[27 ] 36.3 26.7 41.0 54.2 36.7 26.1 41.6 56.8 19.4 11.9 20.5 33.7 RE-GCN[27 ] 37.4 27.4 41.7 57.0 38.0 27.0 43.3 58.9 19.0 11.8 20.3 33.0 rGalT[27 ] 38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8 表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
... [
33 ]
29.7 10.8 41.6 65.5 31.6 11.6 44.5 68.1 11.8 0.0 16.5 32.6 TA-DistMult[33 ] 47.7 36.3 — 68.6 47.4 34.6 — 72.8 20.6 12.4 21.9 36.5 DE-TransE[33 ] 32.6 12.4 46.7 68.6 31.4 10.8 45.3 68.5 12.6 0.0 18.1 35.0 DE-DistMult[33 ] 50.1 39.2 56.9 70.8 48.4 36.6 54.6 71.8 21.3 13.0 22.8 37.6 DE-SimplE[33 ] 52.6 41.8 59.2 72.5 51.3 39.2 57.8 74.8 23.0 14.1 24.8 40.3 ATiSE[34 ] 55.0 43.6 62.9 75.0 51.9 37.8 60.6 79.4 — — — — TeRo[34 ] 56.2 46.8 62.1 73.2 58.6 46.9 66.8 79.5 — — — — RE-Net[27 ] 36.3 26.7 41.0 54.2 36.7 26.1 41.6 56.8 19.4 11.9 20.5 33.7 RE-GCN[27 ] 37.4 27.4 41.7 57.0 38.0 27.0 43.3 58.9 19.0 11.8 20.3 33.0 rGalT[27 ] 38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8 表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
... [
33 ]
47.7 36.3 — 68.6 47.4 34.6 — 72.8 20.6 12.4 21.9 36.5 DE-TransE[33 ] 32.6 12.4 46.7 68.6 31.4 10.8 45.3 68.5 12.6 0.0 18.1 35.0 DE-DistMult[33 ] 50.1 39.2 56.9 70.8 48.4 36.6 54.6 71.8 21.3 13.0 22.8 37.6 DE-SimplE[33 ] 52.6 41.8 59.2 72.5 51.3 39.2 57.8 74.8 23.0 14.1 24.8 40.3 ATiSE[34 ] 55.0 43.6 62.9 75.0 51.9 37.8 60.6 79.4 — — — — TeRo[34 ] 56.2 46.8 62.1 73.2 58.6 46.9 66.8 79.5 — — — — RE-Net[27 ] 36.3 26.7 41.0 54.2 36.7 26.1 41.6 56.8 19.4 11.9 20.5 33.7 RE-GCN[27 ] 37.4 27.4 41.7 57.0 38.0 27.0 43.3 58.9 19.0 11.8 20.3 33.0 rGalT[27 ] 38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8 表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
... [
33 ]
32.6 12.4 46.7 68.6 31.4 10.8 45.3 68.5 12.6 0.0 18.1 35.0 DE-DistMult[33 ] 50.1 39.2 56.9 70.8 48.4 36.6 54.6 71.8 21.3 13.0 22.8 37.6 DE-SimplE[33 ] 52.6 41.8 59.2 72.5 51.3 39.2 57.8 74.8 23.0 14.1 24.8 40.3 ATiSE[34 ] 55.0 43.6 62.9 75.0 51.9 37.8 60.6 79.4 — — — — TeRo[34 ] 56.2 46.8 62.1 73.2 58.6 46.9 66.8 79.5 — — — — RE-Net[27 ] 36.3 26.7 41.0 54.2 36.7 26.1 41.6 56.8 19.4 11.9 20.5 33.7 RE-GCN[27 ] 37.4 27.4 41.7 57.0 38.0 27.0 43.3 58.9 19.0 11.8 20.3 33.0 rGalT[27 ] 38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8 表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
... [
33 ]
50.1 39.2 56.9 70.8 48.4 36.6 54.6 71.8 21.3 13.0 22.8 37.6 DE-SimplE[33 ] 52.6 41.8 59.2 72.5 51.3 39.2 57.8 74.8 23.0 14.1 24.8 40.3 ATiSE[34 ] 55.0 43.6 62.9 75.0 51.9 37.8 60.6 79.4 — — — — TeRo[34 ] 56.2 46.8 62.1 73.2 58.6 46.9 66.8 79.5 — — — — RE-Net[27 ] 36.3 26.7 41.0 54.2 36.7 26.1 41.6 56.8 19.4 11.9 20.5 33.7 RE-GCN[27 ] 37.4 27.4 41.7 57.0 38.0 27.0 43.3 58.9 19.0 11.8 20.3 33.0 rGalT[27 ] 38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8 表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
... [
33 ]
52.6 41.8 59.2 72.5 51.3 39.2 57.8 74.8 23.0 14.1 24.8 40.3 ATiSE[34 ] 55.0 43.6 62.9 75.0 51.9 37.8 60.6 79.4 — — — — TeRo[34 ] 56.2 46.8 62.1 73.2 58.6 46.9 66.8 79.5 — — — — RE-Net[27 ] 36.3 26.7 41.0 54.2 36.7 26.1 41.6 56.8 19.4 11.9 20.5 33.7 RE-GCN[27 ] 37.4 27.4 41.7 57.0 38.0 27.0 43.3 58.9 19.0 11.8 20.3 33.0 rGalT[27 ] 38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8 表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
3
... 本文将提出的TAC方法模型与几种经典的静态知识图谱嵌入[30 ] 模型和动态知识图谱嵌入[31 ] 模型进行比较. 其中,TransE、DistMult、SimplE[32 ] 被选为静态嵌入对比模型,这些传统经典的模型在实验中被广泛使用. HyTE、TTransE、TA-DistMult、DE-SimplE[33 ] 、ATiSE、TeRo[34 ] 、RE-Net[35 ] 、RE-GCN[36 ] 、rGalT[27 ] 、TNTcomplEx、TuckERT[37 ] 被选为动态嵌入对比模型,这些模型在处理时序知识图谱补全任务上都取得了较先进的结果,且一些经典的动态嵌入模型在时序链接预测实验中作为对比模型被广泛使用. ...
... Link prediction results of different embedding methods in ICEWS14 and ICEWS05-15
% Tab.4 模型 ICEWS14 ICEWS05-15 GDELT MRR H@1 H@3 H@10 MRR H@1 H@3 H@10 MRR H@1 H@3 H@10 TransE[33 ] 28.0 9.4 — 63.7 29.4 9.0 — 66.3 11.3 0.0 15.8 31.2 DistMult[33 ] 43.9 32.3 — 67.2 45.6 33.7 — 69.1 19.6 11.7 20.8 34.8 SimplE[33 ] 45.8 34.1 51.6 68.7 47.8 35.9 53.9 70.8 20.6 12.4 22.0 36.6 TTransE[33 ] 25.5 7.4 — 60.1 27.1 8.4 — 61.6 11.5 0.0 16.0 31.8 HyTE[33 ] 29.7 10.8 41.6 65.5 31.6 11.6 44.5 68.1 11.8 0.0 16.5 32.6 TA-DistMult[33 ] 47.7 36.3 — 68.6 47.4 34.6 — 72.8 20.6 12.4 21.9 36.5 DE-TransE[33 ] 32.6 12.4 46.7 68.6 31.4 10.8 45.3 68.5 12.6 0.0 18.1 35.0 DE-DistMult[33 ] 50.1 39.2 56.9 70.8 48.4 36.6 54.6 71.8 21.3 13.0 22.8 37.6 DE-SimplE[33 ] 52.6 41.8 59.2 72.5 51.3 39.2 57.8 74.8 23.0 14.1 24.8 40.3 ATiSE[34 ] 55.0 43.6 62.9 75.0 51.9 37.8 60.6 79.4 — — — — TeRo[34 ] 56.2 46.8 62.1 73.2 58.6 46.9 66.8 79.5 — — — — RE-Net[27 ] 36.3 26.7 41.0 54.2 36.7 26.1 41.6 56.8 19.4 11.9 20.5 33.7 RE-GCN[27 ] 37.4 27.4 41.7 57.0 38.0 27.0 43.3 58.9 19.0 11.8 20.3 33.0 rGalT[27 ] 38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8
表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
... [
34 ]
56.2 46.8 62.1 73.2 58.6 46.9 66.8 79.5 — — — — RE-Net[27 ] 36.3 26.7 41.0 54.2 36.7 26.1 41.6 56.8 19.4 11.9 20.5 33.7 RE-GCN[27 ] 37.4 27.4 41.7 57.0 38.0 27.0 43.3 58.9 19.0 11.8 20.3 33.0 rGalT[27 ] 38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8 表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
1
... 本文将提出的TAC方法模型与几种经典的静态知识图谱嵌入[30 ] 模型和动态知识图谱嵌入[31 ] 模型进行比较. 其中,TransE、DistMult、SimplE[32 ] 被选为静态嵌入对比模型,这些传统经典的模型在实验中被广泛使用. HyTE、TTransE、TA-DistMult、DE-SimplE[33 ] 、ATiSE、TeRo[34 ] 、RE-Net[35 ] 、RE-GCN[36 ] 、rGalT[27 ] 、TNTcomplEx、TuckERT[37 ] 被选为动态嵌入对比模型,这些模型在处理时序知识图谱补全任务上都取得了较先进的结果,且一些经典的动态嵌入模型在时序链接预测实验中作为对比模型被广泛使用. ...
1
... 本文将提出的TAC方法模型与几种经典的静态知识图谱嵌入[30 ] 模型和动态知识图谱嵌入[31 ] 模型进行比较. 其中,TransE、DistMult、SimplE[32 ] 被选为静态嵌入对比模型,这些传统经典的模型在实验中被广泛使用. HyTE、TTransE、TA-DistMult、DE-SimplE[33 ] 、ATiSE、TeRo[34 ] 、RE-Net[35 ] 、RE-GCN[36 ] 、rGalT[27 ] 、TNTcomplEx、TuckERT[37 ] 被选为动态嵌入对比模型,这些模型在处理时序知识图谱补全任务上都取得了较先进的结果,且一些经典的动态嵌入模型在时序链接预测实验中作为对比模型被广泛使用. ...
Tucker decomposition-based temporal knowledge graph completion
4
2022
... 本文将提出的TAC方法模型与几种经典的静态知识图谱嵌入[30 ] 模型和动态知识图谱嵌入[31 ] 模型进行比较. 其中,TransE、DistMult、SimplE[32 ] 被选为静态嵌入对比模型,这些传统经典的模型在实验中被广泛使用. HyTE、TTransE、TA-DistMult、DE-SimplE[33 ] 、ATiSE、TeRo[34 ] 、RE-Net[35 ] 、RE-GCN[36 ] 、rGalT[27 ] 、TNTcomplEx、TuckERT[37 ] 被选为动态嵌入对比模型,这些模型在处理时序知识图谱补全任务上都取得了较先进的结果,且一些经典的动态嵌入模型在时序链接预测实验中作为对比模型被广泛使用. ...
... Link prediction results of different embedding methods in ICEWS14 and ICEWS05-15
% Tab.4 模型 ICEWS14 ICEWS05-15 GDELT MRR H@1 H@3 H@10 MRR H@1 H@3 H@10 MRR H@1 H@3 H@10 TransE[33 ] 28.0 9.4 — 63.7 29.4 9.0 — 66.3 11.3 0.0 15.8 31.2 DistMult[33 ] 43.9 32.3 — 67.2 45.6 33.7 — 69.1 19.6 11.7 20.8 34.8 SimplE[33 ] 45.8 34.1 51.6 68.7 47.8 35.9 53.9 70.8 20.6 12.4 22.0 36.6 TTransE[33 ] 25.5 7.4 — 60.1 27.1 8.4 — 61.6 11.5 0.0 16.0 31.8 HyTE[33 ] 29.7 10.8 41.6 65.5 31.6 11.6 44.5 68.1 11.8 0.0 16.5 32.6 TA-DistMult[33 ] 47.7 36.3 — 68.6 47.4 34.6 — 72.8 20.6 12.4 21.9 36.5 DE-TransE[33 ] 32.6 12.4 46.7 68.6 31.4 10.8 45.3 68.5 12.6 0.0 18.1 35.0 DE-DistMult[33 ] 50.1 39.2 56.9 70.8 48.4 36.6 54.6 71.8 21.3 13.0 22.8 37.6 DE-SimplE[33 ] 52.6 41.8 59.2 72.5 51.3 39.2 57.8 74.8 23.0 14.1 24.8 40.3 ATiSE[34 ] 55.0 43.6 62.9 75.0 51.9 37.8 60.6 79.4 — — — — TeRo[34 ] 56.2 46.8 62.1 73.2 58.6 46.9 66.8 79.5 — — — — RE-Net[27 ] 36.3 26.7 41.0 54.2 36.7 26.1 41.6 56.8 19.4 11.9 20.5 33.7 RE-GCN[27 ] 37.4 27.4 41.7 57.0 38.0 27.0 43.3 58.9 19.0 11.8 20.3 33.0 rGalT[27 ] 38.3 28.6 42.9 58.1 38.9 27.6 44.1 58.1 19.6 12.1 20.9 34.1 TNTComplEx[37 ] 56.0 46.0 61.0 74.0 60.0 50.0 65.0 78.0 22.4 14.4 23.9 38.1 TuckERT[37 ] 59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8
表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
... [
37 ]
59.4 51.8 64.0 73.1 62.7 55.0 67.4 76.9 41.1 31.0 45.3 61.4 TuckERTNT[37 ] 60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8 表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...
... [
37 ]
60.4 52.1 65.5 75.3 63.8 55.9 68.6 78.3 38.1 28.3 41.8 57.6 TAC-TransE 23.3 15.2 38.0 62.7 26.3 17.5 42.0 66.4 9.8 3.7 12.0 28.3 TAC-DistMult 58.7 47.8 65.6 78.3 58.7 46.5 65.6 78.2 25.8 17.4 29.7 45.2 TAC-SimplE 62.5 48.8 74.1 89.4 64.5 52.8 76.9 92.2 52.5 35.7 63.3 79.8 表5 给出在ICEWS14、ICEWS11-14数据集上的实验结果,对比模型的结果均来自文献[29 ],所有模型中的最佳结果以粗体显示,次之的以下划线显示. 从表5 可见,除在ICEWS11-14数据集中T方法在H@1评价标准上优于本文提出的TAC外,TAC方法均优于其他方法. 在ICEWS14数据集上,TAC在MRR、H@1、H@3、H@10评价标准上分别优于次优方法T 15%、11%、4%、2%. 在ICEWS11-14数据集上,TAC在MRR、H@3、H@10评价标准上分别优于次优方法T 7%、18%、20%. 实体预测任务的精度提升效果明显. ...