[1]
BAGHERI-GAVKOSH M, HOSSEINI S, ATAIE-ASHTIANI B, et al Land subsidence: a global challenge
[J]. The Science of the Total Environment , 2021 , 778 : 146493
[本文引用: 1]
[2]
YE S J, XUE Y Q, WU J C, et al. Progression and mitigation of land subsidence in China
[J]. Hydrogeology Journal , 2016 , 24 : 685 - 693
DOI:10.1007/s10040-015-1356-9
[本文引用: 1]
[3]
翟婉明, 赵春发 现代轨道交通工程科技前沿与挑战
[J]. 西南交通大学学报 , 2016 , 51 (2 ): 209
[本文引用: 1]
ZHAI Wanming, ZHAO Chunfa Frontiers and challenges of sciences and technologies in modern railway engineering
[J]. Journal of Southwest Jiaotong University , 2016 , 51 (2 ): 209
[本文引用: 1]
[4]
岳建刚 鲁南高铁沿线地面沉降现状及原因分析
[J]. 铁道勘察 , 2020 , 46 (2 ): 60
[本文引用: 1]
YUE Jiangang Analysis on the current situation and causes of land subsidence along the Lunan high speed railway
[J]. Railway Investigation and Surveying , 2020 , 46 (2 ): 60
[本文引用: 1]
[5]
尚金光, 张献州, 官超伟 高速铁路沉降评估中工程沉降和区域沉降的可区分性研究
[J]. 测绘科学 , 2013 , 38 (1 ): 84 - 86
[本文引用: 1]
SHANG Jinguang, ZHANG Xianzhou, GONG Chaowei Distinguishability of engineering settlement and land subsidence in the settlement evaluation of high-speed railway
[J]. Science of Surveying and Mapping , 2013 , 38 (1 ): 84 - 86
[本文引用: 1]
[6]
卢颖, 郭良杰, 侯云玥, 等 多灾种耦合综合风险评估方法在城市用地规划中的应用
[J]. 浙江大学学报: 工学版 , 2015 , 49 (3 ): 538 - 546
[本文引用: 1]
LU Ying, GUO Liangjie, HOU Yunyue, et al Comprehensive multi-hazard risk assessment method applicated in urban land-use planning
[J]. Journal of Zhejiang university: Engineering Science , 2015 , 49 (3 ): 538 - 546
[本文引用: 1]
[7]
RAJMATIi O, GOLKARIAN A, BIGGS T, et al Land subsidence hazard modeling: machine learning to identify predictors and the role of human activities
[J]. Journal of Environmental Management , 2019 , 236 : 466 - 480
DOI:10.1016/j.jenvman.2019.02.020
[本文引用: 1]
[8]
LYU H M, SHEN S L, ZHOU A, et al Assessment of safety status of shield tunnelling using operational parameters with enhanced SPA
[J]. Tunnelling and Underground Space Technology , 2022 , 123 : 104428
DOI:10.1016/j.tust.2022.104428
[本文引用: 1]
[9]
SU S l, LI D, YU X, et al Assessing land ecological security in Shanghai (China) based on catastrophe theory
[J]. Stochastic Environmental Research and Risk Assessment , 2011 , 25 : 737 - 746
DOI:10.1007/s00477-011-0457-9
[本文引用: 1]
[10]
LYU H M, SUN W J, SHEN S L, et al. Flood risk assessment in metro systems of mega-cities using a GIS-based modeling approach [J]. Science of The Total Environment . 2018, 626: 1012-1025.
[本文引用: 2]
[11]
任娟娟, 刘宽, 王伟华, 等 基于区间层次分析的CRTS Ⅲ型板式无砟轨道开裂状况评估
[J]. 浙江大学学报: 工学版 , 2021 , 55 (12 ): 2267 - 2274
[本文引用: 1]
REN Juanjuan, LIU Kuan, WANG Weihua, et al Evaluation of cracking condition for CRTS Ⅲ prefabricated slab track based on interval analytic hierarchy process
[J]. Journal of Zhejiang University: Engineering Science , 2021 , 55 (12 ): 2267 - 2274
[本文引用: 1]
[12]
SIERRA L, YEPES V, PELLICER E A review of multi-criteria assessment of the social sustainability of infrastructures
[J]. Journal of Cleaner Production , 2018 , 187 : 496 - 513
DOI:10.1016/j.jclepro.2018.03.022
[本文引用: 1]
[13]
DONG Y C, CHEN X, HERRERA F Minimizing adjusted simple terms in the consensus reaching process with hesitant linguistic assessments in group decision making
[J]. Information Sciences , 2015 , 297 : 95 - 117
DOI:10.1016/j.ins.2014.11.011
[本文引用: 1]
[14]
TORRA V Hesitant fuzzy sets
[J]. International Journal of Intelligent Systems , 2010 , 25 (6 ): 529 - 539
[本文引用: 1]
[15]
XIA M M, XU Z Hesitant fuzzy information aggregation in decision making
[J]. International Journal of Approximate Reasoning , 2011 , 52 (3 ): 395 - 407
DOI:10.1016/j.ijar.2010.09.002
[本文引用: 3]
[16]
ZADEH L The concepts of a linguistic variable and its application to approximate reasoning
[J]. Information Sciences , 1975 , 8 (3 ): 199 - 249
DOI:10.1016/0020-0255(75)90036-5
[本文引用: 1]
[17]
HERRERA F, ALONSO S, CHICLANA F, et al Computing with words in decision making: foundations, trends and prospects
[J]. Fuzzy Optimization and Decision Making , 2009 , 8 (4 ): 337 - 364
DOI:10.1007/s10700-009-9065-2
[18]
WANG J, HAO J A new version of 2-tuple fuzzy linguistic representation model for computing with words
[J]. IEEE Transactions on Fuzzy Systems , 2006 , 14 (3 ): 435 - 445
DOI:10.1109/TFUZZ.2006.876337
[本文引用: 2]
[19]
RODRIGUEZ R, LABELLA Á, MARTINEZ L An overview on fuzzy modelling of complex linguistic preferences in decision making
[J]. International Journal of Computational Intelligence Systems , 2016 , 9 : 81 - 94
DOI:10.1080/18756891.2016.1180821
[本文引用: 1]
[20]
LIAO H C, XU Z S, HERRERA-VIEDMA E, et al Hesitant fuzzy linguistic term set and its application in decision making: a state-of-the-art survey
[J]. International Journal of Fuzzy Systems , 2018 , 20 : 2084 - 2110
DOI:10.1007/s40815-017-0432-9
[本文引用: 1]
[21]
廖虎昌, 缑迅杰, 徐泽水 基于犹豫模糊语言集的决策理论与方法综述
[J]. 系统工程理论与实践 , 2017 , 37 (1 ): 35 - 48
[本文引用: 1]
LIAO Huchang, GOU Xunjie, XU Zeshui A survey of decision making theory and methodologies of hesitant fuzzy linguistic term set
[J]. System Engineering Theory and Practice , 2017 , 37 (1 ): 35 - 48
[本文引用: 1]
[22]
MENG F Y, TANG J, LI C L Uncertain linguistic hesitant fuzzy sets and their application in multi-attribute decision making
[J]. International Journal of Intelligent Systems , 2018 , 33 (3 ): 586 - 614
DOI:10.1002/int.21957
[本文引用: 1]
[23]
MENG F Y, CHEN X H A hesitant fuzzy linguistic multi-granularity decision making model based on distance measures
[J]. Journal of Intelligent and Fuzzy Systems: Applications in Engineering and Technology , 2015 , 28 (4 ): 1519 - 1531
[本文引用: 1]
[24]
HUANG J, YOU X Y, LIU H C, et al New approach for quality function deployment based on proportional hesitant fuzzy linguistic term sets and prospect theory
[J]. International Journal of Production Research , 2019 , 57 : 1283 - 1299
DOI:10.1080/00207543.2018.1470343
[本文引用: 1]
[25]
NAZ S, AKRAM M, DAVVAZ B, et al A new decision-making framework for selecting the river crossing project under dual hesitant q-rung orthopair fuzzy 2-tuple linguistic environment
[J]. Soft Computing , 2023 , 27 : 12021 - 12047
DOI:10.1007/s00500-023-08739-z
[本文引用: 1]
[26]
王磊, 赵臣啸 , 薛惠锋, 等. 基于犹豫模糊语言的专家综合集成研讨方法[J]. 系统工程理论与实践, 2021, 41(8): 2157-2168.
[本文引用: 1]
WANG Lei, ZHAO Chenxiao, XUE Huifeng, et al. The expert synthesis and integration research method based on hesitant fuzzy language [J]. System Engineering Theory and Practice , 2021, 41(8): 2157-2168.
[本文引用: 1]
[27]
PRAKASH T, KUMAR A, DURAI C, et al Enhanced Elman spike neural network optimized with flamingo search optimization algorithm espoused lung cancer classification from CT images
[J]. Biomedical Signal Processing and Control , 2023 , 84 : 104948
DOI:10.1016/j.bspc.2023.104948
[本文引用: 1]
[28]
YING X J, NI T, LU M X, et al. Sub-catchment-based urban flood risk assessment with a multi-index fuzzy evaluation approach: a case study of Jinjiang district, China [J]. Geomatics Natural Hazards and Risk , 2023, 14(1): 1–23.
[本文引用: 1]
[29]
ROUYENDEGH B, OZTEKIN A, EKONG J, et al Measuring the efficiency of hospitals: a fully-ranking DEA–FAHP approach
[J]. Annals of Operations Research , 2019 , 278 : 361 - 378
DOI:10.1007/s10479-016-2330-1
[本文引用: 1]
[30]
MOUSAVI-NASAB S H, SOTOUDEH-ANVARI A A comprehensive MCDM-based approach using TOPSIS, COPRAS and DEA as an auxiliary tool for material selection problems
[J]. Materials and Design , 2017 , 121 : 237 - 253
DOI:10.1016/j.matdes.2017.02.041
[本文引用: 1]
[31]
王伟武, 黎菲楠, 王頔, 等 基于通风潜力及风特征量化分析的城市风道构建
[J]. 浙江大学学报: 工学版 , 2019 , 53 (3 ): 470 - 481
[本文引用: 1]
WANG Weiwu, LI Feinan, WANG Di, et al Urban ventilation corridor construction based on ventilation potential and quantitative analysis of wind characteristics
[J]. Journal of Zhejiang University: Engineering Science , 2019 , 53 (3 ): 470 - 481
[本文引用: 1]
[32]
黄赠, 王锐, 赵宇, 等 隐伏断层地震诱发滑坡易发性评价
[J]. 浙江大学学报: 工学版 , 2017 , 51 (11 ): 2136 - 2143
[本文引用: 1]
HUANG Zeng, WANG Rui, ZHAO Yu, et al Susceptibility assessment of landslides triggered by buried fault earthquake
[J]. Journal of Zhejiang University: Engineering Science , 2017 , 51 (11 ): 2136 - 2143
[本文引用: 1]
[33]
RAHMAWATY, SIAHAAN J, NURYAWAN A, et al. Mangrove cover change (2005-2019) in the Northern of Medan City, North Sumatra, Indonesia [J]. Geocarto International , 2023, 38(1): 1–28.
[本文引用: 1]
[34]
WU P, ZHOU L G, MARTINEZ L An integrated hesitant fuzzy linguistic model for multiple attribute group decision-making for health management center selection
[J]. Computers and Industrial Engineering , 2022 , 171 : 108404
DOI:10.1016/j.cie.2022.108404
[本文引用: 9]
[35]
WU P, ZHOU L G, CHEN H Y, et al Additive consistency of hesitant fuzzy linguistic preference relation with a new expansion principle for hesitant fuzzy linguistic term sets
[J]. IEEE Transactions on Fuzzy Systems , 2019 , 27 (4 ): 716 - 730
DOI:10.1109/TFUZZ.2018.2868492
[本文引用: 1]
[36]
COOK W, SEIFORD L Data envelopment analysis (DEA): thirty years on
[J]. European Journal of Operational Research , 2019 , 192 (1 ): 1 - 17
[本文引用: 2]
[37]
LYU H M, SUN W J, SHEN S L, et al Risk assessment using a new consulting process in fuzzy AHP
[J]. Journal of Construction Engineering and Management-ASCE , 2020 , 146 : 04019112
DOI:10.1061/(ASCE)CO.1943-7862.0001757
[本文引用: 4]
[38]
鲁明星. 开采沉陷区残余变形时空演化规律及其对地面建筑影响[D]. 北京: 北京科技大学, 2019.
[本文引用: 4]
LU Mingxing. Research on spatial and temporal evolution of residual deformation in mining subsidence area and the influence of ground buildings [D]. Beijing: University of Science and Technology Beijing, 2019.
[本文引用: 4]
[39]
曹伟伟. 采灌作用下地层变形与含水层水位变化的相关性分析及沉降预测[D]. 上海: 上海交通大学, 2020.
[本文引用: 2]
CAO Weiwei. Correlation analysis of stratum deformation and water level variation of aquifers and land subsidence prediction concerning groundwater exploitation and recharge [D]. Shanghai: Shanghai Jiao Tong University, 2020.
[本文引用: 2]
[40]
国家铁路局. 高速铁路设计规范: TB 10621—2014 [S]. 北京: 中国铁道出版社, 2014.
[本文引用: 6]
[41]
狄胜同. 地下水开采导致地面沉降全过程宏细观演化机理及趋势预测研究[D]. 济南: 山东大学, 2020.
[本文引用: 1]
DI Shengtong. Research on macro-mesoscopic evolution mechanism of whole process and trend prediction of land subsidence caused by groundwater exploitation [D]. Jinan: Shandong University, 2020.
[本文引用: 1]
[43]
边超. 地下水开采引发地面沉降对鲁南高铁沿线的影响性分析及防治[D]. 济南: 山东大学, 2021.
[本文引用: 3]
BIAN Chao. Analysis and prevention of influence of ground subsidence caused by groundwater exploitation on south Shandong high-speed railway [D]. Jinan: Shandong University, 2021.
[本文引用: 3]
[44]
吕海敏. 城市地铁系统沉涝灾害风险评估方法与防灾对策[D]. 上海: 上海交通大学, 2019.
[本文引用: 3]
LV Haimin. Risk assessment methods and countermeasures for floods of metro system in subsidence environment [D]. Shanghai: Shanghai Jiao Tong University, 2019.
[本文引用: 3]
[45]
中华人民共和国交通运输部. 公路工程技术标准: JTG B01—2014 [S]. 北京: 人民交通出版社, 2014.
[本文引用: 3]
[46]
邱颖新, 张献州, 张拯, 等 基于物联网模式的高速铁路工后变形监测预警体系研究
[J]. 铁道科学与工程学报 , 2016 , 13 (4 ): 606 - 612
DOI:10.3969/j.issn.1672-7029.2016.04.003
[本文引用: 3]
QIU Yingxin, ZHANG Xianzhou, ZHANG Zheng, et al Research on high-speed rail post-construction deformation monitoring and warning system based on internet of things
[J]. Journal of Railway Science and Engineering , 2016 , 13 (4 ): 606 - 612
DOI:10.3969/j.issn.1672-7029.2016.04.003
[本文引用: 3]
[47]
陈兆玮. 高速铁路桥墩沉降对行车性能影响的研究[D]. 成都: 西南交通大学, 2017.
[本文引用: 1]
CHEN Zhaowei. Influence of pier settlement on dynamic performance of running trains in high-speed railways [D]. Chengdu: Southwest Jiaotong University, 2017.
[本文引用: 1]
[48]
邵旭东. 桥梁工程[M]. 北京: 人民交通出版社, 2019: 5.
[本文引用: 4]
[49]
王其合, 张鹏, 李程, 等 控制地面沉降的地下水限采方案研究
[J]. 城市轨道交通研究 , 2023 , (Suppl.2 ): 92 - 99
[本文引用: 2]
WANG Qihe, ZHANG Peng, LI Cheng, et al Research on groundwater extraction control scheme for controlling land subsidence
[J]. Urban Mass Transit , 2023 , (Suppl.2 ): 92 - 99
[本文引用: 2]
[50]
邓雪, 李家铭, 曾浩健, 等 层次分析法权重计算方法分析及其应用研究
[J]. 数学的实践与认识 , 2012 , 42 (7 ): 93 - 100
DOI:10.3969/j.issn.1000-0984.2012.07.012
[本文引用: 1]
DENG Xue, LI Jiaming, ZENG Haojian, et al Research on computation methods of AHP weight vector and its applications
[J]. Journal of Mathematics in Practice and Theory , 2012 , 42 (7 ): 93 - 100
DOI:10.3969/j.issn.1000-0984.2012.07.012
[本文引用: 1]
Land subsidence: a global challenge
1
2021
... 地面沉降易导致地下管线破坏、地面高程降低、建筑物倾斜等问题,进而造成重大经济损失[1 -2 ] . 近年来,我国高铁逐渐转入“运营维护”阶段. 在运营阶段,维持线路的高平顺性和高稳定性是高铁安全运营的主要任务[3 ] ,但较多的高铁线路不得不通过沉降严重的区域,使其运营面临巨大的风险[4 -5 ] . ...
al. Progression and mitigation of land subsidence in China
1
2016
... 地面沉降易导致地下管线破坏、地面高程降低、建筑物倾斜等问题,进而造成重大经济损失[1 -2 ] . 近年来,我国高铁逐渐转入“运营维护”阶段. 在运营阶段,维持线路的高平顺性和高稳定性是高铁安全运营的主要任务[3 ] ,但较多的高铁线路不得不通过沉降严重的区域,使其运营面临巨大的风险[4 -5 ] . ...
现代轨道交通工程科技前沿与挑战
1
2016
... 地面沉降易导致地下管线破坏、地面高程降低、建筑物倾斜等问题,进而造成重大经济损失[1 -2 ] . 近年来,我国高铁逐渐转入“运营维护”阶段. 在运营阶段,维持线路的高平顺性和高稳定性是高铁安全运营的主要任务[3 ] ,但较多的高铁线路不得不通过沉降严重的区域,使其运营面临巨大的风险[4 -5 ] . ...
现代轨道交通工程科技前沿与挑战
1
2016
... 地面沉降易导致地下管线破坏、地面高程降低、建筑物倾斜等问题,进而造成重大经济损失[1 -2 ] . 近年来,我国高铁逐渐转入“运营维护”阶段. 在运营阶段,维持线路的高平顺性和高稳定性是高铁安全运营的主要任务[3 ] ,但较多的高铁线路不得不通过沉降严重的区域,使其运营面临巨大的风险[4 -5 ] . ...
鲁南高铁沿线地面沉降现状及原因分析
1
2020
... 地面沉降易导致地下管线破坏、地面高程降低、建筑物倾斜等问题,进而造成重大经济损失[1 -2 ] . 近年来,我国高铁逐渐转入“运营维护”阶段. 在运营阶段,维持线路的高平顺性和高稳定性是高铁安全运营的主要任务[3 ] ,但较多的高铁线路不得不通过沉降严重的区域,使其运营面临巨大的风险[4 -5 ] . ...
鲁南高铁沿线地面沉降现状及原因分析
1
2020
... 地面沉降易导致地下管线破坏、地面高程降低、建筑物倾斜等问题,进而造成重大经济损失[1 -2 ] . 近年来,我国高铁逐渐转入“运营维护”阶段. 在运营阶段,维持线路的高平顺性和高稳定性是高铁安全运营的主要任务[3 ] ,但较多的高铁线路不得不通过沉降严重的区域,使其运营面临巨大的风险[4 -5 ] . ...
高速铁路沉降评估中工程沉降和区域沉降的可区分性研究
1
2013
... 地面沉降易导致地下管线破坏、地面高程降低、建筑物倾斜等问题,进而造成重大经济损失[1 -2 ] . 近年来,我国高铁逐渐转入“运营维护”阶段. 在运营阶段,维持线路的高平顺性和高稳定性是高铁安全运营的主要任务[3 ] ,但较多的高铁线路不得不通过沉降严重的区域,使其运营面临巨大的风险[4 -5 ] . ...
高速铁路沉降评估中工程沉降和区域沉降的可区分性研究
1
2013
... 地面沉降易导致地下管线破坏、地面高程降低、建筑物倾斜等问题,进而造成重大经济损失[1 -2 ] . 近年来,我国高铁逐渐转入“运营维护”阶段. 在运营阶段,维持线路的高平顺性和高稳定性是高铁安全运营的主要任务[3 ] ,但较多的高铁线路不得不通过沉降严重的区域,使其运营面临巨大的风险[4 -5 ] . ...
多灾种耦合综合风险评估方法在城市用地规划中的应用
1
2015
... 风险评估是通过对风险因子的识别、评价、结合,实现某一区域的风险等级划分[6 ] . 众多学者采用神经网络[7 ] 、集对分析法[8 ] 、突变树[9 ] 、层次分析法(analytic hierarchy process, AHP)及模糊层次分析法(fuzzy analytic hierarchy process, FAHP)[10 -11 ] 等理论和方法,量化分析风险等级. AHP是系统化的风险评估方法,广泛运用于各类场景. AHP方法的缺点如下:1)一致性条件难以满足;2)考虑多因子时过于复杂;3)无法处理不确定的数据[12 ] . FAHP是在AHP基础上提出的改进方法,以模糊数建立判断矩阵,在一定程度上克服了AHP的缺点. FAHP要求决策者准确采用某一评分来表述其观点,与决策者固有的犹豫性相悖[13 ] . 犹豫模糊集合理论允许使用者采用多个可能的评分表述其观点,提高了准确性[14 -15 ] . ...
多灾种耦合综合风险评估方法在城市用地规划中的应用
1
2015
... 风险评估是通过对风险因子的识别、评价、结合,实现某一区域的风险等级划分[6 ] . 众多学者采用神经网络[7 ] 、集对分析法[8 ] 、突变树[9 ] 、层次分析法(analytic hierarchy process, AHP)及模糊层次分析法(fuzzy analytic hierarchy process, FAHP)[10 -11 ] 等理论和方法,量化分析风险等级. AHP是系统化的风险评估方法,广泛运用于各类场景. AHP方法的缺点如下:1)一致性条件难以满足;2)考虑多因子时过于复杂;3)无法处理不确定的数据[12 ] . FAHP是在AHP基础上提出的改进方法,以模糊数建立判断矩阵,在一定程度上克服了AHP的缺点. FAHP要求决策者准确采用某一评分来表述其观点,与决策者固有的犹豫性相悖[13 ] . 犹豫模糊集合理论允许使用者采用多个可能的评分表述其观点,提高了准确性[14 -15 ] . ...
Land subsidence hazard modeling: machine learning to identify predictors and the role of human activities
1
2019
... 风险评估是通过对风险因子的识别、评价、结合,实现某一区域的风险等级划分[6 ] . 众多学者采用神经网络[7 ] 、集对分析法[8 ] 、突变树[9 ] 、层次分析法(analytic hierarchy process, AHP)及模糊层次分析法(fuzzy analytic hierarchy process, FAHP)[10 -11 ] 等理论和方法,量化分析风险等级. AHP是系统化的风险评估方法,广泛运用于各类场景. AHP方法的缺点如下:1)一致性条件难以满足;2)考虑多因子时过于复杂;3)无法处理不确定的数据[12 ] . FAHP是在AHP基础上提出的改进方法,以模糊数建立判断矩阵,在一定程度上克服了AHP的缺点. FAHP要求决策者准确采用某一评分来表述其观点,与决策者固有的犹豫性相悖[13 ] . 犹豫模糊集合理论允许使用者采用多个可能的评分表述其观点,提高了准确性[14 -15 ] . ...
Assessment of safety status of shield tunnelling using operational parameters with enhanced SPA
1
2022
... 风险评估是通过对风险因子的识别、评价、结合,实现某一区域的风险等级划分[6 ] . 众多学者采用神经网络[7 ] 、集对分析法[8 ] 、突变树[9 ] 、层次分析法(analytic hierarchy process, AHP)及模糊层次分析法(fuzzy analytic hierarchy process, FAHP)[10 -11 ] 等理论和方法,量化分析风险等级. AHP是系统化的风险评估方法,广泛运用于各类场景. AHP方法的缺点如下:1)一致性条件难以满足;2)考虑多因子时过于复杂;3)无法处理不确定的数据[12 ] . FAHP是在AHP基础上提出的改进方法,以模糊数建立判断矩阵,在一定程度上克服了AHP的缺点. FAHP要求决策者准确采用某一评分来表述其观点,与决策者固有的犹豫性相悖[13 ] . 犹豫模糊集合理论允许使用者采用多个可能的评分表述其观点,提高了准确性[14 -15 ] . ...
Assessing land ecological security in Shanghai (China) based on catastrophe theory
1
2011
... 风险评估是通过对风险因子的识别、评价、结合,实现某一区域的风险等级划分[6 ] . 众多学者采用神经网络[7 ] 、集对分析法[8 ] 、突变树[9 ] 、层次分析法(analytic hierarchy process, AHP)及模糊层次分析法(fuzzy analytic hierarchy process, FAHP)[10 -11 ] 等理论和方法,量化分析风险等级. AHP是系统化的风险评估方法,广泛运用于各类场景. AHP方法的缺点如下:1)一致性条件难以满足;2)考虑多因子时过于复杂;3)无法处理不确定的数据[12 ] . FAHP是在AHP基础上提出的改进方法,以模糊数建立判断矩阵,在一定程度上克服了AHP的缺点. FAHP要求决策者准确采用某一评分来表述其观点,与决策者固有的犹豫性相悖[13 ] . 犹豫模糊集合理论允许使用者采用多个可能的评分表述其观点,提高了准确性[14 -15 ] . ...
2
... 风险评估是通过对风险因子的识别、评价、结合,实现某一区域的风险等级划分[6 ] . 众多学者采用神经网络[7 ] 、集对分析法[8 ] 、突变树[9 ] 、层次分析法(analytic hierarchy process, AHP)及模糊层次分析法(fuzzy analytic hierarchy process, FAHP)[10 -11 ] 等理论和方法,量化分析风险等级. AHP是系统化的风险评估方法,广泛运用于各类场景. AHP方法的缺点如下:1)一致性条件难以满足;2)考虑多因子时过于复杂;3)无法处理不确定的数据[12 ] . FAHP是在AHP基础上提出的改进方法,以模糊数建立判断矩阵,在一定程度上克服了AHP的缺点. FAHP要求决策者准确采用某一评分来表述其观点,与决策者固有的犹豫性相悖[13 ] . 犹豫模糊集合理论允许使用者采用多个可能的评分表述其观点,提高了准确性[14 -15 ] . ...
... 参考不良地质环境作用下线性工程的风险定义[10 ] ,以灾害因子、敏感因子和脆弱因子为输入,构建风险函数如下: ...
基于区间层次分析的CRTS Ⅲ型板式无砟轨道开裂状况评估
1
2021
... 风险评估是通过对风险因子的识别、评价、结合,实现某一区域的风险等级划分[6 ] . 众多学者采用神经网络[7 ] 、集对分析法[8 ] 、突变树[9 ] 、层次分析法(analytic hierarchy process, AHP)及模糊层次分析法(fuzzy analytic hierarchy process, FAHP)[10 -11 ] 等理论和方法,量化分析风险等级. AHP是系统化的风险评估方法,广泛运用于各类场景. AHP方法的缺点如下:1)一致性条件难以满足;2)考虑多因子时过于复杂;3)无法处理不确定的数据[12 ] . FAHP是在AHP基础上提出的改进方法,以模糊数建立判断矩阵,在一定程度上克服了AHP的缺点. FAHP要求决策者准确采用某一评分来表述其观点,与决策者固有的犹豫性相悖[13 ] . 犹豫模糊集合理论允许使用者采用多个可能的评分表述其观点,提高了准确性[14 -15 ] . ...
基于区间层次分析的CRTS Ⅲ型板式无砟轨道开裂状况评估
1
2021
... 风险评估是通过对风险因子的识别、评价、结合,实现某一区域的风险等级划分[6 ] . 众多学者采用神经网络[7 ] 、集对分析法[8 ] 、突变树[9 ] 、层次分析法(analytic hierarchy process, AHP)及模糊层次分析法(fuzzy analytic hierarchy process, FAHP)[10 -11 ] 等理论和方法,量化分析风险等级. AHP是系统化的风险评估方法,广泛运用于各类场景. AHP方法的缺点如下:1)一致性条件难以满足;2)考虑多因子时过于复杂;3)无法处理不确定的数据[12 ] . FAHP是在AHP基础上提出的改进方法,以模糊数建立判断矩阵,在一定程度上克服了AHP的缺点. FAHP要求决策者准确采用某一评分来表述其观点,与决策者固有的犹豫性相悖[13 ] . 犹豫模糊集合理论允许使用者采用多个可能的评分表述其观点,提高了准确性[14 -15 ] . ...
A review of multi-criteria assessment of the social sustainability of infrastructures
1
2018
... 风险评估是通过对风险因子的识别、评价、结合,实现某一区域的风险等级划分[6 ] . 众多学者采用神经网络[7 ] 、集对分析法[8 ] 、突变树[9 ] 、层次分析法(analytic hierarchy process, AHP)及模糊层次分析法(fuzzy analytic hierarchy process, FAHP)[10 -11 ] 等理论和方法,量化分析风险等级. AHP是系统化的风险评估方法,广泛运用于各类场景. AHP方法的缺点如下:1)一致性条件难以满足;2)考虑多因子时过于复杂;3)无法处理不确定的数据[12 ] . FAHP是在AHP基础上提出的改进方法,以模糊数建立判断矩阵,在一定程度上克服了AHP的缺点. FAHP要求决策者准确采用某一评分来表述其观点,与决策者固有的犹豫性相悖[13 ] . 犹豫模糊集合理论允许使用者采用多个可能的评分表述其观点,提高了准确性[14 -15 ] . ...
Minimizing adjusted simple terms in the consensus reaching process with hesitant linguistic assessments in group decision making
1
2015
... 风险评估是通过对风险因子的识别、评价、结合,实现某一区域的风险等级划分[6 ] . 众多学者采用神经网络[7 ] 、集对分析法[8 ] 、突变树[9 ] 、层次分析法(analytic hierarchy process, AHP)及模糊层次分析法(fuzzy analytic hierarchy process, FAHP)[10 -11 ] 等理论和方法,量化分析风险等级. AHP是系统化的风险评估方法,广泛运用于各类场景. AHP方法的缺点如下:1)一致性条件难以满足;2)考虑多因子时过于复杂;3)无法处理不确定的数据[12 ] . FAHP是在AHP基础上提出的改进方法,以模糊数建立判断矩阵,在一定程度上克服了AHP的缺点. FAHP要求决策者准确采用某一评分来表述其观点,与决策者固有的犹豫性相悖[13 ] . 犹豫模糊集合理论允许使用者采用多个可能的评分表述其观点,提高了准确性[14 -15 ] . ...
Hesitant fuzzy sets
1
2010
... 风险评估是通过对风险因子的识别、评价、结合,实现某一区域的风险等级划分[6 ] . 众多学者采用神经网络[7 ] 、集对分析法[8 ] 、突变树[9 ] 、层次分析法(analytic hierarchy process, AHP)及模糊层次分析法(fuzzy analytic hierarchy process, FAHP)[10 -11 ] 等理论和方法,量化分析风险等级. AHP是系统化的风险评估方法,广泛运用于各类场景. AHP方法的缺点如下:1)一致性条件难以满足;2)考虑多因子时过于复杂;3)无法处理不确定的数据[12 ] . FAHP是在AHP基础上提出的改进方法,以模糊数建立判断矩阵,在一定程度上克服了AHP的缺点. FAHP要求决策者准确采用某一评分来表述其观点,与决策者固有的犹豫性相悖[13 ] . 犹豫模糊集合理论允许使用者采用多个可能的评分表述其观点,提高了准确性[14 -15 ] . ...
Hesitant fuzzy information aggregation in decision making
3
2011
... 风险评估是通过对风险因子的识别、评价、结合,实现某一区域的风险等级划分[6 ] . 众多学者采用神经网络[7 ] 、集对分析法[8 ] 、突变树[9 ] 、层次分析法(analytic hierarchy process, AHP)及模糊层次分析法(fuzzy analytic hierarchy process, FAHP)[10 -11 ] 等理论和方法,量化分析风险等级. AHP是系统化的风险评估方法,广泛运用于各类场景. AHP方法的缺点如下:1)一致性条件难以满足;2)考虑多因子时过于复杂;3)无法处理不确定的数据[12 ] . FAHP是在AHP基础上提出的改进方法,以模糊数建立判断矩阵,在一定程度上克服了AHP的缺点. FAHP要求决策者准确采用某一评分来表述其观点,与决策者固有的犹豫性相悖[13 ] . 犹豫模糊集合理论允许使用者采用多个可能的评分表述其观点,提高了准确性[14 -15 ] . ...
... $ X $ $ H $ [15 ] 如下: ...
... $ h = \{ {h_1},{h_2},\cdots ,{h_{{l_h}}}\} $ [15 ] 如下: ...
The concepts of a linguistic variable and its application to approximate reasoning
1
1975
... Zadeh等[16 -18 ] 提出模糊语言模型,发展了一套完备语言计算理论. 与传统语言模型相比,犹豫模糊语言允许专家对评估对象给出几个可能的评价,避免计算中产生信息遗漏[19 -20 ] . 目前,针对犹豫模糊语言集的理论研究主要在以下几个方面:1)集成理论,即通过算子将不确定信息进行集成[21 -22 ] ;2)测度理论,即测量犹豫模糊语言集之间的距离[23 ] ;3)多准则决策方法[24 ] . 犹豫模糊语言集在工程选择[25 ] 、资源评估[26 ] 、深度学习[27 ] 及风险评估[28 ] 等领域取得了不错的成果. 复杂问题的评估需要不同学科与职业背景的专家参与,但忽略了如下问题:1)同一专家在不同领域的专业水平存在差异;2)不同专家在同一领域的专业水平存在差异. 当处理专家意见时,未考虑客观存在的差异,影响了评估结果. ...
Computing with words in decision making: foundations, trends and prospects
0
2009
A new version of 2-tuple fuzzy linguistic representation model for computing with words
2
2006
... Zadeh等[16 -18 ] 提出模糊语言模型,发展了一套完备语言计算理论. 与传统语言模型相比,犹豫模糊语言允许专家对评估对象给出几个可能的评价,避免计算中产生信息遗漏[19 -20 ] . 目前,针对犹豫模糊语言集的理论研究主要在以下几个方面:1)集成理论,即通过算子将不确定信息进行集成[21 -22 ] ;2)测度理论,即测量犹豫模糊语言集之间的距离[23 ] ;3)多准则决策方法[24 ] . 犹豫模糊语言集在工程选择[25 ] 、资源评估[26 ] 、深度学习[27 ] 及风险评估[28 ] 等领域取得了不错的成果. 复杂问题的评估需要不同学科与职业背景的专家参与,但忽略了如下问题:1)同一专家在不同领域的专业水平存在差异;2)不同专家在同一领域的专业水平存在差异. 当处理专家意见时,未考虑客观存在的差异,影响了评估结果. ...
... $ \beta $ a ]为短语的对应数值,在二元组模糊语言和$ \beta $ $ \beta $ $ ({s_i},\alpha ) $ . 映射关系[18 ] 如下: ...
An overview on fuzzy modelling of complex linguistic preferences in decision making
1
2016
... Zadeh等[16 -18 ] 提出模糊语言模型,发展了一套完备语言计算理论. 与传统语言模型相比,犹豫模糊语言允许专家对评估对象给出几个可能的评价,避免计算中产生信息遗漏[19 -20 ] . 目前,针对犹豫模糊语言集的理论研究主要在以下几个方面:1)集成理论,即通过算子将不确定信息进行集成[21 -22 ] ;2)测度理论,即测量犹豫模糊语言集之间的距离[23 ] ;3)多准则决策方法[24 ] . 犹豫模糊语言集在工程选择[25 ] 、资源评估[26 ] 、深度学习[27 ] 及风险评估[28 ] 等领域取得了不错的成果. 复杂问题的评估需要不同学科与职业背景的专家参与,但忽略了如下问题:1)同一专家在不同领域的专业水平存在差异;2)不同专家在同一领域的专业水平存在差异. 当处理专家意见时,未考虑客观存在的差异,影响了评估结果. ...
Hesitant fuzzy linguistic term set and its application in decision making: a state-of-the-art survey
1
2018
... Zadeh等[16 -18 ] 提出模糊语言模型,发展了一套完备语言计算理论. 与传统语言模型相比,犹豫模糊语言允许专家对评估对象给出几个可能的评价,避免计算中产生信息遗漏[19 -20 ] . 目前,针对犹豫模糊语言集的理论研究主要在以下几个方面:1)集成理论,即通过算子将不确定信息进行集成[21 -22 ] ;2)测度理论,即测量犹豫模糊语言集之间的距离[23 ] ;3)多准则决策方法[24 ] . 犹豫模糊语言集在工程选择[25 ] 、资源评估[26 ] 、深度学习[27 ] 及风险评估[28 ] 等领域取得了不错的成果. 复杂问题的评估需要不同学科与职业背景的专家参与,但忽略了如下问题:1)同一专家在不同领域的专业水平存在差异;2)不同专家在同一领域的专业水平存在差异. 当处理专家意见时,未考虑客观存在的差异,影响了评估结果. ...
基于犹豫模糊语言集的决策理论与方法综述
1
2017
... Zadeh等[16 -18 ] 提出模糊语言模型,发展了一套完备语言计算理论. 与传统语言模型相比,犹豫模糊语言允许专家对评估对象给出几个可能的评价,避免计算中产生信息遗漏[19 -20 ] . 目前,针对犹豫模糊语言集的理论研究主要在以下几个方面:1)集成理论,即通过算子将不确定信息进行集成[21 -22 ] ;2)测度理论,即测量犹豫模糊语言集之间的距离[23 ] ;3)多准则决策方法[24 ] . 犹豫模糊语言集在工程选择[25 ] 、资源评估[26 ] 、深度学习[27 ] 及风险评估[28 ] 等领域取得了不错的成果. 复杂问题的评估需要不同学科与职业背景的专家参与,但忽略了如下问题:1)同一专家在不同领域的专业水平存在差异;2)不同专家在同一领域的专业水平存在差异. 当处理专家意见时,未考虑客观存在的差异,影响了评估结果. ...
基于犹豫模糊语言集的决策理论与方法综述
1
2017
... Zadeh等[16 -18 ] 提出模糊语言模型,发展了一套完备语言计算理论. 与传统语言模型相比,犹豫模糊语言允许专家对评估对象给出几个可能的评价,避免计算中产生信息遗漏[19 -20 ] . 目前,针对犹豫模糊语言集的理论研究主要在以下几个方面:1)集成理论,即通过算子将不确定信息进行集成[21 -22 ] ;2)测度理论,即测量犹豫模糊语言集之间的距离[23 ] ;3)多准则决策方法[24 ] . 犹豫模糊语言集在工程选择[25 ] 、资源评估[26 ] 、深度学习[27 ] 及风险评估[28 ] 等领域取得了不错的成果. 复杂问题的评估需要不同学科与职业背景的专家参与,但忽略了如下问题:1)同一专家在不同领域的专业水平存在差异;2)不同专家在同一领域的专业水平存在差异. 当处理专家意见时,未考虑客观存在的差异,影响了评估结果. ...
Uncertain linguistic hesitant fuzzy sets and their application in multi-attribute decision making
1
2018
... Zadeh等[16 -18 ] 提出模糊语言模型,发展了一套完备语言计算理论. 与传统语言模型相比,犹豫模糊语言允许专家对评估对象给出几个可能的评价,避免计算中产生信息遗漏[19 -20 ] . 目前,针对犹豫模糊语言集的理论研究主要在以下几个方面:1)集成理论,即通过算子将不确定信息进行集成[21 -22 ] ;2)测度理论,即测量犹豫模糊语言集之间的距离[23 ] ;3)多准则决策方法[24 ] . 犹豫模糊语言集在工程选择[25 ] 、资源评估[26 ] 、深度学习[27 ] 及风险评估[28 ] 等领域取得了不错的成果. 复杂问题的评估需要不同学科与职业背景的专家参与,但忽略了如下问题:1)同一专家在不同领域的专业水平存在差异;2)不同专家在同一领域的专业水平存在差异. 当处理专家意见时,未考虑客观存在的差异,影响了评估结果. ...
A hesitant fuzzy linguistic multi-granularity decision making model based on distance measures
1
2015
... Zadeh等[16 -18 ] 提出模糊语言模型,发展了一套完备语言计算理论. 与传统语言模型相比,犹豫模糊语言允许专家对评估对象给出几个可能的评价,避免计算中产生信息遗漏[19 -20 ] . 目前,针对犹豫模糊语言集的理论研究主要在以下几个方面:1)集成理论,即通过算子将不确定信息进行集成[21 -22 ] ;2)测度理论,即测量犹豫模糊语言集之间的距离[23 ] ;3)多准则决策方法[24 ] . 犹豫模糊语言集在工程选择[25 ] 、资源评估[26 ] 、深度学习[27 ] 及风险评估[28 ] 等领域取得了不错的成果. 复杂问题的评估需要不同学科与职业背景的专家参与,但忽略了如下问题:1)同一专家在不同领域的专业水平存在差异;2)不同专家在同一领域的专业水平存在差异. 当处理专家意见时,未考虑客观存在的差异,影响了评估结果. ...
New approach for quality function deployment based on proportional hesitant fuzzy linguistic term sets and prospect theory
1
2019
... Zadeh等[16 -18 ] 提出模糊语言模型,发展了一套完备语言计算理论. 与传统语言模型相比,犹豫模糊语言允许专家对评估对象给出几个可能的评价,避免计算中产生信息遗漏[19 -20 ] . 目前,针对犹豫模糊语言集的理论研究主要在以下几个方面:1)集成理论,即通过算子将不确定信息进行集成[21 -22 ] ;2)测度理论,即测量犹豫模糊语言集之间的距离[23 ] ;3)多准则决策方法[24 ] . 犹豫模糊语言集在工程选择[25 ] 、资源评估[26 ] 、深度学习[27 ] 及风险评估[28 ] 等领域取得了不错的成果. 复杂问题的评估需要不同学科与职业背景的专家参与,但忽略了如下问题:1)同一专家在不同领域的专业水平存在差异;2)不同专家在同一领域的专业水平存在差异. 当处理专家意见时,未考虑客观存在的差异,影响了评估结果. ...
A new decision-making framework for selecting the river crossing project under dual hesitant q-rung orthopair fuzzy 2-tuple linguistic environment
1
2023
... Zadeh等[16 -18 ] 提出模糊语言模型,发展了一套完备语言计算理论. 与传统语言模型相比,犹豫模糊语言允许专家对评估对象给出几个可能的评价,避免计算中产生信息遗漏[19 -20 ] . 目前,针对犹豫模糊语言集的理论研究主要在以下几个方面:1)集成理论,即通过算子将不确定信息进行集成[21 -22 ] ;2)测度理论,即测量犹豫模糊语言集之间的距离[23 ] ;3)多准则决策方法[24 ] . 犹豫模糊语言集在工程选择[25 ] 、资源评估[26 ] 、深度学习[27 ] 及风险评估[28 ] 等领域取得了不错的成果. 复杂问题的评估需要不同学科与职业背景的专家参与,但忽略了如下问题:1)同一专家在不同领域的专业水平存在差异;2)不同专家在同一领域的专业水平存在差异. 当处理专家意见时,未考虑客观存在的差异,影响了评估结果. ...
1
... Zadeh等[16 -18 ] 提出模糊语言模型,发展了一套完备语言计算理论. 与传统语言模型相比,犹豫模糊语言允许专家对评估对象给出几个可能的评价,避免计算中产生信息遗漏[19 -20 ] . 目前,针对犹豫模糊语言集的理论研究主要在以下几个方面:1)集成理论,即通过算子将不确定信息进行集成[21 -22 ] ;2)测度理论,即测量犹豫模糊语言集之间的距离[23 ] ;3)多准则决策方法[24 ] . 犹豫模糊语言集在工程选择[25 ] 、资源评估[26 ] 、深度学习[27 ] 及风险评估[28 ] 等领域取得了不错的成果. 复杂问题的评估需要不同学科与职业背景的专家参与,但忽略了如下问题:1)同一专家在不同领域的专业水平存在差异;2)不同专家在同一领域的专业水平存在差异. 当处理专家意见时,未考虑客观存在的差异,影响了评估结果. ...
1
... Zadeh等[16 -18 ] 提出模糊语言模型,发展了一套完备语言计算理论. 与传统语言模型相比,犹豫模糊语言允许专家对评估对象给出几个可能的评价,避免计算中产生信息遗漏[19 -20 ] . 目前,针对犹豫模糊语言集的理论研究主要在以下几个方面:1)集成理论,即通过算子将不确定信息进行集成[21 -22 ] ;2)测度理论,即测量犹豫模糊语言集之间的距离[23 ] ;3)多准则决策方法[24 ] . 犹豫模糊语言集在工程选择[25 ] 、资源评估[26 ] 、深度学习[27 ] 及风险评估[28 ] 等领域取得了不错的成果. 复杂问题的评估需要不同学科与职业背景的专家参与,但忽略了如下问题:1)同一专家在不同领域的专业水平存在差异;2)不同专家在同一领域的专业水平存在差异. 当处理专家意见时,未考虑客观存在的差异,影响了评估结果. ...
Enhanced Elman spike neural network optimized with flamingo search optimization algorithm espoused lung cancer classification from CT images
1
2023
... Zadeh等[16 -18 ] 提出模糊语言模型,发展了一套完备语言计算理论. 与传统语言模型相比,犹豫模糊语言允许专家对评估对象给出几个可能的评价,避免计算中产生信息遗漏[19 -20 ] . 目前,针对犹豫模糊语言集的理论研究主要在以下几个方面:1)集成理论,即通过算子将不确定信息进行集成[21 -22 ] ;2)测度理论,即测量犹豫模糊语言集之间的距离[23 ] ;3)多准则决策方法[24 ] . 犹豫模糊语言集在工程选择[25 ] 、资源评估[26 ] 、深度学习[27 ] 及风险评估[28 ] 等领域取得了不错的成果. 复杂问题的评估需要不同学科与职业背景的专家参与,但忽略了如下问题:1)同一专家在不同领域的专业水平存在差异;2)不同专家在同一领域的专业水平存在差异. 当处理专家意见时,未考虑客观存在的差异,影响了评估结果. ...
1
... Zadeh等[16 -18 ] 提出模糊语言模型,发展了一套完备语言计算理论. 与传统语言模型相比,犹豫模糊语言允许专家对评估对象给出几个可能的评价,避免计算中产生信息遗漏[19 -20 ] . 目前,针对犹豫模糊语言集的理论研究主要在以下几个方面:1)集成理论,即通过算子将不确定信息进行集成[21 -22 ] ;2)测度理论,即测量犹豫模糊语言集之间的距离[23 ] ;3)多准则决策方法[24 ] . 犹豫模糊语言集在工程选择[25 ] 、资源评估[26 ] 、深度学习[27 ] 及风险评估[28 ] 等领域取得了不错的成果. 复杂问题的评估需要不同学科与职业背景的专家参与,但忽略了如下问题:1)同一专家在不同领域的专业水平存在差异;2)不同专家在同一领域的专业水平存在差异. 当处理专家意见时,未考虑客观存在的差异,影响了评估结果. ...
Measuring the efficiency of hospitals: a fully-ranking DEA–FAHP approach
1
2019
... 高铁沿线的风险分布受到多因子的影响,因此,确定因子权重十分重要. 数据包络分析方法(data envelopment analysis, DEA)是根据决策单元的输入和输出进行评估的方法,近年来被广泛应用于复杂问题的因子权重确定问题中[29 -30 ] . 地理信息系统可以完整地展示一定区域内的要素分布,拥有空间分析、可视化分析的功能,被广泛地应用于城市规划[31 ] 、灾害分析[32 ] 、生态环境演化[33 ] 等领域. ...
A comprehensive MCDM-based approach using TOPSIS, COPRAS and DEA as an auxiliary tool for material selection problems
1
2017
... 高铁沿线的风险分布受到多因子的影响,因此,确定因子权重十分重要. 数据包络分析方法(data envelopment analysis, DEA)是根据决策单元的输入和输出进行评估的方法,近年来被广泛应用于复杂问题的因子权重确定问题中[29 -30 ] . 地理信息系统可以完整地展示一定区域内的要素分布,拥有空间分析、可视化分析的功能,被广泛地应用于城市规划[31 ] 、灾害分析[32 ] 、生态环境演化[33 ] 等领域. ...
基于通风潜力及风特征量化分析的城市风道构建
1
2019
... 高铁沿线的风险分布受到多因子的影响,因此,确定因子权重十分重要. 数据包络分析方法(data envelopment analysis, DEA)是根据决策单元的输入和输出进行评估的方法,近年来被广泛应用于复杂问题的因子权重确定问题中[29 -30 ] . 地理信息系统可以完整地展示一定区域内的要素分布,拥有空间分析、可视化分析的功能,被广泛地应用于城市规划[31 ] 、灾害分析[32 ] 、生态环境演化[33 ] 等领域. ...
基于通风潜力及风特征量化分析的城市风道构建
1
2019
... 高铁沿线的风险分布受到多因子的影响,因此,确定因子权重十分重要. 数据包络分析方法(data envelopment analysis, DEA)是根据决策单元的输入和输出进行评估的方法,近年来被广泛应用于复杂问题的因子权重确定问题中[29 -30 ] . 地理信息系统可以完整地展示一定区域内的要素分布,拥有空间分析、可视化分析的功能,被广泛地应用于城市规划[31 ] 、灾害分析[32 ] 、生态环境演化[33 ] 等领域. ...
隐伏断层地震诱发滑坡易发性评价
1
2017
... 高铁沿线的风险分布受到多因子的影响,因此,确定因子权重十分重要. 数据包络分析方法(data envelopment analysis, DEA)是根据决策单元的输入和输出进行评估的方法,近年来被广泛应用于复杂问题的因子权重确定问题中[29 -30 ] . 地理信息系统可以完整地展示一定区域内的要素分布,拥有空间分析、可视化分析的功能,被广泛地应用于城市规划[31 ] 、灾害分析[32 ] 、生态环境演化[33 ] 等领域. ...
隐伏断层地震诱发滑坡易发性评价
1
2017
... 高铁沿线的风险分布受到多因子的影响,因此,确定因子权重十分重要. 数据包络分析方法(data envelopment analysis, DEA)是根据决策单元的输入和输出进行评估的方法,近年来被广泛应用于复杂问题的因子权重确定问题中[29 -30 ] . 地理信息系统可以完整地展示一定区域内的要素分布,拥有空间分析、可视化分析的功能,被广泛地应用于城市规划[31 ] 、灾害分析[32 ] 、生态环境演化[33 ] 等领域. ...
1
... 高铁沿线的风险分布受到多因子的影响,因此,确定因子权重十分重要. 数据包络分析方法(data envelopment analysis, DEA)是根据决策单元的输入和输出进行评估的方法,近年来被广泛应用于复杂问题的因子权重确定问题中[29 -30 ] . 地理信息系统可以完整地展示一定区域内的要素分布,拥有空间分析、可视化分析的功能,被广泛地应用于城市规划[31 ] 、灾害分析[32 ] 、生态环境演化[33 ] 等领域. ...
An integrated hesitant fuzzy linguistic model for multiple attribute group decision-making for health management center selection
9
2022
... 本文提出新的调查问卷收集专家意见,引入犹豫模糊二元语言-DEA[34 ] 方法,针对某地面沉降环境下的高速铁路建立风险评估模型. 采用犹豫模糊二元语言理论处理专家意见,将语言变量转化为数值结果,根据最大共识度模型确定专家权重,利用DEA模型确定风险因子权重,结合GIS系统进行高铁沿线风险等级划分. 结果表明,利用新型调查问卷及其配套计算模型,可以合理、准确、快速地进行高铁沿线地面沉降风险评估,有较好的应用前景. ...
... 对于2个犹豫模糊集$ A、B \in {\varOmega _S} $ $ {l_{{A}}} $ $ {l_{{B}}} $ $ A、B $ [34 ] 如下: ...
... 式中:$ {l_{h_i^k}} $ $ h_i^k $ $ {{\boldsymbol{H}}^{\mathrm{g}}} = {[h_{ij}^{\mathrm{g}}]_{m \times n}} $ [34 ] 如下: ...
... 式中:$ \lambda $ $ \lambda > 0 $ $ \displaystyle \sum\nolimits_{k = 1}^t {{\lambda _k}} = 1 $ . 个体共识度$ {\text{IC}}{{\text{M}}_k} $ [34 ] 如下: ...
... 可以得到集体共识度[34 ] 如下: ...
... 各决策者之间的共识水平越高,则决策结果越合理,越能被决策者所接受. 通过最大化群体共识度量,可以推导得到各决策者的权重. 基于这一观点,建立群体共识优化模型[34 ] 如下: ...
... 将所有风险因子分为以下2类. 1)正因子集,表示为Z 1 ,Z 1 越大越好. 2)负因子集,表示为Z 2 ,Z 2 越小越好. 将正因子u q' vl' 分别作为DEA模型的输出和输入. 将评估者视为独立的决策单元(DMU),假设决策单元有r 个输出与s 个输入. 参考文献[34 ],建立DEA模型如下. ...
... 式中:$ E\left( {{\boldsymbol{h}}_q^{\mathrm{g}}} \right) $ $ E\left( {{\boldsymbol{h}}_l^{\mathrm{g}}} \right) $ $ {\boldsymbol{h}}_q^{\mathrm{g}} $ $ {\boldsymbol{h}}_l^{\mathrm{g}} $ $ {{\boldsymbol{\gamma}} _i} = [{\gamma _{i1}},\cdots ,{\gamma _{im}}] = [{u_{i1}},\cdots ,{u_{iq}},{v_{i1}},\cdots ,{v_{il}}] $ . 其中${u_{i1}},\cdots , {u_{iq}} $ i 个DMU的正因子,${v_{i1}},\cdots ,{v_{il}} $ i 个DMU的负因子. 对于t 个DMU,可以求出t 个权重向量$ {{\boldsymbol{\gamma}} _i} (i=1,2,\cdots ,t)$ . 考虑DMU. 求解的权重可能出现分布不科学的情况,对不同因子求得交叉平均评估(CAA)[34 ] 如下: ...
... 权重$ {w_j} (j = 1,2,\cdots ,m) $ [34 ] 为 ...
Additive consistency of hesitant fuzzy linguistic preference relation with a new expansion principle for hesitant fuzzy linguistic term sets
1
2019
... 语言变量的拓展集$ {h^c} $ [35 ] 如下: ...
Data envelopment analysis (DEA): thirty years on
2
2019
... DEA模型是非参数的线性规划模型,根据每个决策单元(decision making unit, DMU)的输入和输出,评估决策单元的性能[36 ] . 对于n 个DMU,根据m 个输入和s 个输出进行评估. 设x ij y rj j i 个输入和第r 个输出. 给定DMUd [36 ] 计算如下. ...
... [36 ]计算如下. ...
Risk assessment using a new consulting process in fuzzy AHP
4
2020
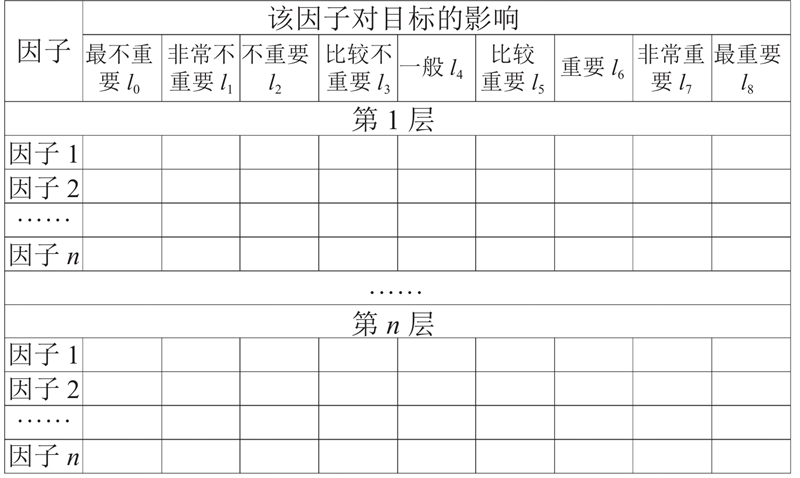
... 在风险评估过程中,专家意见收集是非常重要的环节,传统的AHP的意见收集方法是应用较多的方法. 该方法通过对每个因素进行两两比较,确定该因素的相对重要性. 该方法非常耗时,且一致性条件难满足,对于复杂问题使用难度高. Lyu等[37 ] 提出意见收集方法,该方法采用“1~9度标”来衡量各因子对上一层的影响程度,取代了因子间两两比较的方法. 利用该方法,解决了传统方法一致性检验难以通过的问题. 该方法有以下几个不足. 1)要求在判断过程中选择确定的值表达意见,与模糊性思想相悖. 2)要求采用评分表达评估意见,没有考虑人类的判断是犹豫的. 3)当建立判断矩阵时,确定矩阵中元素的方法不够科学,评估准确性受到影响. 4)群体的共识度为决策者对结果的认可程度,值越高表示决策结果越合理. 为了达到更高的共识度,赋予不同的决策者权重,调整评估结果,得到更合理的结果,在Lyu等[37 ] 的工作中没有考虑这一点. 本文基于Lyu等[37 ] 的工作提出新的意见收集方法,意见收集问卷如图1 所示. 图中,可对一个因子选择1~3个评价,并且同样评价不应重复分配给同一层中的不同因子. 如果一层中的因子数不超过9,建议该层中的各因子评价不允许重复. 如果一层中包含的因子数量为10~18,则该层评价重复次数不应超过2次,且累积重复次数不应超过3次. ...
... [37 ]的工作中没有考虑这一点. 本文基于Lyu等[37 ] 的工作提出新的意见收集方法,意见收集问卷如图1 所示. 图中,可对一个因子选择1~3个评价,并且同样评价不应重复分配给同一层中的不同因子. 如果一层中的因子数不超过9,建议该层中的各因子评价不允许重复. 如果一层中包含的因子数量为10~18,则该层评价重复次数不应超过2次,且累积重复次数不应超过3次. ...
... [37 ]的工作提出新的意见收集方法,意见收集问卷如图1 所示. 图中,可对一个因子选择1~3个评价,并且同样评价不应重复分配给同一层中的不同因子. 如果一层中的因子数不超过9,建议该层中的各因子评价不允许重复. 如果一层中包含的因子数量为10~18,则该层评价重复次数不应超过2次,且累积重复次数不应超过3次. ...
... 参考文献[37 ],采用AHP方法对灾害性因子进行评估,AHP方法的详细评估流程见文献[50 ]. 采用AHP方法,建立判断矩阵如下: ...
4
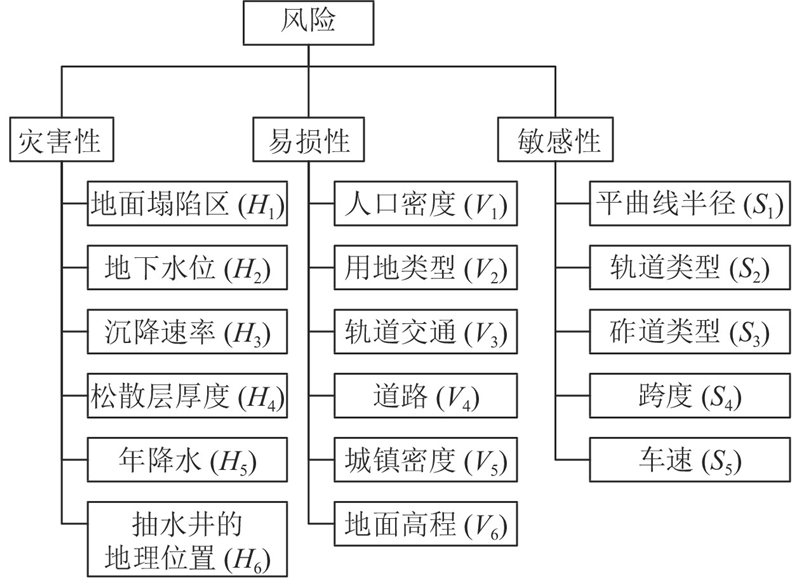
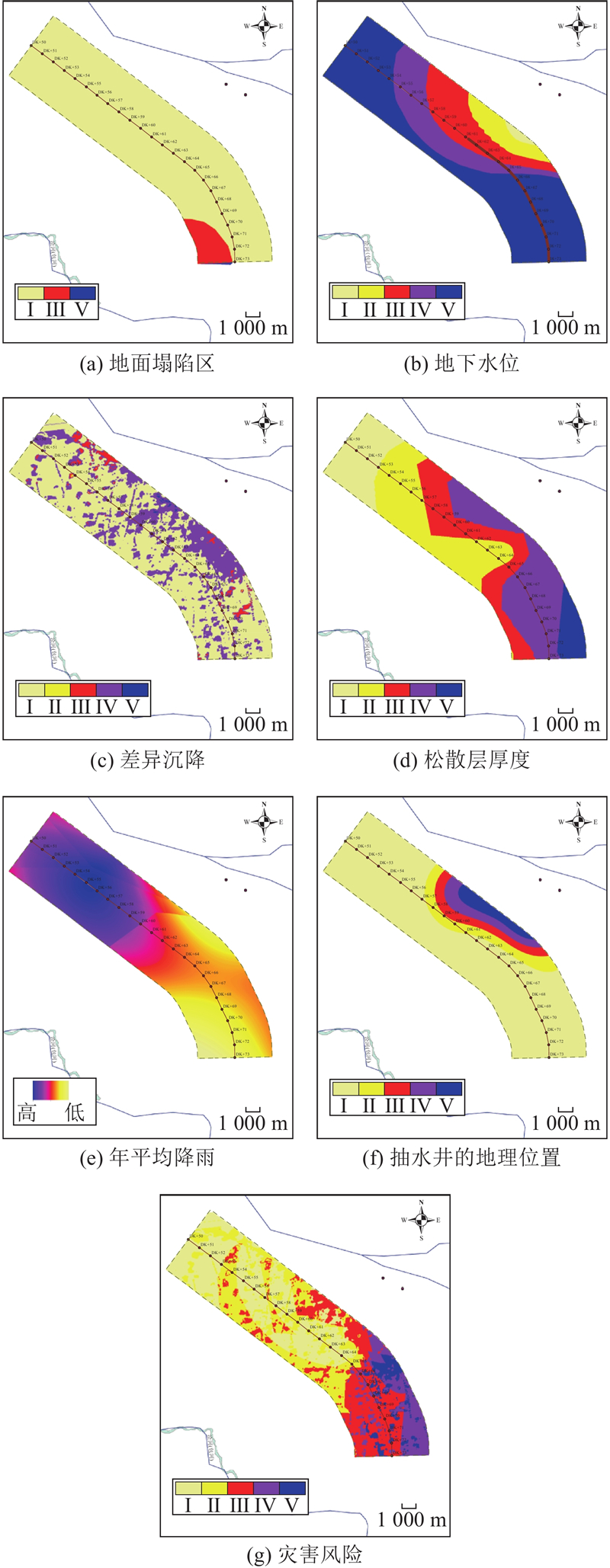
... 式中:$ R $ $ H $ $ S $ $ V $ 38 ~48 ]确定评价因子及其等级划分,构建沉降风险评估体系,如图2 所示,采用的评价语言集为$ L $ . 其中灾害性因子包括地面塌陷区H 1 、地下水位H 2 、差异沉降速率H 3 、松散层厚度H 4 、年降水量H 5 、抽水井的地理位置H 6 . 其中易损性因子包括人口密度V 1 、用地类型V 2 、轨道交通V 3 、道路类型V 4 、城镇密度V 5 、地面高程V 6 . 其中敏感性因子包括平曲线半径S 1 、轨道类型S 2 、砟道类型S 3 、跨度S 4 、车速S 5 . ...
... 灾害因子分级标准[38 -43 ] ...
... Grading standard of hazard factor[38 -43 ] ...
... 开采沉陷区岩层引起的移动和地表变形会持续较长时间,对周边建筑物造成不容忽视的影响[38 ] . 相关资料表明,研究区域部分区段存在塌陷的可能,空间分布如图3 所示. 针对目标工程,将区域内地面塌陷划分为3个等级,依次为未发生地面塌陷、有地面塌陷发展趋势和已发生地面塌陷. ...
4
... 式中:$ R $ $ H $ $ S $ $ V $ 38 ~48 ]确定评价因子及其等级划分,构建沉降风险评估体系,如图2 所示,采用的评价语言集为$ L $ . 其中灾害性因子包括地面塌陷区H 1 、地下水位H 2 、差异沉降速率H 3 、松散层厚度H 4 、年降水量H 5 、抽水井的地理位置H 6 . 其中易损性因子包括人口密度V 1 、用地类型V 2 、轨道交通V 3 、道路类型V 4 、城镇密度V 5 、地面高程V 6 . 其中敏感性因子包括平曲线半径S 1 、轨道类型S 2 、砟道类型S 3 、跨度S 4 、车速S 5 . ...
... 灾害因子分级标准[38 -43 ] ...
... Grading standard of hazard factor[38 -43 ] ...
... 开采沉陷区岩层引起的移动和地表变形会持续较长时间,对周边建筑物造成不容忽视的影响[38 ] . 相关资料表明,研究区域部分区段存在塌陷的可能,空间分布如图3 所示. 针对目标工程,将区域内地面塌陷划分为3个等级,依次为未发生地面塌陷、有地面塌陷发展趋势和已发生地面塌陷. ...
2
... 地下水位是评估地面沉降灾害的重要指标,地下水位高,说明地下水开采量相对较少,地面沉降发展趋势缓慢[39 ] . 针对目标工程,将区域内地下水位划为−20~−16 m、−16~−12 m、−12~−8 m、−8~−4 m、−4~0 m 5个等级. ...
... 抽水是地面沉降发展最主要的原因之一. 目前正逐步封存抽水井,但地下水抽取与地面沉降发展之间存在明显的时滞性[39 ] ,停止抽水后,地面沉降会保持发展. 研究区内的抽水井深度多为120~130 m,抽水强度较大. 本文选取封存时间在2025年及以后的抽水井作为计算依据,假设各抽水井的开采强度相同,影响半径均设为1 500 m[43 ] . 通过ArcGIS计算抽水井影响分布,将区域内的抽水井影响划分为5个等级. ...
2
... 地下水位是评估地面沉降灾害的重要指标,地下水位高,说明地下水开采量相对较少,地面沉降发展趋势缓慢[39 ] . 针对目标工程,将区域内地下水位划为−20~−16 m、−16~−12 m、−12~−8 m、−8~−4 m、−4~0 m 5个等级. ...
... 抽水是地面沉降发展最主要的原因之一. 目前正逐步封存抽水井,但地下水抽取与地面沉降发展之间存在明显的时滞性[39 ] ,停止抽水后,地面沉降会保持发展. 研究区内的抽水井深度多为120~130 m,抽水强度较大. 本文选取封存时间在2025年及以后的抽水井作为计算依据,假设各抽水井的开采强度相同,影响半径均设为1 500 m[43 ] . 通过ArcGIS计算抽水井影响分布,将区域内的抽水井影响划分为5个等级. ...
6
... 《高速铁路设计规范》(TB10621—2014)[40 ] 规定,当列车运营速度达到300 km/h时,有砟轨道路基工后沉降量应不大于5.0 cm,桥台过渡段路基工后沉降量不应大于3.0 cm. 针对区域内2017—2020年的地面沉降监测结果,将区域内地面沉降速率划为0~10 mm/a、11~20 mm/a、21~30 mm/a、31~40 mm/a、>40 mm/a 5个等级. ...
... 敏感因子的分级标准表[40 , 46 -48 ] ...
... Grading standard of sensitivity factor[40 , 46 -48 ] ...
... 平曲线半径是高铁线路的重要指标,影响线路的平顺与相应附属设施的设置. 参考《高速铁路设计规范》(TB10621—2014)[40 ] ,结合目标工程,将目标工程沿线平曲线半径划分为5 000~6 500 m、6 500~8 000 m、8 000~9 500 m、9500~11 000 m、>11 000 m 5个等级. ...
... 高铁设计时常用桥梁、隧道、道路及其组合的形式,但是不同形式的线路对地面沉降的敏感性不同. 考虑到现有研究资料不足与线路较长的问题,参考《高速铁路设计规范》(TB10621—2014)[40 ] 与文献[46 ],将目标工程沿线线路类型划分为路基、桥梁、路桥过渡段3个等级. ...
... 以不同行驶车速跨越地面沉降区域,受沉降的影响不同. 参考《高速铁路设计规范》(TB10621—2014)[40 ] ,结合目标工程,将目标工程沿线车速划分为250 km/h、300 km/h、350 km/h 3个等级. ...
1
... 区域性地面沉降的主要沉降均由厚松散层的变形贡献[41 ] ,较厚的软黏土往往会加剧地面沉降灾害的发展. 将区域内的松散层厚度划分为150~175 mm、175~200 mm、200~225 mm、225~250 mm、250~275 mm 5个等级. ...
1
... 区域性地面沉降的主要沉降均由厚松散层的变形贡献[41 ] ,较厚的软黏土往往会加剧地面沉降灾害的发展. 将区域内的松散层厚度划分为150~175 mm、175~200 mm、200~225 mm、225~250 mm、250~275 mm 5个等级. ...
中国气候区划新方案
1
2010
... 充足的降雨能够及时补充开采的地下水资源,延缓地面沉降灾害的发展. 参考文献[42 ],结合目标工程的地理位置,将区域内年降雨量划分为<200 mm、200~400 mm、400~600 mm、600~800 mm、>800 mm 5个等级. ...
中国气候区划新方案
1
2010
... 充足的降雨能够及时补充开采的地下水资源,延缓地面沉降灾害的发展. 参考文献[42 ],结合目标工程的地理位置,将区域内年降雨量划分为<200 mm、200~400 mm、400~600 mm、600~800 mm、>800 mm 5个等级. ...
3
... 灾害因子分级标准[38 -43 ] ...
... Grading standard of hazard factor[38 -43 ] ...
... 抽水是地面沉降发展最主要的原因之一. 目前正逐步封存抽水井,但地下水抽取与地面沉降发展之间存在明显的时滞性[39 ] ,停止抽水后,地面沉降会保持发展. 研究区内的抽水井深度多为120~130 m,抽水强度较大. 本文选取封存时间在2025年及以后的抽水井作为计算依据,假设各抽水井的开采强度相同,影响半径均设为1 500 m[43 ] . 通过ArcGIS计算抽水井影响分布,将区域内的抽水井影响划分为5个等级. ...
3
... 灾害因子分级标准[38 -43 ] ...
... Grading standard of hazard factor[38 -43 ] ...
... 抽水是地面沉降发展最主要的原因之一. 目前正逐步封存抽水井,但地下水抽取与地面沉降发展之间存在明显的时滞性[39 ] ,停止抽水后,地面沉降会保持发展. 研究区内的抽水井深度多为120~130 m,抽水强度较大. 本文选取封存时间在2025年及以后的抽水井作为计算依据,假设各抽水井的开采强度相同,影响半径均设为1 500 m[43 ] . 通过ArcGIS计算抽水井影响分布,将区域内的抽水井影响划分为5个等级. ...
3
... 易损性因子的分级标准表[44 -45 ] ...
... Grading standards of vulnerability factor[44 -45 ] ...
... 在同一地区内,不同的地区规划,易损性不同[44 ] . 在人流量大、基础设施密集的区域,灾害后潜在损失巨大,易损性较高,考虑将区域内的用地分布划分为工业用地、居住用地、公共服务、农业用地、生态绿地5个等级. ...
3
... 易损性因子的分级标准表[44 -45 ] ...
... Grading standards of vulnerability factor[44 -45 ] ...
... 在同一地区内,不同的地区规划,易损性不同[44 ] . 在人流量大、基础设施密集的区域,灾害后潜在损失巨大,易损性较高,考虑将区域内的用地分布划分为工业用地、居住用地、公共服务、农业用地、生态绿地5个等级. ...
3
... 易损性因子的分级标准表[44 -45 ] ...
... Grading standards of vulnerability factor[44 -45 ] ...
... 参考《公路工程技术标准》(JTG B01—2014)[45 ] ,对不同等级的公路给予不同的权重,以路网为中心,采用不同的影响半径,获得研究区道路易损性分布. 将区域内的道路易损性划分为四级公路、三级公路、二级公路、一级公路、高速公路5个等级. ...
基于物联网模式的高速铁路工后变形监测预警体系研究
3
2016
... 敏感因子的分级标准表[40 , 46 -48 ] ...
... Grading standard of sensitivity factor[40 , 46 -48 ] ...
... 高铁设计时常用桥梁、隧道、道路及其组合的形式,但是不同形式的线路对地面沉降的敏感性不同. 考虑到现有研究资料不足与线路较长的问题,参考《高速铁路设计规范》(TB10621—2014)[40 ] 与文献[46 ],将目标工程沿线线路类型划分为路基、桥梁、路桥过渡段3个等级. ...
基于物联网模式的高速铁路工后变形监测预警体系研究
3
2016
... 敏感因子的分级标准表[40 , 46 -48 ] ...
... Grading standard of sensitivity factor[40 , 46 -48 ] ...
... 高铁设计时常用桥梁、隧道、道路及其组合的形式,但是不同形式的线路对地面沉降的敏感性不同. 考虑到现有研究资料不足与线路较长的问题,参考《高速铁路设计规范》(TB10621—2014)[40 ] 与文献[46 ],将目标工程沿线线路类型划分为路基、桥梁、路桥过渡段3个等级. ...
1
... 不同的砟道形式在不均匀沉降作用下的工作性能存在明显的差异. 参考文献[47 ]与目标工程,将目标工程沿线砟道类型划分为纵连板式、单元板式、双块式3个等级. ...
1
... 不同的砟道形式在不均匀沉降作用下的工作性能存在明显的差异. 参考文献[47 ]与目标工程,将目标工程沿线砟道类型划分为纵连板式、单元板式、双块式3个等级. ...
4
... 式中:$ R $ $ H $ $ S $ $ V $ 38 ~48 ]确定评价因子及其等级划分,构建沉降风险评估体系,如图2 所示,采用的评价语言集为$ L $ . 其中灾害性因子包括地面塌陷区H 1 、地下水位H 2 、差异沉降速率H 3 、松散层厚度H 4 、年降水量H 5 、抽水井的地理位置H 6 . 其中易损性因子包括人口密度V 1 、用地类型V 2 、轨道交通V 3 、道路类型V 4 、城镇密度V 5 、地面高程V 6 . 其中敏感性因子包括平曲线半径S 1 、轨道类型S 2 、砟道类型S 3 、跨度S 4 、车速S 5 . ...
... 敏感因子的分级标准表[40 , 46 -48 ] ...
... Grading standard of sensitivity factor[40 , 46 -48 ] ...
... 跨度较大的桥梁往往受到不均匀沉降的影响较小,桥梁结构产生较小的应力. 参考《桥梁工程》[48 ] ,结合目标工程,将跨度划分为<5 m、5~20 m、20~40 m、40~150 m、>150 m 5个等级. ...
控制地面沉降的地下水限采方案研究
2
2023
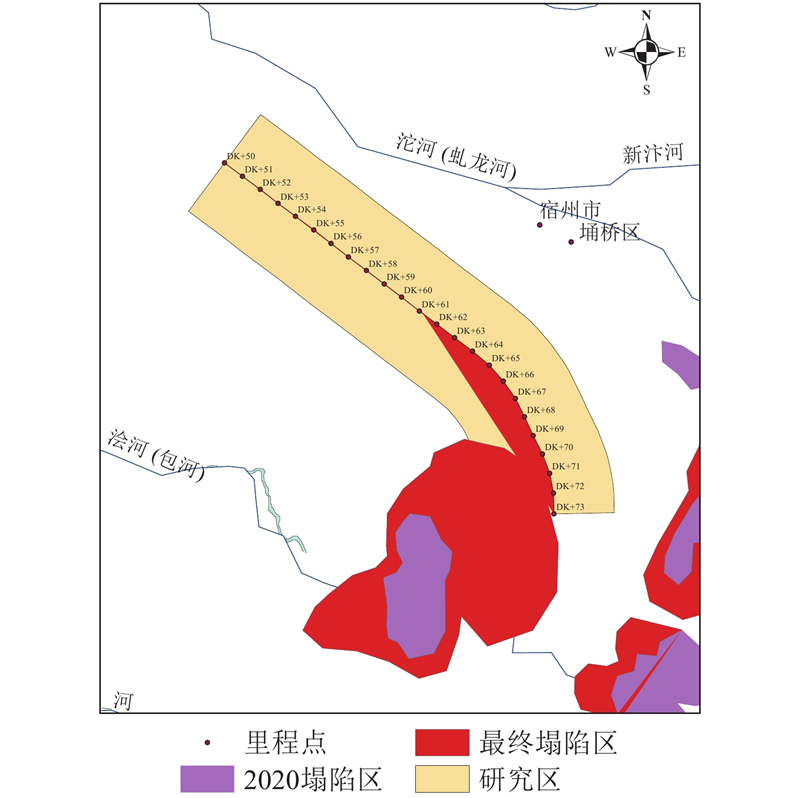
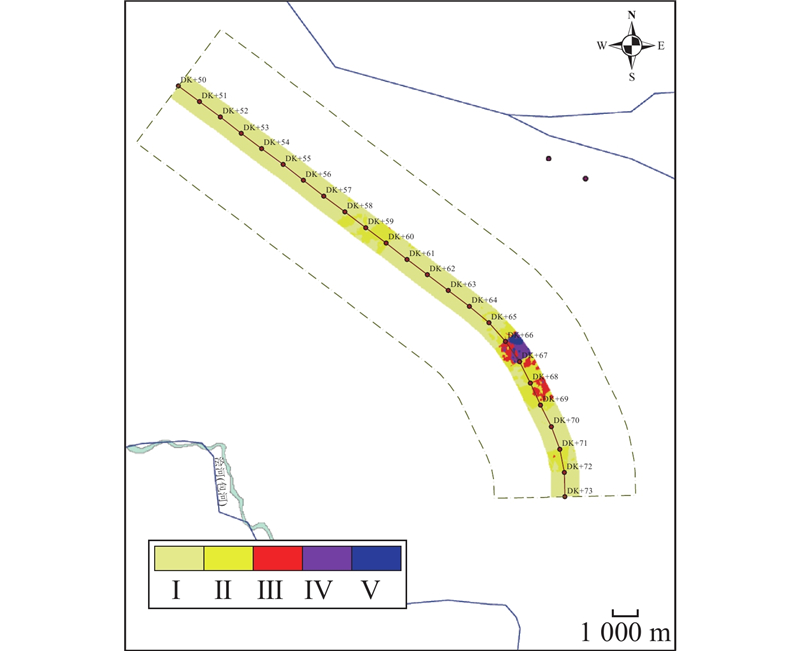
... 研究区的示意图[49 ] ...
... Schematic diagram of study area[49 ] ...
控制地面沉降的地下水限采方案研究
2
2023
... 研究区的示意图[49 ] ...
... Schematic diagram of study area[49 ] ...
层次分析法权重计算方法分析及其应用研究
1
2012
... 参考文献[37 ],采用AHP方法对灾害性因子进行评估,AHP方法的详细评估流程见文献[50 ]. 采用AHP方法,建立判断矩阵如下: ...
层次分析法权重计算方法分析及其应用研究
1
2012
... 参考文献[37 ],采用AHP方法对灾害性因子进行评估,AHP方法的详细评估流程见文献[50 ]. 采用AHP方法,建立判断矩阵如下: ...