在工程实践中,平均腐蚀深度是评估腐蚀程度的重要指标[6]. 目前,预测管道平均腐蚀深度的主流方法包括确定性方法、随机模型和数据驱动模型[8-9]. 确定性方法将平均腐蚀深度的增长用线性或指数型表达式进行模拟[8]. Mazumder等[10]对已有的确定性模型进行总结,利用这些模型建立时间和平均腐蚀深度的关系. 随机模型通常利用不同类型的分布随机模拟腐蚀深度的增长. Dann等[11]获取了多年的管道腐蚀深度检测数据,建立贝叶斯模型,预测腐蚀深度的增长. 数据驱动模型通常是以腐蚀深度数据和运营环境数据为输入,建立机器学习模型,预测腐蚀深度. 蒋白懿等[12]采集得到某条供水管线的管壁内腐蚀速率和水质数据,运用灰关联定权组合法建立预测模型. 上述方法没有考虑钢管腐蚀的电化学机理,因此所建立的预测模型难以泛化到不同的场景中使用.
综上所述,本文在调查钢管内腐蚀电化学机理的基础上,提出基于电化学机理的腐蚀深度预测模型. 结合腐蚀深度-力学性能退化经验公式和Chaboche本构模型,提出化力模型,以预测内腐蚀作用后管壁的应力-应变曲线. 与其他论文的模型预测结果和实测结果进行对比,验证了模型的有效性. 以某服役DN500钢管为例,验证了该模型的实用性.
1. 总体框架
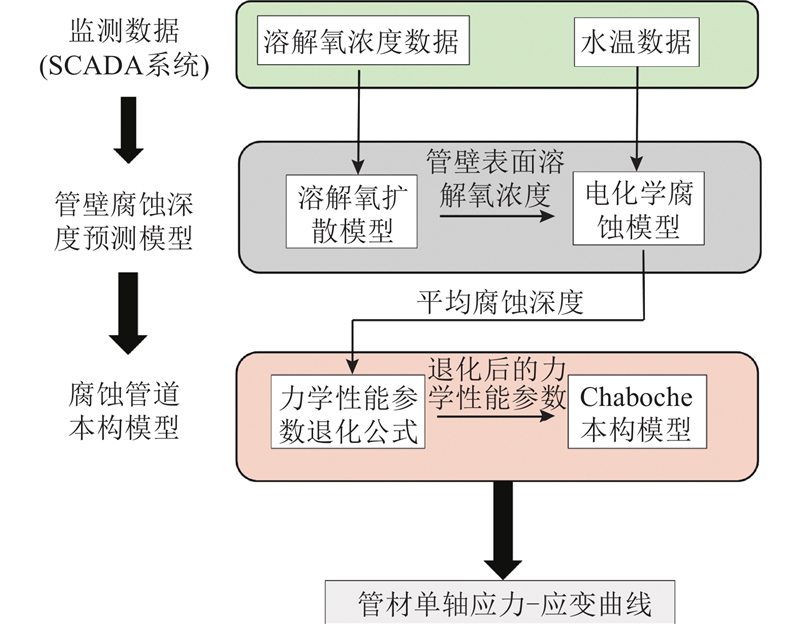
如图1所示为提出的化力模型构建的总体框架. 管壁腐蚀深度预测的电化学模型以数据采集与监测控制 (supervisory control and data acquisition, SCADA)系统所采集到的溶解氧质量浓度和水温作为输入,考虑了水中溶解氧在铁锈中的扩散及管壁的电化学反应,可以准确地预测平均腐蚀深度. 力学模型在已有的力学性能腐蚀退化经验公式基础上,利用Chaboche本构模型模拟在不同时刻下钢管管材在内腐蚀下的单轴拉伸应力-应变曲线. 该曲线可以为全寿命运营周期内管道的安全评估提供依据.
图 1
2. 管壁腐蚀深度预测模型
2.1. 供水钢管的电化学腐蚀机理
图 2
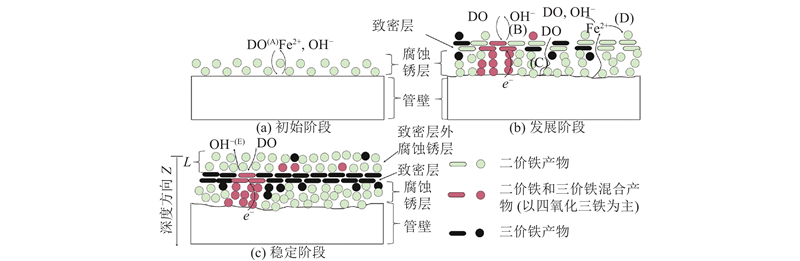
图 2 供水管道电化学腐蚀的三阶段示意图
Fig.2 Three-stage schematic diagram of electrochemical corrosion in water supply pipeline
由式(1)所示反应生成的Fe2+与水中的氢氧根离子、溶解氧和碳酸根离子反应,生成FeCO3、FeOOH和Fe3O4等固体产物,堆积在表面管壁表面,形成锈层. 此阶段由于溶解氧直接与管壁发生反应,腐蚀速率最快. 随着锈层变厚,腐蚀速率变慢,进入到发展阶段.
郭浩[13]通过失重法测得钢管的平均腐蚀速率. 结果显示,前2个阶段持续时间大约为16 d. 在管道几十年的运营周期中,稳定阶段起到控制作用. 综上所述,腐蚀深度预测模型从稳定阶段的机理出发,开展理论建模. 稳定阶段主要包含2个过程:1) 溶解氧扩散到致密层表面;2) 在致密层表面发生电化学反应. 下面对这2个阶段进行建模.
2.2. 溶解氧扩散模型
溶解氧的扩散采用菲克第二定律进行模拟,如下所示:
式中:cO为溶解氧浓度,假定cO在空间上只沿深度方向变化;DO为扩散系数;z为深度. 考虑到外腐蚀锈层的厚度很薄,通常为几百微米. 式(3)可以写成
式中:cOW 、cOS分别为水中和致密层表面的溶解氧浓度;L为外锈层的厚度,Sarin等[15]实测其值均为400 μm,可按400 μm取值;下标d表示由扩散引起的致密层表面溶解氧浓度变化.
2.3. 电化学腐蚀模型
根据化学动力学可知,在初始阶段,当溶解氧与管壁直接接触时,溶解氧浓度变化可以写为
式中:下标r表示由电化学反应引起的致密层表面溶解氧量浓度变化;kO为反应速率常数,需要通过腐蚀试验确定,通常反应速率常数可以写为阿伦尼乌斯公式的形式,
其中,AO为常数,Ea为活化能,这两者需要通过腐蚀试验标定以确定kO;R为摩尔气体常数;Tw为水温.
在稳定阶段,根据图2(c)的过程(E)所示,溶解氧在致密层表面通过可导电的Fe3O4与管壁进行电化学反应. 根据式(5),相应的化学动力学方程可以写为
式中:wFe为外腐蚀锈层中Fe3O4的质量分数.
根据式(7),求得单位时间内由于电化学反应消耗的溶解氧摩尔量后. 考虑到氧化还原反应中氧气在阴极获得的电子数量等于管壁上Fe失去的电子数量,根据溶解氧的反应速率,可以近似估计腐蚀电流密度,估算平均腐蚀速率. 在已知溶解氧的反应速率后,腐蚀电流密度可以按照下式进行估计:
式中:nO为氧气的化合价,取4;V和A分别为单位体积和单位面积;F为法拉第常数.
在已知腐蚀电流密度后,可以通过下式求得年腐蚀速率:
式中:nFe为铁的化合价,取2;MFe为Fe的相对原子质量,取56;ρFe为铁的密度.
综合式(7)~(9)可以推导出在已知致密层表面溶解氧反应速率时的管壁平均腐蚀速率.
对式(10)进行积分,可得管道的平均腐蚀深度:
通过SCADA监测系统可以采集得到水中溶解氧的质量浓度,换算得到cOW,通过2.2节介绍的扩散模型,可以求得cOS. 以此为输入,结合水温监测数据,运用2.3节的电化学模型可以实时估计平均腐蚀深度,为力学性能退化预测提供参考.
2.4. 参数确定与模型验证
目前,模型的反应速率常数kO和溶解氧的扩散系数DO是模型的未知参数. 这2个参数可以通过失重法测得的平均腐蚀速率确定. 运用文献[13]的钢材平均腐蚀速率实测数据,确定这2个参数. 将推导得到的参数值与实测参数值进行对比,验证模型的合理性.
1) 反应速率常数kO.
需要标定AO和Ea,以确定反应速率常数. 利用不同温度下初始时刻的平均腐蚀速率,可以标定这2个参数. 运用式(5)、(6)、(10),标定方程为
cOW可以通过在实验中监测水中溶解氧质量浓度换算得到. 郭浩[13]给出了利用失重法测定平均腐蚀速率时水中的溶解氧质量浓度. 将测得的多组不同温度下的初始时刻的平均腐蚀速率代入式(12)的等号右边项,可以确定AO和Ea.
2) 溶解氧扩散系数DO.
在确定kO后,运用这一标定好的参数,结合稳定阶段的平均腐蚀速率,可以标定DO. 在稳定阶段,腐蚀速率保持恒定不变的数值. 根据式(7)可知,当腐蚀速率不变时,致密层表面的溶解氧浓度保持为定值. 此时通过扩散进入致密层表面的溶解氧等于电化学反应消耗的溶解氧,有
根据式(7)、(10),有
将式(16)代入式(14),除稳定阶段Vy需要进一步测量得到外,其余参数均已知. 在稳定阶段,取一段时间内的平均腐蚀速率均值,可以标定出DO.
3) 模型验证.
表 1 腐蚀速率预测模型的参数识别结果
Tab.1
| 参数 | 标定值 |
| AO/ s−1 | 23.2713 |
| Ea/(kJ‧mol−1) | 23.5 |
| DO/(m2‧s−1) | 1.43×10−11 |
| DOC/(m2‧s−1) | 1.06×10−11 |
郭浩[13]提出的供水管道内腐蚀机理同样适用于球墨铸铁管,且给出使用失重法测得的球墨铸铁试片的平均腐蚀速率. 运用2.4节给出的参数标定方法,获得球墨铸铁管的溶解氧扩散系数DOC,为1.06×10−11 m2/s. 该标定参数在合理范围内. 对于球墨铸铁管的kO,考虑到球墨铸铁管与钢管的电化学腐蚀机理相同,认为其与钢管的kO一致.
3. 腐蚀钢管的本构模型
基于获得的管壁平均腐蚀深度,采用已有的经验公式确定力学性能参数与平均腐蚀深度的定量关系,研究管道力学性能的退化规律. 以力学性能参数作为输入,结合经典的Chaboche本构模型,可以模拟得到腐蚀后的管道单轴拉伸应力-应变曲线.
3.1. 腐蚀深度-力学性能的退化经验曲线
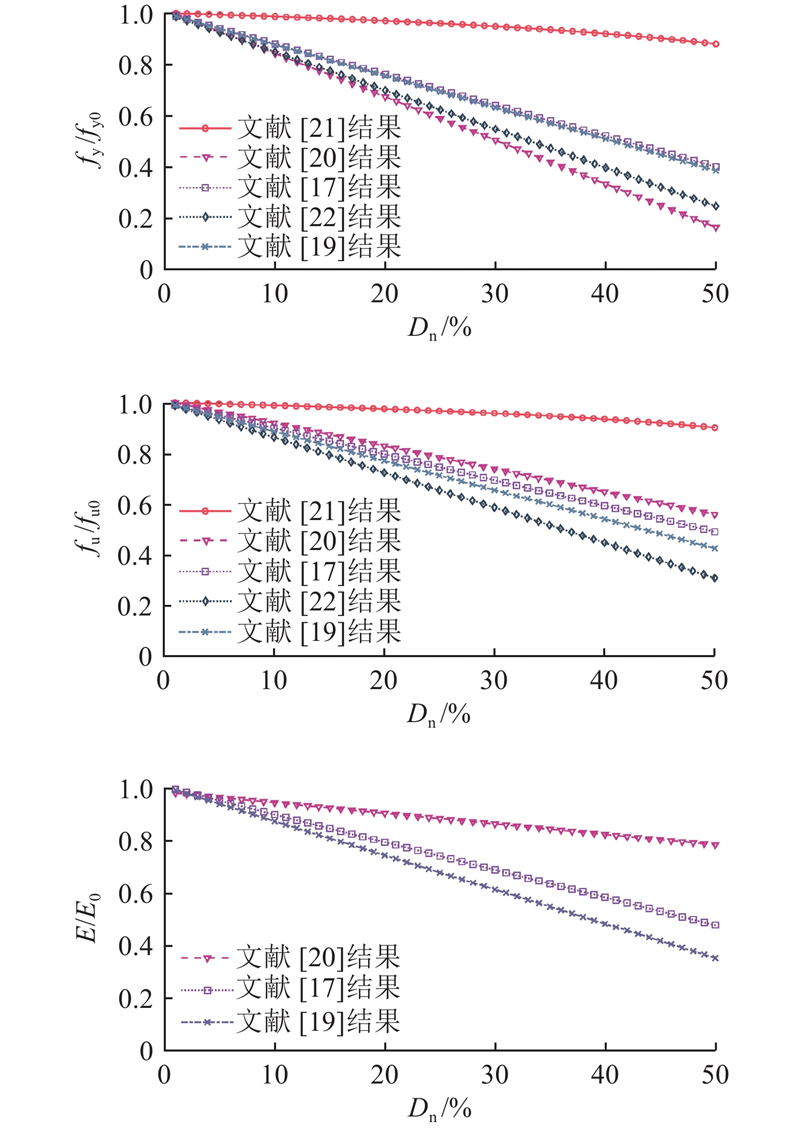
一些学者从已经腐蚀后的构件上切割加工[7, 17-18],或通过加速腐蚀试验获取了腐蚀试件[19-21]. 通过拉伸试验测得不同平均腐蚀深度下钢材力学性能的退化,拟合出了经验公式. 当模拟单轴受拉应力-应变曲线时,应已知弹性模量E、屈服应力fy和极限应力fu的退化. 本文参考了其他学者由腐蚀钢试件拉伸试验归纳出的不同腐蚀深度下单轴力学性能退化的经验公式. 式(17)给出腐蚀程度的定义. 图3给出Wang等[17, 19-22]得到的经验公式,下角标的“0”表示未腐蚀退化构件的力学性能参数. 可以看出,大部分经验公式的预测结果比较接近,验证了这些经验公式的有效性. 为了保证安全,选取其中最不利的公式,预测弹性模量E[19]、屈服应力fy[20]和极限应力fu [22]的退化.
图 3
图 3 不同学者得到的腐蚀程度-钢材力学性能退化经验公式
Fig.3 Empirical law of steel mechanical property degradation due to corrosion obtained by researchers
3.2. Chaboche本构模型
1) 弹性阶段应力-应变关系.
在弹性阶段,Chaboche本构模型服从胡克定律:
式中:
2) 屈服函数.
屈服函数Fy满足Von Mises屈服准则:
式中:
3) 塑性应变演化.
当Fy > 0时,产生塑性应变,弹塑性Chaboche本构模型的塑性应变率遵守正交流动法则,有
式中:
4) 背应力演化.
为了考虑材料的硬化,背应力描述了屈服面中心的移动:
式中:M为背应力的分量的数目,Ci和γi为描述材料硬化的常数.
运用Chaboche本构模型的隐式迭代算法,根据退化后的弹性模量E、fy和fu,可以计算得到腐蚀管道的单轴拉伸应力-应变曲线,为管道在全寿命周期内的安全评估提供依据. 相应的隐式迭代算法可以参考文献[24].
4. 案例分析
4.1. 腐蚀深度预测
本文所使用的数据来源于某正在服役的DN500钢管,由SCADA水质监测系统采集,采样频率为1 min−1,包括溶解氧质量浓度和水温数据. 数据的时间范围为2020年和2021年全年. 运用这2类数据,预测平均腐蚀深度,并以此为输入,采用腐蚀管道本构模型确定管道的时变单轴应力-应变曲线.
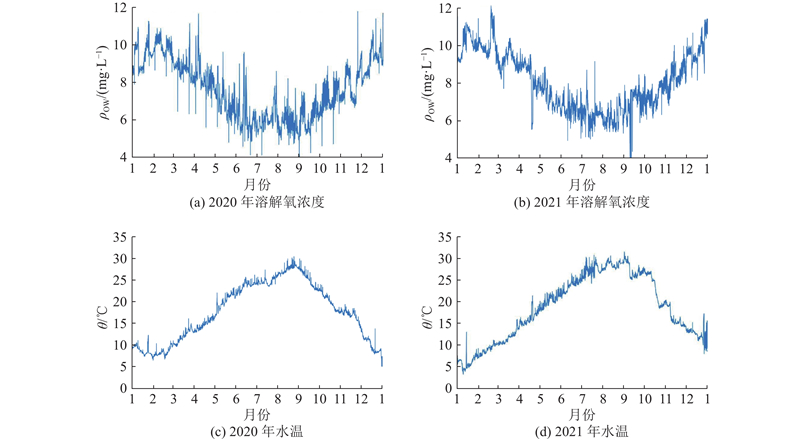
获取2020年和2021年某供水钢管的溶解氧质量浓度ρOW和水温θ数据,由SCADA监测系统采集,如图4、5所示. 由于温度越高,溶解度越小,图4的实测数据在趋势上是合理的. 利用腐蚀深度预测模型计算相应的腐蚀速率,使用的模型参数如表2所示. 如图5所示为计算的结果. 可以看出,两年的计算结果均显示腐蚀速率在0.1 mm/a上下波动. 蒋白懿等[12, 25]对实际运营的管道腐蚀速率进行调查,可知管道的腐蚀速率在0.07~0.13 mm/a波动. 该结果是合理的,证明了所提电化学腐蚀深度预测模型的有效性. 对两年的数据分别进行积分,结果显示,2020年和2021年的年腐蚀深度分别为0.090 8和0.096 3 mm.
图 4
图 4 现场实测得到的溶解氧质量浓度和水温
Fig.4 Measured dissolved oxygen mass concentration and water temperature of field testing
图 5
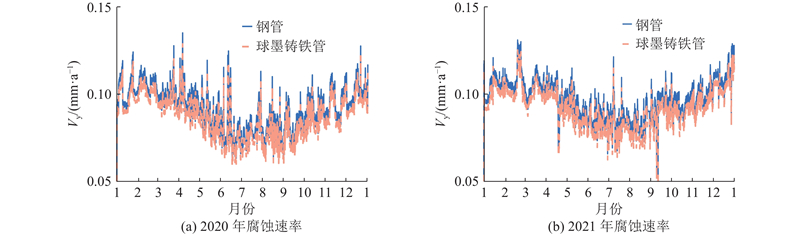
图 5 利用电化学腐蚀速率预测模型计算得到的钢管和球墨铸铁腐蚀速率
Fig.5 Corrosion rate of steel and ductile pipe calculated by electrochemical corrosion rate prediction model
表 2 提出的电化学腐蚀速率预测模型的参数
Tab.2
| 参数 | 数值 |
| wFe | 0.33 |
| L/μm | 400 |
| AO/ s−1 | 23.2713 |
| Ea/( kJ‧mol−1) | 23.5 |
| DO/( m2‧s−1) | 1.43×10−11 |
| DOC/( m2‧s−1) | 1.06×10−11 |
4.2. 腐蚀速率预测模型的对比
图 6
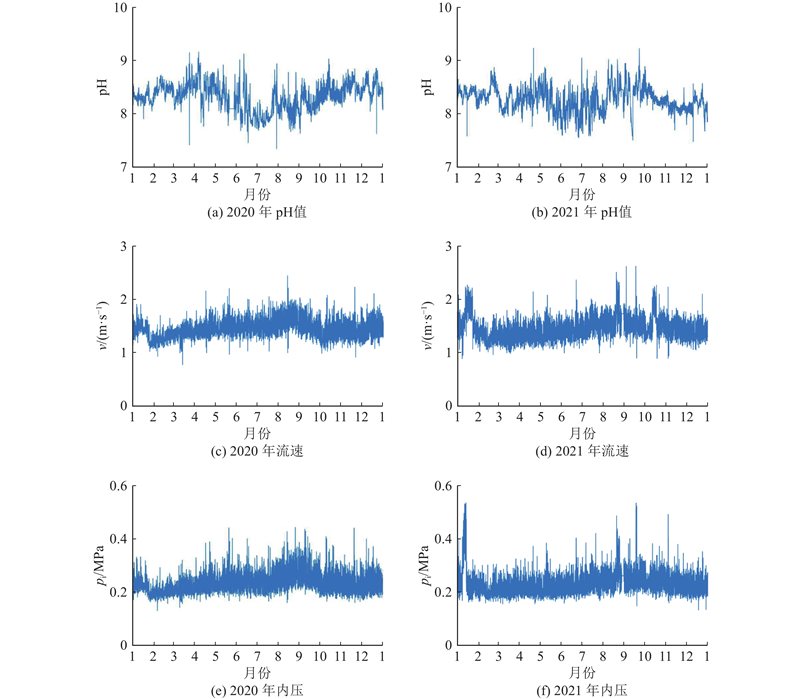
图 6 现场实测得到的pH值、流速和内压数据
Fig.6 Measured pH value, velocity of flow and internal pressure of field testing
运用蒋白懿等[12]归纳总结的经验公式,可以计算得到2020年和2021年的腐蚀速率,如图7所示. 可以看出,除少部分离群值,腐蚀速率为0.07~0.13 mm/a. 与图5所示的本文模型计算得到的腐蚀速率进行对比,可得如下结论. 1) 两者计算得到的腐蚀速率的波动范围基本一致,大都集中在0.07~0.13 mm/a. 2) 运用经验公式计算得到的2020年和2021年管道腐蚀深度为0.085 3和0.088 5 mm;运用提出模型计算得到的2020年和2021年管道腐蚀深度为0.090 8 mm和0.096 3 mm. 利用2类模型计算得到的2020年和2021年年腐蚀深度误差分别为5.95%和8.10%. 可知,本文模型是合理、有效的.
图 7
图 7 使用已有经验模型计算得到的腐蚀速率
Fig.7 Corrosion rate calculated by existing empirical model
4.3. 灵敏度分析
随着服役年限的增加及水力水质条件的变化,管道内壁腐蚀产物层的致密性会发生变化,从而改变溶解氧扩散系数,导致腐蚀速率波动. 针对DO这一参数进行灵敏度分析,讨论在管壁腐蚀过程中铁锈层溶解氧扩散系数的变化对腐蚀速率的影响. 考虑到2020年和2021年水温和溶解氧质量浓度十分接近,不分别进行讨论. 对这2类数据取均值,得到时长为1 a的溶解氧质量浓度和水温数据进行灵敏度分析. 将年平均腐蚀深度作为腐蚀速率的指标.
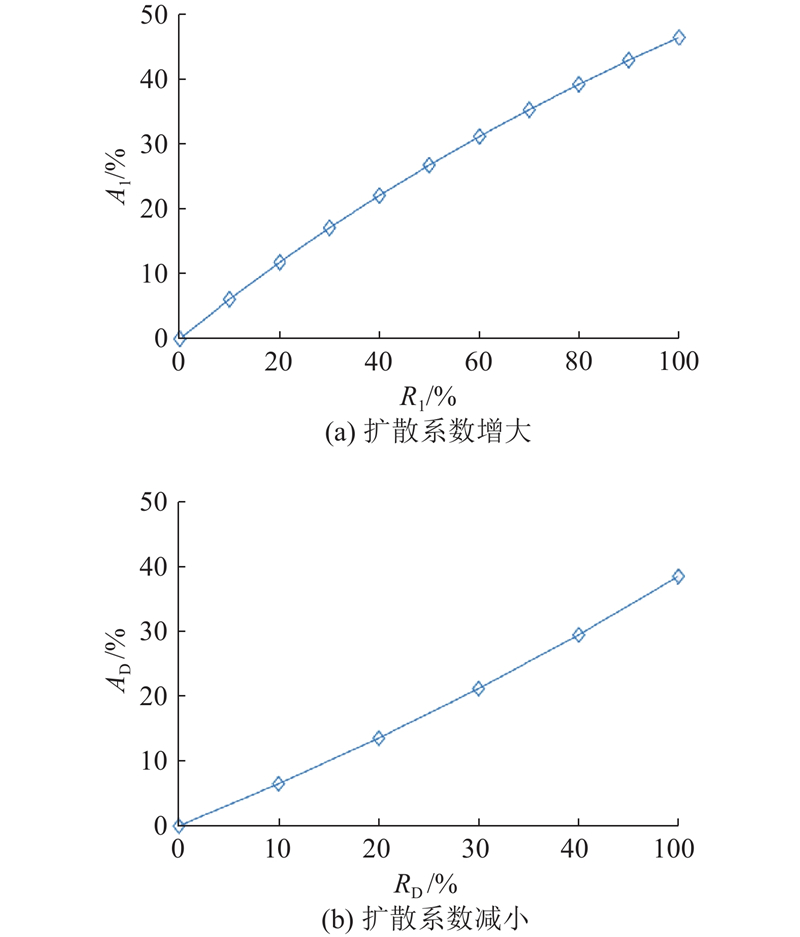
如图8所示为当其他条件不变时,管壁年平均腐蚀深度随扩散系数的变化. 图中,RI和RD分别为扩散系数增大和减小的百分比,AI和AD分别为年平均腐蚀深度增大和减小的百分比. 1) 当DO 减小0~50%时,年平均腐蚀深度减小了40%,从0.0917 mm减小到了0.056 3 mm;当DO增大100%时,年平均腐蚀深度增大近50%,从0.091 7 mm增大到0.132 5 mm. 2) 当DO取值为表1所示的50%~200%时,预测得到的年平均腐蚀深度为0.056~0.133 mm. 蒋白懿等[12]实测得到的年平均腐蚀深度为0.07~0.13 mm,预测年平均腐蚀深度区间与文献[12]实测得到的年平均腐蚀深度接近. 综上可知,年平均腐蚀速率正比于DO的变化. DO具有鲁棒性,在较大的波动范围内,仍能保持结果的合理性.
图 8
图 8 管壁平均腐蚀深度随扩散系数的变化
Fig.8 Variation of average corrosion depth with diffusion coefficient
4.4. 时变单轴-应力应变曲线
| 参数 | 数值 | 参数 | 数值 | |
| fy0/ MPa | 235 | M | 2 | |
| E0/ MPa | 210 000 | C1/ MPa | 2 700 | |
| fu0/ MPa | 375 | C2/ MPa | 800 | |
| Q/ MPa | 200 | γ1 | 200 | |
| b | 40 | γ2 | 50 |
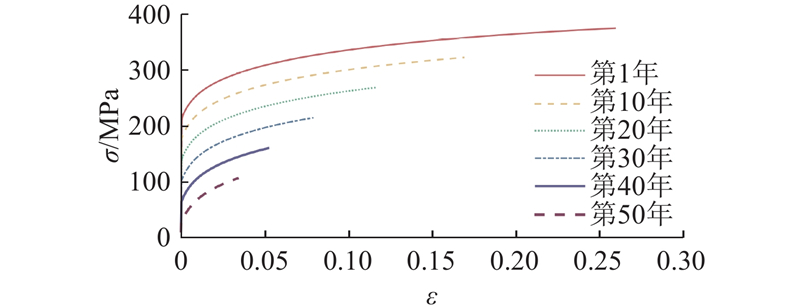
图 9
图 9 内腐蚀作用下钢管的时变单轴应力-应变曲线
Fig.9 Time-varying uniaxial stress-strain curve of pipeline induced by internal corrosion
目前,关于球墨铸铁在不同腐蚀程度下的力学性能退化,相应的实验工作很少. 由于球墨铸铁管的腐蚀深度-力学性能退化的关系研究尚且不充分,本文没有讨论球墨铸铁管腐蚀后管材力学性能的退化. 在获取球墨铸铁的腐蚀深度-力学性能退化经验关系后,可以参考本文的框架,使用相应的本构力学模型计算不同腐蚀深度下球墨铸铁管道的单轴应力-应变曲线.
4.5. 结果讨论
针对采集得到的原始数据、预测得到的管壁平均腐蚀速率和时变应力-应变曲线的合理性进行讨论,结果如下.
1) 从所采集的原始溶解氧数据可知,溶解氧质量浓度随着气温升高而降低. 考虑到温度越高,氧气的溶解度越少,采集的溶解氧质量浓度数据在趋势上是正确的. 针对水温数据可以发现,温度变化趋势与气温波动趋势一致,水温数据在趋势上是合理的. 管道内压、pH值和流速均在正常范围内,波动不大,可以认为是合理的.
5. 结 语
基于供水钢管的电化学腐蚀机理,本文提出化力模型,用以预测管道在内腐蚀作用下的平均腐蚀深度及对应的腐蚀后管材应力-应变曲线,为管道在全寿命周期内的安全评估提供参考.
该化力模型的创新性体现在以下2点. 1) 本文基于供水管道腐蚀的细观机理,提出针对钢管管壁腐蚀深度预测模型. 2)结合现有的腐蚀深度-力学性能退化经验公式和Chaboche本构模型,预测腐蚀后钢管管材的应力-应变曲线. 将化力模型预测得到的年腐蚀速率和腐蚀后管材的应力-应变曲线与已有文献的实测结果进行比较,验证了该化力模型的合理性.
案例中所选取的管线为正在服役的埋地管线,难以直接测量管道的腐蚀深度,因此本文未能获取管道的实际腐蚀情况,以直接验证模型的准确性,是本文目前的不足之处. 后续将退役的废弃管线制成试件,测量腐蚀深度,结合管线历史水质和水力监测数据修正模型,增强该化力模型的准确性.
参考文献
Residual ultimate strength of offshore metallic pipelines with structural damage: a literature review
[J].DOI:10.1080/17445302.2017.1308214 [本文引用: 1]
Degradation of mechanical property of corroded water pipes after long service
[J].DOI:10.1080/1573062X.2019.1687744 [本文引用: 2]
Effect of corrosion and hydrogen embrittlement on microstructure and mechanical properties of mild steel
[J].DOI:10.1016/j.conbuildmat.2018.03.023 [本文引用: 1]
Specific features of hydrogen-induced corrosion degradation of steels of gas and oil pipelines and oil storage reservoirs
[J].
Nanoindentation study of corrosion-induced grain boundary degradation in a pipeline steel
[J].DOI:10.1016/j.elecom.2018.02.001 [本文引用: 2]
Tensile strength assessment of corroded small scale specimens
[J].DOI:10.1016/j.corsci.2014.04.031 [本文引用: 2]
A review on pipeline corrosion, in-line inspection (ILI), and corrosion growth rate models
[J].DOI:10.1016/j.ijpvp.2016.11.007 [本文引用: 2]
Advances in corrosion growth modeling for oil and gas pipelines: a review
[J].
Reliability analysis of water distribution systems using physical probabilistic pipe failure method
[J].DOI:10.1061/(ASCE)WR.1943-5452.0001034 [本文引用: 1]
The effect of inspection sizing uncertainty on the maximum corrosion growth in pipelines
[J].DOI:10.1016/j.strusafe.2017.10.005 [本文引用: 1]
利用灰关联定权组合模型预测城镇给水管道腐蚀速率
[J].
al. Corrosion prediction for pipeline in water supply of town by grey relation weight-making combination forecasting model
[J].
Iron corrosion scales: model for scale growth, iron release, and colored water formation
[J].DOI:10.1061/(ASCE)0733-9372(2004)130:4(364) [本文引用: 1]
Physico-chemical characteristics of corrosion scales in old iron pipes
[J].DOI:10.1016/S0043-1354(00)00591-1 [本文引用: 1]
Enhancement of electric conductivity of the rust layer by adsorption of water
[J].DOI:10.1016/j.corsci.2004.10.010 [本文引用: 1]
Hysteretic behavior and cyclic constitutive model of corroded structural steel under general atmospheric environment
[J].DOI:10.1016/j.conbuildmat.2020.121474 [本文引用: 2]
Stress–strain model of lower corroded steel plates of normal strength for fitness-for-purpose analyses
[J].DOI:10.1016/j.conbuildmat.2022.126560 [本文引用: 1]
Tensile behavior of naturally and artificially corroded steel bars
[J].DOI:10.1016/j.conbuildmat.2015.10.075 [本文引用: 5]
Grey relational analysis of static tensile properties of structural steel subjected to urban industrial atmospheric corrosion and accelerated corrosion
[J].DOI:10.1016/j.conbuildmat.2021.125706 [本文引用: 3]
Tensile and fatigue behavior of corroded rebars
[J].DOI:10.1016/j.conbuildmat.2012.02.071 [本文引用: 1]
Degradation relationships for the mechanical properties of corroded steel rebars
[J].DOI:10.1016/j.conbuildmat.2017.04.209 [本文引用: 2]
A review of some plasticity and viscoplasticity constitutive theories
[J].DOI:10.1016/j.ijplas.2008.03.009 [本文引用: 2]
Extremely-low cycle fatigue fracture of Q235 steel at different stress triaxialities
[J].DOI:10.1016/j.jcsr.2020.106060 [本文引用: 2]