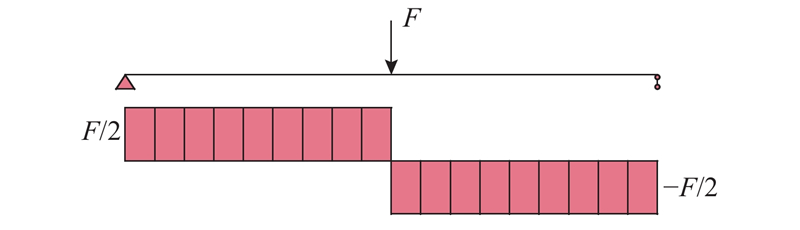
在组合桥面板结构中,明确剪力钉的形式和布置方式及探究对应的剪力钉所受的剪力分布规律是研究中的难点,这三者相互制约,剪力钉的形式、布置方式会改变剪力钉的受力行为.
对于剪力钉在组合桥面板中的受力特点和布置方式,国内外进行了一系列的研究,学者们提出了一些观点. 张士红等[17]认为组合桥面板的横向层间切应力普遍比纵向大,层间横向切应力是决定剪力钉均匀布置间距的主要因素. 史占崇等[18]认为栓钉的布置涉及横桥向及纵桥向2个维度,对于横桥向的布置应当满足构造要求,应避免将栓钉布置在U肋-钢顶板连接位置,纵向布置应考虑静力组合作用,满足疲劳控制要求. 蔡昊[19]研究车辆荷载作用下组合桥面板的层间纵、横向切应力分布规律,认为剪力钉同时受到纵、横向切应力,应综合考虑,将二者矢量叠加进行计算. 聂建国[20]认为对组合桥面板的抗剪连接件进行疲劳验算和正常使用极限状态验算时,需要考虑局部效应(如轮压)和整体效应(如桥梁的整体受弯)下的共同作用,抗剪连接件的剪力设计值取为顺桥向和横桥向2个方向上的剪力的矢量和. 欧洲规范4[21]中规定认为,靠近钢梁腹板位置的抗剪连接件的受力较大,应比其余部位布置得更紧密一些. Hiroshi等[22]采用真实的车轮荷载对组合桥面板结构进行试验,发现剪力钉的受力方向随车轮位置改变而改变,取矢量叠加后的值进行疲劳计算.
综合上述研究现状可知,在剪力钉受力特点方面,组合桥面板结构中的剪力钉是双向受力,在局部车轮荷载作用下会承担纵、横向剪力,整体受弯以纵向剪力为主. 在剪力钉的布置方式上,提出采用纵、横向剪力效应综合布置剪力钉和在横向上避免将栓钉布置在加劲肋上的布置方式. 目前对组合桥面板的整体受弯状态下剪力钉所受的纵向剪力是按组合梁的计算公式进行计算,对剪力钉的横向布置方式没有给出明确的力学解释. 本文从传统的工字形截面的切应力、剪力流分布规律出发,推导得到组合桥面板截面的切应力、剪力流分布公式及特点,根据切应力互等定理,得到组合桥面板独特的剪力流分布对层间纵向剪力的影响,分析剪力钉横向上不同的布置方式.
1. 组合桥面板的剪力流理论
1.1. 组合桥面板结构的剪力流分布规律
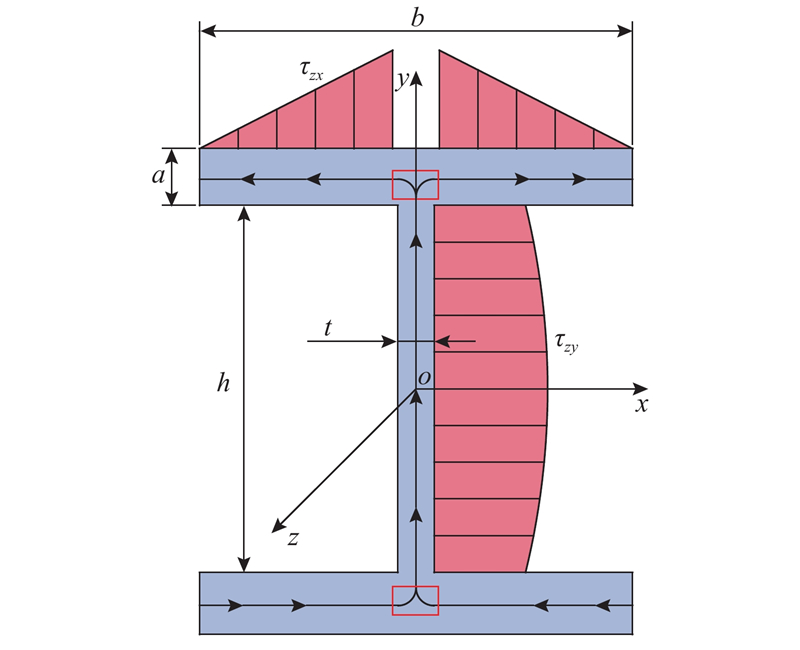
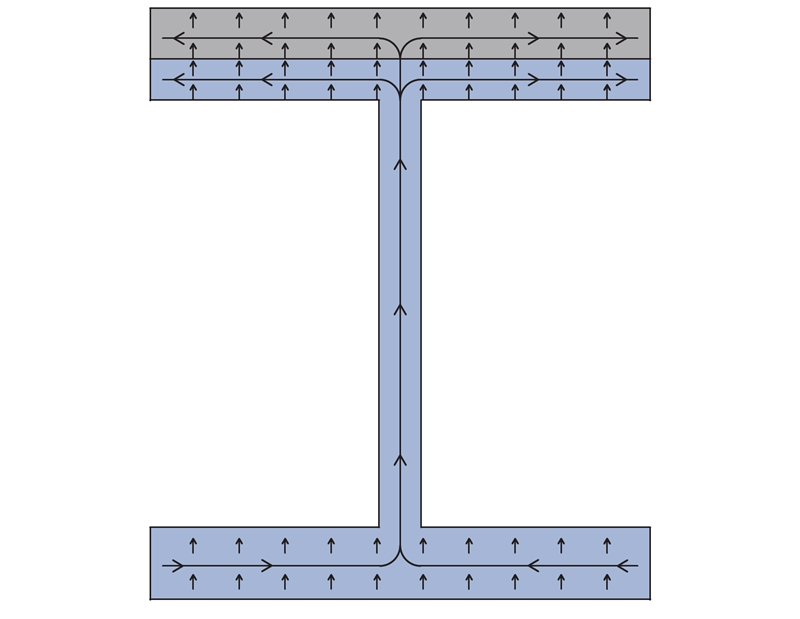
对于传统的工字形梁,根据相关的材料力学理论[23]可知,截面竖向切应力沿腹板和横向切应力沿翼缘分布的计算公式为
式中:V为截面剪力;Ix为截面惯性矩;a、b、t、h分别为上翼缘板高度、上翼缘板宽度、腹板厚度和腹板高度;Sx为计算点以上截面关于x轴的面积矩;x、y分别为图1所示坐标系下计算点到腹板中心的横向距离和竖向距离,取坐标值的绝对值.
图 1
图 1 工字形截面的切应力及剪力流分布
Fig.1 Distribution of shear stress and shear flow in I-shaped section
利用式(1)、(2)得到的切应力和剪力流分布如图1所示. 在顶、底板和腹板的交界处,剪力流由竖向转为横向,变化过程非常复杂,无法精确描述. 根据式(1)、(2),取
对应的剪力流分布规律如下:
若忽略腹板厚度t,可得
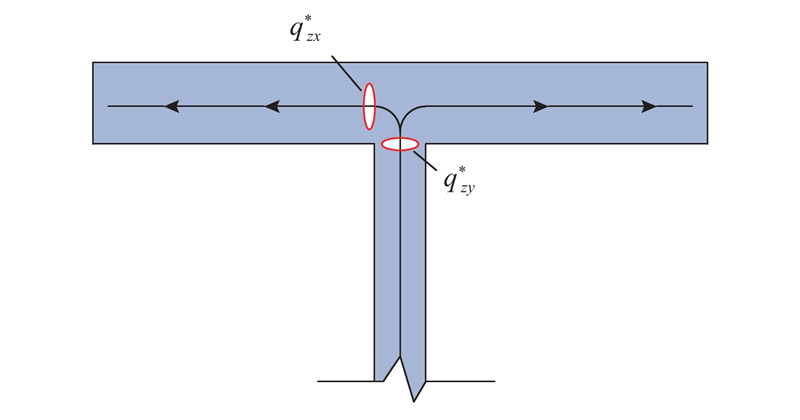
式(7)说明,上翼缘板的横向切应力流为腹板竖向切应力流的一半,两侧翼缘板各承担了从腹板过来的剪力流的一半,剪力流在腹板和翼缘板交接区域方向转换后,总值是固定的.
图 2
图 2 剪力流由腹板流入顶板的示意图
Fig.2 Schematic diagram of shear flow from web to top plate
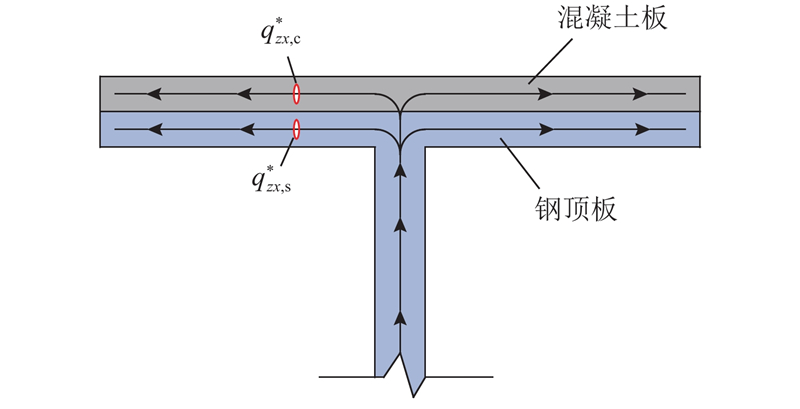
图 3
图 3 剪力流由腹板流入混凝土板和钢顶板的示意图
Fig.3 Schematic diagram of shear flow from web into concrete slab and steel top plate
式中:
假设混凝土板和钢顶板二者完全连接,界面上没有相对位移,此时在界面上混凝土与钢顶板的切应变相等,即
式中:tc和ts分别为混凝土和钢板的厚度.
式(9)说明横向切应力在混凝土和钢顶板中的分配是按切变模量进行分配的,而剪力流的分配受到切变模量和板厚2个因素的共同影响.
1.2. 剪力流分布对纵向剪力的影响
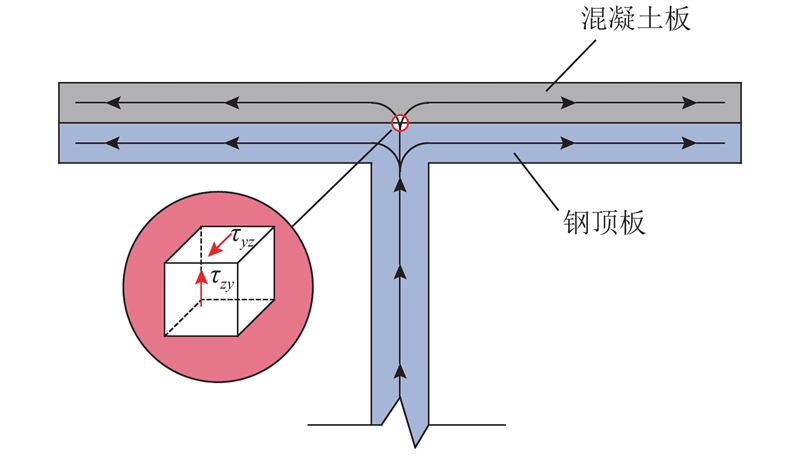
根据切应力互等定理可知,腹板和混凝土板交接处的竖向切应力等于混凝土板-钢顶板结合面的纵向切应力.
如图4所示,腹板的剪力流部分流入钢顶板,剩余部分流入混凝土板,且流入混凝土板的竖向切应力和混凝土板-钢顶板结合面的纵向切应力互等,而不是腹板承担的全部竖向切应力和其相等.
图 4
图 4 混凝土和钢顶板交接处的应力关系
Fig.4 Stress relationship at intersection of concrete and steel top plate
在流入混凝土板的剪力流完全转换成横向后,不产生层间纵向切应力,因此层间纵向切应力集中于腹板的剪力流流入混凝土顶板的区域,但该区域的剪力流分布规律难以通过理论推导得出,可以采用有限元计算的方法确定混凝土板-钢顶板层间纵向切应力沿横截面方向的分布范围及分布规律,和上述理论推导出的结果进行对比印证.
在组合梁相关的计算理论[24]中,用于计算单位长度纵向剪力的公式为
式(10)实质上是计算腹板的剪力流,隐含如下假定:腹板的剪力流不经过钢顶板,直接进入混凝土板. 在组合桥面板结构中,经上述理论分析可知,该公式的假定是不成立的,在该结构中,需要考虑钢顶板对剪力流的分散作用,采用式(10)计算得到的纵向剪力偏大. 组合梁中的钢翼缘由于长度较短,可以忽略,但在组合桥面板计算时,钢顶板不可忽略. 当计算腹板剪力流时,
2. 工字形截面模型的分析
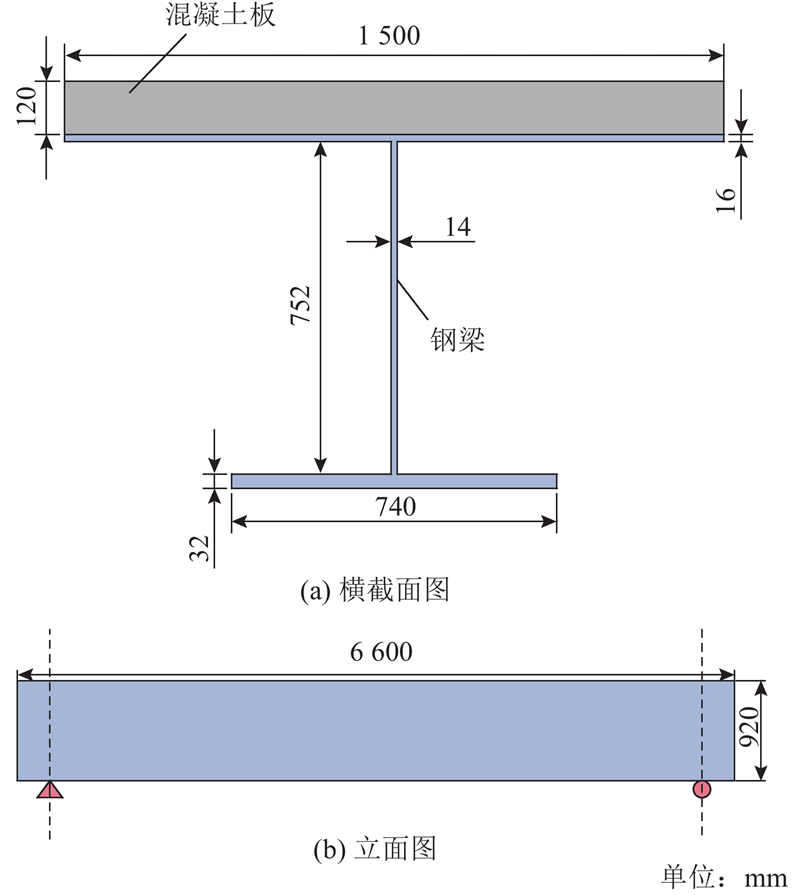
2.1. 剪力流分布规律的验证
图 5
图 6
图 6 工字形组合桥面板结构的简支有限元模型
Fig.6 Simply supported finite element model of I-beam composite bridge deck structure
表 1 有限元模型的网格划分参数
Tab.1
| 构件类型 | 网格编号 | 网格位置 | 网格大小 |
| 混凝土板 | ① | 腹板两侧 | 20 mm×30 mm |
| 混凝土板 | ② | 腹板上方 | 7 mm×30 mm |
| 钢顶板 | ③ | 腹板两侧 | 20 mm×8 mm |
| 钢顶板 | ④ | 腹板上方 | 7 mm×8 mm |
| 钢腹板 | ⑤ | 腹板 | 7 mm×75.2 mm |
| 钢底板 | ⑥ | 腹板两侧 | 36.25 mm×32 mm |
| 钢底板 | ⑦ | 腹板下方 | 7 mm×32 mm |
| 混凝土板、钢梁 | ⑧ | 纵向 | 50 mm |
表 2 组合桥面板结构所用材料的特性
Tab.2
| 材料种类 | E/MPa | ν |
| 混凝土 | 3.45×104 | 0.2 |
| 钢材 | 2.06×105 | 0.3 |
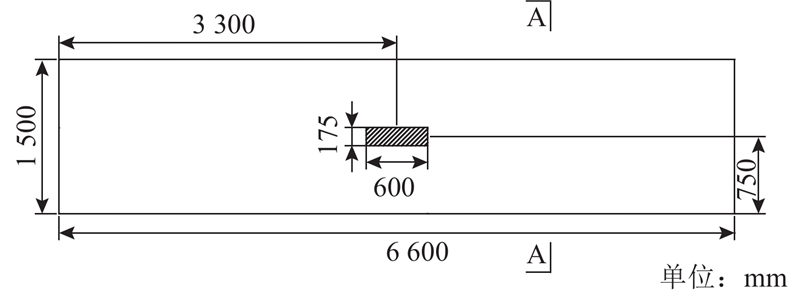
在跨中施加小范围的均布荷载如图7所示,均布荷载为1 MPa. 主要研究整体受弯的纵向剪力,因此避开跨中施加车轮荷载的区域,避免第2体系产生的局部影响,理论计算截面选取1/4截面,即主要考察第1体系1/4梁长截面(图7所示的A-A截面)处的切应力分布情况,组合桥面板结构的1/4梁长截面是一维受力,符合理论计算假定. 二者的横向切应力在腹板两侧沿横向逐渐减小,且远离腹板剪力流方向转换区域后,横向切应力在板厚方向分布都较均匀,取沿板厚方向的单元横向切应力的平均值为
图 7
图 8
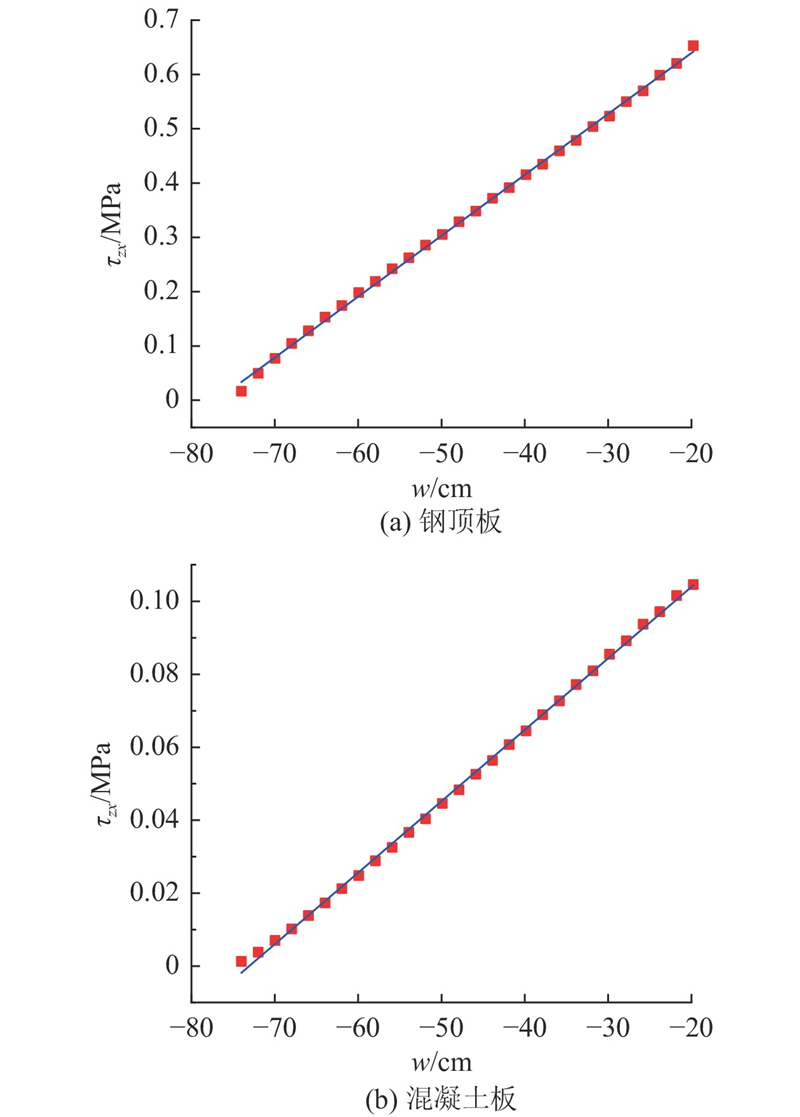
图 8 工字形组合桥面板翼缘的横向切应力分布
Fig.8 Transverse shear stress distribution of I-beam composite deck slab flange
图 9
图 9 横向切应力的线性下降段拟合
Fig.9 Linear descending segment fitting of transverse shear stress
根据式(7)、(9)可知,剪力流从腹板流向翼缘板,剪力流的总值在翼缘板和腹板的交接处转换前后是一定的,且钢顶板和混凝土板在横向切应力和剪力流的分配上存在如下的比例关系:
钢和混凝土的切变模量和弹性模量均存在如下关系:
将式(14)代入式(13),可得
式(15)的计算结果和有限元计算结果较一致,相差3.5%,在误差范围内,证明了理论分析的正确性. 将结果代入切应力和剪力流的关系式,可得
从式(16)可知,钢顶板和混凝土板的横向剪力流承担比例大约为3︰4,与钢顶板和混凝土板的切变模量和厚度有关. 横向剪力流的承担比例会影响钢顶板和混凝土板间的纵向剪力,不同厚度混凝土板和钢顶板的组合中,混凝土板承担剪力流的比例η见表3,即组合板结构中的纵向剪力根据组合梁公式计算得到的折减比例.
表 3 组合桥面结构混凝土板承担的剪力流比例
Tab.3
| ts/mm | η | |||
| tc=15 cm | tc=12 cm | tc=10 cm | tc=8 cm | |
| 10 | 0.731 | 0.685 | 0.645 | 0.592 |
| 12 | 0.694 | 0.645 | 0.602 | 0.547 |
| 14 | 0.660 | 0.609 | 0.565 | 0.509 |
| 16 | 0.630 | 0.576 | 0.531 | 0.476 |
| 18 | 0.602 | 0.547 | 0.502 | 0.446 |
| 20 | 0.576 | 0.521 | 0.476 | 0.421 |
2.2. 层间完全连接下竖向切应力和层间纵向切应力的分布规律
对于截面的竖向应力,根据施加的荷载和结构特性,将施加的小范围均布荷载近似为集中力,将结构按照简支梁计算截面的竖向剪力.
根据均布荷载的大小和施加面积,计算得到集中力为
如图10所示为结构的竖向剪力计算示意图. 在1/4截面处对截面单元的竖向切应力在面积上进行积分,得到1/4截面处的竖向剪力合力:
图 10
表 4 截面的竖向剪力分布
Tab.4
| 截面组成部分 | Vy/kN |
| 混凝土板 | 2.55 |
| 钢顶板 | 0.829 |
| 钢腹板 | 48.1 |
| 钢底板 | 0.927 |
表4的结果表明,组合桥面板结构的截面的竖向剪力几乎都由腹板承担,其次是混凝土板,钢顶、底板承担的竖向剪力最小.
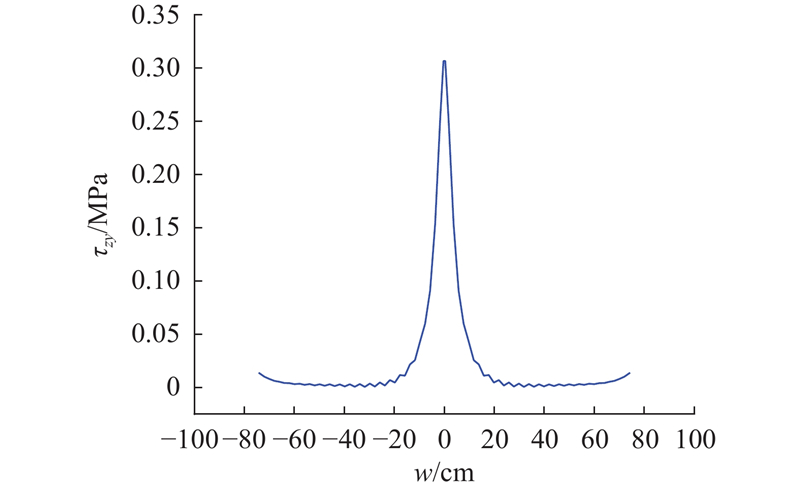
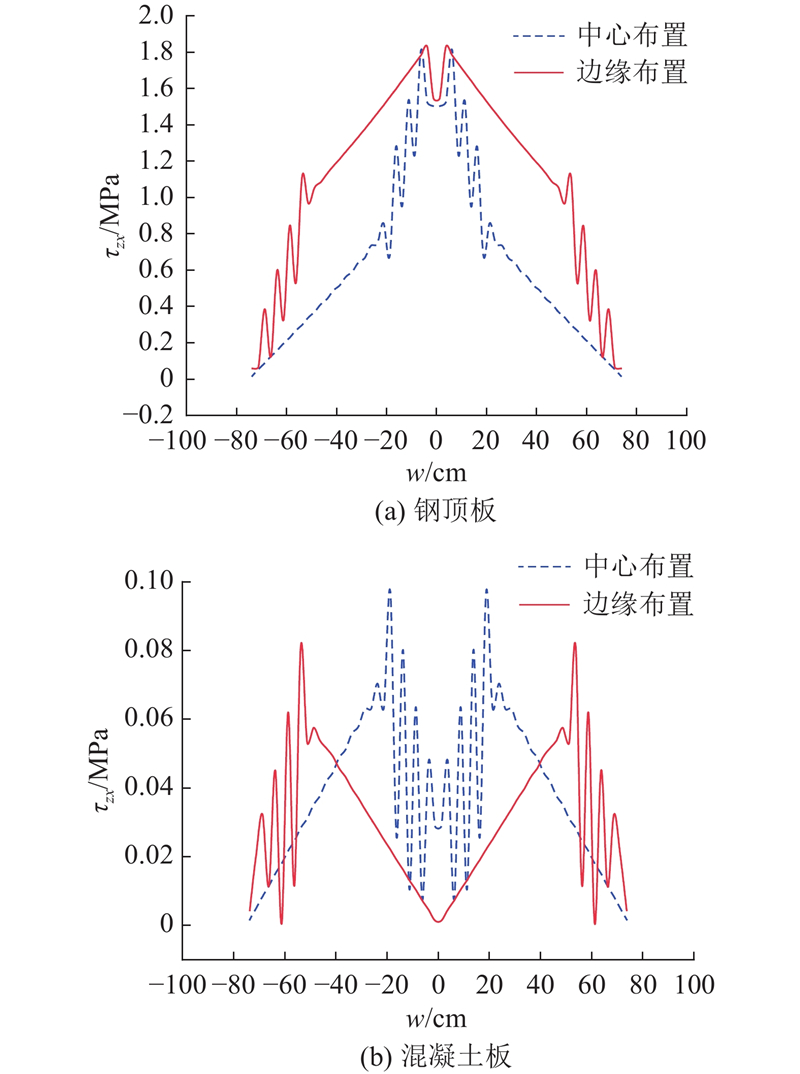
1/4截面处混凝土板-钢顶板结合面的纵向切应力τzy沿横截面方向的分布如图12所示. 层间的纵向切应力主要集中于腹板中心两侧200 mm范围内,在腹板两侧呈急剧下降的趋势.
图 11
图 11 工字形组合桥面板截面的切应力分布
Fig.11 Distribution of shear stress in cross-section of I-beam composite bridge deck slab
图 12
图 12 结合面的纵向切应力分布
Fig.12 Longitudinal shear stress distribution on joint surface
2.3. 层间离散连接下的切应力分布规律和剪力钉布置
上述截面竖向、横向切应力的分配比例理论和仿真均是在界面完全连接的条件下,将连接离散后,在不均匀连接的条件下,对竖向、横向切应力的分配进行分析.
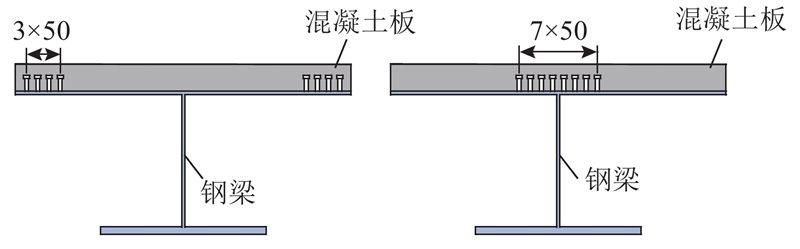
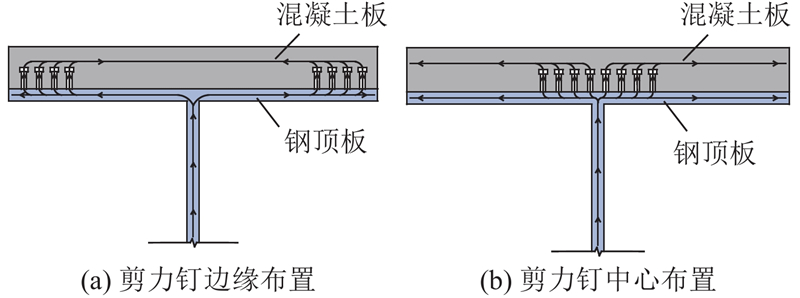
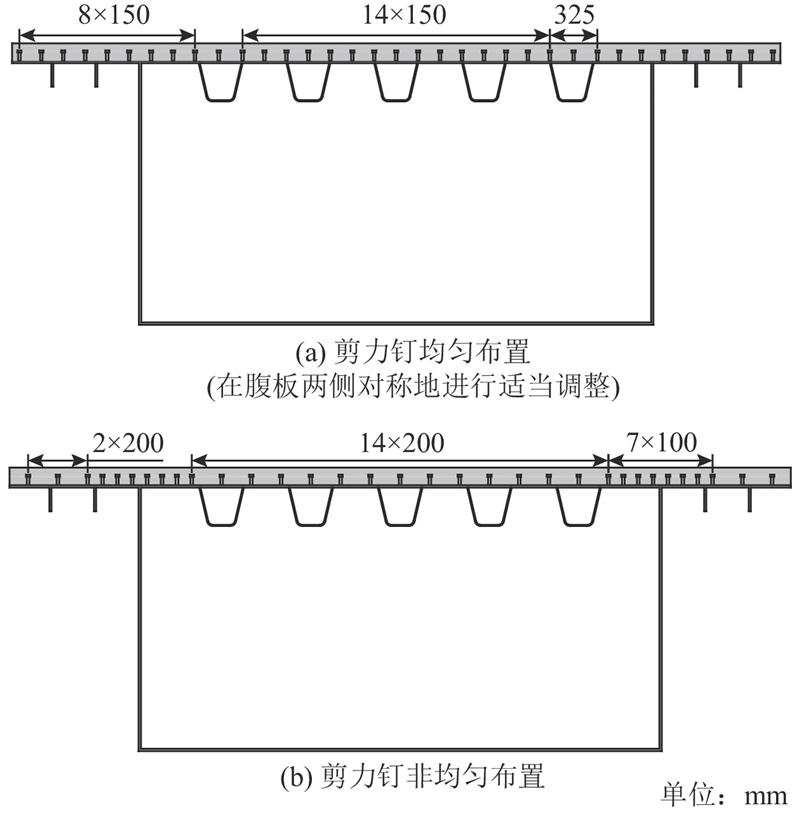
将模型中混凝土板和钢顶板之间节点耦合的连续性连接[25]替换成离散的弹簧连接,模拟直径为16 mm、高为100 mm的剪力钉,纵向间距取为150 mm. 在Abaqus中,采用滑动平面类型的连接截面进行模拟,耦合混凝土板和顶板对应节点的竖向位移,在横向和纵向赋予刚度,纵、横向刚度根据相关剪力钉刚度的研究进行取值,取为220 kN/mm.
图 13
图 14
图 14 离散连接后翼缘的横向切应力分布
Fig.14 Transverse shear stress distribution in flange plate after discrete connection
图 15
图 15 剪力钉连接时的剪力流分布规律
Fig.15 Distribution law of shear flow during shear stud connection
图 16
图 16 剪力钉纵向剪力的计算结果
Fig.16 Calculation results of longitudinal shear force of shear stud
通过上述计算结果和理论分析可知,组合桥面板结构的剪力钉不仅应布置在中心腹板两侧或边缘位置,而应在整个连接面上布置. 局部的剪力钉布置会导致剪力流在界面上传递得不够充分,使得靠边缘的剪力钉承受的纵向剪力较大,不能充分发挥剪力钉的力学性能,减小了结构的安全储备.
图 17
图 18
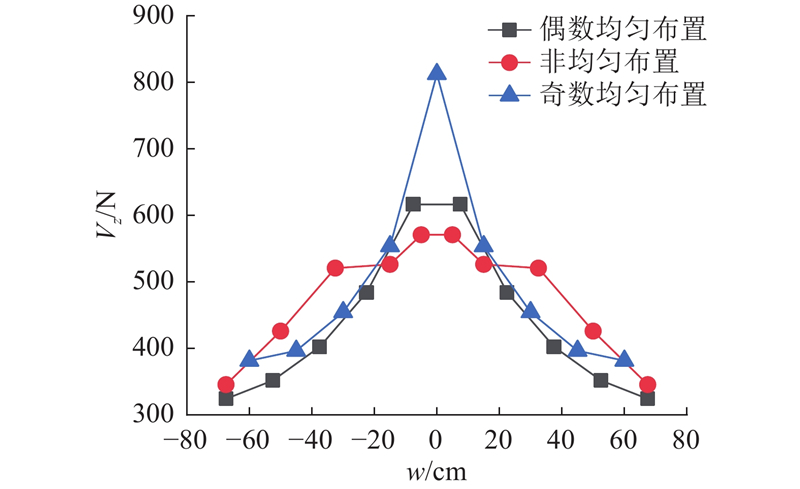
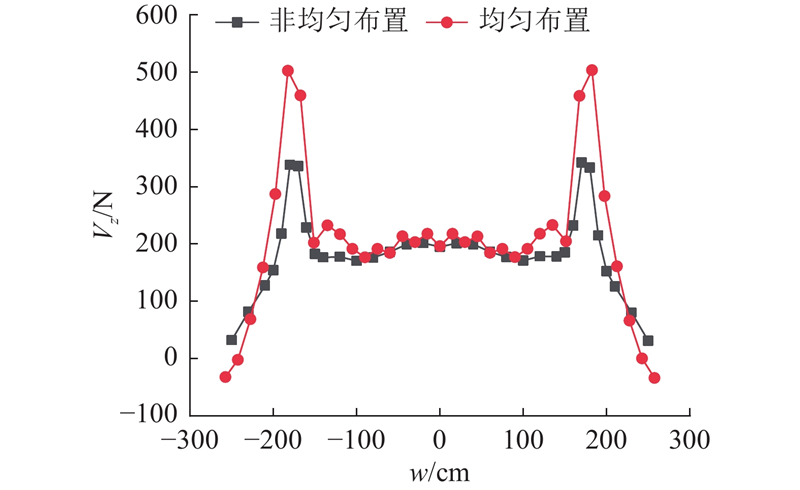
图 18 3种布置方式下剪力钉所受的纵向剪力
Fig.18 Longitudinal shear force on shear stud in three arrangement methods
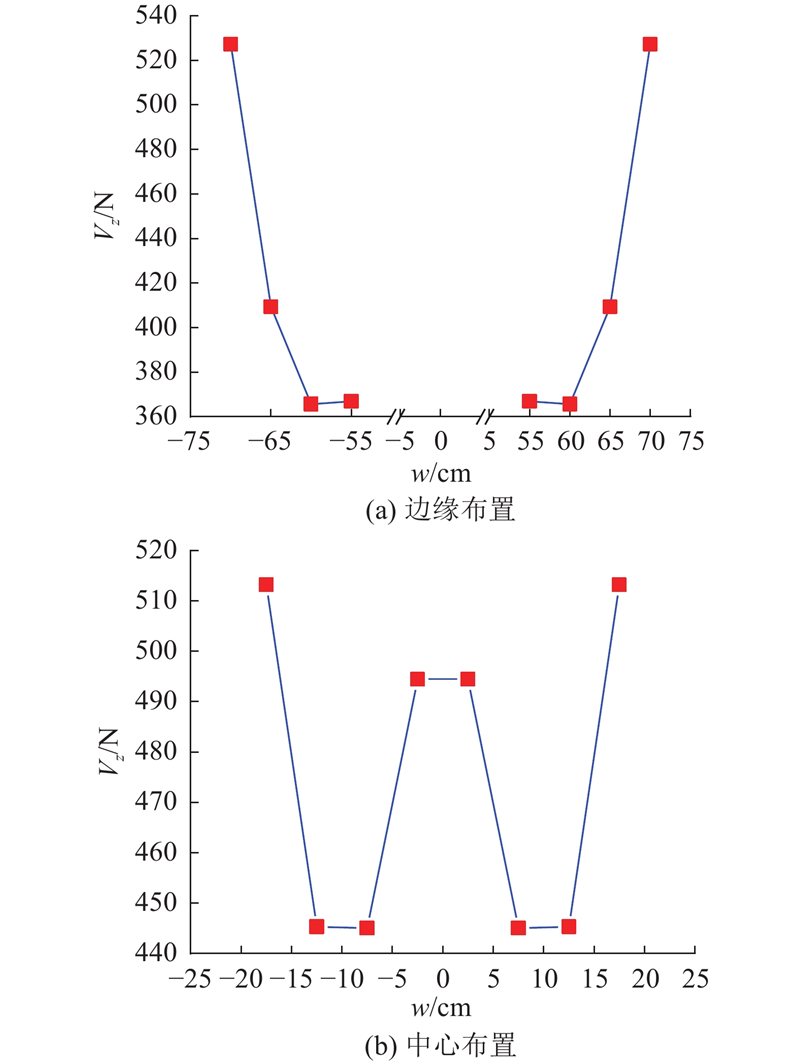
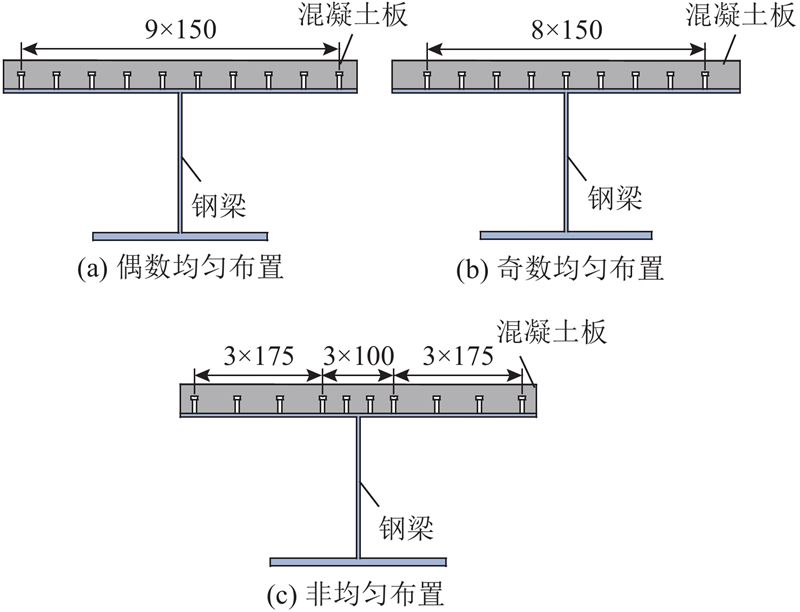
在3种不同的剪力钉布置方式下,剪力钉在不同的横向位置上承受的纵向剪力发生了较大的变化. 在偶数均匀布置下,集中于腹板两侧的层间纵向切应力主要由两侧的剪力钉承担,远离腹板后剪力钉纵向剪力迅速减小. 在腹板两侧对剪力钉进行加密布置后,腹板附近的剪力钉纵向剪力的峰值明显减小,附近6个剪力钉的纵向剪力较等间距布置时更均匀. 当奇数均匀布置时,中间剪力钉受力最不利,其余剪力钉的受力规律和偶数均匀布置时的规律相似,但受力更大,整体剪力钉受力最不均匀.
由图18可知,与在组合桥面板宽度方向均匀布置剪力钉的方式相比,在腹板两侧减小剪力钉的布置间距,对剪力钉进行局部加密,能够使腹板附近较大的纵向剪力由更多的剪力钉均匀分担,而不是由个别剪力钉承受,同时边缘的剪力钉发挥的程度更大. 综上所述,利用非均匀的布置方式,提高了腹板区域剪力钉的构件安全性和远离腹板区域剪力钉的利用效率.
对截面上的竖向切应力进行积分,得到截面各组成部分承受的竖向剪力,如表5所示. 在层间连接离散化后,截面的竖向剪力分配规律大致不变,钢腹板承担的竖向剪力最大,其次是混凝土板,钢顶板和钢底板几乎没有对竖向抗剪作出贡献.
表 5 竖向剪力的计算结果
Tab.5
| 截面组成部分 | Vy/kN |
| 混凝土板 | 2.05 |
| 钢顶板 | 0.868 |
| 钢腹板 | 48.6 |
| 钢底板 | 0.947 |
根据现行的剪力钉设计计算理论,按照剪力流全部由混凝土板承担的计算思想,计算此处一横排剪力钉所承受的纵向剪力,将不同的剪力钉布置方式下单排剪力钉承担纵向剪力的总和进行累加计算,计算结果如表6所示. 由于剪力流会在钢顶板和混凝土板间进行分配,3种布置方式下的纵向剪力和均小于按剪力流完全流入混凝土板的理论计算值.
表 6 单排剪力钉承担的纵向剪力和
Tab.6
| 剪力钉布置方式 | Vz/N |
| 奇数均匀布置 | 4384.50 |
| 偶数均匀布置 | 4357.17 |
| 非均匀布置 | 4778.57 |
| 现有理论计算 | 9689.45 |
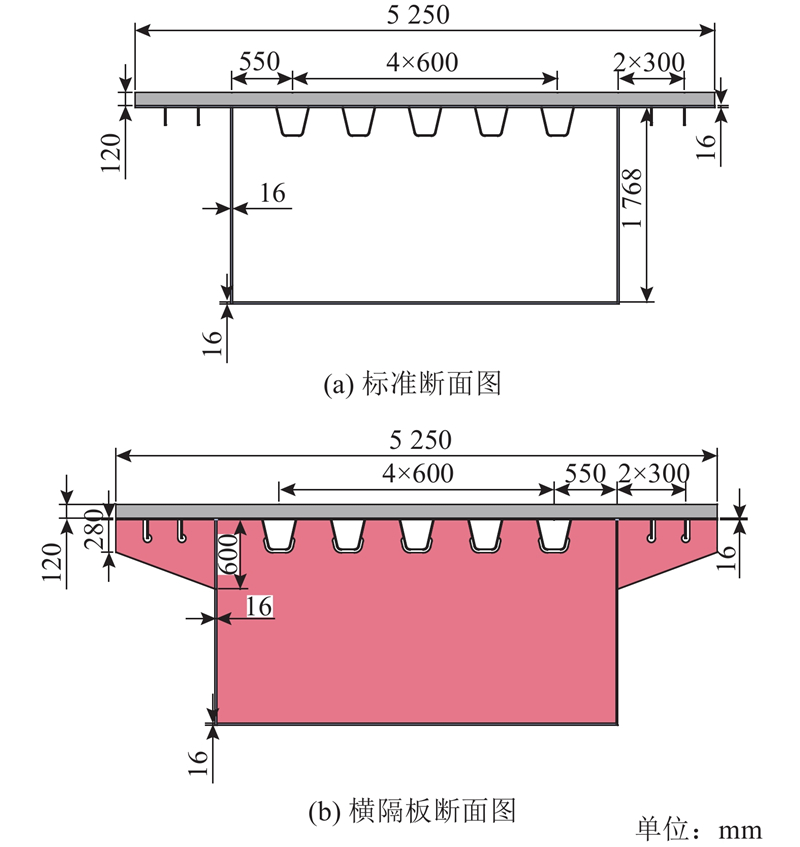
3. 组合桥面板钢箱梁剪力钉的布置
图 19
图 19 组合桥面板钢箱梁的截面
Fig.19 Cross section of composite bridge deck steel box girder
图 20
图 21
在跨中施加小范围的均布荷载如图20所示,均布荷载为1 MPa.
均匀和非均匀布置的剪力钉所受的纵向剪力在1/4横截面上的分布如图22所示. 在均匀布置时腹板两侧的剪力钉受纵向的剪力较大,将腹板两侧的剪力钉进行加密后非均匀布置时,腹板旁的剪力钉受力减小了30%,且剪力钉的整体受力更加均匀.
图 22
图 22 不同布置方法下剪力钉所受的纵向剪力(1/4截面)
Fig.22 Longitudinal shear force on shear stud with different arrangement method (1/4 cross section)
按简支梁计算可知,1/4截面上的竖向剪力为125 kN,对截面单元的竖向切应力在面积上积分,得到1/4截面处的竖向剪力合力:
简支梁公式计算结果和有限元模型积分计算结果相差4.3%,相差较小,原因是没有计入腹板和底板的加劲肋. 承担竖向剪力比例最大的是钢腹板,混凝土板其次,最小的是钢顶板和钢底板.
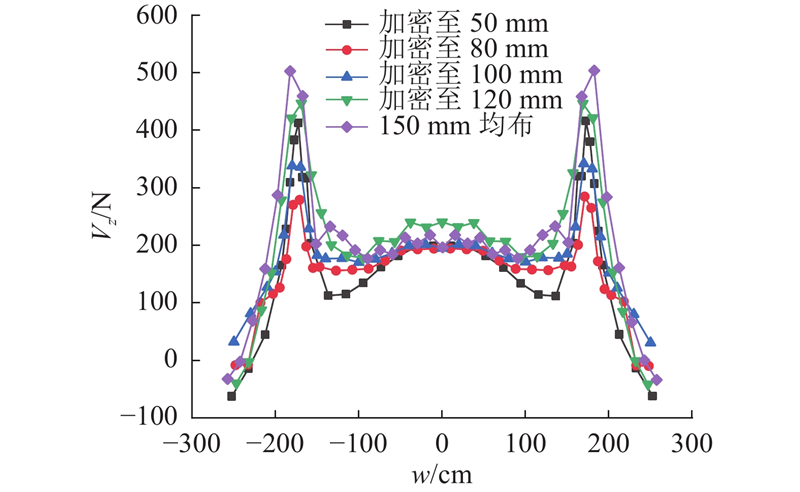
根据竖向剪力的计算结果(见表7),得到单排剪力钉承担剪力的理论计算结果. 将模型中单排剪力钉的剪力进行累加,得到单排剪力钉承受纵向剪力的总和,如表8所示. 非均匀和均匀布置时,截面处的纵向剪力和均小于理论计算值. 计算结果和前文工字形钢梁组合桥面板结构的计算结果相符,说明上述规律在工程实际应用较多的组合桥面板钢箱梁结构中也存在,具有一定的普适性. 上述结果表明,将剪力钉在腹板附近加密是合理的. 为了探究腹板剪力钉加密的程度对剪力钉纵向剪力的影响,以150 mm间距均匀布置下的剪力钉数量为基准,保证截面剪力钉数量较一致,分别将腹板附近的剪力钉加密到50、80、100、120 mm间距(100 mm为前文加密方案),分析整个截面上剪力钉所受的纵向剪力. 分析结果见图23.
表 7 竖向剪力的计算结果
Tab.7
| 截面组成部分 | Vy/kN |
| 混凝土板 | 3.793 |
| 钢顶板 | 0.146 |
| 钢腹板 | 115.519 |
| 钢底板 | 0.350 |
表 8 钢箱梁单排剪力钉承担的纵向剪力和
Tab.8
| 剪力钉的布置方式 | Vz/N |
| 均匀布置 | 7 144.07 |
| 非均匀布置 | 6 169.95 |
| 现有理论计算 | 9 707 |
图 23
图 23 腹板两侧剪力钉不同加密间距下的截面剪力钉纵向剪力分布
Fig.23 Longitudinal shear force distribution of shear stud in cross-section at different encryption spacing for shear stud on both sides of web plate
如图23所示,当腹板附近的剪力钉间距从150 mm改为120、100和80 mm时,整个横截面上的纵向剪力分布逐渐均匀,但加密到50 mm后,会产生反效果,纵向剪力重新变得不均匀.
在组合桥面板结构的腹板附近对剪力钉进行加密,可以在一定程度上避免腹板附近剪力钉所受纵向剪力集中的现象,但不是越密集越好,加密存在合理间距. 在该组合桥面板钢箱梁模型中,当加密间距为80 mm时,横截面上剪力钉的整体受力较均匀,此时大约加密到原基准间距的1/2.
4. 结 论
(1)组合梁的纵向剪力计算公式实质上是计算腹板剪力流,并认为剪力流全部由混凝土板承担,利用切应力互等定理计算混凝土板和钢梁间的纵向剪力. 在组合梁中计算剪力流采用的是混凝土板的换算面积矩,钢顶板可以忽略,但在计算组合桥面板腹板剪力流时,由于钢顶板较宽,需要计入其面积矩.
(2)通过对组合桥面板结构的截面切应力进行分析,证明了钢梁顶板会分担腹板流出的剪力流,使流入混凝土板的剪力流减小,从而减小钢顶板和混凝土板的层间纵向剪力,并给出了二者完全连接时切应力和剪力流的承担比例以及离散剪力钉连接时的变化趋势.
(3)组合桥面板结构和组合梁相似,竖向剪力主要由钢腹板承担,混凝土板有一定的贡献但较小,钢顶、底板的贡献可以忽略.
(4)在组合桥面板结构的剪力钉横向布置中,若仅在腹板两侧或在翼缘边缘布置剪力钉,边缘剪力钉受力非常不利,宜采用在桥面板全宽的非均匀布置方法. 在腹板两侧采用较小的剪力钉布置间距,远离腹板时剪力钉间距增大,且在腹板正上方不宜布置剪力钉. 腹板两侧剪力钉的间距不是越小越好,间距过小会使剪力钉受力重新变得不均匀,文中加密后间距为基准间距的1/2左右时取得了良好的效果.
参考文献
Influence of crossbeam web cutout shape on fatigue performance of steel orthotropic deck
[J].
基于热点应力法的正交异性钢桥面板疲劳验算
[J].DOI:10.3969/j.issn.0258-2724.2013.03.001
Fatigue assessment of orthotropic steel bridge deck based on hot spot stress method
[J].DOI:10.3969/j.issn.0258-2724.2013.03.001
关于正交异性钢桥面板的疲劳
[J].
About the fatigue of orthotropic steel bridge deck
[J].
Failure mechanisms governing fatigue strength of steel–SFRC composite bridge deck with U-ribs
[J].
Static and fatigue behavior of short-headed studs embedded in a thin ultrahigh-performance concrete layer
[J].
基于超短栓钉的钢-超薄UHPC组合桥面性能
[J].
Performance of steel-ultrathin UHPC composite bridge deck based on ultra-short headed studs
[J].
In-service response of an orthotropic steel deck compared with design assumptions
[J].
Fatigue performance of orthotropic steel-concrete composite deck with large-size longitudinal U-shaped ribs
[J].
Behavior of short-headed stud connectors in orthotropic steel-UHPC composite bridge deck under fatigue loading
[J].
Shear behavior of short headed studs in steel-ECC composite structure
[J].
Push-out behavior of headed shear studs welded on thin plates and embedded in UHPC
[J].
钢-UHPC组合桥面板界面抗剪理论及设计方法
[J].
Theory and design method of interfacial shear resistance for steel-UHPC composite bridge deck
[J].
钢桥面沥青铺装层病害及成因分析
[J].DOI:10.3969/j.issn.1674-0610.2010.03.027 [本文引用: 1]
Analysis on diseases and their causes of steel deck asphalt pavement
[J].DOI:10.3969/j.issn.1674-0610.2010.03.027 [本文引用: 1]
钢桥面灌注式树脂混凝土铺装材料与结构研究
[J].
Study on material and structure of PRC for steel bridge deck pavement
[J].
正交异性钢桥面板疲劳问题的研究进展
[J].DOI:10.3969/j.issn.1001-7372.2017.03.002 [本文引用: 1]
Review on fatigue problems of orthotropic steel bridge deck
[J].DOI:10.3969/j.issn.1001-7372.2017.03.002 [本文引用: 1]
横梁腹板切口形状对正交异性钢桥面板疲劳性能的影响研究
[J].
钢-UHPC组合桥面板中焊接栓钉的疲劳性能及设计布置方法
[J].
Fatigue behavior and design layout method of welded stud connectors in steel-UHPC composite bridge deck
[J].
EN 1994 Eurocode 4: design of composite steel and concrete structures
[J].
Evaluation for fatigue strength of shear studs in steel plate-concrete composite deck
[J].