基于递归量化分析的CFRP超声检测缺陷识别方法

doi:10.3785/j.issn.1008-973X.2024.08.008

基于递归量化分析的CFRP超声检测缺陷识别方法

王海军^,, 王涛, 俞慈君^,

1. 浙江大学工程师学院，浙江杭州 310058

2. 浙江大学机械工程学院，浙江杭州 310058

CFRP ultrasonic detection defect identification method based on recursive quantitative analysis

WANG Haijun^,, WANG Tao, YU Cijun^,

1. College of Engineering, Zhejiang University, Hangzhou 310058, China

2. College of Mechanical Engineering, Zhejiang University, Hangzhou 310058, China

通讯作者: 俞慈君，男，副研究员. orcid.org/ 0000-0001-9380-9009. E-mail: yuppy@zju.edu.cn

收稿日期: 2023-07-5

基金资助:

自然科学基金重点资助项目（91748204）；国家自然科学基金创新研究群体科学基金资助项目（51821093）；浙江省重点研发计划资助项目（2020C01039）.

Received: 2023-07-5

Fund supported:

自然科学基金重点资助项目（91748204）；国家自然科学基金创新研究群体科学基金资助项目（51821093）；浙江省重点研发计划资助项目（2020C01039）.

作者简介 About authors

王海军（1998—），男，硕士生，从事超声无损检测的研究.orcid.org/0009-0008-5410-6085.E-mail：navywang@zju.edu.cn , E-mail：navywang@zju.edu.cn

摘要

为了解决碳纤维增强复合材料 (CFRP)超声检测缺陷识别不准确、不可靠的问题，提出自适应变分模态分解(AVMD)与递归量化分析技术(RQAT)特征提取和卷积神经网络(CNN)识别方法. 实验预埋6种模拟缺陷，使用超声相控阵检测后，每种缺陷取500个A扫描波形信号数据，利用蝠鲼智能优化算法优化出变分模态分解(VMD)所需的K、Alpha，使用优化参数的VMD得到本征模态函数(IMF)分量，筛选高频噪声部分，对剩余IMF分量使用递归量化分析技术. 每个信号得到72个特征值，将特征值组成特征向量，输入CNN进行识别，训练集识别正确率为99.94%，验证集识别正确率为98.09%，测试集识别正确率为98.27%. 结果表明，AVMD与RQAT、CNN的结合解决了CFRP超声检测中缺陷的识别分类问题.

关键词： 碳纤维复合材料（CFRP） ; 无损检测 ; 变分模态分解 ; 递归量化分析 ; 特征提取 ; 卷积神经网络 ; 缺陷识别

Abstract

An adaptive variational mode decomposition (AVMD) and recursive quantitative analysis technique (RQAT) for feature extraction was proposed combined with convolutional neural network (CNN) for recognition in order to address the issues of inaccuracy and unreliability in ultrasonic defect detection of carbon fiber reinforced plastics (CFRP). Six types of simulated defects were embedded in the experiments, and 500 A-scan waveform signals were collected for each defect type after ultrasonic phased array detection. The stingray intelligent optimization algorithm was used to optimize the K and Alpha values required for variational mode decomposition (VMD). Intrinsic mode function (IMF) components were obtained by using these optimized parameters, and high-frequency noise parts were filtered out. The remaining IMF components were processed with recursive quantitative analysis technique. Each signal yielded 72 feature values, which were assembled into feature vectors and input into the CNN for recognition. The recognition accuracy was 99.94% for the training set, 98.09% for the validation set, and 98.27% for the test set. Results show that the combination of AVMD, RQAT and CNN solves the defect recognition and classification problem in CFRP ultrasonic testing.

Keywords： carbon fiber reinforced plastics (CFRP) ; non-destructive testing ; variational mode decomposition ; recursive quantitative analysis ; feature extraction ; convolutional neural network ; defect identification

PDF (3095KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王海军, 王涛, 俞慈君. 基于递归量化分析的CFRP超声检测缺陷识别方法. 浙江大学学报(工学版)[J], 2024, 58(8): 1604-1617 doi:10.3785/j.issn.1008-973X.2024.08.008

WANG Haijun, WANG Tao, YU Cijun. CFRP ultrasonic detection defect identification method based on recursive quantitative analysis. Journal of Zhejiang University(Engineering Science)[J], 2024, 58(8): 1604-1617 doi:10.3785/j.issn.1008-973X.2024.08.008

碳纤维增强复合材料（CFRP）因其低密度、高比强度和高比模量，被广泛应用于航空航天^[1]和汽车^[2]领域. 碳纤维复合材料的多层结构和特殊制造工艺常引入缺陷，如分层、夹杂和富树脂，这会降低力学性能. 无损检测方法^[3]如超声检测^[4]、红外热成像^[5]、X射线断层扫描^[6]和声发射^[7]，因不会破坏结构完整性而广泛用于评估这些缺陷，其中超声检测是最常用的方法. 识别CFRP缺陷类型对评估其使用和安全性能至关重要.

目前，CFRP超声检测结果需要专家或有经验的检测人员判别，工作量大、效率低，影响性能评估，因此实现CFRP超声检测缺陷自动识别和分类是亟须解决的问题. 胡业发等^[8]利用小波包分解A扫描信号，通过BP神经网络实现不同夹杂缺陷的识别. Liang等^[9]通过小波包分解，建立SVM缺陷分类模型. Lee等^[10]提出回波边界决策方法，Ge等^[11]使用经验小波变换和模糊相关分类方法，李健等^[12]提出小波包分解和BP神经网络的方法实现缺陷分类. 小波包基函数的人工选取会影响分类结果的稳定性.

Zhang等^[13]提出动态广域网络木材损伤识别方法，Chen等^[14]提出孪生网络元学习方法，邓勇等^[15]提取Volterra级数时域核特征，胡宏伟等^[16]提出基于一维局部二元模式算法和核主成分分析的方法，Rao等^[17]使用脉冲涡流技术. 这些方法对噪声敏感，特征提取不稳定，参数调节复杂，影响算法的效率和泛化能力.

Yang等^[18]提出经验模态分解(EMD)和粗糙集属性约简的方法，Mousavi等^[19]使用EMD分解超声信号，Hassani等^[20]提出基于变分模态分解(VMD)的方法. EMD分解无法确定有效模态数量，VMD分解参数的选择依赖经验，影响分类效果.

本研究提出自适应变分模态分解与递归量化分析 (AVMD-RQAT) 的信号特征提取方法，结合卷积神经网络(CNN)识别，用于CFRP超声检测多种类、大规模缺陷数据，并与文献[12]的结果进行对比验证.

1. 超声相控阵缺陷检测

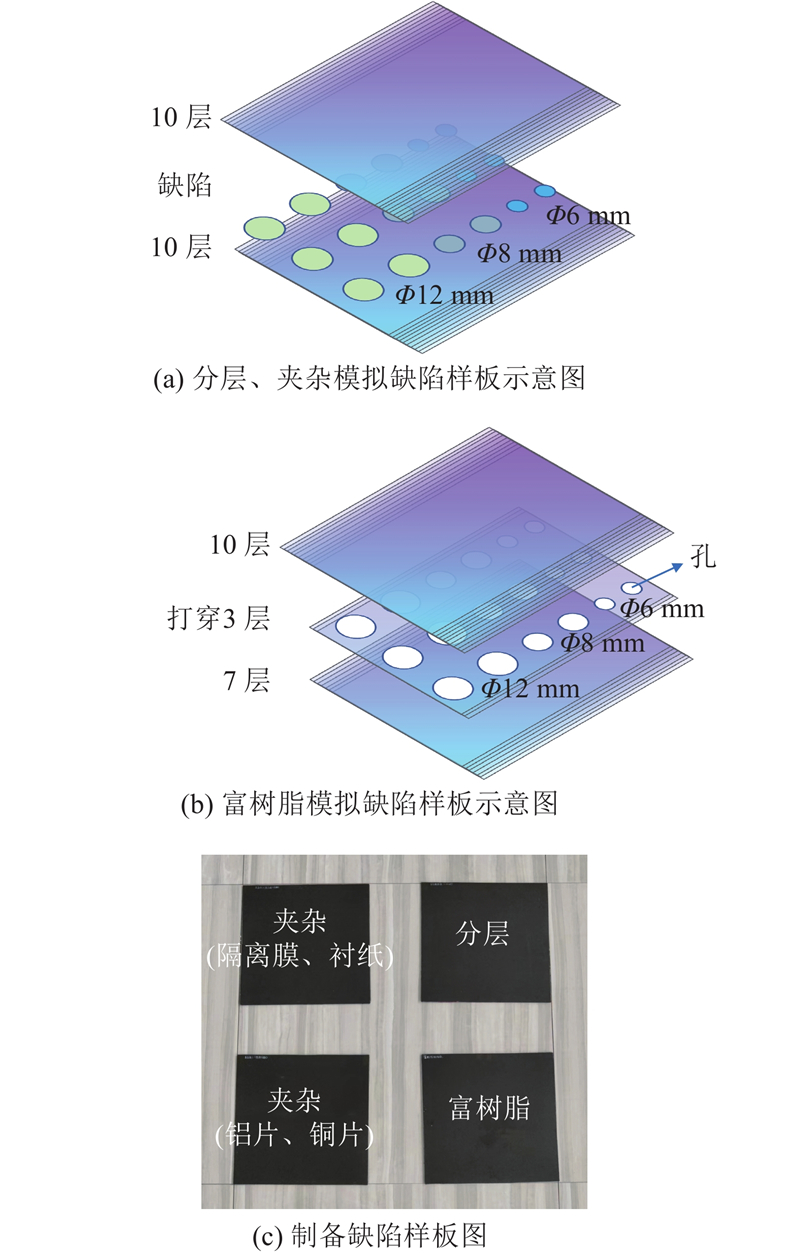
CFRP缺陷样板的制备采用预浸料手工铺层与热压罐工艺固化完成. 预浸料来自威海光威复合材料股份有限公司，型号为GW800G/GS-13，以T800碳纤维为增强体，GS13环氧树脂为基体，GS-13树脂质量分数为34%，厚度为0.187 mm，所裁剪的预浸料尺寸为330 mm×330 mm. 为了更好地模拟实际工况中出现的不同缺陷类型，分别使用聚四氟乙烯、预浸料隔离膜、预浸料衬纸、铜片、铝片模拟缺陷. 其中，利用聚四氟乙烯模拟分层缺陷，利用预浸料隔离膜、预浸料衬纸、铜片、铝片模拟4种夹杂缺陷. 采用打穿预浸料的方式，使其在固化过程中让树脂从孔隙流入，形成富树脂缺陷.

1.1. 超声波传播特性

1.1.1. 声速

简谐波在材料中传播时，单位时间内穿过的距离为该波的传播速度，通常用c表示. 对于不同类型的超声波，传播速度存在差异，固体材料中的声速计算公式如下所示.

$ 纵波： {c_{\text{l}}} = \sqrt {\frac{E}{\rho } \frac{{1 - \sigma }}{{\left( {1 - 2\sigma } \right)\left( {1+\sigma } \right)}}} . $

(1)

$ 横波： {c_{\text{s}}} = \sqrt {\frac{E}{\rho } \frac{1}{{2\left( {1+\sigma } \right)}}} = \sqrt {\frac{G}{\rho }} . $

(2)

式中：E为弹性模量，$\rho $为材料密度，$\sigma $为泊松比，G为切变模量.

1.1.2. 声阻抗

超声波在材料中传播时，任意一点声压p与该点速度振幅$\mu $的比值称为材料的声阻抗，通常用Z表示.

$ Z=\frac{p}{\mu } .$

(3)

对于平面波而言，声阻抗等于材料密度与材料声速的乘积，可以直接表示介质的声学特性，是材料固有的特征参数.

1.1.3. 界面反射与透射

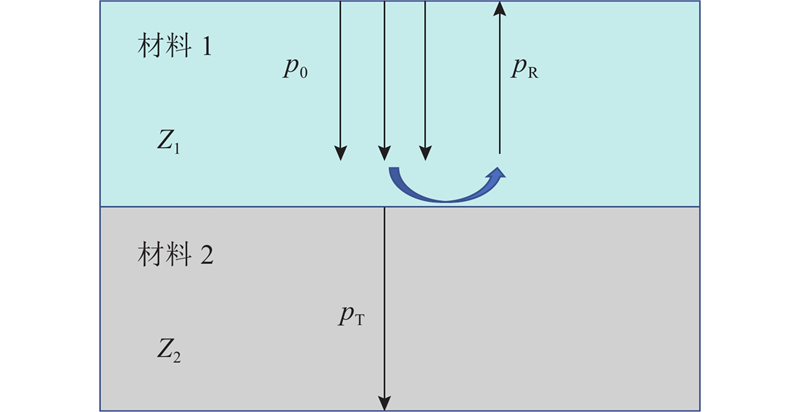
当超声波入射到声阻抗不同的异质界面时，如图1所示，入射波一部分透射进入材料2，另一部分在界面处反射后继续在材料1中传播. 声压反射系数与透射系数的计算公式如下：

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1 超声信号反射透射的示意图

Fig.1 Schematic diagram of ultrasonic signal reflection and transmission

$ {R_{{\text{12}}}} = \frac{{{p_{\text{R}}}}}{{{p_{\text{0}}}}} = \frac{{{Z_{\text{2}}} - {Z_{\text{1}}}}}{{{Z_{\text{2}}}+{Z_{\text{1}}}}}, $

(4)

$ {T_{{\text{12}}}} = \frac{{{p_{\text{T}}}}}{{{p_{\text{0}}}}} = \frac{{2{Z_{\text{2}}}}}{{{Z_{\text{2}}}+{Z_{\text{1}}}}}. $

(5)

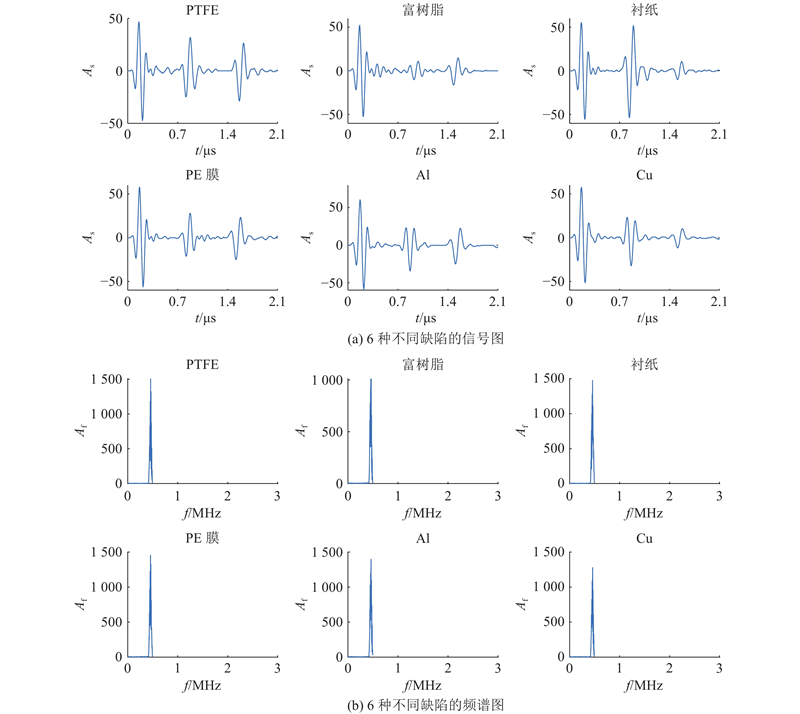
式中：p_R为界面上反射波声压；p₀为入射波声压；p_T为界面上透射波声压；$ {R_{{\text{12}}}} $为材料1到材料2的反射率，反射率为正表示反射波声压与入射波声压的相位相同，为负表示相位相反；${T_{12}}$为材料1到材料2的透射率.

6种模拟缺陷材料的特性如表1所示. 表中，反射率是指从碳纤维复合材料到目标材料时的反射情况，相位表示超声信号从碳纤维复合材料入射到其他材料时相位的变化情况. 6种材料形成的反射波中，有4种材料与入射波相位相反，2种材料与入射波相位相同. 在相位相反的材料中，从环氧树脂到衬纸，反射率的绝对值依次递增，反射波的幅值递增. 在相位相同的材料中，铝比铜的反射率小，故在超声信号中铝的缺陷位置反射回波比铜的波高低.

表 1 6种缺陷材料性能的对比表

Tab.1 Comparison table of property of six defective materials

材料	密度/(kg·m⁻³)	弹性模量/GPa	声速/(m·s⁻¹)	声阻抗/(Pa·s·m⁻¹)	反射率	相位情况
CFRP	1.5×103	89.45	3070	4.61×106	0	无
环氧树脂	1.48×103	3	2972	4.4×106	−0.0228	相位相反
PE膜	1.24×103	0.9	2460	3.05×106	−0.203	相位相反
聚四氟乙烯(PTFE)	2.1×103	0.28	1400	2.94×106	−0.221	相位相反
衬纸	1×103	2	1500	1.5×106	−0.509	相位相反
铜	8.96×103	117	4660	4.18×107	0.801	相位相同
铝	2.7×103	70	6320	1.71×107	0.575	相位相同

新窗口打开| 下载CSV

1.2. 模拟缺陷样板制备

利用上述实验材料，采用手工铺层，铺层方式使用$ {[0/90]_{{\text{2s}}}} $正交，设计缺陷样板为20层，厚度为3.74 mm. 为了避免近、远表面缺陷，夹杂和分层缺陷设计缺陷埋层为第10与11层之间，富树脂缺陷打穿11、12、13层预浸料，在热压过程中树脂流入打穿区域形成富树脂. 设计直径为12、8、6 mm的圆形缺陷各2列，缺陷样板如图2所示. 在缺陷预埋完成后，对完成铺层的CFRP预浸料使用热压罐固化，得到4块缺陷样板，如图2(c)所示.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2 缺陷样板图

Fig.2 Defect boilerplate

1.3. 超声相控阵检测系统的搭建

相控阵设备为Olympus公司的FOCUS PX M/N: FPX-1664PR，楔块是Olympus SNW1-0L-IHC，探头为5L64-NW1，所用软件为Olympus公司配套的FocusPC，扫描时不使用延时法则，相控阵的64个阵元按照编码器每移动1 mm采集一次数据的方式，对缺陷样板扫描. 搭建超声相控阵检测系统，如图3所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3 超声相控阵检测系统

Fig.3 Ultrasonic phased array inspection system

所检测出的不同缺陷信号如图4(a)所示. 图中，A_s为信号幅值，A_f为频率幅值. 由于预埋缺陷深度相同，不同缺陷回波位置相同，且波形相似，波形信号难以区分，对信号进行FFT处理，频谱图如图4(b)所示. 频谱分布具有较大的相似性，对不同类型缺陷难以进行区分，检测者无法对缺陷类型进行定性判断，影响检测结果.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4 6种不同缺陷信号的传统分析图

Fig.4 Traditional analysis plot for six different defect signals

2. 自适应VMD信号分解

测量过程中噪声信号的存在对信号特征的提取存在影响，为了降低噪声信号的影响并充分提取信号的特征信息，对信号进行VMD分解，得到不同的本征模态函数(intrinsic mode functions, IMF)分量. 过滤高频噪声部分实现去噪，利用剩余分量进行特征提取.

2.1. VMD原理

VMD方法是由Dragomiretskiy等^[21]提出，用于迭代求解变分问题，将复杂信号分解成调幅调频的模态分量信号. VMD的目标是将输入信号f分解为离散数量的子信号${u_k}$，是自适应、完全非递归的模态变分和信号处理方法. 假设每个模态在中心频率${\omega _k}$周围是紧密的，模态包含的频率分量都在${\omega _k}$附近，${\omega _k}$随分解信号的特征来确定，解决了EMD方法存在端点效应和模态分量混叠的问题，降低了复杂度高和非线性强的时间序列的非平稳性. 使用频率分别为50、75、100、125 Hz的正弦信号叠加作为模拟信号，分别使用EMD与VMD方法进行分解，如图5所示. 当使用EMD分解时，分解的IMF分量存在模态混叠和端点效应，而VMD方法可以将4种频率信号分解出来.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

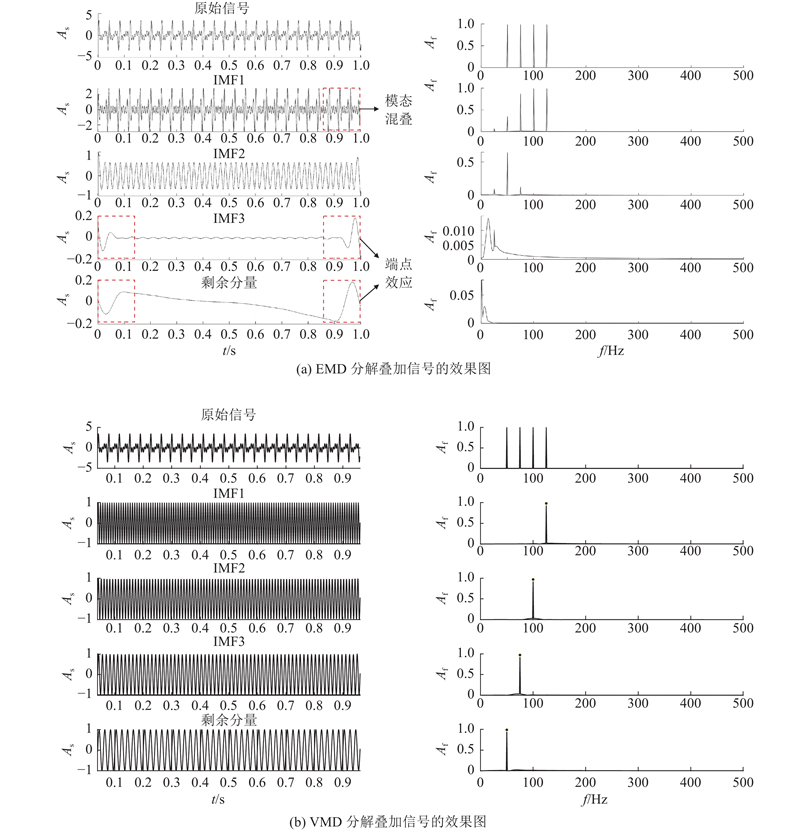
图 5 EMD与VMD分解叠加信号效果的对比图

Fig.5 Comparison chart of EMD and VMD decomposition superposition signal effect

VMD的核心思想是构建和求解变分问题，变分问题的求解过程为模态分解过程，为了评估一个模态的带宽，简要由以下步骤来开展. 1)对于每一个模态${u_k}$，通过Herbert变换，得到${u_k}$的边际谱. 2)每种模态，通过调谐相应估计中心频率的指数混频，将模态的频谱移至“基带”. 3)解调信号的高斯平滑度，即梯度的平方范数来估计带宽.

构造变分问题，假设原始信号f被分解为K个分量，保证分解序列为具有中心频率的有限带宽的模态分量，同时各模态的估计带宽之和最小，约束条件为所有模态之和与原始信号相等. 上述对应的约束变分表达式为

$ \left.\begin{aligned} & {\mathop {\min }\limits_{\left\{ {{\mu _k}} \right\},\left\{ {{\omega _k}} \right\}} {\sum\limits_{k = 1}^K {\left\| {{\partial _t} \left[ {\left( {\delta \left( t \right) + \dfrac{{\text{j}}}{{{\text{π}} t}}} \right){\text{*}}{\mu _k}\left( t \right)} \right]{{\text{exp}}\;{( - {\text{j}}{\omega _k}t)}}} \right\|_2^2;} } } \\ & {{\mathrm{s.t.}}\;\mathop \sum \limits_{k = 1}^K {\mu _k} = f\left( t \right).} \end{aligned}\right\} $

(6)

式中：K为需要分解的模态数；${\mu _k} = \left\{ {{\mu _1}, \cdots ,{\mu _k}} \right\}$、${\omega _k} = \left\{ {{\omega _1}, \cdots ,{\omega _k}} \right\}$分别为第k个模态分量及中心频率；$\delta \left( t \right)$为狄拉克函数.

为了求解上述约束变分问题，引入Lagrange乘法算子λ，将约束变分问题转换为非约束变分问题，得到增广Lagrange表达式：

$ \begin{split} L&\left( {\left\{ {{\mu _k}} \right\},\left\{ {{\omega _k}} \right\},\lambda } \right) = \\ &\alpha \sum\limits_{k = 1}^K {\left\| {{\partial _t}\left[ {\left( {\delta \left( t \right)+\frac{{\text{j}}}{{{\text{π}} t}}} \right){\text{*}}{\mu _k}\left( t \right)} \right]{{\text{exp}}\;{ (- {\text{j}}{\omega _k}t)}}} \right\|_2^2} + \qquad\qquad \\ &\left\| {f\left( t \right) - \sum\limits_{k = 1}^K {{\mu _k}\left( t \right)} } \right\|_2^2+\left\langle {\lambda \left( t \right),f\left( t \right) - \sum\limits_{k = 1}^K {{\mu _k}\left( t \right)} } \right\rangle . \\[-1pt]\end{split}$

(7)

式中：$\alpha $为二次惩罚因子，可以降低高斯噪声干扰. 利用交替方向乘子迭代算法与帕塞瓦尔、傅里叶等距变换，得到各模态分量和中心频率的最优解，搜寻增广Lagrange函数的鞍点. ${\mu _k}、{\omega _k}、\lambda $的迭代优化过程如下：

$ \hat \mu _k^{n+1}\left( \omega \right) \leftarrow \frac{{\hat f\left( \omega \right) - \displaystyle \sum \nolimits_{i/k} {{\hat \mu }_i}\left( \omega \right)+\hat \lambda \left( \omega \right)/2}}{{1+2\alpha {{\left( {\omega - {\omega _k}} \right)}^2}}}, $

(8)

$ \omega _k^{n+1} \leftarrow \frac{{ \displaystyle \int \nolimits_0^\infty \omega {{\left| {\hat \mu _k^{n+1}\left( \omega \right)} \right|}^2}{\mathrm{d}}\omega }}{{ \displaystyle \int \nolimits_0^\infty {{\left| {\hat \mu _k^{n+1}\left( \omega \right)} \right|}^2}{\mathrm{d}}\omega }}, $

(9)

$ {\hat \lambda ^{n+1}}\left( \omega \right) \leftarrow {\hat \lambda ^n}\left( \omega \right)+\gamma \left( {\hat f\left( \omega \right) - \mathop \sum \limits_k \hat \mu _k^{n+1}\left( \omega \right)} \right). $

(10)

式中：$\gamma $为容忍度，$ {\hat{\mu }}_{k}^{n+1}\left(\omega \right)、\hat{f}\left(\omega \right)、{\hat{\mu }}_{i}\left(\omega \right)、\hat{\lambda }\left(\omega \right) $分别为对应$ {\mu }_{k}^{n+1}\left(t\right)、f\left(t\right)、{\mu }_{i}\left(t\right)、\lambda \left(t\right) $的Fourier变换.

通过VMD算法原理可知, K与$\alpha $是2个需要确定的关键参数. 目前对这2个参数的确定大多使用经验法或重复测试选取最优值^[22]，较为耗时，且精度不高，本文提出自适应变分模态分解 (adaptive variational mode decomposition, AVMD) 方法，利用蝠鲼智能优化算法进行优化寻解.

2.2. 蝠鲼智能优化算法

利用该算法模仿蝠鲼在海洋中的觅食过程，针对蝠鲼的不同捕食策略进行数学建模，在复杂解空间中搜索最优解.

2.2.1. 3种觅食方式及数学原理

根据蝠鲼的觅食特点进行数学建模，形成以下3种觅食方式的数学模型.

1）链式觅食.

在链式捕食过程中，蝠鲼种群从头到尾排成一条捕食链. 蝠鲼个体下一位置的移动方向与步长是由当前最优解与前一个体位置共同决定. 该种位置更新方式的数学模型如下：

$ {p}_{i}^{d}\left(t+1\right)=\left\{\begin{array}{l}{p}_{i}^{d}\left(t\right)+r\left({p}_{\text{best}}^{d}\left(t\right)-{p}_{i}^{d}\left(t\right)\right)+\\ \quad \alpha \left({p}_{\text{best}}^{d}\left(t\right)-{p}_{i}^{d}\left(t\right)\right) ,\;i=1;\\ {p}_{i}^{d}\left(t\right)+r\left({p}_{i-1}^{d}\left(t\right)-{p}_{i}^{d}\left(t\right)\right)+\\ \quad \alpha \left({p}_{\text{best}}^{d}\left(t\right)-{p}_{i}^{d}\left(t\right)\right) ,\;i=2,3,\cdots ,N.\end{array}\right. $

(11)

$ \alpha = 2r\sqrt {\left| {{\text{lg}}\left( r \right)} \right|} . $

(12)

式中：r为在(0,1.0)上均匀分布的随机数，$\alpha $为系数权重，$p_i^d\left( t \right)$为第t代、第i个个体在d维上的位置，$p_{{\text{best}}}^d\left( t \right)$为第t代最优个体在d维上的位置，N为个体数量.

2）螺旋觅食.

蝠鲼个体在发现某猎物后，采用螺旋的方式向其靠近，由于链式觅食的存在，在向当前猎物螺旋移动的过程中，受到前一个个体的影响. 该种位置更新方式的数学模型如下.

当t/T > rand时，蝠鲼螺旋状运动的数学方程为

$ {p}_{i}^{d}\left(t+1\right)=\left\{\begin{array}{l}{p}_{\text{best}}^{d}\left(t\right)+r\left({p}_{\text{best}}^{d}\left(t\right)-{p}_{i}^{d}\left(t\right)\right)+\\ \qquad \beta \left({p}_{\text{best}}^{d}\left(t\right)-{p}_{i}^{d}\left(t\right)\right),\; i=1;\\ {p}_{\text{best}}^{d}\left(t\right)+r\left({p}_{i-1}^{d}\left(t\right)-{p}_{i}^{d}\left(t\right)\right)+\\ \qquad \beta \left({p}_{\text{best}}^{d}\left(t\right)-{p}_{i}^{d}\left(t\right)\right) ,\;i=2,3,\cdots ,N.\end{array} \right.$

(13)

$ \beta = 2{{\text{exp}}\;{[{r_1}({{T - i+1}})/{T}}]}{\text{sin}}\left( {2{\text{π}} {r_1}} \right). $

(14)

当t/T $ \leqslant $ rand时，蝠鲼螺旋状运动的数学方程为

$ {p}_{i}^{d}\left(t+1\right)=\left\{\begin{array}{l}{p}_{\text{rand}}^{d}\left(t\right)+r\left({p}_{\text{rand}}^{d}\left(t\right)-{p}_{i}^{d}\left(t\right)\right)+\\\qquad \beta \left({p}_{\text{rand}}^{d}\left(t\right)-{p}_{i}^{d}\left(t\right)\right),\; i=1;\\ {p}_{\text{rand}}^{d}\left(t\right)+r\left({p}_{i-1}^{d}\left(t\right)-{p}_{i}^{d}\left(t\right)\right)+\\\qquad \beta \left({p}_{\text{rand}}^{d}\left(t\right)-{p}_{i}^{d}\left(t\right)\right),\; i=2,3,\cdots ,N.\end{array} \right.$

(15)

$ x_{{\text{rand}}}^d\left( t \right) = {\mathrm{L}}{{\mathrm{b}}^d}+r\left( {{\mathrm{U}}{{\mathrm{b}}^d} - {\mathrm{L}}{{\mathrm{b}}^d}} \right). $

(16)

式中：${r_1}$、rand均为在(0,1.0)上均匀分布的随机数，T为迭代总次数，$x_{{\mathrm{rand}}}^d\left( t \right)$为第t代、第d维的随机位置，${\mathrm{U}}{{\mathrm{b}}^d}$、${\mathrm{L}}{{\mathrm{b}}^d}$分别为d维变量的取值上、下限，$\beta $为权重系数.

3）翻滚觅食.

在翻滚捕食中，蝠鲼个体以当前最优解作为翻滚支点，翻滚至与当前位置成镜像关系的另一侧. 该种位置更新方式的数学模型如下：

$ p_i^d\left( {t+1} \right) = p_i^d\left( t \right)+ S\left( {{r_2}p_{{\text{best}}}^d\left( t \right) - {r_3}p_i^d\left( t \right)} \right);\;i = 1,2, \cdots ,N. $

(17)

$ S = 2. $

(18)

式中：$ {r_2} $、$ {r_3} $均为在(0,1.0)上均匀分布的随机数.

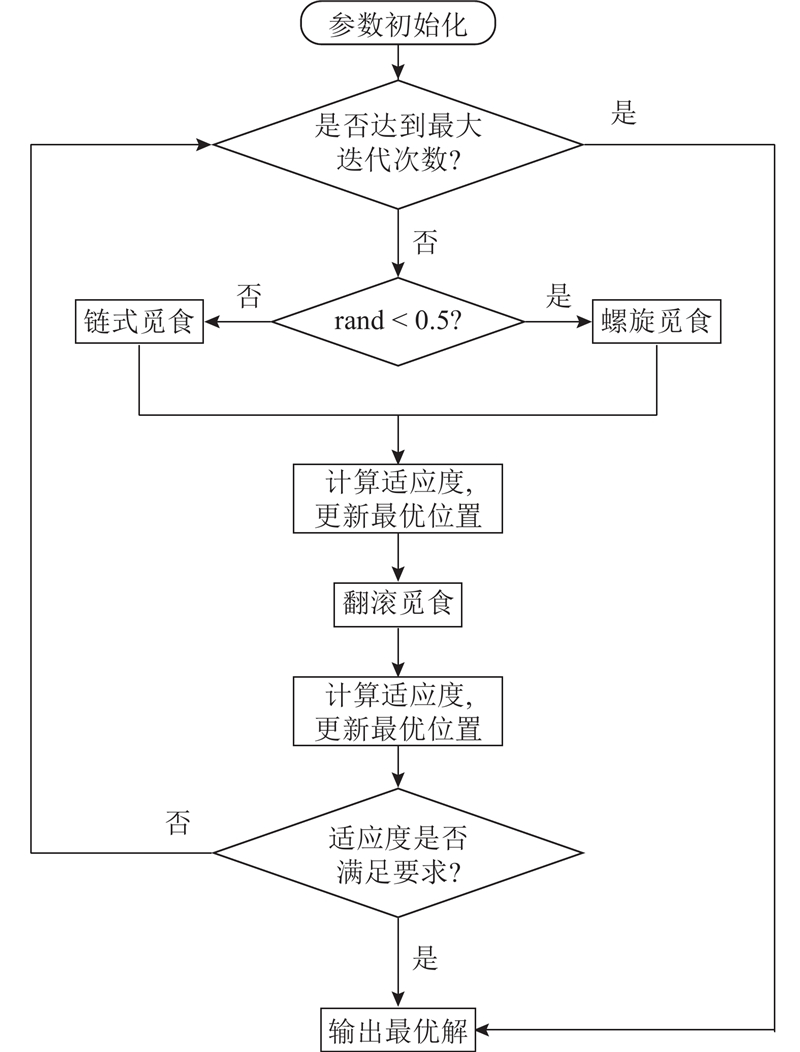
2.2.2. 蝠鲼智能优化算法的执行流程图

初始化种群数量、参数维度、参数上下限、适应度函数、最大迭代次数. 其中种群数量为蝠鲼群体的大小，在同等条件下，群体大小与搜索空间步长成反比. 参数维度为优化参数的个数，如在本场景下，优化参数为K值与Alpha值，则参数维度为2. 参数上下限为搜索空间范围. 适应度函数表示当处于搜索空间某一位置时，该位置处优化参数的评价函数.

根据随机数决定采用何种觅食方式更新位置，再执行翻滚觅食，使用最小包络熵作为适应度函数，计算适应度，适应度与迭代次数决定是否停止迭代. 算法的执行流程如图6所示.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6 蝠鲼智能优化算法的执行流程图

Fig.6 Execution flowchart of manta ray intelligent optimization algorithm

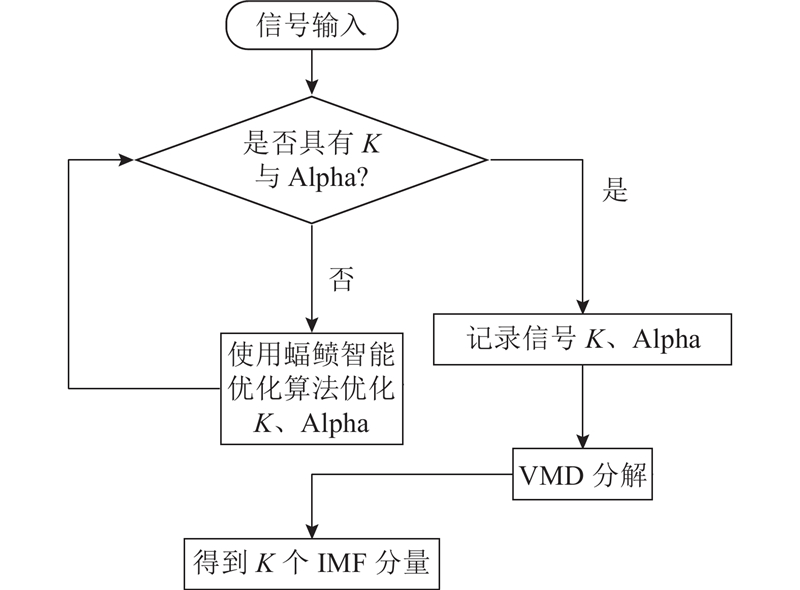
2.3. 自适应信号分解

结合VMD与蝠鲼智能优化算法，提出自适应变分模态分解方法，用于自适应搜寻VMD分解时的最佳参数组合.

该方法通过检验是否存在K、Alpha值，确定是否需要使用蝠鲼智能优化算法进行优化寻解，初始时将信号输入系统，系统检测该信号对象分解参数K与Alpha变量是否有实值. 若不存在实值，则使用蝠鲼智能优化算法优化寻参，直至具备分解参数，完成VMD分解过程. 自适应变分模态分解的执行流程图如图7所示.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7 自适应VMD执行流程图

Fig.7 Adaptive VMD execution flowchart

为了使实验结果更具应用性，分别从分层、富树脂、夹杂-衬纸、夹杂-隔离膜、夹杂-铜片、夹杂-铝片6种模拟缺陷中选取500个缺陷信号，共3 000个数据进行参数优化. 分别采用麻雀优化算法 (sparrow search algorithm，SSA)^[23]与蝠鲼智能优化算法，对K、Alpha进行参数优化. 参数优化后，对优化的结果数据进行统计，3 000个数据分别使用2种优化算法，对K、Alpha进行优化选取，如图8所示. 图中，N_K、N_Alpha分别为K和Alpha的数量. 从图8可以看出，针对不同的优化算法，优化结果存在一定的差异.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

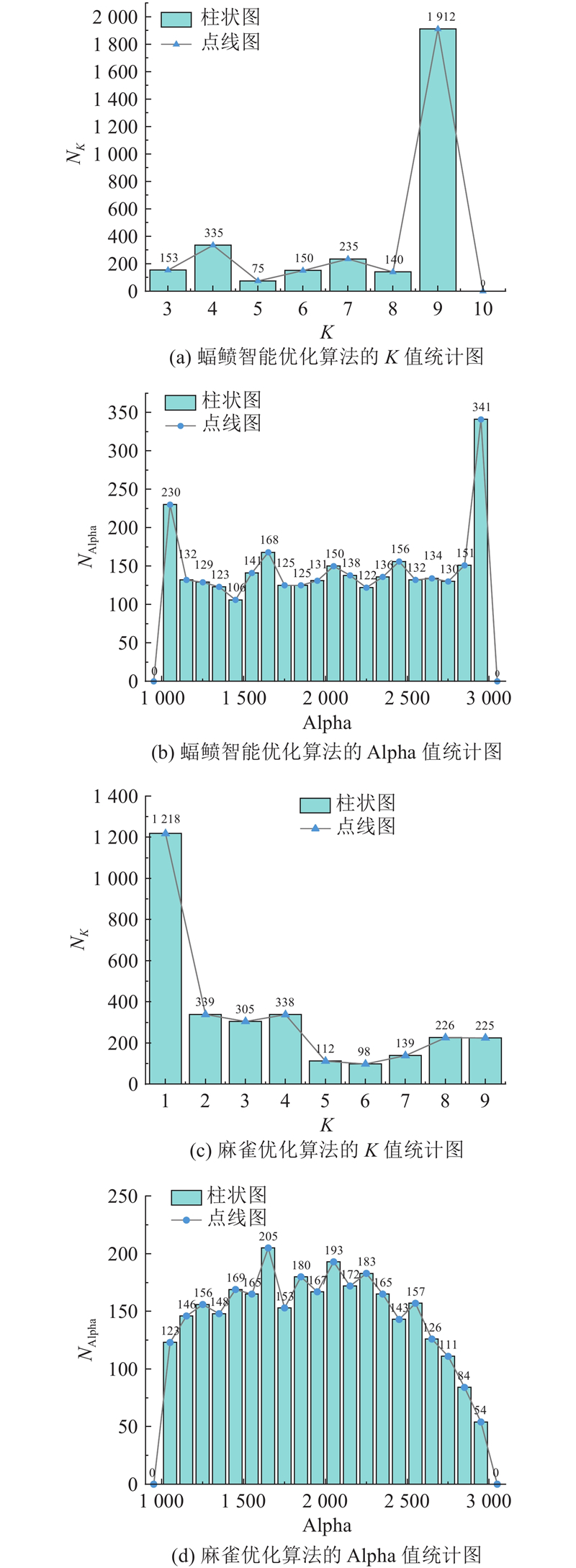
图 8 2种算法参数优化的统计对比图

Fig.8 Statistical comparison chart of parameter optimization of two algorithms

将2种算法优化后的K、Alpha进行数据分析，分别分析均值、标准差、众数、中位数、极差，如表2所示. 2种算法对于K的优化，其中SSA均值、众数、中位数的数值相差较大，且标准差大于MRFO，出现了众数为1的情形；对于Alpha的优化，SSA标准差明显大于MRFO. 综合分析可知，MRFO的优化稳定性明显高于SSA方法.

表 2 2种算法的优化结果对比表

Tab.2 Comparison table of optimization results of two algorithms

方法	参数	均值	标准差	众数	中位数	极差
SSA	K	3.4	2.7	1	2	8
MRFO	K	7.7	2.0	9	9	6
SSA	Alpha	1936.4	625.3	1650	1936.8	1998.7
MRFO	Alpha	2048.6	521.9	2950	2065.7	1999.4

新窗口打开| 下载CSV

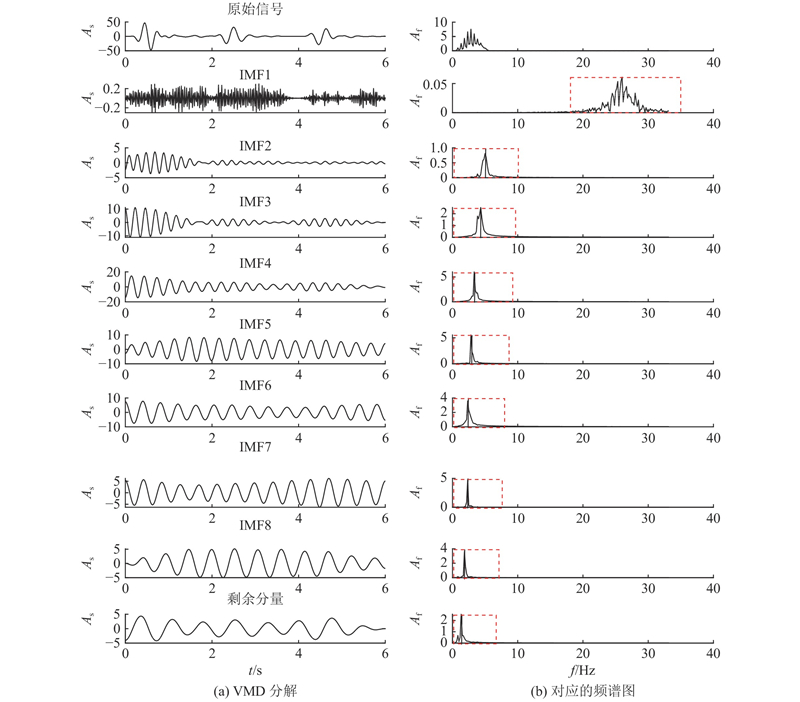
为了使整体数据得到充分分解，降低参数选取对分解结果的影响，分别选取优化K、Alpha的众数作为VMD分解的参数，K选择为9，Alpha选择为2 950. 对6种缺陷进行VMD分解，以分层缺陷为例，分解图如图9所示. 将各IMF分量的频率中心标记为虚线位置，除噪声外，其余每个模态函数的频谱在不同的频率范围内有明显的能量集中. 相邻模态函数的频谱在频域上有明显差异，能够将不同频率范围的IMF分量充分分解，且分解后，各IMF分量的频谱未出现重叠现象，表明AVMD方法对缺陷信号的分解充分且不过度. 分解图中IMF1分量出现高频噪声，对特征提取存在影响，属于无效特征信息，故筛选掉高频IMF1分量，对IMF2~IMF9进行特征提取.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9 分层缺陷自适应VMD分解图

Fig.9 Delamination defect adaptive VMD exploded views

3. 递归量化分析特征提取

缺陷特征是缺陷识别的关键，从缺陷中提取关键信息，找出缺陷间存在的差异，能够提高识别准确率. 对于上述筛选后的IMF分量，采用递归量化分析技术，提取对应的量化特征值，构建缺陷的特征向量.

3.1. 递归量化分析原理

3.1.1. 递归图

递归图(recurrence plots, RP)是由Eckmann等^[24]提出的，用于使动态系统的递归特性可视化. 将递归图应用在时间序列上，将时间序列的时域空间变换到相空间，从而将时域中的每个点${x_i}$变换成相空间的对应状态${{\boldsymbol{ s}}_i}$. 计算2个相邻状态之间的距离，进行阈值二值化，得到递归图中对应2个状态之间的二值化特征. 递归图可以用一系列递归矩阵来表示：

$ {{{R}}}_{i,j}\left(\varepsilon \right)=\textit{Θ}\left({\boldsymbol{\varepsilon}} -{{{\boldsymbol{s}}}}_{i}-{{{\boldsymbol{s}}}}_{j}\right);\text{ }i,j=1,2, \cdots ,N. $

(19)

式中：${{\boldsymbol{R}}}$为$N \times N$的方阵，${\boldsymbol{\varepsilon }}$为距离阈值，使得$ {R}_{i,j}\in \left\{0,1\right\} $；${{\varTheta }}\left( \cdot \right)$为Heaviside函数.

1）相空间重构.

相空间重构是由已知的时间序列来恢复并刻画原动力系统的方法，是由时域空间变换到相空间的过程. 相空间重构过程有2个关键的参数：嵌入维数d、延迟时间$\tau $.

假设一维时间序列为$\left\{ {{\boldsymbol{x}}\left( i \right),i = 1,2, \cdots ,n} \right\}$，当选择延时时间为$\tau $，嵌入维度为$d$进行相空间重构时，得到的相空间矢量为

$ {\boldsymbol{y}}\left( i \right) = \left[ {{\boldsymbol{x}}\left( i \right), \cdots ,{\boldsymbol{x}}\left( {i+\left( {d - 1} \right)\tau } \right)} \right];1 \leqslant i \leqslant n - \left( {d - 1} \right)\tau . $

(20)

延时时间是指在相空间中选择的2个状态之间的时间间隔. 当$\tau $太小时，相空间重构后两坐标分量${\boldsymbol{x}}\left( {i+j\tau } \right)$与${\boldsymbol{x}}\left( {i+\left( {j+1} \right)\tau } \right)$在数值上过于接近，使得相邻两坐标之间的独立性不够；当延时时间$\tau $太大时，相邻两坐标会出现完全独立的情形，混沌吸引子的轨迹在2个方向上的投影无相关性. 选择合适的时间延时来制衡，防止出现2种极端情形.

嵌入维度用于控制相空间重构后高维空间的维数，直接决定系统的几何结构是否被完全打开.

2）延时时间$\tau $的确定.

对于$\tau $，常用的确定方法有自相关系数法、交互信息法. 利用自相关系数法，仅能提取时间序列的线性相关性，不能扩展到高维空间研究. 交互信息法弥补了自相关系数法的缺点，原理如下.

假设2个离散信息系统$\left\{ {{s_1}, {s_2}, \cdots ,{s_m}} \right\}、$$\left\{ {{q_1}, {q_2}, \cdots ,{q_m}} \right\}$构成系统S和Q，通过信息论和遍历论可知，2个系统的信息熵分别为

$ H\left( S \right) = - \mathop \sum \nolimits_{i = 1}^m {P_S}\left( {{s_i}} \right){\mathrm{lo}}{{\mathrm{g}}_2}{P_S}\left( {{s_i}} \right), $

(21)

$ H\left( Q \right) = - \mathop \sum \nolimits_{i = 1}^m {P_Q}\left( {{q_i}} \right){\mathrm{lo}}{{\mathrm{g}}_2}{P_Q}\left( {{q_i}} \right). $

(22)

式中：${P_S}\left( {{s_i}} \right)$和${P_Q}\left( {{q_i}} \right)$分别为S和Q中事件${s_i}$和${q_i}$的概率. 交互信息的计算公式为

$ I\left( {S,Q} \right) = H\left( S \right)+H\left( Q \right) - H\left( {S,Q} \right), $

(23)

$ H\left( {S,Q} \right) = - \mathop \sum \nolimits_{i = 1}^m \mathop \sum \nolimits_{j = 1}^n {P_{S,Q}}\left( {{s_i},{q_j}} \right){\mathrm{lo}}{{\mathrm{g}}_2}{P_{S,Q}}\left( {{s_i},{q_j}} \right). $

(24)

式中：${P_{S,Q}}\left( {{s_i},{q_j}} \right)$为事件${s_i}$和事件${q_j}$的联合分布概率. 交互信息熵标准化为

$ I\left( {S,Q} \right) = I\left( {S,Q} \right)/\sqrt {H\left( S \right) H\left( Q \right)} . $

(25)

以上述理论为基础，计算时间延时，定义

$ \left( {S,Q} \right) = \left( {x\left( i \right),x\left( {i+\tau } \right)} \right);\;1 \leqslant i \leqslant n - \tau . $

(26)

式(26)利用$x\left( i \right)$和$x\left( {i+\tau } \right)$分别替代式(25)中的S和Q，则$I\left( {S,Q} \right)$是关于时间延时的函数，写作$I\left( \tau \right)$. $I\left( \tau \right)$表示2个序列的相关程度，$I\left( \tau \right) = 0$表示$x\left( i \right)$和$x\left( {i+\tau } \right)$完全不可预测，即两者完全不相关. 选择$I\left( \tau \right)$的第1个极小值时对应的$\tau $为最优延时时间. 使用交互信息法得到3 000个数据的延时时间，其中结果为4的个数为123，结果为5的个数为891，结果为6的个数为1 955，结果为7的个数为31. 从上述结果可以看出，时间延时选择众数6.

3）嵌入维度$d$的确定.

常用的嵌入维度确定方法有虚假临近点法和Cao方法. 其中Cao方法克服了虚假临近点法噪声敏感和需要选取阈值的主观性缺点，用较少的数据量便可求出嵌入维度，原理如下.

时间序列$\left\{ {x\left( i \right),i = 1,2, \cdots ,n} \right\}$基于嵌入时间$\tau $构造的向量空间为

$ {{\boldsymbol{y}}_i}\left( d \right) = \left( {{\boldsymbol{x}}\left( i \right), \cdots ,{\boldsymbol{x}}\left( {i+\left( {d - 1} \right)\tau } \right)} \right); i = 1,2, \cdots ,n - \left( {d - 1} \right)\tau . $

(27)

式中：d为嵌入维度，${{\boldsymbol{y}}_i}\left( d \right)$为第i个d维重构向量. 定义变量：

$a\left( {i,d} \right) = \frac{{||{{\boldsymbol{y}}_i}\left( {d+1} \right) - {{\boldsymbol{y}}_{n\left( {i,d} \right)}}\left( {d+1} \right)|{|_\infty }}}{{||{{\boldsymbol{y}}_i}\left( d \right) - {{\boldsymbol{y}}_{n\left( {i,d} \right)}}\left( d \right)|{|_\infty }}}; \;i = 1,2, \cdots ,n - d\tau . $

(28)

式中：$|| \cdot ||$为无穷范数. $ n\left(i,d\right)\in \left\{1,\cdots ,n-d\tau \right\} $是使得${{\boldsymbol{y}}_{n\left( {i,d} \right)}}\left( d \right)$在d维相空间且最大范数下与${{\boldsymbol{y}}_i}\left( d \right)$最近的向量，且$n\left( {i,d} \right) \ne i$. 定义

$ E\left( d \right) = {\left( {n - d\tau } \right)^{ - 1}}\mathop \sum \nolimits_{i = 1}^{n - d\tau } a\left( {i,d} \right). $

(29)

从式（29）可以看出，$E\left( d \right)$与延时时间和嵌入维度有关，当延时时间确定时，只与嵌入维度有关.当嵌入维度大于某个值${d_0}$时，$E\left( d \right)$不再发生变化，即寻找到最小嵌入维度.为了方便量化寻找，定义

$ {E_1}\left( d \right) = \frac{{E\left( {d+1} \right)}}{{E\left( d \right)}}. $

(30)

当$d$>${d_0}$时, ${E_1}\left( d \right)$不再发生变化，则${d_0}+1$是要寻找的最小嵌入维度. 使用Cao方法，得到3 000个数据嵌入维度的汇总结果. 嵌入维度为20的数据个数为674，17为123个，18为176个，19为387个，21为349个，其余嵌入维度从5到27有少量分布. 从结果可知，嵌入维度众数为20，且大多集中于20附近，故嵌入维度选择为20.

根据上述理论，将各缺陷递归图进行绘制. 以分层缺陷为例，递归图如图10所示，各IMF分量的对角线结构较完整，IMF1高频噪声分量递归图的白色区域占比较大，从图10难以对递归图进行直观量化描述. 引入递归量化分析技术，对各递归图进行量化分析.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10 分层缺陷各IMF分量递归图

Fig.10 Recursive plot of each IMF component of delamination defect

3.1.2. 递归量化分析

将时间序列转换为递归矩阵，并进行二值化成像，可以将系统的动力特性可视化，但由于系统呈现形式为图像，易出现分辨率低的问题. 为了解决该问题，Webber等^[25]提出递归量化分析方法，将递归图中的特性以数值量化的形式呈现出来. Gao^[26]补充了更丰富的描述指标，常用的递归量化分析指标如下.

1）递归度(RR)为递归图中递归点数量占总点数的比例，计算公式为

$ {\text{RR}} = \frac{1}{{{N^2}}} \sum \limits_{i=1}^N \sum \limits_{j = 1}^N{{{R}}_{i,j}}. $

(31)

2）确定率(DER)为45°对角线上递归点占总点数的百分比，计算公式为

$ {\text{DER}} = \frac{{\displaystyle \sum \nolimits_{l = {l_{{\mathrm{min}}}}}^N lP\left( l \right)}}{{\displaystyle \sum \nolimits_{i=1}^N\displaystyle \sum \nolimits_{j=1}^N {{{R}}_{i,j}}}}. $

(32)

式中：${l_{{\mathrm{min}}}}$为最小对角线长度，一般取2；$P\left( l \right)$为对角线为l的对角线分布概率.

3）递归熵(ENTR)为45°对角线方向相邻像素点个数的分布概率的香农熵，计算公式为

$ {\text{ENTR}} = - \mathop \sum \nolimits_{l = {l_{{\text{min}}}}}^N P\left( l \right){\text{ln }}P\left( l \right). $

(33)

4）比率(RATIO)为确定率与递归率的比值，计算公式为

$ {\text{RATIO}} = \frac{{{\text{DET}}}}{{{\text{ENTR}}}}. $

(34)

5）平均对角线长度L为递归图中平行于45°对角线方向线段的平均长度，计算公式为

$ L = \frac{{\displaystyle \sum \nolimits_{l = {l_{{\mathrm{min}}}}}^N lP\left( l \right)}}{{\displaystyle \sum \nolimits_{l = {l_{{\mathrm{min}}}}}^N P\left( l \right)}}. $

(35)

6）层状度(LAM)为构成竖直或水平线段结构的递归点的百分比，计算公式为

$ {\text{LAM}} = \frac{{\displaystyle \sum \nolimits_{v = {v_{{\text{min}}}}}^N vP\left( v \right)}}{{\displaystyle \sum \nolimits_{i=1}^N\displaystyle \sum \nolimits_{j=1}^N {{{R}}_{i,j}}}}. $

(36)

式中：${v_{{\text{min}}}}$为最小分析长度，一般取2；$P\left( v \right)$为长度为$v$的竖直/水平线段分布概率.

7）圈闭时间(TT)为递归图中垂直结构长度的均值，计算公式为

$ {\text{TT}} = \frac{{ \displaystyle \sum \nolimits_{v = {v_{{\text{min}}}}}^N v{P^\varepsilon }\left( v \right)}}{{\displaystyle \sum \nolimits_{v = {v_{{\text{min}}}}}^N {P^\varepsilon }\left( v \right)}}. $

(37)

8）最长对角线${L_{{\mathrm{max}}}}$为除45°主对角线外，其余45°最长对角线的元素个数，计算公式为

$ {L_{{\text{max}}}} = {\text{max}}\; {\left\{ {{l_i};i = 1,2, \cdots ,{N_i}} \right\}} . $

(38)

式中：${N_i}$为除主对角线外其余45°对角线的个数.

9）最长水平线段${H_{{\mathrm{max}}}}$为递归图中水平结构的最大长度，计算公式为

$ {H_{{\text{max}}}} = {\text{max}}\; {\left\{ {{h_i};i = 1,2, \cdots ,{N_{\text{h}}}} \right\}} . $

(39)

式中：${N_{\text{h}}}$为水平线段的个数.

利用以上9个指标，可以将递归图中的特征描述为数值参量，开展数值分析. 如图10所示为检测信号每一个IMF分量的递归图. 为了保留缺陷信息的完整性，对除噪声外每一IMF分量的递归图进行量化分析.

3.2. 模态分量递归量化分析

对CFRP超声检测缺陷的3 000个数据进行递归量化分析，发现存在115个问题数据. 原始信号时域上变化较快，频率较高，递归矩阵无法显示系统特性，将115个问题数据过滤筛选，统计剩余2 885个数据的IMF2~IMF9递归量化分析结果. 对6种缺陷信号进行编号，1~6分别表示分层缺陷、富树脂缺陷、夹杂-衬纸缺陷、夹杂-隔离膜缺陷、夹杂-铝片缺陷、夹杂-铜片缺陷，对缺陷信号的每个IMF分量进行递归量化分析. 以IMF3分量为例，递归量化分析结果的平均值如表3所示. 递归度中，2与3明显高于其他缺陷. 确定率中，4明显低于其他缺陷. 递归熵中，1、4明显低于其他缺陷. 比率中，除3、6数值差距较小外，其余缺陷差距较大. 层状度中，1、4明显低于其他缺陷. 圈闭时间中，2、3明显高于其他缺陷. 最长对角线数值中，4明显低于其他缺陷. 最长水平线数值中，1、4、5明显低于6，且6明显低于2、3. 平均对角线长度数值中，5明显高于其他缺陷. 递归量化分析指标中的9个特征能够表征1个IMF分量的特点，为了充分提取缺陷信息，利用IMF2~IMF9递归量化分析后的72个(8×9)特征值构建特征向量，表征一个缺陷.

表 3 2885数据IMF3分量递归量化分析参数平均值的汇总表

Tab.3 Summary table of 2885 data IMF3 component recursive quantitative analysis parameter mean

类型	RR	DER	ENTR	RATIO	LAM	TT	L_max	H_max	L
1	0.03	0.81	1.33	34.12	0.61	2.37	243.27	3.10	45.59
2	0.11	0.93	2.02	11.92	0.92	8.29	258.05	43.36	46.41
3	0.08	0.90	1.91	17.50	0.88	7.43	233.06	40.36	46.26
4	0.02	0.73	1.27	48.63	0.54	2.45	195.46	2.95	47.93
5	0.04	0.87	1.69	26.73	0.81	3.05	235.22	5.59	55.15
6	0.05	0.90	1.87	19.27	0.88	4.16	253.29	15.22	44.34

新窗口打开| 下载CSV

4. CNN神经网络分类识别

卷积神经网络是深度学习模型，广泛应用于计算机视觉任务，如分类和目标检测. CNN的设计灵感来源于生物学中视觉皮层的工作原理，通过一系列的卷积、池化和全连接层，自动学习输入数据的特征表示. 为了提高检测效率，使用轻量级CNN识别模型，模型识别过程能在几秒内完成. 该轻量级模型在保持较高识别性能的同时，减少了模型的计算和存储资源需求. 通过优化网络结构和参数设置，使其在嵌入式设备和资源受限环境下具备更强的实用性. 模型结构如图11所示.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11 CNN模型的结构图

Fig.11 Structure diagram of CNN model

对原始数据进行预处理，包括对数据进行贴标签和特征提取处理，每个缺陷信号的特征被视为8×9×1的模块进行输入. 使用的CNN模型包含输入层、2个卷积块、全连接层和输出层. 每个卷积块由卷积层、批归一化层、ReLU激活层和最大池化层组成. 第1个卷积块有16个输出通道，第2个卷积块有32个输出通道. 全连接层具有64个神经元，使用ReLU激活函数进行非线性变换. 输出层通过softmax函数输出类别概率. 训练时使用随机梯度下降算法，设置最大训练迭代次数为100. 训练集和测试集的准确率通过混淆矩阵进行评估和可视化，使用的CNN神经网络训练模型参数如表4所示.

表 4 CNN神经网络训练模型的参数

Tab.4 Parameter of CNN neural network training model

输入层	卷积层	卷积层	卷积层	池化层	全连接层	全连接层	输出层
8×9×1	3×3,16	2×2,2	3×3,32	2×2,2	64 神经元	6 神经元	6 层

新窗口打开| 下载CSV

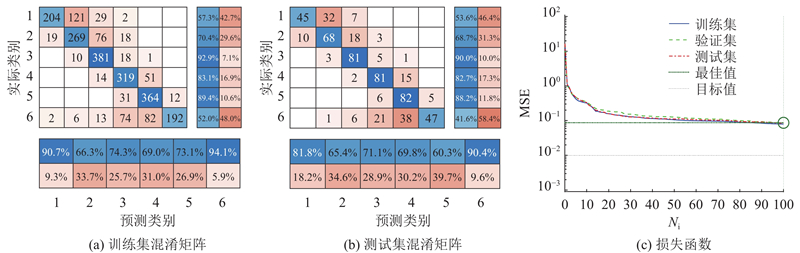
在筛去问题数据后，剩余共2 885个数据，其中分层440个、富树脂481个、夹杂-衬纸500个、夹杂-隔离膜482个、夹杂-铝片500个、夹杂-铜片482个，利用以上数据构建数据集. 分别使用李健等^[12]提出的小波包分解与BP神经网络、本文的特征提取方法结合BP神经网络、本文的特征提取方法结合CNN神经网络3种方法进行识别. 将数据按8∶2的比例划分为训练集与测试集，利用小波包与BP神经网络方法得到的混淆矩阵及误差如图12所示. 图中，N_i为训练轮次，MSE为均方根误差. 训练集的识别正确率为71.66%，测试集的识别正确率为65.86%. 当训练轮次为100时，最佳验证误差为0.09. 从识别结果来看，训练集和测试集的正确率均较低，在实际的大规模扫描数据场景中不适用.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12 小波包转换与BP识别结果

Fig.12 Wavelet packet transform and BP recognition results

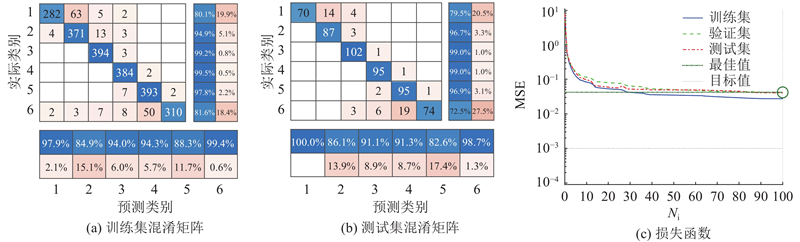
使用本文提出的特征提取方法对缺陷进行特征提取，将提取出的特征值输入BP神经网络识别，其中缺陷的特征数据按8∶2的比例划分为训练集和测试集，识别结果如图13所示. 训练集的识别正确率为91.12%，测试集的识别正确率为87.52%，当训练轮次为100时，最佳验证误差为0.04. 从识别结果来看，训练集和测试集的识别正确率相较于小波包分解特征提取与BP神经网络识别方法有明显提高.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13 RQAT与BP神经网络方法的识别效果图

Fig.13 Identify renderings of RQAT and BP neural network method

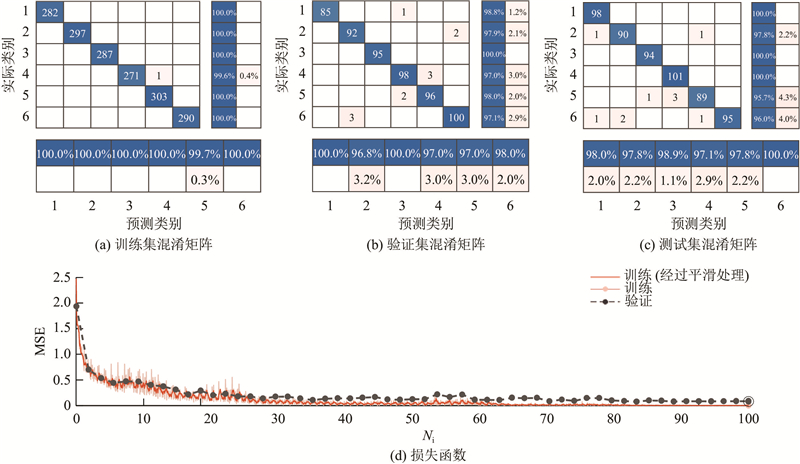
为了进一步提高识别正确率，使用提出的自适应变分模态分解和递归量化分析特征提取方法，对缺陷信号进行特征提取后，输入CNN神经网络识别，在识别过程中增加验证集，将特征提取后的数据按6∶2∶2的比例划分为训练集、验证集、测试集，识别结果如图14所示. 训练集的识别正确率为99.94%，验证集的识别正确率为98.09%，测试集的识别正确率为98.27%. 当训练轮次为100时，最佳验证误差为0.03. 从识别结果来看，将本研究方法特征提取后的缺陷特征输入CNN神经网络后，相较于输入BP神经网络，识别正确率得到提高，能够更好地适应实际工况.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14 新方法的识别结果

Fig.14 Identification result of new method

5. 结　论

（1）利用本文提出的基于蝠鲼智能优化算法的VMD方法，可以有效地解决VMD分解时关键参数K与Alpha的确定问题.

（2）利用本文提出的自适应变分模态分解和递归量化分析方法，能够对CFRP超声无损检测实现去噪与特征提取. 将提取出的72个特征值放入CNN中，能够实现高准确率的识别分类，识别正确率达到98.27%，为后续CFRP缺陷的高质量成像及精确定量研究工作奠定基础.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

MOHAMMADKHANI R, FRAGONARA L Z, PADIYAR J M, et al. Ultrasonic phased array imaging technology for the inspection of aerospace composite structures [C]// IEEE 6th International Workshop on Metrology for Aerospace. New York: IEEE, 2019: 203-208.