海水淡化技术是解决全球淡水危机的有效方法之一[1]. 常见的商用海水淡化技术(如低温多效蒸发和多级闪蒸)不但离不开化石能源,而且不能切实解决边远、区域分散地区的淡水紧缺问题. 太阳能作为可再生的新能源,具有清洁、环保、持续、长久等优势,将太阳能应用到海水淡化系统中,是应对淡水资源短缺、实现可持续发展的有效途径[2]. 太阳能界面蒸发海水淡化技术作为新兴的海水淡化技术,基底结构具备水分稳定输运、抗盐防堵塞和热量隔绝等特性. 毛细作用将海水输运到蒸发界面,高效的光热转换材料将吸收的太阳能转化成热量后蒸发海水中的水分,实现盐水分离[3]. 太阳能界面蒸发系统不消耗化石能源,具有能源利用率高,结构简单,常压运行稳健,成本及维护费用低,可用于海岛等边远地区等优势. 太阳能界面蒸发系统的基底结构的性能直接影响太阳能界面蒸发海水淡化系统的蒸发速率,进而影响系统能量利用率.
为了增加界面蒸发系统的蒸发速率,学者们设计并优化了多种料液输运途径. 有3种代表性的料液输运路径,分别为一维[4]、二维[5],和三维[6]输运结构. 在一维和二维水输运基底结构中,输水通道将料液输运至蒸发界面处,减少了传导至料液池中的热损失,但基底的供水量受输水通道的结构影响小于三维输运基底结构. 三维输运基底结构多采用多孔材料,直接与料液接触,多孔的三维料液输运基底结构毛细作用更强,促进了料液的输运,但是开放孔隙中的料液往往导致更多的热量因被传导到料液池中而损失. 徐凝[7]受睡莲叶片结构的启发,设计多级结构的光热蒸汽转化装置,在处理10%(质量分数)的盐水和30%(质量分数)的污水时,在光照强度为1 kW/m2条件下,系统的光热转换效率达到80%. Liu等[8]将TiAlON涂层作为光热转换界面搭建界面蒸发系统,将单个毛细管作为料液输运通道,基底用泡沫包裹减少热损失,在光照强度为1 kW/m2条件下,该系统的光热转换效率达到73%. Liu等[9]设计的仿生系统以塞有脱脂棉的毛细管和疏水泡沫作为基底结构,该系统在1 kW/m2光照强度下的蒸发速率为0.97 kg/(m2·h),光热转换效率达到89%. Guo等[10]设计并将氧化石墨烯和纸纤维组成装置,在绝热材料中插入多个毛细管,料液持续地通过毛细管传输到光热转换界面处. 该系统在1 kW/m2光强下的光热转换效率达到89.2%. 料液输运过程与蒸发过程息息相关[11-14]. Li等[12]研究了水在矩形纳米毛细通道内的蒸发过程,实验发现蒸发量随着毛细通道温度的升高而增大,随着毛细通道管径的增大而减小,随着毛细通道高度的降低而增大,随着环境空气相对湿度的增加而减小. Ramon等[13]将Lucas-Washburn方程扩展,分析水和乙醚在竖直毛细管中的蒸发与输运过程之间的耦合过程,2种料液的相变影响黏滞力和惯性的大小,最终对平衡上水高度产生影响;随着料液与环境间的温差增大,蒸发时2种料液在通道内输运过程中达到的平衡上水高度降低,气液界面处的振荡现象的频率增大,振荡的幅度减小. Liu等[14]模拟分析蒸发条件下梯形毛细通道内的料液输运过程,发现梯形通道的底角越小,蒸发速率越大,且料液输运过程达到平衡状态的时间随着蒸发速率的增大而增加.
太阳能界面蒸发系统具有协同特征:持续稳定的水分供应,较高的蒸发速率,最小的热损失,三者相互匹配和优化可以提高系统性能. 因此有必要深入研究基底结构对太阳能界面蒸发系统性能的影响规律,以及水分输运过程与蒸发过程间的相互影响机制. 现有研究大多集中于高效光热转换界面的开发和某种特定界面蒸发系统的整体性能,针对系统内部不同基底结构及参数对蒸发性能影响的研究较少. 本研究提出具有板式基底结构的太阳能界面蒸发系统,建立三维数学模型并利用Ansys Fluent软件求解,探究板缝宽度、料液质量分数对界面蒸发过程的影响规律,以及不同条件下液膜在蒸发平台上的动态变化机理.
1. 数学模型
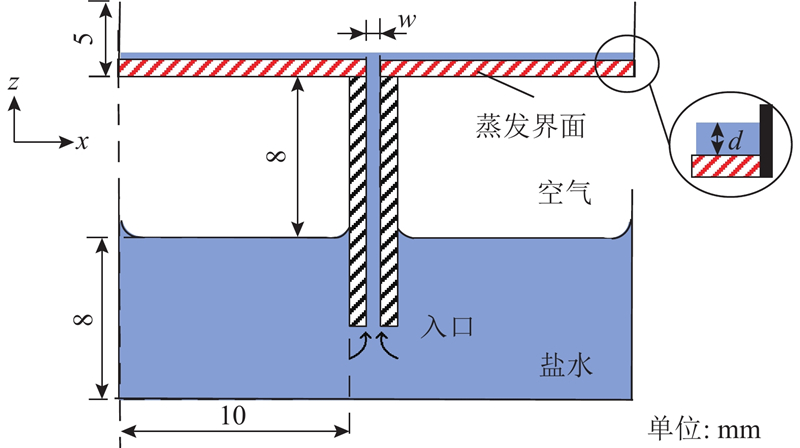
板式基底结构界面蒸发系统的物理模型如图1所示,料液通过毛细作用输运至蒸发界面处,铺展成一层薄薄的液膜并蒸发. 竖板浸入料液的高度为5 mm,料液池内水深为8 mm,板子距同侧水池壁面距离为10 mm,竖直板厚1 mm,通道高度为8 mm,蒸发界面长度为22 mm,蒸发平台高度为5 mm. 定义d为蒸发平台上液膜的厚度,设置初始液膜厚度为1.0 mm;w为板缝宽度,取w=0.5 、0.7、0.8、1.0 、1.4 mm;设置竖直板输水通道内的接触角
图 1
图 1 板式基底结构界面蒸发系统物理模型
Fig.1 Physical model of interfacial evaporation system with plate substrate structure
表 1 盐水的物性参数(T=300 K)
Tab.1
| wB/% | ρ/(kg⋅m−3) | λ/(W⋅m−1⋅K−1) | µ/(kg⋅m−1⋅s−1) | Cp/(J⋅kg−1⋅K−1) | σ/(N⋅m−1) |
| 0 | 996.4 | 0.613 | 0.854×10−3 | 4 185.6 | 71.686×10−3 |
| 3.5 | 1 023.0 | 0.611 | 0.920×10−3 | 4 001.5 | 72.789×10−3 |
| 5.0 | 1 034.4 | 0.610 | 0.953×10−3 | 3 928.1 | 73.262×10−3 |
| 7.0 | 1 049.6 | 0.609 | 1.000×10−3 | 3 835.3 | 73.892×10−3 |
| 13.0 | 1 095.2 | 0.606 | 1.168×10−3 | 3 592.1 | 75.783×10−3 |
按照上述假设,板式基底界面蒸发系统数学模型的连续性方程、动量方程和能量方程分别为
式中:
式中:蒸发适应系数α=0.005;摩尔质量M=0.0585 kg/mol;摩尔气体常数R=8.314 J/(mol⋅K),Zc为气液界面处z方向单元格尺寸;pv、Tv为气相压力与温度;ps(Ti)为气液界面温度Ti对应的饱和水蒸气压力,LH为蒸发过程中盐水的汽化潜热,确定ps(Ti)、LH的方程式[17]分别为
式中:
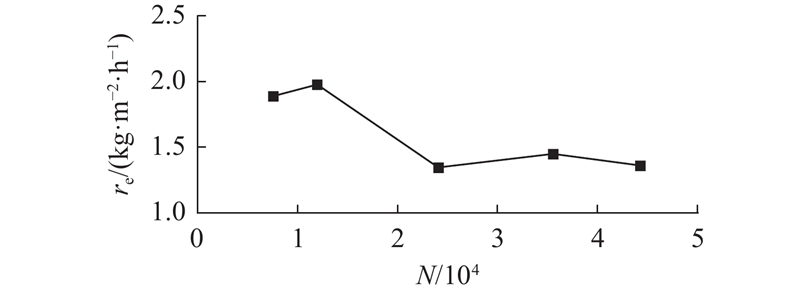
基于瞬态模型,采用压力基求解器求解板式基底结构的太阳能界面蒸发过程,CFD的相关参数设置如下:多相流模型为VOF模型,压力-速度耦合为压力隐式算子分离(pressure implicit with splitting of operators,PISO)算法,体积分数为几何重构(geo-reconstruct),对流项为对流项的二次迎风插值(quadratic upwind interpolation of the convective kinematics,QUICK),压力项为预压交错选项(pressure staggering option,PRESTO),输水通道中心处边界条件设为“对称”,水池以及竖直板设为“壁面,绝热”,蒸发界面处设为“壁面,恒定热通量”,水池以及液膜上方设置为“压力出口”. 蒸发速率直接反映竖直板式基底结构界面蒸发系统的性能,模拟计算中恒定热通量设定为0.98 kW/m2,在板缝宽度为0.8 mm,竖直板输水通道壁面接触角为13°、料液质量分数为3.5%的条件下,不同数量网格计算得到的蒸发速率re如图2所示,网格数N分别为7 516、11 964、24 054、35 550、44 244. 网格数为35 550与44 244相比,蒸发速率相对误差为4%,综合考虑计算耗时和计算精度,选择数量为35 550的网格进行后续研究.
图 2
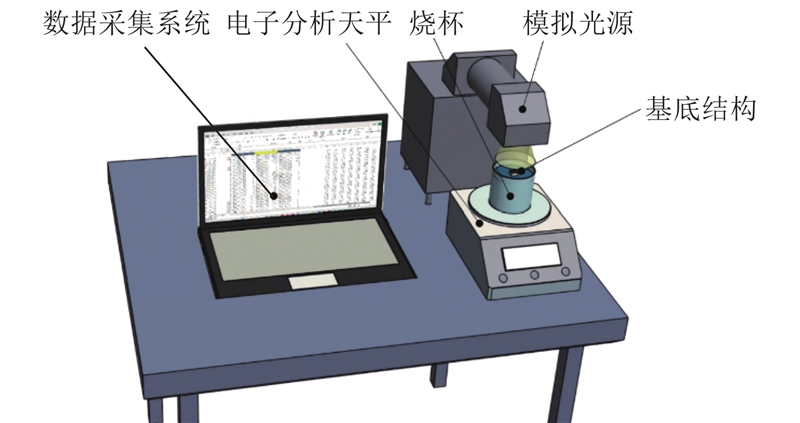
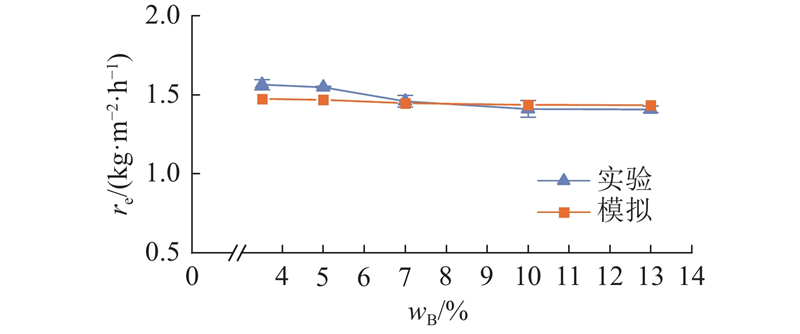
为了验证模拟结果的准确性,搭建如图3所示的蒸发试验台,对板缝宽度为0.8 mm的竖直板基底结构的界面蒸发系统开展料液质量分数分别为3.5%,5%,7%,10%和13%的盐水蒸发实验研究,输水通道接触角为13°,每个工况实验至少重复3次. 实验用到主要仪器设备有电子分析天平(华志电子科技有限公司,PTY-JA1 000S)、光功率计(Thorlabs,PM100D)和太阳光模拟器(中科微能科技有限公司,CME-SL1000)等. 实验的光照强度为1 kW/m2,实验室自主研发的光热转换材料主要由海绵、碳纳米管及聚合物组成,光吸收率为98%,因此将模拟计算中恒定热通量设定为0.98 kW/m2. 不同料液质量分数下的数值模拟计算得到的蒸发速率与实验的蒸发速率对比结果如图4所示. 模拟结果与实验结果基本保持一致,两者的最大相对误差为5.9%,计算模型满足本研究竖直板基底结构界面蒸发系统盐水蒸发进行数值模拟计算的准确性要求.
图 3
图 4
图 4 蒸发速率随料液质量分数的变化
Fig.4 Variation of evaporation rate with mass fraction of feed water
2. 结果与讨论
2.1. 板缝宽度影响
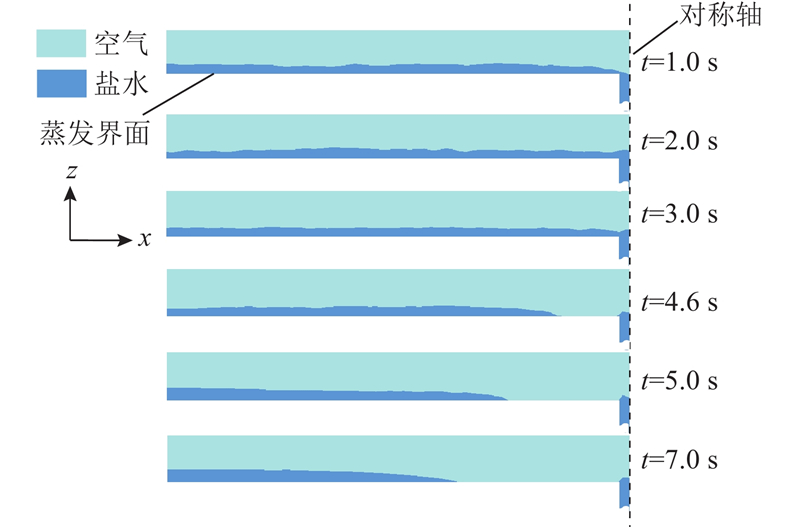
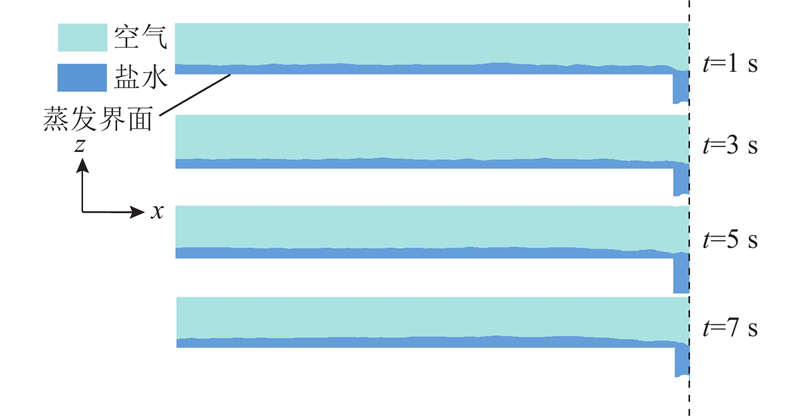
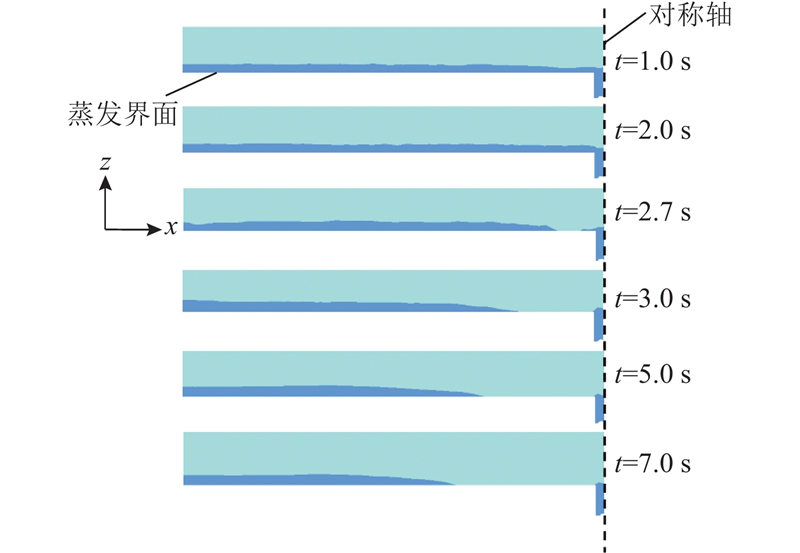
研究料液质量分数为3.5%,输水通道接触角为13°时,板缝宽度对竖直板式基底蒸发过程的影响. 设定板缝宽度分别为0.4、0.5、0.6、0.7、0.8、1.0、1.4 mm. 板缝宽度为0.5 mm,蒸发过程中料液液膜铺展变化过程如图5所示. 该图展示的是轴对称模型计算结果的一半,对称轴为板缝中心线,深色的区域表示盐水,浅色的区域表示空气. 可以看出,蒸发过程中液膜出现2种状态:1)蒸发时间t<4.6 s时,蒸发界面上的液膜与输水通道内的料液相连,液膜厚度基本保持不变,表明输水通道供应的料液能够满足蒸发需求;2)t
图 5
图 5 板缝宽度为0.5 mm时蒸发过程中液膜铺展变化
Fig.5 Changes in liquid film spreading during evaporation at slit width of 0.5 mm
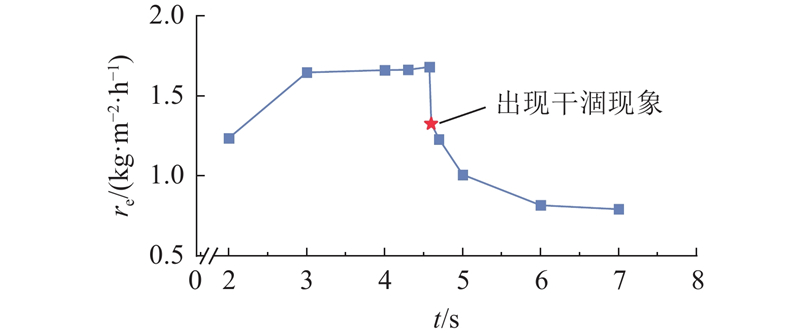
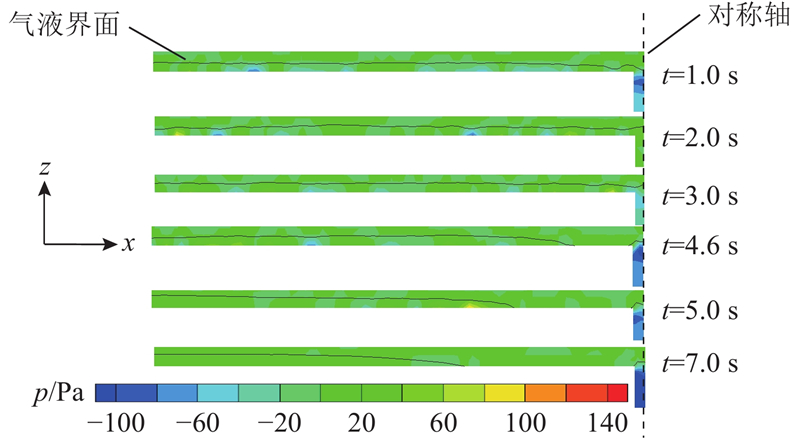
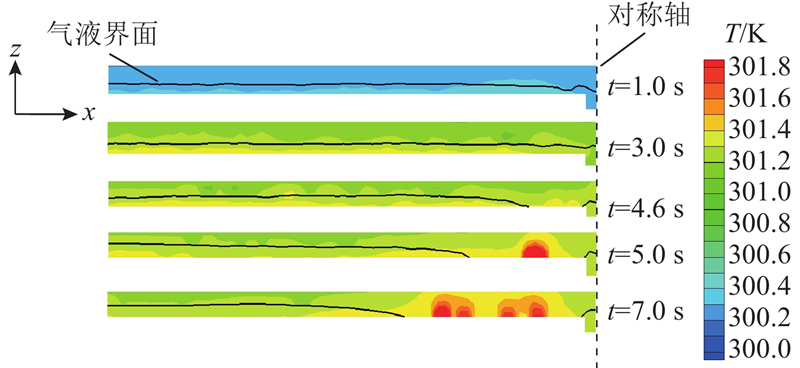
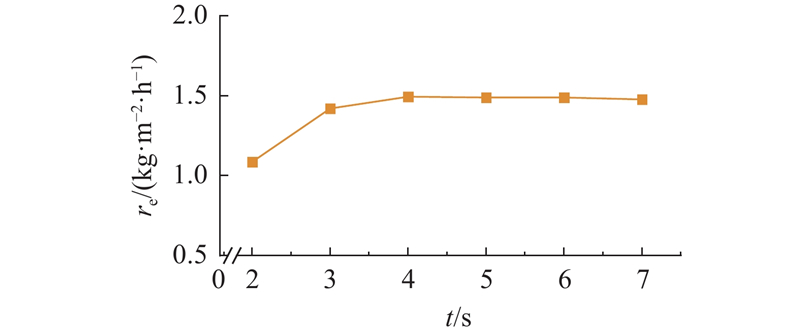
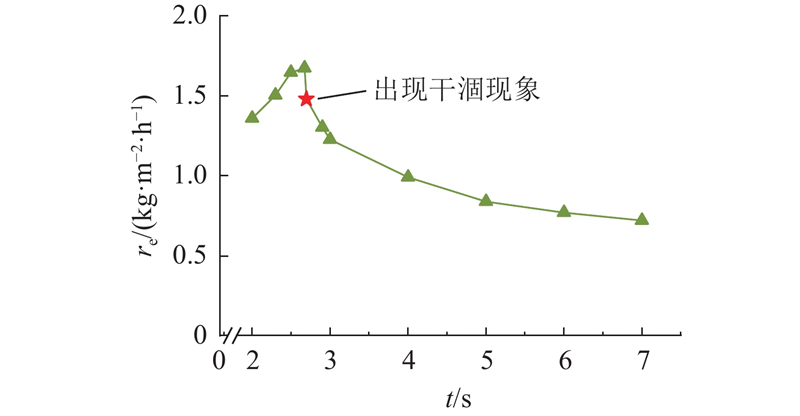
如图6所示为板缝宽度为0.5 mm时蒸发速率随时间的变化曲线. 可以看到,蒸发开始时蒸发速率逐渐增大,t>3 s后趋于稳定,t=4.6 s时蒸发平台上出现干涸现象,蒸发速率逐渐减小. 由如图7所示的气液界面附近以及输水通道内的表压p分布可知,出现干涸现象后,输水通道出口内料液的压力小于外界大气压,料液输运不到蒸发平台,蒸发平台上的液膜不再振荡且料液量减少,导致蒸发速率下降. 出现干涸现象前后,蒸发平台上的温度T分布如图8所示. 可以看出,液膜较薄处(最先出现干涸现象的位置)温度较高,干涸现象出现后,没有液膜的区域温度明显高于液膜内,供水量不足的同时热损失增大. 在料液质量分数和输水通道接触角不变的条件下,板缝宽度为0.4 mm时蒸发过程中液膜铺展变化过程如图9所示. 可以看出,t=2.85 s时蒸发平台上出现干涸现象.
图 6
图 6 板缝宽度为0.5 mm时蒸发速率随时间的变化
Fig.6 Variation of evaporation rate with time at slit width of 0.5 mm
图 7
图 7 蒸发过程中气液界面附近随时间变化的压力云图
Fig.7 Pressure cloud over time near gas-liquid interface during evaporation
图 8
图 8 蒸发平台上的温度分布变化
Fig.8 Changes in temperature distribution on evaporation platform
图 9
图 9 板缝宽度为0.4 mm时蒸发过程中液膜铺展变化
Fig.9 Changes in liquid film spreading during evaporation at slit width of 0.4 mm
图 10
图 10 板缝宽度为0.8 mm时蒸发速率随时间的变化
Fig.10 Variation of evaporation rate with time at slit width of 0.8 mm
图 11
图 11 板缝宽度为0.8 mm时蒸发过程中液膜的动态特性
Fig.11 Dynamic characteristics of liquid film during evaporation at slit width of 0.8 mm
图 12
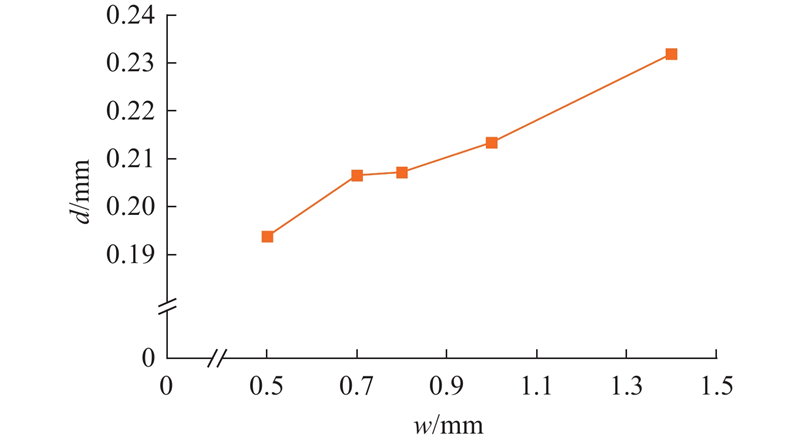
图 12 板缝宽度对液膜厚度的影响 (wB=3.5%)
Fig.12 Effect of slit width on liquid film thickness (wB=3.5%)
图 13
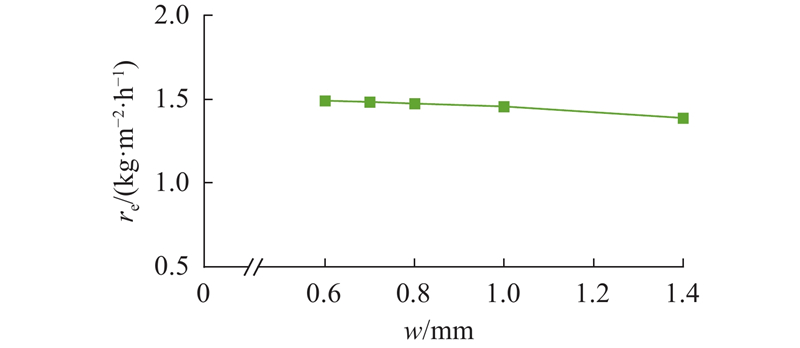
图 13 板缝宽度对蒸发速率的影响 (wB=3.5%)
Fig.13 Effect of slit width on evaporation rate (wB=3.5%)
综上所述,当基底输水量小于蒸发需求时,蒸发界面出现干涸现象,干涸现象出现后蒸发速率显著降低. 在料液质量分数为3.5 %条件下,当板缝宽度w≤0.5 mm时蒸发过程出现干涸现象,当w≥0.6 mm时未出现干涸现象,蒸发速率随板缝宽度的增大而减小,最大蒸发速率对应的板缝宽度在0.5~0.6 mm.
2.2. 料液质量分数影响
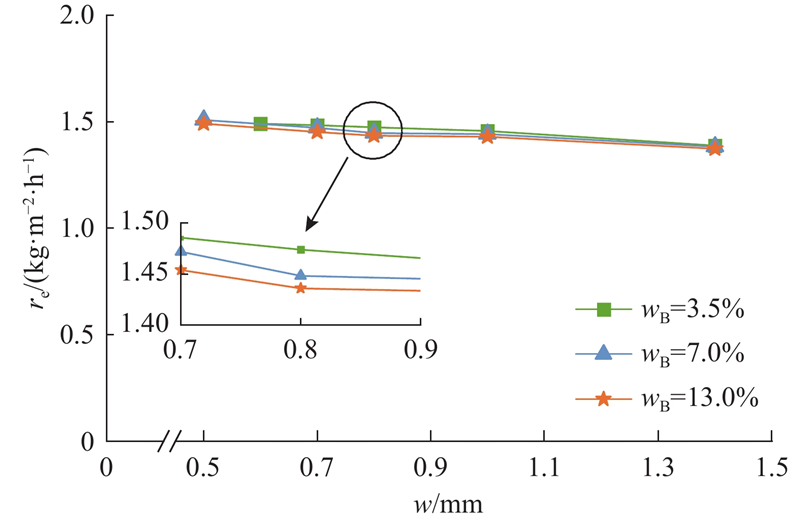
研究当壁面接触角为13°,板缝宽度为0.5 mm时,料液质量分数对板式基底界面蒸发系统蒸发过程的影响,设定料液质量分数分别为0、3.5%、5.0%、7.0%、13.0%. 如图14所示,当板缝宽度为0.5 mm,wB=0时,t=2.7 s时出现干涸现象,液膜与输水通道内的料液相连接时液膜厚度为0.18 mm;如图15所示,蒸发平台上出现干涸现象后蒸发速率逐渐减小. 当wB<3.5%时,t=4.6 s时蒸发过程出现干涸现象;料液质量分数越小,出现干涸现象的时间越早. wB=5.0%、7.0%、13.0%时,没有出现干涸现象,蒸发稳定后蒸发速率分别为1.52、1.51、1.49 kg/(m2·h). 在料液持续供应阶段,液膜厚度基本保持不变,当wB=5.0%、7.0%、13.0%时,液膜平均厚度分别为0.20、0.21、0.22 mm. 随着料液质量分数的增大,蒸发速率逐渐减小,这是由于随着料液质量分数的增大,液膜厚度增大,热阻增大,且料液密度、表面张力、动力黏度都随料液质量分数的增大而增大,水分子间作用力增大,进而蒸发速率越小. 综上所述,当板缝宽度为0.5 mm,wB≤3.5%时蒸发过程出现干涸现象,wB≥5.0%时,没有出现干涸现象,蒸发速率随料液质量分数的增大而减小,最大蒸发速率对应的wB=3.5%~5.0%. 板缝宽度为0.7、0.8、1.0、1.4 mm时,wB=3.5%、7.0%、13.0%的蒸发过程都没有出现干涸现象,板缝宽度越大,料液质量分数越大,液膜越厚,蒸发速率越小,如图16所示.
图 14
图 15
图 16
图 16 不同料液质量分数下蒸发速率随板缝宽度的变化
Fig.16 variation of evaporation rate with slit width for different mass fractions of feed water
系统能量利用率
式中:
式中:
图 17
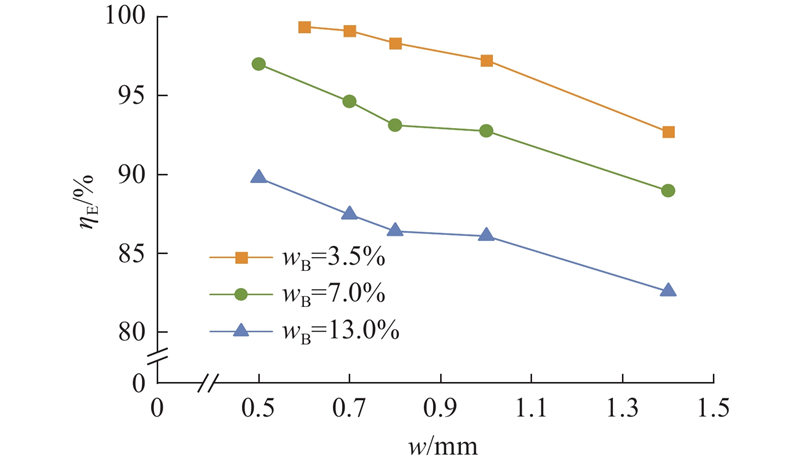
图 17 不同料液质量分数下能量利用率随板缝宽度的变化
Fig.17 variation of energy utilization with slit width for different mass fractions of feed water
3. 结 语
在板式基底结构太阳能界面蒸发研究中,保持输水通道接触角不变,蒸发过程稳定后的蒸发速率随板缝宽度和料液质量分数的减小而增大. 当板缝宽度为0.5 mm,料液质量分数不超过3.5%时,蒸发过程出现干涸现象,出现干涸现象后蒸发速率显著降低;料液质量分数不低于5.0%时,没有出现干涸现象;因此,与最大蒸发速率对应的料液质量分数为3.5%~5.0%,即未发生干涸现象时对应的最小料液质量分数. 当料液质量分数为3.5%,板缝宽度不超过0.5 mm时,蒸发过程出现干涸现象;板缝宽度不小于0.6 mm时,未出现干涸现象;因此,与最大蒸发速率对应的板缝宽度为0.5~0.6 mm. 蒸发过程出现干涸现象后,蒸发速率减小,能量利用率降低,干涸现象严重影响界面蒸发系统的能量利用率;没有干涸现象出现时,能量利用率随着板缝宽度和料液质量分数的增大而减小. 本研究只考虑了输水通道接触角为13°时,不同板缝宽度和料液质量分数对蒸发速率和能量利用率的影响. 输水通道接触角是影响水分输运过程的重要参数,不同输水通道接触角对蒸发性能的影响仍需进一步探讨研究.本研究中界面蒸发系统的水输运通道由2块平行的竖直板构成,导热损失较小,结构简单且容易制备,制造成本低,可进行优化设计,在工程上有较好的应用前景. 在板式基底结构太阳能界面蒸发海水淡化技术的工程应用中,应以获取蒸发稳定后的最大蒸发速率为目标,良好匹配料液质量分数与板缝宽度条件,避开出现干涸现象的工况,获取最优的界面蒸发性能.
参考文献
采用加湿除湿技术处理浓盐水的实验研究
[J].
Experimental study of high salinity water treatment by humidification-dehumidification technology
[J].
A comprehensive review of direct solar desalination techniques and its advancements
[J].DOI:10.1016/j.jclepro.2020.124719 [本文引用: 1]
Scalable fabrication of monolithic porous foam based on cross-linked aromatic polymers for efficient solar steam generation
[J].DOI:10.1016/j.solmat.2019.110111 [本文引用: 1]
Graphene oxide-based efficient and scalable solar desalination under one sun with a confined 2D water path
[J].DOI:10.1073/pnas.1613031113 [本文引用: 1]
Mushrooms as efficient solar steam-generation devices
[J].DOI:10.1002/adma.201606762 [本文引用: 1]
A bioinspired capillary-driven pump for solar vapor generation
[J].DOI:10.1016/j.nanoen.2017.10.039 [本文引用: 1]
High-absorption recyclable photothermal membranes used in a bionic system for high-efficiency solar desalination via enhanced localized heating
[J].DOI:10.1039/C7TA06384A [本文引用: 1]
Fiber-based, double-sided, reduced graphene oxide films for efficient solar vapor generation
[J].DOI:10.1021/acsami.7b07759 [本文引用: 1]
土壤原位热传导修复水-汽-热耦合输运模拟
[J].
Coupled water-vapor-heat transport simulation on in-situ thermal conduction heating remediation of soil
[J].
Exploring ultimate water capillary evaporation in nanoscale conduits
[J].DOI:10.1021/acs.nanolett.7b01620 [本文引用: 1]
Capillary rise of a meniscus with phase change
[J].DOI:10.1016/j.jcis.2008.08.016 [本文引用: 1]
Tuning capillary penetration in porous media: combining geometrical and evaporation effects
[J].DOI:10.1016/j.ijheatmasstransfer.2018.02.101 [本文引用: 2]
Thermophysical properties of seawater: a review of existing correlations and data
[J].
Expressions for the evaporation and condensation coefficients in the Hertz-Knudsen relation
[J].DOI:10.1021/acs.chemrev.5b00511 [本文引用: 1]
Thermophysical properties of seawater: a review and new correlations that include pressure dependence
[J].DOI:10.1016/j.desal.2016.02.024 [本文引用: 1]