坝基的渗流变形和稳定一直是关键的工程问题[1-3]. 坝底基岩包含众多网格状的低序次微小孔隙和数目不多的高序次裂隙,具有典型的孔隙-裂隙结构特征. 孔隙不易压缩,对压力不敏感,渗透能力弱,但具有较强的蓄水能力,在岩体中主要起贮存作用;裂隙易压缩,压敏性较高,渗透能力较强,在岩体中充当渗流通道作用[4-7]. 孔隙和裂隙在尺寸、变形性质和渗透特性中存在显著差异,可根据岩体结构面的分类标准,将孔隙系统归类为Ⅴ级结构面,将裂隙归类为Ⅳ级结构面[8]. 针对上述工程岩体的多尺度特征,Barrenblatt等[4]提出双重孔隙介质概念,在固相刚性条件下建立饱和孔隙-裂隙岩体的渗流耦合方程. Elsworth等[6]应用孔隙和裂隙双有效应力原理直观地反映了孔、裂隙骨架的变形,但没有明确孔隙和裂隙骨架应变的数学定义,根据试验确定的模型参数不符合模型的力学含义. Berryman等[7]唯象地建立了全耦合的线弹性孔隙-裂隙本构模型,该模型参数众多,在实际工程中运用困难. 张玉军[9]在Elsworth等[6]模型的基础上考虑了温度影响,建立孔隙-裂隙岩体多场耦合模型,但没有给出模型参数的取值依据. 上述模型在创建过程中往往基于直觉将单孔介质弹性理论推广到孔隙-裂隙介质中,在建立固相总应变与固相材料应变、孔隙骨架应变和裂隙骨架应变之间的关系时缺少严密的数学推导.
很多学者采用混合物理论来研究饱和孔隙-裂隙介质流固耦合的变形规律,Wilson等[5,10-11]基于混合物理论,直接以组分应力或应变作为状态变量,建立考虑固相变形的流固耦合方程. 这些本构方程的模型参数在工程和试验中难以直接测量,限制了它们在工程中的应用. Borja等[12]基于混合物理论建立孔隙-裂隙非饱和介质的一般本构理论. 在不考虑固流两相材料变形的条件下,Li等[13]推导非饱和孔隙-裂隙膨胀土的外力功表达式,建立非饱和孔隙-裂隙膨胀土的弹塑性本构模型. Guo等[14]在Borja等[12]理论的基础上利用2个固相骨架应变和共轭的2个有效应力建立非饱和孔隙-裂隙土的双有效应力弹塑性模型. 基于嵌套思路,胡亚元[15]建立考虑岩体(固相)材料变形的饱和孔隙-裂隙介质的本构框架,该模型选用的有效应力公式与Terzaghi公式存在较大差异.
本研究1)在小应变条件下,明确孔隙骨架体应变、裂隙骨架体应变、岩块材料体应变的物理含义;基于混合物理论中质量守恒方程,推导固相和流相的应变分解式,揭示流相与固相之间的耦合机理;为了更好地模拟岩体内部各组分之间的相互作用,考虑了更符合工程实际的岩体固相材料变形. 2)将固相骨架体应变、偏斜应变以及固流两相的材料体应变选作本构方程的应变状态变量,推导饱和孔隙-裂隙岩体的能量守恒方程,确定建立本构模型所需的共轭应力状态变量. 3)根据自由能势函数和热力学共轭力学量,建立饱和孔隙-隙岩体的线弹性本构方程,推导模型参数的取值方法.
1. 质量守恒和固流两相应变的分解
1.1. 体积分数和密度
如图1所示,饱和孔隙-裂隙岩体是由岩块固相S、裂隙流相F和孔隙流相P组成的混合物,固体和流体均可压缩. 由于岩体中孔隙和裂隙相互连通,在压力差作用下,孔隙和裂隙中部分流体从孔隙流入裂隙或从裂隙流入孔隙. 假定裂隙流相与孔隙流相间存在质量交换,固相与裂隙和孔隙中的流相不存在质量交换. 令
图 1
1.2. 质量守恒方程
定义固相、孔隙流相和裂隙流相的物质导数为dα(·)/dt. 假定饱和孔隙-裂隙岩体中固相与流相间不存在质量交换,裂隙流相与孔隙流相间存在质量交换,则固相、裂隙流相以及孔隙流相的质量守恒方程分别表示为
式中:t为时间;
1.3. 固流两相应变的分解
在饱和孔隙-裂隙岩体中,裂隙比定义为裂隙体积与固相体积的比值,表达式为
令
由式(11)可知,饱和孔隙-裂隙岩体固相体应变可以分解为裂隙骨架体应变、孔隙骨架体应变与岩块材料体应变.
同理,在小应变条件下,裂隙流相体应变
式(12)、式(13)分别是裂隙流相和孔隙流相体应变的分解式. 由式(11)、式(12)和式(13)可以看出,裂隙骨架体应变和孔隙骨架体应变同时影响固相体应变和流相体应变. 固相、孔隙流相以及裂隙流相之间存在变形耦合效应,这种耦合作用通过裂隙骨架与孔隙骨架之间的变形实现.
2. 本构方程和固结控制方程
2.1. 能量守恒方程
根据混合物理论,令
混合物中应力以拉为正,压力以压为正. 总压力
令
将式(16)等号右边第一项用总平均应力
式中:
2.2. 本构方程
令
根据热力学局部平衡假定,式(18)中的内能可以表示为
其中
引入亥姆霍茨自由能
令饱和孔隙-裂隙岩体混合物的初始平衡状态为
将(22)代入式(21)得到
式中:
式中:
式中:
式(24)、式(25)、式(26)分别为小应变条件下饱和孔隙-裂隙岩体固相、裂隙流相渗入量以及孔隙流相渗入量的本构方程,结合达西定律
3. 模型参数的确定
本研究的饱和孔隙-裂隙岩体水力耦合模型包括以下参数:体积分数
3.1. 完整岩块体积弹性系数的确定
根据文献[15]中式(14)得到饱和孔隙-裂隙岩体中完整岩块的质量守恒方程为
在小应变条件下,
式(31)表明完整岩块的体应变可以分解为岩块材料的体应变和孔隙骨架体应变.
文献[7]的思想实验认为:当围压与裂隙孔压相同(
另一方面,对饱和完整岩块试样单独进行力学试验,测定排水条件下完整岩块的体积模量为
式中:
结合
3.2. 裂隙节理体积弹性系数的确定
在荷载作用下,饱和孔隙-裂隙岩体体应变
对于结构面组数较多,随机定向分布的孔隙-裂隙岩体,通常可以认为是各向同性介质[20]. 因此,裂隙节理变形引起的岩体体应变本构关系为
节理裂隙的法向刚度
3.3. 岩体的剪切弹性系数的确定
令饱和孔隙-裂隙岩体中完整岩块的应变张量为
完整岩块的剪切模量
节理裂隙的剪切模量
将
4. 模型验证
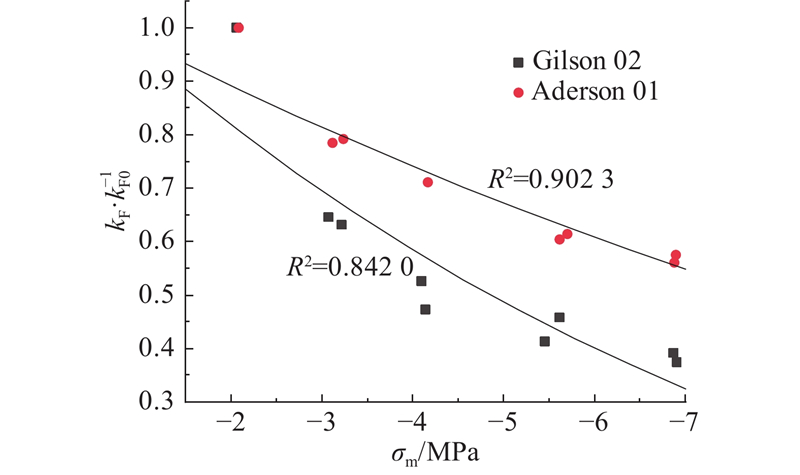
图 2
表 1 模型拟合采用的参数
Tab.1
| 参数 | Anderson 01 | Gilson 02 |
| 裂隙体积分数 | 0.0131[24] | 0.00804[24] |
| 煤块弹性模量 | 1379[24] | 1379[24] |
| 煤块泊松比 | 0.35[24] | 0.35[24] |
| 3×10−4 | 4×10−4 | |
| 9.53×10−4 | 1.1×10−3 | |
| 0.5 | 0.5 |
等式(9)两边对t求积分,得到
将式(45)、
再将式(23b)、式(24)、式(46)、
从图2可以看出,由于压密作用,裂隙体积分数的降低导致渗透率逐渐减小,模型能够较好地拟合试验数据.
5. 一维固结方程及其求解
通过饱和孔隙-裂隙岩体偏斜应变本构方程式(23a)和固相体应变本构方程式(24),推导出一维完全侧限条件下固相本构方程为
式中:
由式(48)、式(49)推导出饱和孔隙-裂隙岩体的固相竖向应力平衡方程为
在一维条件下,
采用厚度
初始条件为
初始孔压
将式(50)两边对
用分离变量法解偏微分方程,得到
式中:
结合边界条件式(53c)、式(53d)、式(58)、式(59),将等式(50)两边在区间
6. 一维固结性状分析
6.1. 不同模型参数取值方法的算例分析
为了直观地展示参数取值方法的理论差异带来的影响,反映岩体固相材料和孔隙骨架变形的影响,以一维固结算例进行比较分析. 饱和孔隙-裂隙岩体深
表 2 完整岩块和节理的力学基本参数
Tab.2
| 参 数 | 数值 |
| 孔隙体积分数 | 0.1,0.05 |
| 形状系数 | 15 |
| 岩块的弹性模量 | 14.4 |
| 岩块材料柔度系数 | 0.025 |
| 孔隙的渗透系数 | 1×10-10 |
| 裂隙渗透系数 | 1×10−7 |
| 岩块泊松比 | 0.2 |
| 节理法向刚度 | 8 |
| 节理间距 | 0.2 |
| 流体材料的柔度系数 | 0.303 |
表 3 饱和孔隙-裂隙岩体的参数
Tab.3
| 参数 | 计算公式 | 数值 | 文献[6]计算公式 | 文献[6]数值 |
| 0.092 | 0.125 | |||
| 0.630 | 0.625 | |||
| 0.033 | — | — | ||
| 0.755 | 0.75 | |||
| 0.123 | 0.125 | |||
| 6 | 6 | |||
| 1.19 | 1.2 | |||
| 0.98 | 0.97 | |||
| 2.631 | 2.627 | |||
| 0.84 | 0.83 | |||
| 式(27) | 1.15×10−4 | 式(27) | 1.19×10−4 | |
| 式(27) | −7.74×10−5 | 式(27) | −1.04×10−4 | |
| 0.12 | 0.17 | |||
| 式(27) | 1.08×10−4 | 式(27) | 1.34×10−4 |
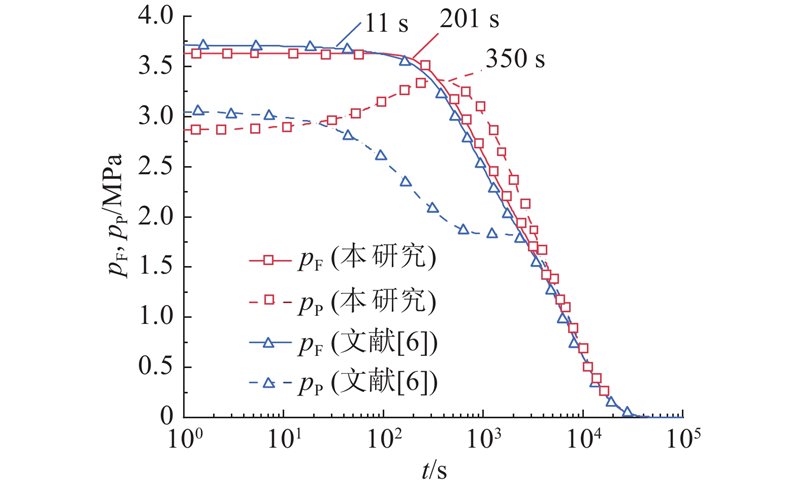
固结过程中基底以下8 m处,按表2、表3中模型参数计算所得的孔隙超孔压和裂隙超孔压的变化情况如图3所示. 可以看出,文献[6]方法计算的初始裂隙超孔压和初始孔隙超孔压分别为3.71 MPa、3.05 MPa,均高于本研究方法计算的3.62 MPa、2.86 MPa. 本研究方法计算得到的裂隙超孔压在均布荷载施加后201 s开始消散,此时孔隙超孔隙压不仅没有下降,反而上升,直到350 s后逐步消散. Khalili[25]认为这是由于裂隙中超孔压消散,荷载从裂隙骨架转移到完整岩块上,体现了孔、裂隙和流体间的微观耦合作用. 相比而言,按照文献[6]方法计算得到的孔隙和裂隙超孔压开始消散时间更接近.
图 3
图 3 不同参数确定方法的孔隙和裂隙超孔压消散
Fig.3 Fracture and pore excess pressure dissipation for different parameter determination methods
如图4所示为2种取值方法对饱和孔隙-裂隙岩体固结沉降的影响. 沉降过程经历3个阶段:缓慢增长、快速增长和沉降稳定,主要受孔隙和裂隙中超孔压消散和固相骨架变形的影响. 固结初期,由于岩体内超孔压较高,且沿深度均匀分布,相邻岩层间超孔压梯度较小,流体很难从排水层排除,沉降处于缓慢增长阶段;随着时间推移,靠近排水层的岩体超孔压率先消散,岩层间超孔压梯度逐渐增大,流体在压力梯度的作用下更易从顶部排水层排除,沉降进入快速增长阶段,直到沉降稳定,固结完成. 由于本研究方法考虑了岩块材料变形的影响,计算的初始沉降量为4.5 mm,大于文献[6]方法计算的初始沉降量(3.03 mm),但总沉降量二者几乎相同.
图 4
图 4 不同参数确定方法的固结沉降
Fig.4 Consolidation settlement for different parameter determination methods
6.2. 模型参数敏感性分析
6.2.1. 渗透系数相对大小的影响
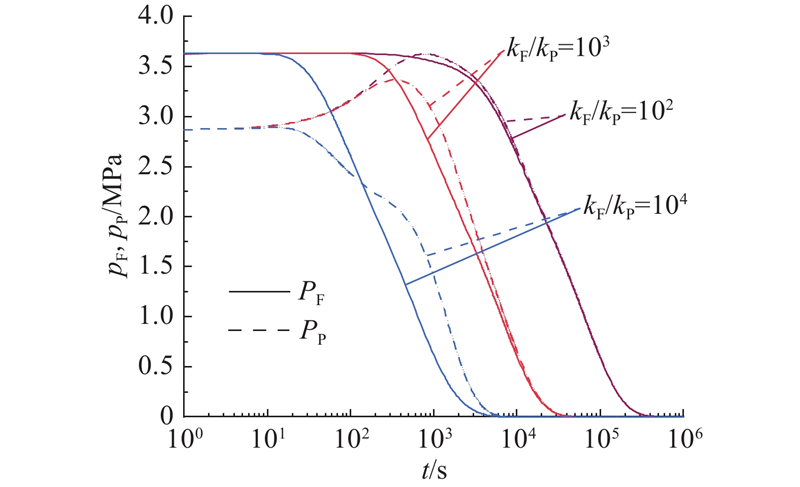
在饱和孔隙-裂隙岩体中,裂隙与孔隙渗透系数的相对大小不仅影响孔隙和裂隙中超孔压的消散,还会影响岩体变形随固结时间变化的规律. 流体交换项
图 5
图 5 不同渗透系数比的裂隙和孔隙超孔压消散图
Fig.5 Diagram of fracture and pore excess pressure dissipation for different permeability coefficient ratios
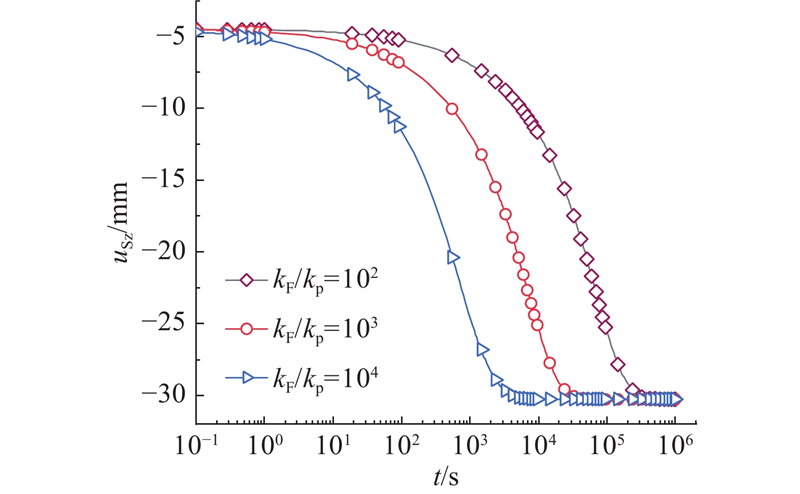
图 6
图 6 不同渗透系数比的固结沉降图
Fig.6 Diagram of consolidation settlement for different permeability coefficient ratios
6.2.2. 形状系数的影响
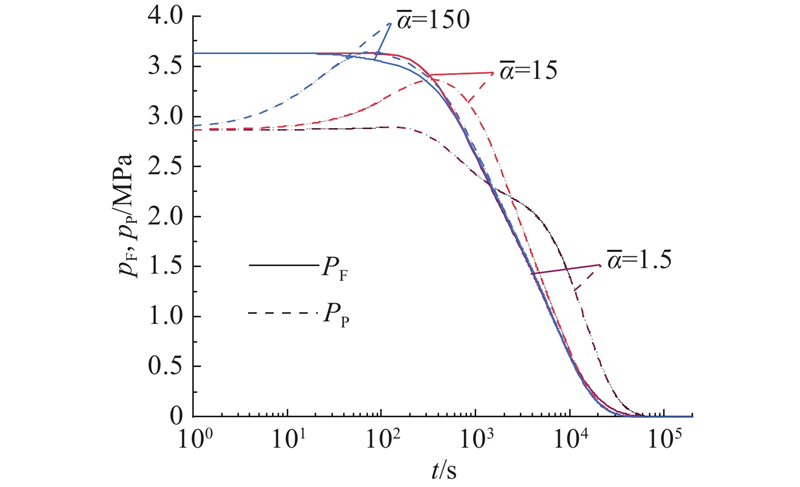
形状系数与正交裂隙的组数和被切割岩块的大小有关,反映孔隙-裂隙中流体相互流动的特性,为此分析形状系数(
图 7
图 7 不同形状系数的裂隙和孔隙超孔压消散图
Fig.7 Diagram of fracture and pore excess pressure dissipation for different shape factors
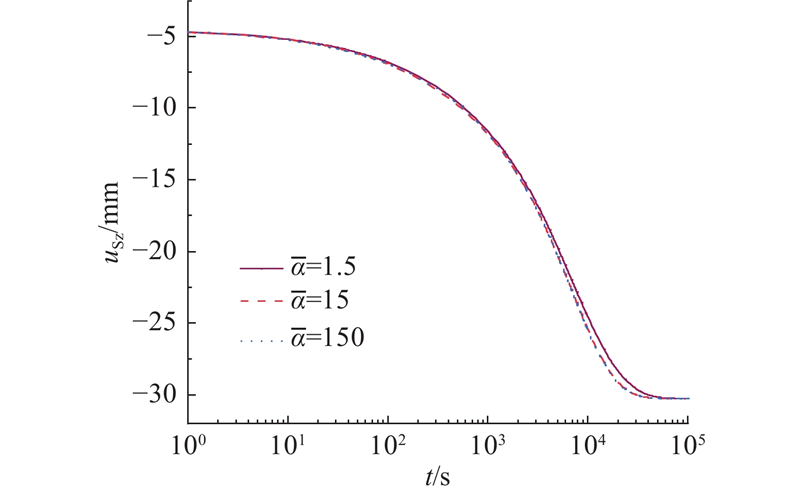
图 8
图 8 不同形状系数的固结沉降图
Fig.8 Diagram of consolidation settlement for different shape factors
7. 结 论
(1)在小应变条件下,固流两相间的耦合作用通过裂隙骨架变形和孔隙骨架变形进行传递和协调;孔隙Terzaghi平均有效应力、裂隙Terzaghi平均有效应力、岩块材料真实压力、固相偏斜应力和流相材料真实压力是建立本构模型需要的应力状态变量.
(2)明确了孔隙、裂隙骨架变形的物理含义,强调了岩块材料的压缩性、岩块基质体积分数对孔隙弹性系数取值,以及孔隙骨架变形对裂隙弹性系数取值的影响,完善了参数的取值方法和理论依据. 一维固结算例表明,按本研究所提参数取值计算的超孔压消散规律以及初始沉降量与按文献[6]参数取值计算的结果差异较大,在岩体中,固相材料变形不可忽略.
(3)一维固结参数敏感性分析表明:1)增大渗透系数比会加快超孔压的消散,提高岩体的固结沉降速度;2)孔隙超孔压比裂隙超孔压对形状系数的变化更敏感,增大形状系数对岩体的固结沉降影响较小.
(4)本研究提出的模型为线性模型,后续计划针对饱和孔隙-裂隙岩体在极端条件下(如高温、高压)的非线性流固耦合行为展开研究.
参考文献
水力耦合裂隙岩体变形破坏机制研究进展
[J].
Research progress of deformation and failure mechanism in fractured rock mass under hydromechanical coupling
[J].
坝基岩体裂隙渗流效应数值模拟方法
[J].
Numerical analysis method of fluid flow in fractured rock mass of dam foundation
[J].
多孔连续介质渗透压力对变形应力影响的数值模拟方法探讨
[J].
Study on numerical simulation method used in analyzing the effect of seepage pressure in continuous medium with pores on deformation and stress
[J].
Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks
[J].DOI:10.1016/0021-8928(60)90107-6 [本文引用: 3]
On the theory of consolidation with double porosity
[J].DOI:10.1016/0020-7225(82)90036-2 [本文引用: 1]
Flow-deformation response of dual-porosity media
[J].DOI:10.1061/(ASCE)0733-9410(1992)118:1(107) [本文引用: 24]
The elastic coefficients of double-porosity models for fluid transport in jointed rock
[J].DOI:10.1029/95JB02161 [本文引用: 3]
遍有节理岩体的双重孔隙-裂隙介质热-水-应力耦合模型及有限元分析
[J].
Coupled thermo-hydro-mechanical model and finite element analyses of dual-porosity fractured medium for ubiquitous-joint rock mass
[J].
Multiporosity multipermeability approach to the simulation of naturally fractured reservoirs
[J].DOI:10.1029/92WR02746 [本文引用: 1]
Constitutive modeling of hydromechanical coupling in double porosity media based on mixture coupling theory
[J].DOI:10.1061/IJGNAI.GMENG-7731 [本文引用: 1]
On the effective stress in unsaturated porous continua with double porosity
[J].DOI:10.1016/j.jmps.2009.04.014 [本文引用: 4]
Work input analysis for soils with double porosity and application to the hydromechanical modeling of unsaturated expansive clays
[J].DOI:10.1139/cgj-2015-0574 [本文引用: 1]
Modelling of dilatancy-controlled gas flow in saturated bentonite with double porosity and double effective stress concepts
[J].DOI:10.1016/j.enggeo.2018.07.002 [本文引用: 1]
基于嵌套思路的饱和孔隙-裂隙介质本构理论
[J].
Constitutive theory of saturated pore-fracture media based on nested way
[J].
Coupling model of saturated fissured porous media based on porosity-dependent skeleton strains and nesting concept
[J].DOI:10.1016/j.compgeo.2022.104942 [本文引用: 2]
岩石细观裂隙组构的平面测定方法
[J].
Determination of mesoscopic crack fabric for rock on plan
[J].
岩石裂隙渗流特性试验研究的新进展
[J].DOI:10.3321/j.issn:1000-6915.2008.12.001 [本文引用: 1]
New advances in experimental study on seepage characteristics of rock fractures
[J].DOI:10.3321/j.issn:1000-6915.2008.12.001 [本文引用: 1]
基于微流控芯片模型的渗流实验与数值模拟
[J].
Seepage experiment and numerical simulation based on microfluidic chip model
[J].
Engineering rock mechanics: an introduction to the principles
[J].
Intrinsic material constants of poroelasticity
[J].DOI:10.1016/j.ijrmms.2021.104754 [本文引用: 1]
Gas seepage in underground coal seams: application of the equivalent scale of coal matrix-fracture structures in coal permeability measurements
[J].DOI:10.1016/j.fuel.2020.119641 [本文引用: 2]
Coupling effects in double porosity media with deformable matrix
[J].