浙江大学学报(工学版)

浙江大学学报(工学版), 2024, 58(7): 1407-1416 doi: 10.3785/j.issn.1008-973X.2024.07.010

交通工程、土木工程

基于多重分形的改进GRU滑坡位移预测模型

徐满,, 张冬梅, 余想, 李江,, 吴益平

1. 中国地质大学（武汉） 计算机学院，湖北 武汉 430074

2. 湖北省自然资源厅 信息中心，湖北 武汉 430071

3. 中国地质大学（武汉） 工程学院，湖北 武汉 430074

Improved GRU landslide displacement prediction model based on multifractal

XU Man,, ZHANG Dongmei, YU Xiang, LI Jiang,, WU Yiping

1. School of Computer Science, China University of Geosciences (Wuhan), Wuhan 430074, China

2. Information Center, Department of Natural Resources of Hubei Province, Wuhan 430071, China

3. Faculty of Engineering, China University of Geosciences (Wuhan), Wuhan 430074, China

通讯作者: 李江，男，教授级高工. orcid.org/0000-0002-1650-9747. E-mail：johnlee1124@126.com

收稿日期: 2023-06-26  

基金资助: 国家自然科学基金联合基金重点支持项目（U1911205）；湖北省自然资源厅科技项目（ZRZY2024KJ22）.

Received: 2023-06-26  

Fund supported: 国家自然科学基金联合基金重点支持项目（U1911205）；湖北省自然资源厅科技项目（ZRZY2024KJ22）.

作者简介 About authors

徐满（2001—），男，硕士生，从事时序预测研究.orcid.org/0009-0002-9741-8181.E-mail：xuman@cug.edu.cn , E-mail：xuman@cug.edu.cn

摘要

门控机制设计难以学习序列变化趋势，导致传统记忆网络模型对滑坡位移非平稳跃变段预测效果较差. 基于多重分形改进门控循环单元（GRU），通过量化序列的变化特征来动态更新门控权重，引入循环神经网络单元的状态融合策略以学习数据的长程相关性特征. 采用变分模态分解算法将滑坡累积位移分解成趋势项、周期项及随机项，利用改进GRU进行位移分量的训练和预测. 选取三峡库区白水河滑坡监测点ZG93、ZG118进行仿真实验. 实验结果表明，相比传统预测模型，新模型的滑坡位移形变趋势特征学习能力更强，预测精度更高.

关键词： 滑坡累积位移 ; 多重分形 ; 门控循环单元(GRU) ; 变分模态分解 ; 循环神经网络

Abstract

The traditional memory network model has poor prediction accuracy on a non-stationary mutation data segment due to the gate mechanism has difficulty in learning sequence change trends. A multifractal algorithm was introduced to improve the gating control of the gated recurrent unit (GRU), and dynamically update the gating weight by quantifying the change characteristics of the sequence. The state fusion of the recurrent neural network unit was introduced to learn the long-range correlation of data. The landslide cumulative displacement was decomposed into trend term, periodic term and random term through the variational mode decomposition algorithm. The decomposed terms were trained and predicted by using the improved GRU. The monitoring points ZG93 and ZG118 of the Baishuihe landslide in the Three Gorges Reservoir area were selected for simulation experiments. Experimental results show that compared with traditional models, the new model learns the characteristics of the landslide displacement deformation trend better and has a higher prediction accuracy.

Keywords： landslide cumulative displacement ; multifractal ; gated recurrent unit (GRU) ; variational mode decomposition ; recurrent neural network

PDF (2282KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

徐满, 张冬梅, 余想, 李江, 吴益平. 基于多重分形的改进GRU滑坡位移预测模型. 浙江大学学报(工学版)[J], 2024, 58(7): 1407-1416 doi:10.3785/j.issn.1008-973X.2024.07.010

XU Man, ZHANG Dongmei, YU Xiang, LI Jiang, WU Yiping. Improved GRU landslide displacement prediction model based on multifractal. Journal of Zhejiang University(Engineering Science)[J], 2024, 58(7): 1407-1416 doi:10.3785/j.issn.1008-973X.2024.07.010

滑坡是受自然地质作用和人类活动因素影响的自然灾害，具有突发性强、危害性大的特点. 根据滑坡的变形-时间曲线特征，滑坡可分为振荡型、直线型和阶跃型，受汛期连续降雨及库水位周期性调度的双重影响，三峡库区内部分滑坡累积位移-时间监测曲线整体上呈现阶跃型动态演化形态[1-3]. 阶跃型滑坡位移的变化是自身地质条件和外界因素共同作用的结果，阶跃型滑坡的预测是非线性非稳态时序预测问题，将位移数据分解为不同尺度后对各分量进行预测叠加可提高总体预测精度，因此在滑坡累积位移预测中数据分解和预测模型构建是研究关键[4].

受自身地质条件、周期性降雨、库水位调度及其他因素影响，滑坡累积位移序列具有不同尺度时序特征. 张俊等[5]利用移动平均法将滑坡累积位移分解成趋势项位移和周期项位移，采用支持向量机(support vector machine, SVM)模型预测周期项位移，由于模型未考虑滑坡演化的动态特征且未能分解出随机项，导致阶跃型滑坡变形期预测误差较大. Xu等[6]提出基于经验模态分解与长短时记忆神经网络(long short-term memory，LSTM)的滑坡位移动态预测模型，进行滑坡位移动态特性和时序数据长期关联特征提取，但经验模态分解会导致位移序列在某些时间步的趋势误差较大. 徐峰等[7]针对经验模态分解和集合经验变分模态分解对滑坡位移序列的分解不可控性问题，使用变分模态分解(variational mode decomposition，VMD)将滑坡位移分解为具有不同尺度特征与实际意义的位移分量. 陈伟等[8]提出基于门控循环单元(gated recurrent unit，GRU)的预测模型，分别预测了基于指数平滑法得到的趋势项和周期项位移分量，该方法在提升预测精度的同时提高了模型的训练效率. 传统指数平滑、移动平均法虽然能分解出物理意义明确的趋势项和周期项，但不能分解出随机项[9-10]；小波分解难以确定小波基和阈值[11]；经验模态分解、集合经验模态分解无法明确各位移分量与实际物理意义的联系[12-13].

受内外因素影响，阶跃型滑坡在变形演化过程中稳定状态和跃变状态交替出现，位移曲线整体呈非线性、非平稳式变化特征[14]. 深度神经网络作为高度复杂的非线性系统，具有处理非平稳数据的优势[15]. 传统循环神经网络（recurrent neural network，RNN）模型存在长期依赖问题[16]， LSTM在RNN基础上增加了细胞状态、输入门、输出门及遗忘门，通过控制信息的传递，LSTM能够较大程度提升长序列处理中信息的表达能力[17]. GRU是在LSTM的基础上将门结构简化，模型的训练效率得到提升[18]. 上述模型的内部门控组件过于简单，门控机制设计难以学习序列变化趋势，对阶跃型滑坡数据台阶状跃变段预测效果较差. 多重分形理论通过计算概率测度求解奇异性指数刻画数据的变化程度，能够较好描述非平稳滑坡位移的变化趋势[19]. 为了自适应学习跃变段数据的变化特征，本研究采用多重分形及状态融合技术对GRU门控机制进行改进，提出新的基于多重分形和状态融合的改进门控循环单元的滑坡位移预测模型(multifractal-statefusion-GRU, MF-SF-GRU)，在门控设计中引入多重分形谱宽量化数据的变化程度，设置新的动态调整矩阵代替传统更新门权重矩阵，各隐藏单元将随时间步进行状态融合. 新的设计加强更新门的记忆能力，可根据谱宽自适应调整权重，学习到由库水位调整、季节性降雨引起的滑坡位移跃变特征. 在循环单元中，各时间步不仅记忆前一层的隐藏层状态，还利用卷积神经网络逐步融合隐藏层的状态来学习滑坡位移数据的历史特征. 本研究将以三峡库区库岸堆积层滑坡白水河滑坡为例，在系统分析外界诱发影响因素的基础上，采用VMD将滑坡位移数据分解为具有不同物理意义与尺度的趋势项、周期项和随机项位移分量，利用MF-SF-GRU对分解的累积位移分量分别进行预测.

1. 相关理论

1.1. 变分模态分解

受季节性降雨和库水位调度影响，滑坡累积位移表现为周期性递增的非平稳时间序列. 滑坡内部的地质条件如岩性、地形地貌为趋势性因素，季节性降雨和库水位调度为周期性因素，非季节性降雨、库水临时调度为随机性因素. 如何对多尺度、多因素非平稳时间序列原始数据进行拆分和预测是滑坡位移预测任务研究的关键. VMD是时间-频率信号分解方法，核心思想是构建和求解变分问题，实现非平稳、非线性的信号处理，具体包括以下过程. 1）构建约束变分问题：将输入的原始信号$ {f_t} $分解成$ K $个分量，对应的约束变分模型表达式为

$ \left. {\begin{array}{*{20}{c}} {\mathop {\min}\limits_{ \left\{ {{\omega _k}} \right\},\left\{ {{u_k}} \right\}} \left\{ {\displaystyle\mathop \sum \nolimits_{k=1}^K \left\| {\partial f/\partial t\left[ {\left( {\delta \left( t \right)+\dfrac{{\mathrm{j}}}{{{\text{π}} t}}} \right){\text{*}}{u_k}\left( t \right)} \right]{{\mathrm{e}}^{ - {\mathrm{j}}{\omega _k}t}}} \right\|_2^2} \right\}.} \\ {{\mathrm{s.t.}}\;\;\displaystyle\mathop \sum \nolimits_{k = 1}^K {u_k} = f(t).} \end{array}} \right\} $
(1)

式中：$ \delta (t) $为狄拉克函数，$\{ {u_k}\} 、\{ {\omega _k}\} $分别为分解后$ k $个分量和中心频率集合，$*$表示卷积运算. 2）求解变分问题：为了求解构建的约束变分模型，引入二次惩罚因子$\beta $和拉格朗日乘法算子$\lambda (t)$将约束性问题转为非约束性问题，增广拉格朗日表达式为

$ \begin{split}& L\left( {\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\},\lambda } \right) = \\&\quad \beta \mathop \sum \nolimits_{k=1}^K \left\| {\partial f/\partial t\left[ {\left( {\delta \left( t \right)+\frac{{\mathrm{j}}}{{{\text{π}} t}}} \right){u_k}\left( t \right)} \right]{{\mathrm{e}}^{ - {\mathrm{j}}{\omega _k}t}}} \right\|_2^2+ \\&\quad \left\| {f\left( t \right) - \mathop \sum \nolimits_{k=1}^K {u_k}\left( t \right)} \right\|_2^2+\left\langle {\lambda \left( t \right),f\left( t \right) - \mathop \sum \nolimits_{k=1}^K {u_k}\left( t \right)} \right\rangle . \end{split} $
(2)

引入交替方向乘子法，结合傅里叶等距变换寻求增广拉格朗日函数的解，

$ \mathop \sum \nolimits_{k=1}^K \frac{{\left\| {u_k^{n+1} - u_k^n} \right\|_2^2}}{{\left\| {u_k^n} \right\|_2^2}} < \varepsilon . $
(3)

${u_k}$、${\omega _k}$、$\lambda $更新，直到满足式（3）则停止迭代. 最终得到最优解，即各分量${u_k}$.

1.2. 门控循环单元

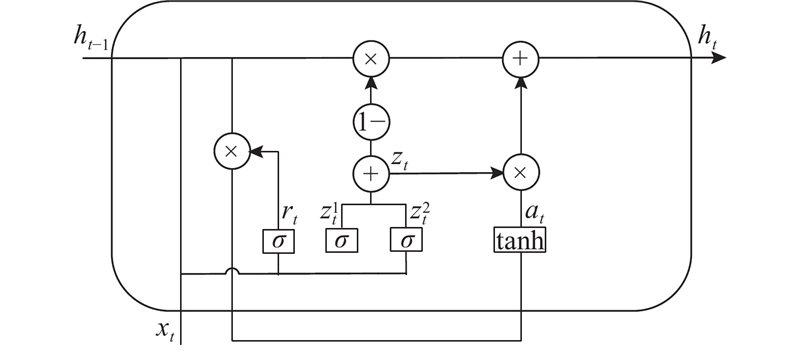
GRU将LSTM中的输入门和遗忘门合并为更新门，简化模型内部结构. 如图1所示，GRU网络模型由多个同构的单元组成，利用重置门、更新门更新隐藏层状态实现长程信息记忆. GRU隐含层状态在时刻t的传递过程为

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   门控循环单元的原理图

Fig.1   Principles of gated recurrent unit


$ {z_t} = \sigma \left( {{{\boldsymbol{W}}_{\text{z}}}\left[ {{h_{t - 1}},{x_t}} \right]+{{\boldsymbol{b}}_{\mathrm{z}}}} \right), $
(4)

$ {r_t} = \sigma \left( {{{\boldsymbol{W}}_{\text{r}}}\left[ {{h_{t - 1}},{x_t}} \right]+{{\boldsymbol{b}}_{\mathrm{r}}}} \right), $
(5)

$ {a_t} = {\mathrm{tanh}}\;\left( {{{\boldsymbol{W}}_{\text{a}}}\left[ {{r_t} \odot {h_{t - 1}},{x_t}} \right]+{{\boldsymbol{b}}_{\mathrm{a}}}} \right), $
(6)

$ {h_t} = {h_{t - 1}}\odot (1 - {z_t})+{z_t}\odot{a_t}. $
(7)

式中：${z_t}、{r_t}$分别为更新门、重置门在时刻t的计算结果，$ {h_{t - 1}}、{h_t} $分别表示时刻$(t - 1)$和时刻$t$的输出，$\odot $表示矩阵对应元素相乘，$ {{\boldsymbol{W}}_{\text{z}}}、{{\boldsymbol{W}}_{\mathrm{r}}}、{{\boldsymbol{W}}_{\mathrm{a}}} $为网络的权重矩阵，${{\boldsymbol{b}}_{\mathrm{z}}}、{{\boldsymbol{b}}_{\mathrm{r}}}、{{\boldsymbol{b}}_{\mathrm{a}}}$为偏置向量.

1.3. 多重分形

多重分形理论以计算序列区间概率测度求解区间奇异性指数，奇异性指数的分布区间可用于刻画非平稳数据段的变化程度.

1.3.1. 概率测度

对$k$维空间${{\bf{R}}^k}(k = 1,2, \cdots ,n)$用尺度为$w$的窗口进行等分，则第$i$个边长为$w$窗口的概率测度表示为

$ {P_i}\left( w \right) = {I_i}\left( w \right)/\mathop \sum \limits_{i = 0}^N {I_i}\left( w \right). $
(8)

式中：${I_i}\left( w \right)$表示窗口大小为$w$时第$i$个区间内所有样品值之和.

1.3.2. 奇异性指数

奇异性指数$\alpha $控制概率测度的奇异性，第$i$个窗口的奇异性指数的表达式为

$ {\alpha _i} = \frac{{\ln {P_i}\left( w \right)}}{{\ln w}}. $
(9)

${\alpha _i}$的大小反映窗口所划分区间测度的概率大小，分布在有限区间$\left[ {{\alpha _{{\mathrm{min}}}},{\alpha _{{\mathrm{max}}}}} \right]$内，$ - \infty \leqslant {\alpha _{{\mathrm{min}}}} \leqslant {\alpha _{{\mathrm{max}}}} \leqslant + \infty $、${\alpha _{{\mathrm{min}}}}$和$ {\mathrm{\alpha }}_{\mathrm{max}} $分别对应变量在空间中分布的奇异性的下限和上限. 把分形上具有相同$\alpha $值的单元的个数记为${N_\alpha }\left( w \right)$，

$ {N_\alpha }\left( w \right) \propto {w^{ - f\left( \alpha \right)}}. $
(10)

式中：$f(\alpha )$为多重分形谱.

1.3.3. 多重分形谱

$f(\alpha )$表示具有相同$\alpha $值的子集分形维数,

$ f\left( \alpha \right) = \mathop {\lim }\limits_{w \to 0} \frac{{\ln {N_\alpha }\left( w \right)}}{{\ln w}}. $
(11)

对于第$i$个窗口大小为w的区间，对应着奇异性集合$\{ {\alpha _i}\} $，谱宽大小表示为

$ \Delta {\alpha _i} = {\mathrm{max}}\left( {{\alpha _i}} \right) - {\mathrm{min}}\left( {{\alpha _i}} \right). $
(12)

$\Delta {\alpha _i}$反映分形结构在概率测度分布上的不均匀程度，用于刻画非平稳时序数据的变化程度. $\Delta {\alpha _i}$越大表示该区间内时序数据分布越不均匀，变化越剧烈.

2. 滑坡位移时序预测模型

传统记忆网络模型缺少学习序列变化趋势的门控机制，导致滑坡跃变数据段预测效果较差. 本研究基于多重分形对GRU进行改进，利用多重分形量化数据变化程度，设置新的动态调整矩阵代替传统更新门权重矩阵. 针对传统循环神经网络历史信息的利用率较低问题，本研究提出循环神经网络的状态融合策略.

2.1. 基于多重分形的改进门控循环单元

研究表明GRU门控中更新门对模型性能影响最大[20]. 当前记忆网络模型的门控组件在训练过程中随机性较强，难以学习非平稳突变特征，影响预测效果，为此引入基于多重分形谱谱宽的改进权重矩阵代替传统更新门权重矩阵，设计MF-GRU. MF-GRU将GRU中的更新门权重矩阵拆分为2个新的更新门矩阵，分别与经激活函数处理后的多重分形谱谱宽矩阵$\sigma \left( {\boldsymbol{E}} \right)$和$\left( {{\boldsymbol{1}} - \sigma \left( {\boldsymbol{E}} \right)} \right)$相乘得到临时门控输出，如图2所示. MF-GRU隐含层状态在时刻$t$将临时更新门输出结果相加得到整体更新门，使用整体更新门代替GRU中的更新门参与计算，其他更新规则与GRU保持一致，对应门控更新公式表示为

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   基于多重分形的改进门控循环单元结构图

Fig.2   Structure of improved gated recurrent unit based on multifractal


$ z_t^1 = \sigma \left( {{{\boldsymbol{W}}_{{\mathrm{z}}1}}\left[ {{h_{t - 1}},{x_t}} \right] \odot \sigma \left( {\boldsymbol{E}} \right)+{{\boldsymbol{b}}_{{\mathrm{z}}1}}} \right), $
(13)

$ z_t^2 = \sigma \left( {{{\boldsymbol{W}}_{{\mathrm{z}}2}}\left[ {{h_{t - 1}},{x_t}} \right] \odot \left( {{\boldsymbol{1}} - \sigma \left( {\boldsymbol{E}} \right)} \right)+{{\boldsymbol{b}}_{{\mathrm{z}}2}}} \right), $
(14)

$ {z_t} = z_t^1+z_t^2. $
(15)

式中：$z_t^1、z_t^2$均为临时更新门，${{\boldsymbol{W}}_{{\rm{z}}1}},{{\boldsymbol{W}}_{{\rm{z}}2}}$均为临时更新门矩阵，${\boldsymbol{E}}$为输入数据的多重分形谱的谱宽矩阵. 新设计的MF-GRU加强了GRU中更新门的记忆能力，能根据多重分形谱谱宽值自适应调整权重.

2.2. 循环神经网络状态融合策略

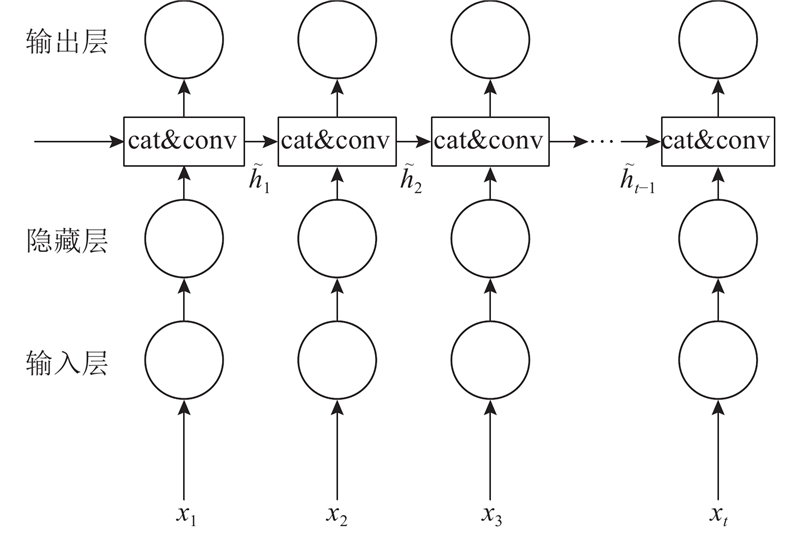
循环神经网络隐藏层输入不仅与当前时间点输入层的输出有关，还与前一时间点隐藏层的输出有关. 各类循环神经网络设计没有考虑历史时间点状态对当前时间点状态的影响，本研究提出改进的循环神经网络状态融合策略. 如图3所示，状态融合的主要思路是利用卷积神经网络对各时间点隐藏层的状态进行融合，以更好地学习到数据长程相关性. 当前时刻隐藏层状态不仅输出到下一时刻，还与下一时刻隐藏层的输出进行融合，随着时间的迭代逐步输出到下一层，循环神经网络隐藏层状态的融合得以实现. 隐藏状态的更新表达式为

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   循环神经网络状态融合

Fig.3   State fusion of recurrent neural network


$ {\tilde h_t} = {\mathrm{conv}}\left( {{\mathrm{cat}}\left( {{{\tilde h}_{t - 1}},{h_t}} \right)} \right). $
(16)

式中：${\tilde h_t}$为时刻t经过循环神经网络状态融合策略隐藏层的输出结果，$ \mathrm{c}\mathrm{a}\mathrm{t}\;(\cdot) $表示指定维度上的拼接操作，$ \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}\;(\cdot) $表示卷积核大小为1的卷积操作.

2.3. 滑坡位移预测流程

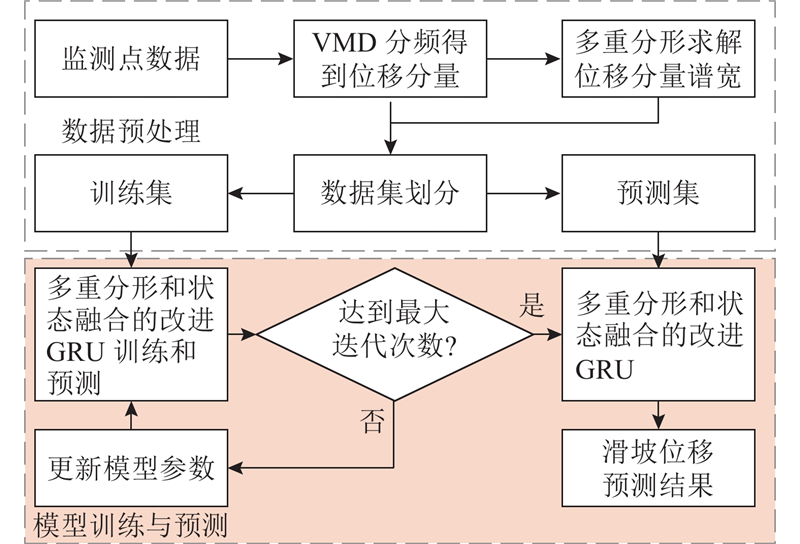
MF-SF-GRU的滑坡位移预测流程如图4所示，主要包括数据预处理、模型训练与预测. VMD将滑坡累积位移数据分解成趋势项、周期项、随机项等位移分量，结合多重分形算法提取各位移分量的变化特征，基于状态融策略逐步融合隐藏层的状态，利用多重分形和状态融合的改进GRU构建滑坡时序预测模型，对各位移分量进行预测并叠加来实现滑坡累积位移预测.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   滑坡位移预测流程图

Fig.4   Flow chart of landslide displacement prediction


3. 白水河滑坡位移预测

3.1. 白水河地质概况及滑坡位移分析

三峡库区白水河滑坡位于湖北省宜昌市秭归县沙镇溪镇，白水河滑坡上设置有11个GPS地表位移监测点，自2003年6月份起，采用GPS、雨量计监测技术对滑坡地表累积位移、降雨量进行长期监测，该区域地质概况及具体监测点分布如图5所示. 在这11个监测点中，监测点ZG118、ZG93的监测周期最长、数据较为完整，且位于滑坡中部，能够较好反映整个滑坡位移演变过程，因此主要针对这2个监测点数据开展相关研究.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   白水河滑坡地质概况图[4]

Fig.5   Geological overview map of Baishuihe landslide[4]


3.2. 评价指标

选取判定系数$ {R^2} $、均方根误差RMSE以及平均绝对百分比误差MAPE作为评价指标对模型预测效果进行评价，各评价指标的计算式分别为

$ {R^2} = 1 - \frac{{\displaystyle\mathop \sum \nolimits_{i = 1}^n {{\left( {{y_i} - {{\hat y}_i}} \right)}^2}}}{{\displaystyle\mathop \sum \nolimits_{i = 1}^n {{\left( {{y_i} - \bar y} \right)}^2}}}, $
(17)

$ {\mathrm{RMSE}} = \sqrt {\frac{{\displaystyle\mathop \sum \nolimits_{i = 1}^n {{\left( {{y_i} - {{\hat y}_i}} \right)}^2}}}{n}} , $
(18)

$ {\mathrm{MAPE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^n \frac{{\left| {{y_i} - {{\hat y}_i}} \right|}}{{\left| {{y_i}} \right|}}. $
(19)

式中：$n$为样本总数，${\hat y_i}$为预测值，${y_i}$为真实值，$ \bar y $为真实值的算术平均值. 白水河滑坡位移监测数据与降雨和库水位相关性较大[21]，为了进一步分析降雨量和库水位的周期性影响，设置不同大小的输入窗口，计算MF-SF-GRU对序列分解得到周期项预测结果的RMSE，结果如表1所示. 由表可知，将三峡水库水位调度和降雨的周期均设为12时，均方根误差最小，因此训练将样本时间步长设置为12，即用前12天的数据对第13天进行预测[22]，使用MSE作为损失函数，tanh作为输出层激活函数，Adam方法作为参数优化算法，其余实验参数设置如表2所示.

表 1   不同输入窗口设置下预测结果的均方根误差

Tab.1  Root mean square error of prediction results under different input window settings

序列长度RMSE/mm序列长度RMSE/mm
60.0896140.1346
80.0844160.0852
100.0836180.0885
120.0809——

新窗口打开| 下载CSV


表 2   对比试验参数设置

Tab.2  Comparative experiment parameter settings

参数取值参数取值
VMD分量数k3迭代次数1200
批处理数量256学习率0.001
隐藏层节点数64隐藏层层数1

新窗口打开| 下载CSV


3.3. 滑坡位移数据分析

3.3.1. 累计位移数据分析

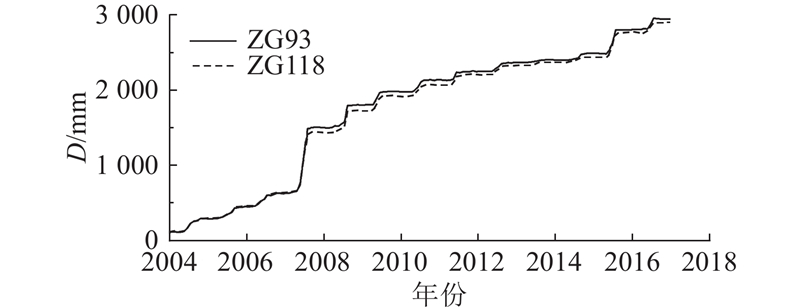
受滑坡自身基础地质构造及工程活动、降雨等外界因素作用，白水河滑坡各监测点位移-时间曲线具有明显阶跃变化特征，ZG93和ZG118的累积位移$D$随时间变化曲线如图6所示.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   不同监测点的累积位移-时间曲线图

Fig.6   Cumulative displacement-time curves for different monitoring points


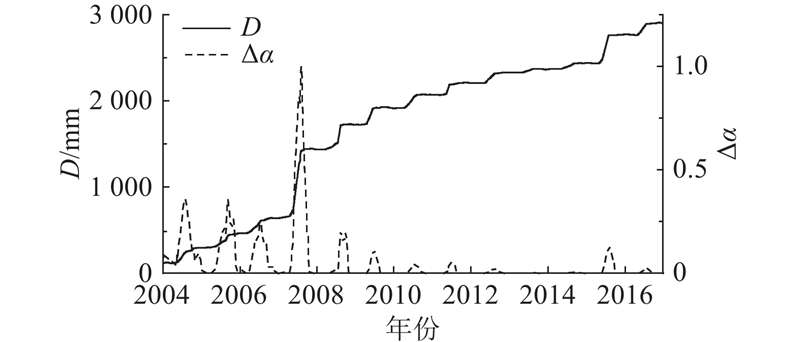
以ZG118为例，研究采用多重分形量化该监测点位移变化，累积位移、谱宽$\Delta \alpha $随时间变化的曲线如图7所示. 由图可知，监测初期滑坡位移变化相对平稳，计算的滑坡位移多重分形谱宽趋于0；季节性降雨（如每年5月到9月）导致库水位急剧下降，改变了坡体的容重、滑带土强度，人工调控库水位改变岩体的物理力学性质、坡体结构（如2004年7月滑坡发生变形导致房屋毁坏，2005年8月地表出现下拉式裂缝，2007年6月预警区发生较大规模的坍塌），监测点累积位移-时间曲线呈台阶状跃变，谱宽-时间曲线变化幅度剧烈，变化区间为[0.2, 1.0]；监测后期滑坡内部地质构造和物理结构逐渐适应库水位和降雨引起的变化，滑坡变形趋于稳定（如2008年9月到2009年4月），谱宽又逐渐趋于0. 综上所述，多重分形谱谱宽参数能够较好刻画监测点滑坡位移的变化程度，度量滑坡状态交替演变过程.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   监测点ZG118的累积位移-时间曲线、谱宽-时间曲线

Fig.7   Cumulative displacement-time curve and spectral width-time curve for monitoring point ZG118


3.3.2. 滑坡位移数据分解

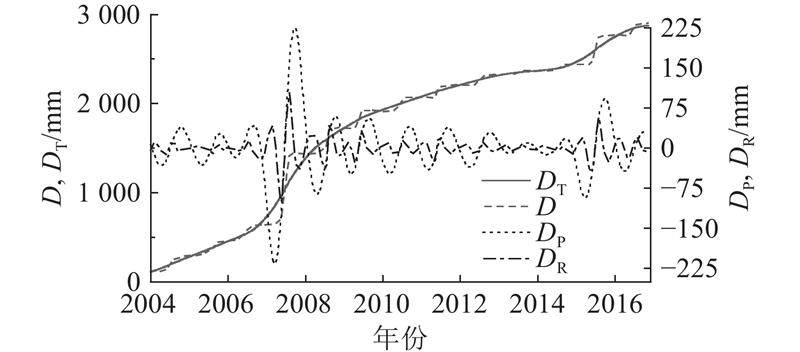
如图8所示，基于滑坡累积位移-时间曲线分析，通过VMD将滑坡累积位移分解成3个位移分量，即趋势${D_{\mathrm{T}}}$、周期${D_{\mathrm{P}}}$及随机项$ {D_{\mathrm{R}}} $. 趋势项位移分量主要与滑坡的内部地质条件有关，周期项位移分量的主要影响因素是季节性降雨和库水位周期调度，随机项位移分量与非季节性降雨等随机性因素有关.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   监测点ZG118的滑坡位移分量-时间曲线

Fig.8   Curves of landslide displacement component-time for monitoring point ZG118


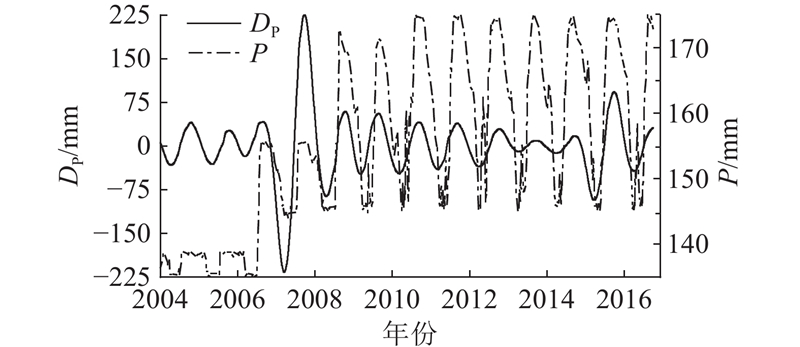
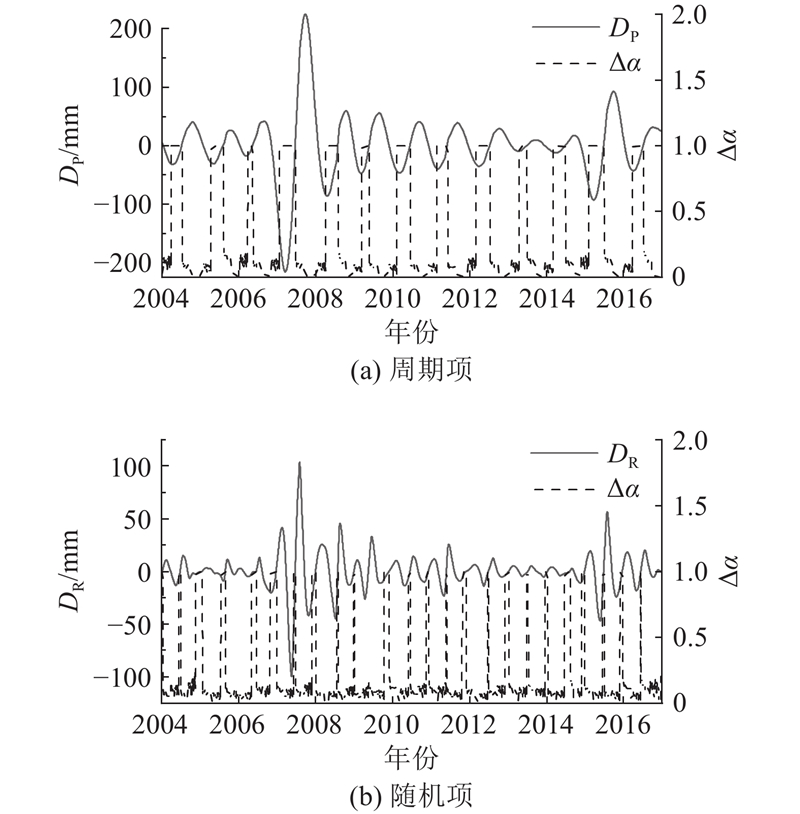
季节性降雨及库水位调度是导致滑坡累积位移周期性阶跃变化的主导因素，位移快速增长往往发生在汛期降雨和库水位调度之后，具有较强的周期性，但库水位变化对滑坡位移变化的影响滞后. 以ZG118为例，库水位P-时间曲线、累积位移周期项-时间曲线如图9所示，每年5月到9月随季节性降雨，库水位调度导致库水位急剧下降，一段时间后滑坡位移周期项发生突变式增长. 如图10(a)所示，累积位移周期项与谱宽变化趋势基本同步，谱宽能较好刻画库水位调度引起的滑坡位移周期变化特征，位移突变数据段谱宽值均较大，趋近于1，变化相对平稳数据段谱宽变化较小，区间为[0, 0.3]. 非季节性降雨是影响随机项位移的主导因素，如图10(b)所示，随机项变化剧烈段谱宽值趋于1，相对平稳数据段谱宽值区间为[0, 0.2]，谱宽能够刻画受外界随机因素导致的随机变化特征. 因此将多重分形引入GRU刻画滑坡位移数据的变化特征和趋势，用谱宽控制、更新门控权重的自适应调整，提高预测精度.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   监测点ZG118的库水位-时间曲线、周期项-时间曲线

Fig.9   Reservoir water level-time curve and periodic term-time curve for monitoring point ZG118


图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   监测点ZG118周期项、随机项及对应谱宽随时间变化的曲线

Fig.10   Curves of periodic term, random term and corresponding spectral width with time at monitoring point ZG118


3.4. 滑坡位移预测

以三峡库区白水河库岸堆积层滑坡为研究对象，选取2004年1月到2009年11月ZG93、ZG118的数据作为训练集，2009年12月到2011年10月ZG93、ZG118的数据作为预测集. 为了进一步验证MF-SF-GRU的有效性和实用性，对比分析多重分形改进GRU模型和传统深度学习模型RNN、LSTM、GRU.

3.4.1. 分频位移预测

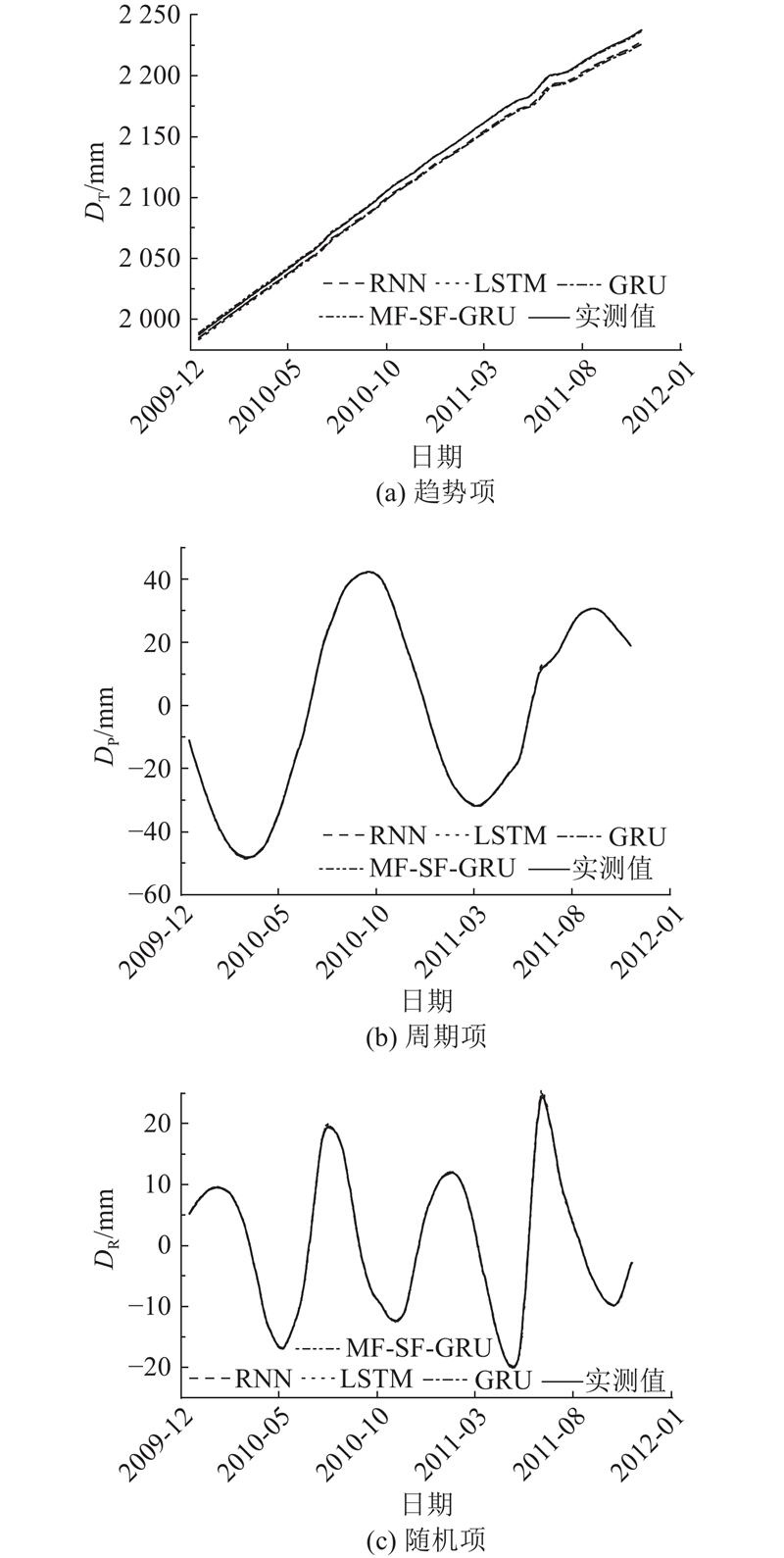
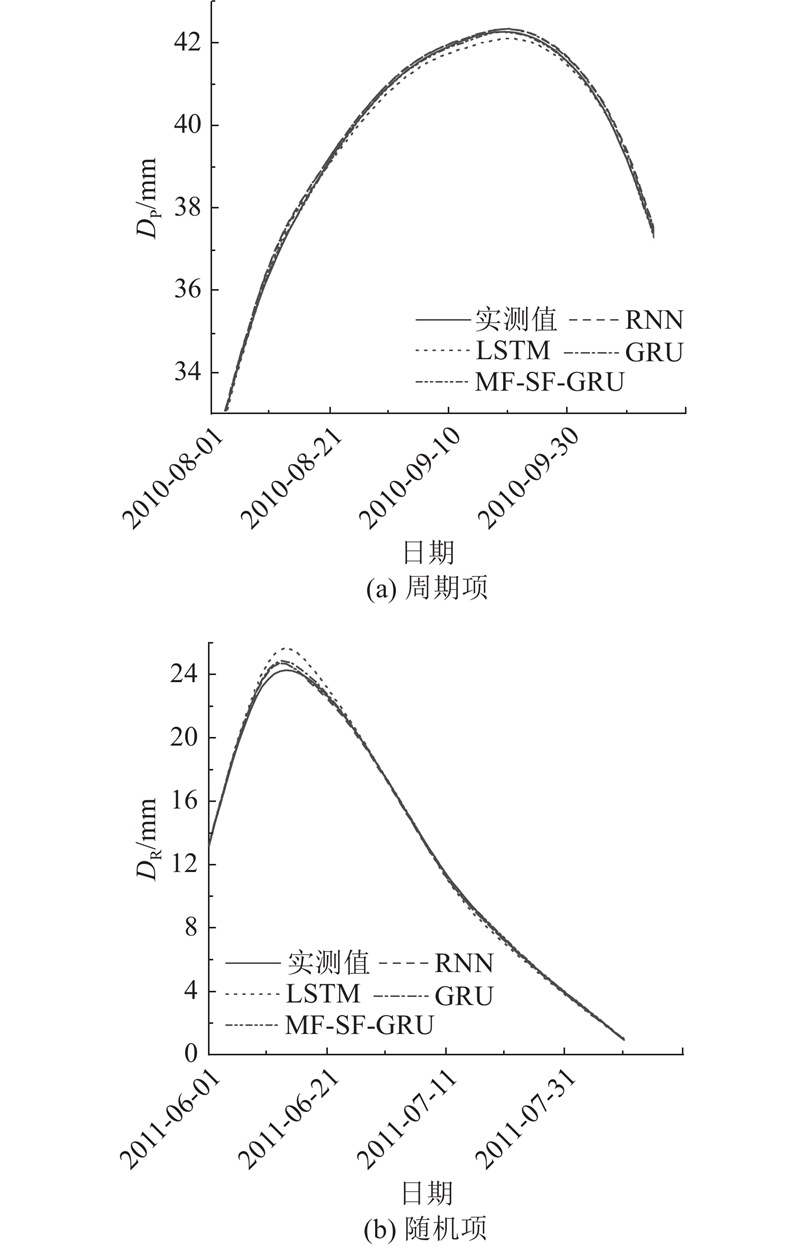
滑坡位移周期项预测选取库水位和降雨量作为影响因素，随机项预测选取降雨量作为影响因素，ZG93各位移分量预测结果如图11所示. 分别绘制2010年8月到10月的周期项位移曲线、2011年6月到8月的随机项位移曲线如图12所示，受降雨和库水位调度的影响区段滑坡位移变化较为剧烈，各模型预测情况如表3所示. 在周期项的预测方面，RNN、LSTM、GRU的预测效果较差，MF-SF-GRU由于引入多重分形加强了更新门的记忆能力，同时影响因素与预测量强相关，根据谱宽自适应调整权重学习到库水位调整和季节性降雨引起的跃变与时滞特征，突变数据段的预测效果有明显提升. 在随机项预测方面，非季节性降雨是影响预测的主导因素，但随机性较大，干扰了门控单元长时序特征的记忆能力，因此随机项预测效果提升不大.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   不同模型滑坡位移分量的预测曲线

Fig.11   Prediction curves of different models for landslide displacement components


图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   不同模型在突变数据段的周期项、随机项预测曲线

Fig.12   Prediction curves of different models for periodic term and random term in mutation data segment


表 3   不同模型的滑坡位移分量预测精度及误差

Tab.3  Prediction accuracy and error of landslide displacement components for different models

模型名称位移分量ZG93ZG118
$ {R}^{2} $RMSE/mmMAPE$ {R}^{2} $RMSE/mmMAPE
RNN趋势项0.992 796.287 050.002 7740.999 932.133 970.002 884
周期项0.999 980.129 220.011 5070.999 930.258 550.020 789
随机项0.999 940.083 460.011 1830.999 720.179 330.014 161
LSTM趋势项0.990 287.302 500.003 3170.988 838.230 300.003 849
周期项0.999 950.198 840.011 3590.999 760.478 830.040 156
随机项0.999 580.229 680.109 0910.998 180.460 150.155 724
GRU趋势项0.989 887.451 830.003 2460.991 477.192 230.003 231
周期项0.999 980.121 790.006 5910.999 530.667 300.057 643
随机项0.999 910.108 200.035 7210.999 840.134 400.016 579
MF-SF-GRU趋势项0.999 870.851 840.000 3460.999 781.142 170.000 433
周期项0.999 990.074 580.004 7570.999 990.061 810.008 133
随机项0.999 950.080 110.023 1860.999 950.075 120.009 470

新窗口打开| 下载CSV


3.4.2. 累积位移预测

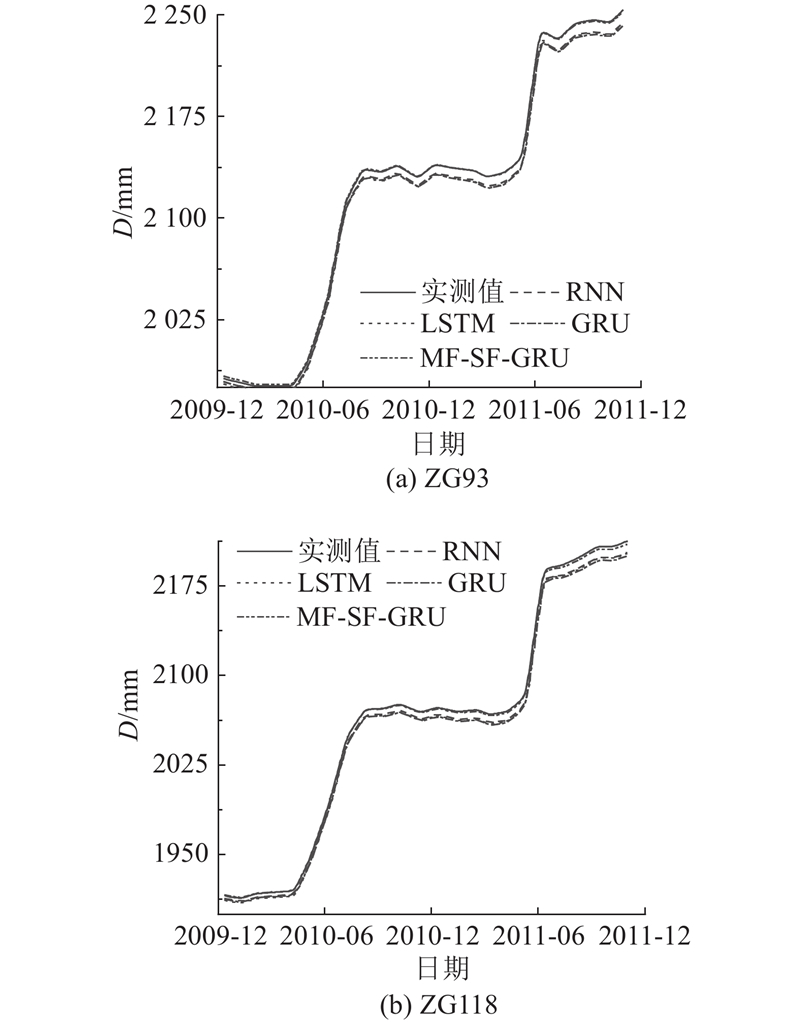
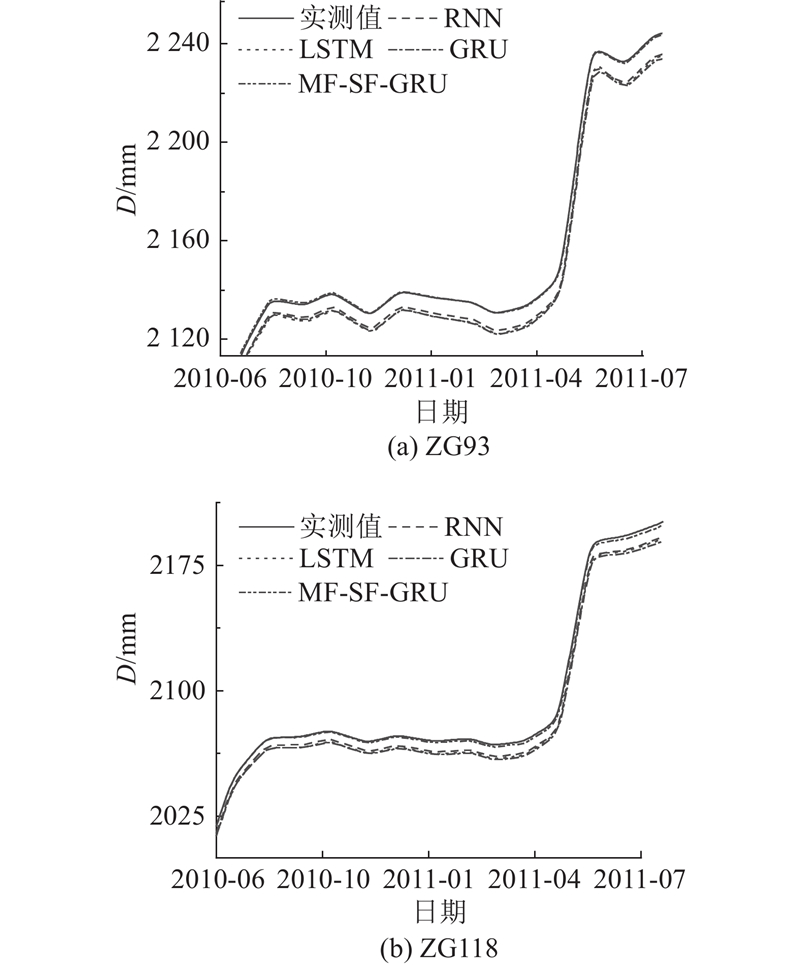
根据时序加法模型将各位移分量预测值叠加得到滑坡累积位移预测值，ZG93和ZG118累积位移的整体数据段和突变数据段如图13、图14所示. 可以看出，RNN、LSTM、GRU在滑坡变化平稳数据段2010年4月到2010年7月，2011年4月到2011年7月预测较为准确，但在滑坡变化较为剧烈的2010年7月到2011年4月，2011年7月到2011年10月突变数据段预测效果较差，说明传统记忆网络模型对非平稳突变数据预测能力较弱. MF-SF-GRU引入多重分形谱，谱宽自适应调整权重，提高了突变数据段的预测能力，特别在2010年7月到12月预测效果较好. 各模型预测精度如表4所示，部分突变数据段2010年7月到2011年4月预测精度如表5所示. 可以看出，RNN、 LSTM、GRU的预测精度相近. 以ZG118为例，较GRU，MF-SF-GRU在整体数据段上RMSE从7.951 10 mm降到1.175 09 mm，$ {R^2} $从0.993 08提高到0.999 85；在部分突变数据段上RMSE从7.280 73 mm下降到0.757 12 mm，$ {R^2} $从0.526 95提升到0.994 88. MF-SF-GRU利用门控机制挖掘影响因素和分频数据的历史信息，多重分形谱宽的引入进一步提高模型学习跃变的能力，历史状态的融合进一步提取数据的历史特征，整体上看，MF-SF-GRU的预测精度是4个模型中最高的.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   不同模型累积位移整体数据段预测曲线

Fig.13   Prediction curves for overall data segment of cumulative displacement with different models


图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   不同模型累积位移突变数据段预测曲线

Fig.14   Prediction curves for mutation data segment of cumulative displacement with different models


表 4   不同模型的累积位移预测精度及误差

Tab.4  Prediction accuracy and error of cumulative displacement for different models

模型名称ZG93ZG118
R2RMSE/mmMAPER2RMSE/mmMAPE
RNN0.995 386.196 620.002 7230.995 786.211 990.002 776
LSTM0.993 527.335 840.003 3360.994 117.339 750.003 401
GRU0.993 367.427 080.003 2280.993 087.951 100.003 557
MF-SF-GRU0.999 910.856 160.000 3490.999 851.175 090.000 437

新窗口打开| 下载CSV


表 5   不同模型部分突变数据段的累积位移预测精度及误差

Tab.5  Prediction accuracy and error of cumulative displacement for partial mutation data segment with different models

模型名称ZG93ZG118
R2RMSE/mmMAPER2RMSE/mmMAPE
RNN0.772 095.797 980.002 6900.715 175.649 480.002 697
LSTM0.656 667.116 380.003 3160.570 336.938 820.003 401
GRU0.674 736.926 570.003 2060.526 957.280 730.003 334
MF-SF-GRU0.998 110.528 220.000 1920.994 880.757 120.000 314

新窗口打开| 下载CSV


4. 结　语

受自身地质条件、降雨、库水位调度的影响，三峡库区部分滑坡呈阶跃式非稳态变化. 在系统分析滑坡位移诱发因素的基础上，本研究引入VMD将滑坡位移数据划分为趋势项、周期项和随机项. 针对滑坡位移预测任务中传统网络对跃变数据段预测效果较差的问题，采用多重分形度量滑坡位移的累积位移变化趋势；新设置动态调整矩阵，根据多重分形谱谱宽自适应调整更新门权重学习滑坡位移跃变趋势，改进GRU的更新门控机制. 针对传统循环神经网络历史信息的利用率较低问题，提出循环神经网络状态融合策略. 以三峡库区白水河滑坡监测点ZG93、ZG118为例，多重分形谱谱宽参数能较好刻画由降雨、库水位调度引起的滑坡位移变化趋势，度量滑坡的演变状态. 实验结果表明，与传统模型相比，MF-SF-GRU能够较好地刻画滑坡位移跃变状态时的变化趋势，有效提高预测精度和实用性. MF-SF-GRU通过动态调整更新门权重矩阵学习滑坡累积位移变化趋势，通过循环单元的历史状态融合学习到数据的长程相关性，后续工作计划采用更为简单的模型结构（如最小门控单元）进行模型改进，以提高模型的训练效率.

参考文献

叶润青, 付小林, 郭飞, 等

三峡水库运行期地质灾害变形特征及机制分析

[J]. 工程地质学报, 2021, 29 (3): 680- 692

[本文引用: 1]

YE Runqing, FU Xiaolin, GUO Fei, et al

Deformation characteristics and mechanism analysis of geological hazards during operation period of Three Gorges Reservoir

[J]. Journal of Engineering Geology, 2021, 29 (3): 680- 692

[本文引用: 1]

李骅锦, 许强, 何雨森, 等

“阶跃式” 滑坡位移预测及阈值分析的 ARMA-(LASSO-ELM)-Copula模型

[J]. 岩石力学与工程学报, 2017, 36 (Suppl.2): 4075- 4084

LI Huajin, XU Qiang, HE Yusen, et al

An ARMA-(LASSO-ELM)-Copula farmework for landslide displacement prediction and threshold computing of the displacement of step-like landslides

[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36 (Suppl.2): 4075- 4084

许强, 汤明高, 徐开祥, 等

滑坡时空演化规律及预警预报研究

[J]. 岩石力学与工程学报, 2008, 27 (6): 1104- 1112

DOI:10.3321/j.issn:1000-6915.2008.06.003      [本文引用: 1]

XU Qiang, TANG Minggao, XU Kaixiang, et al

Research on space-timeevolution laws and early warning-prediction of landslides

[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27 (6): 1104- 1112

DOI:10.3321/j.issn:1000-6915.2008.06.003      [本文引用: 1]

李麟玮, 吴益平, 苗发盛, 等

基于变分模态分解与 GWO-MIC-SVR 模型的滑坡位移预测研究

[J]. 岩石力学与工程学报, 2018, 37 (6): 1395- 1406

[本文引用: 3]

LI Linwei, WU Yiping, MIAO Fasheng, et al

Displacement prediction of landslides based on variational mode decomposition and GWO-MIC-SVR model

[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37 (6): 1395- 1406

[本文引用: 3]

张俊, 殷坤龙, 王佳佳, 等

基于时间序列与 PSO-SVR 耦合模型的白水河滑坡位移预测研究

[J]. 岩石力学与工程学报, 2015, 34 (2): 382- 391

[本文引用: 1]

ZHANG Jun, YIN Kunlong, WANG Jiajia, et al

Displacement prediction of Baishuihe landslide based on time series and PSO-SVR model

[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34 (2): 382- 391

[本文引用: 1]

XU S, NIU R

Displacement prediction of Baijiabao landslide based on empirical mode decomposition and long short-term memory neural network in Three Gorges area, China

[J]. Computers and Geosciences, 2018, 111: 87- 96

DOI:10.1016/j.cageo.2017.10.013      [本文引用: 1]

徐峰, 范春菊, 徐勋建, 等

基于变分模态分解和 AMPSO-SVM 耦合模型的滑坡位移预测

[J]. 上海交通大学学报, 2018, 52 (10): 1388- 1395

[本文引用: 1]

XU Feng, FAN Chunju, XU Jianxun, et al

Displacement prediction of landslide based on variational mode decomposition and AMPSO-SVM coupling model

[J]. Journal of Shanghai Jiao Tong University, 2018, 52 (10): 1388- 1395

[本文引用: 1]

陈伟, 雷帮军, 黄海峰

基于门控循环单元的滑坡位移预测和灾害预警方法

[J]. 长江信息通信, 2021, 34 (5): 19- 21

DOI:10.3969/j.issn.1673-1131.2021.05.006      [本文引用: 1]

CHEN Wei, LEI Bangjun, HUANG Haifeng

Landslide displacement prediction and disaster early warning method based on gated recurrent unit

[J]. Changjiang Information and Communication, 2021, 34 (5): 19- 21

DOI:10.3969/j.issn.1673-1131.2021.05.006      [本文引用: 1]

黄发明, 殷坤龙, 杨背背, 等

基于时间序列分解和多变量混沌模型的滑坡阶跃式位移预测

[J]. 地球科学, 2018, 43 (3): 887- 898

[本文引用: 1]

HUANG Faming, YIN Kunlong, YANG Beibei, et al

Step-like displacement prediction of landslide based on time series decomposition and multivariate chaos model

[J]. Earth Science, 2018, 43 (3): 887- 898

[本文引用: 1]

徐峰, 汪洋, 杜娟, 等

基于时间序列分析的滑坡位移预测模型研究

[J]. 岩石力学与工程学报, 2011, 30 (4): 746- 751

[本文引用: 1]

XU Feng, WANG Yang, DU Juan, et al

Study of displacement prediction model of landslide based on time series analysis

[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30 (4): 746- 751

[本文引用: 1]

朱治军, 李后强

小波分析在分形科学中的应用

[J]. 应用基础与工程科学学报, 1994, 2 (4): 275- 281

[本文引用: 1]

ZHU Zhijun, LI Houqiang

Application of wavelet analysis in fractals

[J]. Journal of Applied Basic and Engineering Science, 1994, 2 (4): 275- 281

[本文引用: 1]

林大超, 安凤平, 郭章林, 等

滑坡位移的多模态支持向量机模型预测

[J]. 岩土力学, 2011, 32 (Suppl.1): 451- 458

[本文引用: 1]

LIN Dachao, AN Fengping, GUO Zhanglin, et al

Prediction of landslide displacements through multimode support vector machine model

[J]. Rock and Soil Mechanics, 2011, 32 (Suppl.1): 451- 458

[本文引用: 1]

邓冬梅. 基于集合经验模态分解的水库库岸滑坡阶跃型位移预测研究[D]. 武汉: 中国地质大学, 2018.

[本文引用: 1]

DENG Dongmei. Study of stepwise displacement prediction for reservoir landslides based on ensemble empirical mode decomposition [D]. Wuhan: China University of Geosciences, 2018.

[本文引用: 1]

李麟玮, 吴益平, 苗发盛, 等

考虑变形状态动态切换的阶跃型滑坡位移区间预测方法

[J]. 岩石力学与工程学报, 2019, 38 (11): 2272- 2287

[本文引用: 1]

LI Linwei, WU Yiping, MIAO Fasheng, et al

Displacement interval prediction method for step-like landslides considering deformation state dynamic switching

[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38 (11): 2272- 2287

[本文引用: 1]

易利容, 王绍宇, 殷丽丽, 等

基于多变量 LSTM 的工业传感器时序数据预测

[J]. 智能计算机与应用, 2018, 8 (5): 13- 16

DOI:10.3969/j.issn.2095-2163.2018.05.003      [本文引用: 1]

YI Lirong, WANG Shaoyu, YIN Lili, et al

Forecasting of industrial sensor time series based on multivariable LSTM

[J]. Intelligent Computer and Applications, 2018, 8 (5): 13- 16

DOI:10.3969/j.issn.2095-2163.2018.05.003      [本文引用: 1]

HOCHREITER S. Untersuchungen zu dynamischen neuronalen Netzen [D]. Munich: Technical University of Munich, 1991. HOCHREITER S. Investigations on dynamic neural networks [D]. Munich: Technical University of Munich, 1991.

[本文引用: 1]

HOCHREITER S, SCHMIDHUBER J

Long short-term memory

[J]. Neural Computation, 1997, 9 (8): 1735- 1780

DOI:10.1162/neco.1997.9.8.1735      [本文引用: 1]

CHO K, VAN MERRIËNBOER B, GULCEHRE C, et al. Learning phrase representations using RNN encoder–decoder for statistical machine translation [C]/ / Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing . Doha: Association for Computational Linguistics, 2014: 1724–1734.

[本文引用: 1]

管孝艳, 杨培岭, 吕烨

基于多重分形理论的农田土壤特性空间变异性分析

[J]. 应用基础与工程科学学报, 2011, 19 (5): 712- 720

DOI:10.3969/j.issn.1005-0930.2011.05.003      [本文引用: 1]

GUAN Xiaoyan, YANG Peiling, LV Ye

Analysis on spatial variability of soil properties based on multifractal theory

[J]. Journal of Basic Science and Engineering, 2011, 19 (5): 712- 720

DOI:10.3969/j.issn.1005-0930.2011.05.003      [本文引用: 1]

ZHOU, G B, WU J, ZHANG C L, et al

Minimal gated unit for recurrent neural networks

[J]. International Journal of Automation and Computing, 2016, 13 (3): 226- 234

DOI:10.1007/s11633-016-1006-2      [本文引用: 1]

张振坤, 张冬梅, 李江, 等

基于多头自注意力机制的LSTM-MH-SA滑坡位移预测模型研究

[J]. 岩土力学, 2022, 43 (Suppl.2): 477- 486

[本文引用: 1]

ZHANG Zhenkun, ZHANG Dongmei, LI Jiang, et al

LSTM-MH-SA landslide displacement prediction model based on multi-head self-attention mechanism

[J]. Rock and Soil Mechanics, 2022, 43 (Suppl.2): 477- 486

[本文引用: 1]

刘艺梁, 殷坤龙, 汪洋, 等

基于经验模态分解和神经网络的滑坡变形预测研究

[J]. 安全与环境工程, 2013, 20 (4): 14- 17

DOI:10.3969/j.issn.1671-1556.2013.04.004      [本文引用: 1]

LIU Yiliang, YIN Kunlong, WANG Yang, et al

Study of landslide deformation prediction based on EMD and neural network

[J]. Safety and Environmental Engineering, 2013, 20 (4): 14- 17

DOI:10.3969/j.issn.1671-1556.2013.04.004      [本文引用: 1]

/

〈 〉