[1]
刘近贞, 叶方方, 熊慧 基于卷积神经网络的多类运动想象脑电信号识别
[J]. 浙江大学学报: 工学版 , 2021 , 55 (11 ): 2054 - 2066
[本文引用: 1]
LIU Jinzhen, YE Fangfang, XIONG Hui Recognition of multi-class motor imagery EEG signals based on convolutional neural network
[J]. Journal of Zhejiang University: Engineering Science , 2021 , 55 (11 ): 2054 - 2066
[本文引用: 1]
[2]
ALTAHERI H, MUHAMMAD G, ALSULAIMAN M, et al Deep learning techniques for classification of electroencephalogram (EEG) motor imagery (MI) signals: a review
[J]. Neural Computing and Applications , 2023 , 35 : 14681 - 14722
DOI:10.1007/s00521-021-06352-5
[本文引用: 1]
[3]
ANG K K, CHIN Z Y, ZHANG H, et al. Filter bank common spatial pattern (FBCSP) in brain-computer interface [C]// 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence) . Hong Kong: IEEE, 2008: 2390–2397.
[本文引用: 1]
[4]
SALAMI A, ANDREU-PEREZ J, GILLMEISTER H EEG-ITNet: an explainable inception temporal convolutional network for motor imagery classification
[J]. IEEE Access , 2022 , 10 : 36672 - 36685
DOI:10.1109/ACCESS.2022.3161489
[本文引用: 1]
[5]
SCHIRRMEISTER R T, SPRINGENBERG J T, FIEDERER L D J, et al Deep learning with convolutional neural networks for EEG decoding and visualization
[J]. Human Brain Mapping , 2017 , 38 (11 ): 5391 - 5420
DOI:10.1002/hbm.23730
[本文引用: 4]
[6]
LAWHERN V J, SOLON A J, WAYTOWICH N R, et al EEGNet: a compact convolutional neural network for EEG-based brain-computer interfaces
[J]. Journal of Neural Engineering , 2018 , 15 (5 ): 056013
DOI:10.1088/1741-2552/aace8c
[本文引用: 3]
[7]
JIA Z, LIN Y, WANG J, et al. GraphSleepNet: adaptive spatial-temporal graph convolutional networks for sleep stage classification [C]// Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence . [S. l.]: ACM, 2020: 1324–1330.
[本文引用: 1]
[8]
李珍琦, 王晶, 贾子钰, 等 融合注意力的多维特征图卷积运动想象分类
[J]. 计算机科学与探索 , 2022 , 16 (9 ): 2050 - 2060
DOI:10.3778/j.issn.1673-9418.2103079
[本文引用: 2]
LI Zhenqi, WANG Jing, JIA Ziyu, et al Attention-based multi-dimensional feature graph convolutional network for motor imagery classification
[J]. Journal of Frontiers of Computer Science and Technology , 2022 , 16 (9 ): 2050 - 2060
DOI:10.3778/j.issn.1673-9418.2103079
[本文引用: 2]
[9]
WANG Q, WU B, ZHU P, et al. ECA-Net: efficient channel attention for deep convolutional neural networks [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 11534–11542.
[本文引用: 2]
[10]
徐冰冰, 岑科廷, 黄俊杰, 等 图卷积神经网络综述
[J]. 计算机学报 , 2020 , 43 (5 ): 755 - 780
DOI:10.11897/SP.J.1016.2020.00755
[本文引用: 1]
TU Bingbing, CEN Keting, HUANG Junjie, et al A survey on graph convolutional neural network
[J]. Chinese Journal of Computers , 2020 , 43 (5 ): 755 - 780
DOI:10.11897/SP.J.1016.2020.00755
[本文引用: 1]
[11]
ZHANG D, CHEN K, JIAN D, et al Motor imagery classification via temporal attention cues of graph embedded EEG signals
[J]. IEEE Journal of Biomedical and Health Informatics , 2020 , 24 (9 ): 2570 - 2579
DOI:10.1109/JBHI.2020.2967128
[本文引用: 2]
[12]
SUN B, ZHANG H, WU Z, et al Adaptive spatiotemporal graph convolutional networks for motor imagery classification
[J]. IEEE Signal Processing Letters , 2021 , 28 : 219 - 223
DOI:10.1109/LSP.2021.3049683
[本文引用: 1]
[13]
HOU Y, JIA S, LUN X, et al Deep feature mining via the attention-based bidirectional long short term memory graph convolutional neural network for human motor imagery recognition
[J]. Frontiers in Bioengineering and Biotechnology , 2022 , 9 : 706229
DOI:10.3389/fbioe.2021.706229
[本文引用: 1]
[14]
HOU Y, JIA S, LUN X, et al. GCNs-Net: a graph convolutional neural network approach for decoding time-resolved EEG motor imagery signals [J]. IEEE Transactions on Neural Networks and Learning Systems , 2022: 1–12.
[本文引用: 1]
[15]
MA W, WANG C, SUN X, et al MBGA-Net: a multi-branch graph adaptive network for individualized motor imagery EEG classification
[J]. Computer Methods and Programs in Biomedicine , 2023 , 240 : 107641
DOI:10.1016/j.cmpb.2023.107641
[本文引用: 1]
[16]
BAHDANAU D, CHO K H, BENGIO Y. Neural machine translation by jointly learning to align and translate [C]// 3rd International Conference on Learning Representations 2015 . San Diego: [s. n.], 2015.
[本文引用: 1]
[17]
LI D, XU J, WANG J, et al A multi-scale fusion convolutional neural network based on attention mechanism for the visualization analysis of EEG signals decoding
[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering , 2020 , 28 (12 ): 2615 - 2626
DOI:10.1109/TNSRE.2020.3037326
[本文引用: 1]
[18]
LI Y, GUO L, LIU Y, et al A temporal-spectral-based squeeze-and-excitation feature fusion network for motor imagery EEG decoding
[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering , 2021 , 29 : 1534 - 1545
DOI:10.1109/TNSRE.2021.3099908
[本文引用: 1]
[19]
YU Z, CHEN W, ZHANG T Motor imagery EEG classification algorithm based on improved lightweight feature fusion network
[J]. Biomedical Signal Processing and Control , 2022 , 75 : 103618
DOI:10.1016/j.bspc.2022.103618
[本文引用: 1]
[20]
DEFFERRARD M, BRESSON X, VANDERGHEYNST P. Convolutional neural networks on graphs with fast localized spectral filtering [C]// Proceedings of the 30th Information Processing Systems . Barcelona: [s. n.], 2016: 3844–3852.
[本文引用: 1]
[21]
TANGERMANN M, MÜLLER K R, AERTSEN A, et al Review of the BCI competition IV
[J]. Frontiers in Neuroscience , 2012 , 6 : 55
[本文引用: 1]
[22]
LEE M H, KWON O Y, KIM Y J, et al EEG dataset and OpenBMI toolbox for three BCI paradigms: an investigation into BCI illiteracy
[J]. GigaScience , 2019 , 8 (5 ): giz002
DOI:10.1093/gigascience/giz002
[本文引用: 1]
[23]
LIU K, YANG M, YU Z, et al FBMSNet: a filter-bank multi-scale convolutional neural network for EEG-based motor imagery decoding
[J]. IEEE Transactions on Biomedical Engineering , 2022 , 70 (2 ): 436 - 445
[本文引用: 1]
[24]
KINGMA D P, BA J. Adam: a method for stochastic optimization [EB/OL]. (2017-01-30)[2023-08-20]. https://arxiv.org/pdf/1412.6980.pdf.
[本文引用: 1]
[25]
WU H, NIU Y, LI F, et al A parallel multiscale filter bank convolutional neural networks for motor imagery EEG classification
[J]. Frontiers in Neuroscience , 2019 , 13 : 1275
DOI:10.3389/fnins.2019.01275
[本文引用: 1]
[26]
MANE R, ROBINSON N, VINOD A P, et al. A multi-view CNN with novel variance layer for motor imagery brain computer interface [C]// 2020 42nd Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) . Montreal: IEEE, 2020.
[本文引用: 1]
[27]
BORRA D, FANTOZZI S, MAGOSSO E Interpretable and lightweight convolutional neural network for EEG decoding: application to movement execution and imagination
[J]. Neural Networks , 2020 , 129 : 55 - 74
DOI:10.1016/j.neunet.2020.05.032
[本文引用: 1]
[28]
CHEN J, YI W, WANG D. Filter bank Sinc-ShallowNet with EMD-based mixed noise adding data augmentation for motor imagery classification [C]// 2021 43rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) . Mexico: IEEE, 2021: 5837–5841.
[本文引用: 1]
[29]
VAN DER MAATEN L, HINTON G Visualizing data using t-SNE
[J]. Journal of Machine Learning Research , 2008 , 9 : 2579 - 2605
[本文引用: 1]
[30]
MISRA D, NALAMADA T, ARASANIPALAI A U, et al. Rotate to attend: convolutional triplet attention module [C]// Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision . Waikoloa: IEEE, 2021: 3139–3148.
[本文引用: 2]
[31]
LIU Y, SHAO Z, TENG Y, et al. NAM: normalization-based attention module [EB/OL]. (2021-11-24)[2023-08-20]. https://arxiv.org/pdf/2111.12419.pdf.
[本文引用: 2]
[32]
YANG L, ZHANG R Y, LI L, et al. Simam: a simple, parameter-free attention module for convolutional neural networks [C]// Proceedings of the 38th International Conference on Machine Learning . [S. l.]: PMLR, 2021: 11863–11874.
[本文引用: 2]
基于卷积神经网络的多类运动想象脑电信号识别
1
2021
... 运动想象(motor imagery,MI)是大脑想象运动动作,但肌肉或肢体不执行该动作而形成的范式. MI可用来判断用户的运动意图[1 ] . 基于MI的脑机接口设备在智能医疗、日常娱乐和运动康复等方面有广阔的应用前景[2 ] . 非侵入式MI系统具有简单、成本低和无创性等优点,但是存在信噪比低、非平稳性和多分类表征能力弱等问题. ...
基于卷积神经网络的多类运动想象脑电信号识别
1
2021
... 运动想象(motor imagery,MI)是大脑想象运动动作,但肌肉或肢体不执行该动作而形成的范式. MI可用来判断用户的运动意图[1 ] . 基于MI的脑机接口设备在智能医疗、日常娱乐和运动康复等方面有广阔的应用前景[2 ] . 非侵入式MI系统具有简单、成本低和无创性等优点,但是存在信噪比低、非平稳性和多分类表征能力弱等问题. ...
Deep learning techniques for classification of electroencephalogram (EEG) motor imagery (MI) signals: a review
1
2023
... 运动想象(motor imagery,MI)是大脑想象运动动作,但肌肉或肢体不执行该动作而形成的范式. MI可用来判断用户的运动意图[1 ] . 基于MI的脑机接口设备在智能医疗、日常娱乐和运动康复等方面有广阔的应用前景[2 ] . 非侵入式MI系统具有简单、成本低和无创性等优点,但是存在信噪比低、非平稳性和多分类表征能力弱等问题. ...
1
... 传统MI分类任务的流程通常为预处理、特征提取和特征分类. 特征提取的主要是信号滤波,包括空间域、时域、频域和多模态信号分析. 常见的空间域分析有滤波器组共空间模式方法[3 ] (filter bank common spatial pattern,FBCSP),时域分析有自回归(autoregressive,AR)模型和Hjorth参数特征提取方法,频域分析常用的是快速傅里叶变换(fast fourier transform,FFT)和功率谱密度(power spectral density,PSD). 这些特征提取方法与传统分类器结合具有较好的分类表现,但上述特征提取算法依赖人工知识和经验,使得解码性能受到很大限制. 深度学习方法的发展使MI的解码性能大大提升,但是当深度学习网络模型参数量大时,容易出现过拟合现象[4 ] . ShallowConvNet[5 ] 仅万位数量级的参数数量却取得了较好的分类表现,表明轻量级网络能够比深层网络更好地适应运动想象脑电信号(electroencephalogram,EEG)分类任务. Lawhern等[6 ] 提出适用于EEG的轻量级卷积神经网络模型EEGNet,该模型是MobileNet的变体,在4种脑机接口(brain-computer interface,BCI)范式中均有良好表现,成为里程碑算法. 虽然传统卷积神经网络的分类准确率较高,但这些方法忽略了大脑非欧式空间的特点[7 -8 ] ,认为通道之间信息是独立的,导致脑电信号的空间特征提取不充分. ...
EEG-ITNet: an explainable inception temporal convolutional network for motor imagery classification
1
2022
... 传统MI分类任务的流程通常为预处理、特征提取和特征分类. 特征提取的主要是信号滤波,包括空间域、时域、频域和多模态信号分析. 常见的空间域分析有滤波器组共空间模式方法[3 ] (filter bank common spatial pattern,FBCSP),时域分析有自回归(autoregressive,AR)模型和Hjorth参数特征提取方法,频域分析常用的是快速傅里叶变换(fast fourier transform,FFT)和功率谱密度(power spectral density,PSD). 这些特征提取方法与传统分类器结合具有较好的分类表现,但上述特征提取算法依赖人工知识和经验,使得解码性能受到很大限制. 深度学习方法的发展使MI的解码性能大大提升,但是当深度学习网络模型参数量大时,容易出现过拟合现象[4 ] . ShallowConvNet[5 ] 仅万位数量级的参数数量却取得了较好的分类表现,表明轻量级网络能够比深层网络更好地适应运动想象脑电信号(electroencephalogram,EEG)分类任务. Lawhern等[6 ] 提出适用于EEG的轻量级卷积神经网络模型EEGNet,该模型是MobileNet的变体,在4种脑机接口(brain-computer interface,BCI)范式中均有良好表现,成为里程碑算法. 虽然传统卷积神经网络的分类准确率较高,但这些方法忽略了大脑非欧式空间的特点[7 -8 ] ,认为通道之间信息是独立的,导致脑电信号的空间特征提取不充分. ...
Deep learning with convolutional neural networks for EEG decoding and visualization
4
2017
... 传统MI分类任务的流程通常为预处理、特征提取和特征分类. 特征提取的主要是信号滤波,包括空间域、时域、频域和多模态信号分析. 常见的空间域分析有滤波器组共空间模式方法[3 ] (filter bank common spatial pattern,FBCSP),时域分析有自回归(autoregressive,AR)模型和Hjorth参数特征提取方法,频域分析常用的是快速傅里叶变换(fast fourier transform,FFT)和功率谱密度(power spectral density,PSD). 这些特征提取方法与传统分类器结合具有较好的分类表现,但上述特征提取算法依赖人工知识和经验,使得解码性能受到很大限制. 深度学习方法的发展使MI的解码性能大大提升,但是当深度学习网络模型参数量大时,容易出现过拟合现象[4 ] . ShallowConvNet[5 ] 仅万位数量级的参数数量却取得了较好的分类表现,表明轻量级网络能够比深层网络更好地适应运动想象脑电信号(electroencephalogram,EEG)分类任务. Lawhern等[6 ] 提出适用于EEG的轻量级卷积神经网络模型EEGNet,该模型是MobileNet的变体,在4种脑机接口(brain-computer interface,BCI)范式中均有良好表现,成为里程碑算法. 虽然传统卷积神经网络的分类准确率较高,但这些方法忽略了大脑非欧式空间的特点[7 -8 ] ,认为通道之间信息是独立的,导致脑电信号的空间特征提取不充分. ...
... 为了验证模型的鲁棒性,采用运动想象范式中常见的跨会话实验(hold-out)方法执行实验[23 ] ,在数据集BCI Competition IV-2a和OpenBMI中进行模型验证. 数据集中的第一个会话脑电数据进行训练,第二个会话的数据进行测试. AFB-DVGCN利用4~14 Hz和14~40 Hz的1阶的巴特沃斯滤波器对脑电信号进行滤波以构建双分支网络,对比方法利用一阶巴特沃斯滤波器在4~40 Hz的频带进行滤波. 随后对滤波后的信号进行指数移动均值标准化[5 ] ,减小数值差异的影响. 将训练数据中80%的数据作为训练集,20%数据作为验证集,划分过程随机. 在训练过程中,采用自适应矩估计Adam[24 ] 优化器进行模型优化,学习率设置为0.001. 批大小设置为64,最大迭代次数为800. 为了防止过拟合,采用早停(early stopping)训练策略,当验证集损失函数连续迭代200次没有改善时,停止训练,选择保存训练过程中验证集损失函数最低的模型. 实验在搭载i9-13900K的CPU、RTX4090显卡和64G内存服务器上进行模型训练和测试. ...
... 对比方法均为深度学习的MI分类方法,方法描述如下. 1)ShallowConvNet[5 ] :轻量级的卷积神经网络,用于提取脑电信号的特征;该网络结合了时域卷积和空域卷积的操作. 2)EEGNet[6 ] :紧凑型的卷积神经网络,采用时域卷积和可分离卷积层来提取脑电信号的时间特征,并利用深度卷积来提取脑电信号的空间特征. 3)MSFBCNN[25 ] :在ShallowConvNet的基础上增加并行的多尺度滤波器组卷积,用于在多个时间尺度上提取特征. 4)FBCNet[26 ] :新型的滤波器组卷积网络,引入方差层来有效地聚合脑电信号的时域信息. 5)Sinc-ShallowNet[27 ] :通过堆叠时间sinc卷积层学习带通滤波器,同时利用深度卷积层来提取脑电信号的空间特征. 6)FB-Sinc-ShallowNet[28 ] :在Sinc-ShallowNet的基础上引入滤波器组结构,以实现对4个频段的时间和空间特征提取. ...
... 如图3 所示为跨会话实验结果的混淆矩阵,主对角线中的数字表示模型正确分类的样本数量,百分数表示该类样本的召回率;非主对角线分别表示每个类别错分类到其他类别的样本数量. 在BCI Competition IV-2a数据集上,舌头类别的召回率明显高于其他3个类别,这与传统的运动想象二分类任务有所不同[5 -6 ] . 在错分的样本中,双脚更容易被分到舌头标签中,原因可能是脚对应于脑沟、脑回区域,脑电采集信号比较微弱. 在OpenBMI数据集中,左手和右手的召回率几乎相同. ...
EEGNet: a compact convolutional neural network for EEG-based brain-computer interfaces
3
2018
... 传统MI分类任务的流程通常为预处理、特征提取和特征分类. 特征提取的主要是信号滤波,包括空间域、时域、频域和多模态信号分析. 常见的空间域分析有滤波器组共空间模式方法[3 ] (filter bank common spatial pattern,FBCSP),时域分析有自回归(autoregressive,AR)模型和Hjorth参数特征提取方法,频域分析常用的是快速傅里叶变换(fast fourier transform,FFT)和功率谱密度(power spectral density,PSD). 这些特征提取方法与传统分类器结合具有较好的分类表现,但上述特征提取算法依赖人工知识和经验,使得解码性能受到很大限制. 深度学习方法的发展使MI的解码性能大大提升,但是当深度学习网络模型参数量大时,容易出现过拟合现象[4 ] . ShallowConvNet[5 ] 仅万位数量级的参数数量却取得了较好的分类表现,表明轻量级网络能够比深层网络更好地适应运动想象脑电信号(electroencephalogram,EEG)分类任务. Lawhern等[6 ] 提出适用于EEG的轻量级卷积神经网络模型EEGNet,该模型是MobileNet的变体,在4种脑机接口(brain-computer interface,BCI)范式中均有良好表现,成为里程碑算法. 虽然传统卷积神经网络的分类准确率较高,但这些方法忽略了大脑非欧式空间的特点[7 -8 ] ,认为通道之间信息是独立的,导致脑电信号的空间特征提取不充分. ...
... 对比方法均为深度学习的MI分类方法,方法描述如下. 1)ShallowConvNet[5 ] :轻量级的卷积神经网络,用于提取脑电信号的特征;该网络结合了时域卷积和空域卷积的操作. 2)EEGNet[6 ] :紧凑型的卷积神经网络,采用时域卷积和可分离卷积层来提取脑电信号的时间特征,并利用深度卷积来提取脑电信号的空间特征. 3)MSFBCNN[25 ] :在ShallowConvNet的基础上增加并行的多尺度滤波器组卷积,用于在多个时间尺度上提取特征. 4)FBCNet[26 ] :新型的滤波器组卷积网络,引入方差层来有效地聚合脑电信号的时域信息. 5)Sinc-ShallowNet[27 ] :通过堆叠时间sinc卷积层学习带通滤波器,同时利用深度卷积层来提取脑电信号的空间特征. 6)FB-Sinc-ShallowNet[28 ] :在Sinc-ShallowNet的基础上引入滤波器组结构,以实现对4个频段的时间和空间特征提取. ...
... 如图3 所示为跨会话实验结果的混淆矩阵,主对角线中的数字表示模型正确分类的样本数量,百分数表示该类样本的召回率;非主对角线分别表示每个类别错分类到其他类别的样本数量. 在BCI Competition IV-2a数据集上,舌头类别的召回率明显高于其他3个类别,这与传统的运动想象二分类任务有所不同[5 -6 ] . 在错分的样本中,双脚更容易被分到舌头标签中,原因可能是脚对应于脑沟、脑回区域,脑电采集信号比较微弱. 在OpenBMI数据集中,左手和右手的召回率几乎相同. ...
1
... 传统MI分类任务的流程通常为预处理、特征提取和特征分类. 特征提取的主要是信号滤波,包括空间域、时域、频域和多模态信号分析. 常见的空间域分析有滤波器组共空间模式方法[3 ] (filter bank common spatial pattern,FBCSP),时域分析有自回归(autoregressive,AR)模型和Hjorth参数特征提取方法,频域分析常用的是快速傅里叶变换(fast fourier transform,FFT)和功率谱密度(power spectral density,PSD). 这些特征提取方法与传统分类器结合具有较好的分类表现,但上述特征提取算法依赖人工知识和经验,使得解码性能受到很大限制. 深度学习方法的发展使MI的解码性能大大提升,但是当深度学习网络模型参数量大时,容易出现过拟合现象[4 ] . ShallowConvNet[5 ] 仅万位数量级的参数数量却取得了较好的分类表现,表明轻量级网络能够比深层网络更好地适应运动想象脑电信号(electroencephalogram,EEG)分类任务. Lawhern等[6 ] 提出适用于EEG的轻量级卷积神经网络模型EEGNet,该模型是MobileNet的变体,在4种脑机接口(brain-computer interface,BCI)范式中均有良好表现,成为里程碑算法. 虽然传统卷积神经网络的分类准确率较高,但这些方法忽略了大脑非欧式空间的特点[7 -8 ] ,认为通道之间信息是独立的,导致脑电信号的空间特征提取不充分. ...
融合注意力的多维特征图卷积运动想象分类
2
2022
... 传统MI分类任务的流程通常为预处理、特征提取和特征分类. 特征提取的主要是信号滤波,包括空间域、时域、频域和多模态信号分析. 常见的空间域分析有滤波器组共空间模式方法[3 ] (filter bank common spatial pattern,FBCSP),时域分析有自回归(autoregressive,AR)模型和Hjorth参数特征提取方法,频域分析常用的是快速傅里叶变换(fast fourier transform,FFT)和功率谱密度(power spectral density,PSD). 这些特征提取方法与传统分类器结合具有较好的分类表现,但上述特征提取算法依赖人工知识和经验,使得解码性能受到很大限制. 深度学习方法的发展使MI的解码性能大大提升,但是当深度学习网络模型参数量大时,容易出现过拟合现象[4 ] . ShallowConvNet[5 ] 仅万位数量级的参数数量却取得了较好的分类表现,表明轻量级网络能够比深层网络更好地适应运动想象脑电信号(electroencephalogram,EEG)分类任务. Lawhern等[6 ] 提出适用于EEG的轻量级卷积神经网络模型EEGNet,该模型是MobileNet的变体,在4种脑机接口(brain-computer interface,BCI)范式中均有良好表现,成为里程碑算法. 虽然传统卷积神经网络的分类准确率较高,但这些方法忽略了大脑非欧式空间的特点[7 -8 ] ,认为通道之间信息是独立的,导致脑电信号的空间特征提取不充分. ...
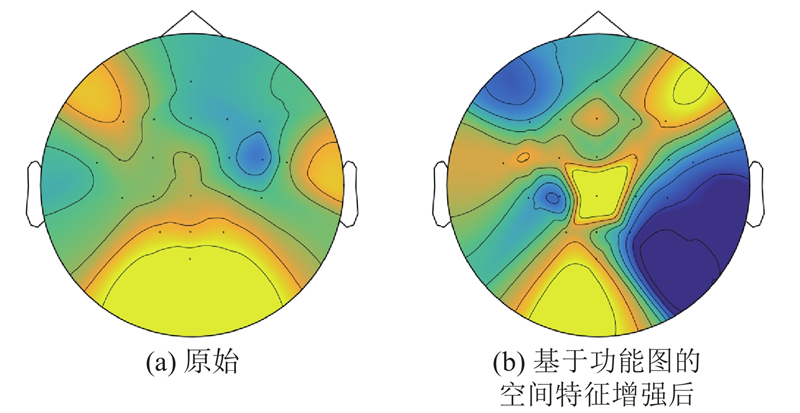
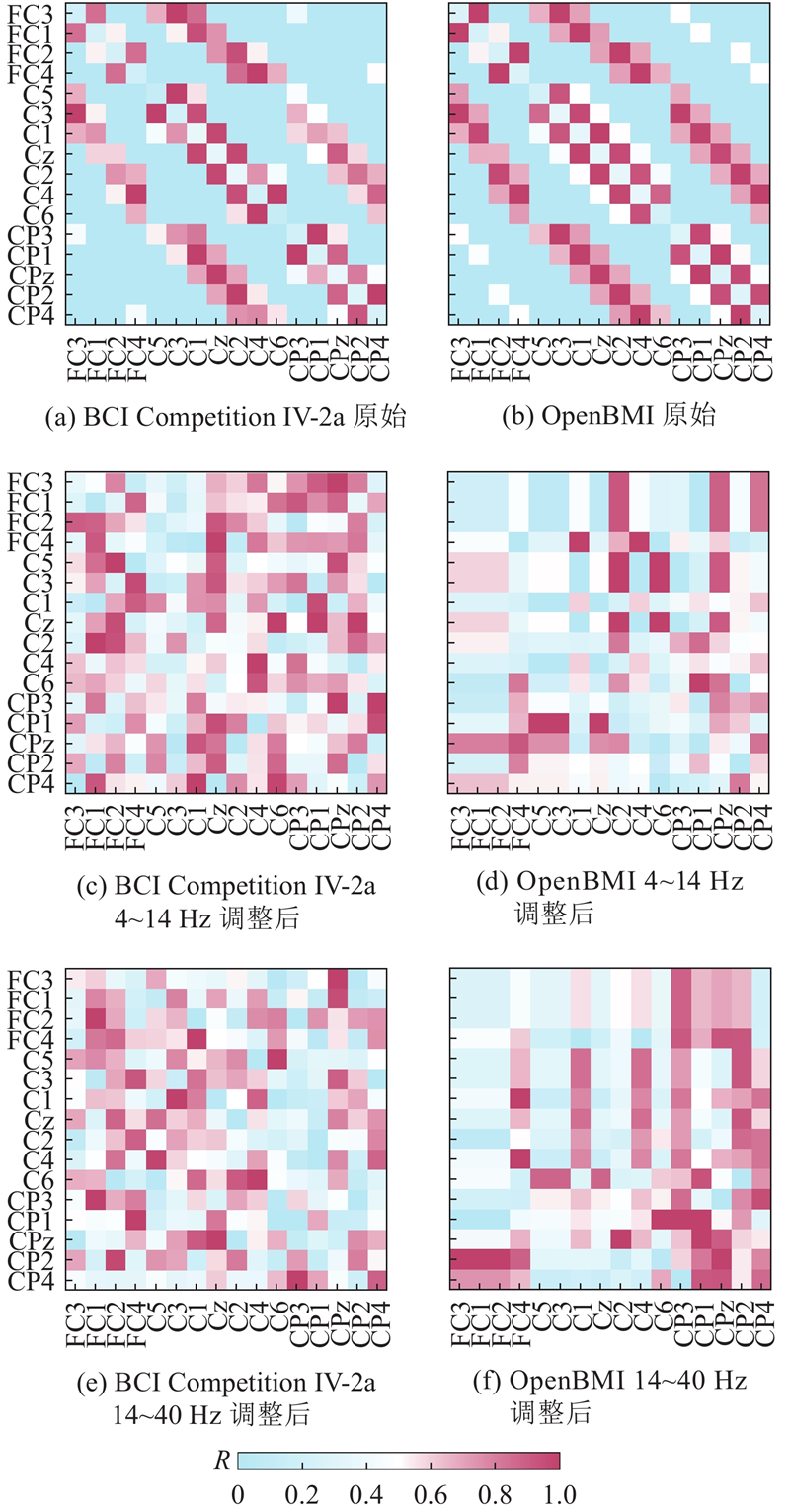
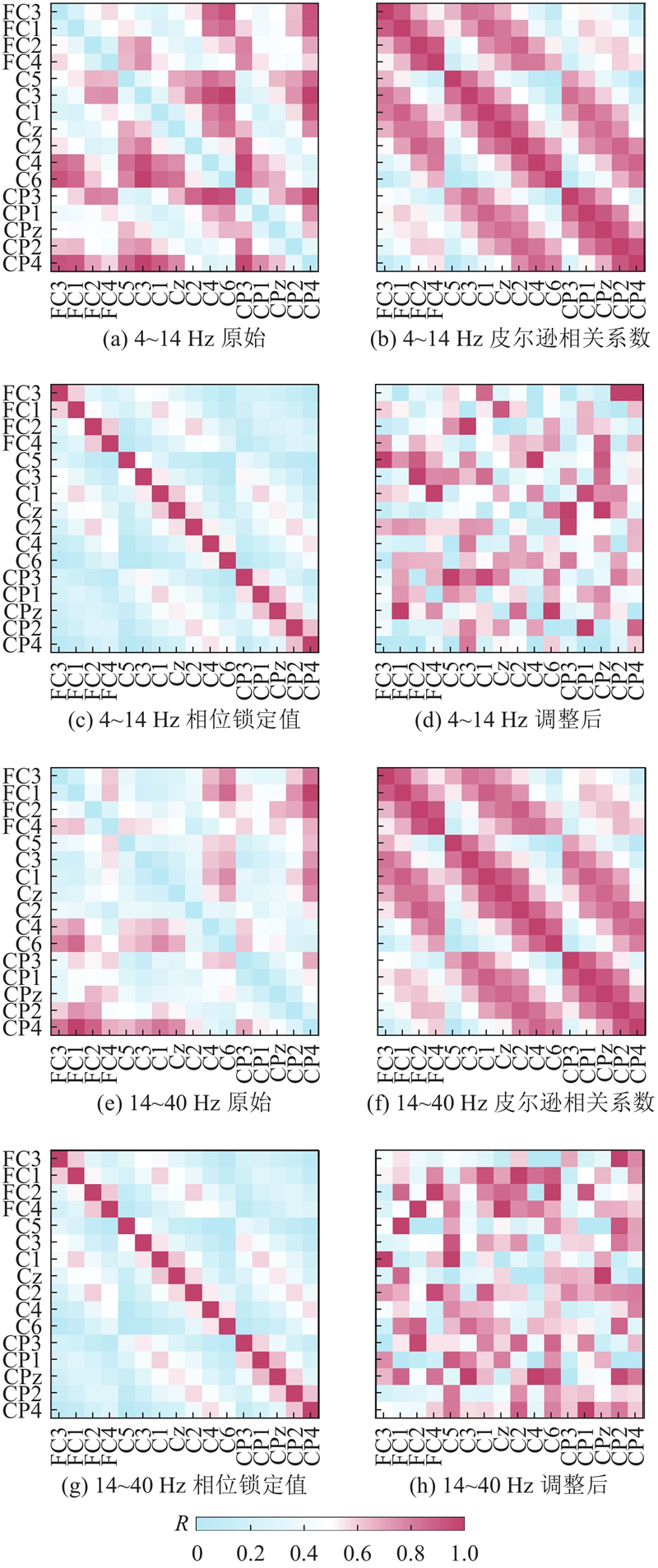
... 基于距离连接的脑视图利用真实世界的3D距离形成邻接矩阵,每个脑电通道视为图上的1个节点. 考虑脑电信号实际特性,相距较近的脑电通道间的电压相互影响较大[8 ] ,相距较远的相互影响较小. 受Zhang等[11 ] 的启发,计算每个节点与其他所有节点的距离值,取平均值作为阈值筛选节点,将平均值作为自身节点值. 定义1个节点和图上所有其他节点的距离集合为$ {D}_{{\mathrm{ds}}}=\left\{{{d}}_{ij}\right|\left({s}^{i},{s}^{j}\right)\in {{V}_{{\mathrm{ds}}}}^{2},i\ne j\} $ $ {{V}}_{\text{ds}} $ $ {{s}}^{{i}} $ $ {{s}}^{{j}} $ $ {V}_{{\mathrm{ds}}} $ $ {{d}}_{ij}=\sqrt[2]{{({x}_{i}-{x}_{j})}^{2}+{({y}_{i}-{y}_{j})}^{2}+{({z}_{i}-{z}_{j})}^{2}} $ $ {x}_{i} $ $ {y}_{i} $ $ {z}_{i} $ $ {D}_{{\mathrm{ds}}} $ ${\boldsymbol{A}}_{\mathrm{ds}} $
融合注意力的多维特征图卷积运动想象分类
2
2022
... 传统MI分类任务的流程通常为预处理、特征提取和特征分类. 特征提取的主要是信号滤波,包括空间域、时域、频域和多模态信号分析. 常见的空间域分析有滤波器组共空间模式方法[3 ] (filter bank common spatial pattern,FBCSP),时域分析有自回归(autoregressive,AR)模型和Hjorth参数特征提取方法,频域分析常用的是快速傅里叶变换(fast fourier transform,FFT)和功率谱密度(power spectral density,PSD). 这些特征提取方法与传统分类器结合具有较好的分类表现,但上述特征提取算法依赖人工知识和经验,使得解码性能受到很大限制. 深度学习方法的发展使MI的解码性能大大提升,但是当深度学习网络模型参数量大时,容易出现过拟合现象[4 ] . ShallowConvNet[5 ] 仅万位数量级的参数数量却取得了较好的分类表现,表明轻量级网络能够比深层网络更好地适应运动想象脑电信号(electroencephalogram,EEG)分类任务. Lawhern等[6 ] 提出适用于EEG的轻量级卷积神经网络模型EEGNet,该模型是MobileNet的变体,在4种脑机接口(brain-computer interface,BCI)范式中均有良好表现,成为里程碑算法. 虽然传统卷积神经网络的分类准确率较高,但这些方法忽略了大脑非欧式空间的特点[7 -8 ] ,认为通道之间信息是独立的,导致脑电信号的空间特征提取不充分. ...
... 基于距离连接的脑视图利用真实世界的3D距离形成邻接矩阵,每个脑电通道视为图上的1个节点. 考虑脑电信号实际特性,相距较近的脑电通道间的电压相互影响较大[8 ] ,相距较远的相互影响较小. 受Zhang等[11 ] 的启发,计算每个节点与其他所有节点的距离值,取平均值作为阈值筛选节点,将平均值作为自身节点值. 定义1个节点和图上所有其他节点的距离集合为$ {D}_{{\mathrm{ds}}}=\left\{{{d}}_{ij}\right|\left({s}^{i},{s}^{j}\right)\in {{V}_{{\mathrm{ds}}}}^{2},i\ne j\} $ $ {{V}}_{\text{ds}} $ $ {{s}}^{{i}} $ $ {{s}}^{{j}} $ $ {V}_{{\mathrm{ds}}} $ $ {{d}}_{ij}=\sqrt[2]{{({x}_{i}-{x}_{j})}^{2}+{({y}_{i}-{y}_{j})}^{2}+{({z}_{i}-{z}_{j})}^{2}} $ $ {x}_{i} $ $ {y}_{i} $ $ {z}_{i} $ $ {D}_{{\mathrm{ds}}} $ ${\boldsymbol{A}}_{\mathrm{ds}} $
2
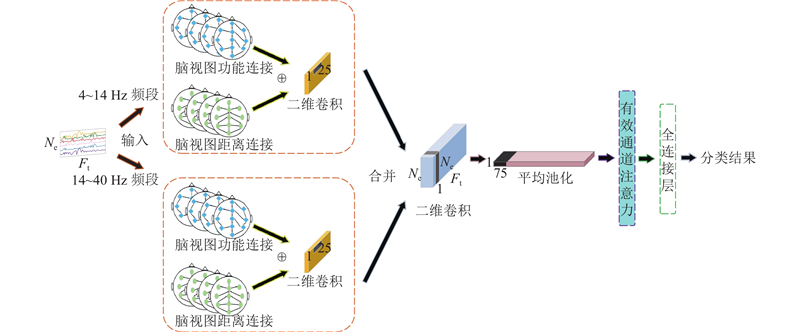
... 本研究提出融合注意力的滤波器组双视图图卷积网络(attention-fused filter bank dual-view graph convolutional network,AFB-DVGCN). 受FBCSP启发,利用滤波器组构建多分支结构网络,充分提取不同频段的时域和空域信息,提高运动想象的分类性能;考虑到传统卷积忽略大脑非欧式空间的特点,提出双视图图卷积(DVGCN)空间特征提取方法,利用功能脑视图和距离脑视图进行空间特征聚合,实现信息互补;利用有效通道注意力机制(efficient channel attention,ECA)[9 ] 进行特征增强,以充分考虑不同特征图间的特征信息,捕捉局部跨通道的交互信息. ...
... Performance comparison of different attention mechanisms in two publicly available datasets
Tab.5 注意力机制 BCI Competition IV-2a OpenBMI acc/% kap std N TP acc/% kap std N TP Triplet Attention[30 ] 72.955 0.655 0.156 129 140 70.065 0.401 0.167 112 702 NAM[31 ] 74.653 0.662 0.108 128 940 69.583 0.392 1.660 112 502 SimAM[32 ] 72.762 0.637 0.116 128 840 67.343 0.347 0.142 112 402 ECA[9 ] 77.392* 0.699 0.103 128 843 72.657* 0.453 0.142 112 405
5. 结 语 本研究利用功能脑视图和距离脑视图进行空间特征提取,充分考虑大脑非欧式空间的特性;利用双分支网络充分考虑不同频段间的特征信息,实现了运动想象不同频域段信息的提取;利用ECA对丢弃层后的特征信息进行交互增强. 对比其他方法,AFB-DVGCN在2个公开数据集上具有更强的分类性能,准确率提高了4.29%,可为后续运动想象范式解码性能提高提供新的思路. AFB-DVGCN只在单被试实验上进行,未来计划在跨被试实验上进行验证,证明网络的泛化性,同时计划精简网络结构,减少参数. ...
图卷积神经网络综述
1
2020
... 图数据为非欧空间数据,每个节点都具有的各自的特征. 脑电信号可以看作2D图结构数据,能够将大脑不同脑电通道映射为图中的不同节点,实现脑电信号的图转换. 传统卷积神经网络卷积和池化操作依赖数据的平移不变性[10 ] ,因此传统神经网络不适用于图结构数据. 图卷积网络有2种方法:谱域和空间域. 谱域方法借助图的拉普拉斯矩阵实现图的傅里叶变换,利用卷积定理实现图上的卷积操作;空间域的方法从节点域出发,通过定义聚合函数来聚合每个中心节点和其邻近节点. Zhang等[11 ] 利用脑电电极的空间位置构建3种距离脑视图对脑电信号进行图嵌入,在区分程度最高的时间段学习空间和时间特征. Sun等[12 ] 提出自适应时空图卷积网络(adaptive spatiotemporal graph convolutional network,ASTGCN),利用自适应矩阵动态调节脑电电极间的关系,实现脑电信号分类. Hou等[13 ] 将注意力机制的双向记忆长短期网络与GCN结合,从特征的内部拓扑结构方面来增强解码性能. Hou等[14 ] 建立图卷积深度学习的框架GCNs-Net,利用功能拓扑关系解码EEG脑电信号. Ma等[15 ] 提出多分支图自适应网络(multi-branch graph adaptive network,MBGA-Net),将每个通道中包含的时域和频域信息作为节点特征来构建连通性图,完成被试自适应匹配充分提取被试的脑电信号特征. 可以看出,利用图卷积神经网络能够增强MI中脑电信号空间特征的提取能力,提高该范式的解码性能,但上述文献未同时关注功能联系和真实空间联系. ...
图卷积神经网络综述
1
2020
... 图数据为非欧空间数据,每个节点都具有的各自的特征. 脑电信号可以看作2D图结构数据,能够将大脑不同脑电通道映射为图中的不同节点,实现脑电信号的图转换. 传统卷积神经网络卷积和池化操作依赖数据的平移不变性[10 ] ,因此传统神经网络不适用于图结构数据. 图卷积网络有2种方法:谱域和空间域. 谱域方法借助图的拉普拉斯矩阵实现图的傅里叶变换,利用卷积定理实现图上的卷积操作;空间域的方法从节点域出发,通过定义聚合函数来聚合每个中心节点和其邻近节点. Zhang等[11 ] 利用脑电电极的空间位置构建3种距离脑视图对脑电信号进行图嵌入,在区分程度最高的时间段学习空间和时间特征. Sun等[12 ] 提出自适应时空图卷积网络(adaptive spatiotemporal graph convolutional network,ASTGCN),利用自适应矩阵动态调节脑电电极间的关系,实现脑电信号分类. Hou等[13 ] 将注意力机制的双向记忆长短期网络与GCN结合,从特征的内部拓扑结构方面来增强解码性能. Hou等[14 ] 建立图卷积深度学习的框架GCNs-Net,利用功能拓扑关系解码EEG脑电信号. Ma等[15 ] 提出多分支图自适应网络(multi-branch graph adaptive network,MBGA-Net),将每个通道中包含的时域和频域信息作为节点特征来构建连通性图,完成被试自适应匹配充分提取被试的脑电信号特征. 可以看出,利用图卷积神经网络能够增强MI中脑电信号空间特征的提取能力,提高该范式的解码性能,但上述文献未同时关注功能联系和真实空间联系. ...
Motor imagery classification via temporal attention cues of graph embedded EEG signals
2
2020
... 图数据为非欧空间数据,每个节点都具有的各自的特征. 脑电信号可以看作2D图结构数据,能够将大脑不同脑电通道映射为图中的不同节点,实现脑电信号的图转换. 传统卷积神经网络卷积和池化操作依赖数据的平移不变性[10 ] ,因此传统神经网络不适用于图结构数据. 图卷积网络有2种方法:谱域和空间域. 谱域方法借助图的拉普拉斯矩阵实现图的傅里叶变换,利用卷积定理实现图上的卷积操作;空间域的方法从节点域出发,通过定义聚合函数来聚合每个中心节点和其邻近节点. Zhang等[11 ] 利用脑电电极的空间位置构建3种距离脑视图对脑电信号进行图嵌入,在区分程度最高的时间段学习空间和时间特征. Sun等[12 ] 提出自适应时空图卷积网络(adaptive spatiotemporal graph convolutional network,ASTGCN),利用自适应矩阵动态调节脑电电极间的关系,实现脑电信号分类. Hou等[13 ] 将注意力机制的双向记忆长短期网络与GCN结合,从特征的内部拓扑结构方面来增强解码性能. Hou等[14 ] 建立图卷积深度学习的框架GCNs-Net,利用功能拓扑关系解码EEG脑电信号. Ma等[15 ] 提出多分支图自适应网络(multi-branch graph adaptive network,MBGA-Net),将每个通道中包含的时域和频域信息作为节点特征来构建连通性图,完成被试自适应匹配充分提取被试的脑电信号特征. 可以看出,利用图卷积神经网络能够增强MI中脑电信号空间特征的提取能力,提高该范式的解码性能,但上述文献未同时关注功能联系和真实空间联系. ...
... 基于距离连接的脑视图利用真实世界的3D距离形成邻接矩阵,每个脑电通道视为图上的1个节点. 考虑脑电信号实际特性,相距较近的脑电通道间的电压相互影响较大[8 ] ,相距较远的相互影响较小. 受Zhang等[11 ] 的启发,计算每个节点与其他所有节点的距离值,取平均值作为阈值筛选节点,将平均值作为自身节点值. 定义1个节点和图上所有其他节点的距离集合为$ {D}_{{\mathrm{ds}}}=\left\{{{d}}_{ij}\right|\left({s}^{i},{s}^{j}\right)\in {{V}_{{\mathrm{ds}}}}^{2},i\ne j\} $ $ {{V}}_{\text{ds}} $ $ {{s}}^{{i}} $ $ {{s}}^{{j}} $ $ {V}_{{\mathrm{ds}}} $ $ {{d}}_{ij}=\sqrt[2]{{({x}_{i}-{x}_{j})}^{2}+{({y}_{i}-{y}_{j})}^{2}+{({z}_{i}-{z}_{j})}^{2}} $ $ {x}_{i} $ $ {y}_{i} $ $ {z}_{i} $ $ {D}_{{\mathrm{ds}}} $ ${\boldsymbol{A}}_{\mathrm{ds}} $
Adaptive spatiotemporal graph convolutional networks for motor imagery classification
1
2021
... 图数据为非欧空间数据,每个节点都具有的各自的特征. 脑电信号可以看作2D图结构数据,能够将大脑不同脑电通道映射为图中的不同节点,实现脑电信号的图转换. 传统卷积神经网络卷积和池化操作依赖数据的平移不变性[10 ] ,因此传统神经网络不适用于图结构数据. 图卷积网络有2种方法:谱域和空间域. 谱域方法借助图的拉普拉斯矩阵实现图的傅里叶变换,利用卷积定理实现图上的卷积操作;空间域的方法从节点域出发,通过定义聚合函数来聚合每个中心节点和其邻近节点. Zhang等[11 ] 利用脑电电极的空间位置构建3种距离脑视图对脑电信号进行图嵌入,在区分程度最高的时间段学习空间和时间特征. Sun等[12 ] 提出自适应时空图卷积网络(adaptive spatiotemporal graph convolutional network,ASTGCN),利用自适应矩阵动态调节脑电电极间的关系,实现脑电信号分类. Hou等[13 ] 将注意力机制的双向记忆长短期网络与GCN结合,从特征的内部拓扑结构方面来增强解码性能. Hou等[14 ] 建立图卷积深度学习的框架GCNs-Net,利用功能拓扑关系解码EEG脑电信号. Ma等[15 ] 提出多分支图自适应网络(multi-branch graph adaptive network,MBGA-Net),将每个通道中包含的时域和频域信息作为节点特征来构建连通性图,完成被试自适应匹配充分提取被试的脑电信号特征. 可以看出,利用图卷积神经网络能够增强MI中脑电信号空间特征的提取能力,提高该范式的解码性能,但上述文献未同时关注功能联系和真实空间联系. ...
Deep feature mining via the attention-based bidirectional long short term memory graph convolutional neural network for human motor imagery recognition
1
2022
... 图数据为非欧空间数据,每个节点都具有的各自的特征. 脑电信号可以看作2D图结构数据,能够将大脑不同脑电通道映射为图中的不同节点,实现脑电信号的图转换. 传统卷积神经网络卷积和池化操作依赖数据的平移不变性[10 ] ,因此传统神经网络不适用于图结构数据. 图卷积网络有2种方法:谱域和空间域. 谱域方法借助图的拉普拉斯矩阵实现图的傅里叶变换,利用卷积定理实现图上的卷积操作;空间域的方法从节点域出发,通过定义聚合函数来聚合每个中心节点和其邻近节点. Zhang等[11 ] 利用脑电电极的空间位置构建3种距离脑视图对脑电信号进行图嵌入,在区分程度最高的时间段学习空间和时间特征. Sun等[12 ] 提出自适应时空图卷积网络(adaptive spatiotemporal graph convolutional network,ASTGCN),利用自适应矩阵动态调节脑电电极间的关系,实现脑电信号分类. Hou等[13 ] 将注意力机制的双向记忆长短期网络与GCN结合,从特征的内部拓扑结构方面来增强解码性能. Hou等[14 ] 建立图卷积深度学习的框架GCNs-Net,利用功能拓扑关系解码EEG脑电信号. Ma等[15 ] 提出多分支图自适应网络(multi-branch graph adaptive network,MBGA-Net),将每个通道中包含的时域和频域信息作为节点特征来构建连通性图,完成被试自适应匹配充分提取被试的脑电信号特征. 可以看出,利用图卷积神经网络能够增强MI中脑电信号空间特征的提取能力,提高该范式的解码性能,但上述文献未同时关注功能联系和真实空间联系. ...
1
... 图数据为非欧空间数据,每个节点都具有的各自的特征. 脑电信号可以看作2D图结构数据,能够将大脑不同脑电通道映射为图中的不同节点,实现脑电信号的图转换. 传统卷积神经网络卷积和池化操作依赖数据的平移不变性[10 ] ,因此传统神经网络不适用于图结构数据. 图卷积网络有2种方法:谱域和空间域. 谱域方法借助图的拉普拉斯矩阵实现图的傅里叶变换,利用卷积定理实现图上的卷积操作;空间域的方法从节点域出发,通过定义聚合函数来聚合每个中心节点和其邻近节点. Zhang等[11 ] 利用脑电电极的空间位置构建3种距离脑视图对脑电信号进行图嵌入,在区分程度最高的时间段学习空间和时间特征. Sun等[12 ] 提出自适应时空图卷积网络(adaptive spatiotemporal graph convolutional network,ASTGCN),利用自适应矩阵动态调节脑电电极间的关系,实现脑电信号分类. Hou等[13 ] 将注意力机制的双向记忆长短期网络与GCN结合,从特征的内部拓扑结构方面来增强解码性能. Hou等[14 ] 建立图卷积深度学习的框架GCNs-Net,利用功能拓扑关系解码EEG脑电信号. Ma等[15 ] 提出多分支图自适应网络(multi-branch graph adaptive network,MBGA-Net),将每个通道中包含的时域和频域信息作为节点特征来构建连通性图,完成被试自适应匹配充分提取被试的脑电信号特征. 可以看出,利用图卷积神经网络能够增强MI中脑电信号空间特征的提取能力,提高该范式的解码性能,但上述文献未同时关注功能联系和真实空间联系. ...
MBGA-Net: a multi-branch graph adaptive network for individualized motor imagery EEG classification
1
2023
... 图数据为非欧空间数据,每个节点都具有的各自的特征. 脑电信号可以看作2D图结构数据,能够将大脑不同脑电通道映射为图中的不同节点,实现脑电信号的图转换. 传统卷积神经网络卷积和池化操作依赖数据的平移不变性[10 ] ,因此传统神经网络不适用于图结构数据. 图卷积网络有2种方法:谱域和空间域. 谱域方法借助图的拉普拉斯矩阵实现图的傅里叶变换,利用卷积定理实现图上的卷积操作;空间域的方法从节点域出发,通过定义聚合函数来聚合每个中心节点和其邻近节点. Zhang等[11 ] 利用脑电电极的空间位置构建3种距离脑视图对脑电信号进行图嵌入,在区分程度最高的时间段学习空间和时间特征. Sun等[12 ] 提出自适应时空图卷积网络(adaptive spatiotemporal graph convolutional network,ASTGCN),利用自适应矩阵动态调节脑电电极间的关系,实现脑电信号分类. Hou等[13 ] 将注意力机制的双向记忆长短期网络与GCN结合,从特征的内部拓扑结构方面来增强解码性能. Hou等[14 ] 建立图卷积深度学习的框架GCNs-Net,利用功能拓扑关系解码EEG脑电信号. Ma等[15 ] 提出多分支图自适应网络(multi-branch graph adaptive network,MBGA-Net),将每个通道中包含的时域和频域信息作为节点特征来构建连通性图,完成被试自适应匹配充分提取被试的脑电信号特征. 可以看出,利用图卷积神经网络能够增强MI中脑电信号空间特征的提取能力,提高该范式的解码性能,但上述文献未同时关注功能联系和真实空间联系. ...
1
... Bahdanau等[16 ] 将注意力机制用于循环神经网络,进一步增强了RNN对全局信息的处理能力. 在计算机视觉领域,注意力能够强化特征信息中的重要部分,提升网络的分类性能. 在BCI中,注意力机制通过神经网络自主学习出权重系数,并以动态加权方式来强化脑电信号的重要信息并抑制非重要信息,可用于提高网络对于特征的表征能力. 有学者尝试将注意力模块应用到运动想象解码工作,Li等[17 ] 利用压缩与激发(squeeze-and-exitation,SE)模块基于全局信息选择性地放大有价值的特征通道并抑制无用的特征通道. Li等[18 ] 引入SE操作的变体挤压-激励-卷积(squeeze-excitation-convolution,SEC)单元来解决特征融合中的冗余问题并增强最具辨别力的特征,在运动想象分类任务中成果显著,证明了SE变体单元的有效性. Yu等[19 ] 将卷积注意力模块 (convolutional block attention module,CBAM)中的通道注意力模块和空间注意力模块进行并联操作,避免了串联模式的相互影响,实现了单一模式注意力机制的较高准确率. 通道注意力模块能够增强提取特征图的特征,本研究充分考虑跨通道间的信息交互,采用ECA来提高分类性能. ...
A multi-scale fusion convolutional neural network based on attention mechanism for the visualization analysis of EEG signals decoding
1
2020
... Bahdanau等[16 ] 将注意力机制用于循环神经网络,进一步增强了RNN对全局信息的处理能力. 在计算机视觉领域,注意力能够强化特征信息中的重要部分,提升网络的分类性能. 在BCI中,注意力机制通过神经网络自主学习出权重系数,并以动态加权方式来强化脑电信号的重要信息并抑制非重要信息,可用于提高网络对于特征的表征能力. 有学者尝试将注意力模块应用到运动想象解码工作,Li等[17 ] 利用压缩与激发(squeeze-and-exitation,SE)模块基于全局信息选择性地放大有价值的特征通道并抑制无用的特征通道. Li等[18 ] 引入SE操作的变体挤压-激励-卷积(squeeze-excitation-convolution,SEC)单元来解决特征融合中的冗余问题并增强最具辨别力的特征,在运动想象分类任务中成果显著,证明了SE变体单元的有效性. Yu等[19 ] 将卷积注意力模块 (convolutional block attention module,CBAM)中的通道注意力模块和空间注意力模块进行并联操作,避免了串联模式的相互影响,实现了单一模式注意力机制的较高准确率. 通道注意力模块能够增强提取特征图的特征,本研究充分考虑跨通道间的信息交互,采用ECA来提高分类性能. ...
A temporal-spectral-based squeeze-and-excitation feature fusion network for motor imagery EEG decoding
1
2021
... Bahdanau等[16 ] 将注意力机制用于循环神经网络,进一步增强了RNN对全局信息的处理能力. 在计算机视觉领域,注意力能够强化特征信息中的重要部分,提升网络的分类性能. 在BCI中,注意力机制通过神经网络自主学习出权重系数,并以动态加权方式来强化脑电信号的重要信息并抑制非重要信息,可用于提高网络对于特征的表征能力. 有学者尝试将注意力模块应用到运动想象解码工作,Li等[17 ] 利用压缩与激发(squeeze-and-exitation,SE)模块基于全局信息选择性地放大有价值的特征通道并抑制无用的特征通道. Li等[18 ] 引入SE操作的变体挤压-激励-卷积(squeeze-excitation-convolution,SEC)单元来解决特征融合中的冗余问题并增强最具辨别力的特征,在运动想象分类任务中成果显著,证明了SE变体单元的有效性. Yu等[19 ] 将卷积注意力模块 (convolutional block attention module,CBAM)中的通道注意力模块和空间注意力模块进行并联操作,避免了串联模式的相互影响,实现了单一模式注意力机制的较高准确率. 通道注意力模块能够增强提取特征图的特征,本研究充分考虑跨通道间的信息交互,采用ECA来提高分类性能. ...
Motor imagery EEG classification algorithm based on improved lightweight feature fusion network
1
2022
... Bahdanau等[16 ] 将注意力机制用于循环神经网络,进一步增强了RNN对全局信息的处理能力. 在计算机视觉领域,注意力能够强化特征信息中的重要部分,提升网络的分类性能. 在BCI中,注意力机制通过神经网络自主学习出权重系数,并以动态加权方式来强化脑电信号的重要信息并抑制非重要信息,可用于提高网络对于特征的表征能力. 有学者尝试将注意力模块应用到运动想象解码工作,Li等[17 ] 利用压缩与激发(squeeze-and-exitation,SE)模块基于全局信息选择性地放大有价值的特征通道并抑制无用的特征通道. Li等[18 ] 引入SE操作的变体挤压-激励-卷积(squeeze-excitation-convolution,SEC)单元来解决特征融合中的冗余问题并增强最具辨别力的特征,在运动想象分类任务中成果显著,证明了SE变体单元的有效性. Yu等[19 ] 将卷积注意力模块 (convolutional block attention module,CBAM)中的通道注意力模块和空间注意力模块进行并联操作,避免了串联模式的相互影响,实现了单一模式注意力机制的较高准确率. 通道注意力模块能够增强提取特征图的特征,本研究充分考虑跨通道间的信息交互,采用ECA来提高分类性能. ...
1
... 式中:$ \odot $ $ {\boldsymbol{g}}_{\mathrm{\theta }}={\boldsymbol{U}}^{\mathrm{T}}\boldsymbol{g} $ $ {\boldsymbol{g}}_{\mathrm{\theta }} $ [20 ] . 利用切比雪夫多项式的K 阶截断展开式近似$ {\boldsymbol{g}}_{\mathrm{\theta }} $
Review of the BCI competition IV
1
2012
... 数据集包含9个受试者的EEG数据[21 ] . 每个受试者进行4类运动想象任务,分别是左手、右手、双脚和舌头. 数据集包含2个会话,每个会话总共有288个试次,每个类别有72个试次. 脑电信号使用22个电极进行记录,并以250 Hz的采样率进行采样. 截取提示后0~4 s的数据,每个试次为1×22×1000的矩阵. ...
EEG dataset and OpenBMI toolbox for three BCI paradigms: an investigation into BCI illiteracy
1
2019
... 数据集为公开数据集,包含54个受试者的脑电信号[22 ] . 该数据集有2类运动想象任务,分别是左手和右手. 脑电信号采集自62个电极,并以1 000 Hz的采样率进行采样. 该数据集包含2个会话,每个会话包含200个试次,每类任务有100个试次. 根据数据集发布者的设置,选取20个运动皮层区域的脑电电极进行分析,包括FC5、FC3、FC1、FC2、FC4、FC6,C5、C3、C1、Cz、C2、C4、C6和CP5、CP3、CP1、CPz、CP2、CP4、CP6. 将原数据降采样到250 Hz,截取提示后0~4 s的数据,每个试次为1×20×1000的矩阵. ...
FBMSNet: a filter-bank multi-scale convolutional neural network for EEG-based motor imagery decoding
1
2022
... 为了验证模型的鲁棒性,采用运动想象范式中常见的跨会话实验(hold-out)方法执行实验[23 ] ,在数据集BCI Competition IV-2a和OpenBMI中进行模型验证. 数据集中的第一个会话脑电数据进行训练,第二个会话的数据进行测试. AFB-DVGCN利用4~14 Hz和14~40 Hz的1阶的巴特沃斯滤波器对脑电信号进行滤波以构建双分支网络,对比方法利用一阶巴特沃斯滤波器在4~40 Hz的频带进行滤波. 随后对滤波后的信号进行指数移动均值标准化[5 ] ,减小数值差异的影响. 将训练数据中80%的数据作为训练集,20%数据作为验证集,划分过程随机. 在训练过程中,采用自适应矩估计Adam[24 ] 优化器进行模型优化,学习率设置为0.001. 批大小设置为64,最大迭代次数为800. 为了防止过拟合,采用早停(early stopping)训练策略,当验证集损失函数连续迭代200次没有改善时,停止训练,选择保存训练过程中验证集损失函数最低的模型. 实验在搭载i9-13900K的CPU、RTX4090显卡和64G内存服务器上进行模型训练和测试. ...
1
... 为了验证模型的鲁棒性,采用运动想象范式中常见的跨会话实验(hold-out)方法执行实验[23 ] ,在数据集BCI Competition IV-2a和OpenBMI中进行模型验证. 数据集中的第一个会话脑电数据进行训练,第二个会话的数据进行测试. AFB-DVGCN利用4~14 Hz和14~40 Hz的1阶的巴特沃斯滤波器对脑电信号进行滤波以构建双分支网络,对比方法利用一阶巴特沃斯滤波器在4~40 Hz的频带进行滤波. 随后对滤波后的信号进行指数移动均值标准化[5 ] ,减小数值差异的影响. 将训练数据中80%的数据作为训练集,20%数据作为验证集,划分过程随机. 在训练过程中,采用自适应矩估计Adam[24 ] 优化器进行模型优化,学习率设置为0.001. 批大小设置为64,最大迭代次数为800. 为了防止过拟合,采用早停(early stopping)训练策略,当验证集损失函数连续迭代200次没有改善时,停止训练,选择保存训练过程中验证集损失函数最低的模型. 实验在搭载i9-13900K的CPU、RTX4090显卡和64G内存服务器上进行模型训练和测试. ...
A parallel multiscale filter bank convolutional neural networks for motor imagery EEG classification
1
2019
... 对比方法均为深度学习的MI分类方法,方法描述如下. 1)ShallowConvNet[5 ] :轻量级的卷积神经网络,用于提取脑电信号的特征;该网络结合了时域卷积和空域卷积的操作. 2)EEGNet[6 ] :紧凑型的卷积神经网络,采用时域卷积和可分离卷积层来提取脑电信号的时间特征,并利用深度卷积来提取脑电信号的空间特征. 3)MSFBCNN[25 ] :在ShallowConvNet的基础上增加并行的多尺度滤波器组卷积,用于在多个时间尺度上提取特征. 4)FBCNet[26 ] :新型的滤波器组卷积网络,引入方差层来有效地聚合脑电信号的时域信息. 5)Sinc-ShallowNet[27 ] :通过堆叠时间sinc卷积层学习带通滤波器,同时利用深度卷积层来提取脑电信号的空间特征. 6)FB-Sinc-ShallowNet[28 ] :在Sinc-ShallowNet的基础上引入滤波器组结构,以实现对4个频段的时间和空间特征提取. ...
1
... 对比方法均为深度学习的MI分类方法,方法描述如下. 1)ShallowConvNet[5 ] :轻量级的卷积神经网络,用于提取脑电信号的特征;该网络结合了时域卷积和空域卷积的操作. 2)EEGNet[6 ] :紧凑型的卷积神经网络,采用时域卷积和可分离卷积层来提取脑电信号的时间特征,并利用深度卷积来提取脑电信号的空间特征. 3)MSFBCNN[25 ] :在ShallowConvNet的基础上增加并行的多尺度滤波器组卷积,用于在多个时间尺度上提取特征. 4)FBCNet[26 ] :新型的滤波器组卷积网络,引入方差层来有效地聚合脑电信号的时域信息. 5)Sinc-ShallowNet[27 ] :通过堆叠时间sinc卷积层学习带通滤波器,同时利用深度卷积层来提取脑电信号的空间特征. 6)FB-Sinc-ShallowNet[28 ] :在Sinc-ShallowNet的基础上引入滤波器组结构,以实现对4个频段的时间和空间特征提取. ...
Interpretable and lightweight convolutional neural network for EEG decoding: application to movement execution and imagination
1
2020
... 对比方法均为深度学习的MI分类方法,方法描述如下. 1)ShallowConvNet[5 ] :轻量级的卷积神经网络,用于提取脑电信号的特征;该网络结合了时域卷积和空域卷积的操作. 2)EEGNet[6 ] :紧凑型的卷积神经网络,采用时域卷积和可分离卷积层来提取脑电信号的时间特征,并利用深度卷积来提取脑电信号的空间特征. 3)MSFBCNN[25 ] :在ShallowConvNet的基础上增加并行的多尺度滤波器组卷积,用于在多个时间尺度上提取特征. 4)FBCNet[26 ] :新型的滤波器组卷积网络,引入方差层来有效地聚合脑电信号的时域信息. 5)Sinc-ShallowNet[27 ] :通过堆叠时间sinc卷积层学习带通滤波器,同时利用深度卷积层来提取脑电信号的空间特征. 6)FB-Sinc-ShallowNet[28 ] :在Sinc-ShallowNet的基础上引入滤波器组结构,以实现对4个频段的时间和空间特征提取. ...
1
... 对比方法均为深度学习的MI分类方法,方法描述如下. 1)ShallowConvNet[5 ] :轻量级的卷积神经网络,用于提取脑电信号的特征;该网络结合了时域卷积和空域卷积的操作. 2)EEGNet[6 ] :紧凑型的卷积神经网络,采用时域卷积和可分离卷积层来提取脑电信号的时间特征,并利用深度卷积来提取脑电信号的空间特征. 3)MSFBCNN[25 ] :在ShallowConvNet的基础上增加并行的多尺度滤波器组卷积,用于在多个时间尺度上提取特征. 4)FBCNet[26 ] :新型的滤波器组卷积网络,引入方差层来有效地聚合脑电信号的时域信息. 5)Sinc-ShallowNet[27 ] :通过堆叠时间sinc卷积层学习带通滤波器,同时利用深度卷积层来提取脑电信号的空间特征. 6)FB-Sinc-ShallowNet[28 ] :在Sinc-ShallowNet的基础上引入滤波器组结构,以实现对4个频段的时间和空间特征提取. ...
Visualizing data using t-SNE
1
2008
... 分别选择BCI Competition IV-2a数据集被试1和OpenBMI数据集被试36的数据特征结果进行t-SNE[29 ] 可视化. AFB-DVGCN中不同计算模块后样本可视化结果分别如图4 和图5 所示. 2个公开数据集上的样本均在模块1处理后有了较明显的分类;随着网络的深度增加,样本的特征可分性不断增强,模型分类效果逐渐明显,在模块2之后不同类别的区分程度更加清晰. ...
2
... 为了充分提取空间时间卷积后的特征信息,模型在丢弃层之后引入注意力机制模块,对选择后的特征进行增强. 如表5 所示为不同注意力机制在2种数据集上的对比结果,其中N TP 为可训练的参数总数. 为了避免过拟合,选择轻量级或无参的注意力机制模块,4种通道注意力方法分别为ECA、Triplet Attention[30 ] 、NAM[31 ] 和SimAM[32 ] . 1)ECA:通过跨局部特征通道进行特征交互和自适应选择一维卷积核的方法实现特征增强;2)Triplet Attention:通过3个分支对交叉维度交互进行捕捉实现注意力计算;3)NAM:通过减小较不显著特征的权重实现注意力计算;4)SimAM:通过3D注意力模块和能量计算函数来计算注意力权值. 由表可知,通过引入注意力机制模块,能够增强特征的表达能力,提高模型的分类性能. 在各种注意力方法中,ECA的性能和稳定性最佳,因此本研究在AFB-DVGCN中采用ECA来增强特征信息. ...
... Performance comparison of different attention mechanisms in two publicly available datasets
Tab.5 注意力机制 BCI Competition IV-2a OpenBMI acc/% kap std N TP acc/% kap std N TP Triplet Attention[30 ] 72.955 0.655 0.156 129 140 70.065 0.401 0.167 112 702 NAM[31 ] 74.653 0.662 0.108 128 940 69.583 0.392 1.660 112 502 SimAM[32 ] 72.762 0.637 0.116 128 840 67.343 0.347 0.142 112 402 ECA[9 ] 77.392* 0.699 0.103 128 843 72.657* 0.453 0.142 112 405
5. 结 语 本研究利用功能脑视图和距离脑视图进行空间特征提取,充分考虑大脑非欧式空间的特性;利用双分支网络充分考虑不同频段间的特征信息,实现了运动想象不同频域段信息的提取;利用ECA对丢弃层后的特征信息进行交互增强. 对比其他方法,AFB-DVGCN在2个公开数据集上具有更强的分类性能,准确率提高了4.29%,可为后续运动想象范式解码性能提高提供新的思路. AFB-DVGCN只在单被试实验上进行,未来计划在跨被试实验上进行验证,证明网络的泛化性,同时计划精简网络结构,减少参数. ...
2
... 为了充分提取空间时间卷积后的特征信息,模型在丢弃层之后引入注意力机制模块,对选择后的特征进行增强. 如表5 所示为不同注意力机制在2种数据集上的对比结果,其中N TP 为可训练的参数总数. 为了避免过拟合,选择轻量级或无参的注意力机制模块,4种通道注意力方法分别为ECA、Triplet Attention[30 ] 、NAM[31 ] 和SimAM[32 ] . 1)ECA:通过跨局部特征通道进行特征交互和自适应选择一维卷积核的方法实现特征增强;2)Triplet Attention:通过3个分支对交叉维度交互进行捕捉实现注意力计算;3)NAM:通过减小较不显著特征的权重实现注意力计算;4)SimAM:通过3D注意力模块和能量计算函数来计算注意力权值. 由表可知,通过引入注意力机制模块,能够增强特征的表达能力,提高模型的分类性能. 在各种注意力方法中,ECA的性能和稳定性最佳,因此本研究在AFB-DVGCN中采用ECA来增强特征信息. ...
... Performance comparison of different attention mechanisms in two publicly available datasets
Tab.5 注意力机制 BCI Competition IV-2a OpenBMI acc/% kap std N TP acc/% kap std N TP Triplet Attention[30 ] 72.955 0.655 0.156 129 140 70.065 0.401 0.167 112 702 NAM[31 ] 74.653 0.662 0.108 128 940 69.583 0.392 1.660 112 502 SimAM[32 ] 72.762 0.637 0.116 128 840 67.343 0.347 0.142 112 402 ECA[9 ] 77.392* 0.699 0.103 128 843 72.657* 0.453 0.142 112 405
5. 结 语 本研究利用功能脑视图和距离脑视图进行空间特征提取,充分考虑大脑非欧式空间的特性;利用双分支网络充分考虑不同频段间的特征信息,实现了运动想象不同频域段信息的提取;利用ECA对丢弃层后的特征信息进行交互增强. 对比其他方法,AFB-DVGCN在2个公开数据集上具有更强的分类性能,准确率提高了4.29%,可为后续运动想象范式解码性能提高提供新的思路. AFB-DVGCN只在单被试实验上进行,未来计划在跨被试实验上进行验证,证明网络的泛化性,同时计划精简网络结构,减少参数. ...
2
... 为了充分提取空间时间卷积后的特征信息,模型在丢弃层之后引入注意力机制模块,对选择后的特征进行增强. 如表5 所示为不同注意力机制在2种数据集上的对比结果,其中N TP 为可训练的参数总数. 为了避免过拟合,选择轻量级或无参的注意力机制模块,4种通道注意力方法分别为ECA、Triplet Attention[30 ] 、NAM[31 ] 和SimAM[32 ] . 1)ECA:通过跨局部特征通道进行特征交互和自适应选择一维卷积核的方法实现特征增强;2)Triplet Attention:通过3个分支对交叉维度交互进行捕捉实现注意力计算;3)NAM:通过减小较不显著特征的权重实现注意力计算;4)SimAM:通过3D注意力模块和能量计算函数来计算注意力权值. 由表可知,通过引入注意力机制模块,能够增强特征的表达能力,提高模型的分类性能. 在各种注意力方法中,ECA的性能和稳定性最佳,因此本研究在AFB-DVGCN中采用ECA来增强特征信息. ...
... Performance comparison of different attention mechanisms in two publicly available datasets
Tab.5 注意力机制 BCI Competition IV-2a OpenBMI acc/% kap std N TP acc/% kap std N TP Triplet Attention[30 ] 72.955 0.655 0.156 129 140 70.065 0.401 0.167 112 702 NAM[31 ] 74.653 0.662 0.108 128 940 69.583 0.392 1.660 112 502 SimAM[32 ] 72.762 0.637 0.116 128 840 67.343 0.347 0.142 112 402 ECA[9 ] 77.392* 0.699 0.103 128 843 72.657* 0.453 0.142 112 405
5. 结 语 本研究利用功能脑视图和距离脑视图进行空间特征提取,充分考虑大脑非欧式空间的特性;利用双分支网络充分考虑不同频段间的特征信息,实现了运动想象不同频域段信息的提取;利用ECA对丢弃层后的特征信息进行交互增强. 对比其他方法,AFB-DVGCN在2个公开数据集上具有更强的分类性能,准确率提高了4.29%,可为后续运动想象范式解码性能提高提供新的思路. AFB-DVGCN只在单被试实验上进行,未来计划在跨被试实验上进行验证,证明网络的泛化性,同时计划精简网络结构,减少参数. ...