超导MRI系统主磁场的被动匀场优化可以构建成一个目标优化的数学模型,以同时对匀场铁片质量和主磁场均匀度进行最小化. 该数学问题的传统求解模型是线性规划(linear programming, LP)模型. 但是LP算法在进行匀场优化后(通常约12
在7 T磁共振被动匀场上,主磁场的均匀度要求将会更高[19]. 并且,既需要考虑主磁场的均匀度,对匀场铁片的消耗量也会有要求,两者的优化需要达到一定的平衡. 整个被动匀场系统的匀场铁片须尽可能的稀疏,这样才能更加有利于实际工程的应用. 本研究提出遗传算法-序列二次规划(genetic algorithm-sequential quadratic programming, GA-SQP),应用到7 T超导磁共振中,既能改善主磁场的均匀度,同时能够满足匀场铁片总量的限制要求. 同时,通过增加L1-Norm正则化实现整个匀场铁片的稀疏分布.
1. 被动匀场方法
在对 MRI 系统进行被动匀场之前,须评估成像区域采样点裸磁场(Bm)的不均匀性. 成像空间的球性表面直径(DSV)也被称为感兴趣区域(volume of interest, VOI). 使用磁场探头/相机记录DSV表面直径上指定测量点的初始磁场数据,这也被称为磁场映射. 此测量磁场Bm可以表示为[B1, B2, B3,···, BN],其中,N为样本点的数量. 平均磁场强度Bavr和磁场峰峰值不均匀性Hp-p可以用于评估磁场质量,表达式[20]如下:
表中:Bm为向量Bm中的元素.
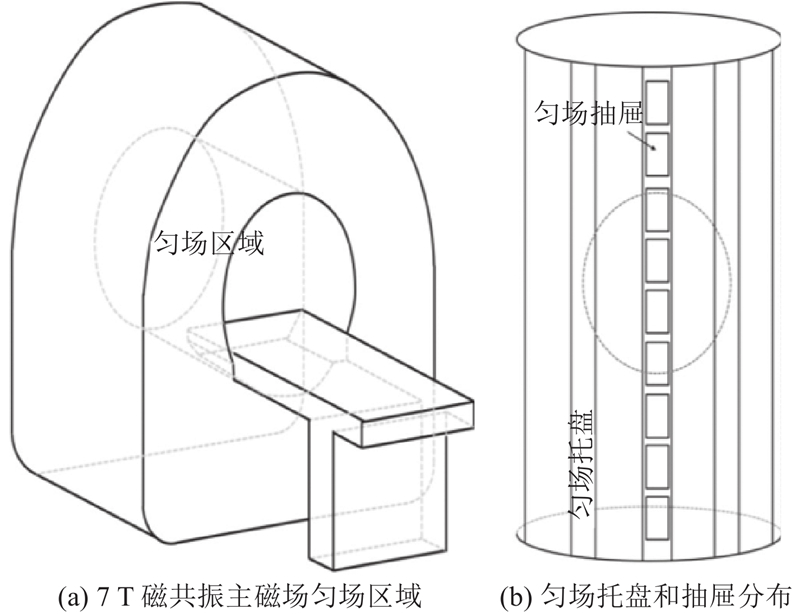
在7 T MRI系统中,将数十个匀场托盘(shim tray)插入梯度线圈组内的被动匀场层中. 每个托盘由数十个匀场抽屉(shim pocket)组成,用于容纳特定尺寸的匀场铁片,如图1所示. 由于超导磁共振磁体的高磁场强度,可以假设匀场铁片都是磁饱和的. 须建立该系统的敏感系数矩阵A,通过数值计算每个单位厚度匀场铁片对DSV 表面上每个测量点的磁场贡献来构建. 敏感系数矩阵可以通过数值计算和实验测试2种方法进行获取. 敏感系数矩阵A的维数为N×M,其中M为匀场抽屉的总数.
图 1
图 2
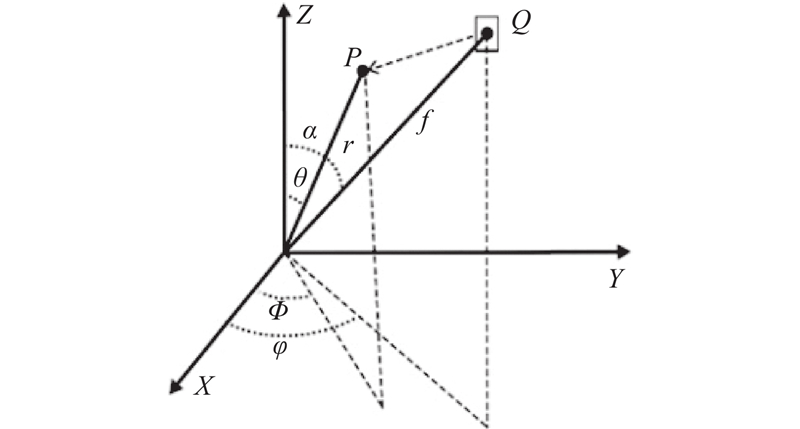
图 2 单元匀场铁片磁场效果示意图
Fig.2 Schematic diagram of magnetic field effect of unit shim iron sheet
式中: μ0为真空磁导率,Mz为匀场铁片的磁化强度,
另外,
2. 优化算法
本研究中磁共振主磁场优化的基本原理如下:以所建立的磁场均匀度非线性数学模型为基础,在特定的优化模式下,选取一定的磁共振性能参数作为优化约束,在确保铁片质量不过高的前提下,寻找最优的磁场均匀度. 在工程实践中,主磁场均匀度是磁共振设备的一项重要技术指标,对磁场均匀度进行优化,经济意义十分明显. 铁片质量下降和稀疏分布可降低人工处理时间,这对磁共振被动匀场工程实践具有重要意义. 该优化目标函数表达式如下:
式中:F(x)为被动匀场后磁场的不均匀性;λ为正则化参数;x为铁片的厚度,是N维向量;xmax为每个匀场袋中铁片的最大厚度. F(x)可进一步描述为
式中:Br为匀场后的磁场强度,Br为其中的元素;A为单位厚度匀场铁片Q对采样点P磁效应的敏感系数矩阵,是N×M的矩阵.
2.1. 遗传优化算法
在计算机科学和运筹学中,遗传优化算法(GA)是受自然选择过程启发的智能算法,属于更大的进化算法(evolutionary algorithm, EA). 它使用随机搜索并从初始成本函数开始寻找最优解,然后仅在成本最低的空间(在引导方向)进行搜索. 这个过程主要涉及3个基本操作:选择、交叉和突变. GA的核心内容包括参数编码、初始种群设置、适应度函数设计、遗传操作设计和对照参数设置. 根据该算法的原理,通过初始种群的逐代演化可以得到最优近似解. 个体的适应度代代相传,通过交叉和变异组合运作,最终产生新的种群,生成近似最优解.
GA算法根据以下6个步骤进行设计[21]:1)针对具体的优化问题,确定目标函数、决策变量和各种约束条件. 2)建立优化问题的数学模型. 3)确定编码方法:MRI被动匀场问题涉及决策变量较多,对一些决策变量的精度要求较高,针对优化问题设计的遗传算法采用浮点数编码方法. 4)确定个体适应度评估的方法:MRI主磁场优化问题属于求目标函数最小值的类型. 5)遗传操作方法设计:尽可能将适应性好的个体保留到下一代,本研究采用改进的最优保存策略进行选择操作.
2.2. SQP优化算法
SQP算法是解决非线性优化问题的有效方法[22]. SQP算法利用函数梯度和约束构造二次规划(quadratic programming, QP)子问题,然后逐步求解一系列QP子问题得到目标函数的最小值. 为了利用SQP算法求解所建立的磁场均匀度模型,将被动匀场系统的磁场均匀度模型转化为非线性约束形式,统一描述为
式中:f(x)为非线性目标函数;
拉格朗日函数可以表示为
基于拉格朗日函数二次逼近的方程的优化问题可以转换为QP子问题:
式中:脚标
式中:αk为步长参数,αk由线性搜索过程确定,以便获得评价函数的充分减小. 在此实现中使用以下形式的评价函数:
式中:
式中:Gi(x)为目标函数的梯度. 这确保了梯度较小的约束对惩罚参数的贡献更大.
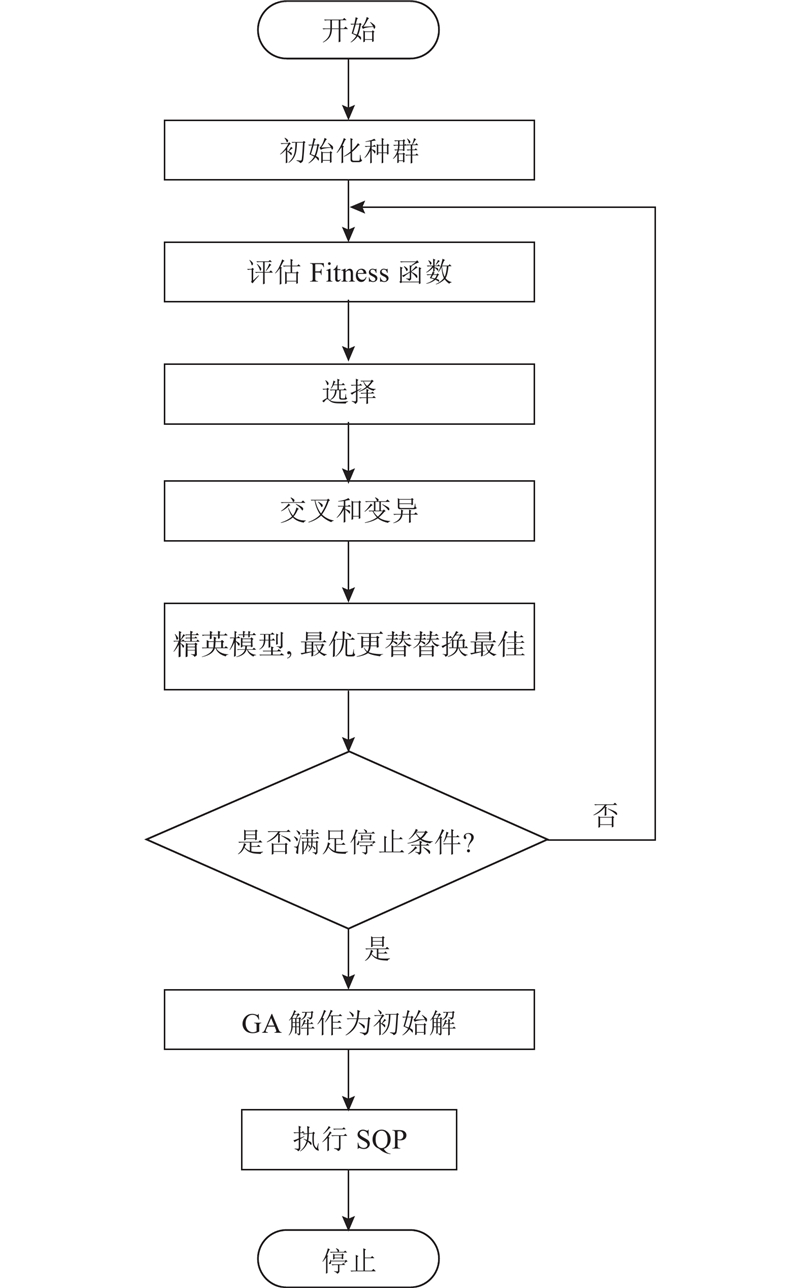
2.3. GA-SQP混合优化算法
图 3
3. 结果和分析
3.1. 初始磁场测量
表 1 7 T磁共振系统被动匀场的系统参数
Tab.1
| 物理量/单位 | 数值 |
| 磁场强度/ T | 7 |
| 球形区域直径/ mm | 400 |
| 匀场托盘半径/ mm | 360 |
| 匀场托盘数量 | 24 |
| 每个托盘匀场抽屉数量 | 24 |
| 匀场片尺寸/ mm | 40 |
| 每个匀场片厚度/ mm | 0.1 |
| 匀场抽屉最大厚度/ mm | 12 |
在所设计的被动匀场系统中,在实验中只使用一种厚度为 0.1 mm的匀场铁片. 匀场铁片尺寸为 40 mm× 50 mm,并且最大允许厚度为 12 mm. 采用塑料厚度为0.5 mm的片材封装匀场铁片. 将24个Shim Tray沿着腔体的圆周安装以进行匀场实现,每个Shim Tray包含24个Shim Pocket. Shim Tray的编号从圆周方向依次为1~24. 匀场铁片工艺采用奇偶匀场方式,一般需要2轮匀场操作执行. 如表1所示,在本超导磁共振被动匀场研究中共有576个匀场铁片位置、576个磁场采样点. 通过标准磁场相机测得磁场初始不均匀度峰峰值在40 cm DSV内为462
图 4
3.2. 基于GA算法的优化
在磁共振磁场强度为7 T,初始磁场B0=462
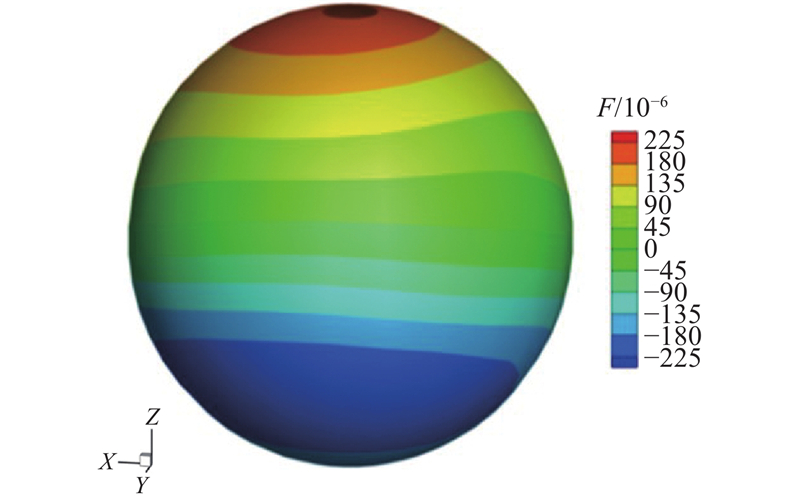
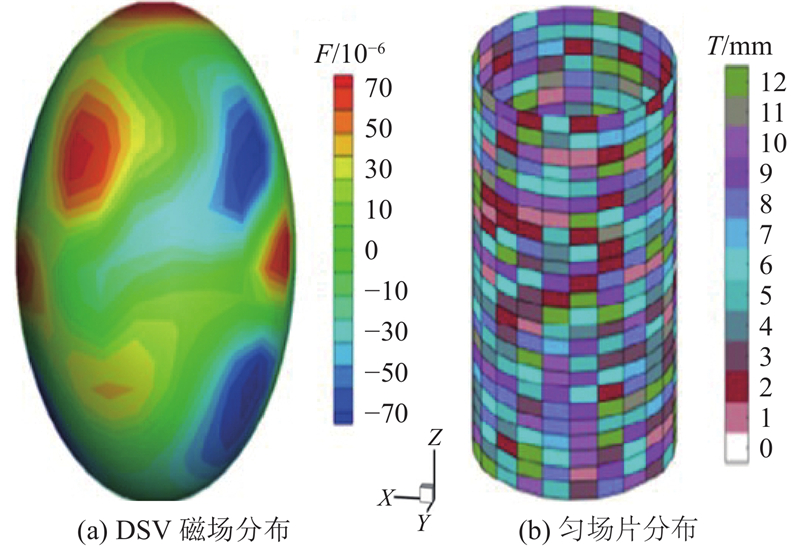
如图5所示为GA算法的仿真模拟结果. GA算法实现了磁共振磁体145
图 5
图 5 GA算法磁场分布和匀场铁片厚度仿真结果
Fig.5 Simulation results of magnetic field distribution and shim iron sheet thickness of GA algorithm
图 6
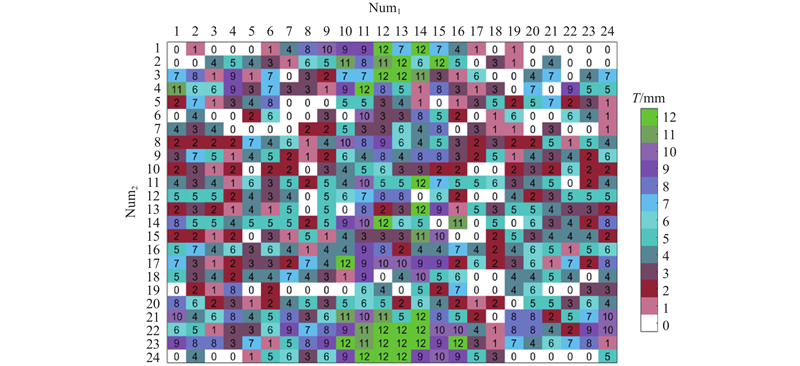
图 6 GA算法获得的匀场铁片平面分布
Fig.6 Planar distribution of iron sheets obtained by GA algorithm
3.3. 基于SQP算法的优化
表 2 不同初始点的SQP算法结果
Tab.2
| 初始点 | 算法 | t | Fo/10−6 |
| Upper bound | SQP | 3 256 | 7.9 |
| Lower bound | SQP | 367 | 5.5 |
| Middle point | SQP | 724 | 6.8 |
| Random | GA | 170 345 | 145.0 |
| GA solution | GA-SQP | 80 367 | 4.5 |
图 7
图 7 SQP算法磁场分布和匀场铁片厚度仿真结果
Fig.7 Simulation results of magnetic field distribution and shim iron sheet thickness of SQP algorithm
图 8
图 8 SQP算法获得的匀场铁片厚度平面分布
Fig.8 Planar distribution of iron sheet obtained by SQP algorithm
3.4. 基于GA-SQP混合算法的优化
在磁共振磁场强度为7 T,初始磁场B0=462
图 9
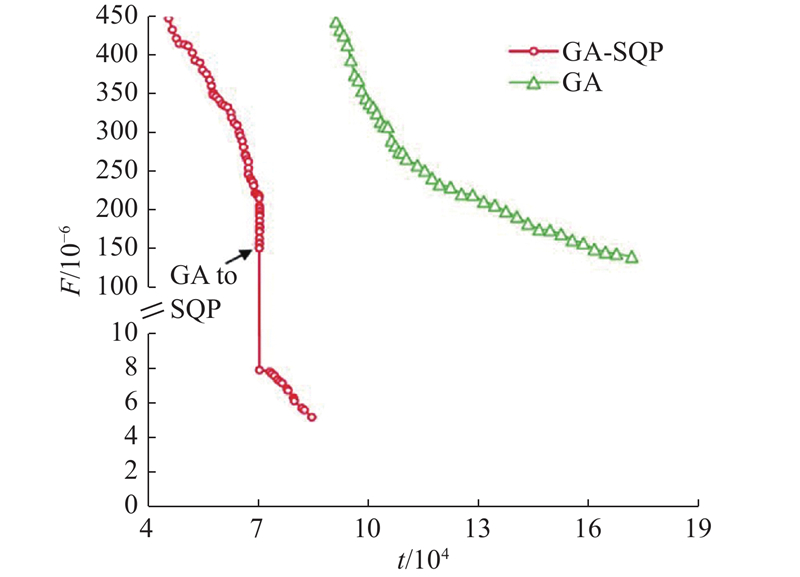
图 9 不同优化方法的优化轨迹
Fig.9 Optimization trajectory of different optimization methods
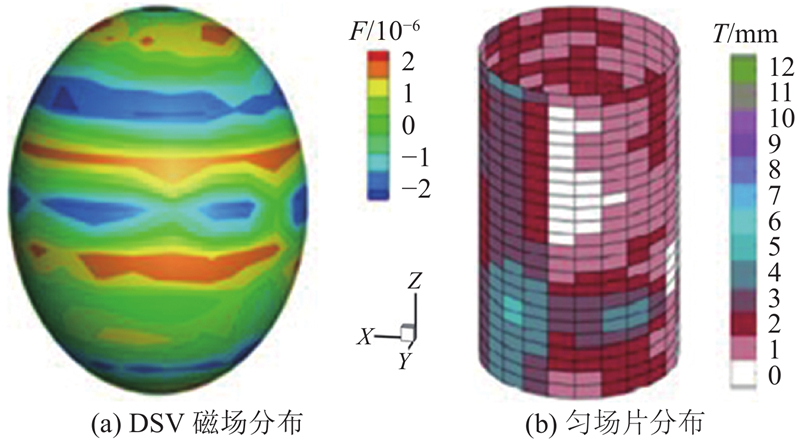
为了找到匀场铁片稀疏的解决方案,在GA-SQP算法中添加 L1-Norm 正则化项. 然后,重新运行优化程序,得到第2个匀场磁场. 在匀场铁片进行四舍五入后,主磁场均匀度约为4.5
图 10
图 10 GA-SQP 算法磁场分布和匀场铁片厚度仿真结果
Fig.10 Simulation results of magnetic field distribution and shim iron sheet thickness of GA-SQP algorithm
图 11
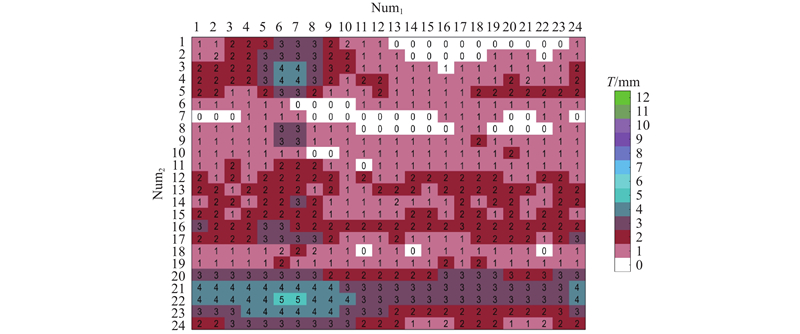
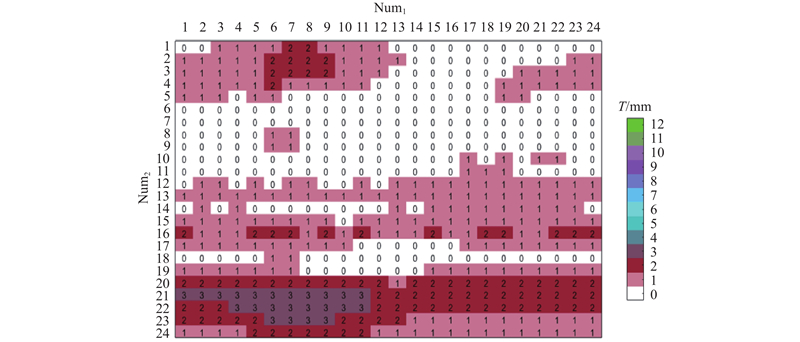
图 11 GA-SQP 混合算法获得的匀场铁片平面分布
Fig.11 Planar distribution of iron sheet obtained by GA-SQP hybrid algorithm
3.5. 多种优化算法对照研究
将GA-SQP混合算法与LS、LP、GA、SQP算法进行比较. 最优磁场均匀度和匀场铁片消耗质量结果如表3所示. 表中,M为匀场铁片消耗质量. 其中,采用Matlab 内置函数 fmincon 用于解决上述被动匀场非线性问题. 同时,通过Matlab内置的GA函数实现GA算法. 仿真计算环境如下:Intel i7,16 G RAM.
表 3 多种优化算法的仿真结果
Tab.3
| 算法 | F/10−6 | M/kg |
| GA | 145.0 | 5.6 |
| GA-SQP | 4.5 | 0.8 |
| SQP | 5.5 | 1.5 |
| LS | 6.8 | 9.6 |
| LP | 12.0 | 9.5 |
4. 讨 论
磁共振主磁场被动匀场是病态问题的数学模型,需要求解的变量高达数百个. 在工程实践中,须在成像区域的整体磁场质量和匀场铁片的总质量之间进行权衡. 本研究所提出的 GA-SQP 算法得到的磁场均匀度为4.5
GA-SQP混合优化算法既保留了GA的全局搜索性能,又吸收了SQP算法的快速收敛优点,整体改善了7 T MRI磁体主磁场的均匀度. GA-SQP混合优化算法将带来几项工程效益. 首先,磁共振磁体的主磁场更加均匀,从而能够生成高质量的MRI图像,有利于接下来的人体或动物组织图像精准分割. 其次,磁共振被动匀场的铁片更加稀疏,减少匀场铁片的使用,可以提高热稳定性并减少涡流效应. 另外,本研究提出的算法具有较强的鲁棒性,同时不需要对标准匀场硬件系统进行任何修改.
由于多种因素,例如匀场片的位置偏差和匀场片的尺寸偏差,模拟和实际之间存在一定差异. 因此,匀场是一个多次迭代过程,可以逐步进行匀场优化(通常需要2~4 次迭代).
还有以下几个方面的问题有待进一步研究:在磁场均匀度的寻优过程中,当采用的不同的正则化参数时,获得的磁场均匀度和匀场铁片厚度将会不同,可能会使优化结果“不优”甚至更差. 因此,须研究如何保证磁场均匀度数学模型与最优匀场铁片的一致性.
5. 结 论
(1)在传统的GA算法下,7 T磁共振磁场均匀度虽然能从462
(2)7 T磁共振被动匀场在SQP优化算法下,磁场均匀度能从462
(3)7 T磁共振被动匀场在GA-SQP混合优化算法下,磁场均匀度能先从462
(4)7 T磁共振被动匀场在GA-SQP混合优化算法下,可以通过L1-Norm正则化实现匀场铁片的稀疏分布要求,满足实际工程的需求.
(5)模拟仿真对比表明,基于GA-SQP混合优化算法的7 T磁共振磁体被动匀场方法,在磁场均匀度和匀场铁片质量消耗方面能得到最佳平衡,同时在匀场铁片厚度分布方面获得较好的稀疏性.
参考文献
Formation of homogeneous field in a shielded superconducting solenoid for an MRI
[J].
Measuring method and magnetic field homogeneity optimization for magnets used in NUM-imaging
[J].
Superconducting systems for MRI-present solutions and new trends
[J].DOI:10.1109/TASC.2005.849580 [本文引用: 1]
Passive shimming of MR magnets: algorithm, hardware and results
[J].DOI:10.1109/77.233719 [本文引用: 1]
Passive shimming of the superconducting magnet for MRI
[J].DOI:10.1109/77.402639 [本文引用: 1]
A hybrid field-harmonics approach for passive shimming design in MRI
[J].DOI:10.1109/TASC.2011.2112358 [本文引用: 2]
Passive shim design and a shimming approach for Biplanar permanent magnetic resonance imaging magnets
[J].DOI:10.1109/TMAG.2007.914770 [本文引用: 1]
A novel design method of passive shimming for 0.7-T Biplanar superconducting MRI magnet
[J].
Passive shimming based on mixed integer programming for MRI magnet
[J].
A novel optimal design method of passive shimming for permanent MRI magnet
[J].DOI:10.1109/TMAG.2007.916267 [本文引用: 1]
A SQP optimization method for shimming a permanent MRI magnet
[J].DOI:10.1016/j.pnsc.2009.04.007 [本文引用: 1]
Passive shimming of a superconducting magnet using the L1-norm regularized least square algorithm
[J].DOI:10.1016/j.jmr.2015.11.019 [本文引用: 1]
Static magnetic field shimming calculation using TSVD regularization with constraints of iron piece placements
[J].
Passive shimming for magic-angle-spinning NMR
[J].
A theoretical design approach for passive shimming of a magic-angle-spinning NMR Magnet
[J].
The optimal target magnetic field method for passive shimming in MRI
[J].DOI:10.1007/s10948-019-05241-2 [本文引用: 1]
On the passive shimming of a 7 T whole-body MRI superconducting magnet: implementation with minimized ferromagnetic materials usage and operable magnetic force control
[J].DOI:10.1002/mp.16538 [本文引用: 1]
A new design method for completely open architecture permanent magnet for MRI
[J].DOI:10.1109/TMAG.2005.845080 [本文引用: 1]
Genetic algorithms in computer aided design
[J].DOI:10.1016/S0010-4485(03)00003-4 [本文引用: 1]
A hybrid GA-SQP optimization technique for determination of kinetic parameters of hydrogenation reactions
[J].DOI:10.1016/j.compchemeng.2007.06.018 [本文引用: 1]
Hybrid GA-SQP algorithms for three-dimensional boundary detection problems in potential corrosion damage
[J].
On-line performance optimization of aero engine control system
[J].DOI:10.1016/S0005-1098(03)00224-3 [本文引用: 1]