随着科学技术的快速发展,人们对轻型、小型电力设备的便携性提出了更高的要求. 因此,如何降低成本、减小设备体积和提高供电电源功率密度等已成为人们关注的重点[1-3]. 单电感双输出(single inductor double output,SIDO) Buck-Boost变换器仅使用一个电感就可以将1路输入电压转换为2路输出电压,减小了设备体积,且具有功率密度高、无电磁干扰的优点,在便携式设备中具有广泛的应用前景[4-7]. 不过,该变换器是强非线性、时变的耦合系统,存在严重的交叉影响,且先导通支路的输出-控制的暂态模型中存在右半平面零点,使得该变换器具有非最小相位特性[8]. 交叉影响以及非最小相位特性导致SIDO Buck-Boost变换器的控制变得更加困难.
为了抑制SIDO DC-DC变换器的交叉影响,国内外学者对SIDO Buck变换器进行了深入研究,提出了许多控制策略,如:电压纹波控制[9]、峰值电流控制[10]、滑模自抗扰控制[11]等. 以上控制策略对于改善SIDO Buck变换器的交叉影响有较好的效果,但SIDO Buck变换器是最小相位系统,这些控制策略直接应用到非最小相位SIDO Buck-Boost变换器上对交叉影响的抑制效果有限. 对于SIDO Buck-Boost变换器的控制策略研究的相关文献较少,已有文献主要针对的是非最小相位Boost变换器. 吴忠等[12]利用电流模式控制解决了Boost变换器的非最小相位特性问题. 舒萤[13]将储能函数引入到控制量中,解决Boost变换器的非最小相位特性. 但由于Boost变换器是单输入单输出的系统,而SIDO Buck-Boost是单输入双输出的强耦合系统,因此以上控制策略对抑制非最小相位SIDO Buck-Boost的交叉影响而言效果有限,仅具有借鉴意义.
受上述文献启发,针对电感电流连续导电模式(continuous conduction mode, CCM)的SIDO Buck-Boost变换器的交叉影响及非最小相位特性,提出基于ESO的改进非奇异快速终端滑模和ADRC相结合的控制策略. 在主路控制中使用ADRC进行解耦. 为了解决先导通支路中的非最小相位特性,在支路中选取系统的储能函数对非奇异快速终端滑模控制(nonsingular fast terminal sliding mode control,NFTSMC)中的状态量进行控制,并结合改进型扩张状态观测器. 利用Lyapunov理论对主路ADRC、支路滑模控制和支路观测器进行稳定性分析. 基于硬件在环(hardware-in-the-loop,HIL)系统搭建实验平台,进行实验验证.
1. CCM SIDO Buck-Boost变换器建模
图 1
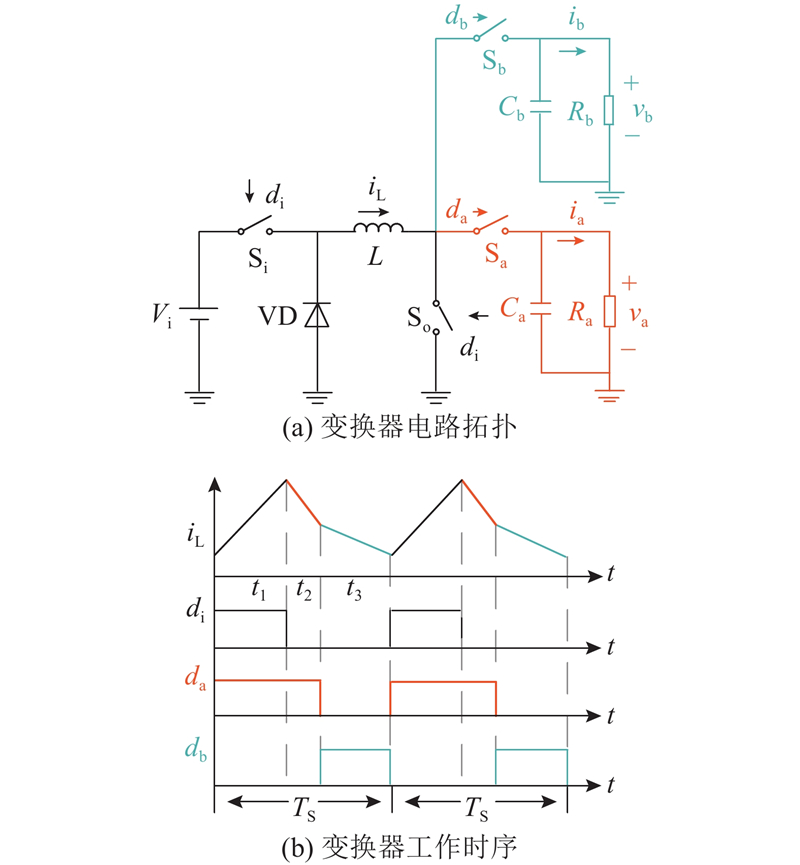
图 1 CCM SIDO Buck-Boost变换器电路拓扑及工作时序
Fig.1 Circuit topology and operating timing of CCM SIDO Buck-Boost converter
由图1可推导出SIDO Buck-Boost变换器的状态空间平均模型:
式中:va、vb为两支路输出电压瞬时值;两支路占空比互补,即满足da+db=1.0.
由式(1)可以推导出两支路的增益表达式如下:
式中:Va和Vb为va和vb的稳态值.
分析式(1)可知,支路a的电压增益中存在支路b的信息,支路b同理,因此两支路存在交叉影响.
根据式(1)可得SIDO Buck-Boost变换器在CCM工作时支路a、b控制/输出的传递函数G1(s)、G2(s)分别为
式中:
分析式(3)可知,先导通的a支路传递函数G1(s)中含有一个右半平面零点,该支路具有非最小相位特性. 非最小相位特性导致SIDO Buck-Boost变换器暂态性能变差,控制器设计变得更加困难.
2. SIDO Buck-Boost控制器设计
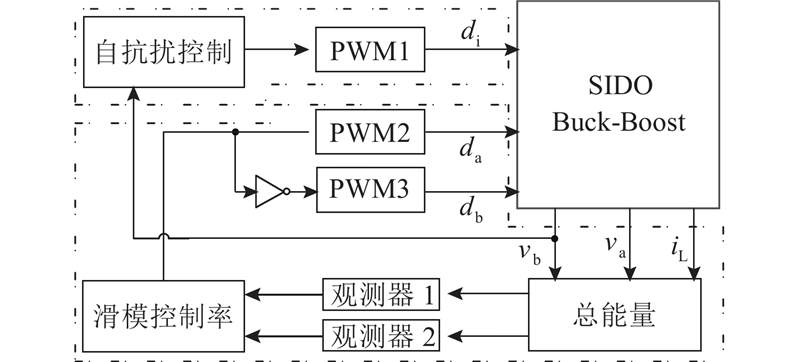
所提系统控制策略结构如图2所示. 主路为自抗扰控制,支路为基于改进扩张状态观测器的非奇异快速终端滑模控制.
图 2
图 2 SIDO Buck-Boost变换器的控制框图
Fig.2 Control block diagram of SIDO Buck-Boost converter
2.1. 主路控制器设计
2.1.1. 主路控制结构
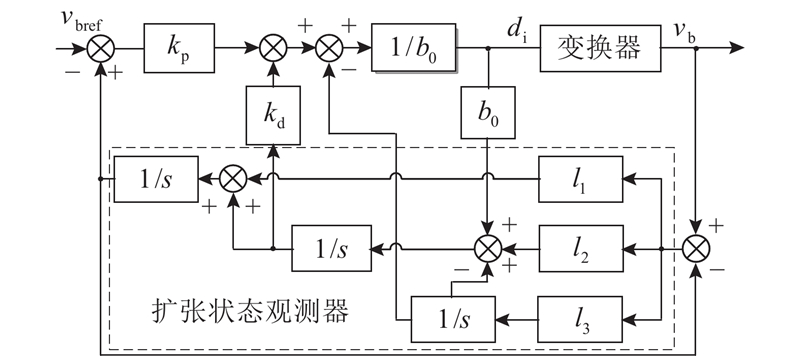
主路开关管Si和So共用一个控制信号. 如图3所示为主路ADRC控制结构框图.
图 3
2.1.2. 自抗扰控制器设计
式(3)中的G2(s)可以拟合为
式中:
根据文献[21]可知,二阶自抗扰范式为
式中:y1=vb,u=di,ω为内部扰动项,g为支路间耦合产生的扰动和外部扰动的总和,b0为控制量增益.
联立式(4)、(5)可得该变换器主路自抗扰范式为
定义系统状态变量为
式中:
根据式(7)设计主路ESO为
式中:
联立式(5)、(8)可得系统状态反馈控制律:
若ESO观测精度足够高,则可忽略观测误差,即
设计ADRC中的PD控制律为
式中:vbref为b支路输出电压参考值,kp和kd为控制器增益.
根据带宽法[21]将ESO所有的极点和反馈控制律中的所有极点分别都配置到ωc和ωo处,可得ADRC中的kp、kd和观测器增益l1、l2和l3分别为
2.2. 支路控制器设计
2.2.1. 支路控制结构
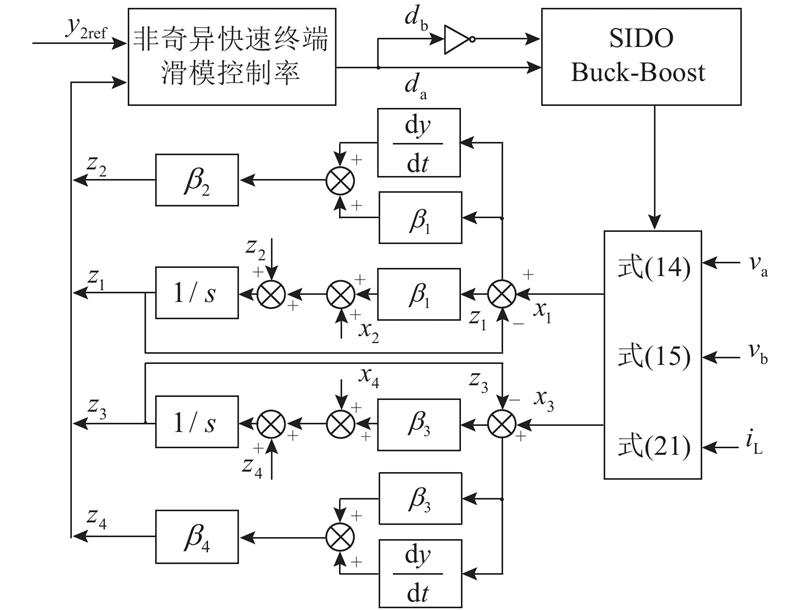
支路开关管Sa和Sb互补导通. 在支路控制中,为了抑制两支路间的交叉影响,须设计ESO对能量函数和所控支路的扰动项进行观测,并结合改进趋近律的非奇异快速终端滑模进行控制,提高系统的暂态和稳态性能. 如图4所示为支路控制结构框图.
图 4
2.2.2. 滑模控制器设计
SIDO Buck-Boost变换器先导通支路具有非最小相位特性,根据文献[16]可知,将变换器中储能元件的能量当作状态量并结合ESO进行控制,可以解决系统的非最小相位问题和强耦合问题,减少传统双环控制中的参数选取,提高系统性能. 因此,构造系统的能量函数为
定义能量的误差为e0,误差的一阶导数为e1,表达式分别为
式中:y2ref为总能量参考值.
对式(14)进行求导可得
式中:
构建非奇异快速终端滑模面表达式为
式中:a、c和β5为系数,均大于0;p大于q,且p和q为正奇数.
对式(16)求导可得
将式(15)代入式(17)可得
由于指数滑模趋近律的开关切换项存在抖振,可对指数滑模趋近律进行改进来消除抖振,改进后的新型滑模趋近律为
改进后的新型趋近律包含2部分,第1部分是含有状态变量(x=e0)和滑模面幂次项的变速趋近律
联立式(18)、(19)可得控制律:
2.2.3. 改进扩张状态观测器设计
传统ESO由于精度不够高,导致扩张项不能完全追踪误差,根据文献[22]可对传统ESO进行改进,从而提高观测精度. 具体改进扩张状态观测器设计如下.
定义x1、x2、x3和x4为
联立式(15)、(21)可得
根据式(22)构建改进型ESO为
式中:z1、z2分别为x1和扰动f1的观测值;z3、z4分别为x3和扰动f2的观测值;
将式(23)代入式(20)可得系统的控制律:
2.3. 稳定性证明
2.3.1. 改进型趋近律的滑模稳定性证明
考虑系统受到不确定扰动后的
式中:f(x)和r(x)为已知量,h为扰动.
将式(25)代入式(16)中,并求导数可得
假设r(x)为非奇异函数,集总扰动h未知且有界,即|h|≤M,M为常数. 可得系统的等效控制律da表达式为
式中:
将式(27)代入式(26)可得
引理1[23]
1) V大于0;
2) V的导数小于0.
3) 存在实数m>0、n>0和一邻域N
则函数
定理1 式(28)中s在有限时间收敛如下区域:
证明 设计Lyapunov函数为
对式(30)求导数可得
式(31)展开为
由引理1可知
联立式(30)、(33)可得
由式(31)可知
因此,由引理可知,s关于平衡点有限时间收敛,收敛区域为
同理,由式(33)、(36)可得出滑模面s的收敛域. 综上所述,当存在扰动时,所提趋近律会在有限时间内收敛到如下区域:
定理1得证.
2.3.2. 支路扩张状态观测器稳定性证明
因文中两路观测器一样,为了节约篇幅,仅证明一路观测器的稳定性.
定义误差h1和h2为
令
构造
式中:
根据式(40)可得系统Lyapunov函数V1为
对式(41)求导可得
分析式(41)可知,
分析式(42),当
当
分析式(42)、(43)可得稳态误差为
2.3.3. ADRC稳定性证明
定义主路的跟踪误差如下:
定义扩张状态观测器的观测误差分别如下:
将式(7)、(8)、(45)代入式(46),化简可得
联立式(8)、(47),可得
选取e=[ev1, ev2, eo1, eo2, eo3]T为新的状态变量,若不考虑外部扰动和模型的不准确性,联立式(47)、(48)可得
式中:
由式(48)、(49)可得系统的特征多项式为
分析式(50)可知该特征方程的特征根都位于s平面的左半平面,因此该系统是大范围渐近稳定的,当
3. 实验分析
为了验证控制算法的有效性及优越性,基于HIL搭建了SIDO Buck-Boost变换器实验平台,该实验平台由MT6020实时仿真器、DSP控制器以及上位机构成,并将本研究所提控制策略与PI、滑模+ESO控制进行实验对比. 实验电路参数为Vi=20 V,Ra=25 Ω,Rb=15 Ω,va=25 V,vb=15 V,fs=20 kHz,L=80 μH,Ca=Cb=260 μF;控制器参数为ωo=2.1×103,ωc=1.5×103,β1=5.5×103,β2=8.5×103,β3=5.0×103,β4=6.5×103,β5=7.2×103,β6=2.2×102,k1=5.0×102,k2=1.1×103,a=7.1×102,c=1.0×103,b0=6.5×107.
3.1. 系统抗负载扰动实验对比分析
图 5
图 5 支路a负载扰动时不同控制策略实验对比
Fig.5 Experimental comparison of different control strategies for branch a load disturbance
图 6
图 6 支路b负载扰动时不同控制策略实验对比
Fig.6 Experimental comparison of different control strategies for branch b load disturbance
图中支路b的一种扰动条件为负载突然加重,即ib由1 A突增到2 A. 分析图6可知,在PI控制策略下,负载扰动导致支路b的电压跌落为1.9 V,过渡过程时间为7 ms;交叉影响导致支路a的电压超调为1.9 V,过渡过程时间为7 ms. 在滑模+ESO控制策略下,负载扰动导致支路b的电压跌落为0.9 V,过渡过程时间为6 ms;交叉影响导致支路a的电压超调量较小,且过渡过程时间较短. 在本研究所提控制策略下,负载扰动导致支路b本身的电压跌落和过渡时间都较小,且交叉影响导致支路a的电压超调和过渡时间较小.
由上述分析可知,在发生负载扰动时,本研究所提控制策略相较于其他2种控制策略具有更优的暂态特性,且较好地抑制了系统的交叉影响.
3.2. 系统抗输入电压扰动实验对比分析
不同控制策略下系统抗输入电压扰动的实验结果如图7所示. 图中,其中一种扰动条件为输入电压突然升高,即Vi由20 V突增到30 V. 在PI控制策略下,输入电压扰动导致支路a的电压超调为2.1 V,过渡过程时间为9 ms;支路b的电压超调为1.9 V,过渡过程时间为7 ms. 在滑模+ESO控制策略下,输入电压扰动对支路a电压和支路b电压造成的波动相较于PI控制较小,并且过渡过程时间较短. 在本研究控制策略下,支路a和支路b的电压的超调和过渡过程时间都极小.
图 7
图 7 输入电压扰动时不同控制策略实验对比
Fig.7 Experimental comparison of different control strategies during input voltage disturbance
另一种扰动条件为输入电压突降,即Vi由30 V突降到20 V. 在PI控制策略下,输入电压扰动导致支路a的电压跌落为1.9 V,过渡过程时间为8 ms;支路b的电压跌落为1.5 V,过渡过程时间为10 ms. 在滑模+ESO控制下,输入电压扰动对支路a电压和支路b电压造成的波动相较于PI控制较小,并且过渡过程时间较短. 在本研究控制策略下,支路a和支路b的电压的超调和过渡过程时间都极小.
由上述分析可知,在输入电压突变时,本研究所提控制策略相较于其他2种控制策略在抑制交叉影响和暂态恢复过渡过程方面都具有良好的性能.
综上实验结果可知,所提控制策略在抑制负载扰动和输入电压扰动方面较传统控制具有更加优越的性能,同时也验证了理论分析的正确性.
4. 结 论
提出基于ESO的改进非奇异快速终端滑模和ADRC复合策略,通过与PI控制以及滑模+ESO进行控制效果对比,可以得出如下结论:
(1) 主路中采用ADRC能较好地进行输出端两支路的解耦效应;支路中利用改进ESO进行解耦,选择改进趋近律的非奇异快速终端滑模能较好地提高系统的暂态性能.
(2) 所提控制策略在系统受到负载和输入电压扰动时,相较于其他2种控制策略,具有暂态响应速度快、超调量小以及抑制交叉影响良好的优点.
(3) 所提控制策略能较好地解决非最小相位SIDO Buck-Boost变换器的交叉影响严重以及暂态性能较差的问题,且具有较好的工程应用价值.
(4) 本研究主要基于电感电流连续模式,未考虑该变换器工作在电感电流断续模式的情况,后续将继续深入研究该变换器在电感电流断续模式下工作的非线性控制策略.
参考文献
Lyapunov-based control strategy for a single-input dual-output three-level DC/DC converter
[J].
A capacitor current and capacitor voltage ripple controlled SIDO CCM buck converter with wide load range and reduced cross regulation
[J].
A pseudo-CCM/DCM SIMO switching converter with freewheel switching
[J].
Single-inductor multiple-output inverter with precise and independent output voltage regulation
[J].
Modular expandable multiinput multioutput (MIMO) high step-up transformerless DC-DC converter
[J].
Choosing coefficient of coupling for coupled SIDO converters
[J].
Effect of coupling on discontinuous conduction mode of coupled inductor SIDO Boost Converter
[J].
单电感双输出Buck-Boost变换器的非最小相位特性分析及控制策略
[J].
Analysis of non-minimum phase characteristics and control strategies for single-inductor dualoutput buck-boost converters
[J].
Dynamic freewheeling control for SIDO buck converter with fast transient performance, minimized cross-regulation, and high efficiency
[J].
Unified model of peak current mode controlled coupled SIDO converters
[J].
基于扩张状态观测器的单电感双输出Buck变换器滑模解耦控制
[J].
Sliding mode decoupling control of single inductor dual output buck converter based on extended state observer
[J].
基于电流模式的DC/DC升压变换器非线性PI控制
[J].
Nonlinear PI control of DC/DC boost power converters based on current mode
[J].
Sliding mode control based on linear extended state observer for DC-to-DC buck-boost power converter system with mismatched disturbances
[J].
Sliding-mode control of a boost converter under constant power loading conditions
[J].
Boost变换器精确反馈线性化滑模变结构控制
[J].
Sliding mode control of boost converter based on exact feedback linearization
[J].
Trajectory tracking strategy for sliding mode control with double closed-loop for lawn mowing robot based on ESO
[J].
自抗扰控制器及其应用
[J].DOI:10.3321/j.issn:1001-0920.1998.01.005 [本文引用: 1]
Auto disturbances rejection controller and its applications
[J].DOI:10.3321/j.issn:1001-0920.1998.01.005 [本文引用: 1]
不稳定对象及非最小相位对象的自抗扰控制仿真研究
[J].
Simulation study on auto-disturbance-rejection control for unstable systems and non-minimum phase systems
[J].
ADRC dynamic stabilization of an unstable heat equation
[J].
线性扩张状态观测器的改进及观测精度分析
[J].DOI:10.11887/j.cn.201706017 [本文引用: 1]
Improvement and observation accuracy analysis of linear extended state observer
[J].DOI:10.11887/j.cn.201706017 [本文引用: 1]