随着“碳达峰，碳中和”目标的提出，以及大规模风电和光伏接入综合能源系统，系统的灵活性需求日益增加^[1]. 区域综合能源系统以输电网和气网为网架，以能量枢纽为节点，是联通能源生产者和消费者的有效手段，可利用自身多种灵活性资源和多能互补特性，满足系统的灵活性需求^[2]. 在综合能源系统灵活性研究方面，Wu等^[3]针对提高综合能源系统运行的灵活性和准确性，提出考虑多能源灵活性的两阶段滚动策略. Sumanth等^[4]针对灵活性评估不稳定问题，提出基于灵活性资源运行范围和爬坡能力的灵活性指标. Jiang等^[5]针对IES电热联合调度问题，提出基于广义蓄热模型的评价体系，并且引入灵活性指标. Huo等^[6]为解决综合能源系统 (integrated energy system, IES)热电联产的电热耦合和可再生能源带来的不稳定性问题，提出涉及灵活性、经济性、安全性和可靠性的指标体系，量化和分析系统的灵活性. 边晓燕等^[7]针对微网有功功率平衡问题，提出考虑灵活性储备的微电网分布式调控策略. 张高航等^[8]为了提高系统的风电接纳能力，提出计及源网荷储灵活性的日前优化调度. 然而，以上研究均只考虑了系统本身的灵活性资源. 合适的灵活性改造对提高灵活性调节能力也有重要意义. 在各种灵活性改造中，碳捕集与封存技术(carbon capture and storage，CCS)作为重要的降碳手段，是我国践行低碳发展战略的重要技术选择以及实现碳中和目标的关键手段^[9]. 崔杨等^[10]为了提高系统低碳性，将价格型需求响应和碳捕集技术引入到调度模型中. 崔杨等^[11]挖掘源荷两侧低碳资源，在碳捕集模型中引入多时间尺度的方法. 齐先军等^[12-14]在碳捕集技术的改造类别中，分别采用加装存储器、运用灵活捕集运行模式技术、运用储液罐缓存的方法，实现碳捕集机组的灵活运行. 吉兴全等^[15]构建了输电网机组组合模型和配电网运行灵活性优化调度模型，高瑞阳等^[16]提出考虑灵活性资源与低碳交互结构的，区域综合能源系统联盟参与配电网调峰调度的优化调度策略. 尽管已有研究分析碳捕集技术的灵活性特点，但较少有研究从系统灵活性需求和资源的角度，引入碳捕集机组的灵活运行模型，分析碳捕集技术对满足灵活性需求的作用.

针对电-气综合能源系统的多主体运营特点，为了调用各能量枢纽的灵活性调节能力，提高各主体的自主性和保护各主体的隐私性，应选取适宜方法进行协调调度. 目标级联分析法作为解决非集中式、层次结构协调问题的方法，允许各元素自主决策，父代元素对子代元素的决策进行协调优化而获得问题的整体最优解^[17]. 已有部分研究将此方法应用于优化问题的求解. 张旋等^[18]利用目标级联分析法求解输电网结构优化问题，谢敏等^[19]针对含多微网的配电系统的动态经济调度问题，利用目标级联分析法进行求解.

为了提高多园区综合能源系统的灵活性和低碳性，同时保证各主体的自主性，提出考虑多种灵活性资源的IES分布式低碳经济调度模型. 主要工作如下：1）对各灵活性资源进行建模，提出IES灵活性裕度约束，建立考虑灵活性的IES双层优化模型. 2）引入碳捕集机组的灵活运行模型和阶梯式碳交易模型，分析碳捕集技术对灵活性的有效性. 3）采用目标级联分析法，实现能源供应商和能源运营商的平衡与协同优化.

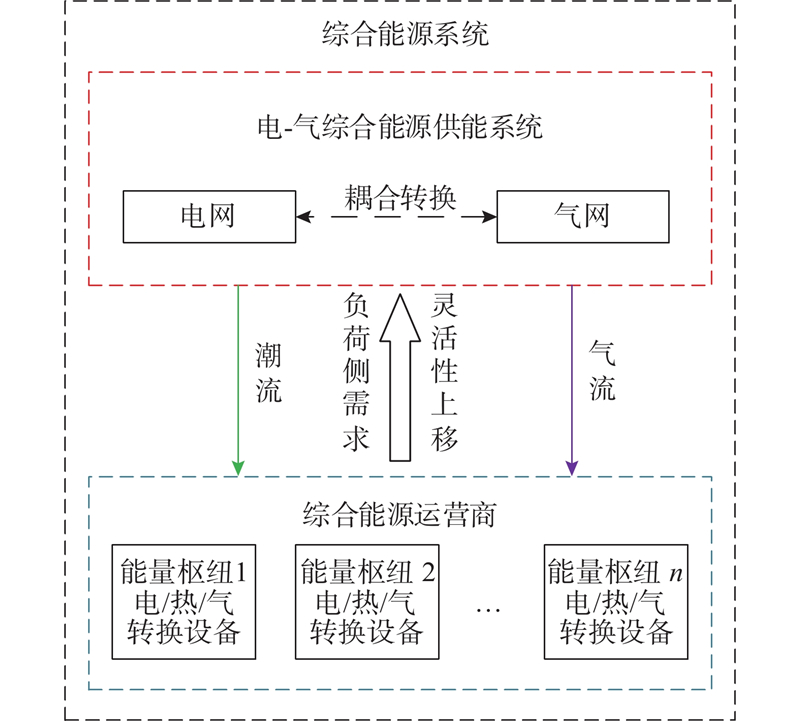
根据IES运营主体结构，本研究所考虑的典型IES如图1所示，由IES能源供应商和IES能源运营商组成. 能源供应商包含电网和气网组成的多能传输网络，侧重于满足负荷需求、降低供能成本以及满足灵活性调节需求. 能源运营商由多能量枢纽组成，侧重于服务用户的多能负荷、提高用能效益和满足能量转换需求等. 系统的灵活性需求多由能量枢纽的负荷端产生，而灵活性资源多由供能系统提供，因此灵活性需求可通过联络线上移至能源供应商.

考虑IES系统多主体运营特性，提出IES双层分布式协调优化调度模型. 上层供能系统以供能成本最小为目标函数，下层IES园区服务系统以各能量枢纽的运行成本最小为目标函数，考虑分散协调优化，采用目标级联分析法进行求解.

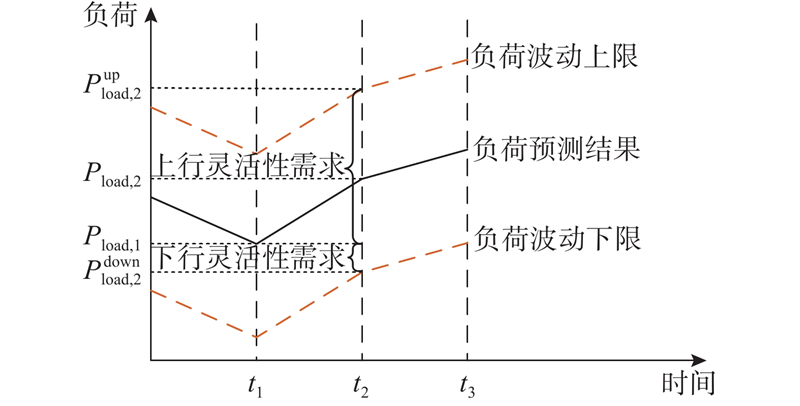
风电光伏等可再生能源的波动、IES电热气负荷预测误差以及多能转换设备的效率等都会影响系统的灵活性调节能力. 通常负荷在某一时刻的灵活性需求是下一时刻的负荷预测值减去该时刻的负荷预测值. 但如果预测结果与实际情况不符，就会导致计算结果产生偏差. 因此，引入上行灵活性安全裕度和下行灵活性安全裕度对灵活性需求进行分析，如图2所示. 图中，$ {P_{{\mathrm{load}},1}} $和$ {P_{{\mathrm{load}},2}} $分别为${t_1}$和${t_2}$时刻的负荷，$ P_{{\mathrm{load}},2}^{{\text{up}}} $和$ P_{{\mathrm{load}},2}^{{\text{down}}} $分别为${t_2}$时刻的负荷波动上限和下限.

可以推导出系统的灵活性需求模型：

(1)$ \left. \begin{gathered} R_t^{{\text{up}}} = \max \;\{ 0,\;{P_{{\text{load}},t+1}} - {P_{{\text{load}},t}}+Y_t^{{\text{up}}}\} , \\ R_t^{{\text{down}}} = \max \;\{ 0,\;{P_{{\text{load}},t}} - {P_{{\text{load}},t+1}}+Y_t^{{\text{down}}}\} . \\ \end{gathered} \right\} $

式中：$ R_t^{{\text{up}}} $和$ R_t^{{\text{down}}} $分别为$t$时刻的上行和下行灵活性需求，$ {P_{{\text{load}},t}} $为$t$时刻的负荷，$ Y_t^{{\text{up}}} $和$ Y_t^{{\text{down}}} $分别为$t$时刻的上行灵活性安全裕度和下行灵活性安全裕度^[20].

灵活性资源模型考虑碳捕集机组、风电、光伏、储能和气网，模型建立如下：

(2)$ \left. \begin{gathered} F_t^{{\text{up}}} = F_{{\text{ccs}},t}^{{\text{up}}}+F_{{\text{wind}},t}^{{\text{up}}}+F_{{\text{pv}},t}^{{\text{up}}}+F_{{\text{soc}},t}^{{\text{up}}}+F_{{\text{gas}},t}^{{\text{up}}}, \\ F_t^{{\text{down}}} = F_{{\text{ccs}},t}^{{\text{down}}}+F_{{\text{wind}},t}^{{\text{down}}}+F_{{\text{pv}},t}^{{\text{down}}}+F_{{\text{soc}},t}^{{\text{down}}}+F_{{\text{gas}},t}^{{\text{down}}}. \\ \end{gathered} \right\} $

式中：$ F_t^{{\text{up}}} $和$ F_t^{{\text{down}}} $分别为$t$时刻系统提供的上行灵活性和下行灵活性；$ F_{{\text{ccs}},t}^{{\text{up}}} $、$ F_{{\text{wind}},t}^{{\text{up}}} $、$ F_{{\text{pv}},t}^{{\text{up}}} $、$ F_{{\text{soc}},t}^{{\text{up}}} $、$ F_{{\text{gas}},t}^{{\text{up}}} $分别为碳捕集机组、风电、光伏、储能和气网$t$时刻提供的上行灵活性能力；$ F_{{\text{ccs}},t}^{{\text{down}}} $、$ F_{{\text{wind}},t}^{{\text{down}}} $、$ F_{{\text{pv}},t}^{{\text{down}}} $、$ F_{{\text{soc}},t}^{{\text{down}}} $和$ F_{{\text{gas}},t}^{{\text{down}}} $分别为碳捕集机组、风电、光伏、储能和气网提供的下行灵活性能力.

考虑到系统的经济性，本研究的灵活性约束为灵活性资源大于灵活性需求^[21]，表达式如下:

(3)$ \left. \begin{gathered} R_t^{{\text{up}}} \leqslant F_t^{{\text{up}}}, \\ R_t^{{\text{down}}} \leqslant F_t^{{\text{down}}}. \\ \end{gathered} \right\} $

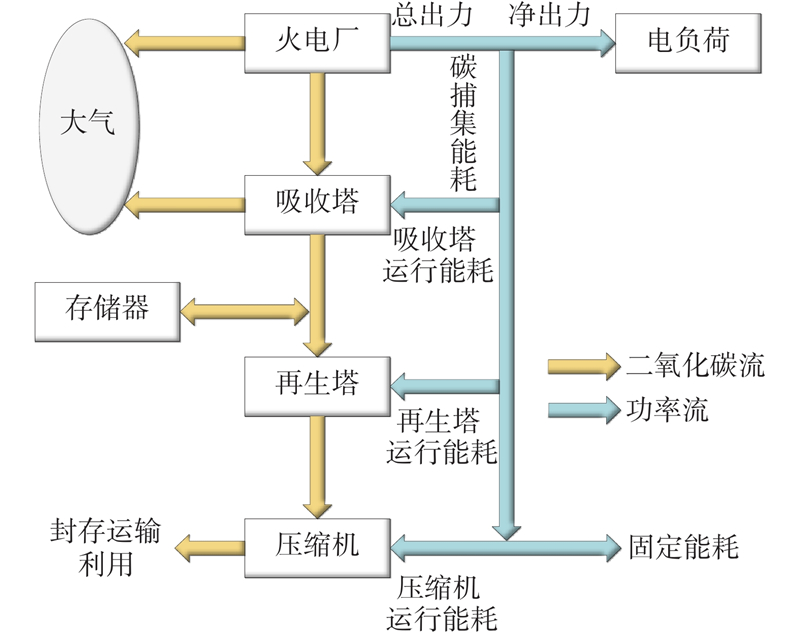
对于碳捕集机组，由于风光存在不确定性，机组需要在上行灵活性不足时提高出力，在下行灵活性不足时减少出力，而碳捕集电厂的综合灵活运行方式是提高系统灵活性的有效手段. 碳捕集电厂灵活运行流程图如图3所示，碳捕集电厂的总出力由净出力和碳捕集能耗组成，吸收的二氧化碳需要经过吸收塔、再生塔和压缩机处理后，进行封存，此外，二氧化碳经过吸收后也可在存储器中备用. 一方面，在高负荷时期，碳捕集电厂可将吸收的二氧化碳储存至存储器中，将高耗能环节如再生环节和压缩环节转移至低负荷时期；另一方面，在低负荷时期，碳捕集电厂可通过增加碳捕集出力的方式消纳风电. 通过灵活运行方式，对存储器内的二氧化碳时移，提高系统的灵活性与低碳性，碳捕集电厂模型如下:

(4)$ \left. \begin{gathered} {E_{{\text{G}}i,t}} = {e_{{\text{G}}i}}{P_{{\text{G}}i,t}}\Delta t, \; {E_{{\text{ccs,G}}i,t}} = {\alpha _i}\eta {E_{{\text{G}}i,t}}+{E_{{\text{sG}}i,t}}, \\ {P_{{\text{ccs}},i,t}} = {P_{{\text{ccsy}},i,t}}+{P_{{\text{ccsg}},i,t}}, \; {P_{{\text{ccsy}},i,t}} = \lambda {E_{{\text{ccs,G}}i,t}}\Delta t, \\ {P_{{\text{G}}i,t}} = {P_{{\text{out,G}}i,t}}+{P_{{\text{ccs}},i,t}}, \; 0 \leqslant {E_{{\text{ccs,G}}i,t}} \leqslant \alpha \eta {e_{{\text{G}}i}}{P_{{\text{G}}i,\max }}, \\ 0 \leqslant {\alpha _i} \leqslant 1.0 . \\\end{gathered} \right\} $

式中：$ {P_{{\text{G}}i,t}} $、$ {P_{{\text{out,G}}i,t}} $和$ {P_{{\text{ccs}},i,t}} $分别为碳捕集机组$i$在$t$时刻的总出力、净出力和碳捕集能耗；$ {P_{{\text{ccsy}},i,t}} $和$ {P_{{\text{ccsg}},i,t}} $分别为碳捕集机组$i$在$t$时刻的碳捕集运行能耗和固定能耗；$ {E_{{\text{G}}i,t}} $、$ {E_{{\text{ccs,G}}i,t}} $和$ {E_{{\text{sG}}i,t}} $分别为碳捕集机组$i$在$t$时刻$ {\text{C}}{{\text{O}}_2} $总产生质量、$ {\text{C}}{{\text{O}}_2} $捕集质量和存储器在碳捕集流程中吸收或释放的CO₂质量；$\Delta t $为单位时间；$ {\alpha _i} $为碳捕集机组$i$的烟气分流比，$ \alpha $、$ \lambda $和$ \eta $分别为再生塔和压缩机最大工作状态系数、单位捕集能耗和碳捕集效率；$ {e_{{\text{G}}i}} $为碳捕集机组$i$的碳排放强度. 存储器模型如下：

(5)$ \left. \begin{aligned} &{V_{{\text{s}},i,t}} = {k_{\text{s}}}{E_{{\text{sG}}i,t}}, \\ &{V_{{\text{m}},i,t}} = {V_{{\text{m}},i,t - 1}} - {V_{{\text{s}},i,t}}, \\& {V_{{\text{p}},i,t}} = {V_{{\text{p}},i,t - 1}}+{V_{{\text{s}},i,t}}, \\ &0 \leqslant {V_{{\text{m}},i,t}} \leqslant {V_{{\text{m,max}},i,t}}, \\& 0 \leqslant {V_{{\text{p}},i,t}} \leqslant {V_{{\text{p,max}},i,t}}, \\& {V_{{\text{m}},i,0}} = {V_{{\text{m}},i,24}}, \\& {V_{{\text{p}},i,0}} ={V_{{\text{p}},i,24}}. \\ \end{aligned} \right\} $

式中：${V_{{\text{s}},i,t}}$为机组$i$在$t$时刻从存储器中释放$ {\text{C}}{{\text{O}}_2} $所需的液体体积，${V_{{\text{m}},i,t}}$为机组$i$在$t$时刻富液存储器内的液体体积，${V_{{\text{p}},i,t}}$为机组$i$在$t$时刻贫液存储器内的液体体积，${V_{{\text{m,max}},i,t}}$为机组$i$的富液存储器最大容量，${V_{{\text{p,max}},i,t}}$为机组$i$的贫液存储器最大容量，${k_{\text{s}}}$为$ {\text{C}}{{\text{O}}_2} $体积质量转换系数.

根据碳捕集模型，推导出碳捕集电厂的出力范围如下：

(6)$ \left. \begin{gathered} {P_{{\text{out,G}}i,t,{\text{max}}}} = {P_{{\text{G}}i,\max }} - {P_{{\text{ccsg}},i,t}}, \\ {P_{{\text{out,G}}i,t,{\text{min}}}} = {P_{{\text{G}}i,\min }} - \lambda {\alpha _{i,\max }}\alpha \eta {e_{{\text{G}}i}}{P_{{\text{G}}i,\max }} - {P_{{\text{ccsg}},i,t}}. \\ \end{gathered} \right\} $

式中：$ {P_{{\text{G}}i,\max }} $和$ {P_{{\text{G}}i,\min }} $分别为碳捕集电厂机组$i$在$t$时刻的总出力的上限和下限；$ {P_{{\text{out,G}}i,t,{\text{max}}}} $和$ {P_{{\text{out,G}}i,t,{\text{min}}}} $分别为碳捕集电厂机组$i$在$t$时刻的净出力的上限和下限.

可以看出碳捕集电厂的净出力范围相较于常规机组大大提高. 碳捕集机组的灵活性模型如下：

(7)$ \left. \begin{gathered} F_{{\text{ccs}},t}^{{\text{up}}} = \sum\limits_{i = 1}^I {\min\; \{ ({P_{{\text{out,G}}i,t,{\text{max}}}} - {P_{{\text{out,G}}i,t}}),\;\Delta {P_{{\text{ccs}},i}}\} ,} \\ F_{{\text{ccs}},t}^{{\text{down}}} = \sum\limits_{i = 1}^I {\min\; \{ ({P_{{\text{out,G}}i,t}} - {P_{{\text{out,G}}i,t,\min }}),\;\Delta {P_{{\text{ccs}},i}}\} .} \\ \end{gathered} \right\} $

式中：$ \Delta {P_{{\text{ccs}},i}} $为机组$i$的爬坡速率，$I$为机组数量.

风电、光伏、储能和气网模型灵活性模型参考文献[21]建立.

上层供能系统以供能总成本最小为目标函数，包括碳捕集电厂总燃料成本、天然气开采成本、弃风成本、碳交易成本以及捕集$ {\text{C}}{{\text{O}}_2} $出售收益.

(8)$ \min \;{F_1} = {f_{\text{e}}}+{f_{\text{g}}}+{f_{{\mathrm{wpv}}}}+{f_{{\text{c}}{{\text{o}}_{\text{2}}}}} - {f_{{\text{ccs}}}}, $

(9)$ \left. \begin{aligned} {f_{\mathrm{e}}} =& \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^I {\left( {{{{a}}_i}P_{Gi,t}^2+{{{b}}_i}{P_{Gi,t}}+{{{c}}_i}} \right),} } \\ {f_{\mathrm{g}}} =& \sum\limits_{t = 1}^T {{\sum\limits_{w = 1}^{\varOmega w}} {{\rho _j}{Q_{w ,t}}} ,} \\ {f_{{\text{wpv}}}} =& \sum\limits_{t = 1}^T \left(\sum\limits_{w = 1}^W {{\rho _{{\text{wind}}}}\left({P_{{\text{wp}},w,t}} - {P_{w,t}}\right)} {\text+}\right.\\ &\left.\sum\limits_{v = 1}^V {\rho _{{\text{pv}}}}({P_{{\text{pv}},v,t}} - {P_{{{v}},t}})\right) , \\ {f_{{\text{c}}{{\text{o}}_2}}} =& \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^I {{c_{{\text{c}}{{\text{o}}_2},i,t}}} ,} \\ {f_{{\text{ccs}}}} =& \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^I {{\rho _{{\text{ccs}}}}{E_{{\text{ccs,G}}i,t}}} .} \\ \end{aligned} \right\}$

式中：$ {f_{\text{e}}} $、$ {f_{\text{g}}} $、$ {f_{{\text{wpv}}}} $、$ {f_{{\text{c}}{{\text{o}}_{\text{2}}}}} $和$ {f_{{\text{ccs}}}} $分别为碳捕集电厂总燃料成本、天然气开采成本、弃电成本、碳交易成本以及捕集$ {\text{C}}{{\text{O}}_2} $出售收益，$ {{{a}}_i} $、$ {{{b}}_i} $和$ {{{c}}_i} $为机组$ i $的发电系数，$ {Q_{w ,t}} $为天然气井$ w $在t时刻的供气量，$ {\varOmega _w } $为天然气井数量，$ {\rho _j} $为天然气单价，$ {\rho _{{\text{wind}}}} $为弃风惩罚成本单价，$ {P_{{\text{wp}},w,t}} $为风电预测值，${P_{w,t}}$为风电出力值，${\rho _{{\text{pv}}}}$为弃光惩罚成本单价，$ {P_{{\text{pv}},v,t}} $为光伏预测值，$ {P_{{\text{v}},t}} $为光伏出力值，$ {c_{{\text{c}}{{\text{o}}_{\text{2}}},i,t}} $为机组$ i $的碳交易成本，$ {\rho _{{\text{ccs}}}} $为出售高浓度$ {\text{C}}{{\text{O}}_2} $的单价，T为调度周期内总时段数，W为风电场总数，V为光伏系统总数.

采用阶梯式碳交易模型计算碳交易成本，机组$ i $的碳交易成本如下：

(10)$ {\begin{split} &{c_{{\rm{c}}{{\rm{o}}_{\rm{2}}},i,t}} =\\&\left\{ \begin{array}{*{20}{l}}{0,}&{0 \le {E_{{\rm{G}}i,t}} \le {\phi _1}};\\{{\lambda _{\rm{1}}}({E_{{\rm{G}}i,t}} - {\phi _1}),}&{{\phi _1} < {E_{{\rm{G}}i,t}} \le {\phi _2}};\\{{\lambda _{\rm{1}}}({\phi _2} - {\phi _1}) + {\lambda _2}({E_{{\rm{G}}i,t}} - {\phi _2}),}&{{\phi _2} < {E_{{\rm{G}}i,t}} \le {\phi _3}};\\{{\lambda _{\rm{1}}}({\phi _2} - {\phi _1}) + {\lambda _2}({\phi _3} - {\phi _2}) + {\lambda _3}({E_{{\rm{G}}i,t}} - {\phi _3}),}&{{\phi _3} < {E_{{\rm{G}}i,t}}}.\end{array} \right.\end{split}} $

式中：$ {\phi _1} $、$ {\phi _2} $和$ {\phi _3} $分别为碳交易三阶段配额，$ {\lambda _{\text{1}}} $、$ {\lambda _2} $和$ {\lambda _3} $分别为碳交易单价.

电力网络约束采用直流潮流约束，天然气网约束主要考虑节点供需平衡约束、节点压力约束、气网管道约束和气源约束. 电力网络及天然气网约束参考文献[22]建立. 天然气网模型非凸，常规求解困难，本研究采用增量分段线性化方法^[23]，将此问题转换为线性规划问题.

储能及燃气轮机约束参考文献[24]设置. 此外，碳捕集机组约束如式（4）所示，灵活性裕度约束如式（3）所示.

下层IES园区服务系统以各能量枢纽购电和购气成本最小为目标函数.

(11)$ \min\; {F_2} = {f_{{\text{EH,e}}}}+{f_{{\text{EH,g}}}}, $

(12)$ {f_{{\text{EH,e}}}} = \sum\limits_{t = 1}^T {\sum\limits_{c = 1}^C {{\lambda _{{\text{e}},t}}{P_{{\text{buy}},c,t}}} } , $

(13)$ {f_{{\text{EH,g}}}} = \sum\limits_{t = 1}^T {\sum\limits_{c = 1}^C {{\lambda _{{\text{g}},t}}{Q_{{\text{buy}},c,t}}} } . $

式中：$ {f_{{\text{EH,e}}}} $为能量枢纽（energy hubs，EH）总购电成本，$ {f_{{\text{EH,g}}}} $为EH总购气成本，$ C $为系统中EH数量，$ {\lambda _{{\text{e}},t}} $和$ {\lambda _{{\text{g}},t}} $分别为t时刻EH购电和购气单价，$ {P_{{\text{buy}},c,t}} $和$ {Q_{{\text{buy}},c,t}} $分别为t时刻第c座EH的购电功率和购气功率.

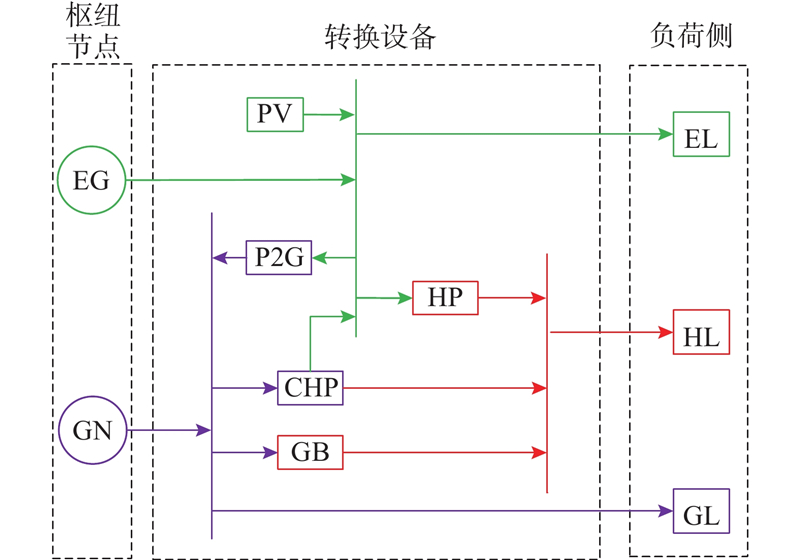
所考虑的能量枢纽模型如图4所示，枢纽节点包括电力网络（EG）、天然气网络（GN），设备包括光伏(PV)、电转气(P2G)、热泵(HP)、热电联产(CHP)和燃气锅炉(GB)，负荷考虑电负荷(EL)、热负荷(HL)和气负荷(GL).

电、气、热母线的功率平衡方程如下：

(14)$ {P_{{\text{buy}},c,t}} + P_{{\text{pv}},c,t}^{{\text{EH}}} + P_{{\text{CHP}},c,t}^{{\text{EH}}} - P_{{\text{P2G}},c,t}^{{\text{EH}}} - P_{{\text{HP}},c,t}^{{\text{EH}}} = {P_{{\text{load}},c,t}}, $

(15)$ {Q_{{\text{buy}},c,t}}+Q_{{\text{P2G}},c,t}^{{\text{EH}}} - Q_{{\text{CHP}},c,t}^{{\text{EH}}} - Q_{{\text{GB}},c,t}^{{\text{EH}}} = {Q_{{\text{load}},c,t}}, $

(16)$ H_{{\text{CHP}},c,t}^{{\text{EH}}}+H_{{\text{HP}},c,t}^{{\text{EH}}}+H_{{\text{GB}},c,t}^{{\text{EH}}} = {H_{{\text{load}},c,t}}. $

式中：$ P_{{\text{pv}},c,t}^{{\text{EH}}} $、$ P_{{\text{CHP}},c,t}^{{\text{EH}}} $、$ P_{{\text{P2G}},c,t}^{{\text{EH}}} $和$ P_{{\text{HP}},c,t}^{{\text{EH}}} $分别为t时刻的EH光伏输出功率、热电联产电功率、电转气电功率和热泵电功率；$ Q_{{\text{P2G}},c,t}^{{\text{EH}}} $、$ Q_{{\text{CHP}},c,t}^{{\text{EH}}} $和$ Q_{{\text{GB}},c,t}^{{\text{EH}}} $分别为t时刻的电转气的用气量、热电联产的用气量和燃气锅炉的用气量；$ H_{{\text{CHP}},c,t}^{{\text{EH}}} $、$ H_{{\text{HP}},c,t}^{{\text{EH}}} $和$ H_{{\text{GB}},c,t}^{{\text{EH}}} $分别为t时刻的热电联产的热功率、热泵的热功率和燃气锅炉的热功率；$ {P_{{\text{load}},c,t}} $、$ {Q_{{\text{load}},c,t}} $和$ {H_{{\text{load}},c,t}} $分别为t时刻的电、气、热负荷.

各设备转换约束及上下限约束参考文献[24]建立.

目标级联分析法是用于快速解决分散式、层次结构协调问题的有效方法，它允许层次结构中各主体自主决策，在各主体对各子主体进行决策时分散协调优化而获得系统整体最优解. 与其他优化方法相比，目标级联法具有可并行优化、级数不受限制和经过严格的收敛证明等优点^[25].

首先，对联络线耦合变量进行解耦，在各主体目标函数中加入拉格朗日罚函数一次和二次项，表达式如下：

(17)$\begin{split} \min\; F_1^{\prime}= & F_1+\sum_{t=1}^T \sum_{c=1}^C\left(\varsigma_{t, c, 1}^{\mathrm{P}}\left(P_{\mathrm{cl}, c, t}-P_{\mathrm{buy}, c, t}\right)+\varsigma_{t, c, 2}^{\mathrm{P}}\right. \times \\&\left.\left.\left(P_{\mathrm{cl}, c, t}-\right.P_{\mathrm{buy}, c, t}\right)^2\right)+\sum_{t=1}^T \sum_{c=1}^C\left(\varsigma_{t, c, 1}^{\mathrm{Q}}\left(Q_{\mathrm{cl}, c, t}-\right.\right. \\& \left.\left.Q_{\mathrm{buy}, c, t}\right)+\varsigma_{t, c, 2}^{\mathrm{Q}}\left(Q_{\mathrm{cl}, c, t}-Q_{\mathrm{buy}, c, t}\right)^2\right) ,\\[-8pt]\end{split} $

(18)$ \begin{split} \min\; F_2^{\prime}= & F_2+\sum_{t=1}^T \sum_{c=1}^C\left(\varsigma_{t, c, 1}^{\mathrm{P}}\left(P_{\mathrm{buy}, c, t}-P_{\mathrm{cl}, c, t}\right)+\varsigma_{t, c, 2}^{\mathrm{P}}\right. \times \\& \left.\left(P_{{{\mathrm{buy}} }, c, t}-P_{\mathrm{cl}, c, t}\right)^2\right)+\sum_{t=1}^T \sum_{c=1}^C\left(\varsigma _ { t , c , 1 } ^ { \mathrm { Q } } \left(Q_{{{\mathrm{buy}} },c,t}-\right.\right. \\& \left.\left.Q_{\mathrm{cl},c,t}\right)+\varsigma_{t,c,2}^{\mathrm{Q}}\left(Q_{ {{\mathrm{buy}} }, c, t}-Q_{\mathrm{cl}, c, t}\right)^2\right) .\\[-5pt]\end{split} $

式中：$ F_1^{'} $和$ F_2^{'} $为修改后的目标函数；$ {P_{{\text{cl}},c,t}} $和$ {Q_{{\text{cl}},c,t}} $分别为电网和气网在t时刻第c座EH的联络线功率，$ \varsigma _{t,c,1}^{\text{P}} $和$ \varsigma _{t,c,1}^{\text{Q}} $分别为电网和气网在t时刻的拉格朗日罚函数的一次项乘子，$ \varsigma _{t,c,2}^{\text{P}} $和$ \varsigma _{t,c,2}^{\text{Q}} $分别为电网和气网在t时刻的拉格朗日罚函数的二次项乘子，拉格朗日罚函数乘子均取1.5. 内循环和外循环的收敛条件分别如下：

(19)$ \left| {{P_{{\text{cl}},c,t}} - {P_{{\text{buy}},c,t}}} \right| \leqslant {\varepsilon _1}, \quad \left| {{Q_{{\text{cl}},c,t}} - {Q_{{\text{buy}},c,t}}} \right| \leqslant {\varepsilon _1}, $

(20)$ \left| {F_{1,k}' - F_{1,k - 1}' } \right| \leqslant {\varepsilon _2}, \quad \left| {F_{2,k}' - F_{2,k - 1}' } \right| \leqslant {\varepsilon _3}. $

式中：$ {\varepsilon _1} $、$ {\varepsilon _2} $和$ {\varepsilon _3} $分别为电网耦合变量、气网耦合变量和目标函数差值的收敛精度，均取0.05 MW；$F_{1,k}' $和$F_{2,k}' $为第k次修改后的目标函数. 拉格朗日乘子更新公式如下：

(21)$ \left. \begin{gathered} \varsigma _{t,c,1}^{{\text{P,}}k} = \varsigma _{t - 1,c,1}^{{\text{P,}}k - 1}+2{(\varsigma _{t,c,2}^{{\text{P,}}k - 1})^2}({P_{{\text{cl}},c,t}} - {P_{{\text{buy}},c,t}}), \\ \varsigma _{t,c,2}^{{\text{P,}}k} = \beta \varsigma _{t,c,2}^{{\text{P,}}k - 1}, \\ \varsigma _{t,c,1}^{{\text{Q,}}k} = \varsigma _{t - 1,c,1}^{{\text{Q,}}k - 1}+2{(\varsigma _{t,c,2}^{{\text{Q,}}k - 1})^2}({Q_{{\text{cl}},c,t}} - {Q_{{\text{buy}},c,t}}), \\ \varsigma _{t,c,2}^{{\text{Q,}}k} = \beta \varsigma _{t,c,2}^{{\text{Q,}}k - 1}. \\ \end{gathered} \right\} $

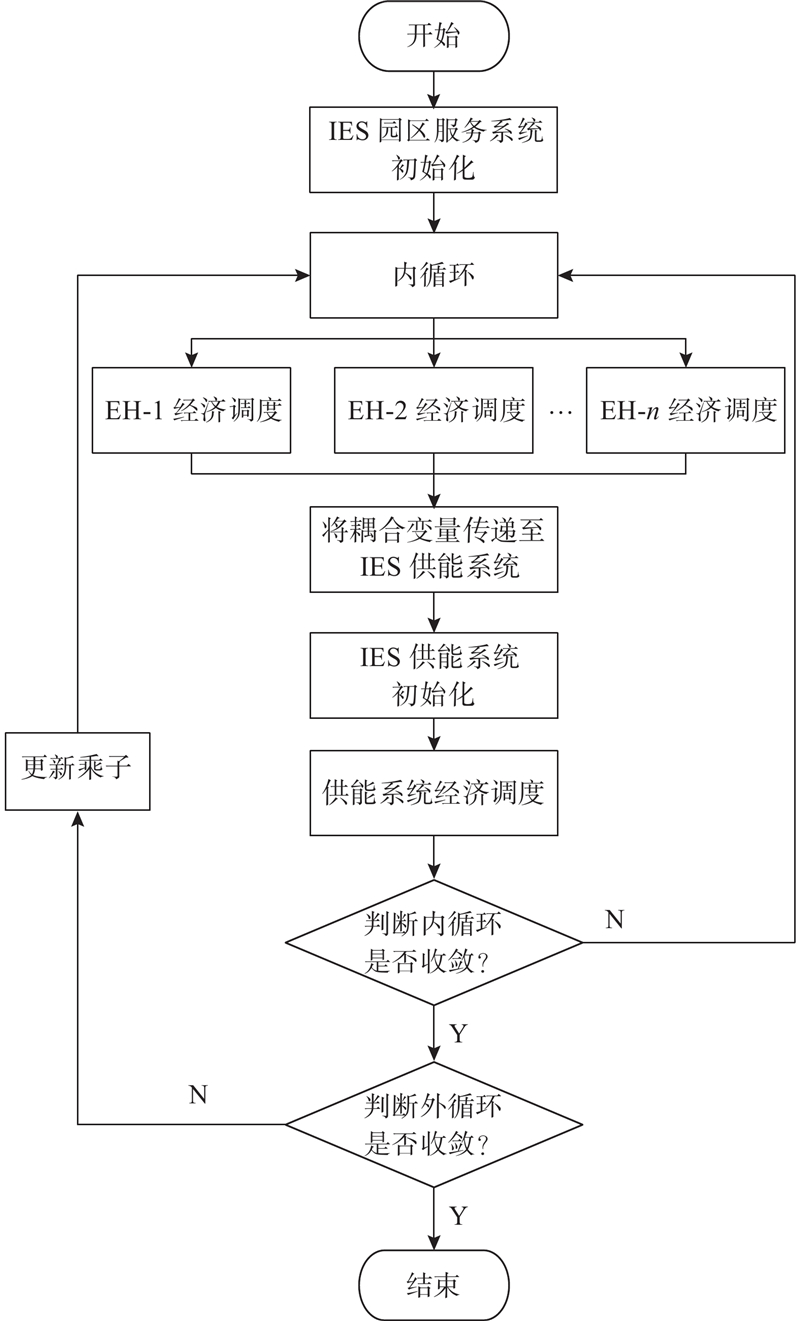
采用目标级联分析法的求解流程图如图5所示.

求解步骤如下.

1） IES 服务系统初始化，进入内循环.

2） 各 EH 进行日前经济调度，目标函数为式（18），约束条件为1.4节中所提约束，并传递耦合变量至IES供能系统.

3） IES供能系统初始化，并进行经济调度，目标函数为式（17），约束条件为1.3节中所提约束.

4） 判断内循环是否收敛，若不收敛则转入 2），若内循环收敛则判断外循环是否收敛.

5） 若外循环不收敛，则更新乘子，转入步骤2），若外循环收敛，则循环结束.

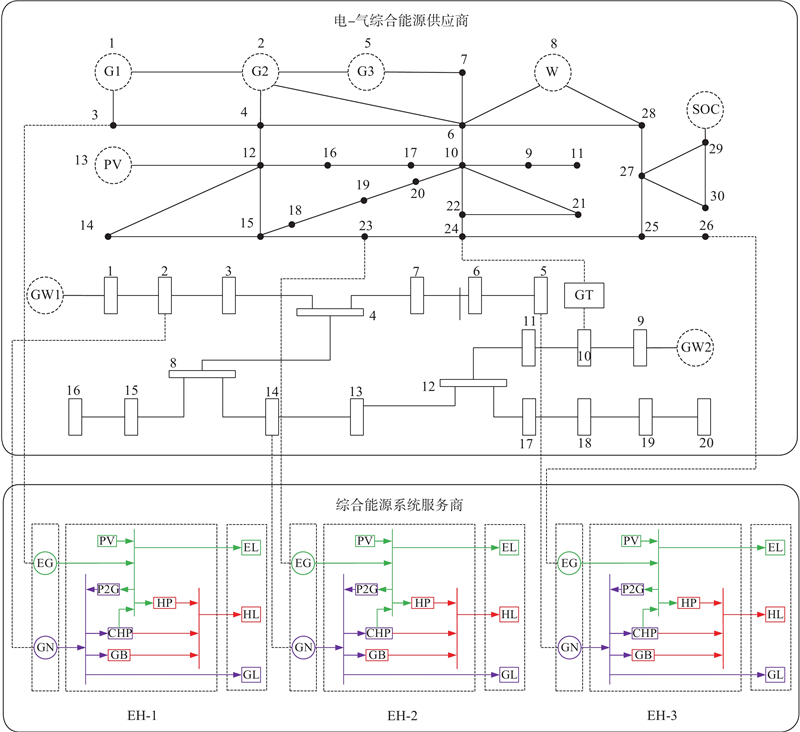
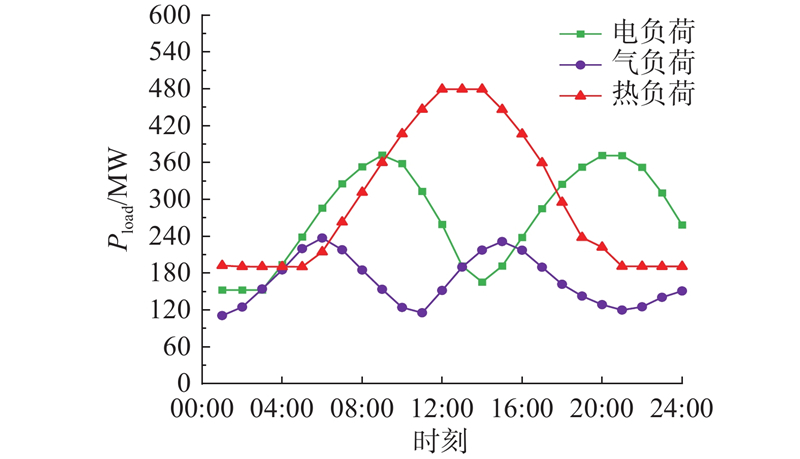
利用IEEE30节点电网和比利时20节点气网构成IES供能系统，3个EH构成IES园区服务系统，与供能系统互联. 其中，IEEE30节点电网包含3个碳捕集电厂、1个风电场、1个光伏系统和1个燃气轮机，风电场额定容量为300 MW，光伏系统额定容量为200 MW；气网系统包含2个气源，如图6所示^[25]. EH内负荷数据如图7所示，图中，${P_{{\text{load}}}}$为综合能源系统负荷. 其他参数如表1~3所示. 表中，$ {P_{{\text{G}}i,\max }} $为碳捕集机组出力最大值，$ {P_{{\text{G}}i,\min }} $为碳捕集机组出力最小值，${Q_{w i,\max }}$为气源供气上限，${Q_{w i,\min }}$为供气下限，${E_{\text{G}}}$为碳排放量.

利用CPLEX进行优化求解，系统以24 h为周期，以1 h为步长进行仿真. 为了分析灵活性约束、碳捕集设备和碳交易对系统的影响，设置以下4个场景.

场景1：考虑灵活性约束、碳交易及碳捕集机组.

场景2：考虑碳捕集机组及碳交易，不考虑灵活性约束.

场景3：考虑灵活性约束及碳交易，不考虑碳捕集机组.

场景4：考虑灵活性约束及碳捕集机组，不考虑碳交易.

如表4所示为4个场景下，供能总成本、碳交易成本、碳捕获收益和碳排放量的数据，其中场景1、3、4的灵活性安全裕度为250 MW. 场景1的总成本比场景2提高了0.47%，碳交易成本提高了2.98%，同时，碳捕获的收益也提高了2.88%，碳排放量减少了4.35%. 说明考虑了灵活性资源后，总成本有小幅上升，系统发挥了灵活性资源的调节能力，减少弃风量，提高了碳交易的效果，并且通过碳捕集技术，有效控制了成本的升高. 相比于场景3，场景1在考虑碳捕集技术后，系统的总成本降低了7.57%，碳排放量大幅减少，说明碳捕集技术有利于提高系统经济性和低碳性，并且大幅降低了碳交易的成本. 在考虑了碳交易后，场景1相比场景4，总成本增加了1.88%，碳排放量减少了3.33%，说明阶梯式碳交易模型在小幅增加总成本的情况下，可大幅减少碳排放，提高系统的经济性，也有利于系统满足灵活性需求.

如图8所示为场景1下的联络线功率. 可以看出，在2:00—9:00和13:00—20:00这2个时间段，联络线功率上升明显，可以得出此阶段的上行灵活性需求较高；而9:00—12:00和22:00—24:00这2个时间段功率下降较大，可判断此时的下行灵活性需求较高.

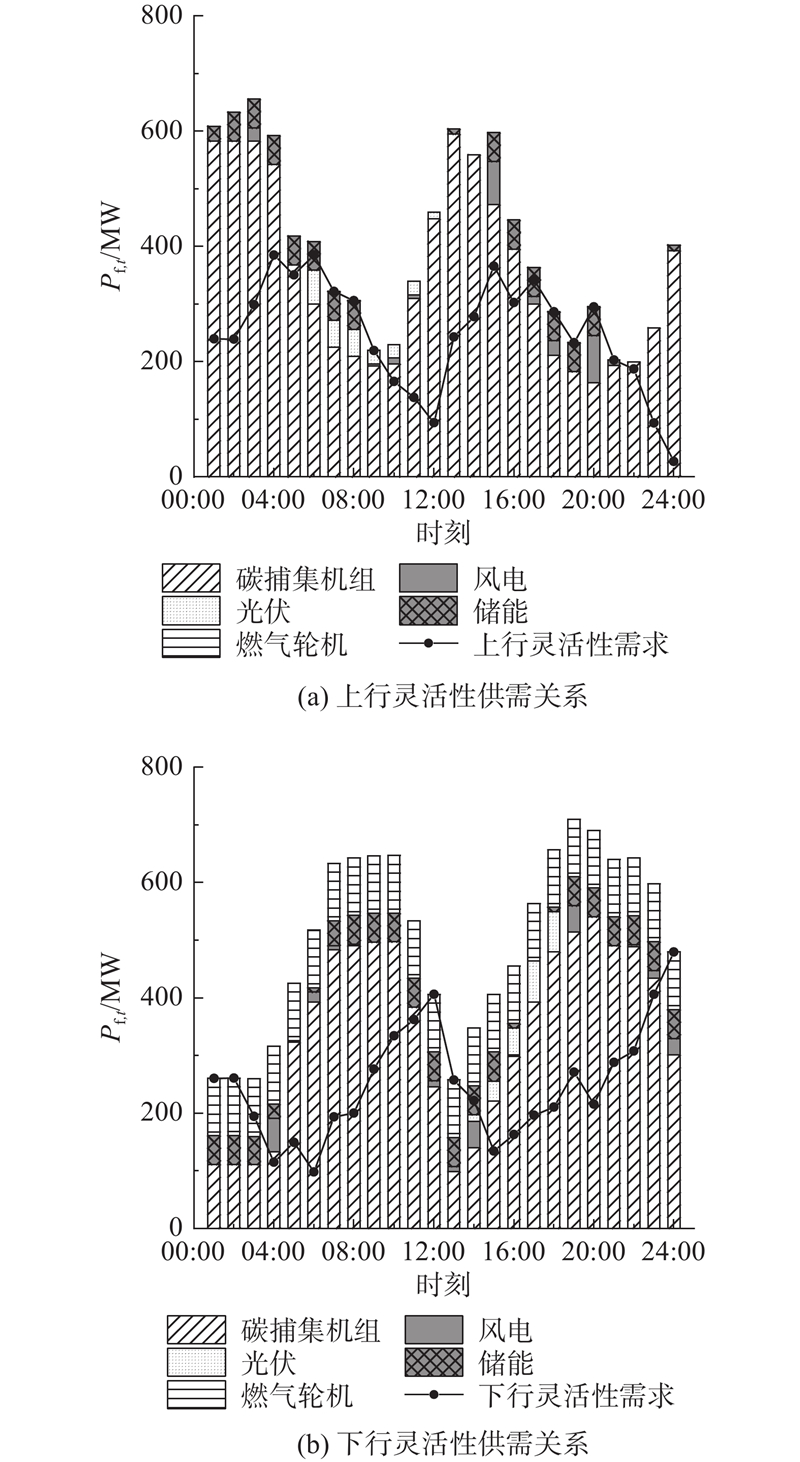
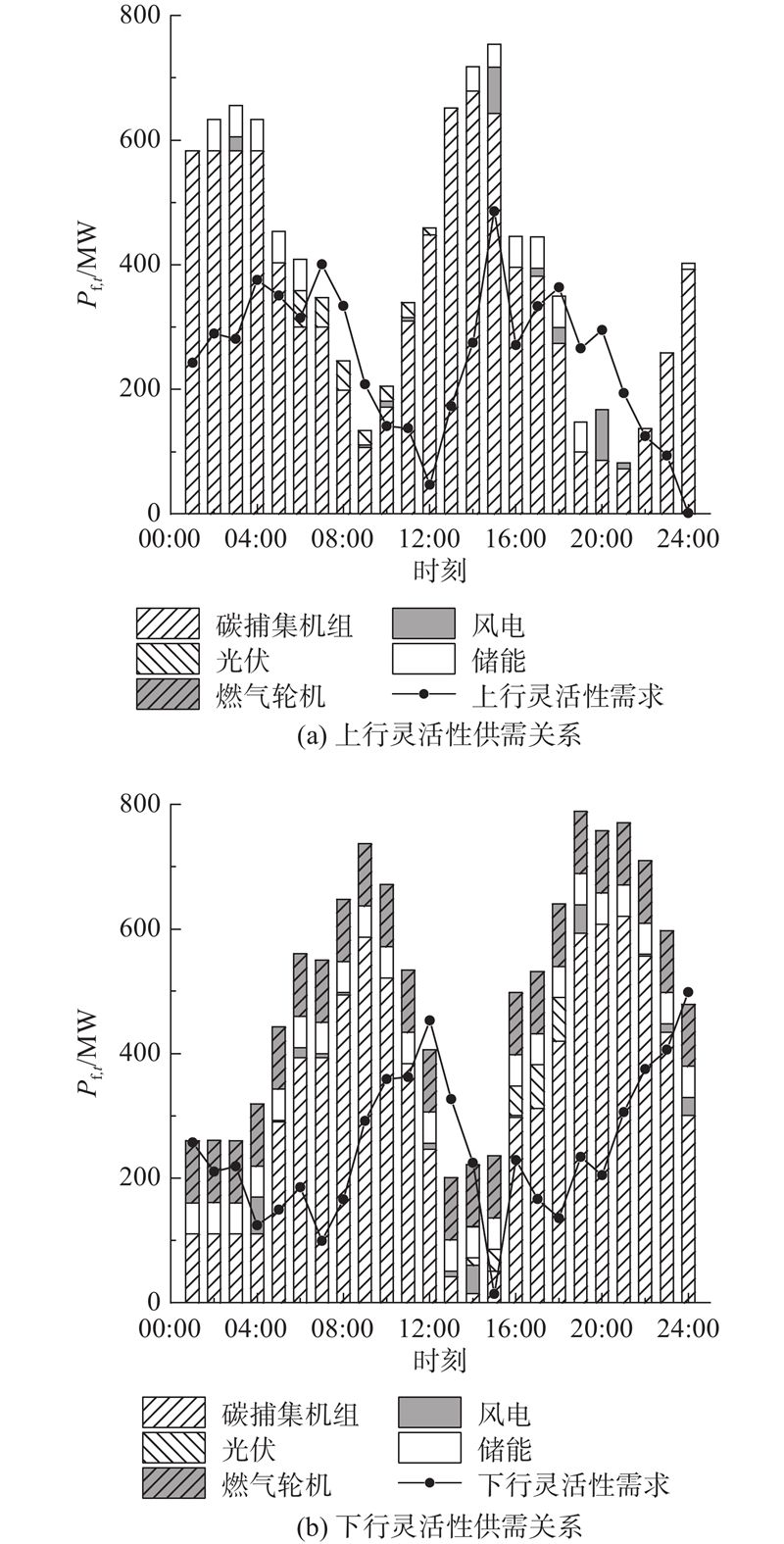
如图9、10所示分别为场景1、2中是否考虑灵活性约束时上行灵活性和下行灵活性的供需关系. 图中，${P_{{\mathrm{f}},t}}$为提供的灵活性功率. 由图9可知，系统的灵活性需求随着EH的负荷需求而变化，灵活性约束可使系统利用多种灵活性资源，调用碳捕集机组、储能、燃气轮机等多种设备，以满足系统的灵活性需求. 从上行灵活性需求的图中可看出，系统的灵活性资源主要由碳捕集机组提供，这是源于机组的出力较大且运行区间较广，而风光出力相对较低. 在0:00—4:00和9:00—15:00，系统的负荷需求和波动较小，因此，此时的上行灵活性需求较小，上行灵活性资源远远大于灵活性需求，表明此时系统有较大的灵活性裕度以满足灵活性，同理，在下行灵活性需求图中5:00—11:00和16:00—23:00，下行灵活性资源远远大于灵活性需求.

若不考虑灵活性约束，由图10可以看出，7:00—9:00和18:00—21:00时的上行灵活性需求无法满足，同理12:00—13:00和23:00—24:00的下行灵活性需求无法得到满足，并且相比与图9，其他时刻的灵活性裕度明显减少. 说明灵活性约束可提高各时刻的灵活性裕度，有效满足系统的灵活性需求.

场景1在1 d内的风电消纳量为5627.5 MW·h，储能在1 d内总的充放电容量为581.1 MW·h，场景2在1 d内的风电消纳量为5627.5 MW·h，储能在1 d内总的充放电容量为552.8 MW·h. 考虑灵活性裕度约束后，系统可以调度灵活性资源满足灵活性上行/下行需求，包括碳捕集机组、储能、燃气轮机等灵活调节，由于灵活性资源的调节，场景1储能利用率提升了5.12%. 由于风电系统灵活性资源充足，风电可以完全消纳，若系统灵活性资源不足或风电渗透率提升，造成低负荷时期可能的弃风，此时可通过灵活性裕度约束，调用系统灵活性资源帮助消纳风电.

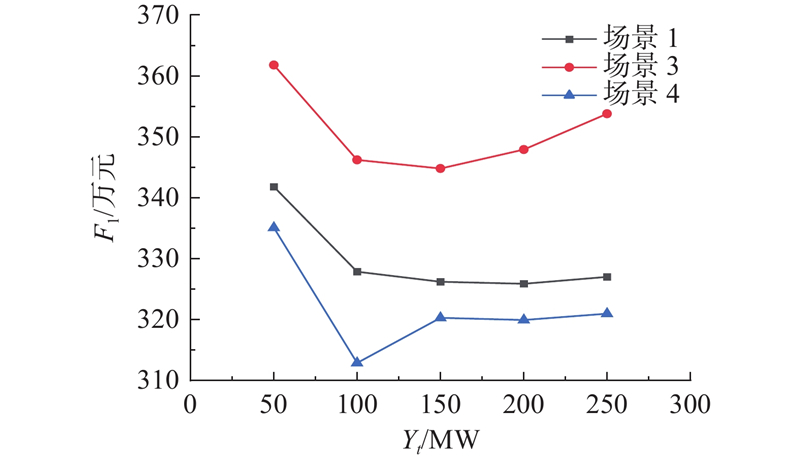
如图11所示为灵活性安全裕度和总成本的关系. 图中，Y_t为灵活性安全裕度. 在场景1中，将灵活性安全裕度从50 MW提高到200 MW后，总成本降低了5.89%，灵活性需求提升到250 MW后，系统的总成本开始提高，说明提升一定的灵活性安全裕度，可有效提高风电的消纳率，提高碳捕集设备的效率，提高捕获收益，降低碳交易成本. 然而，随着灵活性需求的不断提高，系统的灵活性调节能力也消失殆尽，系统的运行成本将开始提高，而将灵活性安全裕度提升至300 MW后，系统将无法满足要求. 场景3没有考虑碳捕集机组，因此在系统提供灵活性需求后，总成本有了较大幅度的提高，这也说明，碳捕集技术的灵活运行模式可以有效缓解系统灵活性需求增加而造成的经济成本压力.

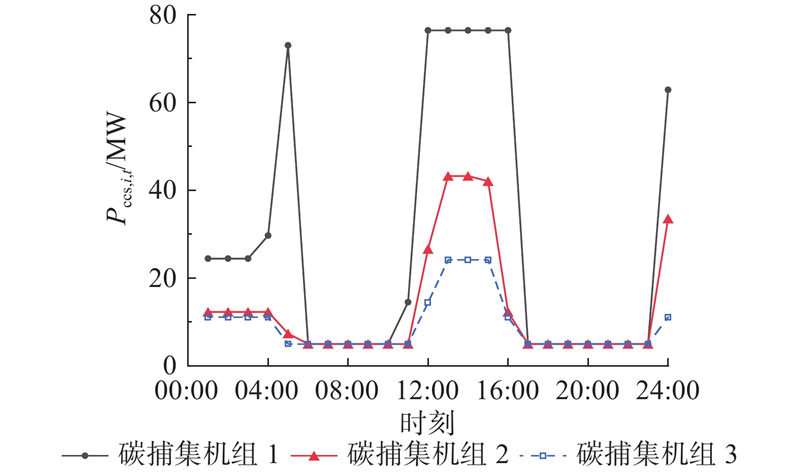
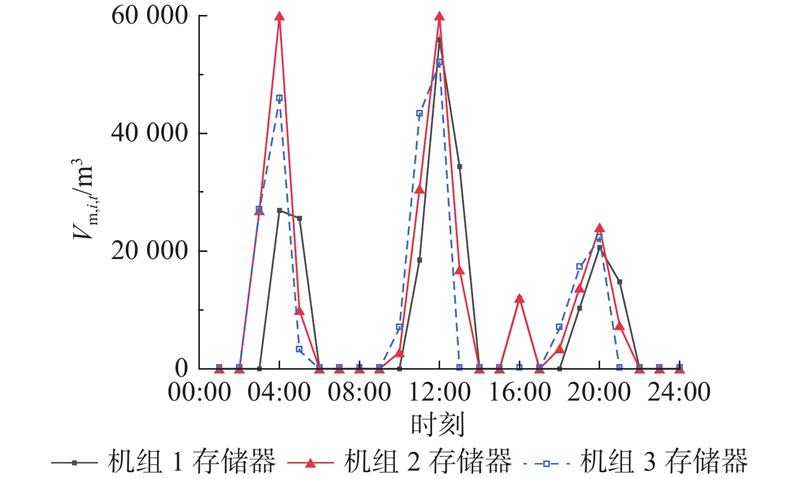
为了研究碳捕集技术对灵活性的有效性，具体对碳捕集设备能耗和碳捕集设备的存储器内的液体体积进行分析. 如图12、13所示分别为场景1下的碳捕集功耗图以及碳捕集存储器中溶液的体积. 由图12可知，在1:00—5:00和11:00—17:00，碳捕集设备功耗较大，说明此时间段，系统负荷较低，上行灵活性需求较小，因此机组出力相对充裕，可增加碳捕集设备的出力，在6:00—11:00和18:00—23:00，由于系统的负荷较大，且上行灵活性需求较高，碳捕集机组没有多余的出力可用于碳捕集. 由图13可知，在2:00—6:00、10:00—14:00及18:00—22:00存储器对二氧化碳进行了存储，说明在负荷较大的时期，碳捕集电厂将吸收的二氧化碳储存至存储器中，将高耗能环节如再生环节和压缩环节转移至低负荷时期. 在低负荷时期，碳捕集电厂通过灵活运行方式，对存储器内的二氧化碳转移至碳捕集设备进行压缩处理，因此，碳捕集设备可以提高系统的灵活性和低碳性.

如图14所示为碳交易价格的变化对系统碳排放的影响，图中，$\varGamma $为碳交易变化率，E_G为系统调度周期内总的碳排放质量. 可以看出，当碳交易价格提升小于40%时，系统的碳排放量会大大降低，而提升到50%以后，碳排放的变化不再明显，说明合理的碳交易价格，可以有效平衡系统的经济性要求和系统性要求.

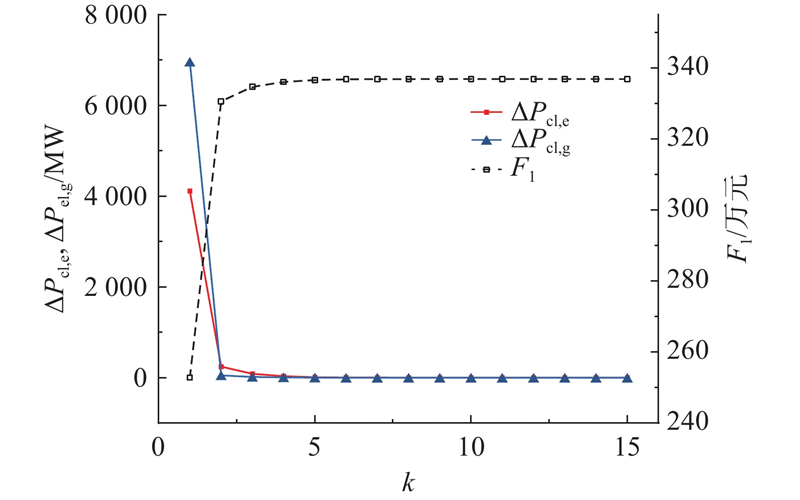
目标级联分析法在迭代过程中联络线电功率差值$\Delta {P_{{\rm{cl,e}}}} $、气功率差值$\Delta {P_{{\rm{cl,g}}}} $以及总成本F₁的变化情况如图15所示. 图中，k为迭代次数. 可以看出，系统在迭代了5次之后，电功率和气功率的差值无限趋近于0，且总成本也趋近稳定，不再变化. 由此可以得出，目标级联分析法具有较好的收敛特性以及较快的迭代速度. 为了进一步证明目标级联分析法的有效性，分别与集中式和分布式求解算法的优化结果进行对比分析. 其中，集中式求解指IES供能系统和IES园区服务系统将各种信息传递至统一的控制中心，然后按照全局进行优化求解. 分层求解算法可以将一个复杂的问题分解成多个简单的子问题,然后逐层求解. 如表5所示为分别采用集中式求解、KKT条件转换以及目标级联分析法进行优化求解的结果. 表中，F_s、F_p分别为IES供能系统、IES园区服务系统成本，tc为耗时. 可以看出，集中式算法的速度较快，但该方法需要将所有信息进行集中，无法解决隐私保护的问题. 以集中式求解的成本为基准，KKT条件转换的求解结果相对于目标级联分析法较为精确，但是该方法耗时较长，且其存在上下层耦合问题. 目标级联分析法求解精确性不如KKT条件转换，但是该方法求解速度较快，且可以根据不同的收敛精度调整收敛速度，较为灵活. 因此，从整体最优的角度，目标级联分析法具有较好的计算效果，能够解决考虑多主体的能源供应商和能源运营商中平衡与协同优化的问题.

（1）考虑灵活性裕度约束，提高了风电的消纳率以及储能的利用率，充分挖掘了各种灵活性资源的调节能力，满足了系统的灵活性需求.

（2）充分利用碳捕集电厂的灵活运行模式，使其在负荷高峰期减少碳捕集出力，并利用存储器存储$ {\text{C}}{{\text{O}}_2} $. 在负荷低谷期，提高碳捕集设备出力，并吸收存储器内的$ {\text{C}}{{\text{O}}_2} $，提高机组的灵活性能力，并且提高了系统的经济性和低碳性.

（3）采用目标级联分析法进行求解，实现了能源供应商和能源服务商上下层协同调度.

本研究提出仅针对于网架侧的灵活性资源，能量枢纽内部的灵活性资源与网侧灵活性资源相互协同配合将是下一步研究方向.