浙江大学学报(工学版)

浙江大学学报(工学版), 2024, 58(6): 1174-1184 doi: 10.3785/j.issn.1008-973X.2024.06.008

土木工程、交通工程

降雨诱发斜坡失稳风险的气象预警

严亮轩,, 张义顺, 龚泉冰, 刘谢攀, 朱浩濛, 殷坤龙,, 陈丽霞

1. 中国地质大学（武汉） 工程学院，湖北 武汉 430074

2. 浙江省地质院 地质灾害防治所，浙江 杭州 310000

3. 中国地质大学（武汉） 地球物理与空间信息学院，湖北 武汉 430074

Meteorological warning for rainfall-induced slope instability risk

YAN Liangxuan,, ZHANG Yishun, GONG Quanbing, LIU Xiepan, ZHU Haomeng, YIN Kunlong,, CHEN Lixia

1. Faculty of Engineering, China University of Geosciences, Wuhan 430074, China

2. Geological Hazard Prevention and Control Institute, Zhejiang Institute of Geosciences, Hangzhou 310000, China

3. Institute of Geophysics and Geomatics, China University of Geosciences, Wuhan 430074, China

通讯作者: 殷坤龙，男，教授. orcid.org/0000-0002-3547-1633. E-mail: yinkl@cug.edu.cn

收稿日期: 2023-06-12  

基金资助: 平阳县地质灾害风险降雨阈值项目（LXCG2022-070）.

Received: 2023-06-12  

Fund supported: 平阳县地质灾害风险降雨阈值项目（LXCG2022-070）.

作者简介 About authors

严亮轩（1994—），男，博士生，从事地质灾害风险评价研究.orcid.org/0000-0002-2207-8461.E-mail：yanliangxuan@cug.edu.cn , E-mail：yanliangxuan@cug.edu.cn

摘要

采用基准阈值和阈值调整方案构建斜坡尺度的降雨诱发斜坡失稳风险的气象预警模型，开展精细化滑坡风险管理. 采用降雨强度-持续时间模型确定基准阈值；分析斜坡地质环境特征，从斜坡几何结构、岩土抗剪强度、水文地质条件、植被等方面选取调整因子，并确定基准斜坡；针对降雨入渗过程分析地质环境变化造成的斜坡稳定性变化，得出阈值调整方案. 以浙江省平阳县为研究区，提出当地阈值计算公式，并根据各斜坡的地质环境形成各自不同等级的预警判据，综合预警有效率达到72%，效果良好. 提出斜坡尺度的风险预警模型，实现了斜坡单元级别的精准预警，能够为“一区一阈值”精细化滑坡气象预警与风险管控提供新思路和参考.

关键词： 滑坡风险 ; 气象预警 ; 阈值 ; 地质环境 ; 斜坡尺度

Abstract

A slope-scale meteorological warning model for rainfall-induced slope instability risk was constructed using benchmark threshold and a threshold adjustment scheme, in order to carry out refined landslide risk management. The benchmark threshold was proposed by the intensity-duration model. Adjusting factors were selected from slope geometry, rock and soil shear strength, hydrogeological conditions and vegetation based on the characteristics of the slope geological environment, and the benchmark slope was determined. The threshold adjustment scheme was obtained from the perspective of rainfall infiltration process, which explored the variation of the slope stability caused by the changes of the geological environment. Taking Pingyang County in Zhejiang Province as the study area, a quantitative formula was defined for calculating the threshold of individual slopes. Thresholds corresponding to different warning levels were formed based on the environment of each slope. The comprehensive early warning effectiveness rate reached 72%, which showed a satisfactory warning effect. An innovative slope-scale risk warning model was proposed. The precise landslide early warning at slope-unit scale was realized, which can provide new ideas and references for refined landslide early warning and risk management on purpose of “each-slope, each-threshold”.

Keywords： landslide risk ; meteorological warning ; threshold ; geological environment ; slope scale

PDF (5548KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

严亮轩, 张义顺, 龚泉冰, 刘谢攀, 朱浩濛, 殷坤龙, 陈丽霞. 降雨诱发斜坡失稳风险的气象预警. 浙江大学学报(工学版)[J], 2024, 58(6): 1174-1184 doi:10.3785/j.issn.1008-973X.2024.06.008

YAN Liangxuan, ZHANG Yishun, GONG Quanbing, LIU Xiepan, ZHU Haomeng, YIN Kunlong, CHEN Lixia. Meteorological warning for rainfall-induced slope instability risk. Journal of Zhejiang University(Engineering Science)[J], 2024, 58(6): 1174-1184 doi:10.3785/j.issn.1008-973X.2024.06.008

滑坡是常见的自然灾害，每年造成大量的人员伤亡和巨大的经济损失[1]. 我国有一半以上的滑坡为降雨诱发型[2]. 降雨入渗，改变坡体的物理力学特性，同时改变地下水位，降低土体抗剪强度，从而影响斜坡的稳定性[3-4]. 目前开展的滑坡气象预警的难点是阈值的选取.

关于降雨诱发地质灾害预警及其阈值的相关研究，国内外学者进行了大量工作[5-7]，可以总结为2类：1）统计分析方法，通过收集历史降雨数据和地质灾害发生情况，进行统计对比分析，从而得到地质灾害和降雨之间的定性、半定量或定量的关系，此方法当前应用较多；2）机理分析方法，主要采用斜坡水文模型，从降雨-渗流-灾害发生机理，分析降雨诱发型滑坡灾害的阈值[8-9]. Caine[10]基于73个灾害数据和降雨数据提出全球性的阈值，并采用降雨持续时间和降雨强度的关系来表示此阈值. Guzzetti等[11]通过对大量诱发滑坡降雨事件的分析将统计阈值分为4个类别：降雨强度-持续时间阈值（I-D）、累计降雨量阈值（E）、累计降雨量-持续时间阈值（E-D）和累计降雨量-降雨强度阈值（E-I）. 降雨强度I和持续时间D是表征降雨事件的主要参数，它们建立了诱发滑坡的降雨强度随持续时间的变化关系[12-13]. E-D阈值建立了诱发滑坡降雨事件的累计降雨量和降雨持续时间之间的关系，随着降雨持续时间增加，诱发滑坡所需的累计降雨量增大[14-15]. E-I阈值建立了诱发滑坡降雨事件的累计降雨量和降雨强度之间的关系. 阈值的建立考虑了研究区内气象、气候和地形地貌特征，适用于定量降雨预报的滑坡预警. 据此，许多国家建立了降雨诱发滑坡的预警系统[16-19].

浙江省作为降雨诱发型滑坡高发省份，自21世纪以来开展了大量的预警模型和阈值研究. 谢剑明等[20]根据浙江省降雨分布特征将浙江省划分为台风暴雨区和非台风影响区，建立了各自的有效降雨量模型. 殷坤龙等[21]建立了基于WEBGIS的浙江省地质灾害预警预报系统，将空间预测和时间预测相结合，在台风降雨过程中进行实时地质灾害预警预报. 鲍其云等[22]对浙江省1990—2013年间发生的1467次滑坡和2457个雨量站降雨数据进行分析，确定62个丘陵山区县引发滑坡和泥石流的I-D阈值，提出了基于I-D模型阈值和滑坡易发程度区划的预报系统模型.

本研究以浙江省平阳县滑坡风险气象预警为研究实例，通过I-D统计模型得到平阳县斜坡失稳的基准阈值，从斜坡孕灾地质环境出发，开展斜坡地质结构的详细分析，进行概化斜坡分析（基准斜坡）. 分析斜坡降雨入渗过程中各地质环境因子对阈值的影响，提出阈值调整方案. 创新性地提出基于地质环境条件的精细化降雨诱发型斜坡失稳风险气象预警模型，为防灾减灾应急工作的介入提供时间参考.

1. 预警模型理论与方法

为了实现精细化的滑坡风险管理，从孕灾斜坡出发，提出基于斜坡地质环境的精细化降雨诱发斜坡失稳风险气象预警模型，能够实现斜坡尺度的气象预警，满足一斜坡一阈值以及动态调整的需求.

预警模型包括基准阈值和斜坡地质环境因子调整方法2部分. 在自然界中，每个斜坡的地质环境条件各不相同，如何刻画斜坡的差异性，以及不同的斜坡地质环境变化所带来的降雨阈值的调整方案是模型的核心内容. 运用I-D统计阈值模型得到斜坡变形破坏的基准阈值. 阈值调整方法则是分析降雨入渗机理，运用数值模拟，探索斜坡地质环境条件改变造成的斜坡稳定性的变化规律. 由具体斜坡与基准斜坡的地质环境变化，对应到基准阈值与具体斜坡阈值的变化，从而得出降雨阈值调整方案.

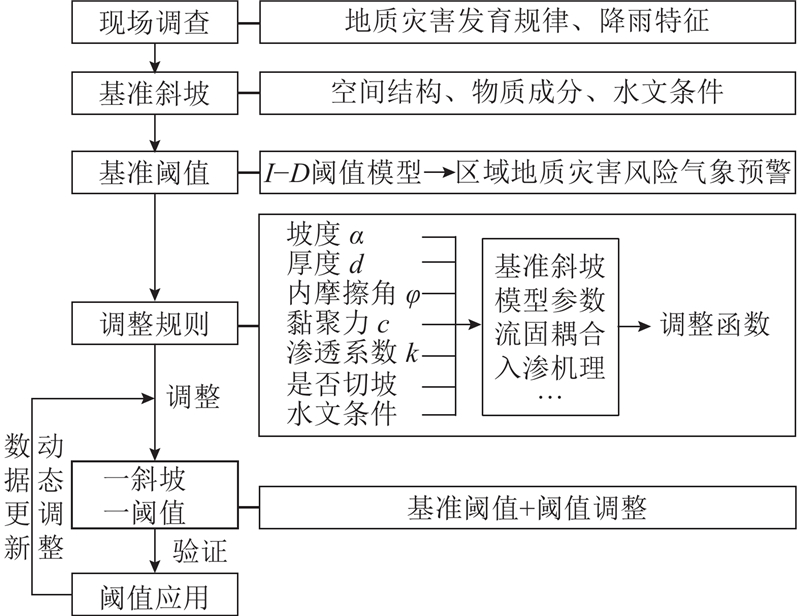
预警模型如图1所示. 预警模型表达式如下：

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   基于地质环境的降雨诱发斜坡失稳风险的气象预警模型

Fig.1   Meteorological warning model for rainfall-induced slope instability based on geological environment


$ R = R_{\mathrm{S}}+\sum\nolimits_{i = 1}^{{n}} {\Delta R_{{i}}} . $
(1)

式中：R为斜坡失稳预警阈值，RS为基准阈值，ΔRi表示第i个地质环境因子带来的阈值调整量.

预警模型通过综合性、有限性和动态性3大原则保证了预警的精准性、科学性和可用性. 综合性指预警模型考虑了多个地质环境因子综合作用的结果，斜坡本身和外部条件这些可能影响阈值变动的主要因素均加以考量，阈值结果总体反映了各指标对阈值变化的作用规律. 有限性指阈值调整是有区间限制的，从各指标对斜坡稳定性作用的实际规律和预警工作的可实现性考虑，结合大量的工程实践案例，本研究中的阈值调整结果限制于基准阈值±20%，使阈值结果处于有效区间内. 动态性是指随着场地地质环境条件的变化，降雨预警的阈值具有时效性，可以根据预警对象的动态变化进行更新和调整.

1.1. 基准阈值的确定

基准阈值是研究区斜坡发生浅层滑坡的普遍阈值，是斜坡对于短时强降雨反应的总体刻画. 基准阈值的作用是确定一定范围内，降雨诱发型滑坡对于某一降雨的反应. 它表征了一定范围内斜坡的特征，同时为斜坡尺度的滑坡预警提供了阈值参考. 须明确的是，基准阈值是基于统计学方法获得的斜坡特性，其本身是脱离地质环境条件的.

滑坡气象预警一般采用统计模型获取阈值. 本研究中，斜坡失稳与短时强降雨关系密切，因此选用I-D阈值模型[10]分析诱发斜坡破坏的降雨阈值：

$ I=C+a D^{\;\beta}. $
(2)

式中：I为降雨强度，D为降雨持续时间，a、β为统计参数，C≥0.

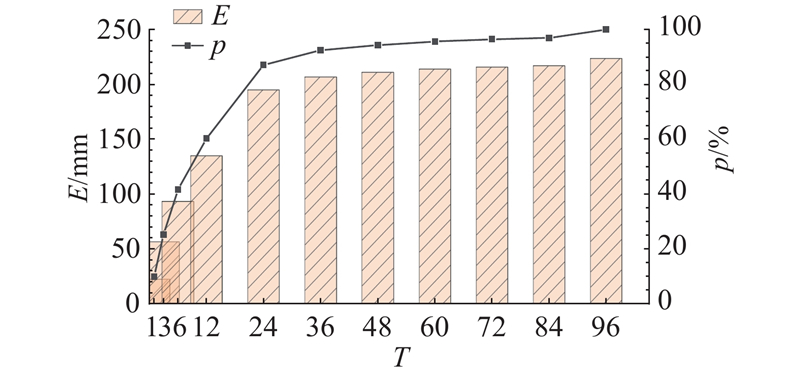
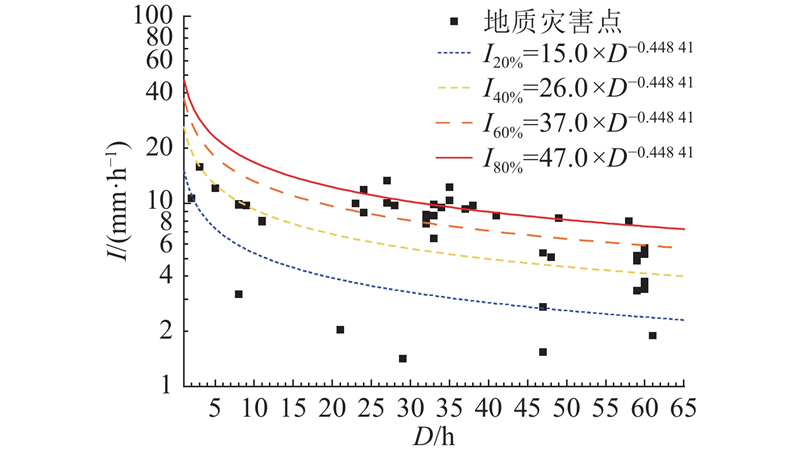
I-D模型以幂指数形式表达：以降雨历时为横轴，平均雨强为纵轴，绘制半对数坐标散点图，拟合得到I-D阈值曲线. 参考中国气象局《暴雨诱发的地质灾害气象风险预警等级QX/T 487—2019》[23]规定，按照20%、40%、60%、80%的灾害发生概率，划分降雨预警等级IV级（蓝色预警）、III级（黄色预警）、II级（橙色预警）、I级（红色预警），分别计算24 h累计降雨量，从而获得基于I-D模型的阈值结果，即基准阈值.

1.2. 斜坡地质环境因子的选取

不同斜坡，由于地质环境条件的差异，在面对同样的外界作用时，其反馈是不一样的. 建立精细化的预警模型，须考虑斜坡地质环境的差异，并赋予预警模型地质学意义.

在选取地质环境评价因子中，遵循2条原则：地质环境因子有效性原则和地质环境因子参数可获取性原则. 地质环境因子的有效性是指所选取的地质环境因子在斜坡降雨入渗变形和破坏过程中起决定作用和主要作用，涉及斜坡变形破坏的机理. 地质环境因子参数可获取性是指在实际调查工作中，因子参数能够获取，且手段简便，数据准确性高. 随着评价单元尺寸的缩小，评价单元数量指数级增长，所带来的数据采集工作是海量的，因此必须保证因子参数的可获取性.

本研究所提出的预警模型考虑了空间几何结构、岩土抗剪强度参数、水文地质条件、植被条件共4类地质环境因子. 其中，斜坡空间几何结构包括斜坡坡度α、松散岩土体厚度d和是否切坡；斜坡岩土抗剪强度参数包括岩土体内聚力c、内摩擦角φ；水文地质条件关注了渗透系数k；植被条件考虑了植被类型.

1.3. 基准斜坡的确定

基准斜坡是能代表研究区斜坡特征的概化斜坡，不一定是实体斜坡，其核心作用是对区内的斜坡地质环境条件进行整体的刻画和描述，它代表区内斜坡的普遍状态. 基准斜坡连接了基准阈值与阈值调整方案：一方面，基准斜坡与基准阈值相对应，两者反映了区域内斜坡的总体特征，基准斜坡反映的是几何和物理力学方面的特征，基准阈值反映的是斜坡在一定的降雨作用下的变化；另一方面，由基准斜坡到某一具体斜坡，地质环境条件会存在变化，伴随着斜坡对降雨反应的变化，这一变化由阈值调整规则进行表达，即达到同样的危险程度，阈值需要一定幅度的增减.

运用前述地质环境因子进行基准斜坡的刻画，上述因子可分为连续型因子和离散型因子2类，对于斜坡坡度、松散岩土体厚度、岩土体内聚力、内摩擦角、渗透系数这5个连续型因子运用平均值刻画基准斜坡；对于是否切坡和植被类型这2个离散型因子，则运用众数刻画基准斜坡.

1.4. 斜坡阈值调整方法

基准阈值是斜坡对降雨总体的反应，阈值调整即针对每个斜坡所具有的个性，从斜坡地质环境条件出发，根据其地质环境的变化，对基准阈值进行修正，从而赋予阈值一定的工程地质学意义.

在预警模型中，阈值调整方法从斜坡降雨入渗机理出发，分析各地质环境因子对岩土体渗流过程的改变或对岩土体强度的改变. 斜坡降雨入渗是水从地表运移到潜水面的过程，也包含了斜坡岩土体从非饱和到饱和的过程. 在此过程中，不同植被的覆盖直接影响了入渗雨量的多少；斜坡渗透系数直接影响渗透的快慢；斜坡坡度、松散岩土体厚度和切坡情况的变化既会改变斜坡渗流场也会影响斜坡稳定性；内聚力和内摩擦角受渗透过程影响，其变化直接改变斜坡的稳定状态.

充分考虑各斜坡地质环境条件差异，建立各因子梯度变化的模型，运用GeoStudio软件SEEP/W模块研究典型斜坡在降雨条件下因子改变后渗流场的变化规律，并使用SLOPE/W模块分析斜坡稳定性变化趋势和规律，从而反演斜坡失稳阈值的变化规律. 最后，根据各斜坡地质环境条件，按照预警模型，形成各自的气象阈值，实现斜坡尺度的斜坡失稳风险气象预警.

2. 平阳县概况

2.1. 地质环境条件

平阳县位于浙江省东南部（120º4ˊ4″E~121º10ˊ55″E，27º20ˊ48″N~27º45ˊ54″N），紧临东海，陆域面积为1051 km2，海域面积为1300 km2，人口稠密. 县内地形复杂，西高东低，最高峰为棋盘山，海拔为1231.1 m，其山地属南雁荡山脉. 区内出露的地层主要为燕山构造层，主体为中生代上侏罗统和下白垩统的火山-沉积岩系；同时伴有燕山晚期侵入的花岗岩、闪长岩、石英正长斑岩等，以岩株产出. 研究区的第四系松散堆积物，有坡洪积物、冲洪积物、人工堆积物等类型，成因复杂，不同的区域厚度变化较大，差异明显，地质构造一般发育.

根据平阳县历年地质灾害调查和县自然资源和规划局数据库资料，平阳县共有地质灾害642处，其中滑坡有542处，绝大多数为浅层降雨诱发型滑坡，受台风暴雨影响强烈. 本次研究使用有准确发生时间（小时精度）的268处滑坡进行分析，滑坡发生时间集中在2005年之后. 滑体主要为含碎石黏性土，结构松散，降雨作用下极易滑动，规模以小型为主（见图2）. 地质灾害集中发生在7、8、9月，具有明显的季节性.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   平阳典型滑坡照片

Fig.2   Photo of typical landslide in Pingyang County


2.2. 降雨特征

采集了平阳县国家级气象站1960年以来日降雨数据和多年小时降雨数据，以及29个地方站小时降雨数据进行降雨分析.

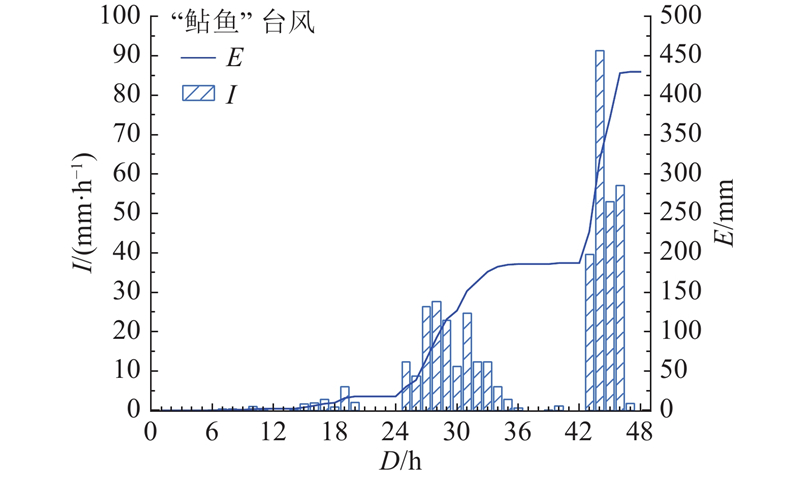
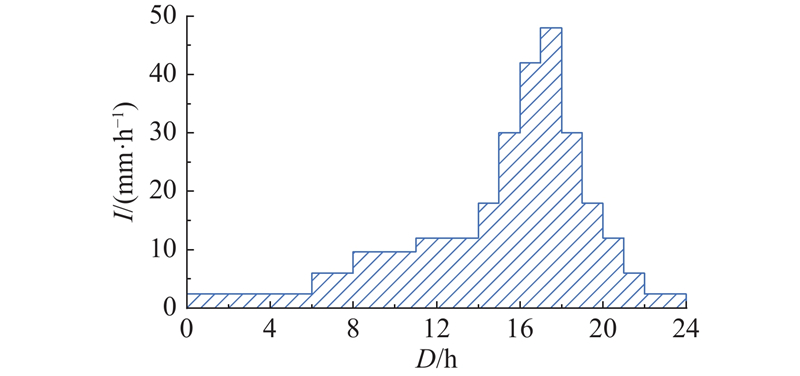
平阳县属亚热带季风气候，平均气温为17.9 ℃，年均降雨量为1703.6 mm. 台风暴雨期（7—9月）降雨量为647.4 mm，占全年的38%，平均雨日43 d，降雨集中，雨量丰沛. 平阳县多次遭受极端台风影响：2005年7月18—21日，“海棠”台风总雨量E超过640 mm，48 h最大雨量达到375 mm. 2009年8月9日，“莫拉克”台风总雨量超过800 mm. 2016年9月27—29日，“鲇鱼”台风48 h最大雨量为425 mm，如图3所示. 上述台风在平阳引发了大量地质灾害，造成人员伤亡及经济损失. 台风带来的降雨强度极大，3次台风降雨过程降雨强度最大值均超过37 mm/h，最大接近50 mm/h；雨型呈“多峰型”[24]. 平阳地区台风暴雨特征为：降雨历时短，降雨集中在24 h以内；短时雨强大，极大值可接近50 mm/h[25].

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   典型台风降雨过程

Fig.3   Typical typhoon rainfall process


2.3. 滑坡与降雨的相关性

台风暴雨的强度较大，往往引起群发性滑坡，将同一时间发生的滑坡定义为一次灾害事件[26]，研究区共55个滑坡事件（268起滑坡）发生在35起降雨过程中. 对滑坡事件与降雨过程相关性展开分析，统计滑坡发生前降雨时间T，累计雨量E和累计降雨占比p，如图4所示. 距离滑坡发生12 h，累计降雨量占降雨过程总雨量的60.3%；距离滑坡发生24 h，累计降雨量占比为84.1%；距离滑坡发生36 h，累计降雨量占比为92.5%，距离滑坡发生48 h，累计降雨量占比为94.3%. 显然，降雨总量集中在滑坡发生前的24 h. 因此，针对滑坡发生前累计24 h降雨开展滑坡风险气象预警研究.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   滑坡发生前累计降雨

Fig.4   Accumulated rainfall before geological disasters


3. 研究结果

3.1. 平阳县降雨诱发型滑坡基准阈值

分析平阳县历史灾害数据，按照前述方法，拟合I-D阈值曲线，如图5所示. 根据20%、40%、60%、80%的滑坡发生概率，得到平阳县降雨诱发型滑坡基准阈值，如表1所示.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   平阳县降雨诱发型滑坡I-D阈值曲线

Fig.5   I-D threshold curve of rainfall-induced landslide in Pingyang County


表 1   平阳县降雨诱发型滑坡预警基准阈值(24 h)

Tab.1  Early warning benchmark threshold (24 h) of rainfall-induced landslide in Pingyang County

预警等级RS/mm
I级（红色预警）[270, +∞)
II级（橙色预警）[210, 270)
III级（黄色预警）[150, 210)
IV级（蓝色预警）[85, 150)

新窗口打开| 下载CSV


3.2. 阈值调整方法

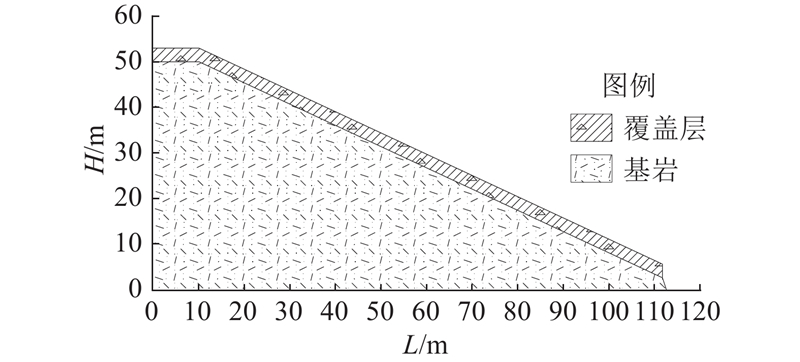
平阳县降雨诱发型滑坡为覆盖层内的浅层斜坡变形破坏，规模小. 以平阳县基准斜坡为基础建立无限斜坡模型，如图6所示. 图中，H、L分别为斜坡模型的高度、长度. 模型为岩土混合斜坡，坡度为25º；上覆松散覆盖层，厚为3 m；坡脚切坡高为5 m，且切穿覆盖层. 斜坡土体内聚力为25 kPa；内摩擦角为25º；渗透系数k=5×10−6 m/s.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   基准斜坡模型

Fig.6   Benchmark slope model


本次降雨工况按照典型致灾的台风降雨过程设置，24 h降雨量为300 mm，整体呈现先增大再减小的趋势[27]，降雨强度在16~17 h达到峰值，如图7所示. 运用数值模拟方法，分析不同地质环境因子变化与斜坡降雨阈值的调整量的关系，结果如下.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   降雨工况分小时雨强

Fig.7   Hourly rainfall intensity under rainfall scenario


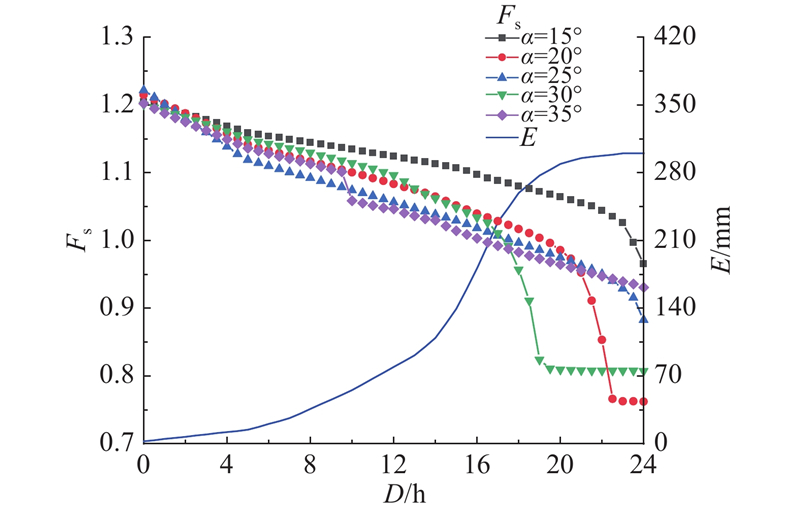
1）坡度α. 斜坡坡度是影响降雨条件下斜坡稳定性的重要因素. 坡度越大，斜坡初始稳定性系数越小，在降雨条件下，斜坡稳定性系数安全裕度小，斜坡更容易失稳. 研究区内斜坡坡度普遍小于35º，因此建立坡度为15º、20º、25º、30º、35º，覆盖层厚度为3 m的斜坡模型.

如图8所示为不同坡度斜坡的稳定性系数Fs变化图，在持续降雨下，斜坡稳定性系数不断降低. 当累计降雨量为205 mm时，35º斜坡稳定性系数降低至1.0，斜坡处于不稳定状态. 对于30º、25º、20º和15º斜坡，临界降雨量分别为237、252、283、300 mm. 根据斜坡失稳时雨量和坡度之间的规律，以25º斜坡对应临界雨量252 mm阈值为基准，拟合不同坡度下阈值的调整值ΔRα（见图9）. 坡度变化值和阈值调整值呈负相关，降雨阈值与斜坡坡度的调整规则为y＝−4.72x+118（R2＝0.9765）.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   不同坡度下的斜坡稳定性系数变化图

Fig.8   Variation of slope stability coefficient with different slope values


图 9

新窗口打开| 下载原图ZIP| 生成PPT

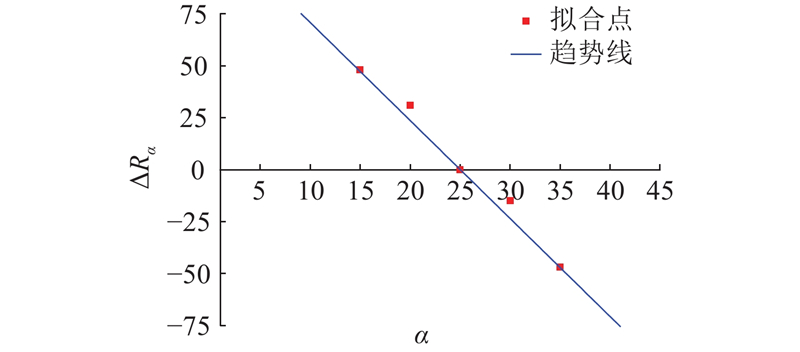
图 9   斜坡坡度因子降雨阈值调整拟合曲线

Fig.9   Rainfall threshold adjustment fitting curve of slope


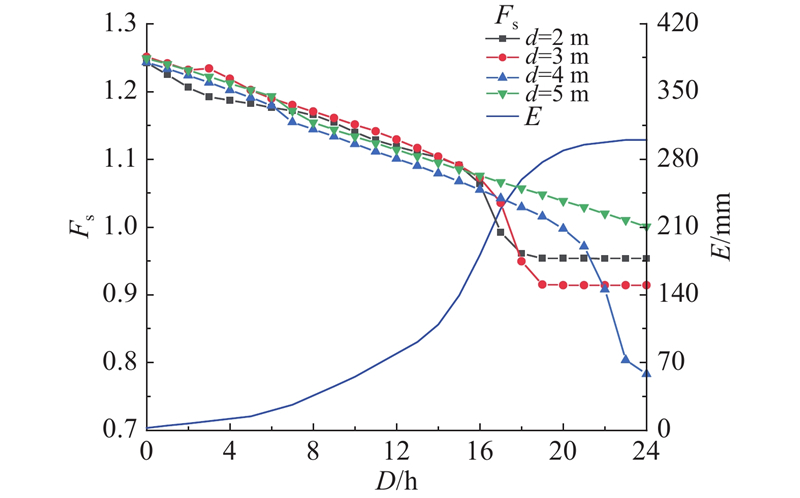
2）覆盖层厚度d. 斜坡覆盖层厚度越大，其初始稳定性系数越小，稳定性系数降低幅度越小[28]. 覆盖层厚度越小，斜坡在降雨入渗条件下更容易饱和，基质吸力丧失，土体抗剪强度降低，斜坡稳定性降低幅度越大. 相反，覆盖层越厚的斜坡，饱和时间拉长甚至不能达到饱和状态，稳定性降低幅度有限. 研究区斜坡覆盖层厚度普遍不超过5 m，建立覆盖层厚度为2、3、4、5 m，坡度为25º的斜坡模型.

如图10所示为不同覆盖层厚度下的斜坡稳定性系数变化图，在持续降雨下，斜坡稳定性系数不断降低. 当累计降雨量为230 mm时，d=2 m的斜坡稳定性系数降低至1.0，斜坡处于不稳定状态. 对于覆盖层厚度为3、4、5 m的斜坡，临界降雨量分别为250、290、300 mm. 以覆盖层厚为3 m的斜坡对应的临界雨量为基准，拟合得到不同覆盖层厚度的斜坡阈值调整值ΔRd满足规则：y＝28.5x−78.5（R2＝0.9627）（见图11），覆盖层厚度变化值与阈值调整值呈正相关.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   不同覆盖层厚度下的斜坡稳定性系数变化图

Fig.10   Variation of slope stability coefficient with different cover layer thicknesses


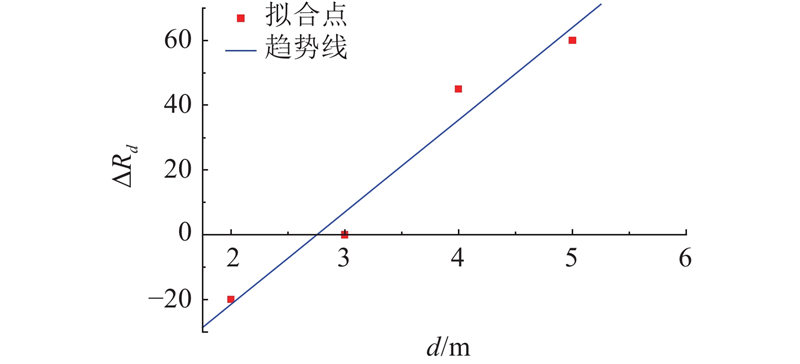
图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   斜坡覆盖层厚度因子降雨阈值调整拟合曲线

Fig.11   Rainfall threshold adjustment fitting curve of slope cover layer thickness


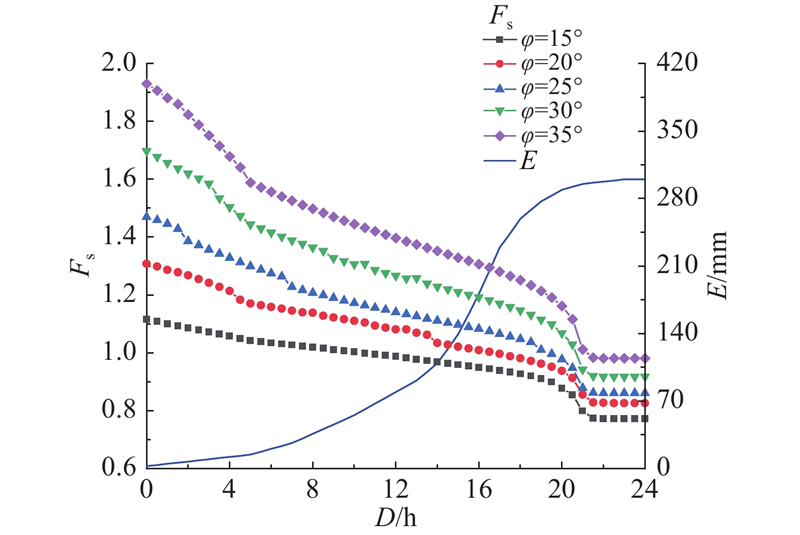
3）内摩擦角φ. 内摩擦角φ是决定土体抗剪强度的重要参数，直接控制斜坡的稳定性：内摩擦角越大，土体抗剪强度越大，斜坡稳定系数越大[29]. 分析坡度为25º、覆盖层厚度为3 m的斜坡，其内摩擦角分别为15º、20º、25º、30º、35º在降雨条件下的稳定性系数变化规律. 总体上，斜坡稳定性随降雨进行持续降低，内摩擦角不影响降雨入渗过程. 当斜坡Fs=1.0时，斜坡失稳，此时的累计降雨量为降雨阈值. 由于斜坡初始Fs的差异，不同内摩擦角的斜坡失稳的时间不同. 初始Fs越大，斜坡失稳所需时间越长，对应的降雨阈值越大.

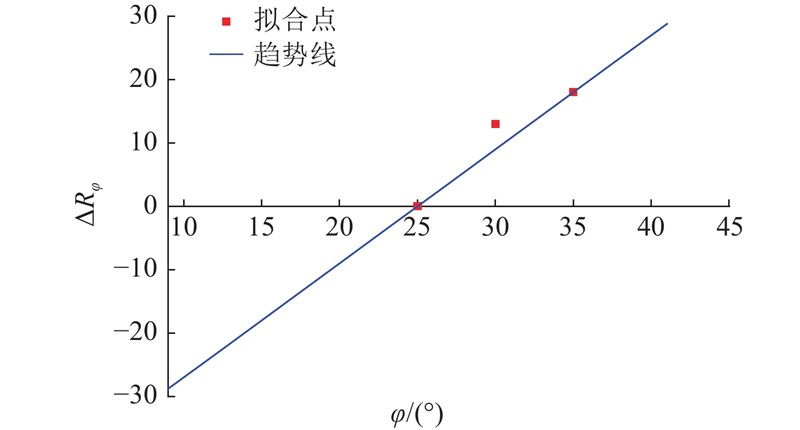
如图12所示为不同内摩擦角斜坡的稳定性系数变化图，斜坡稳定性系数随降雨不断降低. 当累计降雨量为55 mm时，φ=15º的斜坡稳定性系数降低至1.0，斜坡处于不稳定状态. 对于内摩擦角为20º、25º、30º和35º的斜坡，临界降雨量分别为205、277、290、295 mm. 以φ=25º斜坡对应临界雨量277 mm阈值为基准，拟合不同内摩擦角下阈值的调整值（见图13）. 当内摩擦角小于25º时，降雨阈值偏小，即在较小降雨的情况下，斜坡就发生失稳，其规律区别于25º及以上的斜坡，在处理阈值调整规律时，采用25º及以上的阈值结果进行拟合. 坡度变化值和阈值调整值ΔRφ呈正相关，阈值调整规则为y＝1.8x−45（R2＝0.9250）.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   不同内摩擦角下的斜坡稳定性系数变化图

Fig.12   Variation of slope stability coefficient with different internal friction angles


图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   斜坡内摩擦角因子降雨阈值调整拟合曲线

Fig.13   Rainfall threshold adjustment fitting curve of slope internal friction angle


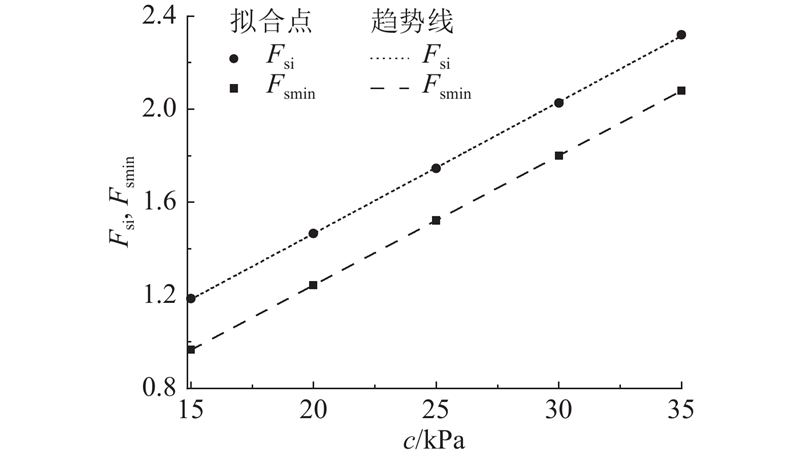
4）内聚力c. 内聚力c也直接控制斜坡的稳定性，内聚力越大，土体抗剪强度越大，斜坡稳定系数越高[30-31]. 以坡度为25º，覆盖层厚度为3 m的斜坡为基础，研究内聚力分别为15、20、25、30、35 kPa的斜坡的稳定性系数变化情况.

如图14所示为不同内聚力斜坡的初始稳定性系数Fsi和最低稳定性系数Fsmin拟合曲线. 内聚力变化直接改变了初始稳定性，与Fsi呈线性变化关系：Fsi=0.0566x+0.3349（R2=0.9998）. 同时，内聚力变化不会导致稳定性系数降低状态的变化，不同内聚力与对应的Fsmin分布也呈线性变化关系：Fsmin=0.0557x+0.1204（R2=0.9999）. 以上结果说明，内聚力c变化仅会导致斜坡Fsi和Fsmin的改变，且呈现高度线性相关的同增同降趋势. 所以，c越大，斜坡的稳定性系数越大，安全裕度越大，诱发斜坡失稳所需的临界降雨阈值越大.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   不同内聚力下的斜坡Fsi和Fsmin拟合曲线

Fig.14   Fitting curves of Fsi and Fsmin of different cohesion forces


在斜坡概化模型中，斜坡的初始稳定性由c和φ共同控制，如图14所示单独反映了c的变化所导致的稳定性系数变化. 以c =25 kPa斜坡模型的降雨阈值为基准，对降雨阈值进行调整. 具体如下：c增大10 kPa，阈值调整至上限，中间线性插值调整；c减小10 kPa，阈值下浮至下限，中间线性插值调整.

5）渗透系数k. 在持续降雨作用下，覆盖层土体渗透系数越大，斜坡渗透性越强，雨水入渗速度就越快、入渗量越多. 斜坡土体中水的体积分数增大速率越快，基质吸力下降幅度越大，斜坡土体抗剪强度下降越明显，最终致使斜坡稳定性大幅下降[32].

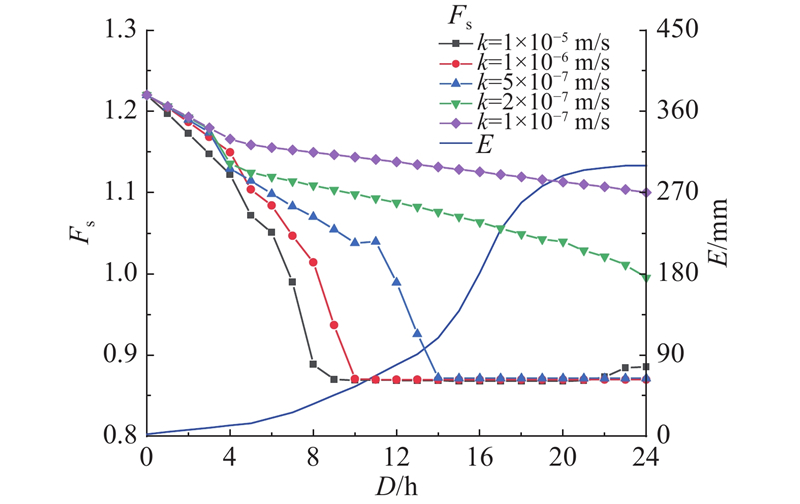
计算不同渗透系数k时基准斜坡的稳定性系数变化情况，如图15所示. 由结果可知，渗透系数变化不会引起斜坡初始稳定性系数的变化，但是会改变降雨条件下斜坡稳定性系数变化过程. 当渗透系数较大时（k≥5×10−7 m/s），斜坡能够完全饱和，此时斜坡稳定性系数降低幅度最大，稳定性系数降至最低，且随着渗透系数的变小，斜坡饱和的速度变慢，稳定性降低的速度减缓；当渗透系数较小时（k≤2×10−7 m/s），斜坡对降雨的响应远不如渗透系数大时敏感，斜坡不能完全饱和，稳定性系数降低幅度有限. 由此可见，渗透系数的变化对于降雨条件下斜坡的稳定性系数变化状态和幅度起了控制作用. 当k=2×10−7 m/s（0.01728 m/d）时，经过24 h降雨，斜坡稳定性系数降低至1.0以下，斜坡处于不稳定状态. 以k=2×10−7 m/s为基准，当k增大至1×10−5 m/s时，斜坡稳定性系数大幅降低，此时斜坡对应的临界降雨阈值最小，取下限阈值. 当k减小至1×10−7 m/s及以下时，斜坡稳定性系数降低幅度有限，斜坡稳定性安全裕度较大，此时斜坡对应的临界降雨阈值更大，取上限阈值.

图 15

新窗口打开| 下载原图ZIP| 生成PPT

图 15   不同渗透系数下的斜坡稳定性系数变化图

Fig.15   Variation of slope stability coefficient with different permeability coefficients


6）切坡条件. 平阳已发生的滑坡中，绝大部分前缘都有切坡. 切坡对于斜坡地质环境条件的改变包括几何形态、植被覆盖、水文条件、应力环境等多个方面，使斜坡初始边界条件发生了极大的变化[33-34]. 计算斜坡坡度为25º，覆盖层厚度为2、3、4、5 m的斜坡模型在有切坡和无切坡2种工况下的初始稳定性系数（见图16），其中切坡坡度为90º，切坡深度大于覆盖层厚度.

图 16

新窗口打开| 下载原图ZIP| 生成PPT

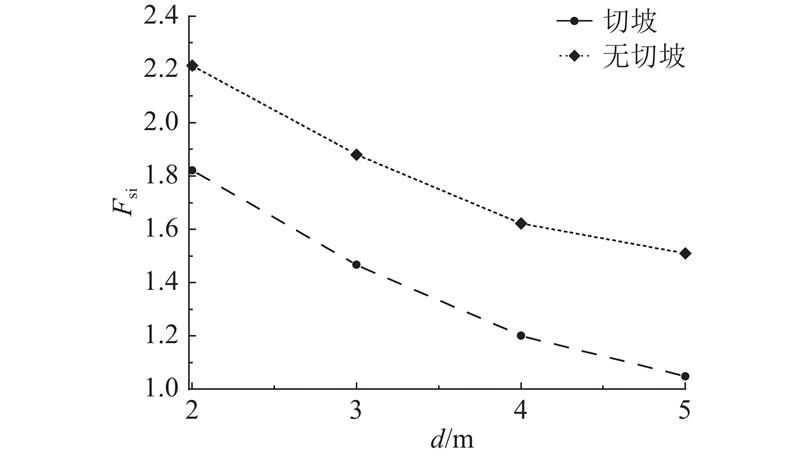
图 16   有无切坡时不同覆盖层厚度斜坡的初始稳定性系数

Fig.16   Initial stability coefficients of slopes under different cover layer thicknesses with or without cutting slope


由图16可知，对于相同覆盖层厚度的斜坡模型，切坡会造成斜坡的初始稳定性大幅降低. 在切坡卸荷后，临空部分应力分布情况改变，此时易发生覆盖层内的小规模滑移. 此类失稳模式下的滑体体积小，但是，由于切坡一般紧邻房屋、道路之类的承灾体，极易造成人员伤亡和经济损失，风险高. 未切坡时斜坡初始稳定性系数较大，安全裕度较高，所以诱发斜坡失稳时的降雨阈值更大，以基准阈值上浮至上限值作为无切坡情况下的降雨阈值.

7）植被类型. 不同植被类型结构不一，其树冠截留降雨的能力不一，对斜坡的稳定性表现出不同的影响[35]. 在短时强降雨过程中，未被冠层拦截的降雨才能有效补给地下水，通过入渗作用降低土体的抗剪强度. 在本研究中，有效降雨系数指未被树冠层截留而穿透下来的雨量与实际雨量值的比例：η=O/P，其中，η为有效降雨系数，P为降雨量，O为穿透树冠层的有效雨量. 对于植被冠层截流造成的阈值调整可按ΔRv=(1−1/η)RS计算，其中，ΔRv为植被类型调整值.

研究区常见植被的有效降雨系数如表2所示.

表 2   常见植被及其有效降雨系数参考值[36]

Tab.2  Common vegetation and its effective rainfall coefficient reference values

植被类型植被特征η
杉木树高约30 m，大枝平展，小枝对生或轮生，常成二列
状，叶子披针形或条状披针形，长2~6 cm，宽3~5 mm		0.82
松树轮状分枝，节间长，小枝较细弱平直，
树冠篷松不紧凑，针叶细长成束		0.85
毛竹竿高可达20多米，末级小枝一般有2~4叶，
叶片较小较薄，披针形		0.93
油茶树树高一般约3 m，单叶互生，其叶子呈椭圆形，
且相对比较茂盛		0.57

新窗口打开| 下载CSV


3.3. 平阳县精细化气象预警

根据式（1）和图1的预警模型，结合平阳灾害得到基准阈值和阈值调整规则，得到平阳县精细化阈值（一斜坡一阈值）：

$ \begin{split} R = & {R_{\rm{S}}} + \displaystyle{\sum} {\left( {\Delta R_{\alpha}} + {\Delta R_{d}} + {\Delta R_{\varphi}} + {\Delta R_{c}} +\right.} \\&\left. {{\Delta R_{k}} + {\Delta R_{\rm{s}}} + {\Delta R_{\rm{v}}}} \right).\end{split} $
(3)

式中：ΔRα、ΔRd、ΔRφ、ΔRc、ΔRk、ΔRs分别为斜坡坡度、覆盖层厚度、内摩擦角、黏聚力、渗透系数和切坡情况对阈值的调整值，具体取值如表3所示. 根据阈值框架，结合现场调查数据，计算得到平阳县风险斜坡的精细化阈值.

表 3   平阳县降雨诱发斜坡失稳预警阈值因子调整规则

Tab.3  Adjustment rules of rainfall-induced slope instability early warning threshold factor in Pingyang County

地质环境因子调整规则
斜坡坡度α/(º)ΔRα=−0.01748(α−25)×RS
覆盖层厚度d/mΔRd=0.1056(d−3)×RS+7
内摩擦角φ/(º)ΔRφ=0.00667(φ−25)×RS
黏聚力c/kPaΔRc=0.02(c−25)×RS
渗透系数k/(m·s−1)$ \Delta R_k=\left\{\begin{array}{*{20}{l}}-0.2 \times R_{\mathrm{S}}, & k>2 \times 10^{-7}\; \mathrm{m / s} \\0, & k=2 \times 10^{-7} \;\mathrm{m / s}\\0.2 \times R_{\mathrm{S}}, & k<2 \times 10^{-7}\; \mathrm{m / s}\end{array}\right. $
切坡情况$ \Delta R_{\rm {s }}=\left\{\begin{array}{*{20}{l}}0,& \text { 有切坡 } \\0.2 \times R_{\mathrm{S}},& \text { 无切坡 }\end{array}\right. $
不同植被类型有效
降雨系数/η		杉木0.82
松树0.85
毛竹0.93
油茶树0.57
荒地1.00

新窗口打开| 下载CSV


4. 预警模型应用与验证

2016年9月27—29日，受“鲇鱼”台风影响，平阳县普降暴雨，过程雨量达461.7 mm，暴雨中心达到643.5 mm，共诱发41处灾害，其中滑坡36处. 平阳现有65个雨量站，按照泰森多边形法则，划分降雨预报区[37]. 36处滑坡根据所处位置，分别获取对应的小时雨量数据（对于新建站点缺失降雨数据的滑坡，使用当时已有站点的降雨数据）.

根据表1中的基准阈值和式（3）阈值调整方法，得到36处滑坡24 h不同等级阈值，如图17所示. 针对发生的36处滑坡，根据雨量数据计算灾害发生前逐小时滚动累计24 h降雨（E24）进行滑坡气象预警复盘. 由滑坡预警复盘可知：1）有34处滑坡，在滑坡发生前10 h进入预警状态；2）所有滑坡在发生前均已达到黄色预警状态，并且35处滑坡黄色预警或更高等级预警至少3 h；3）有23处滑坡最终达到红色预警，3处滑坡最终达到橙色预警，占比分别为64%和8%. 按照浙政办发〔2021〕8号文《浙江省突发地质灾害应急预案》[38]对于橙色预警必要时须进行人员转移安置，对于红色预警必须进行人员转移安置[39]，可以认定预警成功率为72%. 并且，在23个发布红色预警的滑坡中，18个在预警发布后3 h内即发生破坏，由此可见，本套阈值方案灵敏度较高，预警效果较好.

图 17

新窗口打开| 下载原图ZIP| 生成PPT

图 17   “鲇鱼”台风诱发滑坡预警复盘图

Fig.17   Review of early warning of landslides induced by Super Typhoon Megi


针对所获取的有准确时间记录的286处滑坡一一进行验证. 其中，222处滑坡能够在灾害发生前发布红色预警或橙色预警，总体预警成功率为82%.

5. 结　论

为了提高降雨诱发型滑坡风险气象预警的精准性，提出基于地质环境的降雨诱发斜坡失稳风险预警模型，并在平阳县展开实例研究和验证，得到如下结论.

（1）提出基于地质环境的精细化降雨诱发型斜坡失稳风险气象预警模型. 模型以I-D统计阈值为基准阈值，考虑斜坡地质环境因子（斜坡坡度、覆盖层厚度、内摩擦角、内聚力、渗透系数、切坡情况和植被类型）对斜坡稳定性的影响，形成阈值调整规则.

（2）结合统计模型对历史灾害的反演分析，又从降雨入渗过程出发，根据每个斜坡的地质环境变化进行阈值调整，形成了一斜坡一阈值，通过综合性、有限性和动态性3大原则保证了阈值结果的精准性、科学性和可用性.

（3）以浙江省平阳县为例，根据灾害发育情况，运用本研究模型计算出平阳县一斜坡一阈值. 以典型降雨过程为案例进行验证，综合预警率达到72%，效果良好. 该预警模型能够为地质灾害主管部门提供工作介入时机的提示和标准，满足实际工作需求，为浙江省“一区一阈值”的精细化滑坡风险气象预警与风险管控提供新思路和参考.

（4）各斜坡地质环境因子对斜坡稳定性的耦合作用及其在阈值上的反映尚未研究，有待进一步探索.

参考文献

FROUDE M J, PETLEY D N

Global fatal landslide occurrence from 2004 to 2016

[J]. Natural Hazards and Earth System Sciences, 2018, 18 (8): 2161- 2181

DOI:10.5194/nhess-18-2161-2018      [本文引用: 1]

戚国庆. 降雨诱发滑坡机理及其评价方法研究: 非饱和土力学理论在降雨诱发型滑坡研究中的应用[D]. 成都: 成都理工大学, 2004.

[本文引用: 1]

QI Guoqing. Study on the mechanics of rainfall-induced landslide and its evaluating method: the research of landslide due to rainfall applying theories of unsaturated soils mechanics [D]. Chengdu: Chengdu University of Technology, 2004.

[本文引用: 1]

殷坤龙, 汪洋, 唐仲华

降雨对滑坡的作用机理及动态模拟研究

[J]. 地质科技情报, 2002, 21 (1): 75- 78

[本文引用: 1]

YIN Kunlong, WANG Yang, TANG Zhonghua

Mechanism and dynamic simulation of landslide by precipitation

[J]. Geological Science and Technology Information, 2002, 21 (1): 75- 78

[本文引用: 1]

LEPORE C, ARNONE E, NOTO L V, et al

Physically based modeling of rainfall-triggered landslides: a case study in the Luquillo forest, Puerto Rico

[J]. Hydrology and Earth System Sciences, 2013, 17 (9): 3371- 3387

DOI:10.5194/hess-17-3371-2013      [本文引用: 1]

伍宇明, 兰恒星, 高星, 等

台风暴雨型滑坡降雨阈值曲线研究: 以福建地区为例

[J]. 工程地质学报, 2014, 22 (2): 255- 262

DOI:10.3969/j.issn.1004-9665.2014.02.015      [本文引用: 1]

WU Yuming, LAN Hengxing, GAO Xing, et al

Rainfall threshold of storm-induced landslides in typhoon areas: a case study of Fujian Province

[J]. Journal of Engineering Geology, 2014, 22 (2): 255- 262

DOI:10.3969/j.issn.1004-9665.2014.02.015      [本文引用: 1]

CHEN C W, SAITO H, OGUCHI T

Analyzing rainfall-induced mass movements in Taiwan using the soil water index

[J]. Landslides, 2017, 14 (3): 1031- 1041

DOI:10.1007/s10346-016-0788-1     

郭子正, 殷坤龙, 刘庆丽, 等

基于位移比模型的三峡库区云阳县域内蠕变型滑坡降雨预警

[J]. 地球科学, 2020, 45 (2): 672- 684

[本文引用: 1]

GUO Zizheng, YIN Kunlong, LIU Qingli, et al

Rainfall warning of creeping landslide in Yunyang County of Three Gorges Reservoir region based on displacement ratio model

[J]. Earth Science, 2020, 45 (2): 672- 684

[本文引用: 1]

GABET E J, BURBANK D W, PUTKONEN J K, et al

Rainfall thresholds for landsliding in the Himalayas of Nepal

[J]. Geomorphology, 2004, 63 (3/4): 131- 143

[本文引用: 1]

MATSUYAMA H, SAITO H, ZEMTSOV V

Application of soil water index to landslide prediction in snowy regions: sensitivity analysis in Japan and preliminary results from Tomsk, Russia

[J]. Progress in Earth and Planetary Science, 2021, 8 (1): 17

DOI:10.1186/s40645-021-00408-9      [本文引用: 1]

CAINE N

The rainfall intensity-duration control of shallow landslides and debris flows

[J]. Geografiska Annaler. Series A, Physical Geography, 1980, 62 (1/2): 23- 27

DOI:10.2307/520449      [本文引用: 2]

GUZZETTI F, PERUCCACCI S, ROSSI M, et al

Rainfall thresholds for the initiation of landslides in central and southern Europe

[J]. Meteorology and Atmospheric Physics, 2007, 98 (3/4): 239- 267

[本文引用: 1]

LI W, LIU C, SCAIONI M, et al

Spatio-temporal analysis and simulation on shallow rainfall-induced landslides in China using landslide susceptibility dynamics and rainfall I-D thresholds

[J]. Science China Earth Sciences, 2017, 60 (4): 720- 732

DOI:10.1007/s11430-016-9008-4      [本文引用: 1]

MARIN R J, VELÁSQUEZ M F, GARCÍA E F, et al

Assessing two methods of defining rainfall intensity and duration thresholds for shallow landslides in data-scarce catchments of the Colombian Andean Mountains

[J]. Catena, 2021, 206: 105563

DOI:10.1016/j.catena.2021.105563      [本文引用: 1]

PICIULLO L, CALVELLO M, CEPEDA J M

Territorial early warning systems for rainfall-induced landslides

[J]. Earth-Science Reviews, 2018, 179: 228- 247

DOI:10.1016/j.earscirev.2018.02.013      [本文引用: 1]

DIKSHIT A, SARKAR R, PRADHAN B, et al

Estimating rainfall thresholds for landslide occurrence in the Bhutan Himalayas

[J]. Water, 2019, 11 (8): 1616

DOI:10.3390/w11081616      [本文引用: 1]

刘艳辉, 苏永超

四川青川县区域地质灾害气象风险预警模型研究

[J]. 工程地质学报, 2019, 27 (1): 134- 143

[本文引用: 1]

LIU Yanhui, SU Yongchao

Early-warning model of regional geological disasters based on meteorological factor in Qingchuan County, Sichuan Province

[J]. Journal of Engineering Geology, 2019, 27 (1): 134- 143

[本文引用: 1]

BRUNETTI M T, PERUCCACCI S, ROSSI M, et al

Rainfall thresholds for the possible occurrence of landslides in Italy

[J]. Natural Hazards and Earth System Sciences, 2010, 10 (3): 447- 458

DOI:10.5194/nhess-10-447-2010     

ZÊZERE J L, RODRIGUES M L. Rainfall thresholds for landsliding in Lisbon Area (Portugal) [M]// Rybář J, Stemberk J, Wagner P. Landslides . Lisse: Routledge, 2002: 333−338.

DENNIS M S, JOSEPH E G, JASON W K. Objective definition of rainfall intensity-duration thresholds for post-fire flash floods and debris flows in the area burned by the Waldo Canyon Fire, Colorado, USA [M]// Lollino G, Giordan D, Crosta G B, et al. Engineering geology for society and territory: Volume 2 . Cham: Springer International Publishing, 2015: 621−624.

[本文引用: 1]

谢剑明, 刘礼领, 殷坤龙, 等

浙江省滑坡灾害预警预报的降雨阀值研究

[J]. 地质科技情报, 2003, 22 (4): 101- 105

[本文引用: 1]

XIE Jianming, LIU Liling, YIN Kunlong, et al

Study on the threshold valves of rainfall of landslide hazards for early warning and prediction in Zhejiang Province

[J]. Geological Science and Technology Information, 2003, 22 (4): 101- 105

[本文引用: 1]

殷坤龙, 张桂荣, 龚日祥, 等

基于Web-GIS的浙江省地质灾害实时预警预报系统设计

[J]. 水文地质工程地质, 2003, (3): 19- 23

DOI:10.3969/j.issn.1000-3665.2003.03.005      [本文引用: 1]

YIN Kunlong, ZHANG Guirong, GONG Rixiang, et al

A real time warning system design of geo-hazards supported by Web-GIS in Zhejiang Province, China

[J]. Hydrogeology and Engineering Geology, 2003, (3): 19- 23

DOI:10.3969/j.issn.1000-3665.2003.03.005      [本文引用: 1]

鲍其云, 麻土华, 李长江, 等

浙江62个丘陵山区县引发滑坡的降雨强度: 历时阈值

[J]. 科技通报, 2016, 32 (5): 48- 55

DOI:10.3969/j.issn.1001-7119.2016.05.010      [本文引用: 1]

BAO Qiyun, MA Tuhua, LI Changjiang, et al

Rainfall intensity-duration thresholds for the initiation of landslides in 62 hilly and mountainous counties of Zhejiang Province

[J]. Bulletin of Science and Technology, 2016, 32 (5): 48- 55

DOI:10.3969/j.issn.1001-7119.2016.05.010      [本文引用: 1]

中国气象局. 暴雨诱发的地质灾害气象风险预警等级: QX/T 487—2019 [S]. 北京: 气象出版社, 2019.

[本文引用: 1]

林冰. 大连市降雨特性与雨水资源化的研究[D]. 大连: 大连理工大学, 2006.

[本文引用: 1]

LIN Bin. Research on rainfall characteristics and rainwater resources in Dalian City [D]. Dalian: Dalian University of Technology, 2006.

[本文引用: 1]

刘艳辉, 唐灿, 李铁锋, 等

地质灾害与降雨雨型的关系研究

[J]. 工程地质学报, 2009, 17 (5): 656- 661

DOI:10.3969/j.issn.1004-9665.2009.05.012      [本文引用: 1]

LIU Yanhui, TANG Can, LI Tiefeng, et al

Statistical relations between geo-hazards and rain-type

[J]. Journal of Engineering Geology, 2009, 17 (5): 656- 661

DOI:10.3969/j.issn.1004-9665.2009.05.012      [本文引用: 1]

刘书豪. 降雨条件下的输电线路滑坡风险评估与预警技术研究[D]. 武汉: 中国地质大学, 2021.

[本文引用: 1]

LIU Shuhao. Research on risk assessment and early warning of landslides triggered by rainfall along electrical power transmission line [D]. Wuhan: China University of Geosciences, 2021.

[本文引用: 1]

岑国平, 沈晋, 范荣生

城市设计暴雨雨型研究

[J]. 水科学进展, 1998, 9 (1): 41- 46

[本文引用: 1]

CEN Guoping, SHEN Jin, FAN Rongsheng

Research on rainfall pattern of urban design storm

[J]. Advances of Water Science, 1998, 9 (1): 41- 46

[本文引用: 1]

TUFANO R, FORMETTA G, CALCATERRA D, et al

Hydrological control of soil thickness spatial variability on the initiation of rainfall-induced shallow landslides using a three-dimensional model

[J]. Landslides, 2021, 18 (10): 3367- 3380

DOI:10.1007/s10346-021-01681-x      [本文引用: 1]

VITHANA S B, NAKAMURA S, GIBO S, et al

Correlation of large displacement drained shear strength of landslide soils measured by direct shear and ring shear devices

[J]. Landslides, 2012, 9 (3): 305- 314

DOI:10.1007/s10346-011-0301-9      [本文引用: 1]

RAO S M

Role of apparent cohesion in the stability of Dominician allophane soil slopes

[J]. Engineering Geology, 1996, 43 (4): 265- 279

DOI:10.1016/S0013-7952(96)00036-1      [本文引用: 1]

SUN S, PANG B, HU J, et al

Characteristics and mechanism of a landslide at Anqian iron mine, China

[J]. Landslides, 2021, 18 (7): 2593- 2607

DOI:10.1007/s10346-021-01671-z      [本文引用: 1]

吴宏伟, 陈守义, 庞宇威

雨水入渗对非饱和土坡稳定性影响的参数研究

[J]. 岩土力学, 1999, 20 (1): 1- 14

DOI:10.3969/j.issn.1000-7598.1999.01.001      [本文引用: 1]

NG Wangwai Charles, CHEN Shouyi, PANG Yuewai

Parametric study of effects of rain infiltration on unsaturated slopes

[J]. Rock and Soil Mechanics, 1999, 20 (1): 1- 14

DOI:10.3969/j.issn.1000-7598.1999.01.001      [本文引用: 1]

LÓPEZ-VINIELLES J, EZQUERRO P, FERNÁNDEZ-MERODO J A, et al

Remote analysis of an open-pit slope failure: Las Cruces case study, Spain

[J]. Landslides, 2020, 17 (9): 2173- 2188

DOI:10.1007/s10346-020-01413-7      [本文引用: 1]

ZHANG J, LUO Y, ZHOU Z, et al

Research on the rainfall-induced regional slope failures along the Yangtze River of Anhui, China

[J]. Landslides, 2021, 18 (5): 1801- 1821

DOI:10.1007/s10346-021-01623-7      [本文引用: 1]

ZHUANG Y, XING A, JIANG Y, et al

Typhoon, rainfall and trees jointly cause landslides in coastal regions

[J]. Engineering Geology, 2022, 298: 106561

[本文引用: 1]

鲜木斯艳·阿布迪克依木. 高植被覆盖区公路边坡地质灾害危险性评价研究[D]. 赣州: 江西理工大学, 2022.

[本文引用: 1]

Xianmusiyan Abudikeyimu. Study on risk assessment of geological hazards of highway slope in high vegetation coverage area [D]. Ganzhou: Jiangxi University of Science and Technology, 2022.

[本文引用: 1]

MAIR A, FARES A

Comparison of rainfall interpolation methods in a mountainous region of a tropical island

[J]. Journal of Hydrologic Engineering, 2011, 16 (4): 371- 383

DOI:10.1061/(ASCE)HE.1943-5584.0000330      [本文引用: 1]

浙江省人民政府办公厅. 浙江省突发地质灾害应急预案: 浙政办发[2021]8号[EB/OL]. [2023-01-20]. https://www.zj.gov.cn/art/2021/2/18/art_1229019365_2231529.html.

[本文引用: 1]

刘谢攀, 殷坤龙, 肖常贵, 等. 基于I-D-R阈值模型的滑坡气象预警[EB/OL]. (2022-07-11) [2023-01-20]. http://kns.cnki.net/kcms/detail/42.1874.P.20220708.1511.002.html.

[本文引用: 1]

/

〈 〉