[1]
王 丽, 任宇, 邱启仓, 等 多目标进化算法性能评价指标研究综述
[J]. 计算机学报 , 2021 , 44 (8 ): 1590 - 1619
DOI:10.11897/SP.J.1016.2021.01590
[本文引用: 2]
WANG Li, Ren Yu, Qiu Qicang, et al Survey on performance indicator for multi-objective evolutionary algorithms
[J]. Chinese Journal of Computers , 2021 , 44 (8 ): 1590 - 1619
DOI:10.11897/SP.J.1016.2021.01590
[本文引用: 2]
[2]
王万良, 金雅文, 陈嘉诚, 等 多角色多策略多目标粒子群优化算法
[J]. 浙江大学学报: 工学版 , 2022 , 56 (3 ): 531 - 541
WANG Wanliang, JIN Yawen, CHEN Jiachen, et al Multi-objective particle-swarm optimization algorithm with multi-role and multi-strategy
[J]. Journal of Zhejiang University: Engineering Science , 2022 , 56 (3 ): 531 - 541
[3]
LUO Y, ZHANG K, YANG H, et al. A reduced mixed representation based multi-objective evolutionary algorithm for large-scale overlapping community detection [C]// 2021 IEEE Congress on Evolutionary Computation . Kraków: IEEE, 2021: 2435−2442.
[本文引用: 1]
[4]
王万良. 人工智能导论 第5版[M]. 北京: 高等教育出版社, 2022.
[本文引用: 1]
[5]
ZHOU C, DAI G, ZHANG C, et al Entropy based evolutionary algorithm with adaptive reference points for many-objective optimization problems
[J]. Information Sciences , 2018 , 465 : 232 - 247
DOI:10.1016/j.ins.2018.07.012
[本文引用: 1]
[6]
冯茜, 李擎, 全威, 等 多目标粒子群优化算法研究综述
[J]. 工程科学学报 , 2021 , 43 (6 ): 745 - 753
[本文引用: 1]
FENG Qian, LI Qing, QUAN Wei, et al Overview of multiobjective particle swarm optimization algorithm
[J]. Chinese Journal of Engineering , 2021 , 43 (6 ): 745 - 753
[本文引用: 1]
[7]
YUAN Y, XU H, WANG B. An improved NSGA-III procedure for evolutionary many-objective optimization [C]// Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation . New York: [s. n. ], 2014: 661−668.
[本文引用: 1]
[8]
ZHENG J, ZHOU F, ZOU J, et al A dynamic multi-objective optimization based on a hybrid of pivot points prediction and diversity strategies
[J]. Swarm and Evolutionary Computation , 2023 , 78 : 101284
[本文引用: 1]
[9]
ZHANG K, SHEN C, YEN G G, et al Two-stage double niched evolution strategy for multimodal multiobjective optimization
[J]. IEEE Transactionsactions on Evolutionary Computation , 2021 , 25 (4 ): 754 - 768
DOI:10.1109/TEVC.2021.3064508
[本文引用: 1]
[10]
MING M, TRIVEDI A, WANG R, et al A dual-population-based evolutionary algorithm for constrained multiobjective optimization
[J]. IEEE Transactionsactions on Evolutionary Computation , 2021 , 25 (4 ): 739 - 753
DOI:10.1109/TEVC.2021.3066301
[本文引用: 1]
[11]
王万良. 人工智能及其应用 第4版[M]. 北京: 高等教育出版社, 2020.
[本文引用: 1]
[12]
杨辉华, 谢谱模, 张晓凤, 等 求解多目标优化问题的改进布谷鸟搜索算法
[J]. 浙江大学学报: 工学版 , 2015 , 49 (8 ): 1600 - 1608
[本文引用: 1]
YANG Huihua, XIE Pumo, ZHANG Xiaofeng, et al Improved cuckoo search algorithm for multi-objective optimization problems
[J]. Journal of Zhejiang University: Engineering Science , 2015 , 49 (8 ): 1600 - 1608
[本文引用: 1]
[13]
鲁建厦, 翟文倩, 李嘉丰, 等 基于改进混合蛙跳算法的多约束车辆路径优化
[J]. 浙江大学学报: 工学版 , 2021 , 55 (2 ): 259 - 270
[本文引用: 1]
LU Jianxia, ZHAI Wenqian, LI Jiafeng, et al Muti-constraint vehicle routing optimization based on improved hybrid shuffled frog leaping algorithm
[J]. Journal of Zhejiang University: Engineering Science , 2021 , 55 (2 ): 259 - 270
[本文引用: 1]
[14]
CORUS D, DANG D C, EREMEEV A V, et al Level-based analysis of genetic algorithms and other search processes
[J]. IEEE Transactionsactions on Evolutionary Computation , 2018 , 22 (5 ): 707 - 719
DOI:10.1109/TEVC.2017.2753538
[本文引用: 1]
[16]
COLORNI A, DORIGO M, MANIEZZO V, et al. Distributed optimization by ant colonies [C]// Proceedings of ECAL91-European Conference on Artificial Life . Milano: Elsevier, 1992: 134−142.
[本文引用: 1]
[17]
DORIGO M. Optimization, learning and natural algorithms [EB/OL]. [2024-04-09]. https://xueshu.baidu.com/usercenter/paper/show?paperid=1b9ebb7e73db6f097f286e54d5fa31db.
[本文引用: 1]
[18]
KENNEDY J, EBERHART R. Particle swarm optimization [C]// Proceedings of ICNN'95-International Conference on Neural Networks . Perth: IEEE, 1995: 1942−1948.
[本文引用: 2]
[19]
COELLO C A C, LECHUGA M S. MOPSO: a proposal for multiple objective particle swarm optimization [C]// Proceedings of the 2002 Congress on Evolutionary Computation . Honolulu: IEEE, 2002: 1051−1056.
[本文引用: 1]
[20]
毕晓君, 王朝 基于超平面投影的高维多目标进化算法
[J]. 浙江大学学报: 工学版 , 2018 , 52 (7 ): 1284 - 1293
[本文引用: 1]
BI Xiaojun, WANG Chao Many-objective evolutionary algorithm based on hyperplane projection
[J]. Journal of Zhejiang University: Engineering Science , 2018 , 52 (7 ): 1284 - 1293
[本文引用: 1]
[21]
谢承旺, 潘嘉敏, 郭华, 等. 一种采用混合策略的大规模多目标进化算法. 计算机学报[EB/OL]. (2023-07-13) [2023-08-08]. https: //kns.cnki.net/kcms2/detail/11.1826.TP.20230712.1925.021.html
[本文引用: 1]
[22]
XU G, LUO K, JING G, et al On convergence analysis of multi-objective particle swarm optimization algorithm
[J]. European Journal of Operational Research , 2020 , 286 (1 ): 32 - 38
DOI:10.1016/j.ejor.2020.03.035
[本文引用: 1]
[23]
HOUSSEIN E H, GAD A G, HUSSAIN K, et al Major advances in particle swarm optimization: theory, analysis, and application
[J]. Swarm and Evolutionary Computation , 2021 , 63 : 100868 - 100905
DOI:10.1016/j.swevo.2021.100868
[本文引用: 1]
[24]
DE CARVALHO A B, POZO A Measuring the convergence and diversity of CDAS multi-objective particle swarm optimization algorithms: a study of many-objective problems
[J]. Neurocomputing , 2012 , 75 (1 ): 43 - 51
DOI:10.1016/j.neucom.2011.03.053
[本文引用: 1]
[25]
ZAPOTECAS MARTíNEZ S, COELLO COELLO C A. A multi-objective particle swarm optimizer based on decomposition [C]// Proceedings of the Annual Conference on Genetic and Evolutionary Computation . Dublin: IEEE, 2011: 69−76.
[本文引用: 1]
[26]
AL MOUBAYED N, PETROVSKI A, MCCALL J D2MOPSO: MOPSO based on decomposition and dominance with archiving using crowding distance in objective and solution spaces
[J]. Evolution Computation , 2014 , 22 (1 ): 47 - 77
DOI:10.1162/EVCO_a_00104
[本文引用: 1]
[27]
纪昌明, 马皓宇, 李宁宁, 等 基于树形结构无界存档的多目标粒子群算法
[J]. 控制与决策 , 2020 , 35 (11 ): 2657 - 2686
[本文引用: 1]
JI Changming, MA Haoyu, LI Ningning, et al Multi-objective particle swarm optimization algorithm based on tree-structured unbounded archive
[J]. Control and Decision , 2020 , 35 (11 ): 2657 - 2686
[本文引用: 1]
[28]
ZHANG X, ZHENG X, CHENG R, et al A competitive mechanism based multi-objective particle swarm optimizer with fast convergence
[J]. Information Sciences , 2018 , 427 : 63 - 76
DOI:10.1016/j.ins.2017.10.037
[本文引用: 1]
[29]
LIN Q, LIU S, ZHU Q, et al Particle swarm optimization with a balanceable fitness estimation for many-objective optimization problems
[J]. IEEE Transactionsactions on Evolutionary Computation , 2018 , 22 (1 ): 32 - 46
DOI:10.1109/TEVC.2016.2631279
[本文引用: 1]
[30]
余伟伟, 谢承旺, 闭应洲, 等 一种基于自适应模糊支配的高维多目标粒子群算法
[J]. 自动化学报 , 2018 , 44 (12 ): 2278 - 2289
[本文引用: 1]
YU Weiwei, XIE Chengwang, BI Yingzhou, et al Many-objective particle swarm optimization based on adaptive fuzzy dominance
[J]. Acta Automatica Sinica , 2018 , 44 (12 ): 2278 - 2289
[本文引用: 1]
[31]
谭阳, 唐德权, 曹守富 基于超球形模糊支配的高维多目标粒子群优化算法
[J]. 计算机应用 , 2019 , 39 (11 ): 3233 - 3241
[本文引用: 1]
TAN Yang, TANG Dequan, CAO Shoufu Many-objective particle swarm optimization algorithm based on hyper-spherical fuzzy dominance
[J]. Journal of Computer Applications , 2019 , 39 (11 ): 3233 - 3241
[本文引用: 1]
[32]
TANABE R, ISHIBUCHI H A review of evolutionary multimodal multiobjective optimization
[J]. IEEE Transactionsactions on Evolutionary Computation , 2020 , 24 (1 ): 193 - 200
DOI:10.1109/TEVC.2019.2909744
[本文引用: 1]
[33]
QU B, LI C, LIANG J, et al A self-organized speciation based multi-objective particle swarm optimizer for multimodal multi-objective problems
[J]. Applied Soft Computing , 2020 , 86 : 105886
DOI:10.1016/j.asoc.2019.105886
[本文引用: 1]
[35]
公硕鹏. 基于小生境的多模态多目标优化算法研究[D]. 武汉: 华中科技大学, 2022.
[本文引用: 1]
GONG Shuopeng. Research on multimodel multiobjective optimization algorithm based on niching methods [D]. Wuhan: Huazhong University of Science and Technology, 2022.
[本文引用: 1]
[36]
ZAPOTECAS MARTíNEZ S, COELLO COELLO C A. A multi-objective particle swarm optimizer based on decomposition [C]// Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation . Dublin: [s. n.], 2011: 69−76.
[本文引用: 1]
[37]
ZHAN Z H, LI J, CAO J, et al Multiple populations for multiple objectives: a coevolutionary technique for solving multiobjective optimization problems
[J]. IEEE Transactions on Cybernetics , 2013 , 43 (2 ): 445 - 463
DOI:10.1109/TSMCB.2012.2209115
[本文引用: 1]
[38]
DAI C, WANG Y, YE M A new multi-objective particle swarm optimization algorithm based on decomposition
[J]. Information Sciences , 2015 , 325 : 541 - 557
DOI:10.1016/j.ins.2015.07.018
[本文引用: 1]
[39]
黄佩秋, 刘建昌, 谭树彬, 等 混合多目标粒子群优化算法在热精轧负荷分配优化中的应用
[J]. 控制理论与应用 , 2017 , 34 (1 ): 93 - 100
[本文引用: 1]
HUANG Peiqiu, LIU Jianchang, TAN Shubin, et al Application of the hybrid multi-objective particle swarm optimization algorithm in load distribution of hot finishing mills
[J]. Control Theory and Applications , 2017 , 34 (1 ): 93 - 100
[本文引用: 1]
[40]
韩红桂, 阿音嘎, 张璐, 等 自适应分解式多目标粒子群优化算法
[J]. 电子学报 , 2020 , 48 (7 ): 1245 - 1254
DOI:10.3969/j.issn.0372-2112.2020.07.001
[本文引用: 1]
HAN Honggui, A Yinga, ZHANG Lu, et al Adaptive multiobjective particle swarm optimization based on decomposition archive
[J]. Acta Electronica Sinica , 2020 , 48 (7 ): 1245 - 1254
DOI:10.3969/j.issn.0372-2112.2020.07.001
[本文引用: 1]
[41]
CHEN L, LIU H L A region decomposition-based multi-objective particle swarm optimization algorithm
[J]. International Journal of Pattern Recognition and Artificial Intelligence , 2014 , 28 (8 ): 1459009
DOI:10.1142/S0218001414590095
[本文引用: 1]
[42]
LUO J, QI Y, XIE J, et al A hybrid multi-objective PSO-EDA algorithm for reservoir flood control operation
[J]. Applied Soft Computing , 2015 , 34 : 526 - 538
DOI:10.1016/j.asoc.2015.05.036
[本文引用: 1]
[43]
YAO G, DING Y, JIN Y, et al Endocrine-based coevolutionary multi-swarm for multi-objective workflow scheduling in a cloud system
[J]. Soft Computing , 2017 , 21 (15 ): 4309 - 4322
[本文引用: 1]
[44]
YANG Y, ZHANG T, YI W, et al Deployment of multistatic radar system using multi-objective particle swarm optimisation
[J]. IET Radar, Sonar and Navigation , 2018 , 12 (5 ): 485 - 493
DOI:10.1049/iet-rsn.2017.0351
[本文引用: 1]
[45]
张庆科, 孟祥旭, 张化祥, 等 基于随机维度划分与学习的粒子群优化算法
[J]. 浙江大学学报: 工学版 , 2018 , 52 (2 ): 367 - 378
[本文引用: 1]
ZHANG Qingke, MENG Xiangxu, ZHANG Huaxiang, et al Particle swarm optimization based on random vector partition and learning
[J]. Journal of Zhejiang University: Engineering Science , 2018 , 52 (2 ): 367 - 378
[本文引用: 1]
[46]
ZHANG W, LI G, ZHANG W, et al A cluster based PSO with leader updating mechanism and ring-topology for multimodal multi-objective optimization
[J]. Swarm and Evolutionary Computation , 2019 , 50 : 100569
DOI:10.1016/j.swevo.2019.100569
[本文引用: 1]
[47]
刘彬, 刘泽仁, 赵志彪, 等 基于速度交流的多种群多目标粒子群算法研究
[J]. 计量学报 , 2020 , 41 (8 ): 1002 - 1011
DOI:10.3969/j.issn.1000-1158.2020.08.18
[本文引用: 1]
LIU Bin, LIU Zeren, ZHAO Zhibiao, et al Research on multi-population multi-objective particle swarm optimization algorithm based on velocity communication
[J]. Acta Metrologica Sinica , 2020 , 41 (8 ): 1002 - 1011
DOI:10.3969/j.issn.1000-1158.2020.08.18
[本文引用: 1]
[48]
QI Y, MA X, LIU F, et al MOEA/D with adaptive weight adjustment
[J]. Evolution Computation , 2014 , 22 (2 ): 231 - 264
DOI:10.1162/EVCO_a_00109
[本文引用: 1]
[49]
LIN Q, LI J, DU Z, et al A novel multi-objective particle swarm optimization with multiple search strategies
[J]. European Journal of Operational Research , 2015 , 247 (3 ): 732 - 744
[本文引用: 1]
[50]
ZHU Q, LIN Q, CHEN W, et al An external archive-guided multiobjective particle swarm optimization algorithm
[J]. IEEE Transactions on Cybernetics , 2017 , 47 (9 ): 2794 - 2808
DOI:10.1109/TCYB.2017.2710133
[本文引用: 1]
[51]
杨景明, 侯新培, 崔慧慧, 等 基于融合多策略改进的多目标粒子群优化算法
[J]. 控制与决策 , 2018 , 33 (2 ): 226 - 234
[本文引用: 1]
YANG Jingming, HOU Xinpei, CUI Huihui, et al Muti-objective adoptive chaotic particle swarm optimization algorithm
[J]. Control and Decision , 2018 , 33 (2 ): 226 - 234
[本文引用: 1]
[52]
KNOWLES J D, COME D W Approximating the nondominated front using the Pareto archived evolution strategy
[J]. Evolutionary Computation , 2000 , 8 (2 ): 149 - 172
DOI:10.1162/106365600568167
[本文引用: 1]
[53]
李笠, 王万良, 徐新黎, 等 基于网格排序的多目标粒子群优化算法
[J]. 计算机研究与发展 , 2017 , 54 (5 ): 1012 - 1023
[本文引用: 1]
LI Li, WANG Wanliang, XU Xinli, et al Muti-objective particle swarm optimization based on grid ranking
[J]. Journal of Computer Research and Development , 2017 , 54 (5 ): 1012 - 1023
[本文引用: 1]
[54]
LI L, WANG W, XU X Multi-objective particle swarm optimization based on global margin ranking
[J]. Information Sciences , 2017 , 375 : 30 - 47
DOI:10.1016/j.ins.2016.08.043
[本文引用: 1]
[55]
李笠. 基于排序策略的多目标粒子群优化: 研究与应用[D]. 杭州: 浙江工业大学, 2017.
[本文引用: 1]
LI Li. Ranking-based multi-objective particle swarm optimization: rearch and application [D]. Hangzhou: Zhejiang University of Technology, 2017.
[本文引用: 1]
[56]
LENG R, OUYANG A, LIU Y, et al A multi-objective particle swarm optimization based on grid distance
[J]. International Journal of Pattern Recognition and Artificial Intelligence , 2019 , 34 (3 ): 2059008
[本文引用: 1]
[57]
ZOU K, LIU Y, WANG S, et al A multiobjective particle swarm optimization algorithm based on grid technique and multistrategy
[J]. Journal of Mathematics , 2021 , 2021 : 1 - 17
[本文引用: 1]
[59]
YE Q, WANG Z, ZHAO Y, et al A clustering-based competitive particle swarm optimization with grid ranking for multi-objective optimization problems
[J]. Scientific Reports , 2023 , 13 (1 ): 11754
DOI:10.1038/s41598-023-38529-4
[本文引用: 1]
[60]
LI G, WANG W, ZHANG W, et al Grid search based multi-population particle swarm optimization algorithm for multimodal multi-objective optimization
[J]. Swarm and Evolutionary Computation , 2021 , 62 : 100843
DOI:10.1016/j.swevo.2021.100843
[本文引用: 1]
[61]
王学武, 魏建斌, 周昕, 等 一种基于超体积指标的多目标进化算法
[J]. 华东理工大学学报: 自然科学版 , 2020 , 46 (6 ): 780 - 791
[本文引用: 1]
WANG Xuewu, WEI Jianbin, ZHOU Xin, et al Hypervolume-based multi-objective evolutionary algorithm
[J]. Journal of East China University of Science and Technology , 2020 , 46 (6 ): 780 - 791
[本文引用: 1]
[62]
郝秦霞 基于R2指标的高维多目标差分进化推荐式课程系统
[J]. 计算机应用 , 2020 , 40 (10 ): 2951 - 2959
[本文引用: 1]
HAO Qinxia Course recommendation system based on R2 index and multi-objective differential evolution
[J]. Journal of Computer Applications , 2020 , 40 (10 ): 2951 - 2959
[本文引用: 1]
[63]
GARCíA I C, COELLO C A C, ARIAS-MONTAñO A. MOPSOhv: a new hypervolume-based multi-objective particle swarm optimizer [C]// Proceedings of the 2014 IEEE Congress on Evolutionary Computation . Beijing: IEEE, 2014: 266−273.
[本文引用: 1]
[64]
LIANG X, DAI C, YE N. Multi-objective particle swarm optimization algorithm based on decomposition and hypervolume for synthesis gas production [C]// Proceedings of the 2022 18th International Conference on Computational Intelligence and Security . Chengdu: IEEE, 2022: 356−359.
[本文引用: 1]
[65]
LI F, LIU J, TAN S, et al. R2-MOPSO: a multi-objective particle swarm optimizer based on R2-indicator and decomposition [C]// Proceedings of the 2015 IEEE congress on evolutionary computation . Sendai: IEEE, 2015: 3148−3155.
[本文引用: 1]
[66]
WEI L X, LI X, FAN R, et al A hybrid multiobjective particle swarm optimization algorithm based on R2 indicator
[J]. IEEE Access , 2018 , 6 : 14710 - 14721
DOI:10.1109/ACCESS.2018.2812701
[本文引用: 1]
[67]
LI X, LI X L, WANG K, et al A multi-objective particle swarm optimization algorithm based on enhanced selection
[J]. IEEE Access , 2019 , 7 : 168091 - 168103
DOI:10.1109/ACCESS.2019.2954542
[本文引用: 1]
[68]
LIU J, LI F, KONG X, et al Handling many-objective optimisation problems with R2 indicator and decomposition-based particle swarm optimiser
[J]. International Journal of Systems Science , 2019 , 50 (2 ): 320 - 336
DOI:10.1080/00207721.2018.1552765
[本文引用: 1]
[69]
李飞, 吴紫恒, 刘阚蓉, 等 基于R2指标和目标空间分解的高维多目标粒子群优化算法
[J]. 控制与决策 , 2021 , 36 (9 ): 2085 - 2094
[本文引用: 1]
LI Fei, WU Ziheng, LIU Kanrong, et al R2 indicator and objective space partition based many-objective particle swarm optimizer
[J]. Control and Decision , 2021 , 36 (9 ): 2085 - 2094
[本文引用: 1]
[70]
GU Q, JIANG M, JIANG S, et al Multi-objective particle swarm optimization with R2 indicator and adaptive method
[J]. Complex and Intelligent Systems , 2021 , 7 (5 ): 2697 - 2710
DOI:10.1007/s40747-021-00445-3
[本文引用: 1]
[71]
SUN X, CHEN Y, LIU Y, et al Indicator-based set evolution particle swarm optimization for many-objective problems
[J]. Soft Computing , 2016 , 20 (6 ): 2219 - 2232
DOI:10.1007/s00500-015-1637-1
[本文引用: 1]
[72]
WU B, HU W, HE Z, et al. A many-objective particle swarm optimization based on virtual Pareto front [C]// Proceedings of the 2018 IEEE Congress on Evolutionary Computation . Rio de Janeiro: IEEE, 2018: 1−8.
[本文引用: 1]
[73]
LUO J, HUANG X, YANG Y, et al A many-objective particle swarm optimizer based on indicator and direction vectors for many-objective optimization
[J]. Information Sciences , 2020 , 514 : 166 - 202
DOI:10.1016/j.ins.2019.11.047
[本文引用: 1]
[74]
ZAPOTECAS-MARTíNEZ S, LóPEZ-JAIMES A, GARCíA-NáJERA A LIBEA: a lebesgue indicator-based evolutionary algorithm for multi-objective optimization
[J]. Swarm and Evolutionary Computation , 2019 , 44 : 404 - 419
DOI:10.1016/j.swevo.2018.05.004
[本文引用: 1]
[75]
KAWAGUCHI S, FUKUYAMA Y Improved parallel reactive hybrid particle swarm optimization using improved neighborhood schedule generation method for the integrated framework of optimal production scheduling and operational planning of an energy plant in a factory
[J]. Electronics and Communications in Japan , 2020 , 103 (7 ): 37 - 48
DOI:10.1002/ecj.12237
[本文引用: 1]
[76]
SECK-TUOH-MORA J C, MEDINA-MARIN J, MARTINEZ-GOMEZ E S, et al Cellular particle swarm optimization with a simple adaptive local search strategy for the permutation flow shop scheduling problem
[J]. Archives of Control Sciences , 2019 , 29 (2 ): 205 - 226
[本文引用: 1]
[77]
KAYA S, GüMüŞçü A, AYDILEK İ B, et al Solution for flow shop scheduling problems using chaotic hybrid firefly and particle swarm optimization algorithm with improved local search
[J]. Soft Computing , 2021 , 25 (10 ): 7143 - 7154
DOI:10.1007/s00500-021-05673-w
[本文引用: 1]
[78]
谢美华, 李艳武, 葛棚丹 自适应混合粒子群算法求解置换流水车间调度问题
[J]. 计算机应用研究 , 2023 , 40 (11 ): 1 - 8
[本文引用: 1]
XIE Meihua, LI Yanwu, GE Pengdan Self-adaptive hybrid particle swarm optimization for permutation flow shop scheduling problem
[J]. Application Research of Computers , 2023 , 40 (11 ): 1 - 8
[本文引用: 1]
[79]
LONG F, JIN B, XU H, et al Research on multi-objective optimization of smart grid based on particle swarm optimization
[J]. Electrica , 2023 , 23 (2 ): 222 - 230
[本文引用: 1]
[80]
XIONG W, GONG K, SHI W, et al Design and implementation of power mobile inspection system based on improved particle swarm optimization
[J]. Journal of Physics: Conference Series , 2021 , 2033 (1 ): 012202
DOI:10.1088/1742-6596/2033/1/012202
[本文引用: 1]
[81]
DENG C, ZHANG X, HUANG Y, et al Equipping seasonal exponential smoothing models with particle swarm optimization algorithm for electricity consumption forecasting
[J]. Energies , 2021 , 14 (13 ): 4036
DOI:10.3390/en14134036
[本文引用: 1]
[82]
KAHOULI O, ALSAIF H, BOUTERAA Y, et al Power system reconfiguration in distribution network for improving reliability using genetic algorithm and particle swarm optimization
[J]. Applied Sciences , 2021 , 11 (7 ): 3092
DOI:10.3390/app11073092
[本文引用: 1]
[83]
DUMITRU D, DIOȘAN L, ANDREICA A, et al A transfer learning approach on the optimization of edge detectors for medical images using particle swarm optimization
[J]. Entropy , 2021 , 23 (4 ): 414
DOI:10.3390/e23040414
[本文引用: 1]
[84]
HASSAN M U, BADSHAH N, ZAHIR S Automatic initialization for active contour models based on particle swarm optimization and application to medical images
[J]. Journal of Mathematical and Computational Science , 2021 , 11 (1 ): 243 - 264
[本文引用: 1]
[85]
井向阳, 林鹏飞, 游进军, 等 岷江中游梯级闸坝联合优化调度研究
[J]. 水利水电技术 , 2021 , 52 (3 ): 23 - 31
[本文引用: 1]
JIN Xiangyang, LIN Pengfei, YOU Jinjun, et al Study on joint optimal scheduling of cascade sluice on mid-Minjiang River
[J]. Water Resources and Hydropower Engineering , 2021 , 52 (3 ): 23 - 31
[本文引用: 1]
多目标进化算法性能评价指标研究综述
2
2021
... 在生产调度、智能控制和路径规划等多个领域,须同时对多个目标进行优化[1 -3 ] ,且目标之间不能同时达到最优状态,这类问题统称为多目标优化问题[4 ] (multi-objective optimization problems, MOPs). 不同于以往的单目标问题,MOPs无法用线性方法求解,且不具备唯一解,这对MOPs的求解带来了极大挑战,因此,求解MOPs的研究存在一定的实际价值. ...
... 定义1 多目标优化问题 . 为了方便MOPs的求解,对其进行数学建模,假设一个MOP由$ n $ $ m $ [1 ] : ...
多目标进化算法性能评价指标研究综述
2
2021
... 在生产调度、智能控制和路径规划等多个领域,须同时对多个目标进行优化[1 -3 ] ,且目标之间不能同时达到最优状态,这类问题统称为多目标优化问题[4 ] (multi-objective optimization problems, MOPs). 不同于以往的单目标问题,MOPs无法用线性方法求解,且不具备唯一解,这对MOPs的求解带来了极大挑战,因此,求解MOPs的研究存在一定的实际价值. ...
... 定义1 多目标优化问题 . 为了方便MOPs的求解,对其进行数学建模,假设一个MOP由$ n $ $ m $ [1 ] : ...
1
... 在生产调度、智能控制和路径规划等多个领域,须同时对多个目标进行优化[1 -3 ] ,且目标之间不能同时达到最优状态,这类问题统称为多目标优化问题[4 ] (multi-objective optimization problems, MOPs). 不同于以往的单目标问题,MOPs无法用线性方法求解,且不具备唯一解,这对MOPs的求解带来了极大挑战,因此,求解MOPs的研究存在一定的实际价值. ...
1
... 在生产调度、智能控制和路径规划等多个领域,须同时对多个目标进行优化[1 -3 ] ,且目标之间不能同时达到最优状态,这类问题统称为多目标优化问题[4 ] (multi-objective optimization problems, MOPs). 不同于以往的单目标问题,MOPs无法用线性方法求解,且不具备唯一解,这对MOPs的求解带来了极大挑战,因此,求解MOPs的研究存在一定的实际价值. ...
Entropy based evolutionary algorithm with adaptive reference points for many-objective optimization problems
1
2018
... 求解MOPs的基本思想是通过优化过程尽可能找到一组解集,使得多个目标在给定约束范围内尽可能达到最佳,这组折中解集称为Pareto解集[5 ] . 最初,传统的求解方法[6 ] 是将复杂MOPs分解为单目标问题求解,主要包括目标规划法、加权求和法和距离函数法等. 传统的优化方法依赖于先验知识,须运行多次才能逼近Pareto最优解集(Pareto optimal set, PS),不能求得较为理想的折中解集. 此外,当问题复杂化、高维化、动态化、多模态化或遇到带有约束的复杂多目标问题时,很难得到一组理想解,因此,探索新途径新方法来求解高维[7 ] 、复杂的MOPs意义重大. ...
多目标粒子群优化算法研究综述
1
2021
... 求解MOPs的基本思想是通过优化过程尽可能找到一组解集,使得多个目标在给定约束范围内尽可能达到最佳,这组折中解集称为Pareto解集[5 ] . 最初,传统的求解方法[6 ] 是将复杂MOPs分解为单目标问题求解,主要包括目标规划法、加权求和法和距离函数法等. 传统的优化方法依赖于先验知识,须运行多次才能逼近Pareto最优解集(Pareto optimal set, PS),不能求得较为理想的折中解集. 此外,当问题复杂化、高维化、动态化、多模态化或遇到带有约束的复杂多目标问题时,很难得到一组理想解,因此,探索新途径新方法来求解高维[7 ] 、复杂的MOPs意义重大. ...
多目标粒子群优化算法研究综述
1
2021
... 求解MOPs的基本思想是通过优化过程尽可能找到一组解集,使得多个目标在给定约束范围内尽可能达到最佳,这组折中解集称为Pareto解集[5 ] . 最初,传统的求解方法[6 ] 是将复杂MOPs分解为单目标问题求解,主要包括目标规划法、加权求和法和距离函数法等. 传统的优化方法依赖于先验知识,须运行多次才能逼近Pareto最优解集(Pareto optimal set, PS),不能求得较为理想的折中解集. 此外,当问题复杂化、高维化、动态化、多模态化或遇到带有约束的复杂多目标问题时,很难得到一组理想解,因此,探索新途径新方法来求解高维[7 ] 、复杂的MOPs意义重大. ...
1
... 求解MOPs的基本思想是通过优化过程尽可能找到一组解集,使得多个目标在给定约束范围内尽可能达到最佳,这组折中解集称为Pareto解集[5 ] . 最初,传统的求解方法[6 ] 是将复杂MOPs分解为单目标问题求解,主要包括目标规划法、加权求和法和距离函数法等. 传统的优化方法依赖于先验知识,须运行多次才能逼近Pareto最优解集(Pareto optimal set, PS),不能求得较为理想的折中解集. 此外,当问题复杂化、高维化、动态化、多模态化或遇到带有约束的复杂多目标问题时,很难得到一组理想解,因此,探索新途径新方法来求解高维[7 ] 、复杂的MOPs意义重大. ...
A dynamic multi-objective optimization based on a hybrid of pivot points prediction and diversity strategies
1
2023
... 针对MOPs的特点,且考虑到实际生活中的MOPs存在高维、不可导、动态[8 ] 、多模态[9 ] 、带约束[10 ] 等复杂情况,研究者们受生物进化选择和适者生存的启发,将进化思想与元启发算法相结合[11 ] ,提出模拟染色体交叉变异的多目标进化算法[12 -13 ] (multi-objective evolutionary algorithms, MOEAs)来求解MOPs,如基于生物进化选择的遗传算法[14 ] (genetic algorithm, GA)和差分进化算法[15 ] (differential evolution, DE). 不同于传统方法,MOEAs求解MOPs不需要先验知识,只须运行一次就能够得到整个Pareto前沿(Pareto front, PF)的逼近. ...
Two-stage double niched evolution strategy for multimodal multiobjective optimization
1
2021
... 针对MOPs的特点,且考虑到实际生活中的MOPs存在高维、不可导、动态[8 ] 、多模态[9 ] 、带约束[10 ] 等复杂情况,研究者们受生物进化选择和适者生存的启发,将进化思想与元启发算法相结合[11 ] ,提出模拟染色体交叉变异的多目标进化算法[12 -13 ] (multi-objective evolutionary algorithms, MOEAs)来求解MOPs,如基于生物进化选择的遗传算法[14 ] (genetic algorithm, GA)和差分进化算法[15 ] (differential evolution, DE). 不同于传统方法,MOEAs求解MOPs不需要先验知识,只须运行一次就能够得到整个Pareto前沿(Pareto front, PF)的逼近. ...
A dual-population-based evolutionary algorithm for constrained multiobjective optimization
1
2021
... 针对MOPs的特点,且考虑到实际生活中的MOPs存在高维、不可导、动态[8 ] 、多模态[9 ] 、带约束[10 ] 等复杂情况,研究者们受生物进化选择和适者生存的启发,将进化思想与元启发算法相结合[11 ] ,提出模拟染色体交叉变异的多目标进化算法[12 -13 ] (multi-objective evolutionary algorithms, MOEAs)来求解MOPs,如基于生物进化选择的遗传算法[14 ] (genetic algorithm, GA)和差分进化算法[15 ] (differential evolution, DE). 不同于传统方法,MOEAs求解MOPs不需要先验知识,只须运行一次就能够得到整个Pareto前沿(Pareto front, PF)的逼近. ...
1
... 针对MOPs的特点,且考虑到实际生活中的MOPs存在高维、不可导、动态[8 ] 、多模态[9 ] 、带约束[10 ] 等复杂情况,研究者们受生物进化选择和适者生存的启发,将进化思想与元启发算法相结合[11 ] ,提出模拟染色体交叉变异的多目标进化算法[12 -13 ] (multi-objective evolutionary algorithms, MOEAs)来求解MOPs,如基于生物进化选择的遗传算法[14 ] (genetic algorithm, GA)和差分进化算法[15 ] (differential evolution, DE). 不同于传统方法,MOEAs求解MOPs不需要先验知识,只须运行一次就能够得到整个Pareto前沿(Pareto front, PF)的逼近. ...
求解多目标优化问题的改进布谷鸟搜索算法
1
2015
... 针对MOPs的特点,且考虑到实际生活中的MOPs存在高维、不可导、动态[8 ] 、多模态[9 ] 、带约束[10 ] 等复杂情况,研究者们受生物进化选择和适者生存的启发,将进化思想与元启发算法相结合[11 ] ,提出模拟染色体交叉变异的多目标进化算法[12 -13 ] (multi-objective evolutionary algorithms, MOEAs)来求解MOPs,如基于生物进化选择的遗传算法[14 ] (genetic algorithm, GA)和差分进化算法[15 ] (differential evolution, DE). 不同于传统方法,MOEAs求解MOPs不需要先验知识,只须运行一次就能够得到整个Pareto前沿(Pareto front, PF)的逼近. ...
求解多目标优化问题的改进布谷鸟搜索算法
1
2015
... 针对MOPs的特点,且考虑到实际生活中的MOPs存在高维、不可导、动态[8 ] 、多模态[9 ] 、带约束[10 ] 等复杂情况,研究者们受生物进化选择和适者生存的启发,将进化思想与元启发算法相结合[11 ] ,提出模拟染色体交叉变异的多目标进化算法[12 -13 ] (multi-objective evolutionary algorithms, MOEAs)来求解MOPs,如基于生物进化选择的遗传算法[14 ] (genetic algorithm, GA)和差分进化算法[15 ] (differential evolution, DE). 不同于传统方法,MOEAs求解MOPs不需要先验知识,只须运行一次就能够得到整个Pareto前沿(Pareto front, PF)的逼近. ...
基于改进混合蛙跳算法的多约束车辆路径优化
1
2021
... 针对MOPs的特点,且考虑到实际生活中的MOPs存在高维、不可导、动态[8 ] 、多模态[9 ] 、带约束[10 ] 等复杂情况,研究者们受生物进化选择和适者生存的启发,将进化思想与元启发算法相结合[11 ] ,提出模拟染色体交叉变异的多目标进化算法[12 -13 ] (multi-objective evolutionary algorithms, MOEAs)来求解MOPs,如基于生物进化选择的遗传算法[14 ] (genetic algorithm, GA)和差分进化算法[15 ] (differential evolution, DE). 不同于传统方法,MOEAs求解MOPs不需要先验知识,只须运行一次就能够得到整个Pareto前沿(Pareto front, PF)的逼近. ...
基于改进混合蛙跳算法的多约束车辆路径优化
1
2021
... 针对MOPs的特点,且考虑到实际生活中的MOPs存在高维、不可导、动态[8 ] 、多模态[9 ] 、带约束[10 ] 等复杂情况,研究者们受生物进化选择和适者生存的启发,将进化思想与元启发算法相结合[11 ] ,提出模拟染色体交叉变异的多目标进化算法[12 -13 ] (multi-objective evolutionary algorithms, MOEAs)来求解MOPs,如基于生物进化选择的遗传算法[14 ] (genetic algorithm, GA)和差分进化算法[15 ] (differential evolution, DE). 不同于传统方法,MOEAs求解MOPs不需要先验知识,只须运行一次就能够得到整个Pareto前沿(Pareto front, PF)的逼近. ...
Level-based analysis of genetic algorithms and other search processes
1
2018
... 针对MOPs的特点,且考虑到实际生活中的MOPs存在高维、不可导、动态[8 ] 、多模态[9 ] 、带约束[10 ] 等复杂情况,研究者们受生物进化选择和适者生存的启发,将进化思想与元启发算法相结合[11 ] ,提出模拟染色体交叉变异的多目标进化算法[12 -13 ] (multi-objective evolutionary algorithms, MOEAs)来求解MOPs,如基于生物进化选择的遗传算法[14 ] (genetic algorithm, GA)和差分进化算法[15 ] (differential evolution, DE). 不同于传统方法,MOEAs求解MOPs不需要先验知识,只须运行一次就能够得到整个Pareto前沿(Pareto front, PF)的逼近. ...
Review of differential evolution population size
1
2017
... 针对MOPs的特点,且考虑到实际生活中的MOPs存在高维、不可导、动态[8 ] 、多模态[9 ] 、带约束[10 ] 等复杂情况,研究者们受生物进化选择和适者生存的启发,将进化思想与元启发算法相结合[11 ] ,提出模拟染色体交叉变异的多目标进化算法[12 -13 ] (multi-objective evolutionary algorithms, MOEAs)来求解MOPs,如基于生物进化选择的遗传算法[14 ] (genetic algorithm, GA)和差分进化算法[15 ] (differential evolution, DE). 不同于传统方法,MOEAs求解MOPs不需要先验知识,只须运行一次就能够得到整个Pareto前沿(Pareto front, PF)的逼近. ...
1
... 群体智能(swarm intelligence, SI)也被提出用于优化问题的求解,SI是由多个个体组成的群体所产生的智慧集合. 受蚂蚁觅食行为启发提出的蚁群算法[16 -17 ] (ant colony optimization, ACO)是SI的首个成功案例. 随后,由鸟类捕食演化而来的粒子群算法[18 ] (particle swarm optimization, PSO)也被研究者们提出. PSO作为当下最流行的SI优化算法之一,通过个体间的信息交流,能够在复杂空间中快速收敛. 紧接着,Coello等[19 ] 将PSO应用于MOPs的求解,提出了多目标粒子群优化算法(multi-objective particle swarm optimization, MOPSO). ...
1
... 群体智能(swarm intelligence, SI)也被提出用于优化问题的求解,SI是由多个个体组成的群体所产生的智慧集合. 受蚂蚁觅食行为启发提出的蚁群算法[16 -17 ] (ant colony optimization, ACO)是SI的首个成功案例. 随后,由鸟类捕食演化而来的粒子群算法[18 ] (particle swarm optimization, PSO)也被研究者们提出. PSO作为当下最流行的SI优化算法之一,通过个体间的信息交流,能够在复杂空间中快速收敛. 紧接着,Coello等[19 ] 将PSO应用于MOPs的求解,提出了多目标粒子群优化算法(multi-objective particle swarm optimization, MOPSO). ...
2
... 群体智能(swarm intelligence, SI)也被提出用于优化问题的求解,SI是由多个个体组成的群体所产生的智慧集合. 受蚂蚁觅食行为启发提出的蚁群算法[16 -17 ] (ant colony optimization, ACO)是SI的首个成功案例. 随后,由鸟类捕食演化而来的粒子群算法[18 ] (particle swarm optimization, PSO)也被研究者们提出. PSO作为当下最流行的SI优化算法之一,通过个体间的信息交流,能够在复杂空间中快速收敛. 紧接着,Coello等[19 ] 将PSO应用于MOPs的求解,提出了多目标粒子群优化算法(multi-objective particle swarm optimization, MOPSO). ...
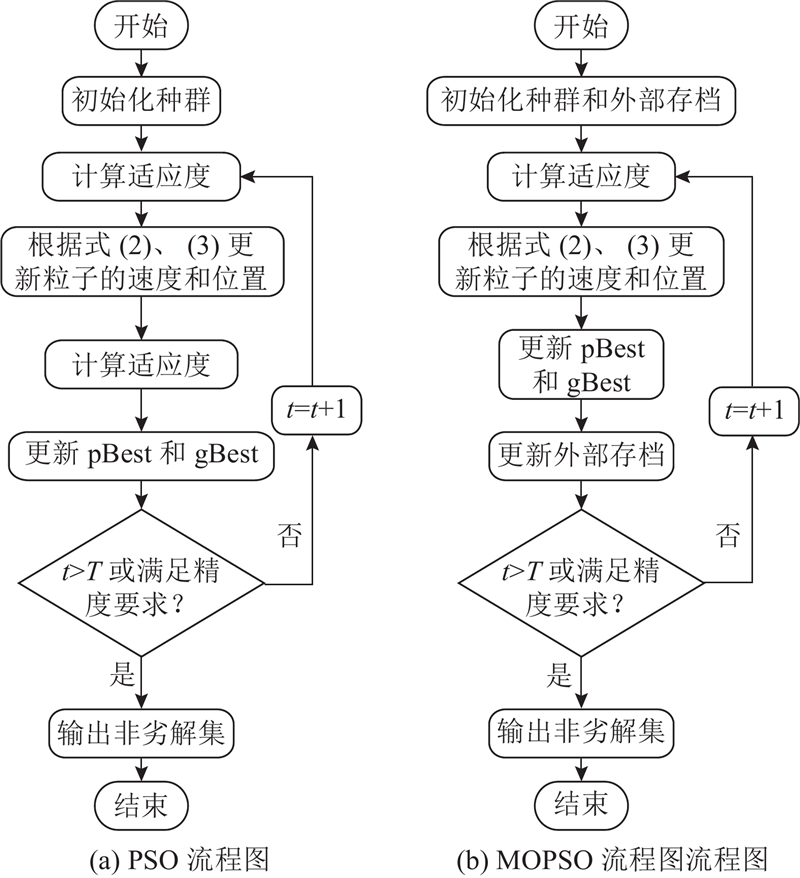
... Kennedy等[18 ] 于1995年提出PSO优化算法,并从理论角度证明了其稳定性和收敛性. 作为群体智能演化算法,PSO模拟自然界中鸟类的觅食行为,将食物的位置类比为优化问题的最优解集,将鸟类的飞行方向与位置类比为粒子的速度和位置. 根据全局最优(gBest)和个体历史最优(pBest)的信息交互,不断更新粒子的位置和速度,提高搜索效率、有效引导种群往PF方向收敛,但这也导致其可能陷入局部最优,其具体更新过程可以表示如下: ...
1
... 群体智能(swarm intelligence, SI)也被提出用于优化问题的求解,SI是由多个个体组成的群体所产生的智慧集合. 受蚂蚁觅食行为启发提出的蚁群算法[16 -17 ] (ant colony optimization, ACO)是SI的首个成功案例. 随后,由鸟类捕食演化而来的粒子群算法[18 ] (particle swarm optimization, PSO)也被研究者们提出. PSO作为当下最流行的SI优化算法之一,通过个体间的信息交流,能够在复杂空间中快速收敛. 紧接着,Coello等[19 ] 将PSO应用于MOPs的求解,提出了多目标粒子群优化算法(multi-objective particle swarm optimization, MOPSO). ...
基于超平面投影的高维多目标进化算法
1
2018
... 值得注意的是,当$ m > 3 $ [20 ] (many-objective optimization problems, MaOPs). 当$ d \geqslant 100 $ [21 ] . ...
基于超平面投影的高维多目标进化算法
1
2018
... 值得注意的是,当$ m > 3 $ [20 ] (many-objective optimization problems, MaOPs). 当$ d \geqslant 100 $ [21 ] . ...
1
... 值得注意的是,当$ m > 3 $ [20 ] (many-objective optimization problems, MaOPs). 当$ d \geqslant 100 $ [21 ] . ...
On convergence analysis of multi-objective particle swarm optimization algorithm
1
2020
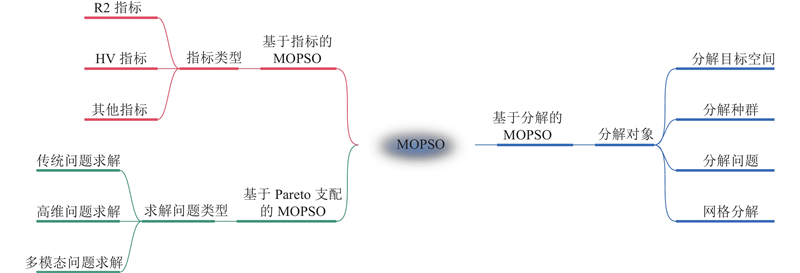
... Xu等[22 ] 通过定义收敛性指标,从理论角度对MOPSO的收敛性进行了分析和证明. 此外,Houssein等[23 ] 对粒子的稳定性、漫游行为以及运动模式等多个特性进行了讨论分析. 根据其特征,MOPSO可以分为3大类:基于Pareto支配的MOPSO、基于分解的MOPSO和基于指标的MOPSO,如图3 所示. ...
Major advances in particle swarm optimization: theory, analysis, and application
1
2021
... Xu等[22 ] 通过定义收敛性指标,从理论角度对MOPSO的收敛性进行了分析和证明. 此外,Houssein等[23 ] 对粒子的稳定性、漫游行为以及运动模式等多个特性进行了讨论分析. 根据其特征,MOPSO可以分为3大类:基于Pareto支配的MOPSO、基于分解的MOPSO和基于指标的MOPSO,如图3 所示. ...
Measuring the convergence and diversity of CDAS multi-objective particle swarm optimization algorithms: a study of many-objective problems
1
2012
... De Carvalho等[24 ] 将多目标控制技术CDAS与PSO相结合,所提出的MOPSO-CDAS优化了非支配档案的更新,有助于解集收敛性和多样性的提高. Zapotecas等[25 ] 将Pareto支配和分解方法集成在求解机制中,提出新的集成PSO算法. 为了进一步提高收敛速度,随后Al Moubayed等[26 ] 又提出新的领导粒子选择和外部存档维护机制,所提出的D2 MOPSO算法引入了目标空间和解空间的拥挤距离概念,且不需要遗传算子即可快速收敛. ...
1
... De Carvalho等[24 ] 将多目标控制技术CDAS与PSO相结合,所提出的MOPSO-CDAS优化了非支配档案的更新,有助于解集收敛性和多样性的提高. Zapotecas等[25 ] 将Pareto支配和分解方法集成在求解机制中,提出新的集成PSO算法. 为了进一步提高收敛速度,随后Al Moubayed等[26 ] 又提出新的领导粒子选择和外部存档维护机制,所提出的D2 MOPSO算法引入了目标空间和解空间的拥挤距离概念,且不需要遗传算子即可快速收敛. ...
D2MOPSO: MOPSO based on decomposition and dominance with archiving using crowding distance in objective and solution spaces
1
2014
... De Carvalho等[24 ] 将多目标控制技术CDAS与PSO相结合,所提出的MOPSO-CDAS优化了非支配档案的更新,有助于解集收敛性和多样性的提高. Zapotecas等[25 ] 将Pareto支配和分解方法集成在求解机制中,提出新的集成PSO算法. 为了进一步提高收敛速度,随后Al Moubayed等[26 ] 又提出新的领导粒子选择和外部存档维护机制,所提出的D2 MOPSO算法引入了目标空间和解空间的拥挤距离概念,且不需要遗传算子即可快速收敛. ...
基于树形结构无界存档的多目标粒子群算法
1
2020
... MOPSO很大程度上依赖于优秀粒子的存储. 通常情况下,外部存档的更新都是在一个固定大小的范围内新增或剔除粒子. 纪昌明等[27 ] 推翻了链表式存档的概念,引入了以树形结构为基础的无界存档机制,并将Pareto支配原则作为粒子能否进入外部存档的衡量标准. 将该机制与PSO结合得到MOPSO/TUA算法,使得存档的更新更加高效. Zhang等[28 ] 提出的基于竞争机制的CMOPSO算法不需要任何额外的存储机制,该算法通过支配关系选出精英粒子,再通过精英粒子间的角度竞争确定获胜粒子,以此更新粒子的速度和位置. ...
基于树形结构无界存档的多目标粒子群算法
1
2020
... MOPSO很大程度上依赖于优秀粒子的存储. 通常情况下,外部存档的更新都是在一个固定大小的范围内新增或剔除粒子. 纪昌明等[27 ] 推翻了链表式存档的概念,引入了以树形结构为基础的无界存档机制,并将Pareto支配原则作为粒子能否进入外部存档的衡量标准. 将该机制与PSO结合得到MOPSO/TUA算法,使得存档的更新更加高效. Zhang等[28 ] 提出的基于竞争机制的CMOPSO算法不需要任何额外的存储机制,该算法通过支配关系选出精英粒子,再通过精英粒子间的角度竞争确定获胜粒子,以此更新粒子的速度和位置. ...
A competitive mechanism based multi-objective particle swarm optimizer with fast convergence
1
2018
... MOPSO很大程度上依赖于优秀粒子的存储. 通常情况下,外部存档的更新都是在一个固定大小的范围内新增或剔除粒子. 纪昌明等[27 ] 推翻了链表式存档的概念,引入了以树形结构为基础的无界存档机制,并将Pareto支配原则作为粒子能否进入外部存档的衡量标准. 将该机制与PSO结合得到MOPSO/TUA算法,使得存档的更新更加高效. Zhang等[28 ] 提出的基于竞争机制的CMOPSO算法不需要任何额外的存储机制,该算法通过支配关系选出精英粒子,再通过精英粒子间的角度竞争确定获胜粒子,以此更新粒子的速度和位置. ...
Particle swarm optimization with a balanceable fitness estimation for many-objective optimization problems
1
2018
... 传统的优化算法由于受到了维数诅咒,在高维问题上表现不佳. 这是由于随着目标空间维度的增加,Pareto支配的优势大大减弱,优化效果不显著. 为了克服这一难题,一方面,Lin等[29 ] 为了增强粒子的选择压力,提出结合粒子收敛性和多样性信息的NMPSO算法,该算法引入平衡适应度估计方法作为多样性保持机制,并利用新的速度更新方程和模拟二进制交叉(simulated binary crossover, SBX)显著提升算法性能. 另一方面,根据维度变化,自适应调整支配条件有助于缓和MOPSO过早收敛的不足,于伟伟等[30 ] 基于自适应模糊支配,改进了原有的MOPSO,用于求解复杂的MaOPs. 同样基于模糊支配的原则,谭阳等[31 ] 从PF的超平面结构考虑,提出了超球形支配域的概念,使得所提出的HFPSO算法在高维空间获得的PS仍保持相对均匀的分布. ...
一种基于自适应模糊支配的高维多目标粒子群算法
1
2018
... 传统的优化算法由于受到了维数诅咒,在高维问题上表现不佳. 这是由于随着目标空间维度的增加,Pareto支配的优势大大减弱,优化效果不显著. 为了克服这一难题,一方面,Lin等[29 ] 为了增强粒子的选择压力,提出结合粒子收敛性和多样性信息的NMPSO算法,该算法引入平衡适应度估计方法作为多样性保持机制,并利用新的速度更新方程和模拟二进制交叉(simulated binary crossover, SBX)显著提升算法性能. 另一方面,根据维度变化,自适应调整支配条件有助于缓和MOPSO过早收敛的不足,于伟伟等[30 ] 基于自适应模糊支配,改进了原有的MOPSO,用于求解复杂的MaOPs. 同样基于模糊支配的原则,谭阳等[31 ] 从PF的超平面结构考虑,提出了超球形支配域的概念,使得所提出的HFPSO算法在高维空间获得的PS仍保持相对均匀的分布. ...
一种基于自适应模糊支配的高维多目标粒子群算法
1
2018
... 传统的优化算法由于受到了维数诅咒,在高维问题上表现不佳. 这是由于随着目标空间维度的增加,Pareto支配的优势大大减弱,优化效果不显著. 为了克服这一难题,一方面,Lin等[29 ] 为了增强粒子的选择压力,提出结合粒子收敛性和多样性信息的NMPSO算法,该算法引入平衡适应度估计方法作为多样性保持机制,并利用新的速度更新方程和模拟二进制交叉(simulated binary crossover, SBX)显著提升算法性能. 另一方面,根据维度变化,自适应调整支配条件有助于缓和MOPSO过早收敛的不足,于伟伟等[30 ] 基于自适应模糊支配,改进了原有的MOPSO,用于求解复杂的MaOPs. 同样基于模糊支配的原则,谭阳等[31 ] 从PF的超平面结构考虑,提出了超球形支配域的概念,使得所提出的HFPSO算法在高维空间获得的PS仍保持相对均匀的分布. ...
基于超球形模糊支配的高维多目标粒子群优化算法
1
2019
... 传统的优化算法由于受到了维数诅咒,在高维问题上表现不佳. 这是由于随着目标空间维度的增加,Pareto支配的优势大大减弱,优化效果不显著. 为了克服这一难题,一方面,Lin等[29 ] 为了增强粒子的选择压力,提出结合粒子收敛性和多样性信息的NMPSO算法,该算法引入平衡适应度估计方法作为多样性保持机制,并利用新的速度更新方程和模拟二进制交叉(simulated binary crossover, SBX)显著提升算法性能. 另一方面,根据维度变化,自适应调整支配条件有助于缓和MOPSO过早收敛的不足,于伟伟等[30 ] 基于自适应模糊支配,改进了原有的MOPSO,用于求解复杂的MaOPs. 同样基于模糊支配的原则,谭阳等[31 ] 从PF的超平面结构考虑,提出了超球形支配域的概念,使得所提出的HFPSO算法在高维空间获得的PS仍保持相对均匀的分布. ...
基于超球形模糊支配的高维多目标粒子群优化算法
1
2019
... 传统的优化算法由于受到了维数诅咒,在高维问题上表现不佳. 这是由于随着目标空间维度的增加,Pareto支配的优势大大减弱,优化效果不显著. 为了克服这一难题,一方面,Lin等[29 ] 为了增强粒子的选择压力,提出结合粒子收敛性和多样性信息的NMPSO算法,该算法引入平衡适应度估计方法作为多样性保持机制,并利用新的速度更新方程和模拟二进制交叉(simulated binary crossover, SBX)显著提升算法性能. 另一方面,根据维度变化,自适应调整支配条件有助于缓和MOPSO过早收敛的不足,于伟伟等[30 ] 基于自适应模糊支配,改进了原有的MOPSO,用于求解复杂的MaOPs. 同样基于模糊支配的原则,谭阳等[31 ] 从PF的超平面结构考虑,提出了超球形支配域的概念,使得所提出的HFPSO算法在高维空间获得的PS仍保持相对均匀的分布. ...
A review of evolutionary multimodal multiobjective optimization
1
2020
... 当决策空间内存在多个等效的Pareto解集的子集或多个等效的PS和局部PS对应于目标空间中相同的PF,这类复杂问题定义为多模态多目标优化问题[32 ] (multimodal multi-objective optimization problems, MMOPs). 研究者们将基于Pareto支配的方法和其他方法相结合,用于MMOPs的求解. Qu等[33 ] 将非支配排序和拥挤距离相结合以保持决策空间和目标空间解集的多样性,提出了基于自组织形态的MOPSO优化算法SS-MOPSO,该算法利用自组织和物种形成策略在快速生成多个小生境[34 -35 ] 的同时避免子种群间的交叉,并采用并行方式搜索PS,有效解决MMOPs,生成均匀分布的非支配解. ...
A self-organized speciation based multi-objective particle swarm optimizer for multimodal multi-objective problems
1
2020
... 当决策空间内存在多个等效的Pareto解集的子集或多个等效的PS和局部PS对应于目标空间中相同的PF,这类复杂问题定义为多模态多目标优化问题[32 ] (multimodal multi-objective optimization problems, MMOPs). 研究者们将基于Pareto支配的方法和其他方法相结合,用于MMOPs的求解. Qu等[33 ] 将非支配排序和拥挤距离相结合以保持决策空间和目标空间解集的多样性,提出了基于自组织形态的MOPSO优化算法SS-MOPSO,该算法利用自组织和物种形成策略在快速生成多个小生境[34 -35 ] 的同时避免子种群间的交叉,并采用并行方式搜索PS,有效解决MMOPs,生成均匀分布的非支配解. ...
基于小生境的多目标进化算法
1
2023
... 当决策空间内存在多个等效的Pareto解集的子集或多个等效的PS和局部PS对应于目标空间中相同的PF,这类复杂问题定义为多模态多目标优化问题[32 ] (multimodal multi-objective optimization problems, MMOPs). 研究者们将基于Pareto支配的方法和其他方法相结合,用于MMOPs的求解. Qu等[33 ] 将非支配排序和拥挤距离相结合以保持决策空间和目标空间解集的多样性,提出了基于自组织形态的MOPSO优化算法SS-MOPSO,该算法利用自组织和物种形成策略在快速生成多个小生境[34 -35 ] 的同时避免子种群间的交叉,并采用并行方式搜索PS,有效解决MMOPs,生成均匀分布的非支配解. ...
基于小生境的多目标进化算法
1
2023
... 当决策空间内存在多个等效的Pareto解集的子集或多个等效的PS和局部PS对应于目标空间中相同的PF,这类复杂问题定义为多模态多目标优化问题[32 ] (multimodal multi-objective optimization problems, MMOPs). 研究者们将基于Pareto支配的方法和其他方法相结合,用于MMOPs的求解. Qu等[33 ] 将非支配排序和拥挤距离相结合以保持决策空间和目标空间解集的多样性,提出了基于自组织形态的MOPSO优化算法SS-MOPSO,该算法利用自组织和物种形成策略在快速生成多个小生境[34 -35 ] 的同时避免子种群间的交叉,并采用并行方式搜索PS,有效解决MMOPs,生成均匀分布的非支配解. ...
1
... 当决策空间内存在多个等效的Pareto解集的子集或多个等效的PS和局部PS对应于目标空间中相同的PF,这类复杂问题定义为多模态多目标优化问题[32 ] (multimodal multi-objective optimization problems, MMOPs). 研究者们将基于Pareto支配的方法和其他方法相结合,用于MMOPs的求解. Qu等[33 ] 将非支配排序和拥挤距离相结合以保持决策空间和目标空间解集的多样性,提出了基于自组织形态的MOPSO优化算法SS-MOPSO,该算法利用自组织和物种形成策略在快速生成多个小生境[34 -35 ] 的同时避免子种群间的交叉,并采用并行方式搜索PS,有效解决MMOPs,生成均匀分布的非支配解. ...
1
... 当决策空间内存在多个等效的Pareto解集的子集或多个等效的PS和局部PS对应于目标空间中相同的PF,这类复杂问题定义为多模态多目标优化问题[32 ] (multimodal multi-objective optimization problems, MMOPs). 研究者们将基于Pareto支配的方法和其他方法相结合,用于MMOPs的求解. Qu等[33 ] 将非支配排序和拥挤距离相结合以保持决策空间和目标空间解集的多样性,提出了基于自组织形态的MOPSO优化算法SS-MOPSO,该算法利用自组织和物种形成策略在快速生成多个小生境[34 -35 ] 的同时避免子种群间的交叉,并采用并行方式搜索PS,有效解决MMOPs,生成均匀分布的非支配解. ...
1
... 受MOEA/D启发,基于分解的方法将MOPs分解为多个子问题,并分别用优化算法求解. Zapotecas Martinez等[36 ] 将分解思想融合入MOPSO,所提出的dMOPSO通过重新初始化策略保持种群的多样性,但由于其缺乏存档机制,无法解决复杂的MOPs. 为了维护外部存档从而提高种群多样性,Zhan等[37 ] 引入协同进化技术并提出新的多目标多种群CMPSO,该算法采用精英学习策略用来更新外部存档以提高多样性,避免陷入局部最优,为了提高收敛速度,CMPSO利用共享存档中的精英信息更新粒子速度. 基于分解的思想根据作用对象的不同,可以分为对目标空间的分解、对种群的分解、对问题的分解和网格分解. ...
Multiple populations for multiple objectives: a coevolutionary technique for solving multiobjective optimization problems
1
2013
... 受MOEA/D启发,基于分解的方法将MOPs分解为多个子问题,并分别用优化算法求解. Zapotecas Martinez等[36 ] 将分解思想融合入MOPSO,所提出的dMOPSO通过重新初始化策略保持种群的多样性,但由于其缺乏存档机制,无法解决复杂的MOPs. 为了维护外部存档从而提高种群多样性,Zhan等[37 ] 引入协同进化技术并提出新的多目标多种群CMPSO,该算法采用精英学习策略用来更新外部存档以提高多样性,避免陷入局部最优,为了提高收敛速度,CMPSO利用共享存档中的精英信息更新粒子速度. 基于分解的思想根据作用对象的不同,可以分为对目标空间的分解、对种群的分解、对问题的分解和网格分解. ...
A new multi-objective particle swarm optimization algorithm based on decomposition
1
2015
... 基于分解的思想可以将目标空间分解为若干子区域求解以保持解的多样性. Dai等[38 ] 提出的MPSO/D算法采用拥挤距离计算适应度以提高收敛性. 为了更好地向具有不同形状的PF收敛,黄佩秋等[39 ] 提出基于分区的分解策略求得均匀分布的解集. 韩红桂等[40 ] 通过自适应分解方法,并对粒子的飞行参数进行调整,在保证多样性的前提下提高了粒子的收敛能力. ...
混合多目标粒子群优化算法在热精轧负荷分配优化中的应用
1
2017
... 基于分解的思想可以将目标空间分解为若干子区域求解以保持解的多样性. Dai等[38 ] 提出的MPSO/D算法采用拥挤距离计算适应度以提高收敛性. 为了更好地向具有不同形状的PF收敛,黄佩秋等[39 ] 提出基于分区的分解策略求得均匀分布的解集. 韩红桂等[40 ] 通过自适应分解方法,并对粒子的飞行参数进行调整,在保证多样性的前提下提高了粒子的收敛能力. ...
混合多目标粒子群优化算法在热精轧负荷分配优化中的应用
1
2017
... 基于分解的思想可以将目标空间分解为若干子区域求解以保持解的多样性. Dai等[38 ] 提出的MPSO/D算法采用拥挤距离计算适应度以提高收敛性. 为了更好地向具有不同形状的PF收敛,黄佩秋等[39 ] 提出基于分区的分解策略求得均匀分布的解集. 韩红桂等[40 ] 通过自适应分解方法,并对粒子的飞行参数进行调整,在保证多样性的前提下提高了粒子的收敛能力. ...
自适应分解式多目标粒子群优化算法
1
2020
... 基于分解的思想可以将目标空间分解为若干子区域求解以保持解的多样性. Dai等[38 ] 提出的MPSO/D算法采用拥挤距离计算适应度以提高收敛性. 为了更好地向具有不同形状的PF收敛,黄佩秋等[39 ] 提出基于分区的分解策略求得均匀分布的解集. 韩红桂等[40 ] 通过自适应分解方法,并对粒子的飞行参数进行调整,在保证多样性的前提下提高了粒子的收敛能力. ...
自适应分解式多目标粒子群优化算法
1
2020
... 基于分解的思想可以将目标空间分解为若干子区域求解以保持解的多样性. Dai等[38 ] 提出的MPSO/D算法采用拥挤距离计算适应度以提高收敛性. 为了更好地向具有不同形状的PF收敛,黄佩秋等[39 ] 提出基于分区的分解策略求得均匀分布的解集. 韩红桂等[40 ] 通过自适应分解方法,并对粒子的飞行参数进行调整,在保证多样性的前提下提高了粒子的收敛能力. ...
A region decomposition-based multi-objective particle swarm optimization algorithm
1
2014
... 基于分解的方法同样可应用于种群的分解,将种群划分为多个子群. Chen等[41 ] 提出基于M2M分解框架的MOPSO优化算法MOPSO-M2M,该算法通过被分解的子种群同时搜索相应的子区域,快速逼近整个PF,此外,MOPSO-M2M采用切比雪夫方法确定pBest,不需要额外的聚类和小生境技术. 当问题复杂化时,Luo等[42 ] 通过建立和更新子种群的概率模型提高算法性能. Yao等[43 ] 提出协同进化多群多目标优化算法ECMSMOO,每个子种群对单个目标进行优化,并引入内分泌激励机制,保证粒子在目标空间的均匀分布. 此外,Yang等[44 ] 提出具有非支配相对拥挤距离的MOPSO优化算法MOPSO-NRCD,将种群动态划分为主群和多个子种群,并通过非支配关系比较和拥挤距离归一化选择最优解. 针对MaOPs,张庆科等[45 ] 以问题维度为划分依据,随机对种群进行维度划分进行降维,子种群之间相互学习,该RVPLO算法在求解单峰、多峰函数时的优势显著. 类似地,聚类策略同样可应用于子种群的分解,Zhang等[46 ] 采用基于决策空间欧氏距离进行种群划分的聚类策略来提高算法性能. 分解方法在重视多样性的同时也要致力于收敛性的维护,刘彬等[47 ] 在分解得到的4个子种群之间实现了速度信息共享,在提高粒子全局搜索能力的同时尽可能向PF收敛. ...
A hybrid multi-objective PSO-EDA algorithm for reservoir flood control operation
1
2015
... 基于分解的方法同样可应用于种群的分解,将种群划分为多个子群. Chen等[41 ] 提出基于M2M分解框架的MOPSO优化算法MOPSO-M2M,该算法通过被分解的子种群同时搜索相应的子区域,快速逼近整个PF,此外,MOPSO-M2M采用切比雪夫方法确定pBest,不需要额外的聚类和小生境技术. 当问题复杂化时,Luo等[42 ] 通过建立和更新子种群的概率模型提高算法性能. Yao等[43 ] 提出协同进化多群多目标优化算法ECMSMOO,每个子种群对单个目标进行优化,并引入内分泌激励机制,保证粒子在目标空间的均匀分布. 此外,Yang等[44 ] 提出具有非支配相对拥挤距离的MOPSO优化算法MOPSO-NRCD,将种群动态划分为主群和多个子种群,并通过非支配关系比较和拥挤距离归一化选择最优解. 针对MaOPs,张庆科等[45 ] 以问题维度为划分依据,随机对种群进行维度划分进行降维,子种群之间相互学习,该RVPLO算法在求解单峰、多峰函数时的优势显著. 类似地,聚类策略同样可应用于子种群的分解,Zhang等[46 ] 采用基于决策空间欧氏距离进行种群划分的聚类策略来提高算法性能. 分解方法在重视多样性的同时也要致力于收敛性的维护,刘彬等[47 ] 在分解得到的4个子种群之间实现了速度信息共享,在提高粒子全局搜索能力的同时尽可能向PF收敛. ...
Endocrine-based coevolutionary multi-swarm for multi-objective workflow scheduling in a cloud system
1
2017
... 基于分解的方法同样可应用于种群的分解,将种群划分为多个子群. Chen等[41 ] 提出基于M2M分解框架的MOPSO优化算法MOPSO-M2M,该算法通过被分解的子种群同时搜索相应的子区域,快速逼近整个PF,此外,MOPSO-M2M采用切比雪夫方法确定pBest,不需要额外的聚类和小生境技术. 当问题复杂化时,Luo等[42 ] 通过建立和更新子种群的概率模型提高算法性能. Yao等[43 ] 提出协同进化多群多目标优化算法ECMSMOO,每个子种群对单个目标进行优化,并引入内分泌激励机制,保证粒子在目标空间的均匀分布. 此外,Yang等[44 ] 提出具有非支配相对拥挤距离的MOPSO优化算法MOPSO-NRCD,将种群动态划分为主群和多个子种群,并通过非支配关系比较和拥挤距离归一化选择最优解. 针对MaOPs,张庆科等[45 ] 以问题维度为划分依据,随机对种群进行维度划分进行降维,子种群之间相互学习,该RVPLO算法在求解单峰、多峰函数时的优势显著. 类似地,聚类策略同样可应用于子种群的分解,Zhang等[46 ] 采用基于决策空间欧氏距离进行种群划分的聚类策略来提高算法性能. 分解方法在重视多样性的同时也要致力于收敛性的维护,刘彬等[47 ] 在分解得到的4个子种群之间实现了速度信息共享,在提高粒子全局搜索能力的同时尽可能向PF收敛. ...
Deployment of multistatic radar system using multi-objective particle swarm optimisation
1
2018
... 基于分解的方法同样可应用于种群的分解,将种群划分为多个子群. Chen等[41 ] 提出基于M2M分解框架的MOPSO优化算法MOPSO-M2M,该算法通过被分解的子种群同时搜索相应的子区域,快速逼近整个PF,此外,MOPSO-M2M采用切比雪夫方法确定pBest,不需要额外的聚类和小生境技术. 当问题复杂化时,Luo等[42 ] 通过建立和更新子种群的概率模型提高算法性能. Yao等[43 ] 提出协同进化多群多目标优化算法ECMSMOO,每个子种群对单个目标进行优化,并引入内分泌激励机制,保证粒子在目标空间的均匀分布. 此外,Yang等[44 ] 提出具有非支配相对拥挤距离的MOPSO优化算法MOPSO-NRCD,将种群动态划分为主群和多个子种群,并通过非支配关系比较和拥挤距离归一化选择最优解. 针对MaOPs,张庆科等[45 ] 以问题维度为划分依据,随机对种群进行维度划分进行降维,子种群之间相互学习,该RVPLO算法在求解单峰、多峰函数时的优势显著. 类似地,聚类策略同样可应用于子种群的分解,Zhang等[46 ] 采用基于决策空间欧氏距离进行种群划分的聚类策略来提高算法性能. 分解方法在重视多样性的同时也要致力于收敛性的维护,刘彬等[47 ] 在分解得到的4个子种群之间实现了速度信息共享,在提高粒子全局搜索能力的同时尽可能向PF收敛. ...
基于随机维度划分与学习的粒子群优化算法
1
2018
... 基于分解的方法同样可应用于种群的分解,将种群划分为多个子群. Chen等[41 ] 提出基于M2M分解框架的MOPSO优化算法MOPSO-M2M,该算法通过被分解的子种群同时搜索相应的子区域,快速逼近整个PF,此外,MOPSO-M2M采用切比雪夫方法确定pBest,不需要额外的聚类和小生境技术. 当问题复杂化时,Luo等[42 ] 通过建立和更新子种群的概率模型提高算法性能. Yao等[43 ] 提出协同进化多群多目标优化算法ECMSMOO,每个子种群对单个目标进行优化,并引入内分泌激励机制,保证粒子在目标空间的均匀分布. 此外,Yang等[44 ] 提出具有非支配相对拥挤距离的MOPSO优化算法MOPSO-NRCD,将种群动态划分为主群和多个子种群,并通过非支配关系比较和拥挤距离归一化选择最优解. 针对MaOPs,张庆科等[45 ] 以问题维度为划分依据,随机对种群进行维度划分进行降维,子种群之间相互学习,该RVPLO算法在求解单峰、多峰函数时的优势显著. 类似地,聚类策略同样可应用于子种群的分解,Zhang等[46 ] 采用基于决策空间欧氏距离进行种群划分的聚类策略来提高算法性能. 分解方法在重视多样性的同时也要致力于收敛性的维护,刘彬等[47 ] 在分解得到的4个子种群之间实现了速度信息共享,在提高粒子全局搜索能力的同时尽可能向PF收敛. ...
基于随机维度划分与学习的粒子群优化算法
1
2018
... 基于分解的方法同样可应用于种群的分解,将种群划分为多个子群. Chen等[41 ] 提出基于M2M分解框架的MOPSO优化算法MOPSO-M2M,该算法通过被分解的子种群同时搜索相应的子区域,快速逼近整个PF,此外,MOPSO-M2M采用切比雪夫方法确定pBest,不需要额外的聚类和小生境技术. 当问题复杂化时,Luo等[42 ] 通过建立和更新子种群的概率模型提高算法性能. Yao等[43 ] 提出协同进化多群多目标优化算法ECMSMOO,每个子种群对单个目标进行优化,并引入内分泌激励机制,保证粒子在目标空间的均匀分布. 此外,Yang等[44 ] 提出具有非支配相对拥挤距离的MOPSO优化算法MOPSO-NRCD,将种群动态划分为主群和多个子种群,并通过非支配关系比较和拥挤距离归一化选择最优解. 针对MaOPs,张庆科等[45 ] 以问题维度为划分依据,随机对种群进行维度划分进行降维,子种群之间相互学习,该RVPLO算法在求解单峰、多峰函数时的优势显著. 类似地,聚类策略同样可应用于子种群的分解,Zhang等[46 ] 采用基于决策空间欧氏距离进行种群划分的聚类策略来提高算法性能. 分解方法在重视多样性的同时也要致力于收敛性的维护,刘彬等[47 ] 在分解得到的4个子种群之间实现了速度信息共享,在提高粒子全局搜索能力的同时尽可能向PF收敛. ...
A cluster based PSO with leader updating mechanism and ring-topology for multimodal multi-objective optimization
1
2019
... 基于分解的方法同样可应用于种群的分解,将种群划分为多个子群. Chen等[41 ] 提出基于M2M分解框架的MOPSO优化算法MOPSO-M2M,该算法通过被分解的子种群同时搜索相应的子区域,快速逼近整个PF,此外,MOPSO-M2M采用切比雪夫方法确定pBest,不需要额外的聚类和小生境技术. 当问题复杂化时,Luo等[42 ] 通过建立和更新子种群的概率模型提高算法性能. Yao等[43 ] 提出协同进化多群多目标优化算法ECMSMOO,每个子种群对单个目标进行优化,并引入内分泌激励机制,保证粒子在目标空间的均匀分布. 此外,Yang等[44 ] 提出具有非支配相对拥挤距离的MOPSO优化算法MOPSO-NRCD,将种群动态划分为主群和多个子种群,并通过非支配关系比较和拥挤距离归一化选择最优解. 针对MaOPs,张庆科等[45 ] 以问题维度为划分依据,随机对种群进行维度划分进行降维,子种群之间相互学习,该RVPLO算法在求解单峰、多峰函数时的优势显著. 类似地,聚类策略同样可应用于子种群的分解,Zhang等[46 ] 采用基于决策空间欧氏距离进行种群划分的聚类策略来提高算法性能. 分解方法在重视多样性的同时也要致力于收敛性的维护,刘彬等[47 ] 在分解得到的4个子种群之间实现了速度信息共享,在提高粒子全局搜索能力的同时尽可能向PF收敛. ...
基于速度交流的多种群多目标粒子群算法研究
1
2020
... 基于分解的方法同样可应用于种群的分解,将种群划分为多个子群. Chen等[41 ] 提出基于M2M分解框架的MOPSO优化算法MOPSO-M2M,该算法通过被分解的子种群同时搜索相应的子区域,快速逼近整个PF,此外,MOPSO-M2M采用切比雪夫方法确定pBest,不需要额外的聚类和小生境技术. 当问题复杂化时,Luo等[42 ] 通过建立和更新子种群的概率模型提高算法性能. Yao等[43 ] 提出协同进化多群多目标优化算法ECMSMOO,每个子种群对单个目标进行优化,并引入内分泌激励机制,保证粒子在目标空间的均匀分布. 此外,Yang等[44 ] 提出具有非支配相对拥挤距离的MOPSO优化算法MOPSO-NRCD,将种群动态划分为主群和多个子种群,并通过非支配关系比较和拥挤距离归一化选择最优解. 针对MaOPs,张庆科等[45 ] 以问题维度为划分依据,随机对种群进行维度划分进行降维,子种群之间相互学习,该RVPLO算法在求解单峰、多峰函数时的优势显著. 类似地,聚类策略同样可应用于子种群的分解,Zhang等[46 ] 采用基于决策空间欧氏距离进行种群划分的聚类策略来提高算法性能. 分解方法在重视多样性的同时也要致力于收敛性的维护,刘彬等[47 ] 在分解得到的4个子种群之间实现了速度信息共享,在提高粒子全局搜索能力的同时尽可能向PF收敛. ...
基于速度交流的多种群多目标粒子群算法研究
1
2020
... 基于分解的方法同样可应用于种群的分解,将种群划分为多个子群. Chen等[41 ] 提出基于M2M分解框架的MOPSO优化算法MOPSO-M2M,该算法通过被分解的子种群同时搜索相应的子区域,快速逼近整个PF,此外,MOPSO-M2M采用切比雪夫方法确定pBest,不需要额外的聚类和小生境技术. 当问题复杂化时,Luo等[42 ] 通过建立和更新子种群的概率模型提高算法性能. Yao等[43 ] 提出协同进化多群多目标优化算法ECMSMOO,每个子种群对单个目标进行优化,并引入内分泌激励机制,保证粒子在目标空间的均匀分布. 此外,Yang等[44 ] 提出具有非支配相对拥挤距离的MOPSO优化算法MOPSO-NRCD,将种群动态划分为主群和多个子种群,并通过非支配关系比较和拥挤距离归一化选择最优解. 针对MaOPs,张庆科等[45 ] 以问题维度为划分依据,随机对种群进行维度划分进行降维,子种群之间相互学习,该RVPLO算法在求解单峰、多峰函数时的优势显著. 类似地,聚类策略同样可应用于子种群的分解,Zhang等[46 ] 采用基于决策空间欧氏距离进行种群划分的聚类策略来提高算法性能. 分解方法在重视多样性的同时也要致力于收敛性的维护,刘彬等[47 ] 在分解得到的4个子种群之间实现了速度信息共享,在提高粒子全局搜索能力的同时尽可能向PF收敛. ...
MOEA/D with adaptive weight adjustment
1
2014
... 在处理复杂PSO问题时,为了降低问题的复杂度,分解方法还可以将要求解的MOPs分解为多个子问题. 自适应的分解方法在MOEAAWA[48 ] 中被提出,动态调整每个子问题的权值,在节省计算最优子问题时间的同时保证粒子的多样性. Lin等[49 ] 提出的MMOPSO算法为每个分解得到的聚合问题分配相应的粒子,并引入多样化的搜索策略对粒子的速度进行更新. Zhu等[50 ] 提出新颖的外部存档引导的AgMOPSO算法,对每个分解得到的子问题分配相应的粒子进行优化,其领导者都是从外部存档中选择的. 杨景明等[51 ] 通过分解MOPs保证多样性,结合非支配排序增强收敛性,引入动态变异机制避免局部最优,从而得到与真实PF尽量吻合的最终种群. ...
A novel multi-objective particle swarm optimization with multiple search strategies
1
2015
... 在处理复杂PSO问题时,为了降低问题的复杂度,分解方法还可以将要求解的MOPs分解为多个子问题. 自适应的分解方法在MOEAAWA[48 ] 中被提出,动态调整每个子问题的权值,在节省计算最优子问题时间的同时保证粒子的多样性. Lin等[49 ] 提出的MMOPSO算法为每个分解得到的聚合问题分配相应的粒子,并引入多样化的搜索策略对粒子的速度进行更新. Zhu等[50 ] 提出新颖的外部存档引导的AgMOPSO算法,对每个分解得到的子问题分配相应的粒子进行优化,其领导者都是从外部存档中选择的. 杨景明等[51 ] 通过分解MOPs保证多样性,结合非支配排序增强收敛性,引入动态变异机制避免局部最优,从而得到与真实PF尽量吻合的最终种群. ...
An external archive-guided multiobjective particle swarm optimization algorithm
1
2017
... 在处理复杂PSO问题时,为了降低问题的复杂度,分解方法还可以将要求解的MOPs分解为多个子问题. 自适应的分解方法在MOEAAWA[48 ] 中被提出,动态调整每个子问题的权值,在节省计算最优子问题时间的同时保证粒子的多样性. Lin等[49 ] 提出的MMOPSO算法为每个分解得到的聚合问题分配相应的粒子,并引入多样化的搜索策略对粒子的速度进行更新. Zhu等[50 ] 提出新颖的外部存档引导的AgMOPSO算法,对每个分解得到的子问题分配相应的粒子进行优化,其领导者都是从外部存档中选择的. 杨景明等[51 ] 通过分解MOPs保证多样性,结合非支配排序增强收敛性,引入动态变异机制避免局部最优,从而得到与真实PF尽量吻合的最终种群. ...
基于融合多策略改进的多目标粒子群优化算法
1
2018
... 在处理复杂PSO问题时,为了降低问题的复杂度,分解方法还可以将要求解的MOPs分解为多个子问题. 自适应的分解方法在MOEAAWA[48 ] 中被提出,动态调整每个子问题的权值,在节省计算最优子问题时间的同时保证粒子的多样性. Lin等[49 ] 提出的MMOPSO算法为每个分解得到的聚合问题分配相应的粒子,并引入多样化的搜索策略对粒子的速度进行更新. Zhu等[50 ] 提出新颖的外部存档引导的AgMOPSO算法,对每个分解得到的子问题分配相应的粒子进行优化,其领导者都是从外部存档中选择的. 杨景明等[51 ] 通过分解MOPs保证多样性,结合非支配排序增强收敛性,引入动态变异机制避免局部最优,从而得到与真实PF尽量吻合的最终种群. ...
基于融合多策略改进的多目标粒子群优化算法
1
2018
... 在处理复杂PSO问题时,为了降低问题的复杂度,分解方法还可以将要求解的MOPs分解为多个子问题. 自适应的分解方法在MOEAAWA[48 ] 中被提出,动态调整每个子问题的权值,在节省计算最优子问题时间的同时保证粒子的多样性. Lin等[49 ] 提出的MMOPSO算法为每个分解得到的聚合问题分配相应的粒子,并引入多样化的搜索策略对粒子的速度进行更新. Zhu等[50 ] 提出新颖的外部存档引导的AgMOPSO算法,对每个分解得到的子问题分配相应的粒子进行优化,其领导者都是从外部存档中选择的. 杨景明等[51 ] 通过分解MOPs保证多样性,结合非支配排序增强收敛性,引入动态变异机制避免局部最优,从而得到与真实PF尽量吻合的最终种群. ...
Approximating the nondominated front using the Pareto archived evolution strategy
1
2000
... Knowles等[52 ] 首先将网格机制引入多目标优化中,从而确保外部存档中非劣解的多样性. 对网格坐标的映射能够将粒子的多样性可视化,以图4 (a)为例,尝试在不同网格中选择粒子,可以观察到$ {p_2} $ $ {p_3} $ [53 ] 引入网格距离的概念,兼顾了粒子的收敛性和多样性从而实现粒子间的网格排序,在增强粒子选择压力的同时提高了排序效率. 该团队还在网格的基础上提出融合粒子密度信息的全新的MOPSO/GMR算法[54 -55 ] ,该方法不仅考虑了种群的多样性,还通过粒子的位置信息来协助pBest和gBest的选择. 为了避免局部最优,提高算法的鲁棒性,Leng等[56 ] 提出基于网格距离的GDMOPSO算法. 这些算法只在低维MOPs上表现良好,对高维空间上的优化问题帮助不大. ...
基于网格排序的多目标粒子群优化算法
1
2017
... Knowles等[52 ] 首先将网格机制引入多目标优化中,从而确保外部存档中非劣解的多样性. 对网格坐标的映射能够将粒子的多样性可视化,以图4 (a)为例,尝试在不同网格中选择粒子,可以观察到$ {p_2} $ $ {p_3} $ [53 ] 引入网格距离的概念,兼顾了粒子的收敛性和多样性从而实现粒子间的网格排序,在增强粒子选择压力的同时提高了排序效率. 该团队还在网格的基础上提出融合粒子密度信息的全新的MOPSO/GMR算法[54 -55 ] ,该方法不仅考虑了种群的多样性,还通过粒子的位置信息来协助pBest和gBest的选择. 为了避免局部最优,提高算法的鲁棒性,Leng等[56 ] 提出基于网格距离的GDMOPSO算法. 这些算法只在低维MOPs上表现良好,对高维空间上的优化问题帮助不大. ...
基于网格排序的多目标粒子群优化算法
1
2017
... Knowles等[52 ] 首先将网格机制引入多目标优化中,从而确保外部存档中非劣解的多样性. 对网格坐标的映射能够将粒子的多样性可视化,以图4 (a)为例,尝试在不同网格中选择粒子,可以观察到$ {p_2} $ $ {p_3} $ [53 ] 引入网格距离的概念,兼顾了粒子的收敛性和多样性从而实现粒子间的网格排序,在增强粒子选择压力的同时提高了排序效率. 该团队还在网格的基础上提出融合粒子密度信息的全新的MOPSO/GMR算法[54 -55 ] ,该方法不仅考虑了种群的多样性,还通过粒子的位置信息来协助pBest和gBest的选择. 为了避免局部最优,提高算法的鲁棒性,Leng等[56 ] 提出基于网格距离的GDMOPSO算法. 这些算法只在低维MOPs上表现良好,对高维空间上的优化问题帮助不大. ...
Multi-objective particle swarm optimization based on global margin ranking
1
2017
... Knowles等[52 ] 首先将网格机制引入多目标优化中,从而确保外部存档中非劣解的多样性. 对网格坐标的映射能够将粒子的多样性可视化,以图4 (a)为例,尝试在不同网格中选择粒子,可以观察到$ {p_2} $ $ {p_3} $ [53 ] 引入网格距离的概念,兼顾了粒子的收敛性和多样性从而实现粒子间的网格排序,在增强粒子选择压力的同时提高了排序效率. 该团队还在网格的基础上提出融合粒子密度信息的全新的MOPSO/GMR算法[54 -55 ] ,该方法不仅考虑了种群的多样性,还通过粒子的位置信息来协助pBest和gBest的选择. 为了避免局部最优,提高算法的鲁棒性,Leng等[56 ] 提出基于网格距离的GDMOPSO算法. 这些算法只在低维MOPs上表现良好,对高维空间上的优化问题帮助不大. ...
1
... Knowles等[52 ] 首先将网格机制引入多目标优化中,从而确保外部存档中非劣解的多样性. 对网格坐标的映射能够将粒子的多样性可视化,以图4 (a)为例,尝试在不同网格中选择粒子,可以观察到$ {p_2} $ $ {p_3} $ [53 ] 引入网格距离的概念,兼顾了粒子的收敛性和多样性从而实现粒子间的网格排序,在增强粒子选择压力的同时提高了排序效率. 该团队还在网格的基础上提出融合粒子密度信息的全新的MOPSO/GMR算法[54 -55 ] ,该方法不仅考虑了种群的多样性,还通过粒子的位置信息来协助pBest和gBest的选择. 为了避免局部最优,提高算法的鲁棒性,Leng等[56 ] 提出基于网格距离的GDMOPSO算法. 这些算法只在低维MOPs上表现良好,对高维空间上的优化问题帮助不大. ...
1
... Knowles等[52 ] 首先将网格机制引入多目标优化中,从而确保外部存档中非劣解的多样性. 对网格坐标的映射能够将粒子的多样性可视化,以图4 (a)为例,尝试在不同网格中选择粒子,可以观察到$ {p_2} $ $ {p_3} $ [53 ] 引入网格距离的概念,兼顾了粒子的收敛性和多样性从而实现粒子间的网格排序,在增强粒子选择压力的同时提高了排序效率. 该团队还在网格的基础上提出融合粒子密度信息的全新的MOPSO/GMR算法[54 -55 ] ,该方法不仅考虑了种群的多样性,还通过粒子的位置信息来协助pBest和gBest的选择. 为了避免局部最优,提高算法的鲁棒性,Leng等[56 ] 提出基于网格距离的GDMOPSO算法. 这些算法只在低维MOPs上表现良好,对高维空间上的优化问题帮助不大. ...
A multi-objective particle swarm optimization based on grid distance
1
2019
... Knowles等[52 ] 首先将网格机制引入多目标优化中,从而确保外部存档中非劣解的多样性. 对网格坐标的映射能够将粒子的多样性可视化,以图4 (a)为例,尝试在不同网格中选择粒子,可以观察到$ {p_2} $ $ {p_3} $ [53 ] 引入网格距离的概念,兼顾了粒子的收敛性和多样性从而实现粒子间的网格排序,在增强粒子选择压力的同时提高了排序效率. 该团队还在网格的基础上提出融合粒子密度信息的全新的MOPSO/GMR算法[54 -55 ] ,该方法不仅考虑了种群的多样性,还通过粒子的位置信息来协助pBest和gBest的选择. 为了避免局部最优,提高算法的鲁棒性,Leng等[56 ] 提出基于网格距离的GDMOPSO算法. 这些算法只在低维MOPs上表现良好,对高维空间上的优化问题帮助不大. ...
A multiobjective particle swarm optimization algorithm based on grid technique and multistrategy
1
2021
... 面对复杂MOPs,Zou等[57 ] 结合网格机制和多策略机制并提出GTMSMOPSO算法,该算法同时采用基于收敛性和多样性的评价策略,用来维护外部存档,选择高质量的解. 为了使得粒子初始化时具备良好的分布,吴耀威等[58 ] 提出基于网格密度的GDHMOPSO算法,同时通过选择每个网格中的最优粒子来避免算法陷入局部最优. Ye等[59 ] 改进了传统的网格机制,引入分层聚类思想并通过增强的网格排名对粒子的收敛性和多样性进行更全面的评价,提出全新的EGCCMOPSO算法. 如图4 (b)所示,GDR和GD的比值以及EGD决定了粒子$ {p_1}、 {p_4} 、{p_6} $ $ {p_7} $
基于网格密度的混合新型多目标粒子群算法
1
2021
... 面对复杂MOPs,Zou等[57 ] 结合网格机制和多策略机制并提出GTMSMOPSO算法,该算法同时采用基于收敛性和多样性的评价策略,用来维护外部存档,选择高质量的解. 为了使得粒子初始化时具备良好的分布,吴耀威等[58 ] 提出基于网格密度的GDHMOPSO算法,同时通过选择每个网格中的最优粒子来避免算法陷入局部最优. Ye等[59 ] 改进了传统的网格机制,引入分层聚类思想并通过增强的网格排名对粒子的收敛性和多样性进行更全面的评价,提出全新的EGCCMOPSO算法. 如图4 (b)所示,GDR和GD的比值以及EGD决定了粒子$ {p_1}、 {p_4} 、{p_6} $ $ {p_7} $
基于网格密度的混合新型多目标粒子群算法
1
2021
... 面对复杂MOPs,Zou等[57 ] 结合网格机制和多策略机制并提出GTMSMOPSO算法,该算法同时采用基于收敛性和多样性的评价策略,用来维护外部存档,选择高质量的解. 为了使得粒子初始化时具备良好的分布,吴耀威等[58 ] 提出基于网格密度的GDHMOPSO算法,同时通过选择每个网格中的最优粒子来避免算法陷入局部最优. Ye等[59 ] 改进了传统的网格机制,引入分层聚类思想并通过增强的网格排名对粒子的收敛性和多样性进行更全面的评价,提出全新的EGCCMOPSO算法. 如图4 (b)所示,GDR和GD的比值以及EGD决定了粒子$ {p_1}、 {p_4} 、{p_6} $ $ {p_7} $
A clustering-based competitive particle swarm optimization with grid ranking for multi-objective optimization problems
1
2023
... 面对复杂MOPs,Zou等[57 ] 结合网格机制和多策略机制并提出GTMSMOPSO算法,该算法同时采用基于收敛性和多样性的评价策略,用来维护外部存档,选择高质量的解. 为了使得粒子初始化时具备良好的分布,吴耀威等[58 ] 提出基于网格密度的GDHMOPSO算法,同时通过选择每个网格中的最优粒子来避免算法陷入局部最优. Ye等[59 ] 改进了传统的网格机制,引入分层聚类思想并通过增强的网格排名对粒子的收敛性和多样性进行更全面的评价,提出全新的EGCCMOPSO算法. 如图4 (b)所示,GDR和GD的比值以及EGD决定了粒子$ {p_1}、 {p_4} 、{p_6} $ $ {p_7} $
Grid search based multi-population particle swarm optimization algorithm for multimodal multi-objective optimization
1
2021
... 基于网格分解的方法同样适用于MMOPs的求解,Li等[60 ] 采用网格搜索决策空间中的高质量解,提出的GSMPSO-MM算法中的网格机制对维持决策空间中PS的多样性和目标空间中PS的收敛性意义重大. ...
一种基于超体积指标的多目标进化算法
1
2020
... 除了基于Pareto支配和基于分解的方法,研究者们还通过评价指标的引入增加选择压力,常见的评价指标有超体积指标[61 ] (hypervolume, HV)和R2指标[62 ] 等. ...
一种基于超体积指标的多目标进化算法
1
2020
... 除了基于Pareto支配和基于分解的方法,研究者们还通过评价指标的引入增加选择压力,常见的评价指标有超体积指标[61 ] (hypervolume, HV)和R2指标[62 ] 等. ...
基于R2指标的高维多目标差分进化推荐式课程系统
1
2020
... 除了基于Pareto支配和基于分解的方法,研究者们还通过评价指标的引入增加选择压力,常见的评价指标有超体积指标[61 ] (hypervolume, HV)和R2指标[62 ] 等. ...
基于R2指标的高维多目标差分进化推荐式课程系统
1
2020
... 除了基于Pareto支配和基于分解的方法,研究者们还通过评价指标的引入增加选择压力,常见的评价指标有超体积指标[61 ] (hypervolume, HV)和R2指标[62 ] 等. ...
1
... 采用HV指标求解MOPs的瓶颈在于难以衡量不同解的HV贡献,如图5 所示为HV指标的定义以及HV贡献的示意图. 其中,集合$\left\{ {{p_1},{p_2},{p_3}} \right\}$ ${p_2}$ [63 ] 为MOPSO开发了基于HV指标的领导粒子选择策略,其中使用了基于存档粒子的HV贡献来指导领导粒子的选择. Liang等[64 ] 构建了结合分解思想和HV的优化算法MPSO/DN,在每个分解得到的子区域中依次选择HV贡献最大的解. ...
1
... 采用HV指标求解MOPs的瓶颈在于难以衡量不同解的HV贡献,如图5 所示为HV指标的定义以及HV贡献的示意图. 其中,集合$\left\{ {{p_1},{p_2},{p_3}} \right\}$ ${p_2}$ [63 ] 为MOPSO开发了基于HV指标的领导粒子选择策略,其中使用了基于存档粒子的HV贡献来指导领导粒子的选择. Liang等[64 ] 构建了结合分解思想和HV的优化算法MPSO/DN,在每个分解得到的子区域中依次选择HV贡献最大的解. ...
1
... 基于R2指标,Li等[65 ] 提出选择最优粒子的R2-MOPSO算法. 考虑到MOPSO算法在处理复杂的MOPs时容易陷入局部最优,导致分布不均匀,为此,文献[66 ]中提出的R2HMOPSO混合优化算法通过利用Sigmoid函数映射方法调整惯性权值和学习因子,还设计了SBX算子对粒子进行重新初始化. ...
A hybrid multiobjective particle swarm optimization algorithm based on R2 indicator
1
2018
... 基于R2指标,Li等[65 ] 提出选择最优粒子的R2-MOPSO算法. 考虑到MOPSO算法在处理复杂的MOPs时容易陷入局部最优,导致分布不均匀,为此,文献[66 ]中提出的R2HMOPSO混合优化算法通过利用Sigmoid函数映射方法调整惯性权值和学习因子,还设计了SBX算子对粒子进行重新初始化. ...
A multi-objective particle swarm optimization algorithm based on enhanced selection
1
2019
... 基于R2指标的MOPSO在求解简单MOPs时具有较好的收敛性和多样性,但在高维目标空间内仍有一定缺陷. 当目标函数的数目大于3时,为了提高开发能力,Li等[67 ] 设计了基于增强选择的MOPSO优化算法ESMOPSO,采用目标函数加权自适应更新全局最优粒子,并将R2指标引入到成果分级函数中,对归档中的粒子进行分层,促进了归档的更新. 针对MaOPs的挑战,Liu等[68 ] 将R2指标和基于分解的归档剪枝策略融入PSO优化算法中,同时,在新提出的算法R2-MaPSO中嵌入了精英学习策略和智能高斯学习策略,采用了新的速度更新方法. 李飞等[69 ] 也提出基于R2指标和目标空间分解的R2-MOPSO-II优化算法,设计了双层存档机制,并采用了新的向导选择策略来连接目标空间和决策变量空间. Gu等[70 ] 在R2基础上融入自适应策略,在收敛性和多样性之间达到了平衡. ...
Handling many-objective optimisation problems with R2 indicator and decomposition-based particle swarm optimiser
1
2019
... 基于R2指标的MOPSO在求解简单MOPs时具有较好的收敛性和多样性,但在高维目标空间内仍有一定缺陷. 当目标函数的数目大于3时,为了提高开发能力,Li等[67 ] 设计了基于增强选择的MOPSO优化算法ESMOPSO,采用目标函数加权自适应更新全局最优粒子,并将R2指标引入到成果分级函数中,对归档中的粒子进行分层,促进了归档的更新. 针对MaOPs的挑战,Liu等[68 ] 将R2指标和基于分解的归档剪枝策略融入PSO优化算法中,同时,在新提出的算法R2-MaPSO中嵌入了精英学习策略和智能高斯学习策略,采用了新的速度更新方法. 李飞等[69 ] 也提出基于R2指标和目标空间分解的R2-MOPSO-II优化算法,设计了双层存档机制,并采用了新的向导选择策略来连接目标空间和决策变量空间. Gu等[70 ] 在R2基础上融入自适应策略,在收敛性和多样性之间达到了平衡. ...
基于R2指标和目标空间分解的高维多目标粒子群优化算法
1
2021
... 基于R2指标的MOPSO在求解简单MOPs时具有较好的收敛性和多样性,但在高维目标空间内仍有一定缺陷. 当目标函数的数目大于3时,为了提高开发能力,Li等[67 ] 设计了基于增强选择的MOPSO优化算法ESMOPSO,采用目标函数加权自适应更新全局最优粒子,并将R2指标引入到成果分级函数中,对归档中的粒子进行分层,促进了归档的更新. 针对MaOPs的挑战,Liu等[68 ] 将R2指标和基于分解的归档剪枝策略融入PSO优化算法中,同时,在新提出的算法R2-MaPSO中嵌入了精英学习策略和智能高斯学习策略,采用了新的速度更新方法. 李飞等[69 ] 也提出基于R2指标和目标空间分解的R2-MOPSO-II优化算法,设计了双层存档机制,并采用了新的向导选择策略来连接目标空间和决策变量空间. Gu等[70 ] 在R2基础上融入自适应策略,在收敛性和多样性之间达到了平衡. ...
基于R2指标和目标空间分解的高维多目标粒子群优化算法
1
2021
... 基于R2指标的MOPSO在求解简单MOPs时具有较好的收敛性和多样性,但在高维目标空间内仍有一定缺陷. 当目标函数的数目大于3时,为了提高开发能力,Li等[67 ] 设计了基于增强选择的MOPSO优化算法ESMOPSO,采用目标函数加权自适应更新全局最优粒子,并将R2指标引入到成果分级函数中,对归档中的粒子进行分层,促进了归档的更新. 针对MaOPs的挑战,Liu等[68 ] 将R2指标和基于分解的归档剪枝策略融入PSO优化算法中,同时,在新提出的算法R2-MaPSO中嵌入了精英学习策略和智能高斯学习策略,采用了新的速度更新方法. 李飞等[69 ] 也提出基于R2指标和目标空间分解的R2-MOPSO-II优化算法,设计了双层存档机制,并采用了新的向导选择策略来连接目标空间和决策变量空间. Gu等[70 ] 在R2基础上融入自适应策略,在收敛性和多样性之间达到了平衡. ...
Multi-objective particle swarm optimization with R2 indicator and adaptive method
1
2021
... 基于R2指标的MOPSO在求解简单MOPs时具有较好的收敛性和多样性,但在高维目标空间内仍有一定缺陷. 当目标函数的数目大于3时,为了提高开发能力,Li等[67 ] 设计了基于增强选择的MOPSO优化算法ESMOPSO,采用目标函数加权自适应更新全局最优粒子,并将R2指标引入到成果分级函数中,对归档中的粒子进行分层,促进了归档的更新. 针对MaOPs的挑战,Liu等[68 ] 将R2指标和基于分解的归档剪枝策略融入PSO优化算法中,同时,在新提出的算法R2-MaPSO中嵌入了精英学习策略和智能高斯学习策略,采用了新的速度更新方法. 李飞等[69 ] 也提出基于R2指标和目标空间分解的R2-MOPSO-II优化算法,设计了双层存档机制,并采用了新的向导选择策略来连接目标空间和决策变量空间. Gu等[70 ] 在R2基础上融入自适应策略,在收敛性和多样性之间达到了平衡. ...
Indicator-based set evolution particle swarm optimization for many-objective problems
1
2016
... 基于指标的求解方法同样适用于MaOPs. Sun等[71 ] 提出基于质量指标的改进S-MOPSO算法,根据参考点动态决定gBest和pBest,通过解分层技术更新粒子,有效求解MaOPs. S-MOPSO的成功主要归因于将MaOPs转换为2个或3个基于指标的目标,从而增加了粒子的选择压力. Wu等[72 ] 根据构建的虚拟Pareto前沿(virtual Pareto front, vPF)提出MaOPSO/vPF算法,采用新的指标来评价外部档案中解的综合质量,提高近似PF的收敛性和多样性. Luo等[73 ] 提出基于单目标指标和方向向量的IDMOPSO优化算法,基于epsilon指标和Pareto支配选择pBest,以增强局部探索能力,有助于MaOPs的求解. ...
1
... 基于指标的求解方法同样适用于MaOPs. Sun等[71 ] 提出基于质量指标的改进S-MOPSO算法,根据参考点动态决定gBest和pBest,通过解分层技术更新粒子,有效求解MaOPs. S-MOPSO的成功主要归因于将MaOPs转换为2个或3个基于指标的目标,从而增加了粒子的选择压力. Wu等[72 ] 根据构建的虚拟Pareto前沿(virtual Pareto front, vPF)提出MaOPSO/vPF算法,采用新的指标来评价外部档案中解的综合质量,提高近似PF的收敛性和多样性. Luo等[73 ] 提出基于单目标指标和方向向量的IDMOPSO优化算法,基于epsilon指标和Pareto支配选择pBest,以增强局部探索能力,有助于MaOPs的求解. ...
A many-objective particle swarm optimizer based on indicator and direction vectors for many-objective optimization
1
2020
... 基于指标的求解方法同样适用于MaOPs. Sun等[71 ] 提出基于质量指标的改进S-MOPSO算法,根据参考点动态决定gBest和pBest,通过解分层技术更新粒子,有效求解MaOPs. S-MOPSO的成功主要归因于将MaOPs转换为2个或3个基于指标的目标,从而增加了粒子的选择压力. Wu等[72 ] 根据构建的虚拟Pareto前沿(virtual Pareto front, vPF)提出MaOPSO/vPF算法,采用新的指标来评价外部档案中解的综合质量,提高近似PF的收敛性和多样性. Luo等[73 ] 提出基于单目标指标和方向向量的IDMOPSO优化算法,基于epsilon指标和Pareto支配选择pBest,以增强局部探索能力,有助于MaOPs的求解. ...
LIBEA: a lebesgue indicator-based evolutionary algorithm for multi-objective optimization
1
2019
... 为了对MOPSO的算法性能进行定量评估,研究者们通常采用逆世代距离(inverted generational distance, IGD)[74 ] 和HV这2个常用的性能指标. ...
Improved parallel reactive hybrid particle swarm optimization using improved neighborhood schedule generation method for the integrated framework of optimal production scheduling and operational planning of an energy plant in a factory
1
2020
... 生产调度是以生产计划为依据,将生产计划变成最终产品所做的一系列工作. 在生产过程中容易发生一些突发事故,如:设备突发性故障、在制品返修和网络波动导致测试产品功能时间大量延长. 为了解决这些问题,MOPSO被成功引入,可以根据现场的实际情况进行实时调度,确保快速恢复生产,不耽误生产进度. 通过改进邻域调度生成方法,Kawaguchi等[75 ] 提出了并行反应混合PSO优化算法IPRHPSO,可以在同时考虑最小化生产时间的基础上,最小化工厂二次能源成本. ...
Cellular particle swarm optimization with a simple adaptive local search strategy for the permutation flow shop scheduling problem
1
2019
... 置换流水车间调度问题(permutation flow shop scheduling problem, PFSP)是当今热门的生产调度问题之一. PFSP的本质是调度一组机器采用相同的顺序处理多个作业的生产计划. 随着作业数量和机器数量的增加,找到调度问题的最优解决方案的难度也在增加. 针对此类NP问题,研究者们提出了多种基于MOPSO的求解方法. 基于原始的ATPPSO和蜂窝PSO算法的邻域概念,Seck-Tuoh-Mora等[76 ] 提出自适应局部搜索策略CAPSO-SALS,通过每个解的邻域增强本地搜索能力. Kaya等[77 ] 将混沌混合萤火虫算法和MOPSO相结合,改进了局部搜索策略,以最大化完工时间最小化作为目标函数用于流水车间环境下的调度问题求解. 此外,改进的混合粒子群算法SHPSO[78 ] 同样可以用于求解PFSP,其通过实施粒子停滞判断方法避免陷入局部最优,并将Q学习融入参数自适应更新策略中,有效提升求解质量. ...
Solution for flow shop scheduling problems using chaotic hybrid firefly and particle swarm optimization algorithm with improved local search
1
2021
... 置换流水车间调度问题(permutation flow shop scheduling problem, PFSP)是当今热门的生产调度问题之一. PFSP的本质是调度一组机器采用相同的顺序处理多个作业的生产计划. 随着作业数量和机器数量的增加,找到调度问题的最优解决方案的难度也在增加. 针对此类NP问题,研究者们提出了多种基于MOPSO的求解方法. 基于原始的ATPPSO和蜂窝PSO算法的邻域概念,Seck-Tuoh-Mora等[76 ] 提出自适应局部搜索策略CAPSO-SALS,通过每个解的邻域增强本地搜索能力. Kaya等[77 ] 将混沌混合萤火虫算法和MOPSO相结合,改进了局部搜索策略,以最大化完工时间最小化作为目标函数用于流水车间环境下的调度问题求解. 此外,改进的混合粒子群算法SHPSO[78 ] 同样可以用于求解PFSP,其通过实施粒子停滞判断方法避免陷入局部最优,并将Q学习融入参数自适应更新策略中,有效提升求解质量. ...
自适应混合粒子群算法求解置换流水车间调度问题
1
2023
... 置换流水车间调度问题(permutation flow shop scheduling problem, PFSP)是当今热门的生产调度问题之一. PFSP的本质是调度一组机器采用相同的顺序处理多个作业的生产计划. 随着作业数量和机器数量的增加,找到调度问题的最优解决方案的难度也在增加. 针对此类NP问题,研究者们提出了多种基于MOPSO的求解方法. 基于原始的ATPPSO和蜂窝PSO算法的邻域概念,Seck-Tuoh-Mora等[76 ] 提出自适应局部搜索策略CAPSO-SALS,通过每个解的邻域增强本地搜索能力. Kaya等[77 ] 将混沌混合萤火虫算法和MOPSO相结合,改进了局部搜索策略,以最大化完工时间最小化作为目标函数用于流水车间环境下的调度问题求解. 此外,改进的混合粒子群算法SHPSO[78 ] 同样可以用于求解PFSP,其通过实施粒子停滞判断方法避免陷入局部最优,并将Q学习融入参数自适应更新策略中,有效提升求解质量. ...
自适应混合粒子群算法求解置换流水车间调度问题
1
2023
... 置换流水车间调度问题(permutation flow shop scheduling problem, PFSP)是当今热门的生产调度问题之一. PFSP的本质是调度一组机器采用相同的顺序处理多个作业的生产计划. 随着作业数量和机器数量的增加,找到调度问题的最优解决方案的难度也在增加. 针对此类NP问题,研究者们提出了多种基于MOPSO的求解方法. 基于原始的ATPPSO和蜂窝PSO算法的邻域概念,Seck-Tuoh-Mora等[76 ] 提出自适应局部搜索策略CAPSO-SALS,通过每个解的邻域增强本地搜索能力. Kaya等[77 ] 将混沌混合萤火虫算法和MOPSO相结合,改进了局部搜索策略,以最大化完工时间最小化作为目标函数用于流水车间环境下的调度问题求解. 此外,改进的混合粒子群算法SHPSO[78 ] 同样可以用于求解PFSP,其通过实施粒子停滞判断方法避免陷入局部最优,并将Q学习融入参数自适应更新策略中,有效提升求解质量. ...
Research on multi-objective optimization of smart grid based on particle swarm optimization
1
2023
... 国家电力系统同样可以从多目标优化中受益,降低运营成本,提高服务可靠性. Long等[79 ] 通过对量子PSO的改进,使其在保证计算速度的前提下,能够较好地完成电网规划任务. ...
Design and implementation of power mobile inspection system based on improved particle swarm optimization
1
2021
... 除了电网规划外,电力线路巡检、电力消耗预测和配电网络优化等同样可视为MOPs. 改进的粒子群优化组合算法IPSO[80 ] 采用多元线性回归法、BP神经网络法和灰色系统理论法得到的检测结果进行优化组合,有效提高电力线路巡检的精度,提高输电线路的安全性,减少了故障的发生. 在季节性指数平滑模型的基础上,Deng等[81 ] 通过PSO找到一组近乎最优的平滑参数,这对电力消耗预测意义重大. 此外,针对配电系统中的网络重构问题,Kahouli等[82 ] 采用MOPSO来优化配电网拓扑结构,结果表明MOPSO的引入能够有效提高可靠性,降低功率损耗和计算时间. ...
Equipping seasonal exponential smoothing models with particle swarm optimization algorithm for electricity consumption forecasting
1
2021
... 除了电网规划外,电力线路巡检、电力消耗预测和配电网络优化等同样可视为MOPs. 改进的粒子群优化组合算法IPSO[80 ] 采用多元线性回归法、BP神经网络法和灰色系统理论法得到的检测结果进行优化组合,有效提高电力线路巡检的精度,提高输电线路的安全性,减少了故障的发生. 在季节性指数平滑模型的基础上,Deng等[81 ] 通过PSO找到一组近乎最优的平滑参数,这对电力消耗预测意义重大. 此外,针对配电系统中的网络重构问题,Kahouli等[82 ] 采用MOPSO来优化配电网拓扑结构,结果表明MOPSO的引入能够有效提高可靠性,降低功率损耗和计算时间. ...
Power system reconfiguration in distribution network for improving reliability using genetic algorithm and particle swarm optimization
1
2021
... 除了电网规划外,电力线路巡检、电力消耗预测和配电网络优化等同样可视为MOPs. 改进的粒子群优化组合算法IPSO[80 ] 采用多元线性回归法、BP神经网络法和灰色系统理论法得到的检测结果进行优化组合,有效提高电力线路巡检的精度,提高输电线路的安全性,减少了故障的发生. 在季节性指数平滑模型的基础上,Deng等[81 ] 通过PSO找到一组近乎最优的平滑参数,这对电力消耗预测意义重大. 此外,针对配电系统中的网络重构问题,Kahouli等[82 ] 采用MOPSO来优化配电网拓扑结构,结果表明MOPSO的引入能够有效提高可靠性,降低功率损耗和计算时间. ...
A transfer learning approach on the optimization of edge detectors for medical images using particle swarm optimization
1
2021
... 边缘检测作为一项基本的图像分析任务,存在边缘断开、无法检测分支边缘的特殊情况. 针对这些复杂的边缘检测任务,Dumitru等[83 ] 将迁移学习和MOPSO结合用于边缘检测. 批量优化可以有效提高边缘检测质量,可广泛应用于医学图像处理中的结构识别. ...
Automatic initialization for active contour models based on particle swarm optimization and application to medical images
1
2021
... 图像处理中的轮廓分割易受背景复杂程度、图像轮廓和初始位置等的影响. 最新的粒子群轮廓搜索算法PSCS[84 ] 可以有效解决这一难题,首先在图像上应用平滑滤镜以消除高强度噪声,其次通过该算法找到物体边界周围的主导点,采用其生成的点计算物体的中心位置和半径,初始化轮廓. MOPSO的引入使得PSCS的初始化更加快速,在复杂背景的环境下,可以成功分割图像中的期望对象. ...
岷江中游梯级闸坝联合优化调度研究
1
2021
... 在水环境研究中主要以水质和运行费用为调度目标,在应急调度研究中,主要以水动力指标为评估闸坝调度效果的主要优化目标. 井向阳等[85 ] 以闸坝系统的供水保证率最大和下泄水量最少为优化目标,构建岷江中游梯级闸坝联合调度2目标优化模型,并使用MOPSO算法求解,其结果同样显示了智能优化算法良好的收敛稳定性. 但是目前调度优化研究还存在诸多局限性. ...
岷江中游梯级闸坝联合优化调度研究
1
2021
... 在水环境研究中主要以水质和运行费用为调度目标,在应急调度研究中,主要以水动力指标为评估闸坝调度效果的主要优化目标. 井向阳等[85 ] 以闸坝系统的供水保证率最大和下泄水量最少为优化目标,构建岷江中游梯级闸坝联合调度2目标优化模型,并使用MOPSO算法求解,其结果同样显示了智能优化算法良好的收敛稳定性. 但是目前调度优化研究还存在诸多局限性. ...