在工程领域内，许多结构在服役期间会不可避免地受到外部冲击载荷的作用^[1-3]，这将严重影响结构的稳定和安全性能，甚至引发重大工程事故. 为此，需要对工程结构进行健康监测，其关键是监测结构外部载荷及动力学响应^[4-6]. 实际上，由于结构复杂或现场安装条件的限制，无法获得较完备的测量数据，并且外部冲击载荷具有稀疏性^[7]，往往难以直接精确测量. 重构冲击载荷及未安装或无法安装传感器位置处的响应具有重要意义^[8-10].

目前，结构响应重构技术主要有以下3类方法：模态分析类方法^[11-13]、传递矩阵类方法^[14-16]及滤波类方法^[17-19]. 其中，传递矩阵类和滤波类方法是目前应用最广泛的响应重构方法. Ribeiro等^[14]最先给出传递率矩阵的概念. Law等^[15]提出基于频域广义传递率的结构响应重构方法，通过7层平面框架验证了方法的精度. 毛羚等^[16]结合响应重构和遗传算法进行结构损伤识别，利用少数测量响应重构了目标位置响应. 此外，卡尔曼滤波(Kalman filter, KF)算法能够考虑结构系统和测量中的不确定性. 张笑华等^[17]基于KF提出结构多类型响应重构的方法，对不同类型传感器的位置进行优化，用于响应重构. Zhang等^[18]提出用于结构响应优化重构的KF自适应模态选择方法. KF能够取得最优估计，但忽略了工程中常见的有色噪声，难以保证重构结果的可靠性. 粒子滤波(particle filter, PF)算法能够弥补这一空缺，史鹏程等^[19]提出2步结构响应重构方法，在一步重构基础上引入PF方法，考虑了有色噪声的影响. 上述方法均需要在外部载荷已知的前提下重构，但外部冲击载荷往往难以直接获得，在工程应用中综合考虑外载荷识别与响应重构显得十分重要. 目前，针对载荷识别的正则化方法主要有L2正则化^[20]和L1正则化^[21]. 前者即Tikhonov正则化，根据最小化原理识别冲击载荷，能够满足光滑度要求，但正则化参数选取困难且L2解通常是非稀疏的，在载荷的非加载区域振荡较大. L1正则化能够保留解的稀疏特征，但光滑度较差，且噪声较大时会降低识别结果的稳定性，甚至造成识别错误.

针对上述问题，本文采用单类型传感器及小样本的测量信息，提出基于修正-联合正则化的冲击载荷识别与结构响应重构方法，旨在克服响应重构中冲击载荷的识别振荡、光滑度较差及识别精度易受噪声干扰等问题. 推导结构冲击载荷及动态响应的重构方程. 探究新型的修正-联合正则化方法并用于冲击载荷的求解，以提高冲击载荷峰值的识别精度与非加载区域识别结果的稳定性. 利用传递矩阵法和PF算法重构结构动态响应，通过某动车轮对数值算例和外伸梁试验验证了所提方法的有效性.

结构在外部载荷作用下的运动方程可以表示为

(1)$ {\boldsymbol{M}}\ddot {\boldsymbol{x}}(t)+{\boldsymbol{C}}\dot {\boldsymbol{x}}(t)+{\boldsymbol{Kx}}(t) = {\boldsymbol{f}}(t) . $

式中：M、C、K分别为质量、阻尼和刚度矩阵，$ \ddot {\boldsymbol{x}}(t) $、$ \dot {\boldsymbol{x}}(t) $和$ {\boldsymbol{x}}(t) $分别为加速度、速度和位移响应，$ {\boldsymbol{f}}(t) $为外部载荷向量. 假设结构阻尼是质量矩阵和刚度矩阵的组合，即瑞利阻尼模型，表示为

(2)$ {\boldsymbol{C}} = \alpha {\boldsymbol{M}}+\beta {\boldsymbol{K}} . $

式中：$ \alpha $、$ \beta $为瑞利阻尼比例系数，分别具有s⁻¹和s的量纲.

通过定义${\boldsymbol{z}}(t)$，将式(1)表示为连续时间的状态空间形式^[16]：

(3)$ \dot {\boldsymbol{z}}(t) = {{\boldsymbol{A}}_{\text{c}}}{\boldsymbol{z}}(t)+{{\boldsymbol{B}}_{\text{c}}}{\boldsymbol{f}}(t). $

式中：

$\begin{split} {{\boldsymbol{A}}_{\text{c}}} = &\left[ {\begin{array}{*{20}{c}} {\boldsymbol{0}}&{\boldsymbol{I}} \\ { - {{\boldsymbol{M}}^{ - 1}}{\boldsymbol{K}}}&{ - {{\boldsymbol{M}}^{ - 1}}{\boldsymbol{C}}} \end{array}} \right]\text{，}{{\boldsymbol{B}}_{\text{c}}} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{0}} \\ {{{\boldsymbol{M}}^{ - 1}}} \end{array}} \right]\text{，}\\{\boldsymbol{z}(t)} =& \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{x}}(t)} \\ {\dot {\boldsymbol{x}}(t)} \end{array}} \right]， \end{split}$

下标c表示连续时间系统. 输出响应为

(4)$ {\boldsymbol{y}}(t) = {{\boldsymbol{C}}_{{\text{ac}}}}\ddot {\boldsymbol{x}}(t)+{{\boldsymbol{C}}_{{\text{ve}}}}\dot {\boldsymbol{x}}(t)+{{\boldsymbol{C}}_{{\text{di}}}}{\boldsymbol{x}}(t). $

式中：${{\boldsymbol{C}}_{{\text{ac}}}}$、${{\boldsymbol{C}}_{{\text{ve}}}}$和${{\boldsymbol{C}}_{{\text{di}}}}$分别为加速度、速度和位移的映射矩阵，与输出数据类型相关.

根据式(1)、(4)，可得

(5)$ {\boldsymbol{y}}(t) = {{\boldsymbol{C}}_{\text{c}}}{\boldsymbol{z}}(t)+{{\boldsymbol{D}}_{\text{c}}}{\boldsymbol{f}}(t) . $

式中：$ {{\boldsymbol{C}}_{\text{c}}} = [\begin{array}{*{20}{c}} {{{\boldsymbol{C}}_{{\text{di}}}} - {{\boldsymbol{C}}_{{\text{ac}}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{K}}}&{{{\boldsymbol{C}}_{{\text{ve}}}} - {{\boldsymbol{C}}_{{\text{ac}}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{C}}} \end{array}] $，$ {{\boldsymbol{D}}_{\text{c}}} = {{\boldsymbol{C}}_{{\text{ac}}}}{{\boldsymbol{M}}^{ - 1}} $. 将式(3)、(5)转换为离散时间模型：

(6)$ \left. {\begin{array}{*{20}{l}} {\boldsymbol{z}(k+1) = {{\boldsymbol{A}}_{\text{d}}}{\boldsymbol{z}}(k)+{{\boldsymbol{B}}_{\text{d}}}{\boldsymbol{f}}(k)}, \\ {{\boldsymbol{y}}(k) = {{\boldsymbol{C}}_{\text{d}}}{\boldsymbol{z}}(k)+{{\boldsymbol{D}}_{\text{d}}}{\boldsymbol{f}}(k)} . \end{array}} \right\} $

式中：${\boldsymbol{f}}(k)$、${\boldsymbol{y}}(k)$和${\boldsymbol{z}}(k)$分别为离散后的外载荷向量、观测向量和状态向量；k为观测时刻，$k = 0,1, \cdots ,N$；下标d表示离散时间系统；${{\boldsymbol{A}}_{\text{d}}}$和${{\boldsymbol{B}}_{\text{d}}}$分别为离散后状态矩阵和外载荷输入矩阵；${{\boldsymbol{C}}_{\text{d}}}$和${{\boldsymbol{D}}_{\text{d}}}$分别为离散后输出矩阵和直接传输矩阵.

将状态向量代入观测向量，可得

(7)$ \begin{split} {\boldsymbol{y}}(k) =& {{\boldsymbol{C}}_{\text{d}}}{\boldsymbol{A}}_{\text{d}}^k{\boldsymbol{z}}(0)+{{\boldsymbol{C}}_{\text{d}}}{\boldsymbol{A}}_{\text{d}}^{k - 1}{{\boldsymbol{B}}_{\text{d}}}{\boldsymbol{f}}(0)+{{\boldsymbol{C}}_{\text{d}}}{\boldsymbol{A}}_{\text{d}}^{k - 2}{{\boldsymbol{B}}_{\text{d}}}{\boldsymbol{f}}(1) + \\ &\cdots +{{\boldsymbol{C}}_{\text{d}}}{{\boldsymbol{B}}_{\text{d}}}{\boldsymbol{f}}(k - 1)+{{\boldsymbol{D}}_{\text{d}}}{\boldsymbol{f}}(k). \end{split}$

假设初始条件${{\boldsymbol{z}}}(0) = {\boldsymbol{0}}$，${\boldsymbol{f}}(0) = {\boldsymbol{0}}$，式(7)简化为

(8)$ {\boldsymbol{Y}} = {\boldsymbol{Hf}}. $

式中：$\boldsymbol{f} $为外载荷，${\boldsymbol{f}} = {\left[ {{\boldsymbol{f}}(1){\text{ , }}{\boldsymbol{f}}(2){\text{ , }} \cdots {\text{ , }}{\boldsymbol{f}}(N)} \right]^{\text{T}}}$；Y为响应，$ {\boldsymbol{Y}} = {\left[ {{\boldsymbol{y}}(1){\text{ , }}{\boldsymbol{y}}(2){\text{ , }} \cdots {\text{ , }}{\boldsymbol{y}}(N)} \right]^{\text{T}}} $；H为传递矩阵，

(9)$ {\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{D}}_{\text{d}}}}&{\boldsymbol{0}}& \cdots &{\boldsymbol{0}} \\ {{{\boldsymbol{C}}_{\text{d}}}{{\boldsymbol{B}}_{\text{d}}}}&{{{\boldsymbol{D}}_{\text{d}}}}& \cdots &{\boldsymbol{0}} \\ \vdots & \vdots & & \vdots\\ {{{\boldsymbol{C}}_{\text{d}}}{\boldsymbol{A}}_{\text{d}}^{N - 2}{{\boldsymbol{B}}_{\text{d}}}}&{{{\boldsymbol{C}}_{\text{d}}}{\boldsymbol{A}}_{\text{d}}^{N - 3}{{\boldsymbol{B}}_{\text{d}}}}& \cdots &{{{\boldsymbol{D}}_{\text{d}}}} \end{array}} \right]. $

式(8)为响应传递方程. 测量位置的响应传递方程可以表示为

(10)$ {{\boldsymbol{Y}}_{\text{m}}} = {{\boldsymbol{H}}_{\text{m}}}{\boldsymbol{f}}. $

式中：${{\boldsymbol{Y}}_{\text{m}}}$和${{\boldsymbol{H}}_{\text{m}}}$分别为测量位置的响应和传递矩阵.

依据式(10)可得外载荷f的解，即载荷反演的数学模型，表示为

(11)$ {\boldsymbol{f}} = {\boldsymbol{H}}_{\text{m}}^+{{\boldsymbol{Y}}_{\text{m}}}. $

式中：${\boldsymbol{H}}_{\text{m}}^+$为伪逆. 借助测量位置处响应及式(11)，可以求得未知外部载荷f.

传递矩阵的结构响应重构方法^[16]的基本思想是通过建立测量位置处响应与待重构位置响应间的传递函数，重构目标位置处的动态响应. 响应重构方程可以表示为

(12)$ {{\boldsymbol{Y}}_{\text{r}}} = {{\boldsymbol{H}}_{\text{r}}}{\boldsymbol{f}}. $

式中：${{\boldsymbol{Y}}_{\text{r}}}$和${{\boldsymbol{H}}_{\text{r}}}$分别为结构待重构位置的响应和传递矩阵.

基于传递矩阵的结构响应重构方法可能会因为系统模型误差而导致重构精度大幅下降，PF算法能够很好地处理系统模型误差及有色噪声，因此引入PF方法进行结构响应重构.

基于PF算法类结构响应重构方法^[19,22]的核心思想是将系统状态的后验概率密度函数由含有权重的离散随机采样点表征，根据贝叶斯准则进行加权和递归，获取系统状态估计向量，将系统状态估计向量用于结构响应重构. PF算法的原理见文献[22]，本文不作赘述.

引入模态坐标q，通过$ {\boldsymbol{z}}(t) = {\boldsymbol{\varPhi q}}(t) $模态坐标变换，将结构的运动方程转换到模态坐标系下，具体表示为

(13)$ \ddot {\boldsymbol{q}}+2{\boldsymbol{\xi}} {{\boldsymbol{\omega}} _0}\dot {\boldsymbol{q}}+{\boldsymbol{\omega}} _0^2{\boldsymbol{q}} = {{\boldsymbol{\varPhi}} ^{\text{T}}}{\boldsymbol{Lu}} . $

式中：$ {\boldsymbol{\xi}} $为阻尼矩阵，$ {{\boldsymbol{\omega}} _{\text{0}}} $为模态频率矩阵，$ {\boldsymbol{\varPhi}} $为位移振型矩阵，L为外部载荷的映射矩阵，u为模态坐标系下的外部载荷向量.

将式(13)转化为状态空间模型并离散化：

(14)$ \left. {\begin{array}{*{20}{l}} {{{\boldsymbol{z}}_{k+1}} = {\boldsymbol{A}}{{\boldsymbol{z}}_k}+{\boldsymbol{B}}{{\boldsymbol{u}}_k}+{{\boldsymbol{w}}_k}}, \\ {{{\boldsymbol{y}}_k}{\text{ }} = {\boldsymbol{C}}{{\boldsymbol{z}}_k}+{\boldsymbol{D}}{{\boldsymbol{u}}_k}+{{\boldsymbol{v}}_k}}. \end{array}} \right\} $

式中：${{\boldsymbol{u}}_k}$、${{\boldsymbol{y}}_k}$和${{\boldsymbol{z}}_k}$分别为离散后的外载荷向量、观测向量和状态向量；A、B分别为系统离散后的状态矩阵和外载荷输入矩阵；C、D分别为观测输出矩阵和直接传输矩阵；$ {{\boldsymbol{w}}_k} $为系统的过程噪声，以考虑模型不确定性所带来的误差；$ {{\boldsymbol{v}}_k} $为传感器的测量噪声. 各矩阵具体表示为

(15)$ \begin{aligned}& \boldsymbol{A}=\exp {({\boldsymbol{\delta }}\Delta t)}, \quad \boldsymbol{B}=\boldsymbol{\delta}^{-1}(\boldsymbol{A}-\boldsymbol{I})\left[\begin{array}{c}\mathbf{0} \\\boldsymbol{\varPhi}^{\mathrm{T}} \boldsymbol{L}\end{array}\right], \\& z_k=\left[\begin{array}{c}\boldsymbol{q}_k \\\dot{\boldsymbol{q}}_k\end{array}\right], \quad \boldsymbol{\delta}=\left[\begin{array}{cc}\boldsymbol{0} & \boldsymbol{I} \\ -{\boldsymbol{\omega}}_0^2 &-2 \boldsymbol{\xi} {\boldsymbol{\omega}}_0\end{array}\right] .\end{aligned}$

当观测类别为速度和加速度时，C和D为

(16)$\boldsymbol{C}=\left[\begin{array}{cc}\boldsymbol{0} & \boldsymbol{\varPhi} \\ -\boldsymbol{\varPhi} {\boldsymbol{\omega}}_0^2 & -2 \boldsymbol{\varPhi} {\boldsymbol{\xi \omega}}_0\end{array}\right], \quad \boldsymbol{D}=\left[\begin{array}{c}\boldsymbol{0} \\ \boldsymbol{\varPhi} \boldsymbol{\varPhi}^{\mathrm{T}} \boldsymbol{L}\end{array}\right]. $

结构待重构位置的响应重构方程为

(17)$ {{\boldsymbol{Y}}_{\text{r}}} = {{\boldsymbol{C}}_{\text{r}}}{{{{\boldsymbol{z}}}}_{{\text{PF}}}}+{{\boldsymbol{D}}_{\text{r}}}{\boldsymbol{u}} = {{\boldsymbol{C}}_{\text{r}}}{{\boldsymbol{z}}_{{\text{PF}}}}+{{\boldsymbol{D}}_{\text{r}}}{\boldsymbol{f}}. $

式中：${{\boldsymbol{Y}}_{\text{r}}}$为待重构位置的响应；$ {{\boldsymbol{C}}_{\text{r}}} $、$ {{\boldsymbol{D}}_{\text{r}}} $分别为矩阵C和D的子矩阵，分别表示待重构位置的观测输出矩阵和直接传输矩阵；${{\boldsymbol{z}}_{{\text{PF}}}}$为利用PF算法估计的系统状态向量.

载荷${\boldsymbol{f}} $ 的最小二乘解可写为

(18)$ {\boldsymbol{f}} = {({\boldsymbol{H}}_{\text{m}}^{{{\mathrm{T}}}}{{\boldsymbol{H}}_{{{\mathrm{m}}}}})^{ - 1}}{\boldsymbol{H}}{_{\mathrm{m}}^{\mathrm{T}}}{{\boldsymbol{Y}}_{\text{m}}} . $

式中：上标T表示共轭转置. 当$ {{\boldsymbol{H}}_{\text{m}}} $的奇异值趋于零或其条件数太大时，该问题属于不适定问题^[23]. 引入L2正则化(Tikhonov正则化)方法，获得稳定解. 实际测量响应含有噪声，定义该噪声引起的误差e为

(19)$ {\boldsymbol{e}} = {{\boldsymbol{Y}}_{\text{m}}} - {{{{\boldsymbol{H}}}}_{\text{m}}}{\boldsymbol{f}}. $

Tikhonov正则化方法可以描述为最优化问题：

(20)$ \min \left\{ {\left\| {\boldsymbol{e}} \right\|_2^2+\lambda \left\| {\boldsymbol{f}} \right\|_2^2} \right\} = \min \left\{ {\left\| {{{\boldsymbol{Y}}_{\text{m}}} - {{{{{{\boldsymbol{H}}}}}}_{\text{m}}}{\boldsymbol{f}}} \right\|_2^2+\lambda \left\| {\boldsymbol{f}} \right\|_2^2} \right\} . $

式中：$\lambda \gt 0$为正则化参数，${\left\| \cdot \right\|_2}$为L2范数. 为了使e最小，Tikhonov给出目标函数：

(21)$ \begin{split} J =&\left(\boldsymbol{e}^{\mathrm{T}} \boldsymbol{e}\right)+\lambda\left(\boldsymbol{f}^{\mathrm{T}} \boldsymbol{f}\right) =\\&\left(\boldsymbol{Y}_{\mathrm{m}}-\boldsymbol{H}_{\mathrm{m}} \boldsymbol{f}\right)^{\mathrm{T}}\left(\boldsymbol{Y}_{\mathrm{m}}-\boldsymbol{H}_{\mathrm{m}} \boldsymbol{f}\right)+\lambda\left(\boldsymbol{f}^{\mathrm{T}} \boldsymbol{f}\right) .\end{split} $

从式（21）可以看出，正则化方法本质上是带有惩罚项或约束项的最小二乘方法^[24]. 以载荷f为自变量对函数J求导，并令${{{\text{d}}J}}/{{{\text{d}}{\boldsymbol{f}}}} = {\boldsymbol{0}}$，可得e最小所对应的外载荷，表示为

(22)$ {{\boldsymbol{f}}_{{\text{L2}}}} = {({\boldsymbol{H}}_{\text{m}}^{\text{T}}{{\boldsymbol{H}}_{\text{m}}}+\lambda {\boldsymbol{I}})^{ - 1}}{\boldsymbol{H}}_{\text{m}}^{\text{T}}{{\boldsymbol{Y}}_{\text{m}}}. $

式中：I为单位矩阵，${{\boldsymbol{f}}_{{\text{L2}}}}$为Tikhonov正则化的载荷识别结果. 对${{\boldsymbol{H}}_{\text{m}}}$进行奇异值分解：

(23)$ {{\boldsymbol{H}}_{\text{m}}} = {\boldsymbol{U}}{\boldsymbol{\varSigma}} {{\boldsymbol{V}}^{\text{T}}} . $

式中：${{\boldsymbol{H}}_{\text{m}}}$为$p \times N$的矩阵，${\boldsymbol{U}} = [{{\boldsymbol{u}}_1},{{\boldsymbol{u}}_2}, \cdots ,{{\boldsymbol{u}}_p}]$和${\boldsymbol{V}} = [{{\boldsymbol{v}}_1},{{\boldsymbol{v}}_2}, \cdots ,{{\boldsymbol{v}}_N}]$分别为左、右奇异值矩阵；${\boldsymbol{\varSigma}} = {\text{diag}}\;\left[ {{\sigma _1},{\sigma _2}, \cdots ,{\sigma _N}} \right]$为奇异值矩阵，奇异值${\sigma _i}$越小，对应的${{\boldsymbol{u}}_i}$和${{\boldsymbol{v}}_i}$中元素正负符号的变化越多^[25].

基于奇异值分解的正则化解可以表示为

(24)$ {{\boldsymbol{f}}_{{\text{L2}}}} = \sum\limits_{i = 1}^N {\frac{{\sigma _i^2}}{{\sigma _i^2+{\lambda ^2}}}} \cdot \frac{{{\boldsymbol{u}}_i^{\text{T}} {{\boldsymbol{Y}}_{\text{m}}}}}{{{\sigma _i}}}{{\boldsymbol{v}}_i} . $

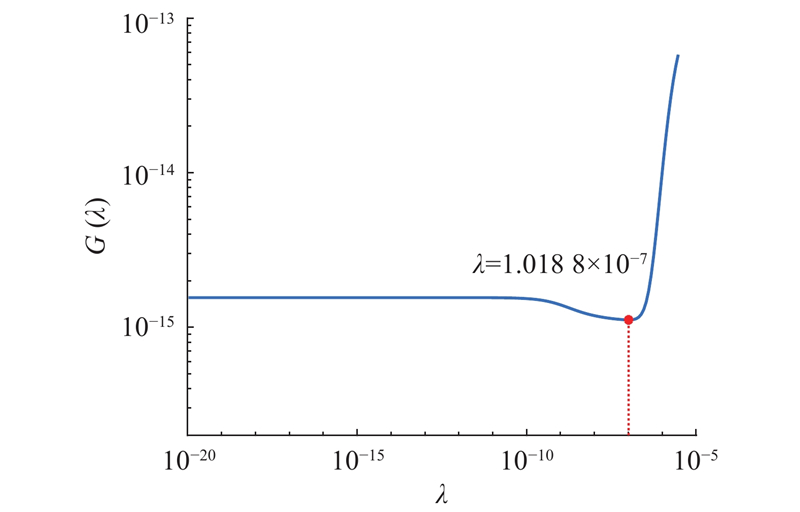
Tikhonov正则化能否有效求解反问题的关键在于正则化参数$\lambda $的选取，本文采用GCV(generalized cross-validation)准则确定正则化参数$\lambda $. GCV函数最小化所对应的$\lambda $为所选取的正则化参数. GCV函数的具体表达式^[26]为

(25)$ G = \frac{{\left\| {{{\boldsymbol{H}}_{\text{m}}}{{\boldsymbol{f}}_{{\text{reg}}}} - {{\boldsymbol{Y}}_{\text{m}}}} \right\|_2^2}}{{{{({\text{trace}}\;({\boldsymbol{I}} - {{\boldsymbol{H}}_{\text{m}}}{\boldsymbol{H}}_{\text{m}}^{{\text{reg}}}))}^2}}}. $

式中：trace为矩阵的迹，${\boldsymbol{H}}_{\text{m}}^{{\text{reg}}} = {({\boldsymbol{H}}_{\text{m}}^{\text{T}}{{\boldsymbol{H}}_{\text{m}}}+\lambda {\boldsymbol{I}})^{ - 1}}{\boldsymbol{H}}_{\text{m}}^{\text{T}}$，${{\boldsymbol{f}}_{{\text{reg}}}} = {\boldsymbol{H}}_{\text{m}}^{{\text{reg}}}{{\boldsymbol{Y}}_{\text{m}}}$.

为了充分考虑冲击载荷的稀疏性，建立L1正则化载荷识别模型^[27]. 对于稀疏正则化，基于无约束凸优化的系统模型可以表示为

(26)$ \min \left\{ {\left\| {{{\boldsymbol{Y}}_{\text{m}}} - {{{{\boldsymbol{H}}}}_{\text{m}}}{\boldsymbol{f}}} \right\|_2^2+\lambda {{\left\| {\boldsymbol{f}} \right\|}_1}} \right\}. $

式中：$\lambda \gt 0$为正则化参数.

L1正则化求解未知荷载，即凸优化问题的求解，可以采用梯度法^[28]、内点法^[29]和迭代阈值收缩算法^[30]等进行求解，本文采用常用的截断牛顿内点法求解. 稀疏正则化对正则化参数不敏感^[27]，正则化参数在$ \left[0.001{\lambda }_{\mathrm{max}}\text{ }，\text{ }0.1{\lambda }_{\mathrm{max}}\right] $内均可求得较准确的稀疏正则化解，本文参考文献[27]设置正则化参数$\lambda = 0.01{\lambda _{\max }}$，${\lambda _{\max }}$表示为

(27)$ {\lambda _{\max }} = {\left\| {{{{\boldsymbol{H}}}}_{\text{m}}^{\text{T}}{{\boldsymbol{Y}}_{\text{m}}}} \right\|_\infty }. $

当外部载荷类型为冲击载荷时，采用L2正则化方法能够保证加载区域载荷识别的光滑度，但会出现非加载区域的识别振荡问题，且振荡较明显. L1正则化方法保留了解的稀疏特征，但识别结果的光滑度较差且易受噪声干扰，在噪声较大时甚至难以识别.

为了提高载荷识别的精度，提出新型的修正-联合(updating-combination)正则化方法，即Luc正则化，用以冲击载荷的识别. 该方法基于传统L2与L1正则化，具体的计算过程可以归纳为“修正-联合”的步骤，即修正步与联合步. 先引入小波变换阈值法^[31]对测量数据进行降噪预处理，以获得降噪后的响应${{\boldsymbol{Y}}_{{\text{de}}}}$. 现有已知点测量响应${{\boldsymbol{Y}}_{\text{m}}}$、小波降噪后测量响应${{\boldsymbol{Y}}_{{\text{de}}}}$、L2正则化识别的载荷$ {{\boldsymbol{f}}_{{\text{L2}}}} $及L1正则化识别的载荷$ {{\boldsymbol{f}}_{{\text{L1}}}} $. 采用$ {{\boldsymbol{f}}_{{\text{L2}}}} $重构已知测量点处的响应：

(28)$ {{\boldsymbol{Y}}_{{\text{L2}}}} = {{\boldsymbol{H}}_{\text{m}}}{{\boldsymbol{f}}_{{\text{L2}}}} . $

式中：$ {{\boldsymbol{Y}}_{{\text{L2}}}} $为L2正则化识别结果计算的响应(下述简称L2识别计算响应). 计算${{\boldsymbol{Y}}_{{\text{de}}}}$与$ {{\boldsymbol{Y}}_{{\text{L2}}}} $的差值$ {{\boldsymbol{Y}}_{\text{e}}} $：

(29)$ {{\boldsymbol{Y}}_{\text{e}}} = {{\boldsymbol{Y}}_{{\text{de}}}} - {{\boldsymbol{Y}}_{{\text{L2}}}} = {{\boldsymbol{H}}_{\text{m}}}{{\boldsymbol{f}}_{\text{e}}} . $

式中：${{\boldsymbol{f}}_{\text{e}}}$为差值载荷.

${{\boldsymbol{f}}_{\text{e}}}$的求解可以表示为

(30)$ {{\boldsymbol{f}}_{\text{e}}} = {\boldsymbol{H}}_{\text{m}}^+{{\boldsymbol{Y}}_{\text{e}}}. $

差值载荷较小不需要考虑振荡问题，仅满足其光滑性即可，故采用L2正则化方法求解${{\boldsymbol{f}}_{\text{e}}}$. 一步修正载荷可以表示为

(31)$ {{\boldsymbol{f}}_{{\text{Lu}}}} = {{\boldsymbol{f}}_{{\text{L2}}}} \pm {{\boldsymbol{f}}_{\text{e}}}. $

式中：$ {{\boldsymbol{f}}_{{\text{Lu}}}} $为修正后的冲击载荷. 引入a、b判断式（31）的符号，表示为

(32)$ a={\displaystyle \sum\limits_{k = 1}^N {{{f}}}_{\text{e}}}(k)\text{ }\text{，}{b}^{j}={\displaystyle \sum \left(\left|{{{Y}}}_{\text{de}}^{j}\right|-\left|{{{Y}}}_{\text{L2}}^{j}\right|\right)} . $

式中：a为各时刻差值载荷之和；k为观测时刻，$k = {1, 2,\cdots ,N} $；$ {b^j} $为测量位置j处的绝对值响应差值之和；$ {{Y}}_{{\text{de}}}^j $为去噪后测量位置j处的响应；$ {{Y}}_{{\text{L2}}}^j $为测量位置j处的L2识别计算响应；上标$j $表示可测量位置，可测量位置共有n个.

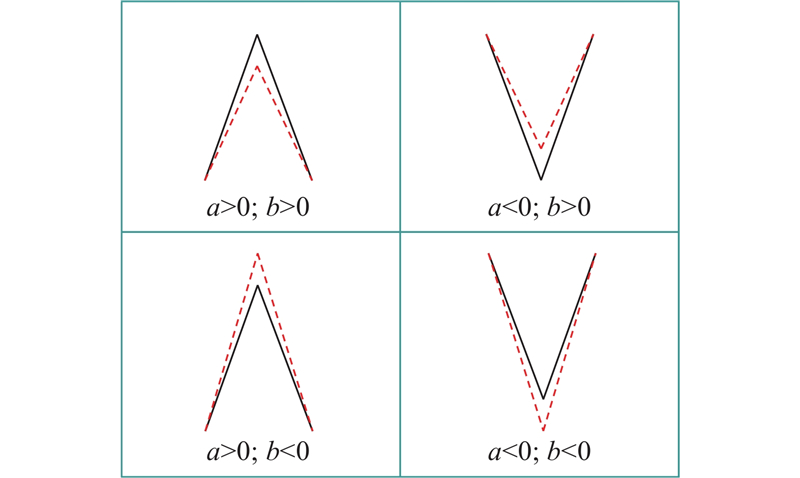
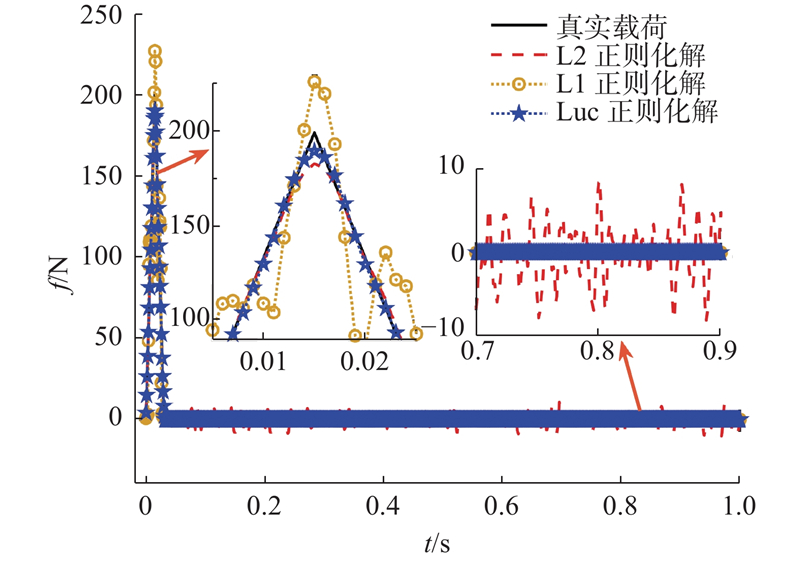
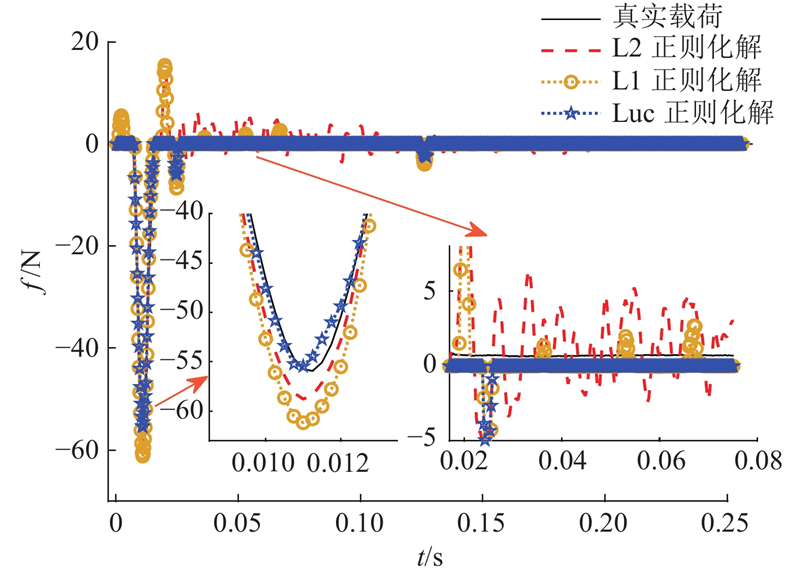
载荷的具体识别情况如图1所示. 图中，实线为理论真实载荷，虚线为L2正则化识别载荷，分别有以下4种识别情况. $ a \gt 0 $表示载荷方向为正，反之则为负. 当多数$b \gt 0$时，说明L2正则化方法所识别的载荷偏小，则式(31)取正号，故一步修正载荷为$ {{\boldsymbol{f}}_{{\text{Lu}}}} = {{\boldsymbol{f}}_{{\text{L2}}}}+{{\boldsymbol{f}}_{\text{e}}} $，反之则取负号.

目前已完成载荷的修正步工作，可以满足冲击载荷峰值的识别，但是非加载区的载荷存在振荡情况，故引入载荷联合步. 在修正后载荷结果的基础上联合L1正则化方法，融入非加载区域识别稳定的优势，保留待重构载荷的稀疏特征. 采用式(33)、(34)求解最终的冲击载荷识别结果.

当冲击载荷方向为正，即$a \gt 0$时，

(33)$ {{{f}}_{{\text{Luc}}}}(k) = \left\{ {\begin{array}{*{20}{c}} 0,& {{{f}}_{{\text{L1}}}}(k) \lt {\text{const}}; \\ {{{f}}_{{\text{Lu}}}}(k),& {{{f}}_{{\text{L1}}}}(k) \geqslant {\text{const}} .\end{array}} \right. $

当冲击载荷方向为负，即$a \lt 0$时，

(34)$ {{{f}}_{{\text{Luc}}}}(k) = \left\{ {\begin{array}{*{20}{c}} 0,& {{{f}}_{{\text{L1}}}}(k) \gt - {\text{const}}; \\ {{{f}}_{{\text{Lu}}}}(k),& {{{f}}_{{\text{L1}}}}(k) \leqslant - {\text{const}} .\end{array}} \right. $

式中：$ {{{f}}_{{\text{Luc}}}} (k)$为修正-联合冲击载荷，const为常数.

在联合步中，对L1正则化方法的载荷识别结果$ {\text{ }}{{{f}}_{{\text{L1}}}} (k) $进行判断，以设置的const常数为判断标准. 当冲击载荷方向为正时，若$ {\text{ }}{{{f}}_{{\text{L1}}}}(k) \geqslant $const，则说明此处为载荷加载区，令$ {{{f}}_{{\text{Luc}}}} (k)$为一步修正载荷$ {{{f}}_{{\text{Lu}}}}(k) $；若$ {\text{ }}{{{f}}_{{\text{L1}}}} (k)$<const，则说明此处为载荷非加载区，令$ {{{f}}_{{\text{Luc}}}}(k) $= 0. 同理，当冲击载荷方向为负时，可以依据是否为加载区进行判断. 通常依据常数const的取值判断是否为加载区，若$ {{{f}}_{{\text{L1}}}}(k) \ne 0 $则说明有载荷加载，若$ {{{f}}_{{\text{L1}}}}(k) = 0 $则说明无加载，但由于获得的数据含有一定的误差，可能导致L1正则化方法所识别的非加载区载荷有偏差，影响常数const的取值. 具体的const取值需要以真实载荷及L1正则化方法非加载区域的识别载荷为依据进行选取，使其尽可能避免非加载区域的波动. 不同载荷和噪声水平下的const取值不同，当噪声较小时，0 < const < 1.0；当噪声增大时，为了减小载荷振荡，const的取值可以适当增加.

具体来说，Luc正则化方法如下. 对传统L2正则化解进行修正，联合L1正则化解的稀疏性优势，使其能够在满足冲击载荷识别结果光滑度的基础上，提高冲击载荷的识别精度与鲁棒性，保证冲击载荷非加载区域识别结果趋于稳定.

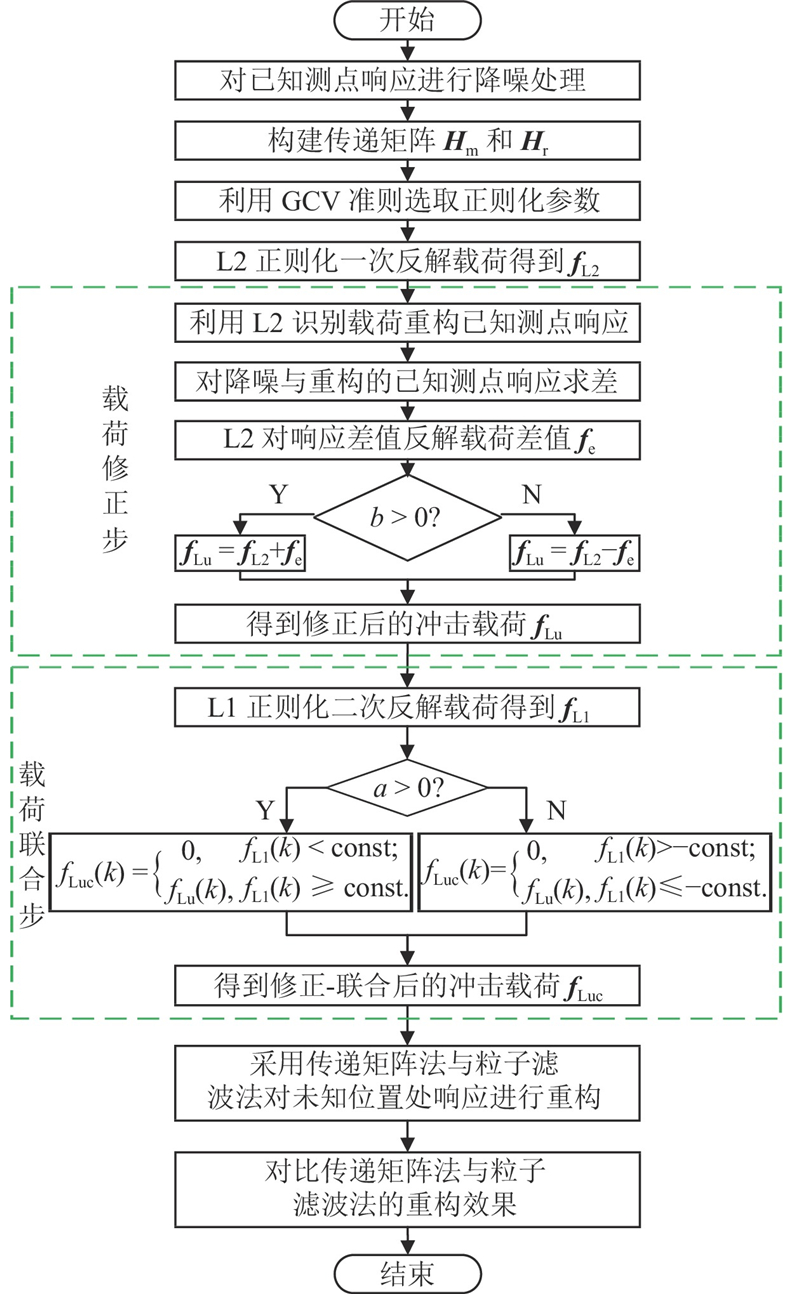
基于修正-联合正则化方法的冲击载荷识别与结构响应重构方法的具体流程如图2所示. 在获得结构测量响应后，引入小波变换阈值法对测量响应进行降噪处理. 构建测量位置处的传递矩阵H_m及待重构位置处的传递矩阵H_r. 利用去噪后响应、传递矩阵及提出的Luc正则化方法，对结构外部的冲击载荷进行识别，具体的Luc正则化方法分为“载荷修正”与“载荷联合”2个步骤. 利用Luc冲击载荷识别结果，结合传递矩阵法与PF算法，分别对待重构位置处的动态响应进行计算，对比2种方法的重构效果.

利用传递矩阵法计算待重构响应，可以表示为

(35)$ {{\boldsymbol{Y}}_{{\mathrm{rc}}}} = {{\boldsymbol{H}}_{\mathrm{r}}}{{\boldsymbol{f}}_{{\mathrm{Luc}}}}. $

式中：${{\boldsymbol{Y}}_{{\text{rc}}}}$为传递矩阵重构结果.

利用PF算法计算待重构响应，可以表示为

(36)$ {{\boldsymbol{Y}}_{{\text{rp}}}} = {{\boldsymbol{C}}_{\text{r}}}{{\boldsymbol{z}}_{{\text{PF}}}}+{{\boldsymbol{D}}_{\text{r}}}{{\boldsymbol{f}}_{{\text{Luc}}}}. $

式中：${{\boldsymbol{Y}}_{{\text{rp}}}}$为粒子滤波重构结果.

评估载荷误差的指标为

(37)$ {\text{RP}}{{\text{E}}_{\boldsymbol{f}}} = \frac{{\left\| {{{\boldsymbol{f}}^{{\text{re}}}} - {{\boldsymbol{f}}^{{\text{true}}}}} \right\|}}{{\left\| {{{\boldsymbol{f}}^{{\text{true}}}}} \right\|}} \times 100 {\text{%}}{\text{.}} $

式中：${{\boldsymbol{f}}^{{\text{re}}}}$为外载荷识别结果，${{\boldsymbol{f}}^{{\text{true}}}}$为真实载荷.

评估响应误差的指标为

(38)$ {\text{RP}}{{\text{E}}_{\boldsymbol{Y}}} = \frac{{\left\| {{{\boldsymbol{Y}}^{{\text{re}}}} - {{\boldsymbol{Y}}^{{\text{true}}}}} \right\|}}{{\left\| {{{\boldsymbol{Y}}^{{\text{true}}}}} \right\|}} \times 100\text{%} . $

式中：${{\boldsymbol{Y}}^{{\text{re}}}}$为重构响应，${{\boldsymbol{Y}}^{{\text{true}}}}$为真实响应.

高速列车轮对作为列车的关键部件，其动力学特性直接关系到列车的行车稳定与安全，对其重要位置的响应进行重构显得尤为重要. 以CRH2型动车组非动力轮对为研究对象，模拟整个响应的重构流程，轮对的有限元模型如图3所示. 车轮密度为8500 kg/m³，弹性模量为212 GPa，泊松比为0.264. 车轴密度为7 850 kg/m³，弹性模量为206 GPa，泊松比为0.281. 由于轨道线路及复杂运行工况极易对轮对产生冲击载荷^[32]，在轮对踏面处模拟施加列车所承受的冲击载荷.

轴颈用来安装滚动轴承，承担车辆质量，并传递各个方向上的静、动载荷，轴颈的动态响应对轮对动力学分析十分重要. 利用A、B和C节点的垂向加速度响应来识别冲击载荷f，重构轴颈上D和E节点处的垂向速度v_D和v_E、D和E节点处的加速度响应a_D、a_E. 在结构动力学领域，各阶模态响应按响应因子来表征其重要性，各阶模态的响应因子1/(2k−1)²随着阶数k的增大而减少^[33]，模态阶数越低，响应因子越大，该阶模态对于结构动力学信息越重要. 通常情况下，低阶模态包含结构的主要信息，反映结构的动力学行为. 工程上一般仅关心低阶模态，且通常选择4~8阶模态作为感兴趣模态. 将该轮对划分为31 778个节点、11 596个单元，开展模态分析，获取前8阶的弹性模态频率分别为89.22、102.84、103.02、167.88、168.64、274.97、308.03和309.29 Hz. 在响应数据中添加噪声，以模拟真实测量响应，具体表示为

(39)$ {{\boldsymbol{Y}}_{\text{m}}} = {{\boldsymbol{Y}}_{{\text{cal}}}}+\alpha \cdot {\text{std}}\; ({{\boldsymbol{Y}}_{{\text{cal}}}}) \cdot {{\boldsymbol{R}}_{{\text{noise}}}} . $

式中：$ {{\boldsymbol{Y}}_{\text{m}}} $为含噪的测量响应，$ {{\boldsymbol{Y}}_{{\text{cal}}}} $为计算响应，$ {{\boldsymbol{R}}_{{\text{noise}}}} $为正态随机噪声，$ {\text{std}}\; ( \cdot ) $为标准差，$ \alpha $为表示噪声水平的噪声因子.

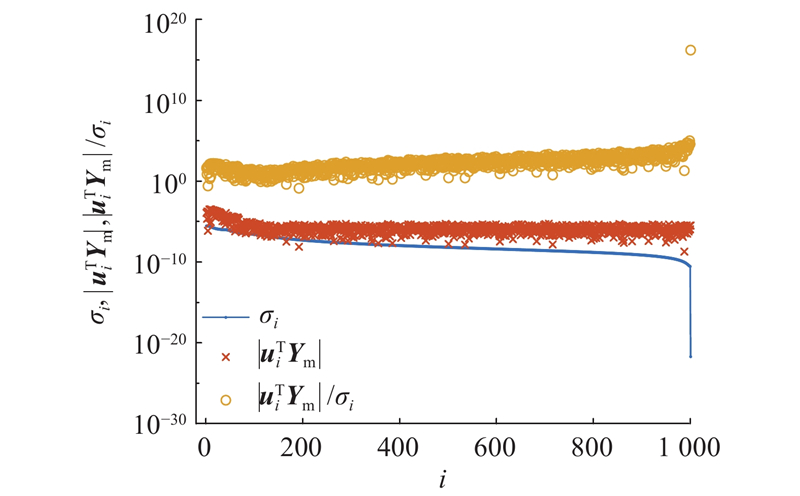
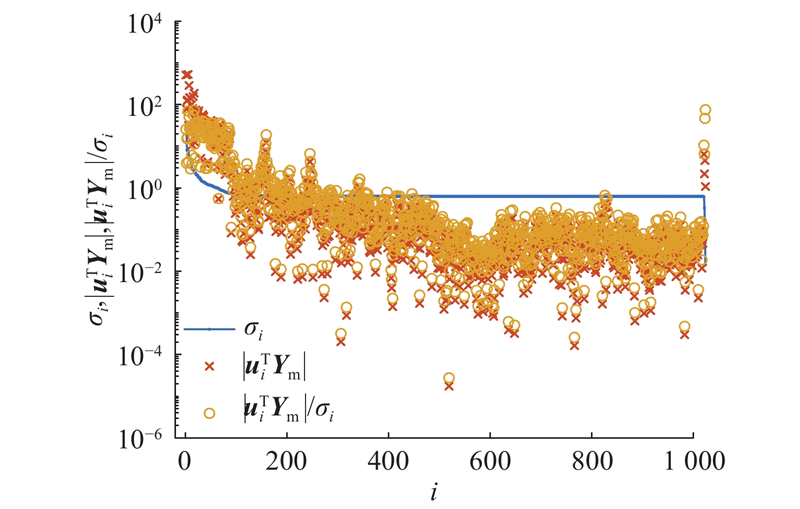
载荷识别问题是否适定，须引入Picard条件^[34]进行判断，即随着奇异值个数i的增加，系数$ \left| {{{\boldsymbol{u}}_i}^{\text{T}}{{\boldsymbol{Y}}_{\text{m}}}} \right| $的减小速度比奇异值$ {\sigma _i} $更快. 若满足Picard条件，则判定为适定问题，否则为不适定问题. 如图4所示为当噪声因子为0.10，即噪声水平为10%时测量响应的Picard图. 可以看出，该问题不满足Picard条件，即载荷识别问题为不适定问题. 求解不适定问题的普遍方法是将不适定问题替换为对扰动不太敏感的“附近”的适定问题^[34]，以与原不适定问题相“邻近”的适定问题的解去逼近原问题的解，称为正则化方法. 为了解决逆问题的不适定性，获得稳定解，引入该方法.

如图5所示为当噪声因子为0.10时测量响应的GCV函数图. 可知，正则化参数λ为1.02×10⁻⁷. 分别采用L2、L1和Luc正则化方法进行载荷识别，经反复试验，取const常数为0.5，识别结果如图6所示. 可以看出，利用L2正则化方法识别的载荷在峰值位置处精度不高，在非加载区振荡较大. 利用L1正则化方法识别的载荷在非加载区识别效果稳定，但不能保证冲击载荷识别的光滑性. 利用Luc正则化方法识别的载荷在峰值处和非加载区均能够较好地拟合真实载荷.

为了验证所提Luc正则化方法的有效性，计算3种方法冲击载荷的识别误差，L2、L1和Luc正则化的误差分别为17.69%、23.42%和3.23%. Luc正则化的误差明显小于其他2种正则化方法，表明本文方法能够获得较好的冲击载荷识别结果. 探究不同噪声等级下冲击载荷的识别情况，分别加入噪声因子为0.03、0.05、0.10及0.30的测量噪声. 不同噪声等级下3种冲击载荷识别方法独立运行10次，计算误差均值的结果如表1所示. 经反复试验确定，当噪声因子为0.03、0.05、0.10时const取0.5，当噪声因子为0.30时const取2. 由表1可以看出，Luc正则化方法对冲击载荷的识别精度更高，在不同等级噪声的干扰下，Luc正则化均能表现出良好的识别精度，表明所提方法具有较强的鲁棒性.

利用Luc正则化的冲击载荷结果，重构D和E节点响应，分别采用传递矩阵法与粒子滤波法进行重构. 如图7所示为10%的噪声干扰下，轮对轴颈D和E节点的真实响应与传递矩阵法重构响应的对比图. 图中，v_D、a_D分别为D节点的速度和加速度，v_E、a_E分别为E节点的速度和加速度. 从图7可以看出，速度和加速度的重构值都与结果的真实值具有良好的一致性.

为了对比L1、L2及Luc正则化获得的冲击载荷用于结构响应重构的差别，基于传递矩阵法分别对图3轮对轴颈D和E节点的响应进行重构，计算重构结果的误差，结果如图8所示. 可以看出，采用Luc正则化方法获得的重构精度最高，重构结果的误差明显小于其他2种正则化方法.

假设数值算例的模型准确，且加入的噪声为高斯白噪声，在重构过程中不考虑结构模型误差及有色噪声的影响. 基于粒子滤波法与传递矩阵法的重构误差如表2所示，误差均小于11%，而所提Luc正则化方法识别出的冲击载荷结果用于结构响应重构的误差明显小于其他2种正则化方法.

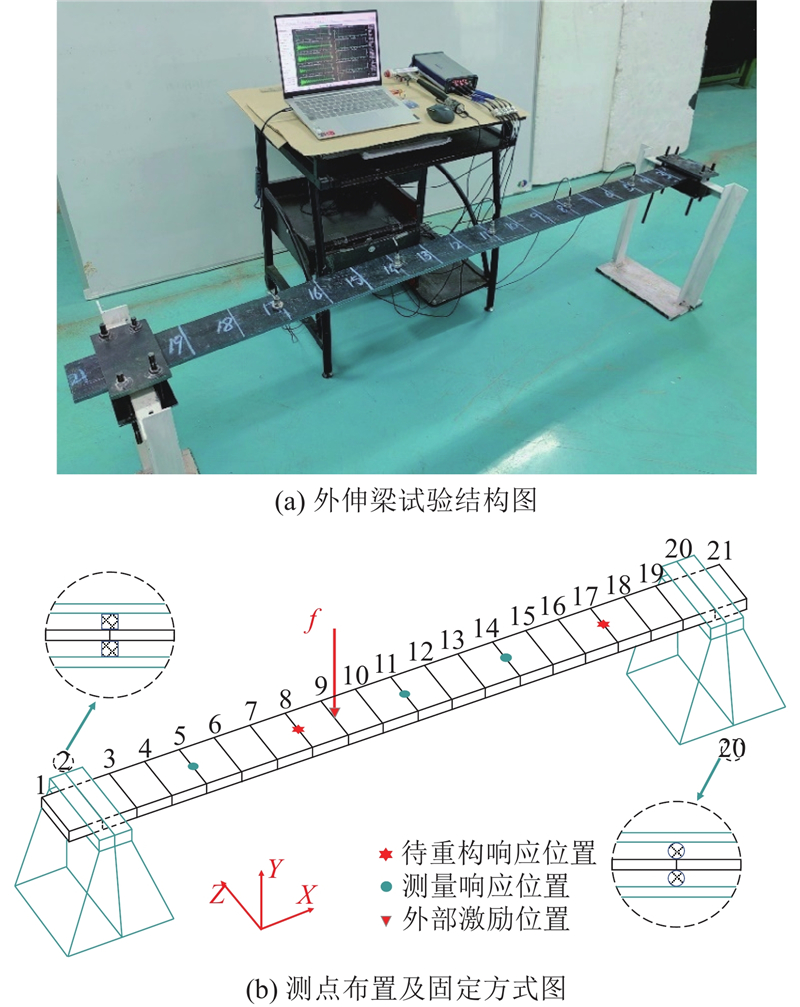
为了验证本文方法在工程实际中的可行性与适用性，根据结构力学，将数值算例中的高速列车轮对简化等效为两端都伸出支座的外伸梁. 搭建相应的外伸梁试验台，对所提方法进行试验验证. 外伸梁试验结构如图9(a)所示. 该外伸梁尺寸为2 000 mm×200 mm×10 mm，将其划分为20个单元、21个节点，只考虑Y方向的自由度，外伸梁第2节点为固定端，第20节点为简支端，具体的测点布置及固定方式如图9(b)所示. 在第9节点Y方向施加一锤击激励，测量第5、11和14节点的Y方向加速度信号，用于外部冲击载荷识别与第8、17节点Y方向加速度响应a₈、a₁₇的重构. 采集第8、17节点的Y方向加速度信号，与重构信号进行对比，验证所提方法的有效性.

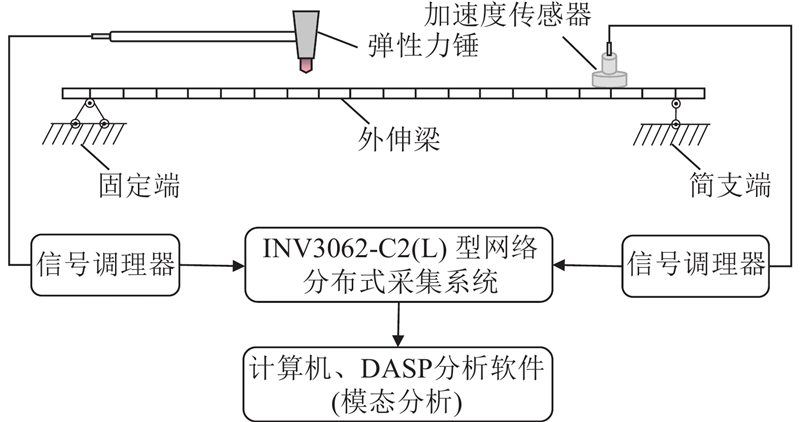
测试系统框架如图10所示，试验测得该外伸梁结构的前4阶模态频率分别为7.82、28.12 、60.86 和106.13 Hz. 经反复试验，外伸梁算例中参数const取0.4.

引入Picard条件判断问题的适定性，如图11所示为实测数据的Picard图. 可以看出，该问题不满足Picard条件，引入正则化方法处理. 如图12所示为测量响应的GCV函数图，正则化参数$ \lambda $为0.38.

分别采用L2正则化、L1正则化及本文的Luc正则化方法对外部冲击载荷进行识别，如图13所示为冲击载荷识别结果. 可以看出，与L2和L1正则化方法相比，本文的Luc正则化方法无论是在载荷峰值位置还是非加载区域位置，均能较好地吻合实测载荷.

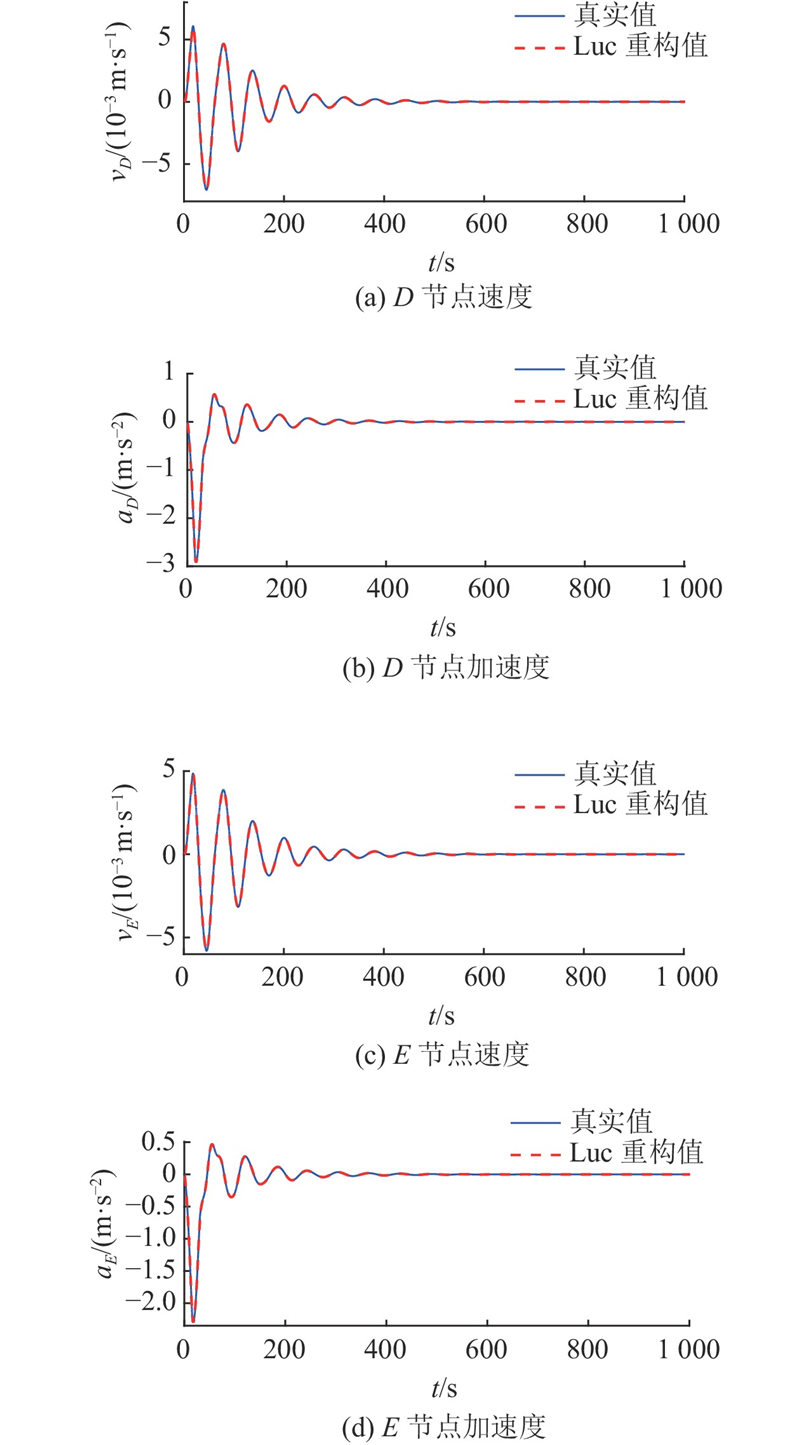
为了验证所提Luc正则化方法的有效性，计算并对比利用3种方法进行冲击载荷识别的误差. L2正则化的误差为31.72%，L1正则化的误差为24.55%，Luc正则化的误差为13.11%. 本文的Luc正则化方法用于载荷识别的误差更小，表明该方法对于冲击载荷的识别精度较高. 利用Luc正则化方法识别的冲击载荷，结合传递矩阵法、粒子滤波法重构外伸梁第8和第17节点响应，与测量响应进行对比. 时程拟合曲线如图14所示. 图中，a₈、a₁₇分别为第8、17节点的垂向加速度. 从图14可以看出，利用传递矩阵法和粒子滤波法重构的响应均能与结构真实响应保持良好的一致性，说明利用这2种方法都能描述结构动态响应的时间历程.

为了对比传递矩阵与PF算法下3种正则化方法用于响应重构的效果，分别对外伸梁的第8、17节点的加速度进行重构，重构响应与测量响应的误差如表3所示.

从表3可以看出，将Luc正则化引入基于传递矩阵的响应重构方法时，响应的重构精度较低. 原因是试验算例存在模型误差，即重构算法与试验系统采集算法间的机制差异，利用引入的PF算法，能够有效地降低结构模型误差及有色噪声的影响，较传递矩阵法具有更高的响应重构精度，但存在部分算法机制的差异. 在试验研究中有2种算法机制：一种是DASP软件内部的模态分析算法，用于获得结构的加速度响应；一种是结合模态试验与状态空间模型的算法，用于获得结构的理论加速度响应. 利用状态空间模型得到的加速度响应不能与实测加速度响应完全拟合，状态空间模型存在建模误差. 综上，模型误差与载荷识别精度共同影响最终的响应重构结果. 整体而言，存在模型误差时，采用Luc正则化与PF算法进行冲击载荷识别与结构响应重构，能够获得更高精度的冲击载荷识别结果与响应重构结果.

假设模型准确，在传递矩阵方法下将重构响应与理论真实响应进行对比，结果如表4所示. 由表4可以看出，Luc正则化重构响应的误差均小于L2正则化与L1正则化方法重构响应的误差. 在不考虑模型误差的情况下，响应重构精度与载荷识别精度正相关.

(1) 利用本文所提Luc正则化方法对Tikhonov正则化解进行修正，能够在满足载荷识别结果光滑的同时，提高冲击载荷峰值的识别精度. 引入L1正则化中一范数项的稀疏性优势，对修正解进行联合优化，保留了冲击载荷非加载区域的稀疏特征.

(2) 所提正则化方法在30%的噪声情况下，仍可以获得较好的冲击载荷识别结果，具有良好的抗噪性. 修正-联合正则化方法可以看作是2种传统正则化的推广和改进版本.

(3) 与传递矩阵法相比，粒子滤波算法能够考虑模型误差及算法间的不确定性，获得更高精度的重构响应.