既有研究主要针对有滑移组合梁受梁端弯矩、轴向拉压及均布荷载等作用下的界面和内力响应,而年温变化、太阳辐射或寒潮引起的温度变化为非荷载作用,会引起界面滑移和弯曲变形,在截面产生的温度应力不容忽视. 目前,刘永健等[2]总结了既有学者对组合梁桥温度梯度作用模式的研究,在现有的桥梁规范体系下,多数学者在计算组合梁的温度效应时均认为钢和混凝土完全连接,在温度作用下不产生滑移,且对组合梁桥温度效应的研究主要以有限元模拟为主. 采用理论解析方法计算组合梁温度效应,有利于从机理上认识温度对组合梁的作用规律,欧洲规范Eurocode-4[14]和周良等[15]给出不考虑界面滑移时的组合梁温度应力计算方法,吴迅等[16-19]考虑滑移,建立组合梁桥温度作用下界面滑移、剪力及截面应力的解析计算方法. 以上研究多假定组合梁为钢-混均匀温差或线性温差,与实际组合梁桥的温度分布相差较大. 笔者等[20]的研究表明,不考虑组合梁截面的非线性温差分布会使应力计算结果产生偏差,偏差随着非线性温差的增大而增大. 目前,有滑移组合梁温度效应解析解均基于简支梁提出,关于连续梁温度次生效应的求解是在假设无滑移基础上通过结构力学的方法得到的,这显然不够严谨. 此外,界面滑移组合梁仍缺乏温度和荷载共同作用下的统一解析模型.
本文基于欧拉伯努利梁理论,提出侧向非均布荷载、轴向拉(压)力、梁端弯矩和任意非线性温度分布等共同作用下有滑移组合梁的理论解析模型. 推导了简支和连续组合梁的挠度、界面剪力、滑移及截面应力计算的解析公式,开展了组合梁温度效应的算例分析,对温度作用引起的界面滑移和组合梁挠度进行讨论,为组合梁桥的设计计算提供参考.
1. 有滑移组合梁的挠度微分方程
1.1. 基本假定
1)将组合梁视为欧拉伯努利梁,即忽略剪切变形对总变形的影响.
2)桥面板与钢梁均为理想线弹性体,拉压模量相同.
3)混凝土桥面板与钢梁均服从平截面假定.
4)考虑混凝土桥面板与钢梁之间的界面滑移,滑移与界面切应力线性相关.
5)混凝土桥面板与钢梁间无掀起,曲率相同.
1.2. 挠度微分方程的建立
1.2.1. 挠度微分方程
图 1
图 2
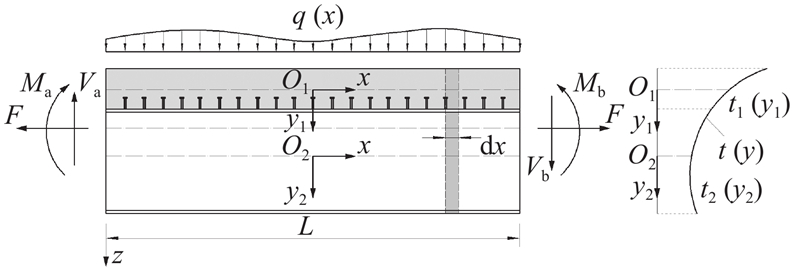
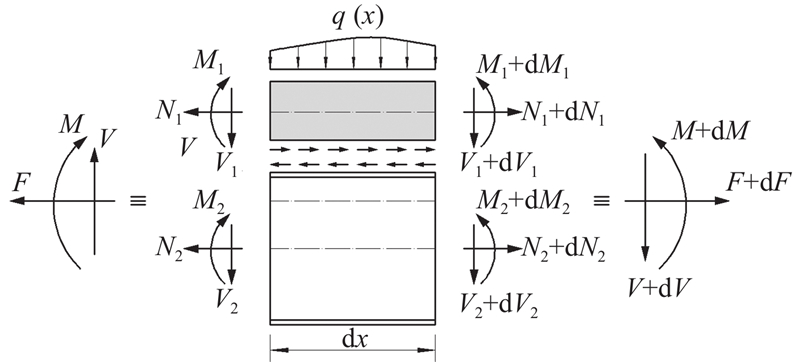
取组合梁dx微段为研究对象,考虑混凝土和钢梁之间相互作用的微段受力图,见图3,由整个微段平衡可知,
图 3
考虑组合梁截面的内力平衡条件,则
根据混凝土桥面板和钢梁局部平衡,则有
根据假定可知,界面剪力τ与界面滑移∆u成正比,
式中:Δu为钢梁和混凝土板之间的滑移;K为组合梁等效剪切滑移刚度,与界面剪力连接件的抗剪刚度和布置形式有关,若采用栓钉连接件,则按式(5)计算;d为相邻栓钉之间的间距;n为横向每排栓钉的个数;kss为栓钉连接件抗剪刚度,
其中dss为栓钉连接件杆部的直径,E1为混凝土的弹性模量,fck为混凝土抗压强度的标准值.
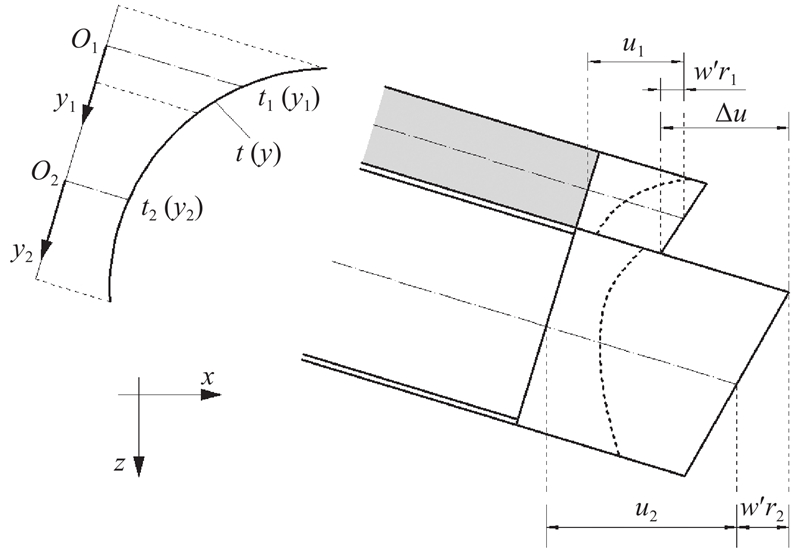
组合梁微段在多种荷载组合作用下发生变形,见图4. 根据变形协调条件,有
图 4
式中:u1、u2分别为混凝土桥面板和钢梁形心处沿x方向的变形,w为组合梁的挠度,w′和w″分别为组合梁的转角和曲率,
式中:
式中:E1和E2、I1和I2、A1和A2分别为混凝土和钢的弹性模量、各自形心处的惯性矩和面积;te1和te2分别为桥面板和钢梁截面的平均温度,
ty1和ty2分别为桥面板和钢梁截面的竖向线性温度梯度,
根据式(10)、(11),可得
将式(13)代入式(2),可得
式中:
将式(14)等式两边同时取梁长x的二阶导数,可得
将式(2)、(3)、(12)、(14)代入式(8),令
可得
式中:εm为组合梁完全无剪力连接时桥面板和钢梁平均温度te1和te2产生的应变差,εm=α1te1 −α2te2.
联立式(14)~(16),可得
式中:
根据式(18)可知,作用于组合梁上的外力荷载与温度作用对组合梁挠度的影响不耦合. 当计算外力及温度共同作用下组合梁桥的结构效应时,可以简化挠度微分方程,分别计算外力荷载和温度作用的效应,随后进行叠加.
1.2.2. 界面剪力、滑移与应力计算
通过求解挠度微分方程,得到挠度w沿组合梁梁长x方向的表达式. 根据式(18)、(14)、(3)和(4),可以推出均布荷载q与温度分布T(y)共同作用下弯矩M、桥面板轴力N1、界面剪力τ和滑移Δu的表达式如下:
根据式(9)可知,桥面板和钢梁的应力分布σ1(y1)和σ2(y2)分别为
求得N1后,则可知N2=F−N1,代入式(12)可得桥面板和钢梁形心处的应变
1.3. 挠度微分方程的求解
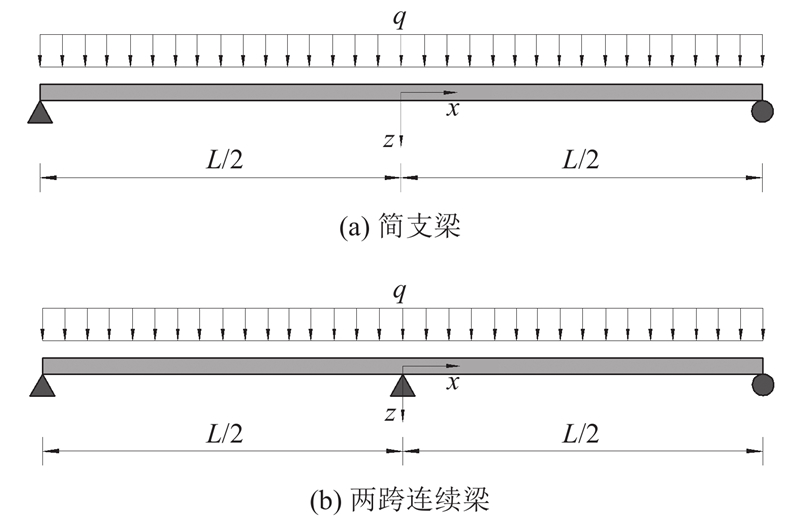
分别以一跨简支梁(静定梁)和两跨连续梁(超静定梁)为例,对均布荷载q和任意温度分布t(y)作用下的挠度方程进行求解. 简支梁以跨中为坐标原点,跨径为L,连续梁以中支点为坐标原点,总长度为L,单跨跨径为L/2,如图5所示.
图 5
1.3.1. 均布荷载下的解析解
当仅考虑均布荷载q时,取εm = 0,χt = 0,则组合梁的挠度微分方程为
式(24)等号右边M为梁长x的函数. 对式(24)两边同时取x的二次导数,可得
式(25)为关于挠度w的6阶常系数微分方程,其通解为
式中:C1~C6为待定常数.
对于对称荷载作用下的简支梁,两端支点处位移为零,跨中截面的转角为零,又由两端支点弯矩为零,即M(L/2)=M(−L/2)=0,两端支点界面剪力为零,即N1(L/2)=N1(−L/2)=0. 对于对称荷载作用下的两跨连续梁,根据对称性,仅对0 ≤ x ≤ L/2跨进行计算. 中支点和端支点位移为零,中支点截面转角为零;端支点弯矩为零,即M(L/2)=0,端支点界面剪力为零,即N1(L/2)=0,又有中支点的界面滑移为零. 结合式(14)、(24),可得边界条件如下.
进一步可以求解得到待定系数如下.
两跨连续梁:限于篇幅,不再给出.
1.3.2. 温度作用下的解析解
对于仅受温度分布T(y)作用的简支组合梁,取q=0,M=0,则挠度微分方程由式(18)变为
式(27)为关于挠度w的4阶常系数微分方程,令
式中:C7~C10为待定常数.
对于仅受温度分布t(y)作用的连续组合梁,结构会产生次弯矩,故M ≠ 0. 对式(18)两边同时取梁长x的二次导数,取q=0,M″=0,可得
式(32)的通解为
式中:C11~C16为待定系数.
简支梁两端支点处位移为零,跨中截面处转角为零;支点弯矩为零,支点界面剪力为零. 对于连续梁,当0 ≤ x ≤ L/2时,中支点和端支点位移为零,中支点截面转角为零;端支点弯矩为零,端支点界面剪力为零,且中支点的界面滑移为零. 结合式(14)、(27),可得边界条件如下.
进一步可以求解得到待定系数如下.
两跨连续梁:限于篇幅,不再给出.
2. 温度效应的求解方法
2.1. 温度作用的基本参数
由微分方程的建立和求解可知,在结构尺寸确定的情况下,组合梁温度产生的挠度与界面滑移仅由εm和χt决定,计算挠度与滑移时,应先计算这2个参数:
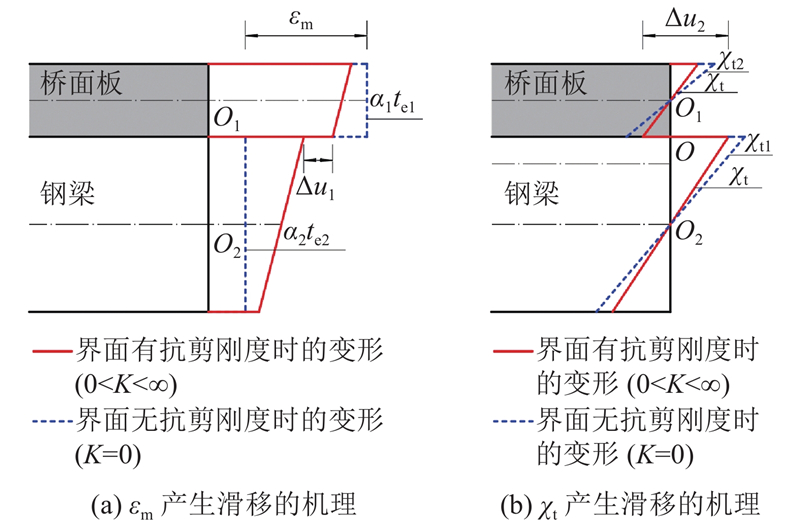
式中:εm1、εm2分别为界面完全自由时桥面板和钢梁在温度作用下形心的自由应变,εm1 = α1te1,εm2 = α2te2;χt1、χt2分别为界面完全自由时的温度作用引起的桥面板和钢梁的曲率,χt1 = α1ty1,χt2 = α2ty2. 可见,εm的本质为K=0时桥面板和钢梁的应变差,故定义为等效温度滑移应变,当0 < K < ∞时,产生界面滑移Δu1,见图6 (a). χt为χt1和χt2关于桥面板和钢梁各自抗弯刚度的加权平均数,即K=0时组合梁的曲率,故定义为等效温度曲率,当0<K<∞时,产生界面滑移Δu2,如图6 (b)所示. 组合梁在温度作用下产生的界面总滑移为Δu = Δu1+Δu2.
图 6
2.2. 温度作用分解方法
图 7
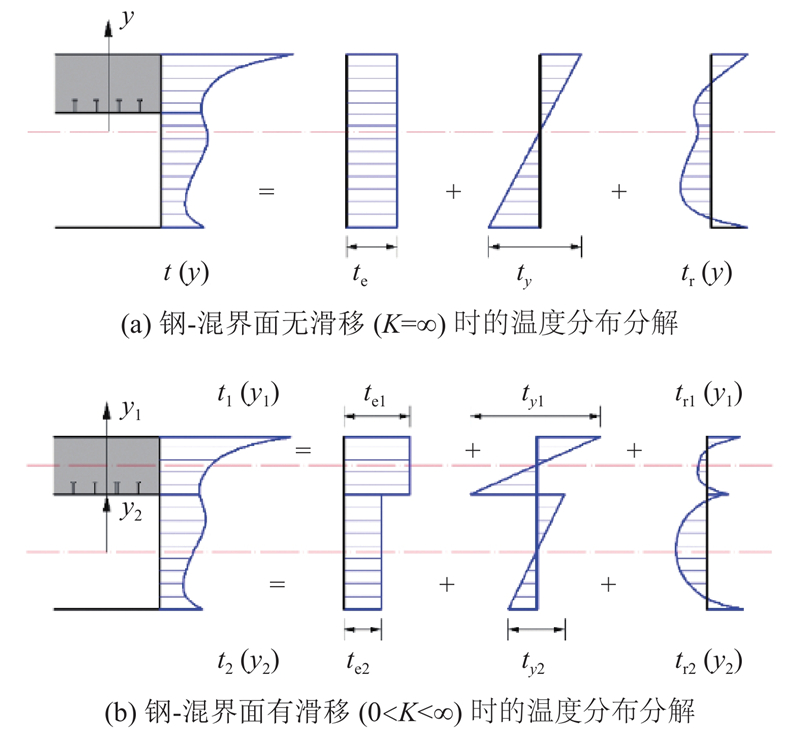
类似地,当认为界面存在滑移(0 < K < ∞)时,桥面板和钢梁应视为各自满足平截面假定且相互独立的2个部件,则组合梁的任意温度分布由桥面板的t1(y1)和钢梁的t2(y2)组成,可以分别分解为有效温度te1和te2、竖向线性温差ty1和ty2、残余温度分布tr1(y1)和tr2(y2),见图7 (b). 当K=0时,桥面板和钢梁的温度自应力完全由tr1(y1)和tr2(y2)引起;当0 < K < ∞时,桥面板和钢梁相互约束产生温度次应力,再叠加自应力即可得到有滑移静定组合梁的温度应力. 组合梁截面桥面板和钢梁相互约束产生的次生效应是计算的关键,可在求得te1、te2和ty1、ty2的基础上,按式(37)、(38)计算得到εm和χt,再进一步通过本文建立的微分方程计算.
3. 温度效应计算
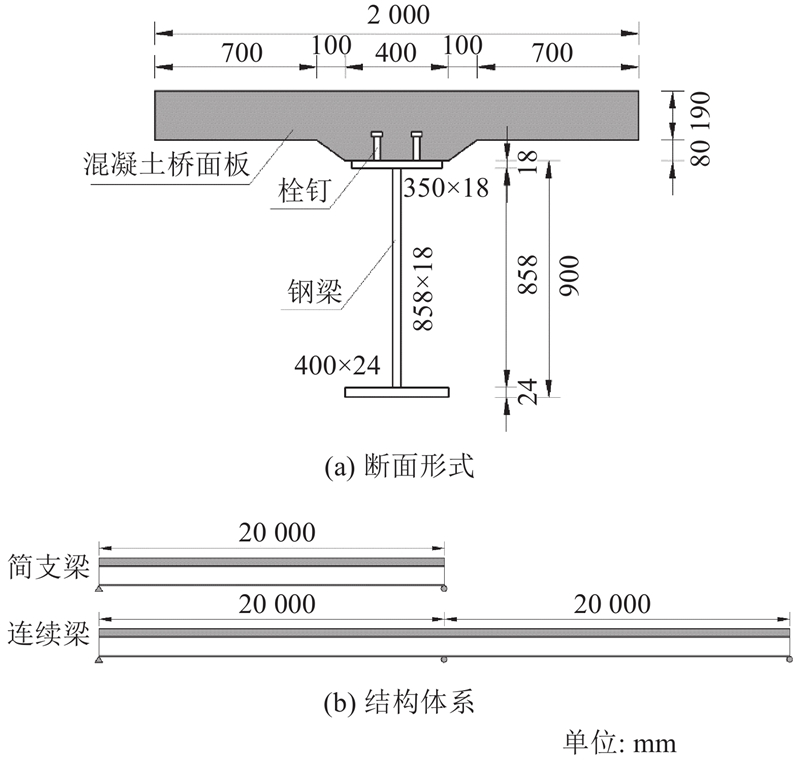
3.1. 计算模型与温度梯度模式
图 8
图 9
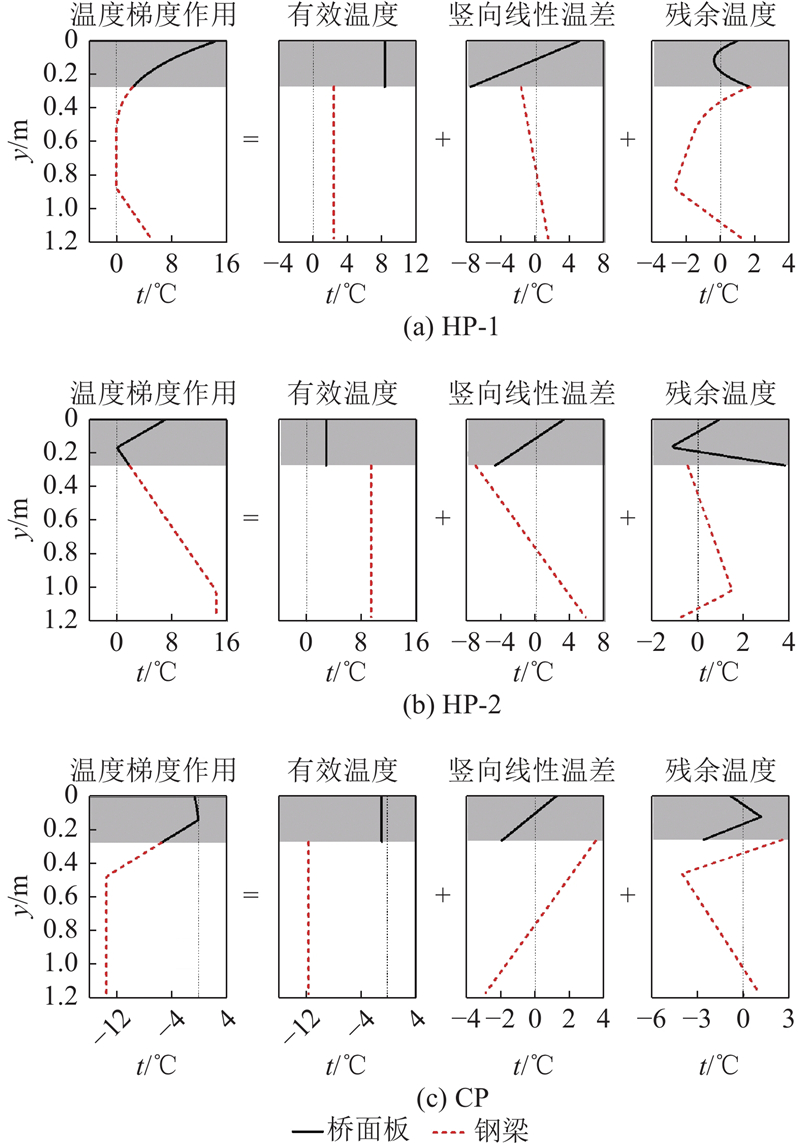
图 10
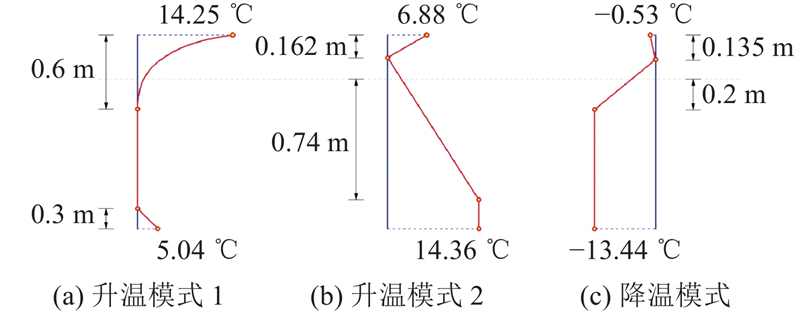
图 10 竖向温度梯度模式的分解
Fig.10 Decomposition of vertical temperature gradient pattern
表 1 温度参数εm和χt的取值
Tab.1
| 温度作用模式 | te1/℃ | te2/℃ | ty1/(℃·mm−1) | ty2/(℃·mm−1) | εm | χt / mm−1 |
| 升温模式1(HP-1) | 8.29 | 2.38 | −4.68×10−2 | 3.49×10−3 | 5.43×10−5 | 5.83×10−9 |
| 升温模式2(HP-2) | 2.79 | 9.34 | −2.95×10−2 | 1.43×10−2 | −8.41×10−5 | 1.39×10−7 |
| 降温模式(CP) | −0.18 | −11.52 | −1.21×10−2 | −7.17×10−3 | 1.30×10−4 | −8.86×10−8 |
3.2. 解析模型的验证
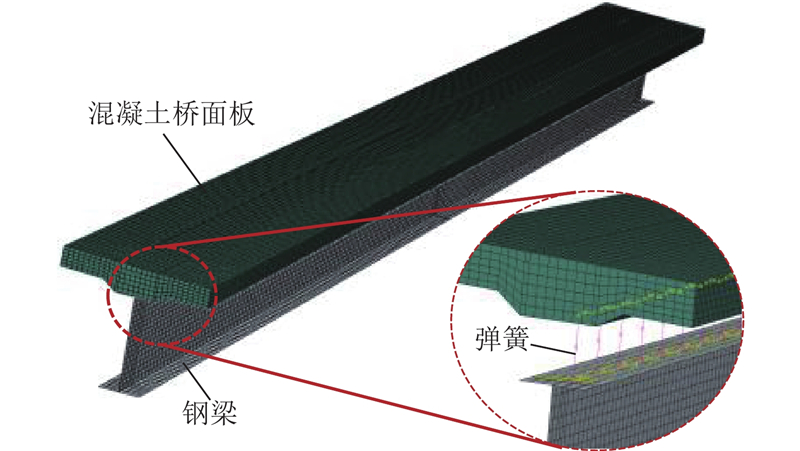
基于ABAQUS建立上述组合梁有限元模型(见图11),桥面板和钢梁分别采用C3D20R和S4R单元模拟. 栓钉模拟采用弹簧单元Spring 2,以设置界面剪切和竖向刚度. 其中,竖向刚度设置无穷大,保证钢梁和混凝土桥面板的曲率一致,根据栓钉布置,可得界面等效剪切滑移刚度K=5 008.4 N/mm2.
图 11
表 2 挠度和端部滑移的有限元解与解析解的对比(K = 5 000.8 N/mm2)
Tab.2
| 作用类型 | 计算结果 | 简支梁 | 2跨连续梁 | |||
| wmax/mm | Δu/mm | wmax/mm | Δu/mm | |||
| q=16 N/mm | 解析解 | 12.075 | 0.0317 | 2.121 | 0.0122 | |
| 有限元解 | 12.221 | 0.0322 | 2.221 | 0.0126 | ||
| HP-1 | 解析解 | −2.736 | 0.0331 | −0.875 | 0.0357 | |
| 有限元解 | −2.815 | 0.0345 | −0.923 | 0.0375 | ||
| HP-2 | 解析解 | 6.573 | 0.0482 | 0.671 | 0.0463 | |
| 有限元解 | 6.733 | 0.0498 | 0.695 | 0.0483 | ||
| CP | 解析解 | −8.176 | 0.0122 | −1.619 | 0.0144 | |
| 有限元解 | −8.456 | 0.0127 | −1.678 | 0.0149 | ||
3.3. 界面滑移与挠度
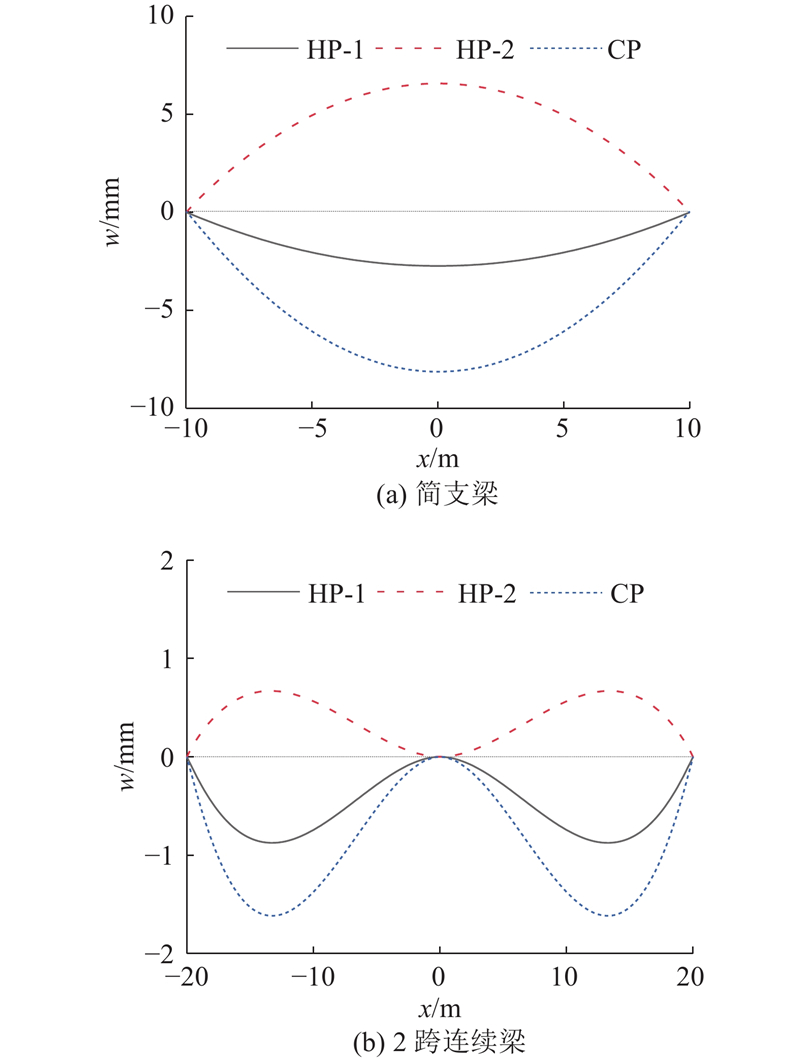
通过有滑移组合梁解析模型计算简支梁和2跨连续梁的挠度,如图12所示,正值为向下挠曲,负值为向上挠曲. 挠度是εm和χt综合作用的结果,升温模式1和降温模式使组合梁上挠曲,升温模式2使组合梁向下挠曲,其中降温模式的竖向挠度最大,可以达到8.18 mm,连续梁的规律与此一致.
图 12
图 12 温度作用下组合梁的挠度分布
Fig.12 Distribution of temperature caused deflection of composite girder
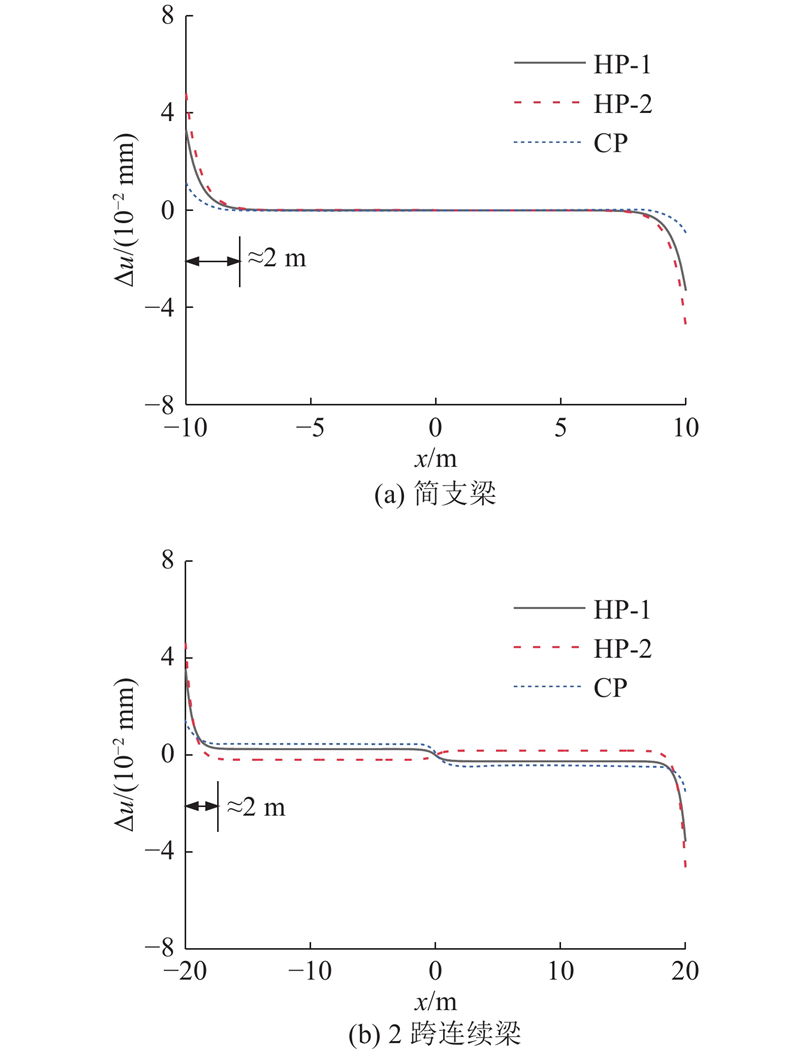
图13给出各温度作用下简支梁和连续梁的界面滑移分布. 可以看出,简支梁在温度作用下的界面滑移沿梁长呈现反对称分布,梁端最大,向跨中逐渐减小至0. 连续梁的分布与之类似,但在中支点处存在反弯点,在端部和中支点间存在等值段. 在相同温度作用下,简支梁与连续梁端部的滑移接近,其中升温模式2的滑移最大,达到0.048 mm. 滑移主要分布在距组合梁端部小于2 m的范围内,即温度梯度引起的剪力在界面的传递范围为0~2 m,在此范围外简支梁的界面滑移均基本为0,连续梁的界面滑移基本无变化.
图 13
图 13 温度作用下组合梁的界面滑移分布
Fig.13 Distribution of temperature caused interfacial slip of composite girder
3.4. 温度应力
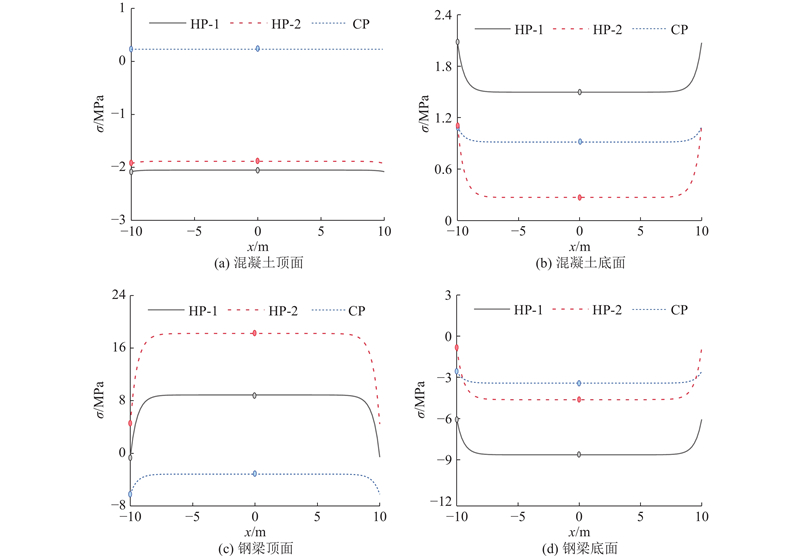
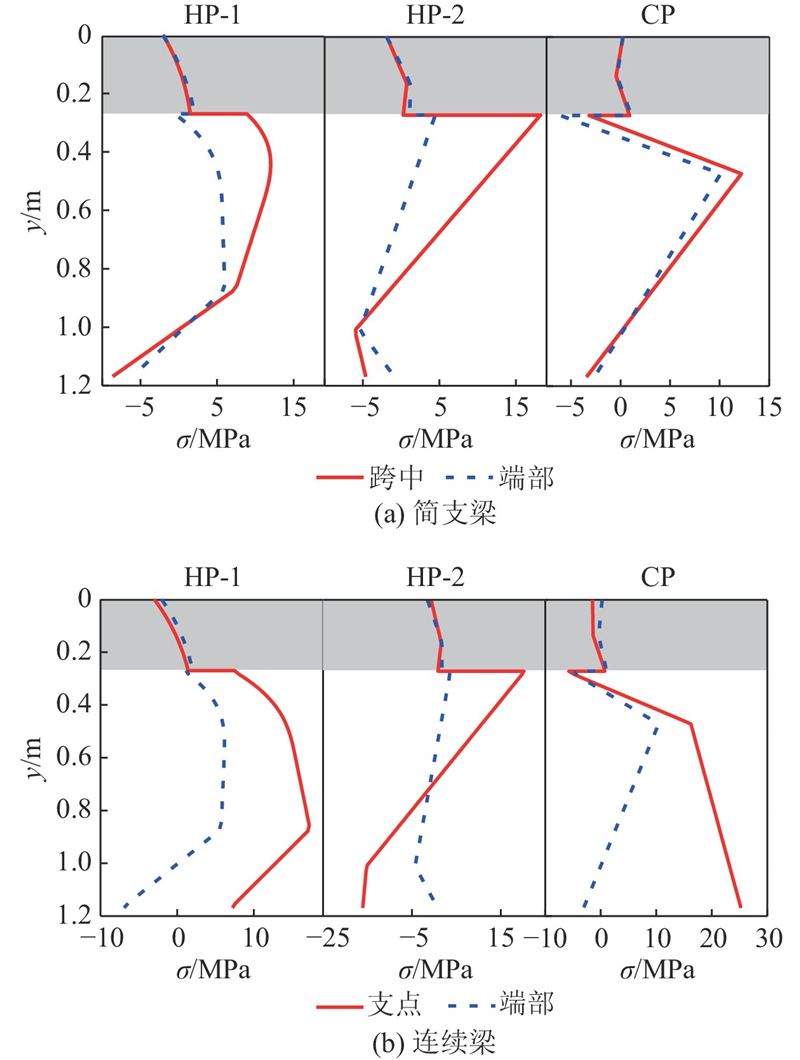
通过式(23)计算可得简支梁和2跨连续梁在各温度作用下的温度应力,选取混凝土顶面(CT)、混凝土底面(CB)、钢梁顶面(ST)和钢梁底面(SB)4个位置,绘制温度应力沿梁长的分布,如图14、15所示,其中2跨连续梁仅给出右跨的结果,左跨完全对称. 可以看出,受界面滑移的影响,组合梁的温度应力在距梁端部小于2 m的范围内沿梁长有明显的曲线变化,其中,界面CB处和ST处的温度应力变化最显著,在如图16所示的竖向应力分布中可以看出. 以升温模式1为例,CB处温度应力由跨中的1.49 MPa变化至端部的2.07 MPa,ST处应力由跨中的8.88 MPa变化至端部的−0.58 MPa,变化率分别为38.9%和106.5%,远大于CT处的1.5%和SB处的29.8%.
图 14
图 14 简支梁温度应力沿纵向的分布
Fig.14 Longitudinal distribution of thermal stress of simply supported girder
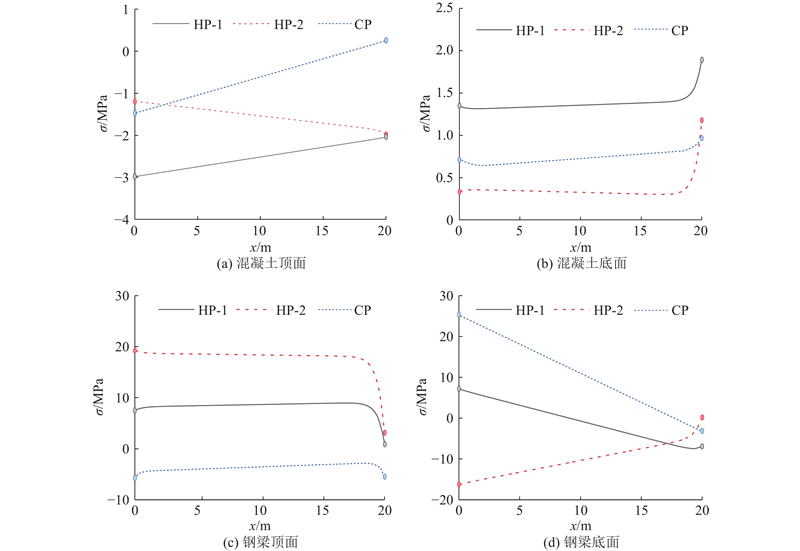
图 15
图 15 连续梁温度应力沿纵向的分布(右跨)
Fig.15 Longitudinal distribution of thermal stress of continuous girder (right span)
图 16
图 16 组合梁温度应力的竖向分布
Fig.16 Vertical distribution of thermal stress of composite girder
4. 挠度影响系数
以简支梁为例,讨论温度作用下界面等效刚度K对组合梁梁端滑移和跨中挠度的影响规律. 根据前文求解可以得到挠度和滑移沿梁长的分布函数,将x = 0代入w(x)和x = L/2代入∆u(x),经过整理,可以分别得到wmax和∆umax的计算公式如下.
式中:w∞,max为无界面滑移(K→∞)时的跨中挠度,∆wmax为有界面滑移产生的附加挠度.
滑移效应对组合梁挠度的影响可以通过如下的挠度影响系数Φ来表示:
根据前文推导,可以求得均布荷载作用下组合梁挠度影响系数Φq. 由于Φq>1,一般称为挠度放大系数,
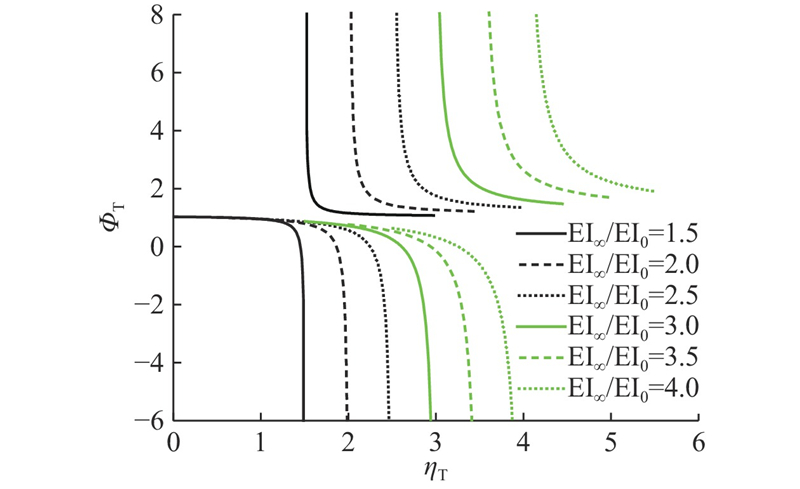
对于温度作用,一般情况下εm不为0,滑移引起的附加挠度可能是正值或负值,则滑移对组合梁挠度的影响可以采用温度作用下的挠度影响系数ΦT来表示:
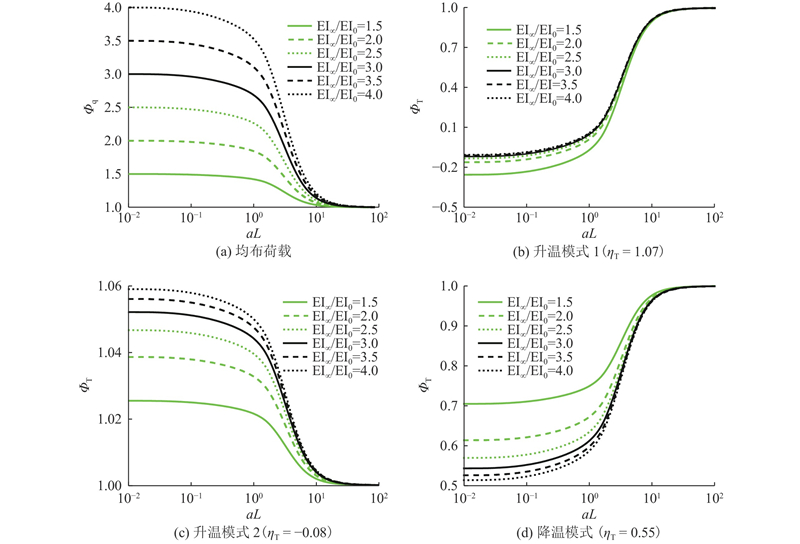
图 17
图 17 不同荷载作用下的挠度影响系数
Fig.17 Influencing factor of deflection under different loads
图 18
图 18 温度作用系数对挠度影响系数的影响
Fig.18 Effects of temperature effect coefficient on deflection influence coefficient
对于温度作用下的简支组合梁(见图17(b)~(d)),ΦT不仅与aL和EI∞/EI0有关,还与由温度作用模式确定的温度作用系数ηT有关. 当aL趋于0时,可以求得ΦT趋近于式(40),是EI∞/EI0和ηT的函数,在不同的作用模式下,可能大于1或小于1,甚至小于0. 无论何种温度作用模式,当aL不断增大时,界面滑移逐渐消失,与均布荷载作用一样,ΦT均趋于1.
温度作用引起组合梁挠曲的机理较常规荷载更复杂,存在某一温度作用模式下,随着aL的变化,挠度影响系数出现正负转变的现象,也存在某一温度作用下挠度刚好为0的情况. 其中特例为当aL=0(即K = 0)且ηT =1(即χt = 0)时,ΦT = 0,其含义如下:界面完全无抗剪作用的组合梁在钢梁和混凝土均匀温差作用下,组合梁挠度为0. 这个论述显然是成立的,进一步印证了温度作用下界面滑移对组合梁挠度影响系数推导的准确性.
5. 结 论
(1)建立外力-温度共同作用下的有滑移钢-混组合梁解析模型,提出有滑移组合梁挠度、界面剪力及滑移的计算公式,通过与有限元计算结果对比,验证了公式的准确性.
(2)有滑移组合梁温度作用产生的挠度与界面滑移由等效温度滑移应变εm和等效温度曲率χt决定,可将桥面板与钢梁的温度分布各自分解为有效温度、竖向线性温差和残余温度这相互独立的3部分,计算εm和χt.
(3)算例分析表明,简支梁和2跨连续梁在温度作用下的界面滑移沿梁长呈现反对称分布,滑移主要集中在端部,分布范围约为2 m,由梁端向跨中逐渐减小至0,连续梁的界面滑移在中支点处存在反弯点. 受滑移的影响,组合梁端部桥面板底面的拉应力水平显著提高,超过2 MPa,增大了桥面板底面的开裂风险.
(4)提出温度作用下组合梁考虑界面滑移的挠度影响系数计算方法,其大小由温度作用系数ηT、完全剪力连接与界面无连接时组合梁的抗弯刚度比EI∞/EI0和组合效应系数aL这3个无量纲参数决定.
参考文献
中小跨径钢-混凝土组合梁桥技术经济性分析
[J].DOI:10.3969/j.issn.1001-7372.2017.03.001 [本文引用: 1]
Technical and economic analysis in steel-concrete composite girder bridges with small and medium span
[J].DOI:10.3969/j.issn.1001-7372.2017.03.001 [本文引用: 1]
钢-混凝土组合梁桥温度作用及效应研究综述
[J].
Review on temperature action and effect of steel-concrete composite girder bridge
[J].
桥梁结构日照温度作用研究综述
[J].
Review on solar thermal actions of bridge structures
[J].
Performance of shear connection in composite beams with profiled steel sheeting
[J].DOI:10.1016/j.jcsr.2005.11.004 [本文引用: 1]
钢-混凝土组合结构桥梁研究新进展
[J].
Advances of research on steel-concrete composite bridges
[J].
Tests and analysis of composite beams with incomplete interaction
[J].
Composite beam-columns with interlayer slip: exact analysis
[J].DOI:10.1061/(ASCE)0733-9445(1993)119:4(1265) [本文引用: 1]
滑移效应对钢-混凝土组合梁弯曲强度的影响及其计算
[J].
Influence of slip effect on bending strength of steel-concrete composite beams and its calculation
[J].
Static, dynamic, and buckling analysis of partial interaction composite members using Timosinco's beam theory
[J].DOI:10.1016/j.ijmecsci.2007.02.006
A steel–concrete composite beam model with partial interaction including the shear deformability of the steel component
[J].DOI:10.1016/j.engstruct.2007.02.007
Analytical solution of two-layer beam taking into account interlayer slip and shear deformation
[J].DOI:10.1061/(ASCE)0733-9445(2007)133:6(886)
Mixed formulation of nonlinear steel-concrete composite beam element
[J].DOI:10.1061/(ASCE)0733-9445(2000)126:3(371)
Nonlinear finite element analysis of composite planar frames with an interlayer slip
[J].DOI:10.1016/j.compstruc.2004.03.070 [本文引用: 1]
钢-混凝土组合梁的温度应力计算
[J].DOI:10.3969/j.issn.1002-0268.2012.05.014 [本文引用: 1]
Calculation of temperature stress of steel-concrete composite beam
[J].DOI:10.3969/j.issn.1002-0268.2012.05.014 [本文引用: 1]
温差、收缩引起的钢-混凝土组合梁界面处剪力作用研究
[J].
Study on shear effect caused by temperature and shrinkage on the interface of steel-concrete composite beams
[J].
温差和荷载引起的FRP-钢组合梁界面剪应力分析
[J].
Interfacial shear stress of FRP-steel composite beams subjected to temperature and load action
[J].
钢-混凝土组合梁的温度骤变效应分析
[J].DOI:10.3969/j.issn.1671-1637.2013.01.004 [本文引用: 1]
Effect analysis of steel-concrete composite beam caused by sudden change of temperature
[J].DOI:10.3969/j.issn.1671-1637.2013.01.004 [本文引用: 1]
钢-混凝土组合梁温度效应的解析解
[J].DOI:10.3969/j.issn.1671-1637.2017.04.002 [本文引用: 1]
Analytical solution of temperature effects of steel-concrete composite girder
[J].DOI:10.3969/j.issn.1671-1637.2017.04.002 [本文引用: 1]
钢-混凝土组合梁桥的温度梯度作用:作用模式与极值分析
[J].
Temperature gradient action of steel-concrete composite girder bridge: action pattern and extreme value analysis
[J].