在“碳中和,碳达峰”的背景下,我国风电机组装机容量不断提高,大型新能源送端电网呈现低短路比特征[1],电网的电压支撑能力变弱,导致宽频振荡问题频发[2-3],极大限制了风电的送出能力. 与传统电流源型直驱风电机组在弱电网下稳定性较差不同[4-5],电压源型直驱风电机组对弱电网具备更好的适应性,且可主动提升对电网的电压/频率支撑能力[6]. 与小容量的微电网系统不同,若大规模新能源基地完全依赖自同步型储能来提升送端系统短路比,所需储能的建设成本将极为高昂. 因此,依赖风机自身能量环节的自同步型直驱风电机组逐渐受到工程界和学术界的广泛关注[7-8]. 典型的自同步控制结构主要有2种[9]:功率自同步控制[10-11]和直流电压自同步控制[12-13].
自同步型直驱风电机组主要关注低频振荡问题,相关分析已较为成熟. Qu等[14-15]建立风电机组的状态空间模型,指出直流电容及机侧动态会极大影响风电机组的低频稳定性. 通过改变机侧外环控制参数[16]或增加类似同步机的虚拟励磁[17]均可有效抑制系统的低频振荡. 相较于小干扰下的低频振荡问题,自同步型直驱风电机组在大干扰下的暂态稳定问题更加复杂,相关研究尚处于起步阶段. Qi等[18]通过流形刻画分析下垂变流器的平衡点吸引域,并得到系统的暂态稳定边界. Chen等[19-20]基于等面积定则和能量函数法分析了电压外环对暂态特性的影响. 秦垚等[21]基于传统同步机的暂态分析方法分析直流电压同步直驱风电机组的暂态响应,指出暂态下风机系统容易发生暂态过流. 由于过流能力有限,变流器往往会设置限流环节,且电流限幅会极大影响系统暂态稳定性[22]. Huang等[23]基于“虚拟功角”分析下垂控制电流饱和导致的特性切换,指出电流限幅会导致系统暂态稳定裕度降低,并提出暂态增强控制以提升变流器暂态稳定性能. 姜卫同等[24]考虑电流限幅分析虚拟同步机的暂态特性,提出混合控制以提高系统暂态稳定裕度. 上述研究大都针对储能变流器进行分析,忽略了风电机组机侧和直流电容动态对风机系统同步动态的负面作用[25],自同步型直驱风电机组的暂态特性须进一步研究.
本研究针对功率自同步和直流电压自同步2种典型的控制结构,分别建立对应的风机系统暂态模型,揭示机侧动态和直流电容动态对风机系统暂态特性的影响. 1)针对频率跌落及电压跌落,分别分析机侧动态对功率自同步型风电机组的暂态动态的影响,揭示系统暂态失稳机理. 2)针对直流电压自同步型风电机组,考虑直流电压动态揭示系统的直流电压崩溃失稳风险. 3)总结对比储能和风电机组的暂态特性差异,讨论直驱风电机组的暂态控制设计思路. 4)基于Matlab/Simulink的时域仿真模型验证理论分析的准确性及控制的有效性.
1. 功率自同步型直驱风电机组暂态分析
1.1. 计及机侧动态的风机系统暂态模型
图 1
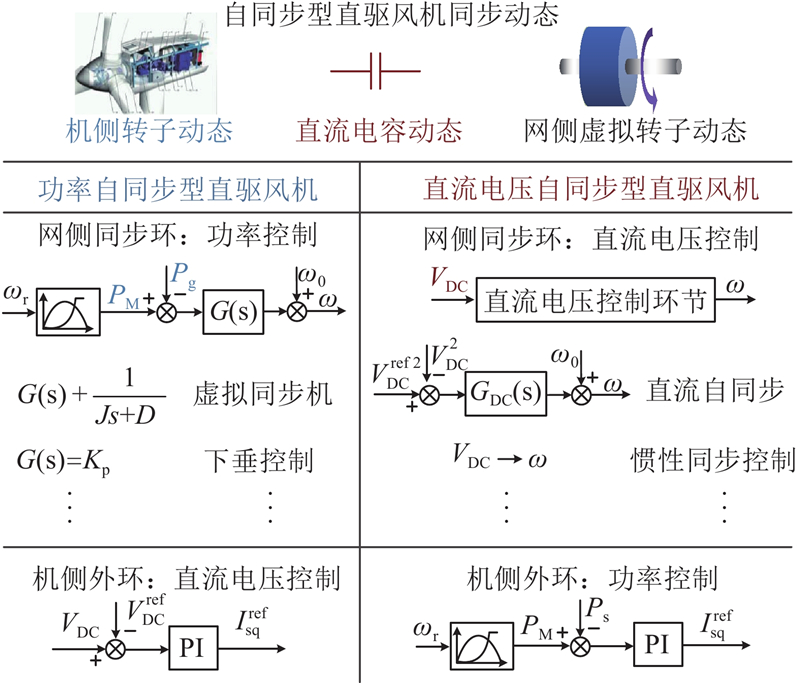
图 1 自同步型直驱风电机组控制结构
Fig.1 Control structure of direct-driven wind turbines based on self-synchronous control
式中:
本研究关注暂态下风机系统的虚拟功角(网侧变流器dq旋转坐标系的d轴与电网电压的夹角[27])变化以分析系统暂态特性,为此作如下简化:1)不考虑谐波分量与零序、负序分量;2)电流内环响应速度远快于同步环,因此忽略内环的暂态过程,认为电流内环的给定值等于实际值;3)忽略风速、浆距角变化.
对于功率自同步型直驱风电机组,机侧直流电压控制动态相较于网侧同步动态具有更快的响应速度[28],因此认为暂态过程中直流电压控制能够实现理想跟踪,即
式中:
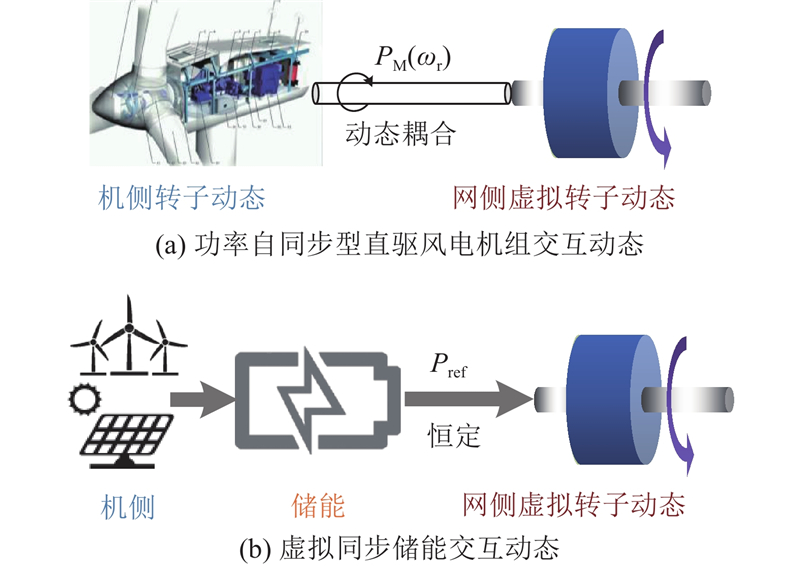
由式(3)、(4)可知,机侧动态通过网侧功率跟踪与网侧同步动态耦合,如图2所示. 与功率自同步型直驱风电机组不同,储能的存在使得虚拟同步储能(基于储能实现虚拟同步控制的新能源设备)的直流电容电压恒定,储能与网侧虚拟转子实现能量交互,机侧与网侧无明显的耦合关系.
图 2
此外,由于变流器的过流能力有限,自同步型设备广泛采用网侧电流环限幅以应对暂态过流问题. 当电流饱和后,风机系统由电压源特性切换为电流源特性,饱和前后的网侧电磁功率输出表达式[27]为
式中:
1.2. 频率跌落下的风机系统暂态稳定分析
由于网侧动态与机侧动态存在耦合,在电网频率波动下,机侧转子通过调整自身转速参与系统频率调节,风机系统的动态响应更为复杂. 为了分析频率变化下的风机系统响应特性,由式(3)、(4)得到系统的频率响应:
式中:
在频率波动下,风机系统会调整运行点以响应网侧频率变化. 频率波动下风机系统的
图 3
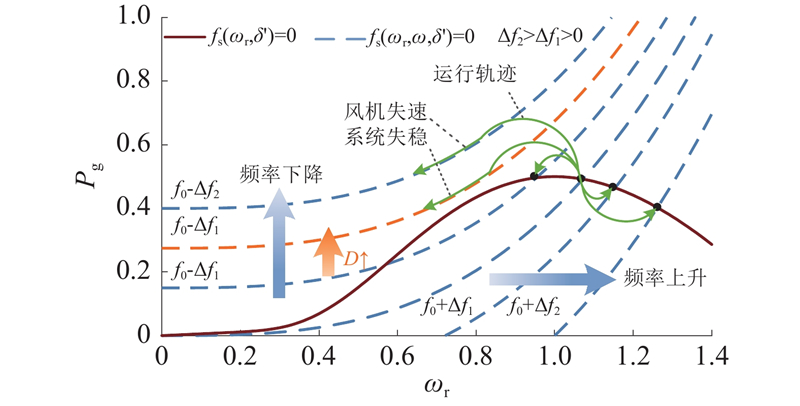
图 3 频率波动下风机系统暂态响应
Fig.3 Transient response of wind turbines under frequency deviations
如图3所示,在频率上升时,风机系统转子会经历一个加速过程,吸收有功功率为电网提供频率支撑. 在频率剧烈上升时,风机系统往往具有稳定平衡点,且当转速超过允许范围时,风机系统会通过俯仰角控制以防止转子超速. 因此,功率自同步型直驱风电机组在频率上升时可维持稳定运行. 当频率下降时,风机转子将减速以释放储存在转子中的动能,进而参与电网频率调节,但转子转速低于允许范围或失去平衡点,风机系统可能会失去同步稳定性. 例如,当频率下降到图3中的
1.3. 电压跌落下的风机系统暂态稳定分析
除了电网频率波动,短路故障也会引起等效无穷大电网的电压跌落,相应的暂态特性更加复杂. 为了对比只考虑网侧动态的虚拟同步储能,仍关注网侧同步动态,揭示机侧动态对风机系统暂态特性的影响.
由式(2)和式(5)可知,在稳态下,网侧
图 4
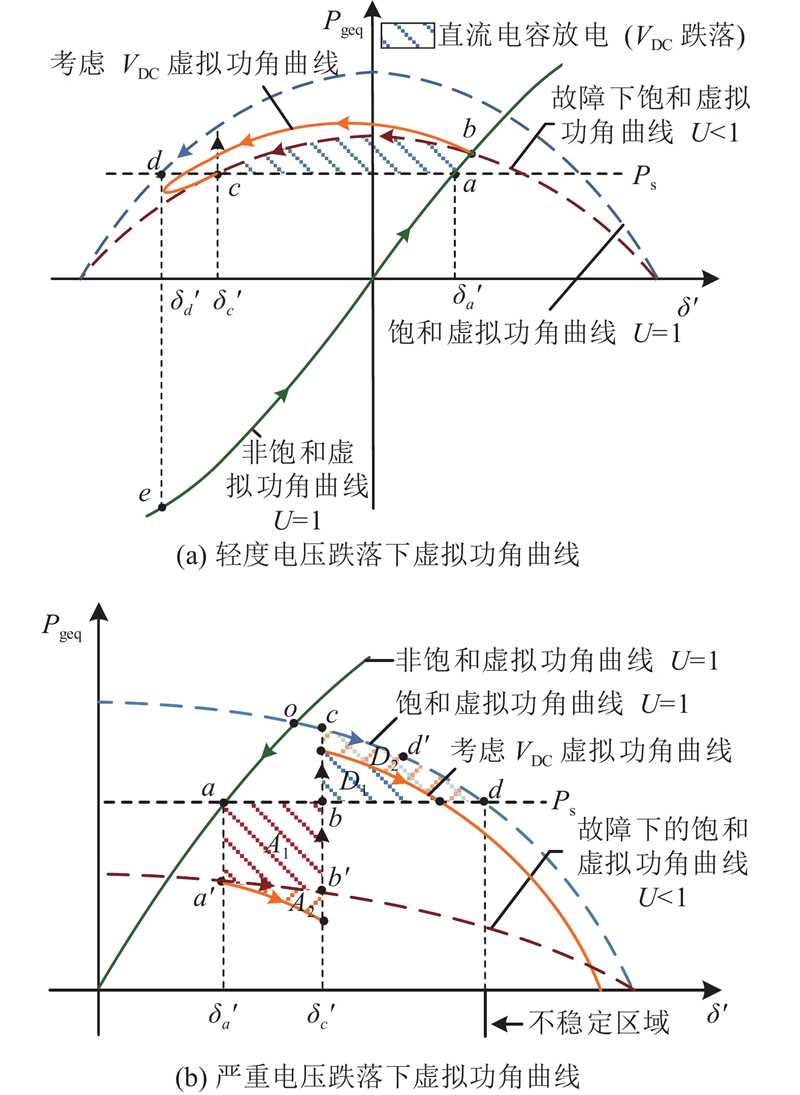
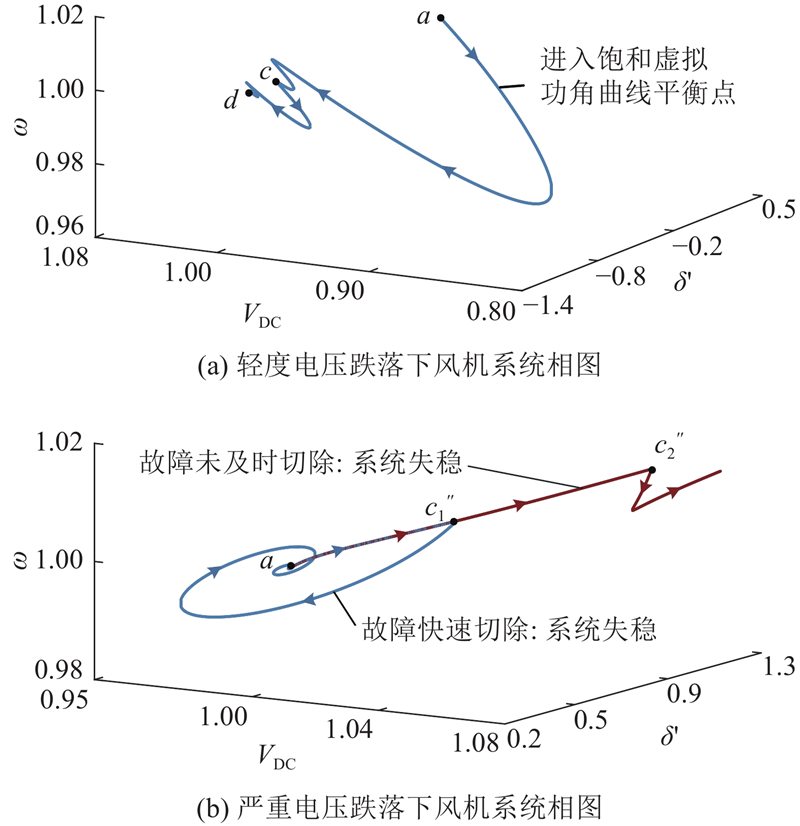
图 4 功率自同步型直驱风机虚拟功角曲线
Fig.4 Virtual power angle curve of direct-driven wind turbines based on power self-synchronous control
1)
2)
上述分析主要适用于强电网,弱电网由于系统短路比(short circuit ratio, SCR)较小,因此电网远端故障对并网点电压的影响往往较小,且受到线路电抗的限流作用,弱电网下风机系统相较强电网更难进入电流限幅. 在轻度电压跌落下,弱电网下风机系统可能不存在
2. 直流电压自同步型直驱风电机组暂态分析
2.1. 计及直流电压动态的风机系统暂态模型
直流自同步控制在取合适参数时具有和惯性同步控制相似的特性,因此以直流自同步直驱风电机组为例,分析直流电压自同步型直驱风电机组的暂态特性,将同步原理表示为
式中:
其中等效惯性系数
式中:
2.2. 电压跌落下的风机系统暂态稳定分析
不同于功率自同步型直驱风电机组,直流电压自同步型直驱风电机组的机侧转子几乎不响应网侧,因此不存在频率跌落下的转子失速问题. 在电压跌落下,由式(5)和式(9)可知,风机系统由于电流饱和也会发生特性切换,其平衡点的存在由机侧功率输出
图 5
图 5 直流电压自同步型直驱风机虚拟功角曲线
Fig.5 Virtual power angle curve of direct-driven wind turbines based on DC voltage self-synchronous control
1)
图 6
2)
3. 暂态特性对比及控制设计思路
3.1. 储能与风机系统暂态特性对比总结
为了进一步揭示机侧动态和直流电容动态对风机系统暂态特性的影响,总结传统直流电压恒定的虚拟同步储能与2种自同步型直驱风电机组的暂态特性如表1所示. 对于虚拟同步储能,直流电压恒定,机侧及直流电压动态可忽略,暂态特性仅由网侧变流器决定. 在轻度电压跌落下,虚拟功角减小并进入不期望平衡点;在严重电压跌落下,虚拟功角增大,并可能越过不稳定平衡点而失稳.
表 1 储能与直驱风机的暂态特性对比
Tab.1
| 设备类型 | 动态影响 | 暂态特性 | ||||
| 机侧 | 直流电压 | 频率跌落 | 电压轻度跌落 | 电压严重跌落 | ||
| 虚拟同步储能 | 无影响 | 直流电压恒定 | 储能支撑电网 | 虚拟功角减小,进入不期望 平衡点 | 虚拟功角增大,存在越过不稳定平衡点的失稳风险 | |
| 功率自同步型直驱 风电机组 | 机侧与网侧 动态耦合强 | 直流电压近似 恒定 | 风机失去平衡点 机侧转子失速切机 | 机侧动态→减速面积增大→ 进入平衡点时间增加 | 机侧动态→加速面积增大减速面积减小→增加失稳风险 | |
| 直流电压自同步型 直驱风电机组 | 机侧与网侧 动态耦合弱 | 直流电压与网 侧动态耦合 | 无转子失速风险 | 直流电容释放能量→存在直 流电压崩溃失稳风险 | 直流电压动态→加速面积增大减速面积减小→增加失稳风险 | |
对于功率自同步型直驱风电机组,考虑机侧直流电压控制相较网侧同步动态具有更快的响应速度,可以认为直流电压恒定,机侧转子与网侧动态交互耦合. 考虑机侧转子动态后,在频率跌落下,风机系统由于转子减速可能失去平衡点,导致机侧转子失速切机. 在电压跌落下,机侧动态使暂态过程中的
对于直流电压自同步型直驱风电机组,由于机侧几乎不响应网侧及直流侧,可以认为机侧为功率源,直流电压动态与网侧动态交互耦合. 相较于虚拟同步储能,在轻度电压跌落下,风机系统虚拟功角将减小,且直流电压不断降低,可能引发直流电压崩溃失稳;在严重电压跌落下,虚拟功角将增大,且直流电压不断升高,可能引起chopper动作,导致加速面积增大及减速面积减小,增加减速面积不足的风机系统失稳风险.
3.2. 风机系统暂态控制设计思路
基于前文分析可知,自同步型直驱风电机组的网侧动态均具有摇摆特性,其参数在不同控制下有不同的形式,具体如表2所示. 因此,可基于图7(a)的网侧等效动态进行控制设计,并使现有控制适用多种自同步控制. 例如,文献[23]通过增加q轴电压分量改变
表 2 网侧等效动态参数
Tab.2
| 风机类型 | 网侧控制 | Jg | Dg | Pref | f(VDC) |
| 功率自同步 | 虚拟同步机 | J | D | PM | 0 |
| 下垂控制 | 0 | 1/ Kp | PM | 0 | |
| 直流电压自同步 | 直流自同步 | Ps | |||
| 惯性同步 | CDC VDC0 | 0 | Ps | 0 |
图 7
图 7 网侧等效动态及暂态控制实例
Fig.7 Equivalent dynamic of grid side and transient control examples
4. 仿真验证
4.1. 功率自同步型风电机组暂态验证
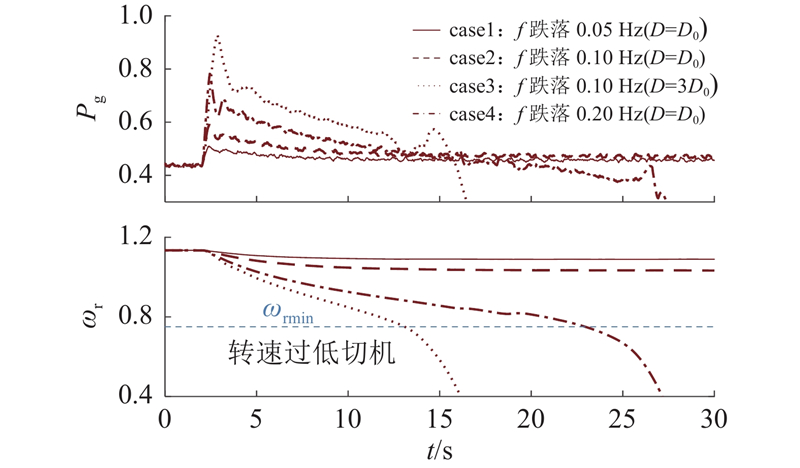
为了验证频率跌落下的稳定分析,搭建功率自同步型风电机组仿真模型,主要系统参数如下:额定线电压Vnom=690 V,额定容量Pnom=1.5 MW,额定频率fnom=50 Hz,永磁直驱电机的惯量系数Js=4,永磁直驱电机极对数为48,直流电容CDC=0.38(标幺值),其他参数参考文献[12]及文献[25]. 在t=2 s发生电网频率跌落,如图8所示为不同工况下的风机系统时域仿真波形,其中case1和case2的电网频率分别跌落0.05、0.10 Hz,
图 8
图 8 频率跌落下的风机系统时域仿真波形
Fig.8 Time domain simulation waveform of wind turbines under frequency drop
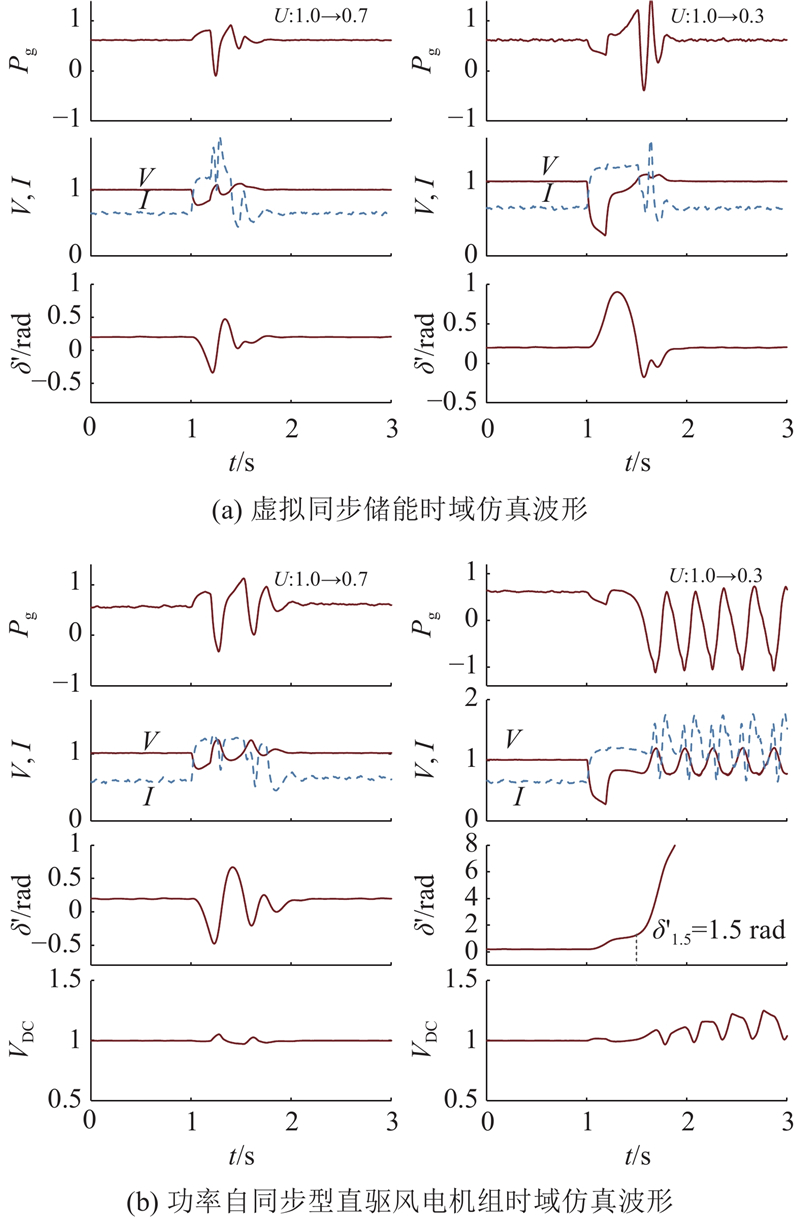
为了验证电压跌落下的暂态稳定分析,基于虚拟同步储能及功率自同步型风电机组的仿真模型,在t=1 s发生电网电压跌落,并于1.2 s恢复,如图9所示为2种机组在不同工况下的系统时域仿真波形. 图中,Pg、V、I、
图 9
图 9 功率自同步型风电机组时域仿真波形(SCR=5)
Fig.9 Time domain simulation waveform of direct-driven wind turbines based on power self-synchronous control (SCR=5)
表 3 系统极限故障切除时间
Tab.3
| SCR | U | tcut,1 | tcut,2 |
| 5 | 0.3 | 0.184 | 0.207 |
| 5 | 0.2 | 0.148 | 0.174 |
| 2 | 0.3 | 0.152 | 0.168 |
| 2 | 0.2 | 0.125 | 0.137 |
4.2. 直流电压自同步型风电机组暂态验证
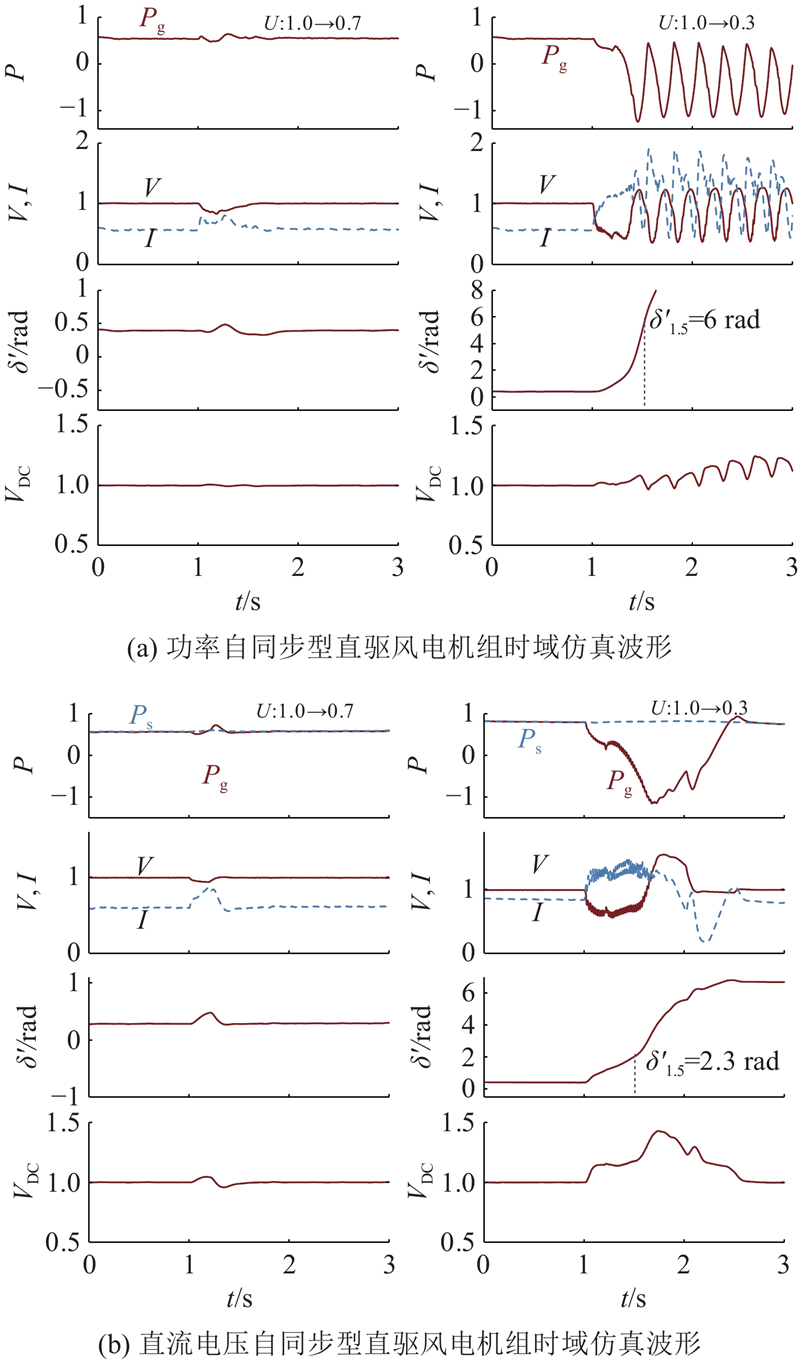
为了验证电压跌落下的暂态稳定分析,基于直流电压自同步型风电机组仿真模型,在1.0 s给予电网电压跌落,并于1.2 s恢复,如图10所示为不同工况下的风机系统时域仿真波形. 在电网电压跌落至0.7后(
图 10
图 10 直流电压自同步型风电机组时域仿真波形(SCR=5)
Fig.10 Time domain simulation waveform of direct-driven wind turbines based on DC voltage self-synchronous control (SCR=5)
为了验证不同电网强度下的风电机组的暂态特性,对比不同电网强度下的风电机组极限故障切除时间. 可以发现,弱电网下(SCR=2)风机并网系统的极限故障切除时间明显低于强电网,具有更高的暂态失稳风险. 当电网于1.0 s发生电压跌落并于1.2 s切除时,如图11所示为不同电网强度下的功率自同步型直驱风电机组和直流电压自同步型直驱风电机组的暂态时域波形. 通过对比轻度电压跌落下不同电网强度的2种风机系统的暂态时域波形可以发现,弱电网下(SCR=2)风电机组不会进入限幅,而是维持电压源运行. 在严重电压跌落下,通过对比可以发现,弱电网下风电机组在故障切除后的减速过程变短,更容易越过不稳定平衡点,并引起风电机组暂态失稳.
图 11
图 11 电压跌落下的时域仿真波形(SCR=2)
Fig.11 Time domain simulation waveform under voltage drop(SCR=2)
4.3. 暂态控制验证
为了验证控制设计实例的有效性,基于直流电压自同步型风电机组仿真模型,在1.0 s给予电网电压跌落,并于1.2 s恢复电网电压,图10(b)为增加暂态控制的风机系统时域仿真波形. 在电网电压跌落至0.3后(
5. 结 语
针对自同步型直驱风电机组忽略机侧及直流电压动态导致的暂态分析不准确问题,建立功率自同步型及直流电压自同步型直驱风电机组暂态模型,揭示了机侧动态和直流电压动态对风机系统暂态特性的影响机理,并得到如下结论. 1)对于功率自同步型直驱风电机组,在频率波动下,过大的阻尼系数或严重频率跌落均易引发机侧转子失速,导致风机系统切机;在电压跌落下,机侧转子动态使加速面积增大及减速面积减小,增加风机系统的暂态失稳风险. 2)对于直流电压自同步型直驱风电机组,直流电压动态加剧暂态期间的功率不平衡,且在直流电压约束下可能引发直流电压崩溃失稳及减速面积不足失稳. 3)现有暂态控制广泛忽略机侧和直流电压动态,针对网侧进行控制设计,现有控制须加以改进才能适用于各类自同步型直驱风电机组. 合理利用机侧参与暂态穿越,也能有效提升风机系统暂态稳定性能. 考虑多机设备交互及控制耦合,分析风机系统的暂态特性是未来计划开展的工作之一.
参考文献
高比例新能源电力系统的惯量控制技术与惯量需求评估综述
[J].
Review of inertia control technology and requirement evaluation inrenewable-dominant power system
[J].
新能源并网系统引发的复杂振荡问题及其对策研究
[J].
Study of complex oscillation caused by renewable energy integration and its solution
[J].
电力系统次同步谐振/振荡的形态分析
[J].
Analysis of subsynchronous resonance/oscillation types in power systems
[J].
直驱风机变流控制系统对次同步频率分量的响应机理研究
[J].
Study on response characteristics of grid converter control system of permanent magnet synchronous generators (PMSG) to subsynchronous frequency component
[J].
Subsynchronous interaction between direct-drive PMSG based wind farms and weak AC networks
[J].DOI:10.1109/TPWRS.2017.2682197 [本文引用: 1]
Response of a grid forming wind farm to system events, and the impact of external and internal damping
[J].DOI:10.1049/iet-rpg.2020.0638 [本文引用: 1]
虚拟同步发电机技术在风力发电系统中的应用与展望
[J].
Application and prospect of virtual synchronous generator in wind power generation system
[J].
电压源型构网风电机组研究现状及展望
[J].
Review of the voltage-source grid forming wind turbine
[J].
基于虚拟同步控制的电压源型直驱风电机组并网稳定性分析
[J].
Analysis of grid-connected stability of voltage-source-type PMSG-based wind turbine based on virtual synchronous control
[J].
适应于弱电网的永磁直驱风电机组虚拟惯量协调控制策略
[J].
A virtual inertia coordinated control scheme of PMSG-based wind turbines in weak grids
[J].
全功率变换风电机组的电压源控制(一): 控制架构与弱电网运行稳定性分析
[J].
et al. Voltage source control of wind turbines with full-scale converters (part I): control architecture and stability analysis under weak grid conditions
[J].
Modeling and analysis of inner controls effects on damping and synchronizing torque components in VSG-controlled converter
[J].DOI:10.1109/TEC.2020.3010049 [本文引用: 1]
考虑源端特性的虚拟同步直驱风机小信号建模与稳定性分析
[J].
Small-signal modeling and stability analysis of virtual synchronous PMSG considering source characteristics
[J].
虚拟同步直驱风电场经MMC-HVDC并网的低频振荡特性分析
[J].
Low-frequency oscillation characteristic analysis of grid-connected VSG-PMSG via MMC-HVDC system
[J].
改善虚拟同步发电机阻尼特性的设计方法
[J].
Design method for improving damping characteristics of virtual synchronous generator
[J].
Transient angle stability of inverters equipped with robust droop control
[J].
Enhanced transient angle stability control of grid-forming converter based on virtual synchronous generator
[J].DOI:10.1109/TIE.2021.3114723 [本文引用: 1]
Transient angle stability of virtual synchronous generators using Lyapunov’s direct method
[J].DOI:10.1109/TSG.2018.2866122 [本文引用: 1]
全功率变换风电机组的电压源控制(二): 电网故障穿越控制与保护
[J].
Voltage source control of wind turbine generators with full-scale converters (part II): control and protection of grid fault ride-through
[J].
Virtual impedance current limiting for inverters in microgrids with synchronous generators
[J].DOI:10.1109/TIA.2014.2345877 [本文引用: 1]
Transient stability analysis and control design of droop-controlled voltage source converters considering current limitation
[J].DOI:10.1109/TSG.2017.2749259 [本文引用: 3]
基于虚拟同步机的变流器暂态稳定分析及混合同步控制策略
[J].
Transient stability analysis and hybrid synchronization control strategy of converter based on virtual synchronous generator
[J].
虚拟同步直驱风机低频振荡机理分析及阻尼补偿控制
[J].
Low-frequency oscillation mechanism analysis and damping compensation control of permanent magnet synchronous generator with virtual synchronous control
[J].
Equivalence of virtual synchronous machines and frequency-droops for converter-based microgrids
[J].DOI:10.1109/TSG.2013.2288000 [本文引用: 1]
下垂控制逆变器的虚拟功角稳定机理分析
[J].
Mechanism analysis of virtual power angle stability in droop-controlled inverters
[J].
电力电子化电力系统多尺度电压功角动态稳定问题
[J].
Multi-time scale voltage and power angle dynamics in power electronics dominated large power systems
[J].
Low-voltage ride-through control strategy for a virtual synchronous generator based on smooth switching
[J].DOI:10.1109/ACCESS.2017.2784846 [本文引用: 1]