撞击坑成坑规律研究最初主要集中在高速撞击领域,其成坑过程及机理涉及材料的热力学相变与破碎[4],由于数值模拟十分困难,研究以试验居多. Schmidt[5]基于爆炸与高速撞击在成坑过程中的相似性,将爆炸成坑规律与结论推广应用至高速撞击成坑,提出撞击成坑相似理论. Holsapple等[6-8]在常重力和超重力(500g)条件下开展球体高速(2 km/s)撞击干砂靶成坑试验,验证了撞击成坑相似理论在高速撞击情况下的适用性. 之后,不少学者开展低速(100~102 m/s)撞击验证试验. Yamamoto等[9]对不同撞击速度(11~329 m/s)下球体撞击玻璃珠成坑瞬时过程及成坑尺寸进行试验研究,验证了低速撞击条件下Schmidt等[8]提出的相似律的适用性.Tsujido等[10]研究了撞击速度约为200 m/s的弹体密度对成坑尺寸的影响. De Vet等[11]进行速度为0.6~4.4 m/s的撞击试验,验证了成坑尺寸的撞击能量依赖性. Takizawa等[12]在砂土斜坡上进行速度为1~97 m/s撞击试验,提出综合考虑靶体倾角与撞击角度的相似律关系,并验证了该相似关系的适用性.
关于球体低速斜撞击水平颗粒材料成坑效应的研究较少,对成坑效应的分析多集中在成坑深度和成坑直径,对成坑体积和撞击角度的分析相对匮乏. 本研究通过系统开展不同撞击角度下球体低速斜撞击干砂靶成坑试验,进一步修正低速斜撞击水平靶体条件下考虑撞击角度的成坑相似律,探讨该相似律的适用性及其在天文学上的应用.
1. 试验方案
为了研究低速斜撞击条件下的成坑机理及规律,设计利用重力的球体发射装置,系统开展不同角度条件下球体撞击干砂靶成坑试验,并利用手持式三维激光扫描仪定量测量坑型几何参数.
1.1. 试验装置
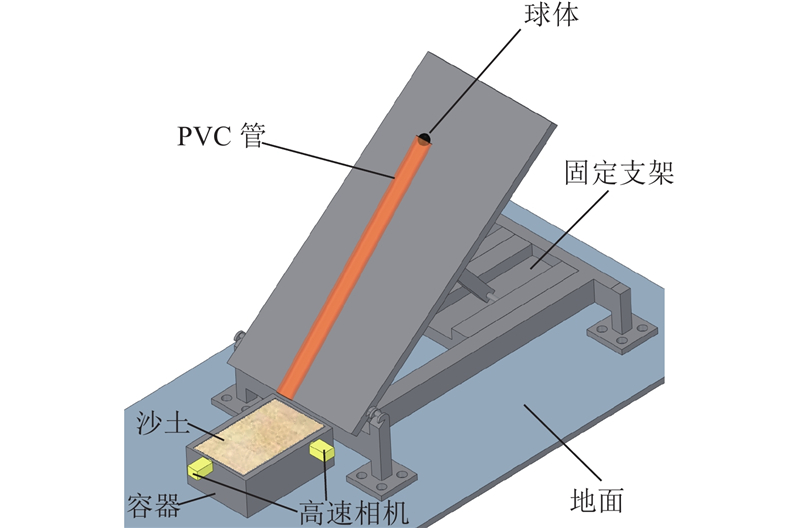
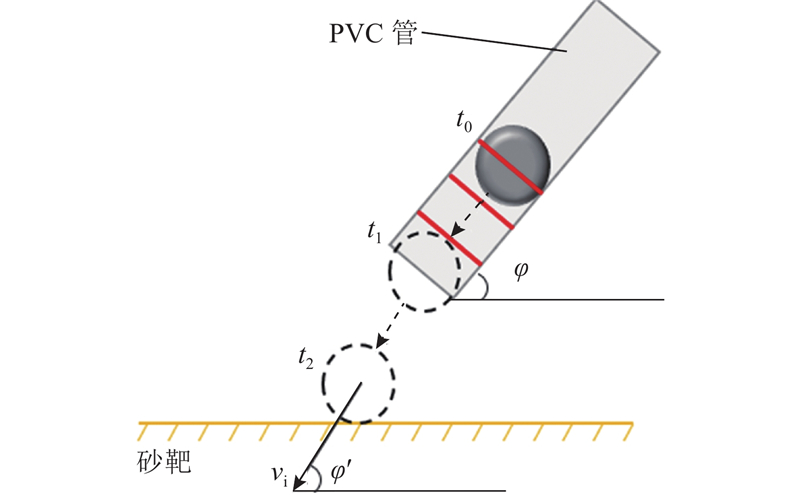
如图1所示为可控制撞击角度的试验装置. 试验装置由发射系统、砂靶系统和测量系统组成,各装置材料的具体规格参数如表1所示. 发射系统由球体、PVC管、涤纶纤维、固定支架组成. PVC管固定于固定支架上,固定支架可自由调节以控制撞击角度,涤纶纤维置于PVC管内部,在PVC管底部0~3 cm范围进行特征标记. 控制PVC管位于砂靶中心上方约1 cm,通过高速相机后续观测可知,PVC管对成坑过程中砂土溅射物分布几乎无影响. 砂靶由长方体开口容器、福建标准砂组成,撞击点控制在容器中间区域,容器尺寸大于球体直径的5倍,以忽略在撞击过程中容器壁对试验结果的影响[14]. 测量系统由角度仪、手持式三维激光扫描仪、高速相机组成,角度仪控制PVC管固定角度,手持式三维激光扫描仪测量坑型几何参数,高速相机记录撞击过程及速度,撞击速度过程记录如图2所示. 时刻
图 1
图 1 球体发射低速撞击试验装置示意图
Fig.1 Schematic illustration of low-speed impact test device for sphere launch
表 1 球体发射低速撞击试验装置的材料及规格参数
Tab.1
| 试验装置 | 试验材料 | 规格参数 |
| 发射系统 | 球形弹丸 | 表面光滑,材质为304不锈钢;直径Di=18 mm,中间有3 mm通孔;质量mi = 23.093 g |
| PVC透明硬管 | 外径为25 mm,壁厚为2.5 mm;长度分别为1.0、1.5、2.0 m,与球体的摩擦系数约为0.01 | |
| 涤纶纤维 | 直径为0.2 mm,抗拉强度≥500 MPa | |
| 固定支架 | 角度可调整,不锈钢材料 | |
| 砂靶系统 | 长方体开口容器 | 木制;内径尺寸为480 mm×280 mm×190 mm,壁厚为10 mm |
| 福建标准砂 | 真实密度 | |
| 测量系统 | 角度仪 | 型号为JZC-B2,测量范围为−130°~ 130°,测量精度为±1° |
| 手持式三维激光扫描仪 | 型号为SIMSCAN30,最高精度为0.020 mm,最大扫描面幅为410 mm×400 mm | |
| 高速相机 | 型号为Photron,MH6;帧率为2640 帧/s;分辨率为1 280×600 |
图 2
图 2 撞击速度计算过程示意图
Fig.2 Schematic illustration of impact speed calculation process
1.2. 试验方案及工况
每次试验开始前,取39.07 kg砂土置于容器内,轻轻振动容器并将砂靶表面整平,控制砂土密实度为0.73. 随后利用角度仪调整PVC管至控制角度并固定于固定支架上,将涤纶纤维穿入管内,将球体沿通孔方向穿入涤纶纤维,限制球体沿速度方向的角速度,并从PVC管顶部释放,撞击砂靶成坑,全过程由高速相机记录. 试验结束后,使用手持式三维激光扫描仪扫描,得到坑型三维点云模型. 如表2所示为设计试验工况,共开展127组试验,获得有效试验数据107组. 表中,
表 2 球体发射低速撞击试验工况
Tab.2
| L/m | n | L/m | n | |||
| 45 | 1.0 | 5 | 70 | 1.5 | 5 | |
| 1.5 | 5 | 2.0 | 5 | |||
| 2.0 | 5 | 75 | 1.0 | 5 | ||
| 50 | 1.0 | 5 | 1.5 | 5 | ||
| 1.5 | 5 | 2.0 | 5 | |||
| 2.0 | 5 | 90 | 0.5 | 2 | ||
| 55 | 1.0 | 5 | 0.6 | 2 | ||
| 1.5 | 5 | 0.7 | 2 | |||
| 2.0 | 5 | 0.8 | 2 | |||
| 60 | 1.0 | 5 | 0.9 | 2 | ||
| 1.5 | 5 | 1.0 | 2 | |||
| 2.0 | 5 | 1.1 | 2 | |||
| 65 | 1.0 | 5 | 1.2 | 2 | ||
| 1.5 | 5 | 1.3 | 2 | |||
| 2.0 | 5 | 1.4 | 2 | |||
| 70 | 1.0 | 5 | 1.5 | 2 |
2. 试验结果
2.1. 成坑过程与成坑形状
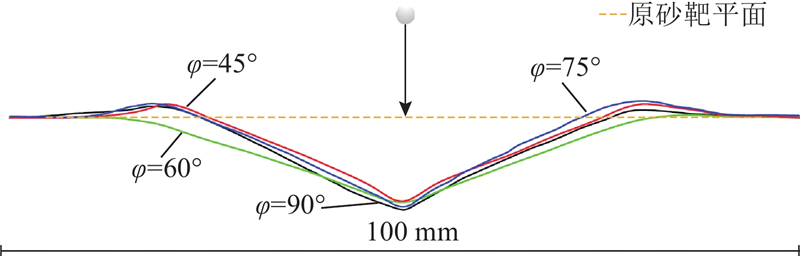
如图3所示为不同撞击角
图 3
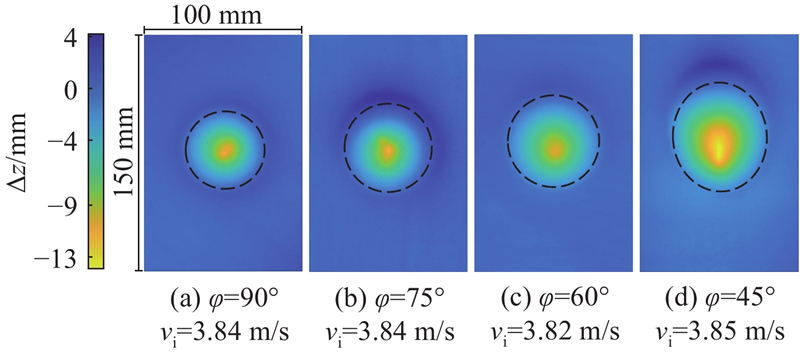
图 4
图 4 不同撞击角度的撞击坑型颜色深度图
Fig.4 Impact crater shapes color depth map at different impact angles
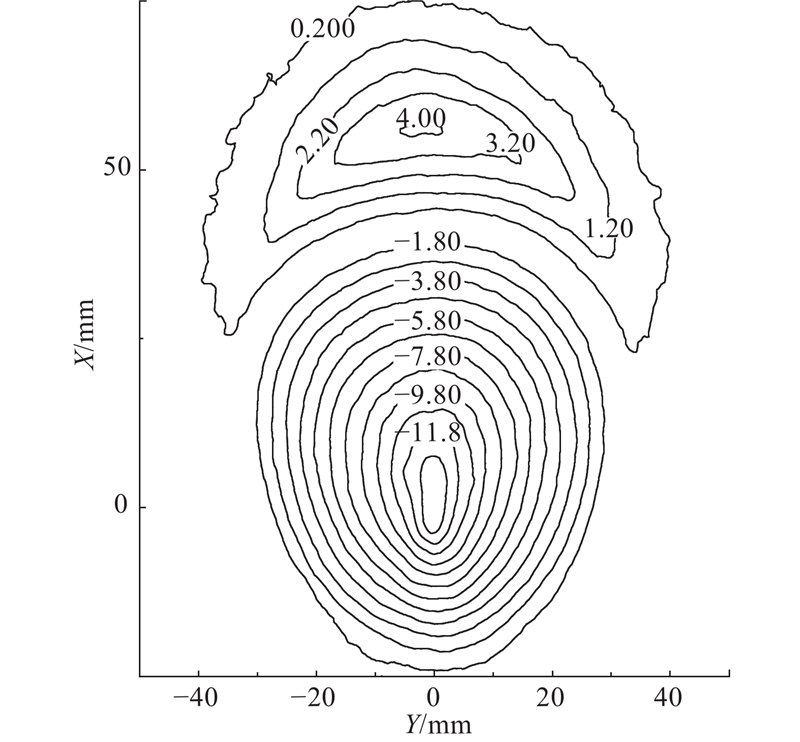
图 5
图 5
撞击坑型等高线图(
Fig.5
Impact crater shape contour map (
图 6
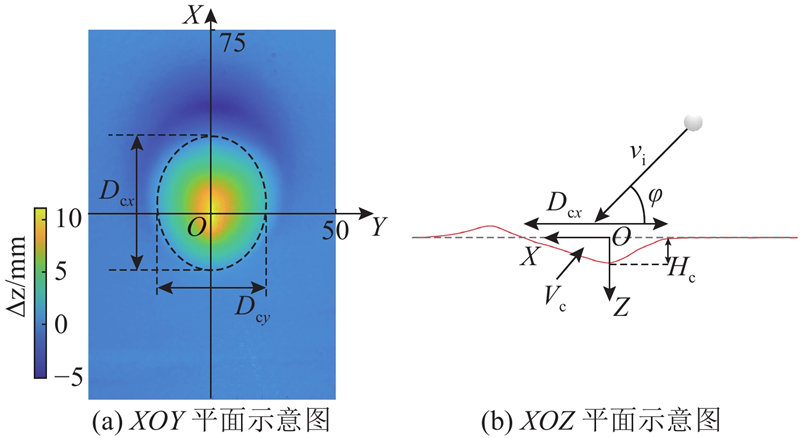
图 6 成坑参数及坐标系定义示意图
Fig.6 Schematic illustrations of crater parameters and coordinate system definition
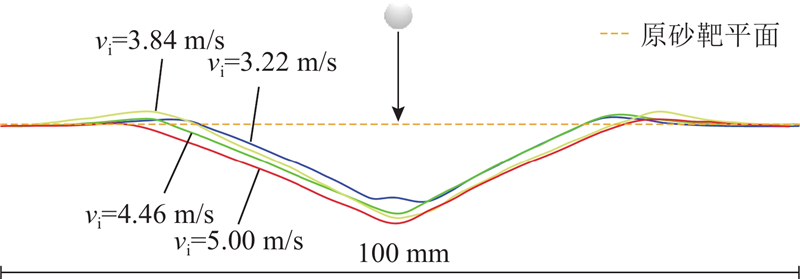
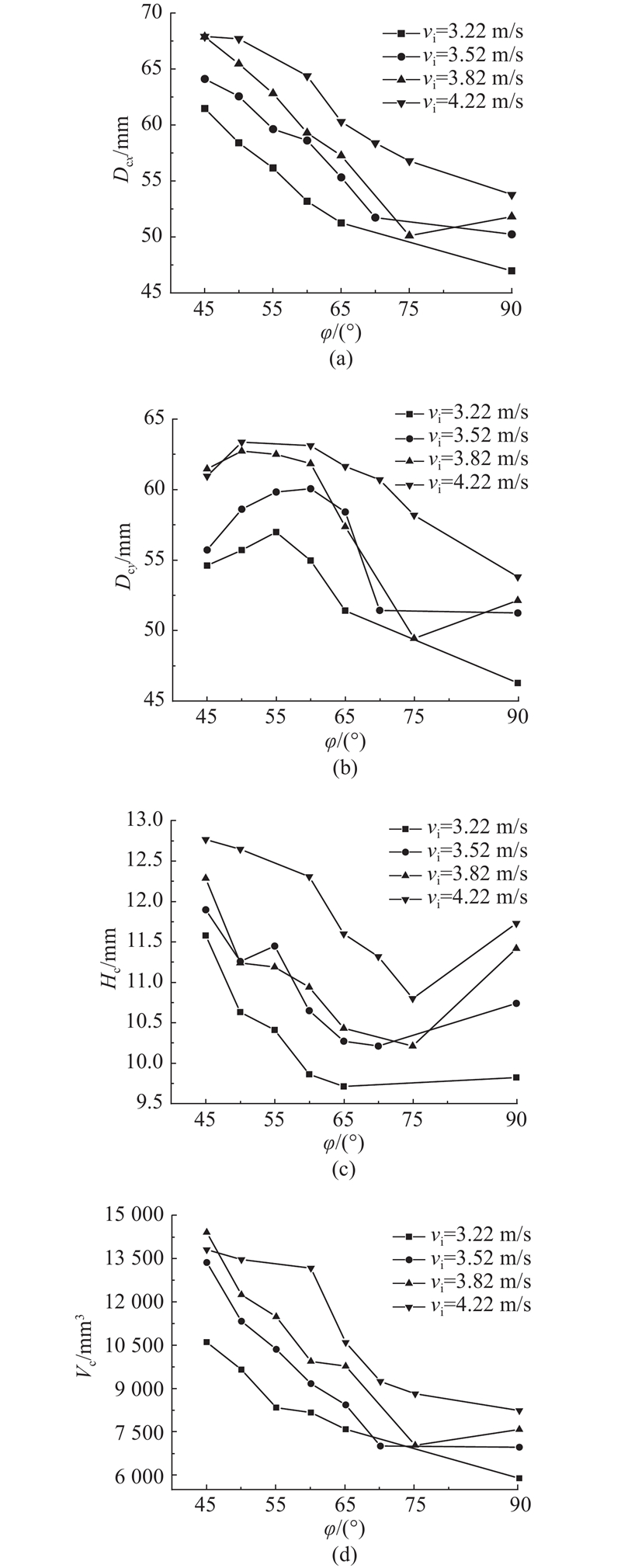
2.2. 撞击速度对坑型的影响
如图7所示为垂直撞击下不同撞击速度的坑型截面图. 坑长、坑深随着撞击速度的增加而增加,坑型左右几乎对称,坡度几乎相等. 当撞击速度
图 7
图 7 不同撞击速度下的正撞击YOZ平面成坑剖面图
Fig.7 Vertical impact YOZ plane crater profile at different impact speeds
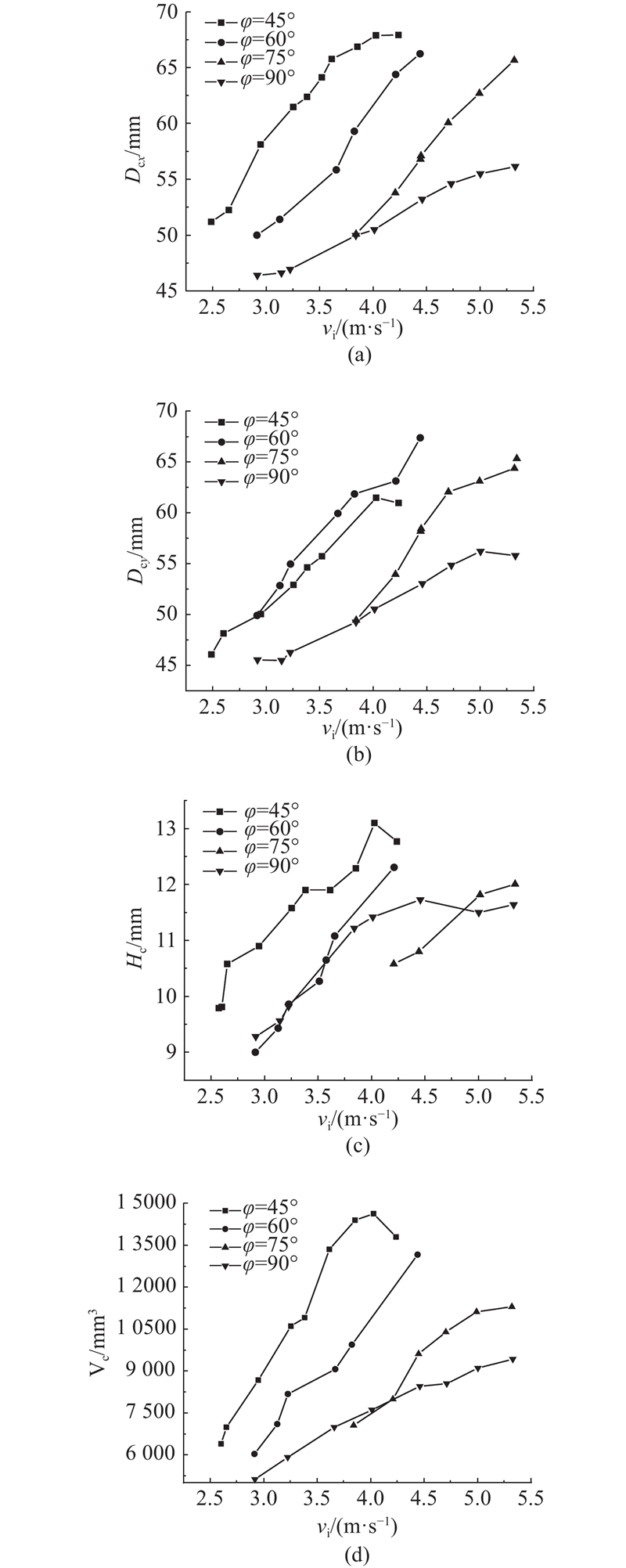
如图8所示为不同
图 8
图 8 坑型参数随撞击速度的变化曲线
Fig.8 Variation curve of crater parameters with impact speed
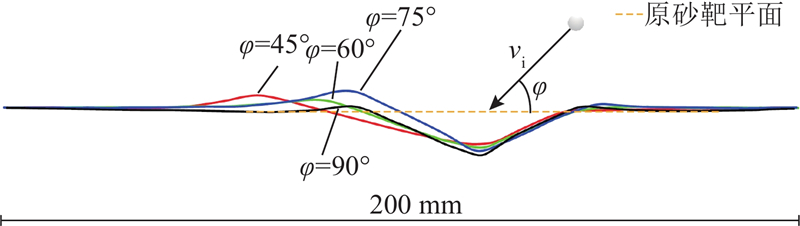
2.3. 撞击角度对坑型的影响
如图9所示为不同
图 9
图 9 不同撞击角度下的XOZ平面成坑剖面图
Fig.9 XOZ plane crater profile at different impact angles
图 10
图 10 不同撞击角度下的YOZ平面成坑剖面图
Fig.10 YOZ plane crater profile at different impact angles
如图11所示为不同
图 11
图 11 坑型参数随撞击角度的变化曲线
Fig.11 Variation curve of crater parameters with impact angle
3. 试验分析
3.1. 成坑过程及机理分析
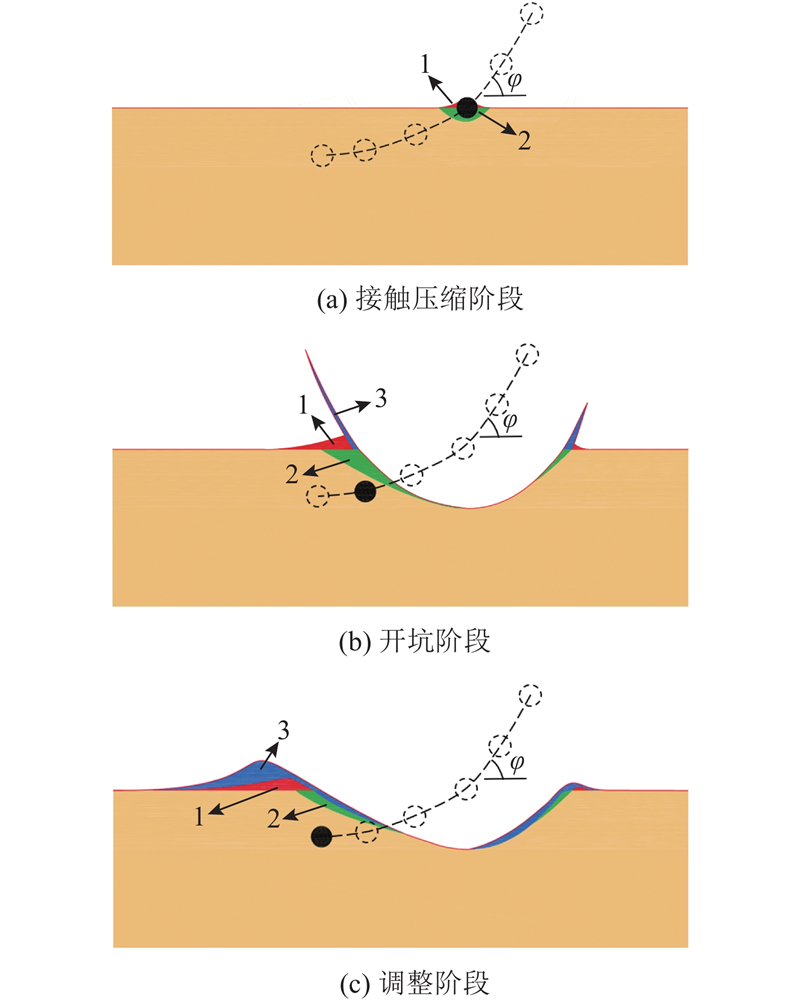
基于上述试验结果,将低速斜撞击成坑过程分为接触压缩、开坑及调整3个阶段. 如图12所示,虚线代表小球运动轨迹,深色球形代表小球所处位置. 土体表面产生隆起部分用区域1表示,溅射物回落到表面产生的堆积部分用区域2部分表示,成坑过程中产生的溅射物部分用区域3表示. 在接触压缩阶段,随着球体侵彻砂坑,只存在部分因球体侵彻产生的土体挤压隆起,此时并未产生溅射物;在开坑阶段,球体完全没入砂靶中,撞击动能在冲击过程中转换为砂靶颗粒的动能,产生溅射物,土体表面出现更大隆起;在调整阶段,冲击作用结束,此时砂坑开始卸载,土体表面略微回弹,溅射物回落到表面产生堆积,最终成坑形状由崩塌的坑壁及溅射物回落共同构成.
图 12
图 12 撞击成坑过程XOZ截面示意图
Fig.12 Schematic illustration of XOZ section of impact cratering mechanism
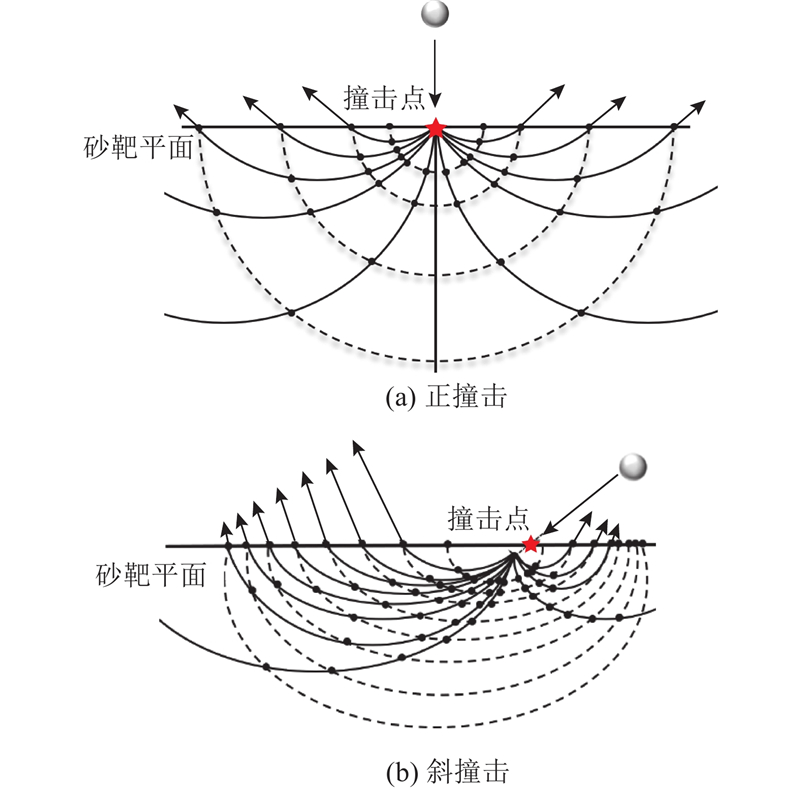
为了描述低速斜撞击条件下成坑过程中颗粒流场的运动特性,采用Maxwell[15]提出的半经验Z模型. 如图13所示,假设在撞击发生后,靶体材料内瞬时形成一簇以撞击点为中心的流线,且处于不同流线上的材料颗粒相互不存在干扰,溅射颗粒速度与撞击点距离呈反比. 在正撞击时,颗粒流场中心发生竖向位移,颗粒流场以撞击点为中心表现出较好的各向同性,最终产生的溅射颗粒以撞击点为圆心均匀分布,坑型截面为圆形. 在斜撞击时,颗粒流场中心发生沿撞击速度投影方向的位移,最终产生的溅射颗粒在速度投影方向上呈弯月形分布,在速度投影反向上溅射颗粒较少,坑型截面近似为蛋形截面. 值得注意的是,Z模型假定靶体材料的溅射角与其初始位置无关,这与试验过程中高速相机的实际观测到的现象存在些许差异. 但基于最终坑型的观测结果,Z模型能够在一定程度上说明低速正撞击及斜撞击条件下成坑过程中颗粒流场的运动特性.
图 13
图 13 半经验Z模型中靶体颗粒运动规律示意图
Fig.13 Schematic diagram of target particle movement in semi-empirical Z model
3.2. 成坑长径比尺度分析
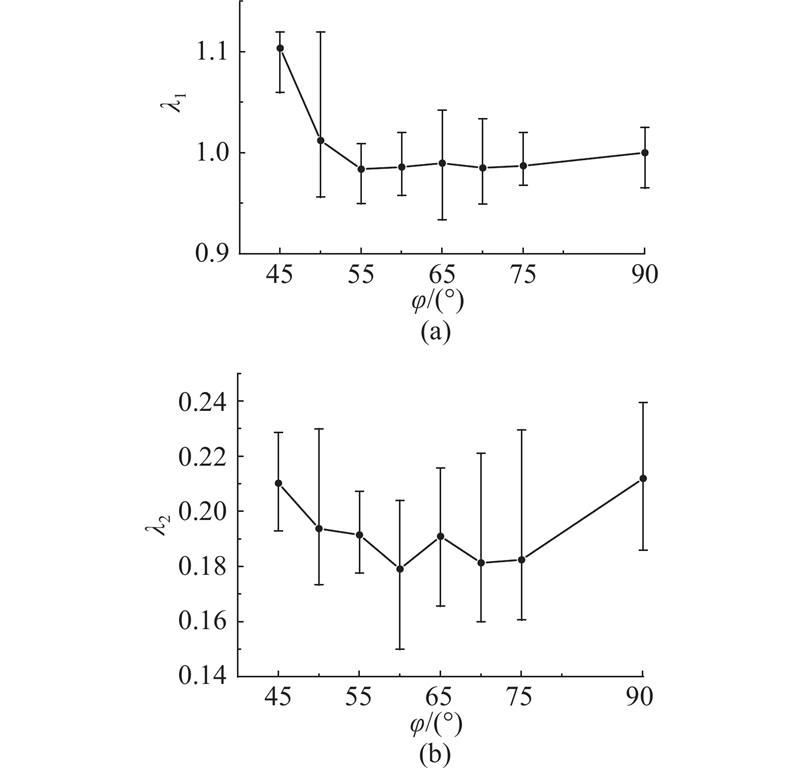
为了解撞击角度
图 14
图 14 坑形长度比和深宽比随撞击角度的变化曲线
Fig.14 Variation curve of length-to-width and depth-to-width ratios of cratering shapes with impact angle
3.3. 成坑尺寸的能量依赖性
分析撞击动能与成坑参数的关系,为了解成坑过程及机理,受初始试验条件控制,近似认为弹丸角度为0,因此弹丸撞击动能为
如图15所示为在不同
图 15
表 3 撞击动能与坑型参数的指数值
Tab.3
| k | k | |||||
| 坑长 | 坑体积 | 坑长 | 坑体积 | |||
| 45 | 0.30 | 0.87 | 65 | 0.35 | 0.90 | |
| 50 | 0.34 | 0.81 | 70 | 0.39 | 0.88 | |
| 55 | 0.35 | 0.74 | 75 | 0.39 | 0.88 | |
| 60 | 0.35 | 1.07 | 90 | 0.18 | 0.48 | |
3.4. 相似律分析
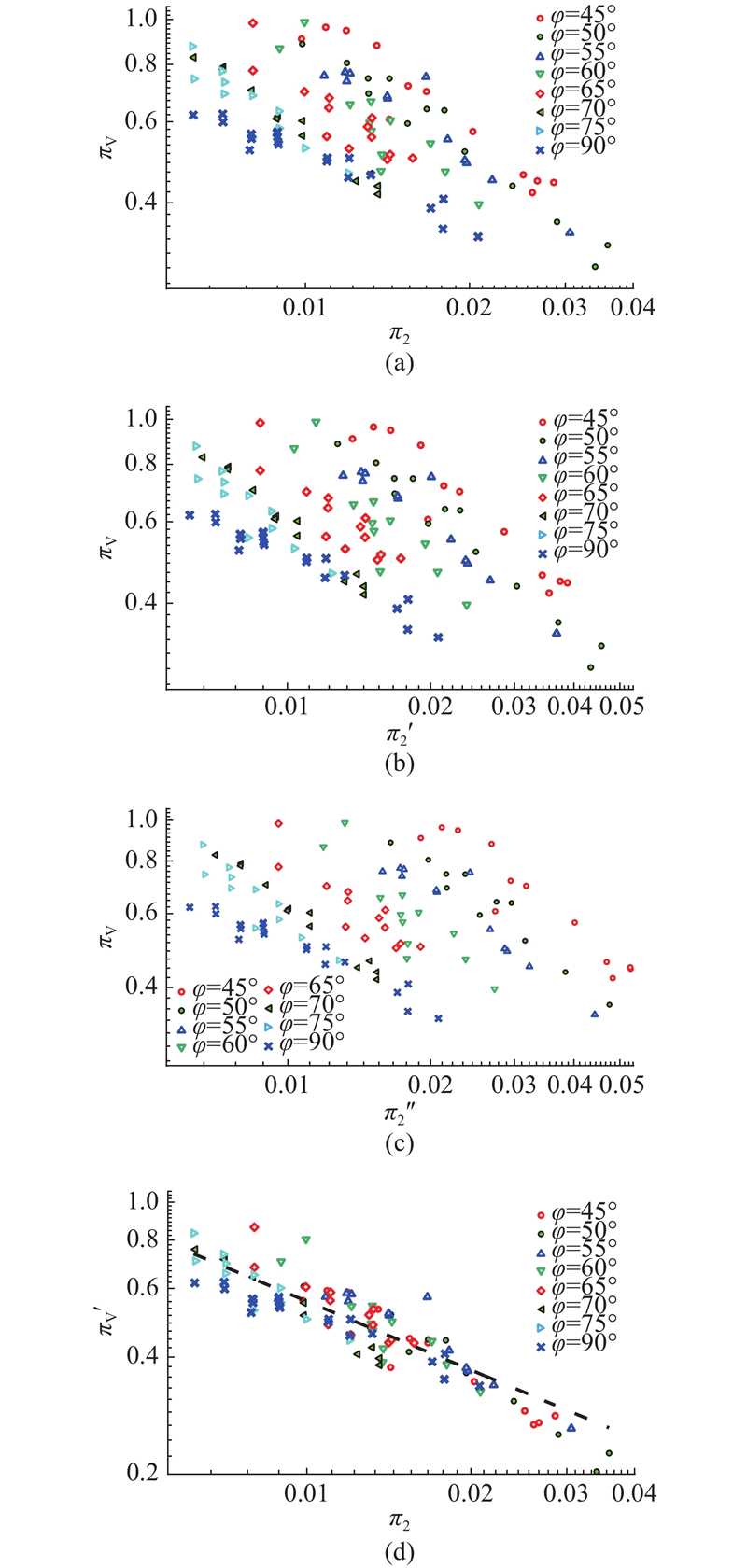
为了进一步了解成坑过程以及考虑将试验室结果应用于天文学上的可能性,基于
式中:
图 16
式中:
在早期相似律的研究中,部分学者使用动量描述弹丸的撞击,部分学者采用动能描述弹丸撞击,所获得的相似律形式不一致. 为了获得形式统一的相似律形式,Housen等[22]引入耦合参数,实现对动量与能量的综合考量. 定义耦合参数
式中:
3.5. 修正成坑相似理论适用性及其应用
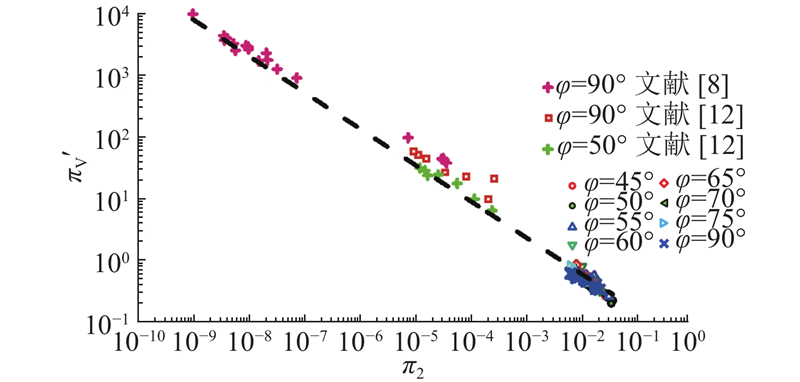
式(9)形式与高速撞击(
图 17
图 17 相似律关系在不同试验中的适用性
Fig.17 Scaling law relation applicability for different experiments
基于上述分析,可以通过水平靶体表面撞击坑的探测数据估计撞击发生的初始条件,如弹体直径、撞击角度、撞击速度等. 例如,在执行天体探测任务时,测量水平表面上发现的撞击坑相关尺寸,获得参量如坑长、坑体积,撞击角度与长宽比、深宽比之间的关系,估算得到撞击角度;基于遥感数据以及对靶体材料的分析,估算得到天体表面重力水平以及靶体密度,此时剩下撞击体质量、撞击体直径以及撞击速度3个未知参量. 假定撞击体为球体,且撞击体密度与天体表面颗粒相同,基于Takizawa等[12]的成坑宽度计算方法和式(8)的修正相似关系,计算获得弹体质量、弹体直径以及撞击速度. 撞击引起的地震动会导致撞击坑变形,从而影响撞击坑形状[18],本研究修正的相似律关系仅适用于刚形成的撞击坑. 此外,角度对纵横比、深宽比的影响很可能取决于撞击坑的规模[25].
4. 结 语
为了了解撞击坑的形成过程及规律,本研究针对水平砂靶表面进行球体低速斜撞击试验,得到如下结论. 1)基于
参考文献
Trajectory estimation for particles observed in the vicinity of (101955) Bennu
[J].DOI:10.1029/2019JE006363 [本文引用: 1]
Regolith migration and sorting on asteroid Itokawa
[J].DOI:10.1126/science.1134390 [本文引用: 1]
Craters, boulders and regolith of (101955) Bennu indicative of an old and dynamic surface
[J].DOI:10.1038/s41561-019-0326-6 [本文引用: 1]
On the scaling of crater dimensions: 2. impact processes
[J].DOI:10.1029/JB087iB03p01849 [本文引用: 1]
Crater ejecta scaling laws: fundamental forms based on dimensional analysis
[J].DOI:10.1029/JB088iB03p02485 [本文引用: 1]
Some recent advances in the scaling of impact and explosion cratering
[J].DOI:10.1016/0734-743X(87)90069-8 [本文引用: 3]
Transient crater growth in granular targets: an experimental study of low velocity impacts into glass sphere targets
[J].DOI:10.1016/j.icarus.2006.02.002 [本文引用: 1]
Ejecta velocity distribution of impact craters formed on quartz sand: effect of projectile density on crater scaling law
[J].DOI:10.1016/j.icarus.2015.08.035 [本文引用: 1]
Shape of impact craters in granular media
[J].DOI:10.1103/PhysRevE.76.041306 [本文引用: 1]
Scaling laws for the oblique impact cratering on an inclined granular surface
[J].DOI:10.1016/j.icarus.2019.113409 [本文引用: 5]
砂土液化后再固结体变规律表征与离心模型试验验证
[J].DOI:10.11779/CJGE201410011 [本文引用: 1]
Characterization of reconsolidation volumetric strain of liquefied sand and validation by centrifuge model tests
[J].DOI:10.11779/CJGE201410011 [本文引用: 1]
Influence of confinement on granular penetration by impact
[J].
Impact cratering on slopes
[J].DOI:10.1016/j.icarus.2017.02.021 [本文引用: 1]
The global effects of impact-induced seismic activity on fractured asteroid surface morphology
[J].DOI:10.1016/j.icarus.2005.07.005 [本文引用: 2]
Morphology and scaling of impact craters in granular media
[J].DOI:10.1103/PhysRevLett.91.104301 [本文引用: 1]
Impact of a liquid drop on a granular medium: inertia, viscosity and surface tension effects on the drop deformation
[J].DOI:10.1016/j.expthermflusci.2012.03.007 [本文引用: 1]
Ejecta from impact craters
[J].DOI:10.1016/j.icarus.2010.09.017 [本文引用: 1]
A strain-based porosity model for use in hydrocode simulations of impacts and implications for transient crater growth in porous targets
[J].DOI:10.1016/j.icarus.2005.10.013 [本文引用: 1]
Scaling of oblique impacts in frictional targets: implications for crater size and formation mechanisms
[J].DOI:10.1016/j.icarus.2009.07.018 [本文引用: 1]
The size-frequency distribution of elliptical impact craters
[J].