浙江大学学报(工学版)

浙江大学学报(工学版), 2024, 58(4): 817-827 doi: 10.3785/j.issn.1008-973X.2024.04.017

土木工程

斜拉桥钢塔地震损伤特性及输入地震动参数的影响

郏洲,, 谢旭,, 王天佳, 成程

1. 浙江大学 建筑工程学院，浙江 杭州 310058

Seismic damage characteristics of steel tower of cable-stayed bridge and influence of input ground motion parameters

JIA Zhou,, XIE Xu,, WANG Tianjia, CHENG Cheng

1. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China

通讯作者: 谢旭，男，教授，博士. org.orcid/0000-0002-4247-0487. E-mail：xiexu@zju.edu.cn

收稿日期: 2023-04-8  

基金资助: 国家自然科学基金资助项目（52178174，51878606）.

Received: 2023-04-8  

Fund supported: 国家自然科学基金资助项目（52178174，51878606）.

作者简介 About authors

郏洲（1999―），男，硕士生，从事桥梁抗震研究.org.orcid/0009-0002-2580-2432.E-mail：22112280@zju.edu.cn , E-mail：22112280@zju.edu.cn

摘要

以主跨为165 m的独塔钢斜拉桥为研究对象，建立精细化钢塔计算模型. 选取经峰值加速度调整后的历史地震记录作为地震动输入，分析顺桥向弹塑性时程反应，研究钢塔的钢板局部失稳以及超低周疲劳开裂特性，讨论纤维模型的适用性. 结果表明，沿高度方向加载的Pushover法能够预测钢塔顺桥向地震塑性发展的顺序和位置；纤维模型能够获得钢塔的弹塑性地震位移反应以及地震损伤位置，不能精确评价结构残余变形与损伤程度；输入地震动的峰值地面速度（PGV）/峰值地面加速度（PGA）值是影响结构地震损伤程度的指标；当PGA相同时，PGV/PGA值越大的地震动引起的钢塔地震损伤越显著，钢塔斜拉桥抗震性能验算应选用PGV/PGA值大的地震动时程.

关键词： 钢塔 ; 地震损伤 ; 近断层地震动 ; 钢板局部失稳 ; 超低周疲劳损伤

Abstract

Taking a single-tower steel cable-stayed bridge with a main span of 165 m as a research object, a refined calculation model of the steel tower was established. The historical seismic records adjusted by peak acceleration were selected as the ground motion input for the elasto plastic time-history analysis in the longitudinal direction of the bridge. The local instability of the steel plates and ultra-low cycle fatigue cracking characteristics of the steel tower were studied, and the applicability of the fiber model was discussed. Results show that the Pushover analysis method loaded along the height can predict the sequence and location of the seismic plastic development in the longitudinal direction of the steel tower. Although the fiber model can obtain the elastic-plastic seismic displacement response and the seismic damage location of the steel tower, it cannot accurately evaluate the residual deformation and the damage degree of the structure. The peak ground velocity (PGV)/peak ground acceleration (PGA) value of the input ground motion is an indicator that affects the degree of structural seismic damage. Under the same PGA, the seismic damage of the steel tower caused by ground motions with larger PGV/PGA values is significant. Therefore, the seismic performance verification of steel towers cable-stayed bridges should adopt the ground motion time history with larger PGV/PGA values.

Keywords： steel tower ; seismic damage ; near-fault ground motions ; local instability of steel plate ; ultra-low cycle fatigue damage

PDF (5212KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

郏洲, 谢旭, 王天佳, 成程. 斜拉桥钢塔地震损伤特性及输入地震动参数的影响. 浙江大学学报(工学版)[J], 2024, 58(4): 817-827 doi:10.3785/j.issn.1008-973X.2024.04.017

JIA Zhou, XIE Xu, WANG Tianjia, CHENG Cheng. Seismic damage characteristics of steel tower of cable-stayed bridge and influence of input ground motion parameters. Journal of Zhejiang University(Engineering Science)[J], 2024, 58(4): 817-827 doi:10.3785/j.issn.1008-973X.2024.04.017

在1995年日本阪神地震中，由于钢板局部失稳和钢材超低周疲劳开裂导致许多钢结构桥梁遭到严重的地震破坏[1-2]. 此后，考虑地震损伤影响的钢桥抗震设计方法开始受到关注，一系列试验研究和理论分析随之开展，钢桥墩地震反应计算方法以及结构抗震性能验算方法初步建立[2-9].

与钢桥墩相比，针对受力复杂的斜拉桥钢塔结构的地震损伤特性研究鲜少. 虽然神户大桥、天保山大桥、六甲大桥和摩耶大桥等钢斜拉桥在历史地震中有一定程度的损伤[1]，由于损伤集中在支座、伸缩缝以及阻尼器连接构件等附属结构部位，震害不能体现钢塔结构的地震破坏机理. 受到1995年日本阪神地震的影响，一些学者曾对斜拉桥钢塔结构的抗震性能进行数值模拟；如Raheem等[10]采用弯曲-曲率模型计算考虑钢塔塑性发展影响的结构地震反应，和崎宏一等[11-12]采用纤维模型分析桥塔在强震作用下的抗震性能. 由于弯曲-曲率模型、纤维模型引入平截面假定，结果不能反映钢板面外变形的影响，也不能计算塑性应变循环引起的钢材超低周疲劳开裂特性，只适用于结构损伤程度轻微的情形[13]. 精细的板壳模型是分析薄壁钢结构在强地震作用下塑性发展和钢板局部变形过程的有效方法，但是这种方法建模复杂且自由度多、计算效率低，在钢塔结构弹塑性地震反应分析中鲜有应用.

斜拉桥是大跨度桥梁的主要结构形式之一，在我国已广泛应用. 迄今为止，我国大部分的斜拉桥为混凝土索塔结构设计[14]，随着我国经济的发展和钢材产量的增加，钢塔结构逐渐成为斜拉桥结构的一种选项[15]，采用精细的计算模型对钢塔结构开展地震破坏机理研究将有助于结构设计的优化. 历史地震灾害表明，近断层地震动对桥梁具有强大的破坏力，特别是对于具有长周期振动特性的斜拉桥而言，近断层地震动可以造成严重的结构地震损伤[16-18]，分析近断层地震作用下的结构地震反应是评估斜拉桥钢塔结构抗震性能不可忽视的地震工况. 鉴于针对斜拉桥钢塔在强地震作用下的结构地震损伤特性的研究鲜少，本研究以跨度为（105+165） m的独塔钢斜拉桥为例，以历史地震中近断层地震记录的调整波作为输入地震动，采用精细的桥塔有限元计算模型分析钢塔的结构损伤特性以及地震动特性对计算结果的影响，讨论不考虑钢板变形影响的纤维模型在结构抗震设计中的适用性.

1. 计算模型及结构自振特性

1.1. 桥梁概况

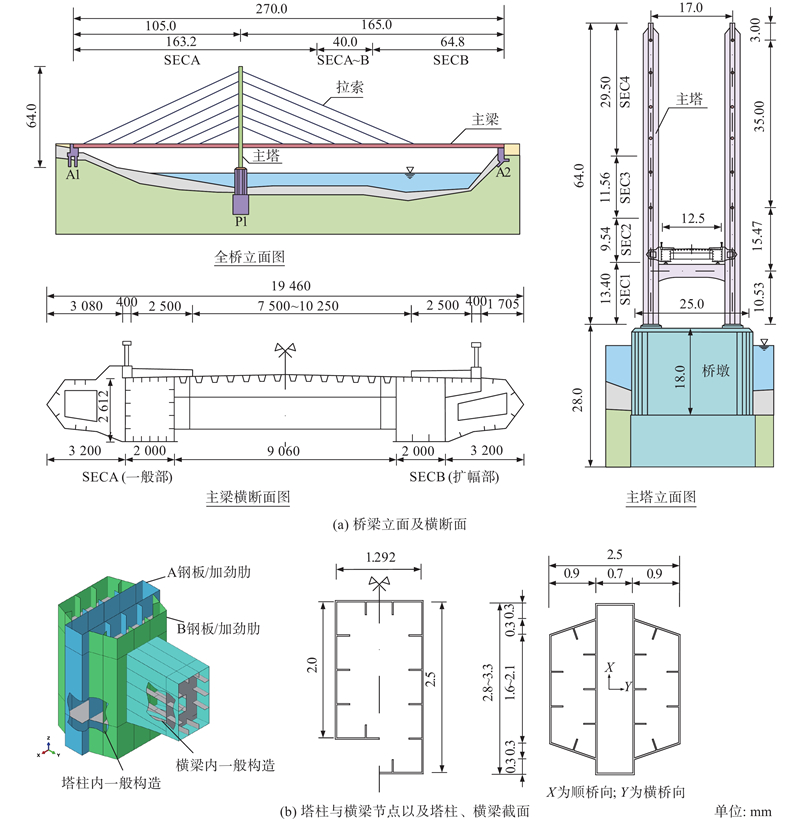
如图1所示(a)为跨度（105 +165） m的独塔钢斜拉桥[19]. H型钢塔高64 m，其中桥面以上的塔高50.19 m，横梁位于主梁下方，塔柱间距为17.0 m；塔柱采用单箱三室变截面，截面尺寸如图1(b)所示，基部至塔顶顺桥向的截面高度由3.3 m缩小至2.8 m，截面参数如表1所示. 表中，δA、δB分别为A板厚、B板厚，bR-A、bR-B分别为A板肋宽、B板肋宽，δR-A、δR-B分别为A板肋厚、B板肋厚. 钢材根据强度同等的原则改用Q355. 主梁为双箱单室截面，箱梁高2.6 m，单侧梁宽2.24 m，箱梁之间横梁连接，横梁净长9.05 m. 箱梁之间采用正交异性钢桥面板，U型加劲肋. 斜拉索采用平行钢丝束，竖琴型双索面布置.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   斜拉桥概况

Fig.1   Overview of cable-stayed bridge


表 1   主塔截面参数

Tab.1  Section parameters of main tower

mm
截面号δAδBbR-A×δR-AbR-B×δR-B
SEC13232230×22230×22
SEC22825230×22200×19
SEC32525200×19200×19
SEC42222200×19200×19

新窗口打开| 下载CSV


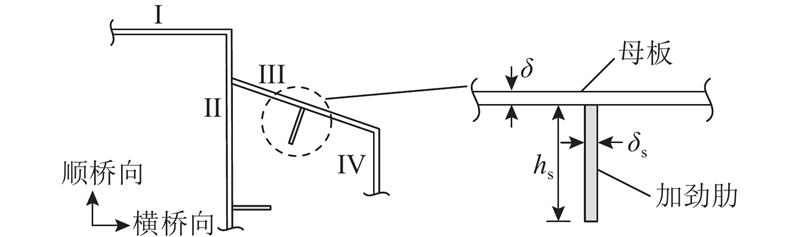
钢板的宽厚比R（母板宽厚比RR和加劲板整体宽厚比RF）和横隔板间距是影响钢板面外失稳的重要参数. 横隔板间距为3.08 m，与塔底截面钢板宽厚比[20]相关的计算式为

$ \left.\begin{array}{l}R_{\mathrm{R}}=\dfrac{b}{\delta} \sqrt{\dfrac{\sigma_{\mathrm{y}}}{E} \dfrac{12\left(1-v^{2}\right)}{4 n^{2} {\text{π}}^{2}}}, \\R_{\mathrm{F}}=\dfrac{b}{\delta} \sqrt{\dfrac{\sigma_{{\mathrm{y}}}}{E} \dfrac{12\left(1-v^{2}\right)}{{\text{π}}^{2} k_{\mathrm{F}}}}.\end{array}\right\} $

式中：v为泊松比；$ \sigma_{{\mathrm{y}}} $为屈服应力；E为弹性模量；b为受压翼缘板的宽度；δ为受压翼缘板的厚度；n为受压翼缘板被纵向加劲肋的分隔数；kF为屈曲系数，计算式为

$ k_{\mathrm{F}}=\left\{ \begin{array}{l}\dfrac{\left(1+\alpha^{2}\right)^{2}+n \gamma}{a^{2}\left(1+n \lambda_{{\mathrm{L}}}\right)},\;\;\; a \leqslant \sqrt[4]{1+n \gamma}; \\\dfrac{2(1+\sqrt{1+n y})}{1+n \lambda_{{\mathrm{L}}}},\;\;\; a > \sqrt[4]{1+n \gamma}.\end{array}\right. $

式中：$ \alpha $为翼缘板的相对尺寸，即横隔板间距a与翼缘板宽度b的比值（a/b）；$ \gamma $为纵向加劲肋的相对刚度，λL为单根纵向加劲肋截面积与母板的截面积之比，

$ \gamma=\dfrac{E I_{{\mathrm{L}}}}{b D^{'}}, \;\lambda_{{\mathrm{L}}}=\dfrac{A_{{\mathrm{s}}}}{b \delta}. $

式中：$ D^{\prime} $为单位宽度的钢板抗弯刚度，表达式为$ D^{\prime}=E t^{3} /\left[12\left(1-\mu^{2}\right)\right] $；IL为单根纵向加劲肋对翼缘板的抗弯惯性矩；As为单根纵向加劲肋的截面积. 如表2所示为由式（1）得到的塔底截面钢板宽厚比，钢板位置如图2所示.

表 2   塔底截面钢板宽厚比

Tab.2  Width-thickness ratios of steel plate at tower bottom

钢板位置RRRF
I0.5290.529
II0.4950.701
III0.3430.329
IV0.5090.706

新窗口打开| 下载CSV


图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   钢板位置

Fig.2   Position of steel plates


本桥在罕遇地震作用下的水平设计反应谱如图3所示[20]，其中S为加速度反应谱值，T为结构周期. 桥梁在罕遇地震动作用下容许发生有限的损伤.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   桥梁设计反应谱

Fig.3   Response spectra for seismic design


1.2. 计算模型

如图4所示为钢塔斜拉桥地震响应分析计算模型，主梁、拉索按弹性杆系单元模拟，考虑地震损伤的桥塔采用板壳模型，以模拟主塔截面局部失稳的力学行为. 为了使得主梁在面外和面内的变形刚度与实际截面等效，在左右箱梁之间引入一对斜向的桁架. 板壳单元的尺寸约为0.15 m. 拉索与桥塔和主梁的连接采用刚臂连接，忽略锚固部位的构造细节. 两端桥台和中间桥塔的约束方式分别如图4(b)、(c)所示. 计算模型不含承台质量的影响，在基础上表面用水平刚性杆连接两塔柱，并在中间设集中的基础弹簧模拟边界.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   桥梁计算模型

Fig.4   Analysis model of bridge


计算采用有限元通用程序ABAQUS 2018，同时考虑材料和几何非线性的影响. 桥梁的初始应力根据恒载和斜拉索张力作用下的平衡条件计算得到，并根据Ernst公式进行弹性模量修正以考虑斜拉索垂度的影响. 钢材滞回本构模型采用Chaboche提出的混合强化模型，材料参数如表3所示[21]，其中σ0为等效塑性应变为0时的应力，Q∞为屈服面的最大变化值，biso为屈服面随塑性应变发展变化的比率，Ckin,i为随动强化模量的初始值，$\xi_i $为塑性变形增加时随动强化模量减小的比率[22]. 结构阻尼采用Rayleiy阻尼，设定结构阻尼比约为2%.

表 3   Q355钢材的Chaboche模型参数

Tab.3  Chaboche model parameters of Q355 steel

参数数值参数数值
σ0/MPa391.2ξ1245
Q∞/MPa21ξ2155
biso10ξ350
Ckin,i (i=1, 2, 3, 4)/MPa1 800ξ430

新窗口打开| 下载CSV


1.3. 结构自振特性

如图5所示为斜拉桥前10阶振型，对应的自振频率及振型特征如表4所示. 表中，f为自振频率，Meff为有效质量率，坐标X、Y和Z分别表示顺桥向、横桥向和竖向. 结果表明，桥梁在面内的振型主要为主梁纵飘，X方向的有效质量率达到80%；在面外，一阶侧弯振型的影响较大，Y方向的有效质量率为31%.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   桥梁主要振型

Fig.5   Main modes of bridge


表 4   桥梁自振特性

Tab.4  Natural vibration characteristics of bridge

模态振型f/HzMeff/%
XYZ
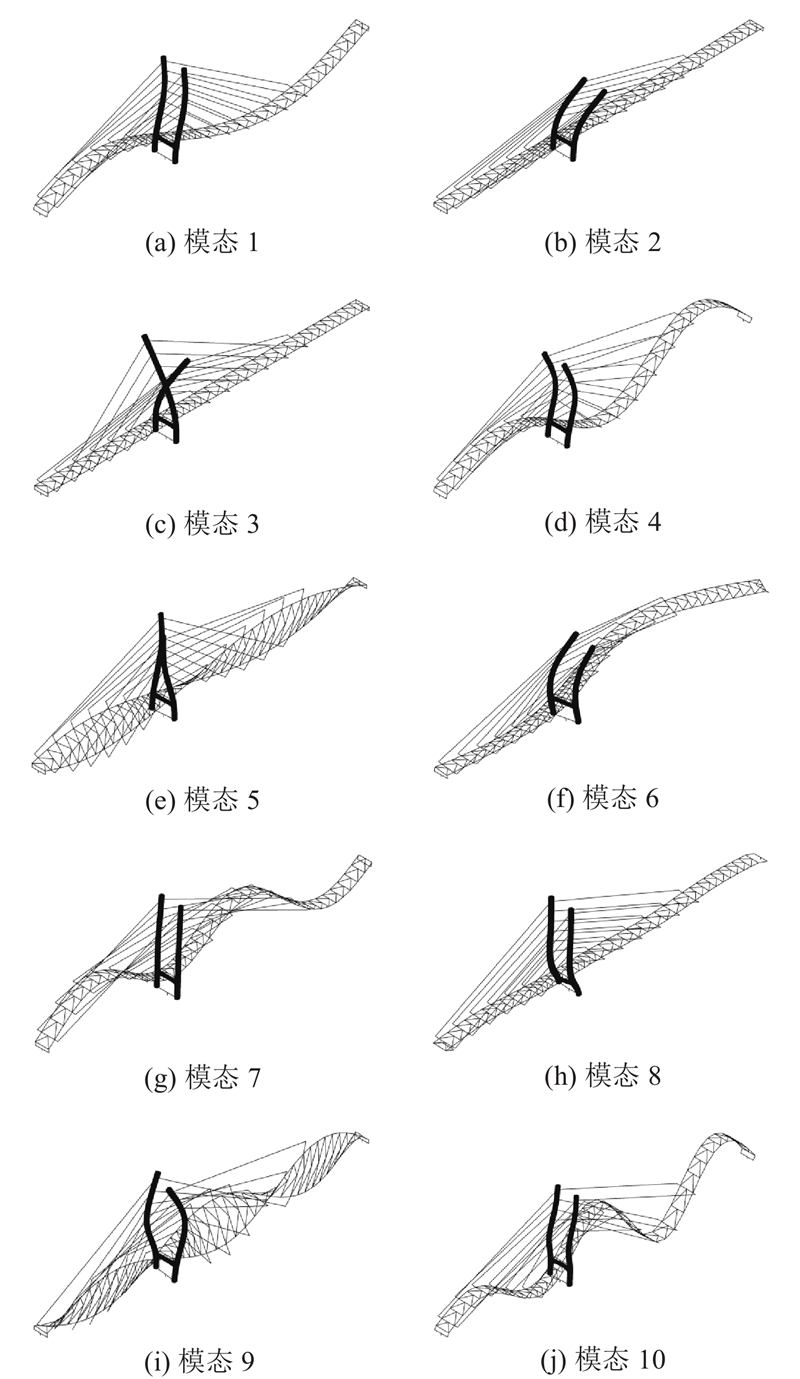
1主梁一阶竖弯(面内)0.451011
2塔对称侧弯0.670140
3塔反对称侧弯0.74000
4主梁二阶竖弯(面内)0.852021
5主梁一阶扭转1.06000
6主梁一阶侧弯1.150310
7主梁三阶竖弯(面内)1.250031
8主梁纵飘(面内)1.578001
9主梁二阶扭转1.75000
10主梁四阶竖弯(面内)1.84106

新窗口打开| 下载CSV


2. 结构地震损伤特性

本桥的塔梁之间采用铰接体系，桥梁面内的抗震性能比横桥向薄弱，因此以面内的地震反应为对象进行分析.

2.1. 基于Pushover法的计算结果

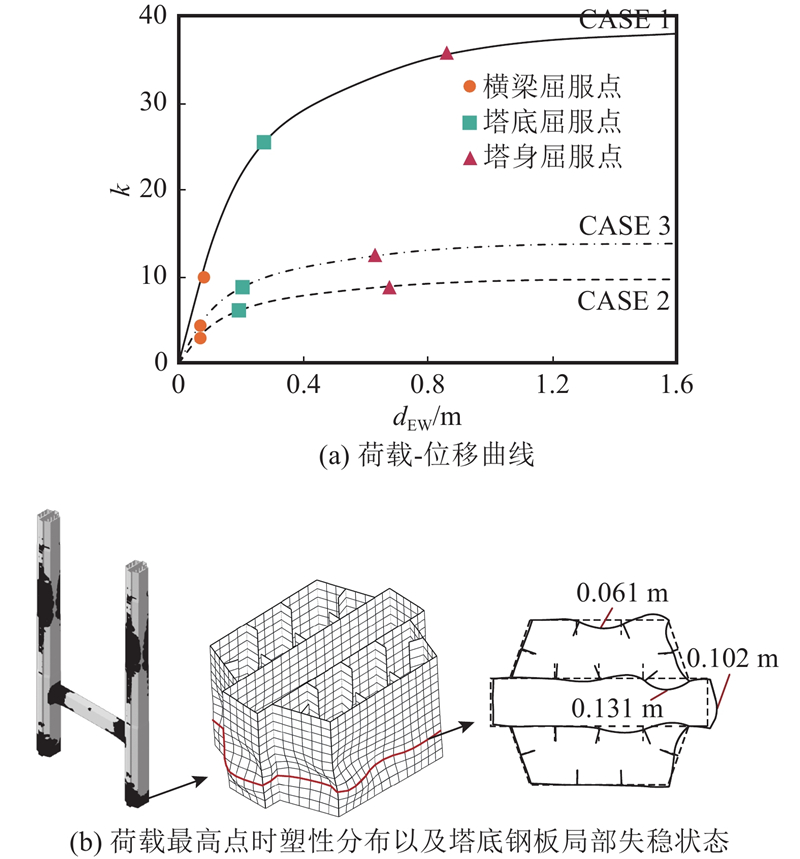
Pushover法是分析简单结构地震损伤特性的常用方法，研究者利用这种方法通过对结构施加单调递增的水平荷载来研究结构在地震作用下的损伤过程以及非线性变形性能. 由于Pushover法采用固定的荷载模式，一般适用于结构地震反应受单一振型控制的情形[2]. 本桥虽然结构形式复杂，但是在顺桥向第8阶振型的有效质量率为80%（不考虑桥塔基础质量），满足Pushover法计算结构破坏过程的振型有效质量率条件[20,23]，因此Pushover法仍不失为预测桥梁地震损伤的有效方法.

如图6所示，为了分析荷载模式对桥梁结构的损伤位置和损伤过程计算结果的影响，分析采用3种荷载模式进行：沿桥塔高度方向的倒三角形（CASE1）、矩形（CASE2），顺桥向卓越振型（CASE3）. 图中，ϕ为荷载沿高度方向的分布函数， CASE3为第8阶振型的水平向模态位移分量. 计算时，在顺桥向逐渐增加荷载系数k，用弹塑性静力方法计算桥梁的变形和应力.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   Pushover法加载模式

Fig.6   Load modes of Pushover analysis method


如图7(a)所示为3种加载模式得到的荷载-塔顶水平位移曲线，其中dEW为塔顶顺桥向位移. 结果表明，3种加载模式获得的荷载-位移曲线相似，初始屈服发生在塔梁连接的横梁位置，随着荷载增加，塔底和塔身相继进入塑性. 由于3种模式的水平荷载合力不同，荷载系数k有较大的差异，但屈服位移接近，且均表现出良好的结构延性. 塔底承受全桥的水平地震作用，随着水平荷载的增加，塔底受压侧发生钢板局部变形. 如图7(b)所示，以CASE3为例给出荷载最高点时的塑性分布和塔底钢板局部变形，结果表明，钢板的最大面外变形超过13 cm，发生在内部的腹板位置，由表2不难看出，该部位钢板的宽厚比相对较大.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   Pushover法的计算结果

Fig.7   Calculation results of Pushover analysis method


2.2. 基于弹塑性时程分析的计算结果

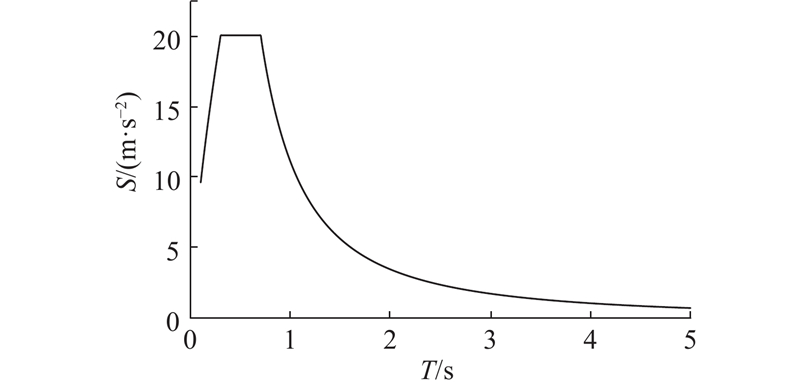
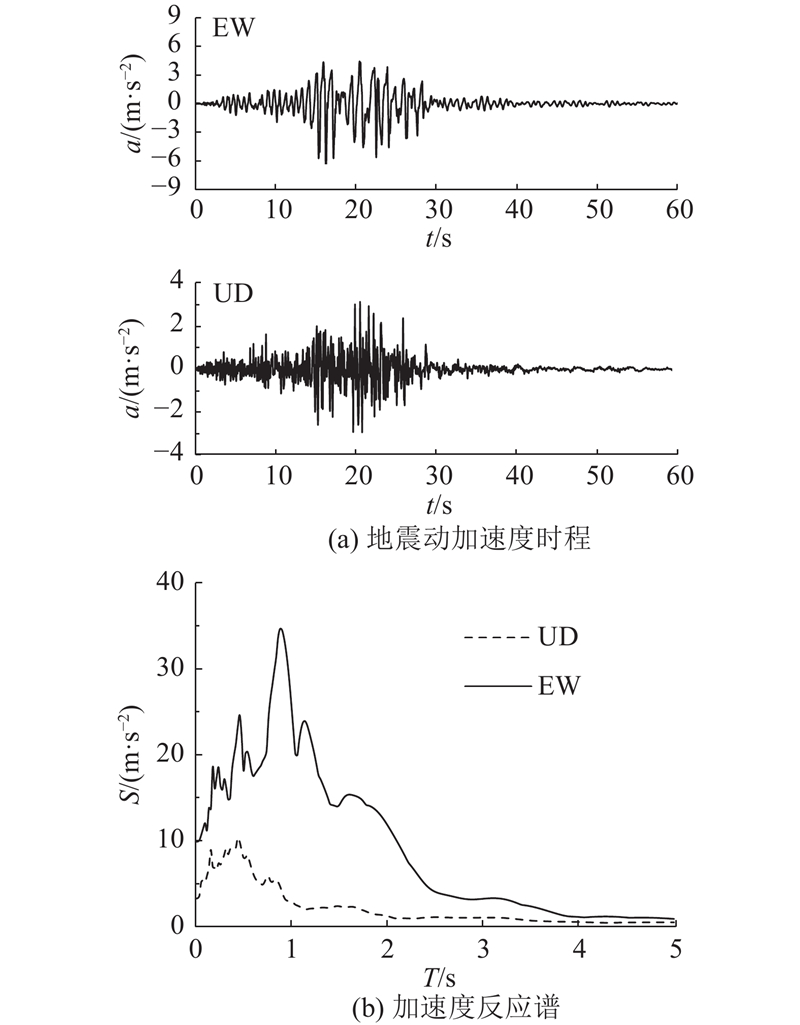
为了使桥梁在地震作用下能够进入弹塑性状态，选取1999年集集地震TCU-084台站记录作为输入地震动. 该台站位于断层上盘，断层距离为8.2 km，水平东西EW向地震动的峰值地面加速度（peak ground acceleration , PGA）与图3的设计地震作用在T=0.1 s的加速度反应谱值接近. 如图8所示为输入地震动加速度时程a和阻尼比取5%的加速度反应谱，竖直上下UD向和水平EW向加速度峰值分别为3.14、9.87 m/s2. 由于近断层地震动包含长周期成分，在周期1.0~3.0 s的地震动明显大于本桥的设计加速度反应谱，在短周期范围内(0~1.0 s)该台站EW向地震动反应谱值与设计反应谱接近.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   输入地震动及反应谱

Fig.8   Input ground motion and response spectrum


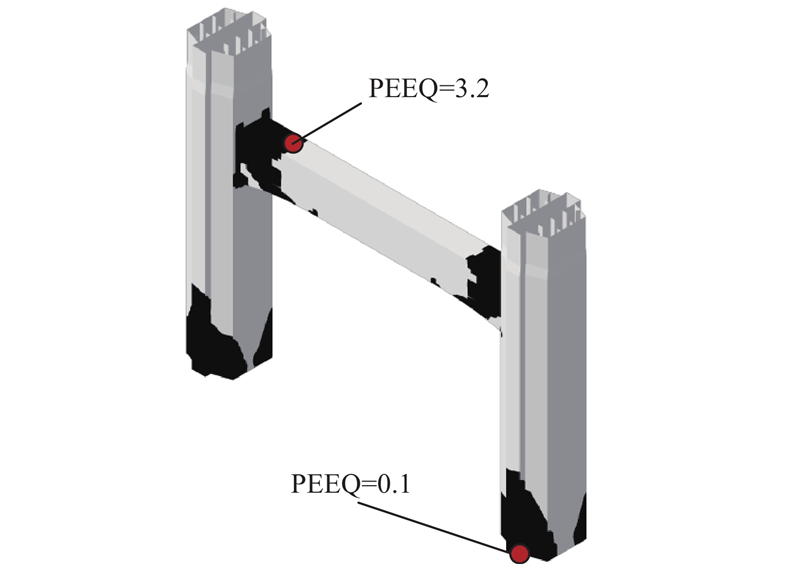
如图9所示为桥塔塑性区分布，其中PEEQ为等效塑性应变. TCU-084台站地震记录输入时钢板没有发生局部失稳，地震损伤仅限于塔底和横梁进入塑性，其中横梁位置的塑性程度明显大于桥塔底部，结果与Pushover法大致相似，可以认为Pushover法能够预测桥梁的地震损伤过程以及桥塔破坏状态.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   桥塔塑性区域分布

Fig.9   Plastic zone distribution of bridge tower


3. 地震动参数对钢塔地震损伤的影响

3.1. 输入地震动参数

为了研究地震动参数对斜拉桥钢塔地震损伤特性的影响，将集集地震6个台站的地震记录经峰值加速度调整一致后作为输入地震动，比较地震动参数对结构地震反应的影响. 集集地震的震中位于台湾西部，震级为Mw7.6，属于逆冲型断层. 断层倾角约30°，在断层北端转变成以左旋斜滑为主的运动，沿着车笼埔活断层形成长约100 km的地表破裂带，其中近南北向的破裂长度约85 km，在丰原发生转折，向东破裂长度约15 km[24-26]. 如表5所示为各台站的地理位置，其中λ为台站经度，ω为台站纬度. 如图10所示为调整后的地震动反应谱. 6个台站包括断层前方（TCU-036）、上盘（TCU-052、TCU-084）、下盘（TCU-076、TCU-109）和后方（CHY-087）. EW向和UD向分别作为顺桥向及竖向输入，水平向地震动的PGA根据该桥的设计地震作用统一调整到9.87 m/s2，竖向地震按照同样比例调整. 为了保持地震动的原始特性，对波形不做改变. 各台站的断层距和地震动的峰值地面速度（peak ground velocity, PGV）/PGA值如表6所示，其中G为断层距. 下盘台站TCU-109短周期竖向地震动卓越，水平地震动在1.0~5.0 s的周期范围内卓越；下盘台站TCU-076虽然断层距小，竖向和水平向的地震动仅在短周期区域卓越. 后方的地震动在短周期0.3~0.7 s相对于其他台站较强；上盘台站TCU-052和前方台站TCU-036长周期相对较卓越，但周期范围相对比较小. 对比如表6所示的PGV/PGA值可以发现，PGV/PGA值较大的地震动时程，卓越周期范围宽、长周期地震动较强，反之则小；还可以发现，6个台站的地震动PGV/PGA指标与台站位置没有明显的相关性.

表 5   各台站地理位置

Tab.5  Geographic location of stations

位置台站号λ/（°）ω/（°）
破裂前方TCU-036120.69624.449
破裂前方TCU-052120.73924.198
破裂区上盘TCU-084120.90023.883
破裂区下盘TCU-076120.67623.908
破裂后方TCU-109120.57124.085
破裂后方CHY-087120.51923.385

新窗口打开| 下载CSV


图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   调整后的地震动反应谱

Fig.10   Adjusted seismic response spectrums


表 6   台站的断层距和地震动的PGV/PGA值

Tab.6  Fault distance of stations and PGV/PGA values of ground motion

位置台站号G/km(PGV/PGA)/s
破裂前方TCU-036-EW19.830.429
破裂区上盘TCU-052-EW0.660.431
破裂区上盘TCU-084-EW8.200.130
破裂区下盘TCU-076-EW2.740.153
破裂区下盘TCU-109-EW13.060.383
破裂后方CHY-087-EW37.480.077

新窗口打开| 下载CSV


3.2. 地震动参数对钢塔地震损伤的影响

如表7所示为桥塔地震反应计算结果，其中dx为塔顶顺桥向残余位移，μm为塔底部位最大PEEQ的板单元积分点的塑性率. 当输入PGV/PGA值大于0.3的3个台站（TCU-036、TCU-052、TCU-109）地震动时，塔顶均产生残余位移，其中TCU-109的地震残余位移和塑性率最大，残余变形为塔高的0.26%，塑性率为10.68. PGV/PGA值小于0.2的其他3个台站（TCU-084、TCU-076、CHY-087）地震动没有残余位移，且塑性率小. 结果表明，PGV/PGA值大、长周期范围内强度大的地震动，会对斜拉桥产生很强的地震作用.

表 7   桥塔地震反应计算结果

Tab.7  Calculation results of seismic response of bridge tower

位置台站号dx/mμm
拉应变压应变
破裂前方TCU-0360.0774.43−3.90
破裂区上盘TCU-0520.08211.80−6.82
破裂区上盘TCU-0840.0004.58−4.12
破裂区下盘TCU-0760.0001.41−4.07
破裂区下盘TCU-1090.16510.66−10.68
破裂后方CHY-0870.0001.52−2.63

新窗口打开| 下载CSV


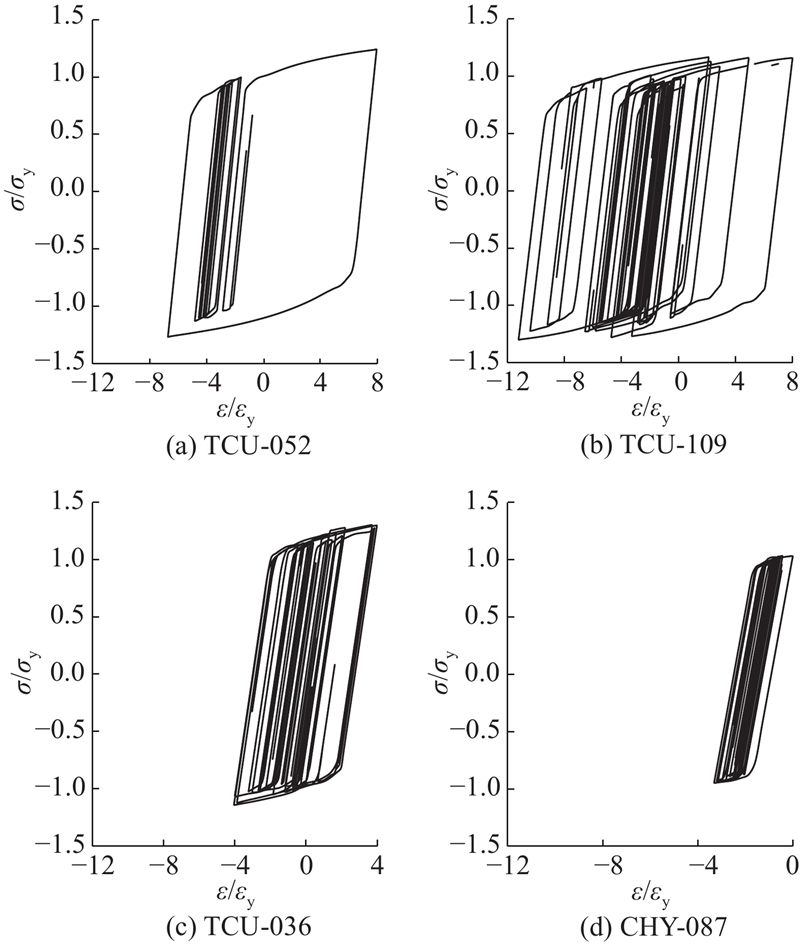
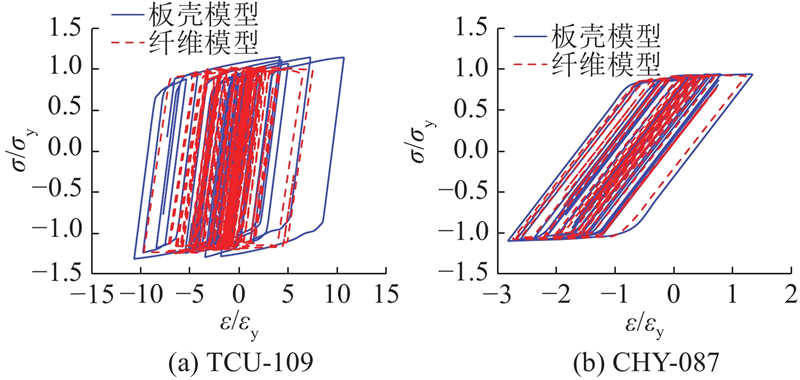
如图11所示为4个方位的地震动引起的塔底塑性应变最大位置的滞回曲线. 图中，σ、ε为纵向应力和应变，σy、εy为屈服应力和屈服应变. 由图可见，除长周期卓越的台站TCU-109、TCU-052外，其他台站的地震动在塔底基本上没有产生钢板面外局部变形，结构的地震损伤主要表现为塑性发展，特别是在后方台站（CHY-087）地震作用下，结构塑性应变非常小.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   塔底最大等效塑性应变位置的滞回曲线

Fig.11   Hysteretic curves of maximum equivalent plastic strain position at tower bottom


选取1979年Imperial Valley地震以及1994年Northridge地震中2组持时基本相同、断层类型不同的近断层地震动进行弹塑性时程分析. 如表8所示为2个台站的断层信息和地震动的PGV/PGA值. 表中，LV-3为Leona Valley #3台站，EL-10为EL Centro Array #10台站. 按照相同的地震动处理方法进行计算， 如表9所示为2组地震动作用下桥塔地震反应计算结果. PGV/PGA值较大的EL-10台站地震损伤程度明显大于PGV/PGA值较小的LV-3台站.

表 8   台站的断层信息和地震动的PGV/PGA值[27]

Tab.8  Fault information of stations and PGV/PGA values of ground motion[27]

地震名称断层类型台站号G/km(PGV/PGA)/s
Imperial Valley走滑断层EL-108.600.298
Northridge逆冲断层LV-337.330.077

新窗口打开| 下载CSV


表 9   不同断层类型的桥塔地震反应计算结果

Tab.9  Calculation results of seismic response of bridge tower with different fault types

台站号dx/mμmPEEQ
拉应变压应变
EL-100.1094.85−1.110.016
LV-30.0000.65−1.620.002

新窗口打开| 下载CSV


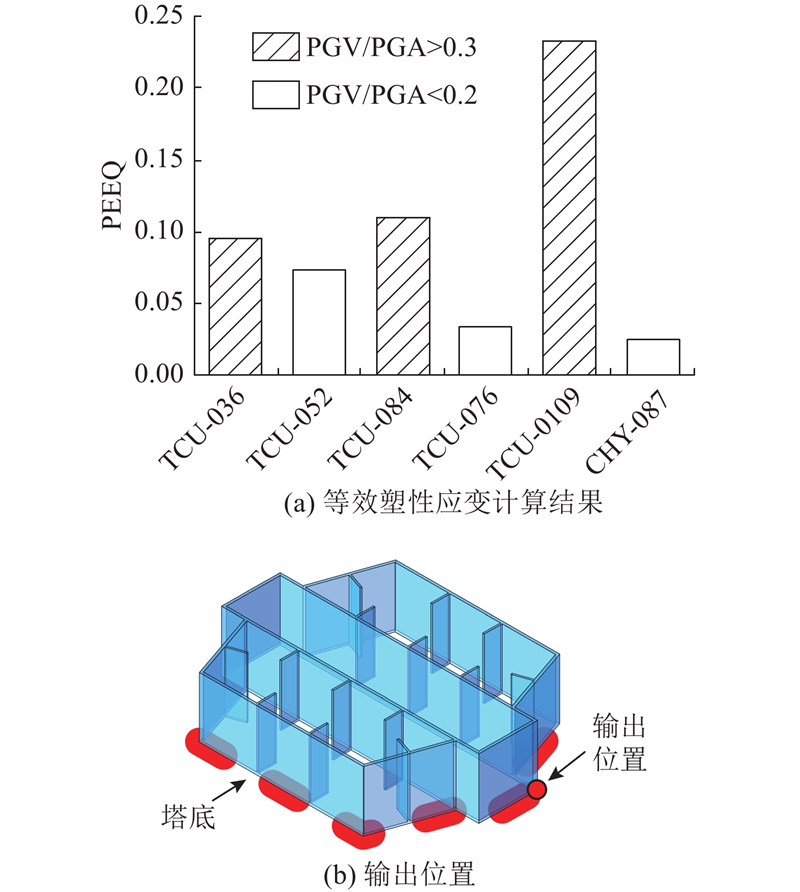
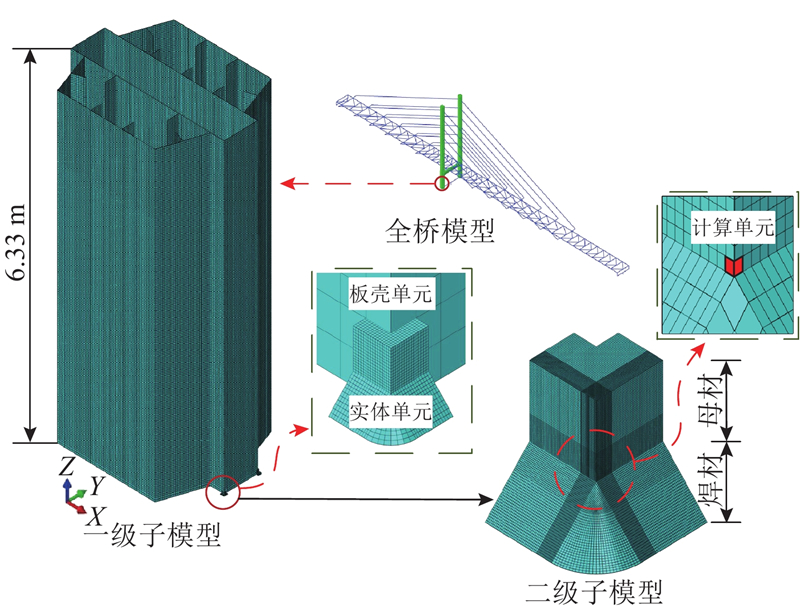
如图12所示为集集地震6个台站地震动作用下塔底的等效塑性应变计算结果以及输出位置，当输入TCU-109台站地震动时，等效塑性应变明显大于其他台站地震动输入，最有可能发生超低周疲劳破坏. 为了分析桥塔发生超低周疲劳破坏的可能性，采用子模型技术计算局部塑性应变，用考虑应力三轴度影响的循环空穴成长模型（CVGM）[28-29]计算超低周疲劳开裂强度. 计算模型如图13所示，采用精细实体单元的二级子模型计算塔底应变集中部位的应力三轴度和等效塑性应变，板壳单元和实体单元的连接方式采用ABAQUS软件中的Shell-Soild耦合. 在一级子模型和二级子模型的边界上，利用软件中子模型节点驱动技术，分别输入在全桥和一级子模型计算得到的结构变形和内力时程. 二级子模型的单元尺寸大致为0.3 mm，满足材料超低周疲劳验算特征长度的要求[29]. 假定塔底焊接部位的焊脚尺寸为32 mm×32 mm，材料参数采用文献[30]的标定结果，如表10所示.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   塔底等效塑性应变计算结果以及输出位置

Fig.12   Calculation results of equivalent plastic strain at tower bottom and output points


图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   超低周疲劳验算的子模型

Fig.13   Submodel for ultra-low cycle fatigue verification


表 10   焊缝材料的Chaboche混合强化模型参数

Tab.10  Chaboche combined hardening model parameters of weld material

参数数值参数数值参数数值
σ0/MPa428.5Ckin,1/MPa12752.3ξ2160
Q∞/MPa17.4ξ1160Ckin,3/MPa630.5
biso0.4Ckin,2/MPa1111.2ξ326

新窗口打开| 下载CSV


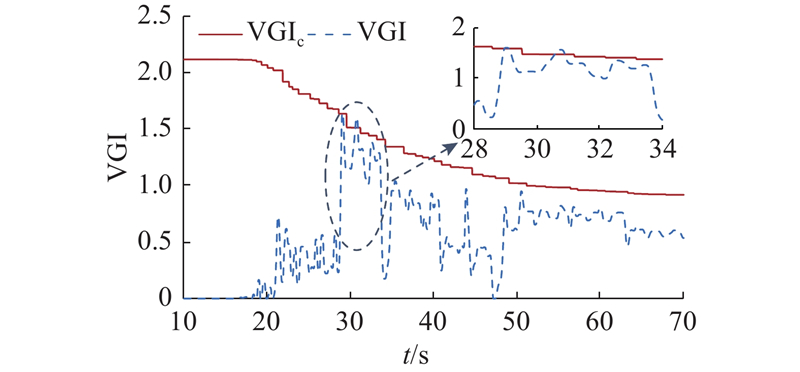
在循环空穴成长模型（cyclic void growth model，CVGM）中，循环荷载作用下的空穴成长指数VGI被作为超低周疲劳断裂预测指标，临界空穴成长指数VGIc随着循环荷载作用下塑性损伤的累积逐步下降，当VGI达到临界空穴成长指数VGIc时，认为材料发生韧性开裂. 如图14所示为输入TCU-109台站的地震动时得到的VGI和VGIc计算结果. 结果表明，在30 s附近两者相交，结构达到发生超低周疲劳开裂的条件，表明在进行钢塔结构抗震设计时，须关注塑性应变集中部位发生超低周疲劳开裂的可能性.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   地震作用下塔底的空穴成长指数履历

Fig.14   Void growth index evolution process at tower bottom under seismic effects


3.3. 纤维模型的适用性

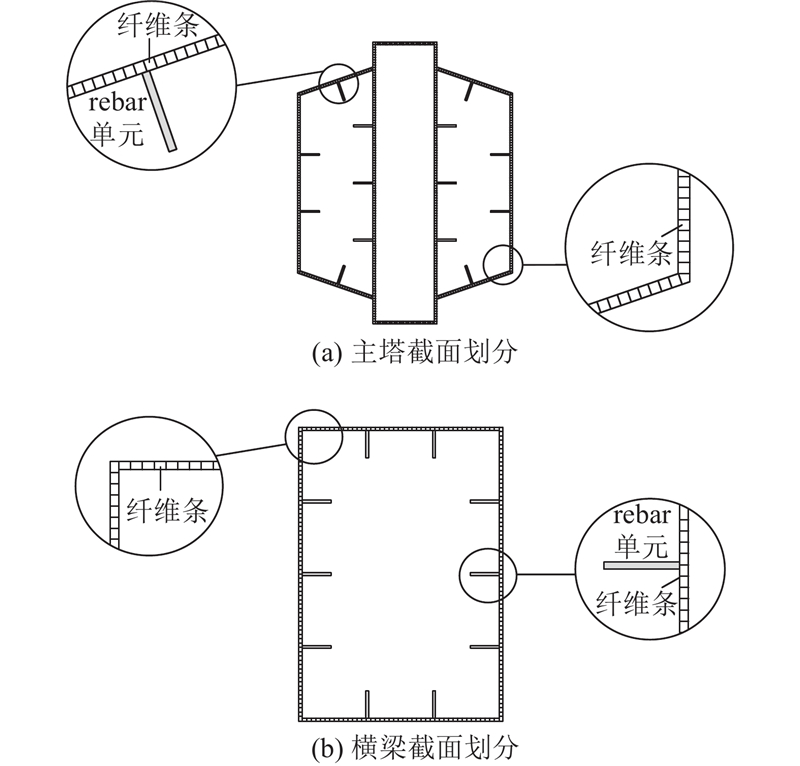
纤维模型是结构弹塑性地震反应分析的实用计算模型，与板壳有限元计算模型相比，具有计算量小、容易收敛的优点. 常用的纤维模型基于平截面假定，不能考虑钢板面外变形的影响，为了检验纤维模型在本桥中的适用性，塔身和横梁改用纤维单元并进行弹塑性地震反应计算. 如图15所示为塔、横梁截面纤维划分情况，其中加劲肋用rebar单元模拟，其余钢板每20~50 mm宽划分一条纤维，塔柱和横梁截面纤维数为210~700. 由于ABAQUS软件没有单轴应力的Chaboche混合强化模型，考虑材料硬化的影响，计算采用双直线随动强化模型，屈服以后的弹性模量取初始弹性模量的1%.

图 15

新窗口打开| 下载原图ZIP| 生成PPT

图 15   截面纤维条划分情况

Fig.15   Fiber division of sections


如表11所示为2种计算模型在面内的自振周期对比，其中Meff-X为X向有效质量率，Meff-Z为Z向有效质量率. 由计算结果可知，纤维模型的结构动力特性与板壳模型基本一致，在弹性范围内结构特性相同. 如表12所示为由纤维模型得到的桥塔地震反应及与板壳模型计算结果对比，其中Dx为塔顶顺桥向峰值位移，括号内为2种计算模型的结果差异. 可以发现，当输入TCU-109和TCU-052台站的地震动时，因结构的应变塑性率超过5.0，2种计算模型的结果差异超过25%，而输入其他地震动时的最大差异在10%左右. 表明当塑性应变较大时，不考虑钢板局部变形的纤维模型会带来较大的应变计算结果误差，并低估结构的残余变形. 如图16所示为应变塑性最大（TCU-109）和最小（CHY-087）时2种模型得到的塔底应力－应变履历对比. 由图可知，虽然2种模型得到的计算结果趋势一致，但差异随着塑性应变增大而增加.

表 11   自振特性比较

Tab.11  Comparison of natural vibration characteristics

模态f/HzMeff-X/%Meff-Z /%
板壳模型纤维模型板壳模型纤维模型板壳模型纤维模型
10.4450.437111111
40.8500.847212121
71.2541.248013131
81.5671.558807910

新窗口打开| 下载CSV


表 12   纤维和板壳单元模型的桥塔地震反应计算结果比较

Tab.12  Calculation results comparison of seismic responses of bridge tower with fiber and shell elements models

台站位置台站号Dx/mdx/mμmPEEQ
拉应变压应变
破裂前方TCU-036-EW0.412（3.51%）0.069（10.39%）4.25（4.06%）−3.72（4.62%）0.087（8.42%）
破裂区上盘TCU-052-EW0.626（7.26%）0.062（24.39%）8.42（28.64%）−6.25（8.36%）0.061（15.28%）
破裂区上盘TCU-084-EW0.275（0.73%）0.000（0.00%）4.33（5.46%）−3.88（5.83%）0.098（10.09%）
破裂区下盘TCU-076-EW0.269（2.28%）0.000（0.00%）1.37（2.84%）−3.85（5.41%）0.031（6.45%）
破裂区下盘TCU-109-EW0.603（8.77%）0.118（28.48%）7.36（30.96%）−9.33（12.64%）0.183（21.46%）
破裂后方CHY-087-EW0.163（1.81%）0.000（0.00%）1.47（3.29%）−2.57（2.28%）0.024（5.30%）

新窗口打开| 下载CSV


图 16

新窗口打开| 下载原图ZIP| 生成PPT

图 16   不同模型塔底最大等效塑性应变位置的滞回曲线

Fig.16   Hysteretic curves of maximum equivalent plastic strain position at tower bottom for different models


4. 结　论

（1）当基础以上桥梁结构在水平方向存在有效质量率较大的振型时（本桥为80%），按Pushover法能够预测桥梁结构地震损伤的发展过程和位置，且沿高度方向的加载模式对计算结果的影响不大.

（2）当PGA相同时，输入PGV/PGA值较大的地震动引起的钢塔地震损伤程度较大. 因此，钢塔斜拉桥抗震性能验算应选用PGV/PGA值大的地震动时程作为输入条件.

（3）在PGA=9.87 m/s2的强地震作用下，本桥塔身虽然没有发生明显的钢板局部变形，结构整体的抗震性能较好，但是在塑性应变集中部位仍有发生超低周疲劳的可能性. 因此，钢塔抗震设计时，须关注塑性应变集中部位的超低周疲劳损伤状况.

（4）对于翼缘钢板宽厚比为0.529的钢塔截面，当应变塑性率小于5.0时，纤维模型能得到的应变和残余变形与板壳模型的差异最大为10%左右，随着应变塑性率增大，两者的差异增大. 因此，当应变塑性率不超过3.0时，抗震设计可采用纤维模型来验算结构抗震性能.

（5）本研究建立精细化钢桥塔有限元模型，分析斜拉桥钢塔结构在强震作用下的损伤特性以及与地震动参数的相关性. 研究以特定的桥梁为对象，有待通过对其他桥梁的研究获得具有普遍适用性的结论.

参考文献

日本土木学会. 阪神淡路大震災における鋼構造物の震災の実態と分析[M]. 東京: 丸善, 1999.

[本文引用: 2]

宇佐美勉. 鋼橋の耐震·制震設計ガイドライン[M]. 東京: 丸善, 2006.

[本文引用: 3]

ZHUGE H, XIE X

Hysteresis model for fiber elements in effective damaged zone of square-section steel piers considering local instability effect of steel plates

[J]. Journal of Structural Engineering, 2020, 146 (8): 04020156

DOI:10.1061/(ASCE)ST.1943-541X.0002698     

CHEN S, XIE X, ZHUGE H

Hysteretic model for steel piers considering the local buckling of steel plates

[J]. Engineering Structures, 2019, (183): 303- 318

刘乃藩, 高圣彬

带肋圆形截面钢桥墩的延性性能预测

[J]. 哈尔滨工业大学学报, 2017, 49 (3): 138- 143

LIU Naifan, GAO Shengbin

Ductility prediction of stiffened steel pipe-section bridge piers

[J]. Journal of Harbin Institute of Technology, 2017, 49 (3): 138- 143

KANG L, GE H

Predicting ductile crack initiation in steel bridge piers with unstiffened box section under specific cyclic loadings using detailed and simplified evaluation methods

[J]. Advances in Structural Engineering, 2015, 18 (9): 1427- 1442

DOI:10.1260/1369-4332.18.9.1427     

USAMI T, GAO S, GE H

Stiffened steel box columns. Part 2: ductility evaluation

[J]. Earthquake Engineering and Structural Dynamics, 2000, 29 (11): 1707- 1722

DOI:10.1002/1096-9845(200011)29:11<1707::AID-EQE990>3.0.CO;2-7     

JENOTHAN M, JAYASINGHE J, BANDARA C

Lateral behaviour and performance evaluation of steel piers under cyclic lateral loading

[J]. Journal of Constructional Steel Research, 2023, 201: 107764

DOI:10.1016/j.jcsr.2022.107764     

谢旭, 唐站站. 钢桥抗震设计[M]. 北京: 科学出版社, 2019.

[本文引用: 1]

RAHEEM S E A, HAYASHIKAWA T, DORKA U

Ground motion spatial variation effects on seismic response control of cable-stayed bridges

[J]. Earthquake Engineering and Engineering Vibration, 2011, 10: 37- 39

[本文引用: 1]

和崎宏一, 柳野和也, 廣住敦士, など

長大斜張橋の想定大規模地震時の非線形挙動に関する研究

[J]. 構造工学論文集, 2007, 53A: 388- 397

[本文引用: 1]

WASAKI Kouichi, YANAGINO Kazuya, HIROZUMI Atsushi, et al

Nonlinear seismic behaviors of a long-span cable-stayed bridge in major earthquakes

[J]. Journal of Structural Engineering, 2007, 53A: 388- 397

[本文引用: 1]

OKAMOTO Y, NAKAMURA S

Static and seismic studies on steel/concrete hybrid towers for multi-span cable-stayed bridges

[J]. Journal of Constructional Steel Research, 2011, 67 (2): 203- 210

DOI:10.1016/j.jcsr.2010.08.008      [本文引用: 1]

谢旭, 唐站站, 胡欣科, 等

纤维模型在钢拱桥抗震设计中的适用性研究

[J]. 中国公路学报, 2015, 28 (2): 33- 42

DOI:10.3969/j.issn.1001-7372.2015.02.005      [本文引用: 1]

XIE Xu, TANG Zhanzhan, HU Xinke, et al

Study on applicability of fiber model in seismic design for steel arch bridge

[J]. China Journal of Highway and Transport, 2015, 28 (2): 33- 42

DOI:10.3969/j.issn.1001-7372.2015.02.005      [本文引用: 1]

张鸿. 千米级斜拉桥施工关键技术研究与实践[M]. 北京: 人民交通出版社, 2015.

[本文引用: 1]

朱家豪, 叶爱君, 韩大章, 等

钢塔斜拉桥地震反应特性分析

[J]. 建筑钢结构进展, 2020, 22 (2): 36- 40

[本文引用: 1]

ZHU Jiahao, YE Aijun, HAN Dazhang, et al

Seismic response analysis of steel-tower cable-stayed bridges

[J]. Progress in Steel Building Structures, 2020, 22 (2): 36- 40

[本文引用: 1]

李帅, 王景全, 颜晓伟, 等

近断层地震动空间分布特征对斜拉桥地震响应影响

[J]. 土木工程学报, 2016, 49 (6): 94- 104

[本文引用: 1]

LI Shuai, WANG Jingquan, YAN Xiaowei, et al

Influence of spatial distribution characteristics of near-fault ground motion on seismic response of cable-stayed bridges

[J]. China Civil Engineering Journal, 2016, 49 (6): 94- 104

[本文引用: 1]

LI S, ZHANG F, WANG J Q, et al

Seismic responses of super-span cable-stayed bridges induced by ground motions in different sites relative to fault rupture considering soil-structure interaction

[J]. Soil Dynamics and Earthquake Engineering, 2017, 101: 295- 310

DOI:10.1016/j.soildyn.2017.07.016     

陈扬, 张铭, 王秋良, 等

近断层脉冲型地震动作用下大跨斜拉桥的地震响应特征分析

[J]. 公路, 2022, 67 (1): 97- 104

[本文引用: 1]

CHEN Yang, ZHANG Ming, WANG Qiuliang, et al

Analysis seismic response characteristics of cable stayed bridges under near-fault pulse ground motion

[J]. Highway, 2022, 67 (1): 97- 104

[本文引用: 1]

辰巳正明. 鋼斜張橋-技術とその変遷[M]. 東京: 丸善, 2010: 231.

[本文引用: 1]

Japanese Road Association. Specifications for highway bridges part V: seismic design [S]. Tokyo: Maruzen, 2012.

[本文引用: 3]

王彤. 桥梁结构钢材滞回本构模型改进及其应用研究[D]. 杭州: 浙江大学, 2016.

[本文引用: 1]

WANG Tong. Improvement of the hysteretic constitutive model for bridge structural steels and its application [D]. Hangzhou: Zhejiang University, 2016.

[本文引用: 1]

CHABOCHE J L

Time-independent constitutive theories for cyclic plasticity

[J]. International Journal of Plasticity, 1986, 2 (2): 149- 188

DOI:10.1016/0749-6419(86)90010-0      [本文引用: 1]

CHEN W F, DUAN L. Bridge engineering handbook: seismic design [M]. Boca Raton: CRC Press, 2014.

[本文引用: 1]

黄蓓. 基于集集地震记录的近断层地震动特性分析[D]. 北京: 中国地震局地球物理研究所, 2003.

[本文引用: 1]

HUANG Bei. Study on near-field characteristics of strong ground motion during the Chi-Chi, Taiwan, earthquake [D]. Beijing: Institute of Geophysics, China Earthquake Administration, 2003.

[本文引用: 1]

罗全波, 陈学良, 高孟潭, 等

集集地震近断层速度脉冲分析

[J]. 国际地震动态, 2019, (10): 2- 11

LUO Quanbo, CHEN Xueliang, GAO Mengtan, et al

Analysis of near-fault velocity pulses in the Chi-Chi earthquake

[J]. International Seismological Dynamics, 2019, (10): 2- 11

SHIN T C

An overview of the 1999 ChiChi, Taiwan, earthquake

[J]. Bulletin of the Seismological Society of America, 2001, 91 (5): 895- 913

[本文引用: 1]

李帅. 近断层地震动工程特性及其作用下大跨斜拉桥地震响应分析[D]. 南京: 东南大学, 2018.

[本文引用: 2]

LI Shuai. Characteristics of near fault ground motions and its influence on the seismic performance of long-span cable-stayed bridge [D]. Nanjing: Southeast University, 2018.

[本文引用: 2]

KANVINDE A, DEIERLEIN G

Cyclic void growth model to assess ductile fracture initiation in structural steels due to ultra low cycle fatigue

[J]. Journal of Engineering Mechanics, 2007, 133 (6): 701

DOI:10.1061/(ASCE)0733-9399(2007)133:6(701)      [本文引用: 1]

诸葛翰卿, 谢旭, 廖燕华, 等

横桥向地震作用对钢拱桥地震损伤发展的影响

[J]. 浙江大学学报: 工学版, 2019, 53 (4): 702- 712

[本文引用: 2]

ZHUGE Hanqing, XIE Xu, LIAO Yanhua, et al

Effect of transverse earthquake action on development of seismic damage of steel arch bridges

[J]. Journal of Zhejiang University: Engineering Science, 2019, 53 (4): 702- 712

[本文引用: 2]

廖燕华. 钢桥焊接节点超低周疲劳性能与断裂机理研究[D]. 杭州: 浙江大学, 2018.

[本文引用: 1]

LIAO Yanhua. Research on ultra low cycle fatigue performance and fracture mechanism of steel bridge welded joint [D]. Hangzhou: Zhejiang University, 2018.

[本文引用: 1]

/

〈 〉