伴随着信息技术的蓬勃发展，结构安全自动监测系统已成为结构工程建设和运营安全保障必不可少的组成部分. 通过大量传感器采集结构工程状态数据预测结构的变形趋势，是防止和减少安全事故的重要手段；利用监测数据建立基于数据驱动的预测模型预测结构变形数据，更成为结构自动监测系统研究的关键技术之一.

结构变形预测的模型主要包含回归预测模型^[1-3]、灰色模型^[4-8]、时间序列模型^[9-13]和人工智能模型^[14]. 为了更加准确地预测土坝沉降，Chen等^[3]在传统回归模型中加入物理因子，利用安装在大坝内部的综合监测系统采集沉降数据. 测试结果表明，Chen等^[3]所提模型平均误差为1.02%~4.48%，略低于传统的多元非线性回归模型. 回归预测模型属于静态模型，当监测数据量大且精准时，预测效果较好，但在实际使用过程中物理因子的选用对模型影响较大，模型的鲁棒性有待提高. 张立亚等^[8]利用隧道拱顶和地表的沉降序列数据建立强、弱随机性非等间隔灰色预测模型，由隧道累计沉降量的增长、减速增长及平缓增长3个阶段的数据测试结果得出当预测步数≥8 时，强随机模型的精度仍能达到2.96%，但弱随机在这3个阶段的预测效果均不佳. 灰色模型要求数据呈指数增长趋势，只适合中短期的预测，使该模型在实际工程中的应用受限. He等^[15]利用小基线子集干涉合成孔径雷达（small baseline subset interferometric synthetic aperture radar，SBAS-InSAR）技术获得矿区表面变形的时空演化特征. 时间序列InSAR数据通过具有窥视孔长短期记忆的卷积神经网络（convolutional neural network with peephole long short time memory，CNN-PhLSTM）进行预测，得到的预测结果与不同轨道的InSAR数据具有高度相关性，但当缺失数据量大时，时间序列模型预测结果将受到较大影响.

随着结构安全自动监测系统的广泛使用，结构监测数据正逐步进入大数据的时代，机器学习特别是深度学习研究浪潮的兴起，基于深度学习的结构监测数据预测成为该领域的研究热点. Qiu等^[16]提出基于莱文贝格-马夸特（Levenberg-Marquardt，LM）优化的条件深度信念网络（conditional deep belief network，CDBN）模型，并采用该模型预测超高层建筑变形，结果表明，优化的CBDN具有较高的预测精度. Yang等^[17]利用长短时记忆网络^[18-21]（long short term memory，LSTM）模型预测边坡周期性位移，结果表明，LSTM模型可以充分利用历史信息来提高预测性能. Luo等^[22]为了在不增加运算量的同时扩大感受视野，更多地利用时间序列的长周期特征，提出基于时间卷积网络（temporal convol-utional network，TCN）的结构变形预测模型，并通过正交试验优化模型参数，实测数据的测试结果表明，该模型预测精度良好且有效减少了运算时间. 针对LSTM只能提取数据的前向信息而对数据的时间特征利用效果不佳，王亚飞等^[23]提出双向长短时记忆网络^[24-25]（Bi-LSTM）的结构变形预测模型，利用2个不相关的LSTM模型从前向和后向分别提取数据的时间信息. 测试结果表明，相比小波神经网络^[26]（wavelet neural network，WNN）、LSTM、门控循环单元^[27] (gated recurrent unit，GRU)模型，王亚飞等^[22]所提模型具有更高的准确性. 基于深度学习的预测模型因良好的预测性能得到广泛的应用，但深度学习为了建立准确的映射关系，须增加隐含层层数，导致模型训练时间复杂度剧增，限制了模型在实际中的应用.

作为新的机器学习方法，宽度学习系统^[28]（broad learning system, BLS）在保障良好性能的同时使运算时间大幅度下降. 为了改善深度学习预测模型运算时间的问题，本研究充分利用监测数据的双向变化规律并结合GRU和BLS，提出基于双向门控式宽度学习系统（bi-directional gated broad learning system，Bi-G-BLS）的监测数据结构变形预测模型（以下简称为Bi-G-BLS预测模型或Bi-G-BLS）. 研究工作包括：对BLS的特征节点增加循环反馈和遗忘门结构，克服BLS模型对监测数据的长期依赖，提高当前节点对前一节点的依赖关系；分别从正向和反向提取时间序列的内部特征，有效挖掘监测数据的双向变化规律，在提高预测精度的同时有效降低深度学习模型的预测时间.

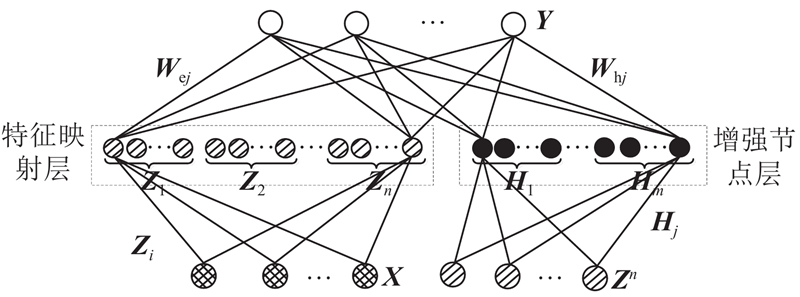
BLS是在改进随机向量函数连接神经网络（random vector functional-link neural network，RVFLNN）输入层组成结构的基础上提出机器学习算法，模型的网络结构如图1所示. 假设$ \{ {\boldsymbol{X}} \in {{\bf{R}}^{a \times l}},{\text{ }}{\boldsymbol{Y}} \in {{\bf{R}}^{a \times 1}}\} $分别为模型初始的输入和最终输出，其中$a$为训练数据集的大小，$ l $为模型预测步长. $ {{\boldsymbol{Z}}_i} $为第$i$组特征映射节点输出，由${u_i}$个映射节点组成；${{\boldsymbol{Z}}^n} \in {{\bf{R}}^{a \times \mu }}$为整个特征映射层输出，其中$ \mu = \displaystyle\sum\nolimits_{i = 1}^n {{u_i}} $；计算式分别为

(1)$ \left. {\begin{array}{*{20}{l}} {{{\boldsymbol{Z}}_i} = {\varphi _i}\left( {{{\boldsymbol{XW}}_{{\mathrm{e}}i}}+{{\boldsymbol{\beta}} _{{\mathrm{e}}i}}} \right){\text{； }}i = 1,2, \cdots ,n.} \\ {{{\boldsymbol{Z}}^n} = \left[ {{{\boldsymbol{Z}}_1},{{\boldsymbol{Z}}_2}, \cdots ,{{\boldsymbol{Z}}_n}} \right].} \end{array}} \right\} $

式中：$ {\varphi }_{i}(\cdot) $为激活函数，${{\boldsymbol{W}}_{{\mathrm{e}}i}} \in {{\bf{R}}^{l \times {u_i}}}$为经过稀疏自编码器产生的输入权重，${{\boldsymbol{\beta}} _{{\mathrm{e}}i}} \in {{\bf{R}}^{a \times {u_i}}}$为第$i$组映射特征节点的偏置矩阵. 输入连接矩阵的维度和特征组的节点数相同. 将特征映射节点数据通过映射函数变换为增强节点输出值. ${{\boldsymbol{H}}_j}$为第$j$组增强节点组输出值，由${v_j}$个增强节点组成；${{\boldsymbol{H}}^m} \in {{\bf{R}}^{a \times \eta }}$为整个增强节点层输出，其中$\eta =\displaystyle\sum\nolimits_{j = 1}^m {{v_j}} $；计算式分别为

(2)$ \left. {\begin{array}{*{20}{l}} {{{\boldsymbol{H}}_j} = {\xi _j}\left( {{{\boldsymbol{W}}_{{\mathrm{h}}j}} {{\boldsymbol{Z}}^n}+{{\boldsymbol{\beta}} _{{\mathrm{h}}j}}} \right)；{\text{ }}j = 1,2, \cdots ,m}. \\ {{{\boldsymbol{H}}^m} = \left[ {{{\boldsymbol{H}}_1},{{\boldsymbol{H}}_2}, \cdots ,{{\boldsymbol{H}}_m}} \right].} \end{array}} \right\} $

式中：${\xi _j}$为非线性激活函数，${{\boldsymbol{W}}_{{\mathrm{h}}j}} \in {{\bf{R}}^{\mu \times {v_j}}}$为第$j$组增强节点的随机连接权值矩阵，${{\boldsymbol{\beta}} _{{\mathrm{h}}j}} \in {{\bf{R}}^{a \times {v_j}}}$为偏置矩阵，$m$为增强节点层的组数. 将特征映射节点和增强节点组输出共同作为模型输入，模型预测输出${\boldsymbol{Y}}$的表达式为

(3)$ \begin{split} {\boldsymbol{Y}} =& \left[ {{{\boldsymbol{Z}}^n}|{{\boldsymbol{H}}^m}} \right]{\boldsymbol{W}}_n^m =\\&\left[ {{{\boldsymbol{Z}}_1},{{\boldsymbol{Z}}_2},{{\boldsymbol{Z}}_3}, \cdots ,\left. {{Z_n}} \right|{{\boldsymbol{H}}_1},{{\boldsymbol{H}}_2}} \right.\left. {{{\boldsymbol{H}}_3}, \cdots ,{{\boldsymbol{H}}_m}} \right]{\boldsymbol{W}}_n^m. \end{split} $

其中组合矩阵$\left[ {{{\boldsymbol{Z}}^n}|{{\boldsymbol{H}}^m}} \right]$为模型输入；${\boldsymbol{W}}_n^m \in {{\bf{R}}^{(\mu+\eta ) \times 1}}$为求解岭回归得到的连接权值矩阵，表达式为

(4)$ {{\boldsymbol{W}}}_{n}^{m}={\left[({{\boldsymbol{A}}}_{n}^{m})^{{\mathrm{T}}}{{\boldsymbol{A}}}_{n}^{m}+\lambda {\boldsymbol{I}}\right]}^{-1}{({{\boldsymbol{A}}}_{n}^{m})}^{{\rm T}}{\boldsymbol{Y}}. $

式中：${\boldsymbol{A}}_n^m = \left[ {{{\boldsymbol{Z}}^n}|{{\boldsymbol{H}}^m}} \right] \in {{\bf{R}}^{a \times (\mu+\eta )}}$为模型输入，$ \lambda $为正则项参数，$ {\boldsymbol{I}} $为单位矩阵.

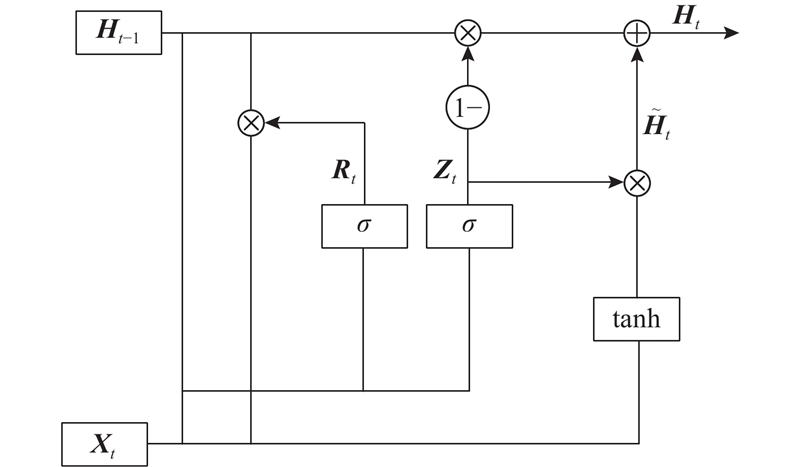
GRU是常用的门控循环神经网络. 除了解决循环神经网络（recurrent neural network，RNN）容易丢失时间序列时间步长较大时信息的依赖关系问题，GRU还能够解决梯度消失与爆炸问题. 如图2所示，GRU主要由重置门和更新门组成，重置门决定是否保留上一时刻隐藏状态输出的信息，更新门可以控制隐藏状态如何对当前时间步信息的候选隐藏状态进行更新. 重置门和更新门的输入均为当前时刻的输入$ {{ {\boldsymbol{X}}}_t} $和上一时刻隐藏层输出$ {{\boldsymbol H}_{t - 1}} $，输出由激活函数$ \sigma $计算得出，表达式分别为

(5)$ {{\boldsymbol{R}}_t} = \sigma \left( {{{\boldsymbol X}_t}{{\boldsymbol{W}}_{{\mathrm{xr}}}}+{{\boldsymbol{H}}_{t - 1}}{{\boldsymbol{W}}_{{\mathrm{Hr}}}}+{{\boldsymbol{b}}_{\mathrm{r}}}} \right), $

(6)$ {{\boldsymbol{Z}}_t} = \sigma \left( {{{\boldsymbol{X}}_t}{{\boldsymbol{W}}_{{\mathrm{xz}}}}+{{\boldsymbol{H}}_{t - 1}}{{\boldsymbol{W}}_{{\mathrm{Hz}}}}+{{\boldsymbol{b}}_{\mathrm{z}}}} \right). $

式中：$ {{\boldsymbol{W}}_{{\mathrm{xr}}}} $、$ {{\boldsymbol{W}}_{{\mathrm{xz}}}} $、$ {{\boldsymbol{W}}_{{\mathrm{Hx}}}} $、$ {{\boldsymbol{W}}_{{\mathrm{Hz}}}} $为权重矩阵，$ {{\boldsymbol{b}}_{{\mathrm{r}}}} $、$ {{\boldsymbol{b}}_{\mathrm{z}}} $均为偏置矩阵. 重置门的输出$ {{\boldsymbol{R}}_t} $与上一时刻隐藏状态输出$ {{\boldsymbol{H}}_{t - 1}} $相乘，若重置门输出接近0则将隐藏状态重置，若接近1则保留上一时刻隐藏状态输出，相乘结果和当前时刻输入通过激活函数$ \tanh $输出为候选隐藏状态，表达式为

(7)$ {\widetilde {\boldsymbol{H}}_t} = \tanh \left( {{{\boldsymbol{X}}_t}{{\boldsymbol{W}}_{{\mathrm{xH}}}}+\left( {{{\boldsymbol{R}}_t} \times {{\boldsymbol{H}}_{t - 1}}} \right){{\boldsymbol{W}}_{{{\mathrm{HH}}}}}+{{\boldsymbol{b}}_{\mathrm{H}}}} \right). $

式中：$ {{\boldsymbol{W}}_{{\mathrm{xH}}}} $、$ {{\boldsymbol{W}}_{{\mathrm{HH}}}} $为权重矩阵，$ {{\boldsymbol{b}}_{\mathrm{H}}} $为偏置矩阵. $t$时刻的隐藏状态$ {{\boldsymbol{H}}_t} $由当前时间步的更新门$ {{\boldsymbol{Z}}_t} $、前一时间步的隐藏状态$ {{\boldsymbol{H}}_{t - 1}} $和当前时间步的候选隐藏状态$ \widetilde {\boldsymbol{H}} $共同作用得到，表达式为

(8)$ {{\boldsymbol{H}}_t} = {{\boldsymbol{Z}}_t} \odot {\tilde {\boldsymbol{H}}_t}+\left( {{\boldsymbol{1}} - {{\boldsymbol{Z}}_t}} \right) \odot {{\boldsymbol{H}}_{t - 1}}. $

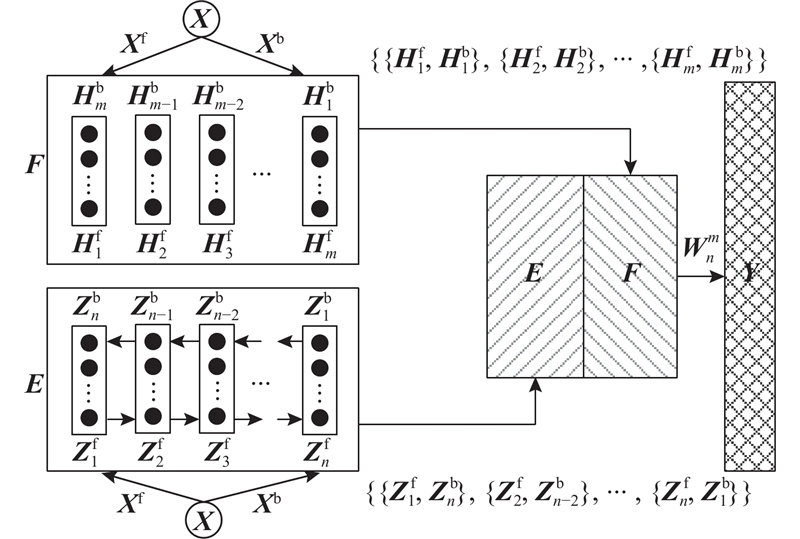
BLS模型有结构简单、训练速度快、实时性高的优点，但它对所有数据都赋予相同的权值，无法区分不同输入数据的重要程度. 结合循环网络结构的特点，本研究在BLS模型的特征节点层增加门控式结构来控制特征节点提取信息，并充分考虑监测数据的前后相关性，借鉴Bi-LSTM构建思路，对特征节点增加循环结构和遗忘门，以增强当前提取的时间信息与前一时刻的相关性，由于门控式结构能够控制信息流的提取，对参与预测值的权重和的特征节点进行筛选，构建结构变形数据Bi-G-BLS预测模型，模型的结构如图3所示.

特征节点层从2个方向对输入数据$ {\boldsymbol{X}} $进行特征提取，得到映射特征输出$ {\boldsymbol{E}} $和增强节点输出$ {\boldsymbol{F}} $，其中$ {\boldsymbol{E}} $包括$ k $个正向特征节点组$ {\boldsymbol{Z}}_q^{{\mathrm{f}}}(q\text{mod} c = 0) $，与$ k $个反向特征节点组$ {\boldsymbol{Z}}_q^{{\mathrm{b}}}\left( {q\text{mod} c = 0} \right) $，在$ {\boldsymbol{F}} $中包括$ k $个正向增强节点组$ {\boldsymbol{H}}_q^{{\mathrm{f}}}(q\text{mod} c = 0) $，与$ k $个反向增强节点组$ {\boldsymbol{H}}_q^{{\mathrm{b}}}\left( {q\text{mod} c = 0} \right) $，其中$ q $为组数，$ c $为遗忘门间隔参数，$ q\text{mod} c = 0 $时$ {{\boldsymbol{Z}}_q} $重置为零，数据输入$ {\boldsymbol{X}} $被分成前向输入$ {{\boldsymbol{X}}_{{\mathrm{f}}}} $和反向输入$ {{\boldsymbol{X}}_{{\mathrm{b}}}} $，2种输入分别通过特征节点层提取得到$ {\boldsymbol{Z}}_q^{{\mathrm{f}}} $和$ {\boldsymbol{Z}}_q^{{\mathrm{b}}} $，通过增强节点层提取得到$ {\boldsymbol{H}}_j^{{\mathrm{f}}} $和$ {\boldsymbol{H}}_j^{{\mathrm{b}}} $，各特征节点的计算式分别为

(9)$ {\boldsymbol{Z}}_q^{{\mathrm{f}}} = f({{\boldsymbol{X}}_{{\mathrm{f}}}}{\boldsymbol{W}}_{{{\mathrm{e}}_,q}}^{{\mathrm{f}}}+{\boldsymbol{Z}}_{q - 1}^{{\mathrm{f}}}{{\boldsymbol{U}}^{{\mathrm{f}}}}+{\boldsymbol{b}}_{{{\mathrm{e}}_,q}}^{{\mathrm{f}}}). $

(10)$ {\boldsymbol{Z}}_{q+1}^{{\mathrm{f}}}=\left\{ {\begin{array}{*{20}{c}} {f({{\boldsymbol{X}}_{{\mathrm{f}}}}{\boldsymbol{W}}_{{{{\mathrm{e}}}_,{q+1}}}^{{\mathrm{f}}}+{\boldsymbol{Z}}_0^{{\mathrm{f}}}{{\boldsymbol{U}}^{{\mathrm{f}}}}+{\boldsymbol{b}}_{{{{\mathrm{e}}}_,{q+1}}}^{{\mathrm{f}}}),\;\;{\;}q\text{mod} c = 0;} \\ {f({{\boldsymbol{X}}_{{\mathrm{f}}}}{\boldsymbol{W}}_{{{{\mathrm{e}}}_,{q+1}}}^{{\mathrm{f}}}+{\boldsymbol{Z}}_q^{{\mathrm{f}}}{{\boldsymbol{U}}^{{\mathrm{f}}}}+{\boldsymbol{b}}_{{{{\mathrm{e}}}_,{q+1}}}^{{\mathrm{f}}}),\;\;{\;}q\text{mod} c \ne 0.} \end{array}} \right.$

(11)$ {\boldsymbol{Z}}_q^{{\mathrm{b}}} = f({{\boldsymbol{X}}_{b}}{\boldsymbol{W}}_{{{{\mathrm{e}}}_,q}}^{{\mathrm{b}}}+{\boldsymbol{Z}}_{q - 1}^{{\mathrm{b}}}{{\boldsymbol{U}}^{{\mathrm{b}}}}+{\boldsymbol{b}}_{{{{\mathrm{e}}}_,q}}^{{\mathrm{b}}}). $

(12)$ {\boldsymbol{Z}}_{q+1}^{{\mathrm{b}}}=\left\{ {\begin{array}{*{20}{c}} {f({{\boldsymbol{X}}_{{\mathrm{b}}}}{\boldsymbol{W}}_{{{{\mathrm{e}}}_,{q+1}}}^{{\mathrm{b}}}+{\boldsymbol{Z}}_0^{{\mathrm{b}}}{{\boldsymbol{U}}^{{\mathrm{b}}}}+{\boldsymbol{b}}_{{{{\mathrm{e}}}_,{q+1}}}^{{\mathrm{b}}}),\;\;{\;}q\text{mod} c = 0;} \\ {f({{\boldsymbol{X}}_{{\mathrm{b}}}}{\boldsymbol{W}}_{{{{\mathrm{e}}}_,{q+1}}}^{{\mathrm{b}}}+{\boldsymbol{Z}}_q^{{\mathrm{b}}}{{\boldsymbol{U}}^{{\mathrm{b}}}}+{\boldsymbol{b}}_{{{{\mathrm{e}}}_,{q+1}}}^{{\mathrm{b}}}),\;\;{\;}q\text{mod} c \ne 0.} \end{array}} \right.$

式中：$ {\boldsymbol{W}}_{{{{\mathrm{e}}}_,q}}^{{\mathrm{f}}} $、$ {\boldsymbol{W}}_{{{{\mathrm{e}}}_,q}}^{{\mathrm{b}}} $、$ {{\boldsymbol{U}}^{{\mathrm{f}}}} $、$ {{\boldsymbol{U}}^{{\mathrm{b}}}} $为第$ q $个随机生成的前向和后向特征节点输入权重，$ {\boldsymbol{b}}_{{{{\mathrm{e}}}_,q}}^{{\mathrm{f}}} $、$ {\boldsymbol{b}}_{{{{\mathrm{e}}}_,q}}^{{\mathrm{b}}} $为偏置矩阵，$ f(\cdot) $为激活函数. 特征节点层提取步长$ c $的最后一组值$ {{\boldsymbol{Z}}^k} = [{{\boldsymbol{Z}}_q}],q\text{mod} c = 0 $，因此前向映射特征节点隐含状态输出$ {\boldsymbol{Z}}_{{\mathrm{f}}}^k = [{\boldsymbol{Z}}_c^{{\mathrm{f}}},{\boldsymbol{Z}}_{2c}^{{\mathrm{f}}}, \cdots ,{\boldsymbol{Z}}_{kc}^{{\mathrm{f}}}] $，后向映射特征节点隐含状态输出$ {\boldsymbol{Z}}_{{\mathrm{b}}}^k = [{\boldsymbol{Z}}_c^{{\mathrm{b}}},{\boldsymbol{Z}}_{2c}^{{\mathrm{b}}}, \cdots ,{\boldsymbol{Z}}_{kc}^{{\mathrm{b}}}] $，把$ {\boldsymbol{Z}}_{\mathrm{f}}^k $和$ {\boldsymbol{Z}}_{\mathrm{b}}^k $进行拼接得到最终特征节点输出$ {{\boldsymbol{Z}}^k} $，

(13)$ {{\boldsymbol{Z}}^k} = [{{\boldsymbol{Z}}_1},{{\boldsymbol{Z}}_2}, \cdots ,{{\boldsymbol{Z}}_k}], $

(14)$ {{\boldsymbol{Z}}_i} = [{\boldsymbol{Z}}_{i \times c}^{{\mathrm{f}}}{\boldsymbol{Z}}_{i \times c}^{{\mathrm{b}}}];{\;}i = 1,2, \cdots ,k. $

在增强节点层$ {\boldsymbol{F}} $中，前向输入数据$ {{\boldsymbol{X}}^{{\mathrm{f}}}} = [{\boldsymbol{X}}_1^{{\mathrm{f}}}, {\boldsymbol{X}}_2^{{\mathrm{f}}}, \cdots , {\boldsymbol{X}}_n^{{\mathrm{f}}}] $通过激活函数$ \xi (\cdot) $处理生成增强节点$ {\boldsymbol{H}}_j^{{\mathrm{f}}} $：

(15)$ {\boldsymbol{H}}_j^{{\mathrm{f}}} = \xi ({\boldsymbol{X}}_i^{{\mathrm{f}}}{\boldsymbol{W}}_{{{\mathrm{h}},j}}^{{\mathrm{f}}}+{\boldsymbol{b}}_{{{\mathrm{h}},j}}^{{\mathrm{f}}});{\;}j = 1,2, \cdots ,m. $

同理，后向输入数据

(16)$ {{\boldsymbol{X}}^{{\mathrm{b}}}} = [{\boldsymbol{X}}_1^{{\mathrm{b}}},{\boldsymbol{X}}_2^{{\mathrm{b}}}, \cdots ,{\boldsymbol{X}}_n^{{\mathrm{b}}}]. $

通过激活函数$ \xi (\cdot) $处理生成增强节点$ {\boldsymbol{H}}_j^{\mathrm{b}} $，

(17)$ {\boldsymbol{H}}_j^{{\mathrm{b}}} = \xi ({\boldsymbol{X}}_j^{{\mathrm{b}}}{\boldsymbol{W}}_{{{{\mathrm{h}}}_,j}}^{{\mathrm{b}}}+{\boldsymbol{b}}_{{{{\mathrm{h}}},j}}^{{\mathrm{b}}});\;j = 1,2, \cdots ,m. $

拼接生成的前向和后向增强节点，得到最终增强层节点输出$ {{\boldsymbol{H}}^m} $，

(18)$ {{\boldsymbol{H}}^m} = [{{\boldsymbol{H}}_1},{{\boldsymbol{H}}_2}, \cdots ,{{\boldsymbol{H}}_m}]. $

(19)$ {{\boldsymbol{H}}_j} = [{\boldsymbol{H}}_j^{{\mathrm{f}}},{\boldsymbol{H}}_j^{{\mathrm{b}}}];{\;}j = 1,2, \cdots ,m. $

将特征节点和增强节点进行组合，并与连接矩阵$ {\boldsymbol{W}}_k^m $的乘积得到模型最终输出：

(20)$ {\boldsymbol{Y}} = [{{\boldsymbol{Z}}^k}|{{\boldsymbol{H}}^m}]{\boldsymbol{W}}_k^m. $

其中$ [{{\boldsymbol{Z}}^k}|{{\boldsymbol{H}}^m}] $作为模型输入，$ {\boldsymbol{Y}} $为模型输出. 连接$ [{{\boldsymbol{Z}}^k}|{{\boldsymbol{H}}^m}] $输入和$ {\boldsymbol{Y}} $输出的矩阵$ {\boldsymbol{W}}_k^m $通过求解岭回归矩阵伪逆得到，

(21)$ {\boldsymbol{W}}_k^m = {\left[ {{{\left( {{\boldsymbol{A}}_k^m} \right)}^{\mathrm{T}}}{\boldsymbol{A}}_k^m+\lambda {\boldsymbol{I}}} \right]^{ - 1}}{\left( {{\boldsymbol{A}}_k^m} \right)^{\rm T}}{\boldsymbol{Y}}. $

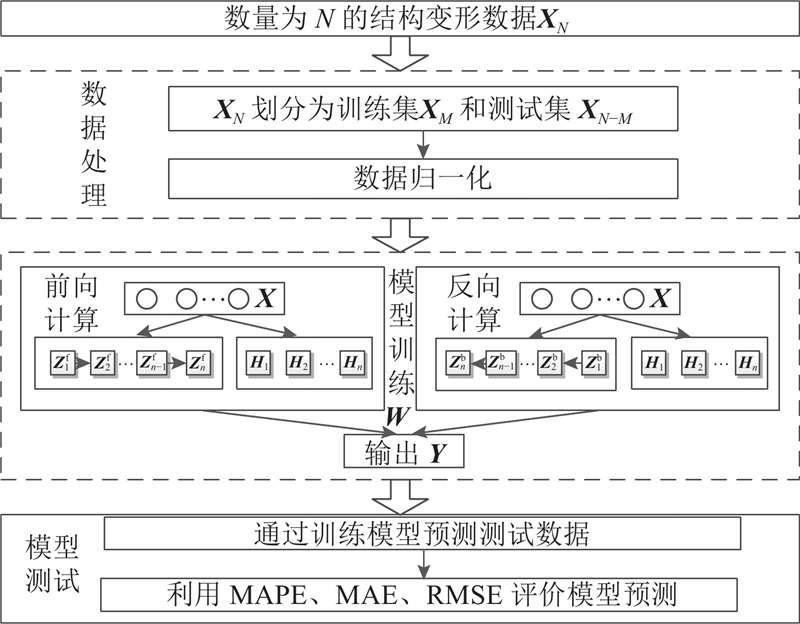
Bi-G-BLS预测模型训练过程和BLS模型相似，无需利用梯度下降算法训练模型参数取得最优解，该模型把模型训练的迭代运算转化为矩阵求解问题. 预测模型的具体流程如图4所示. 假设传感器采集的一组结构监测数据为${{\boldsymbol{X}}_N} = [{x_1},{x_2}, {x_3}, \cdots ,{x_N}]$，其中$ {{{N}}} $为采样点数. 假定训练集数据为M，测试集数据为N−M，L为设定的模型步长，分别构造模型训练输入$ {{\boldsymbol{X}}_{{\mathrm{tr}}}} \in {{\bf{R}}^{(M - L) \times L}} $，测试输入$ {{\boldsymbol{X}}_{{{\mathrm{te}}}}} \in {{\bf{R}}^{(N - M - L) \times L}} $. 将模型训练输入划分成正向结构变形数据$ {\boldsymbol{X}}_{{{\mathrm{tr}}}}^{{\mathrm{f}}} $和反向训练数据$ {\boldsymbol{X}}_{{{\mathrm{tr}}}}^{{\mathrm{b}}} $，

(22)$ {\boldsymbol{X}}_{{{\mathrm{tr}}}}^{{\mathrm{f}}} = {\left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}& \cdots &{{x_L}} \\ {{x_2}}&{{x_3}}& \cdots &{{x_{L+1}}} \\ \vdots & \vdots & & \vdots \\ {{x_{M - L}}}&{{x_{M - L+2}}}& \cdots &{{x_{M - 1}}} \end{array}} \right]_{(M - L) \times L}}, $

(23)$ {\boldsymbol{X}}_{{{\mathrm{tr}}}}^{{\mathrm{b}}} = {\left[ {\begin{array}{*{20}{c}} {{x_L}}&{{x_{L - 1}}}& \cdots &{{x_1}} \\ {{x_{L+1}}}&{{x_L}}& \cdots &{{x_2}} \\ \vdots & \vdots & & \vdots \\ {{x_{M - 1}}}&{{x_{M - 2}}}& \cdots &{{x_{M - L - 1}}} \end{array}} \right]_{(M - L) \times L}}. $

正向输入数据$ {\boldsymbol{X}}_{{{\mathrm{tr}}}}^{{\mathrm{f}}} $和反向输入数据$ {\boldsymbol{X}}_{{{\mathrm{tr}}}}^{{\mathrm{b}}} $分别作为2个不相关门控单元的特征映射层输入，代入式(9)~式(12)，初步获得2组经循环反馈结构和遗忘门处理的隐含状态数据；分别对每组状态数据以步长$ c $进行提取，得到正向和反向映射特征节点的状态输出；对2组隐含状态进行拼接得到最终特征点输出. Bi-G-BLS预测模型的特征节点层对输入数据的信息进行隔段提取，捕捉数据的整体特征，具体计算步骤如下. 1）将沉降数据划分成测试集和训练集，并进行归一化处理. 2）设置模型参数$ L $、$ c $、$ {\boldsymbol{W}}_{{{{\mathrm{e}}}_,i}}^{{\mathrm{f}}} $、$ {\boldsymbol{W}}_{{{{\mathrm{e}}}_,i}}^{{\mathrm{b}}} $、$ {\boldsymbol{b}}_{{{{\mathrm{e}}}_,i}}^{{\mathrm{f}}} $、$ {\boldsymbol{b}}_{{{{\mathrm{e}}}_,i}}^{{\mathrm{b}}} $、$ {\boldsymbol{W}}_{{{{\mathrm{h}}}_,j}}^{{\mathrm{f}}} $、$ {\boldsymbol{W}}_{{{{\mathrm{h}}}_,j}}^{{\mathrm{b}}} $、$ {\boldsymbol{b}}_{{{{\mathrm{h}}}_,j}}^{{\mathrm{f}}} $、$ {\boldsymbol{b}}_{{{{\mathrm{h}}}_,j}}^{{\mathrm{b}}} $，并进行初始化. 3）将$ {\boldsymbol{X}}_{{{\mathrm{tr}}}}^{{\mathrm{f}}} $通过正向门控单元的特征映射节点处理得到正向特征节点组输出$ \{ {\boldsymbol{Z}}_1^{{\mathrm{f}}},{\boldsymbol{Z}}_2^{{\mathrm{f}}}, \cdots ,{\boldsymbol{Z}}_k^{{\mathrm{f}}}\} $. 4）将$ {\boldsymbol{X}}_{{{\mathrm{tr}}}}^{{\mathrm{b}}} $利用反向门控单元的特征映射节点处理得到反向特征节点组输出$ \{ {\boldsymbol{Z}}_k^{{\mathrm{b}}}, {\boldsymbol{Z}}_{k - 1}^{{\mathrm{b}}}, \cdots ,{\boldsymbol{Z}}_1^{{\mathrm{b}}}\} $. 5）结合从正、反方向提取的2组特征映射层隐含状态，得到最终的特征节点层输出为$ \{ \{ {\boldsymbol{Z}}_1^{{\mathrm{f}}},{\boldsymbol{Z}}_k^{{\mathrm{b}}}\} ,\{ {\boldsymbol{Z}}_2^{{\mathrm{f}}},{\boldsymbol{Z}}_{k - 1}^{{\mathrm{b}}}\} , \cdots ,\{ {\boldsymbol{Z}}_k^{{\mathrm{f}}},{\boldsymbol{Z}}_1^{{\mathrm{b}}}\} \} $.6）$ {\boldsymbol{X}}_{{{\mathrm{tr}}}}^{{\mathrm{f}}} $和$ {\boldsymbol{X}}_{{{\mathrm{tr}}}}^{{\mathrm{b}}} $依然作为2个不相关门控单元增强节点的输入代入式(15)~式(19)，得到增强节点的最终状态输出$ {{\boldsymbol{H}}^L} \in {{\bf{R}}^{2(M - L) \times L}} $. 增强层的输入数据和增强节点进行单连接，提取输入数据的个体特征，实现对序列局部信息的捕捉.

(24)$ {{\boldsymbol{H}}^L} = \{ \{ {\boldsymbol{H}}_1^{{\mathrm{f}}},{\boldsymbol{H}}_L^{{\mathrm{b}}}\} ,\{ {\boldsymbol{H}}_2^{{\mathrm{f}}},{\boldsymbol{H}}_{L - 1}^{{\mathrm{b}}}\} , \cdots ,\{ {\boldsymbol{H}}_L^{{\mathrm{f}}},{\boldsymbol{H}}_1^{{\mathrm{b}}}\} \} . $

7）将Bi-G-BLS提取的特征节点状态与增强节点状态进行拼接，得到连接矩阵$ {\boldsymbol{W}}_k^L $的输入$ {\boldsymbol{A}}_k^L $.$ {\boldsymbol{A}}_k^L $捕捉数据的正向规律和反向规律，完成整体特征和局部特征的提取. $ {\boldsymbol{A}}_k^L $和连接矩阵$ {\boldsymbol{W}}_k^L $运算得到结构变形预测输出$ {\boldsymbol{Y }}$. 8）利用训练后的模型对测试集数据进行预测，由各评价指标实现模型误差分析.

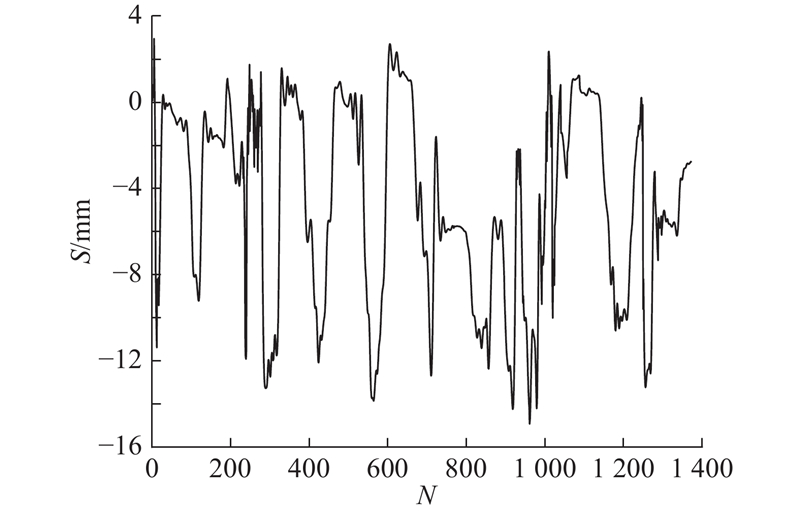
如图5所示，为了研究实验方法的预测效果，使用某地在建地铁基坑地表沉降数据作为本次实验的监测数据集，数据由静力水准仪测得，包含1373个沉降位移量. 图中，S为沉降位移. 实验中将数据70%划分为训练集，30%作为测试集. 沉降数据分布区间广，为了防止不同评价指标的量纲对结果的影响，消除奇异样本数据，在实验前进行数据归一化处理，映射区间为$ [ - 1,1] $，计算式为

(25)$ \widetilde {{x_i}} = \frac{{{x_i} - {X_{\min }}}}{{{X_{\max }} - {X_{\min }}}}. $

式中：$ {x_i} $为第$ i $个监测数据，$ \widetilde {{x_i}} $为归一化后的数据，$ {X_{\min }} $和$ {X_{\max }} $是原始数据的最小值和最大值. 本实验在96 G内存，安装有64位操作系统的 Windows10系统上进行，处理器为Intel(R) Core(TM) i5-6200U @2.30 GHz，RAM为4G，配置3组NVIDIA GeForce RTX 2080 Ti显卡和480 G固态硬盘. 实验平台为Anaconda3-4.10.3，编程语言版本为 Python-3.6，实验框架为Tensorflow2.2.0-gpu.

衡量预测模型性能的常用指标为均方误差MSE、均方根误差 RMSE、平均绝对误差 MAE、平均绝对百分比误差 MAPE，本研究采用RMSE、MAE和MAPE 衡量模型的预测效果，各项指标的计算式分别为

(26)$ {\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{({y_i} - {{\hat y}_i})}^2}} } , $

(27)$ {\text{MAE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^N |{\hat y_i} - {y_i}|, $

(28)$ {\text{MAPE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^N \left|\frac{{{{\hat y}_i} - {y_i}}}{{{y_i}}}\right|. $

式中：${\hat y_i}$为模型预测值，$ {y_i} $为实际沉降值.

为了检验Bi-G-BLS预测模型的精准度和有效性，对影响预测的模型参数进行多次重复实验，当遗忘门间隔参数$ c $=6，映射特征节点数为15，映射特征组数为22时，模型的预测结果最佳. 利用测试输入数据预测沉降值，并将预测结果与真实值进行对比，预测结果和真实值对比如图6所示. 由图可知，Bi-G-BLS的预测曲线和真实值曲线拟合度很高，仅少量点的预测数据和实际沉降值有些许偏差. 在整体上，模型预测值准确反映了真实数据的变化趋势；在局部数据变化较剧烈处，预测曲线也能够贴近数据的真实曲线，各个峰值的预测值与沉降数据也较相近. Bi-G-BLS的预测误差RMSE、MAE、MAPE分别为0.905 4、0.449 8、0.793 2，完成数据预测所需的时间为2.07 s. 综合可知，Bi-G-BLS预测结构沉降具有良好的准确性和处理速度.

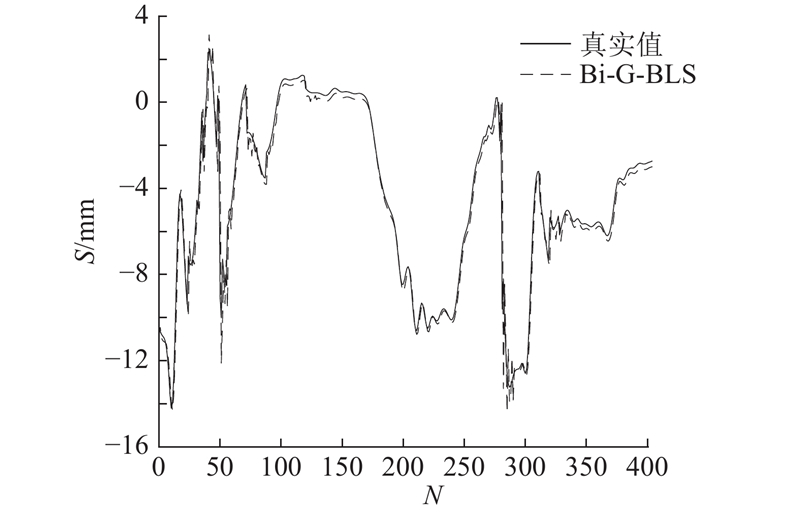
将Bi-G-BLS与GRU、BLS、Bi-LSTM、G-BLS进行对比，并对把对比结果的局部变化进行放大，各预测模型对比结果如图7所示. 由图可知，BLS的预测效果最差，在多处采样点的预测值和真实值存在较大误差.与BLS相比，GRU效果更好，在整体上能够反映出沉降数据的变化趋势. 原因是GRU利用2个门把有用信息保留下来，将时间跨度过大的不相关信息滤除掉，保留了与当前数据时间相关度高的数据.GRU处理数据花费时间长，仅利用单侧信息的特征进行预测，精准度也有待提高，在采样点100~180，前后数据变化幅度小时预测效果较好，在采样点250~300，沉降数据出现较大变化，模型的预测结果出现很大误差. G-BLS整体上反映了沉降数据的变化趋势，但在一些局部峰值处的预测值和真实值相差较大. 从整体上看，Bi-G-BLS和Bi-LSTM的预测值和真实值接近，由图7(b)可以看出，Bi-G-BLS在数据峰值出的预测曲线和真实拟合程度最高，预测效果最好. Bi-G-BLS结合了BLS运算时间短和GRU运算精度高的优点，利用在BLS的特征节点层加入的循环反馈与遗忘门，使上一时刻的特征节点输出为当前特征节点的输入，能够有选择地提取时间序列的相关特征，并通过提取数据的正向规律和反向规律对结构变形数据进行预测，使得数据的精度得到进一步提高.

对比各预测模型误差，综合RMSE、MAE、MAPE及运行时间判断模型性能如表1所示. 表中，t为运算时间. 可以看出，与GRU、BLS、Bi-LSTM、G-BLS相比，Bi-G-BLS的预测误差RMSE分别降低了35.31%、23.77%、9.01%、16.05%，MAE分别降低了6.64%、29.99%、5.11%、9.51%，MAPE分别降低了33.25%、34.89%、27.48%、2.03%. 还可以看出， Bi-G-BLS与Bi-LSTM的预测误差接近，运算时间比Bi-LSTM降低了503.82 s，模型的运算效率得到显著提高. 综合分析可知，Bi-G-BLS不仅提高了BLS的预测精确度，实现结构变形所需的时间较传统BLS和Bi-LSTM显著降低. 对比结果表明，新模型是满足现代工程结构变形预测要求的良好模型，能够为大型工程提供科学有效的数据支持.

针对传统的深度学习预测模型运算时间问题，本研究提出Bi-G-BLS预测模型. 所提模型结合Bi-LSTM和BLS模型优点，从正向和反向采集时间序列的内部特征，利用监测数据的前后时间变化规律在提高预测精度的同时降低了运算时间. 结合GRU，所提模型对BLS特征层增加循环反馈结构和遗忘门，利用历史时刻与当前时刻数据关联性，进一步提高了预测精度. 工程实测数据测试结果表明，所提模型相较于GRU、BLS、Bi-LSTM、G-BLS模型的MAPE、RMSE和MAE均有下降，是行之有效的结构监测预测模型，具有良好的实际应用价值. 结构变形数据受外部因素多，未来将考虑外界因素对预测模型的影响，并利用多组传感器对结构变形进行监测，充分利用多传感器监测数据的相关性，通过数据融合综合预测结构状态的变化情况，为结构健康自动化监测系统辅助决策提供支撑.