出行目的地识别方法主要分为2个大类:模型驱动和数据驱动. 在模型驱动方面,Qiao等[3]通过构建混合马尔可夫模型来提高个体出行目的地识别精度,考虑出行数据的非高斯和时空特征来计算位置转移概率. 随着人口流动性研究的深入,引力模型、辐射模型及改进的辐射模型等被用于人类移动模式识别. Yan等[4-5]提出识别城市人群移动量的人口权重机会模型以及同时识别个体和群体移动模式的统一模型. 上述模型驱动研究提出的模型均在宏观层面进行出行识别,未实现微观层面的个体出行目的地识别. 在数据驱动方面,大数据和人工智能算法被广泛应用于智慧交通领域. Feng等[6]将多模态数据嵌入基于注意力机制的循环神经网络,通过联合嵌入控制人类移动的多种因素来捕获复杂的顺序转换,以规则的方式刻画多层次周期性,并利用周期性特征来增强循环神经网络的识别精度. 桂志鹏等[7]提出结合长短时记忆模型和注意力机制的端到端出行目的地实时识别模型,该模型能够兼顾轨迹点的位置语义和重要性. 现有数据驱动方面的研究侧重于利用大量数据训练神经网络,大多数模型较为复杂,缺乏可解释性且泛化能力有限.
基于位置的服务(location based services,LBS)经地理位置坐标脱敏处理后,有助于向用户提供与位置相关的增值服务. 虽然LBS数据覆盖范围广,定位精度高,但存在数据质量参差不齐的问题[8],如手机定位关闭、信号中断导致的定位数据存在数据稀疏、信息缺失、位置偏移. 因此,基于局部可观测LBS数据识别出行目的地具有重要的理论和实际意义. 本研究提出基于个体记忆效应和距离效应的出行目的地识别(memory-distance effect,MDE)模型,通过研究出行者的历史出行行为习惯,识别出行目的地;利用杭州市LBS数据进行参数标定、性能评估、模型对比与敏感性分析.
1. 基于个体记忆效应和距离效应的出行目的地识别模型
1.1. 个体记忆效应
个体出行轨迹存在部分缺失的情况,为此通过挖掘个体出行行为特征,构建出行目的地识别模型. 记忆效应是个体连续移动行为中的重要特征[9],它使个体倾向于频繁返回访问过的地点. 例如,在探索优先返回(exploration and preferential return,EPR)模型[10]中,假设个体访问新地点的概率
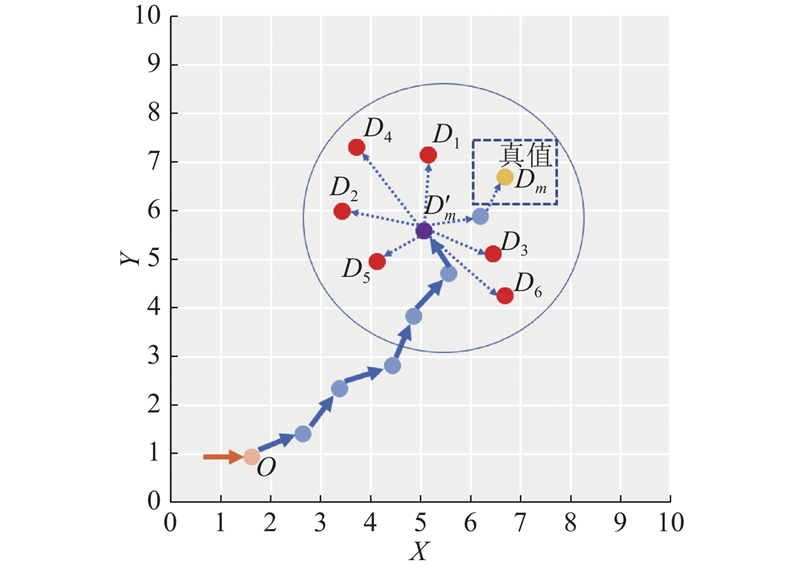
图 1
图 1 基于个体记忆效应和距离效应的出行目的地识别模型示意图
Fig.1 Illustration of trip destination recognition model based on individual memory effect and distance effect
式中:
1.2. 距离效应
引力模型又称重力模型[12]:两地间的出行量与两地活力乘积成正比,与两地间距离的幂成反比,表达式为
式中:
式中:
式中:
1.3. 模型参数标定方法
由于个体出行特征存在异质性,采用随机缺失方法构建数据集,设定随机缺失率
1.4. 计算流程
LBS数据记录出行者不同时刻的出行位置信息,通过分析LBS数据可以挖掘历史出行起讫点(OD)和活动轨迹信息从而识别出行者真实出行目的地,具体流程如图2所示. 1)对LBS数据进行预处理,提取以活动为目的的分段出行数据片段. 2)采用GeoHash网格编码方法[13]对轨迹点进行网格编码,叠加历史出行轨迹得到用户的历史目的地集合. 3)利用部分个体出行轨迹观测数据识别真实出行目的地,建立MDE模型. 4)对预处理后的个体出行历史轨迹数据进行随机剔除,构建训练集和测试集,采用非线性最小二乘法进行模型参数标定. 由上述流程可知,所建模型具有2个特点:1)综合考虑个体记忆效应和距离效应,具有良好的可解释性;2)模型结构简洁,参数数量少,便于标定和迁移.
图 2
2. 案例分析
2.1. 数据准备
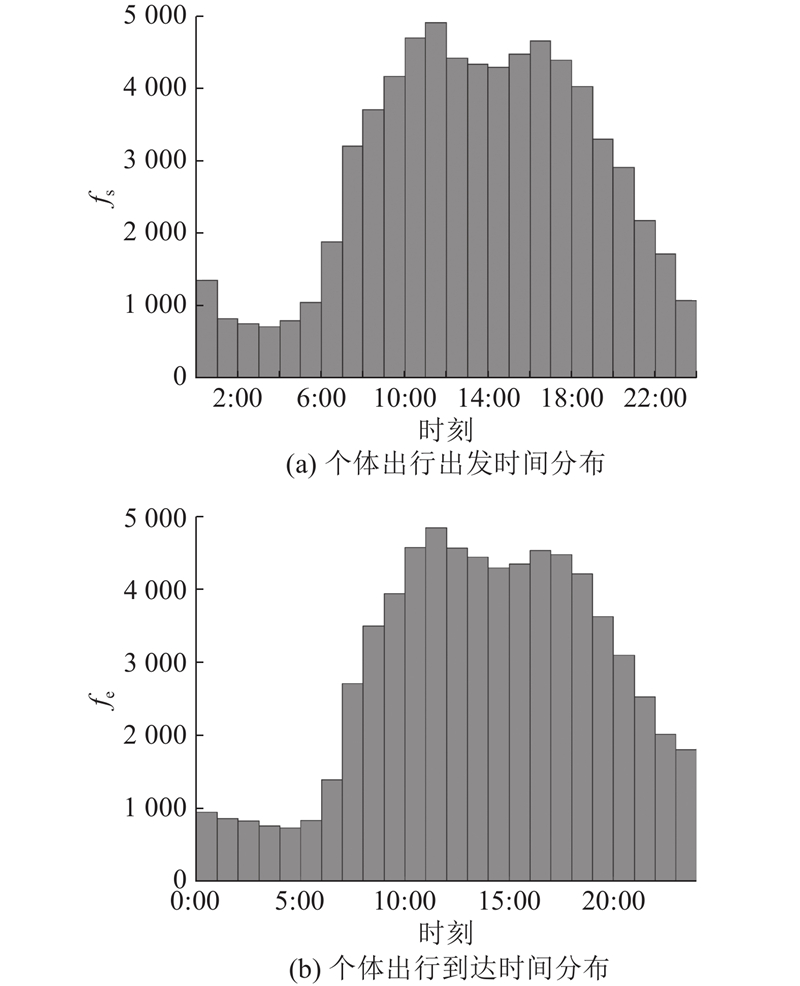
采用2021年1月6日至2月5日杭州市200名匿名个体、62 800次出行的LBS数据进行实证分析. 通过删除重要特征值缺失的异常数据,设置速度阈值对噪声数据进行清洗,删除不合理的轨迹点,构造分类决策树来识别驻留点,将出行行程分段,得到包括用户ID、起讫点时间和经纬度、中间轨迹点时间和经纬度等信息的一次出行数据. 通过人工随机抽样部分出行轨迹来判断出行行程分段的合理性. 如图3所示为个体出行次数分布,s为用户出行次数. 除少量个体出行次数较多以外(如快递配送员),出行次数普遍位于300~500. 如图4所示为个体出行时间分布,
图 3
图 4
图 4 个体出行时间分布
Fig.4 Departure and arrival time distribution of individual trips
数据集所有轨迹点均由经纬度表示,若直接用于个体出行目的地表征,在数据量较大的情况下经纬度变化极大,容易造成维度灾问题,此时不仅训练模型困难,而且计算效率低下. 在诸如个性化服务推荐的实际应用中无须精准预测个体的经纬度信息. 与此同时,基于GeoHash的网格编码技术已被广泛应用于出行流动性挖掘研究[14-15],用GeoHash对轨迹数据进行编码能以较小网格表示目的地,对于出行目的地识别有较高的应用价值. 本研究采用GeoHash网格地理位置编码算法表示轨迹点的位置特征. 网格化编码精度与GeoHash编码长度有关,编码长度越长,网格划分越小[15]. 网格划分过小会导致数据覆盖过于稀疏,不利于模型训练. 为此采用GeoHash6进行编码,所划分网格的长为1.22 km,宽为0.61 km.
通过对杭州市域范围进行GeoHash网格编码,将200个匿名个体共计62 800次出行的目的地与相应网格进行匹配和叠加,结果如图5所示. 可以看出,这200个匿名个体出行聚焦在主城区,城区的出行分布较为密集.
图 5
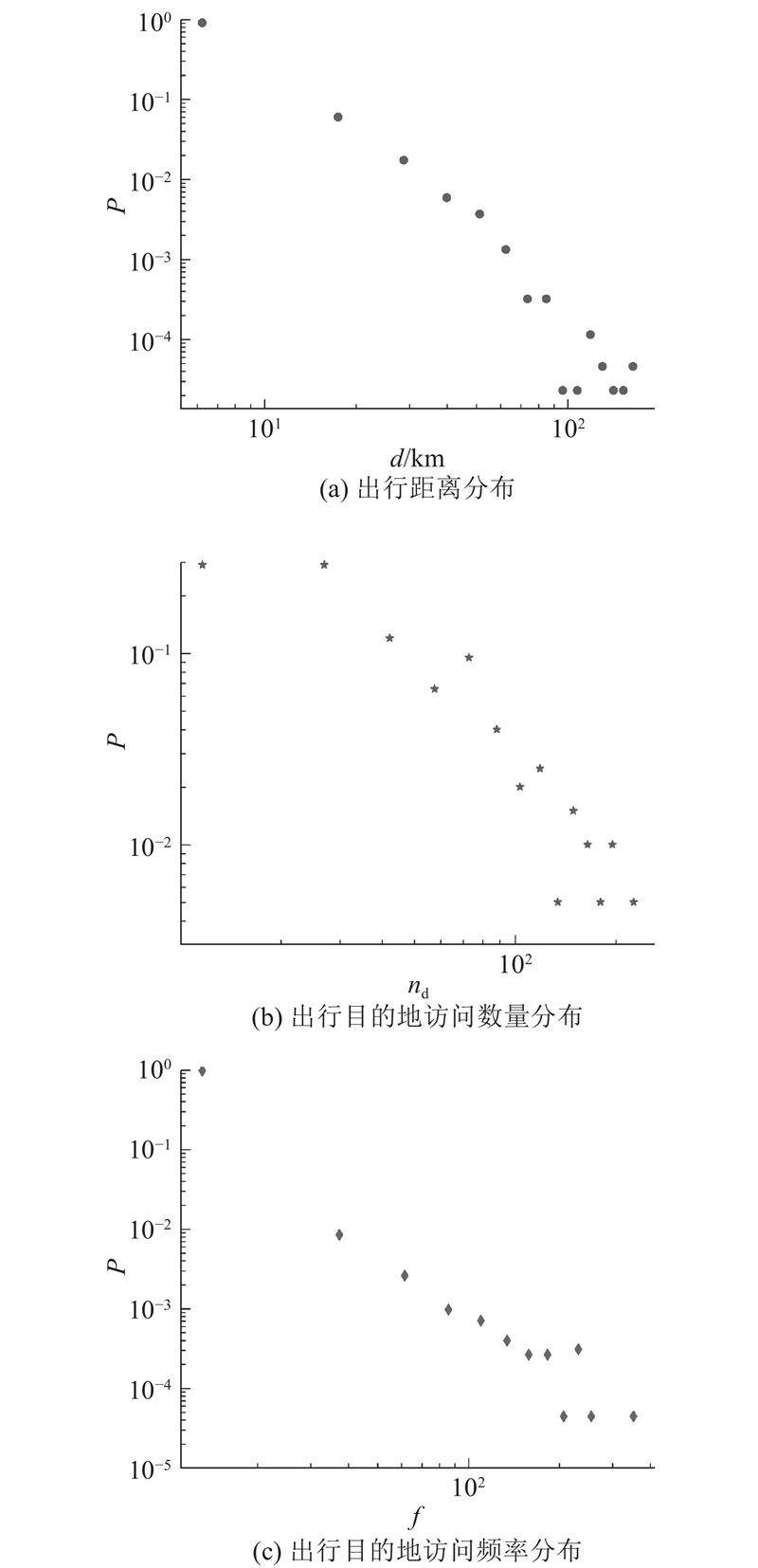
如图6所示为个体水平层面出行距离分布、出行目的地访问数量分布以及出行目的地访问频率分布情况,其中
图 6
2.2. 模型识别结果分析
采用部分观测数据缺失的数据集训练模型,得到参数估计值λ=0.832, β=1.809. 为了直观展示测试集识别效果,识别出的测试集部分个体目的地分布如图7所示. 可以看出,模型识别结果与真实数据非常相近,表明市中心各目的地的出行人数都与实际值具有很好的吻合度.
图 7
图 7 真实与识别目的地分布对比
Fig.7 Comparison of real and recognized destination distribution
2.3. 模型性能对比分析
为了量化评估模型识别性能并进行性能对比,将马尔可夫链[17](Markov chain,MC)模型、决策树(decision tree,DT)模型[18]以及随机森林(random forest,RF)模型[19]作为基准模型. 其中MC模型基于所有个体的历史出行记录来构建出行转移矩阵,并基于出行者当前所在位置来预测出行目的地;DT模型是经典的基于树的分类方法,能够通过学习样本发现个体出行的转移规律,并对新的数据做出正确分类;RF模型是集成多个决策树的分类器. 在对比实验中,各基准模型的输入与MDE模型的输入保持相同. MDE模型的输出为按照概率由大到小排序的位置列表,即top-
式中:若第
式中:
不同识别模型的性能对比结果如表1所示. 可以看出,
表 1 不同目的地识别模型性能对比
Tab.1
| 模型 | 训练集 | 测试集 | |||||||||||||
| r1 | r3 | r5 | g1 | g3 | g5 | F1 | r1 | r3 | r5 | g1 | g3 | g5 | F1 | ||
| MDE | 0.59 | 0.85 | 0.91 | 0.59 | 0.75 | 0.77 | 0.61 | 0.56 | 0.83 | 0.89 | 0.56 | 0.72 | 0.74 | 0.57 | |
| MC | 0.54 | 0.60 | 0.61 | 0.54 | 0.58 | 0.58 | 0.38 | 0.55 | 0.62 | 0.62 | 0.55 | 0.59 | 0.59 | 0.39 | |
| DT | 0.57 | 0.69 | 0.70 | 0.57 | 0.65 | 0.65 | 0.45 | 0.56 | 0.71 | 0.71 | 0.56 | 0.65 | 0.65 | 0.43 | |
| RF | 0.57 | 0.69 | 0.70 | 0.57 | 0.65 | 0.65 | 0.45 | 0.56 | 0.71 | 0.72 | 0.56 | 0.65 | 0.65 | 0.43 | |
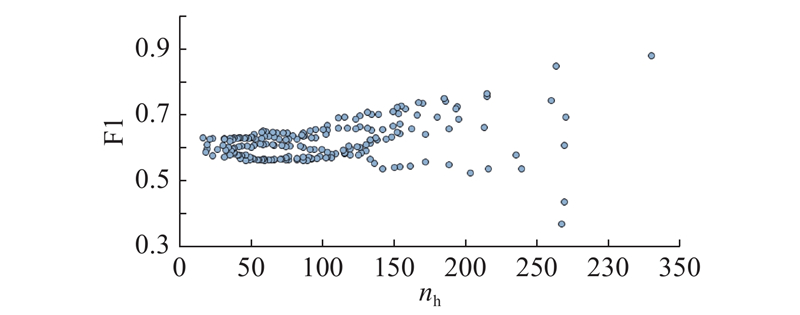
图 8
图 8 不同访问目的地个数的F1分数
Fig.8 F1-score for different numbers of destinations visited
为了探究所提模型中距离效应和记忆效应的有效性,进行消融实验,实验结果如表2所示. 将只考虑个体记忆效应的出行目的地识别模型(memory effect,ME)和只考虑距离效应的出行目的地识别模型(distance effect,DE)作为对比模型,在实验中与MDE模型保持相同的输入输出. 可以看出,综合考虑个体记忆效应和距离效应的MDE模型比对比模型的识别效果好. MDE模型在r1指标上相比DE模型提升了4个百分点,在r3指标上相比DE模型提升了13个百分点,MDE模型在F1分数指标上相比ME模型提升了18个百分点,验证了双效应融合的必要性.
表 2 个体记忆效应和距离效应模型的消融实验
Tab.2
| 模型 | 训练集 | 测试集 | |||||||||||||
| r1 | r3 | r5 | g1 | g3 | g5 | F1 | r1 | r3 | r5 | g1 | g3 | g5 | F1 | ||
| MDE | 0.59 | 0.85 | 0.91 | 0.59 | 0.75 | 0.77 | 0.61 | 0.56 | 0.83 | 0.89 | 0.56 | 0.72 | 0.74 | 0.57 | |
| ME | 0.54 | 0.82 | 0.90 | 0.54 | 0.70 | 0.74 | 0.38 | 0.55 | 0.83 | 0.91 | 0.55 | 0.71 | 0.74 | 0.39 | |
| DE | 0.56 | 0.74 | 0.82 | 0.56 | 0.66 | 0.70 | 0.60 | 0.52 | 0.70 | 0.79 | 0.52 | 0.62 | 0.66 | 0.43 | |
2.4. 出行特征对比分析
为了进一步对比模型识别效果,从个体层面对比个体回转半径分布、访问频率分布. 定义个体回转半径为
式中:
访问频率为在一定时间内个体访问某个地点的次数. 如图9所示,
图 9
为了更直观地对比所有个体出行特征刻画效果,使用JS散度(Jensen-Shannon divergence,JSD)进行评价. JSD能够定量地度量2个概率分布的相似性[21],本质上是KL散度(Kullback-Leibler divergence,KLD)的变体,与KLD类似,若2种分布越相似,JSD越小. JSD的值域范围为[0,1.0],完全相同为0,完全相反为1.0. 相较于KLD,JSD对相似度的判别更加确切. KLD的计算式为
式中:
统计MDE模型、MC模型、DT模型以及RF模型下所有个体回转半径分布和访问频率分布的JSD的计算结果如表3所示. 可以看出,MDE模型的JS散度远小于其他3种基准模型,表明MDE模型能够更好地展现个体出行特征分布.
表 3 不同对比模型出行特征分布的JS散度
Tab.3
| 模型 | rg | f | 模型 | rg | f | |
| MDE | 0.0150 | 0.0012 | DT | 0.0362 | 0.0023 | |
| MC | 0.0297 | 0.0022 | RF | 0.0378 | 0.0022 |
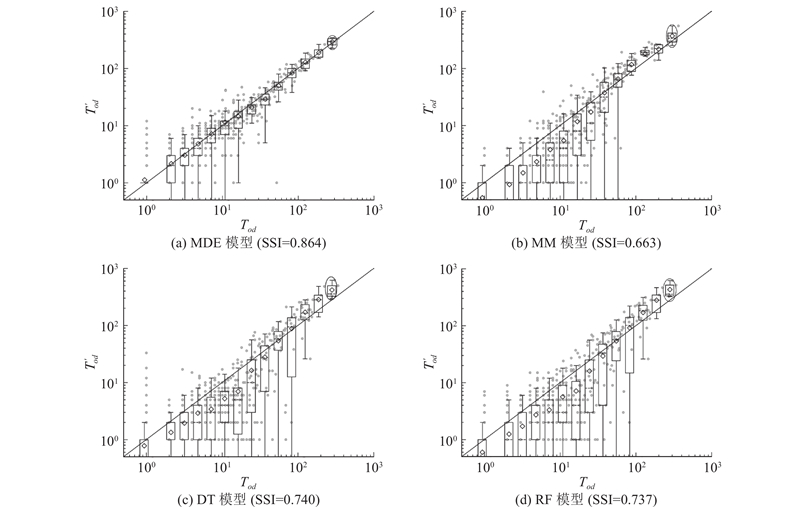
从群体层面对比模型,识别结果如图10所示. 通过散点图直观对比模型出行量的识别值和实际值,出行量为2个GeoHash网格之间的移动量统计值,成对的灰色点表示模型识别值和真实值分布;空心点表示在不同分位数箱中识别结果的平均值;箱线图是可视化数据分布的方法,表示识别行程数在观测行程数的不同分位数箱中的分布,箱线图中的虚线代表中位数,下线为下四分位数(25%分位数),上线为上四分位数(75%分位数). 箱线图的绘制方法:先找出1组数据的中位数和2个四分位数,然后连接2个四分位数画出箱体,中位数在箱体中间. 如果Y=X位于10%到90%置信区间之间,则用矩形标记框,否则用矩形叠加椭圆形标记框. 可以看出,MDE模型能够比基准模型更准确地识别出行目的地. 在出行次数为1~50时,MC模型、DT模型以及RF模型均低估了真实的出行次数,原因在于基准模型在影响个体出行目的地选择的因素上考虑不够全面,MDE模型通过考虑个体历史出行习惯及其对出行距离选择的影响来识别个体出行目的地,因此在识别效果上表现更佳. MC模型设每个状态只依赖前一个状态,不依赖过去的历史,这简化了计算和分析,但不能充分利用历史数据. DT模型可以较好地处理非线性关系,由于只考虑每个变量的影响,忽略了变量之间的相互关系,可能会导致模型的性能下降. RF模型的泛化能力较强,但是在解决回归问题时效果不是很好,不能做出超越训练集数据范围的识别,因此在测试集上训练出的结果较真实值低. 为了直观地对比群体层面的特征刻画效果,采用Sørensen相似性指数(Sørensen similarity index,SSI)来衡量各模型的识别效果. SSI是常用的统计工具,用于评估2个样本的相似度. Lenormand等[22]使用修改版本的SSI来衡量流动性识别模型是否正确地再现真实出行量(平均),计算式为
图 10
图 10 不同模型的出行散点图对比
Fig.10 Comparison of travel scatter plot for different models
式中:
3. 敏感性分析
3.1. 缺失率敏感性分析
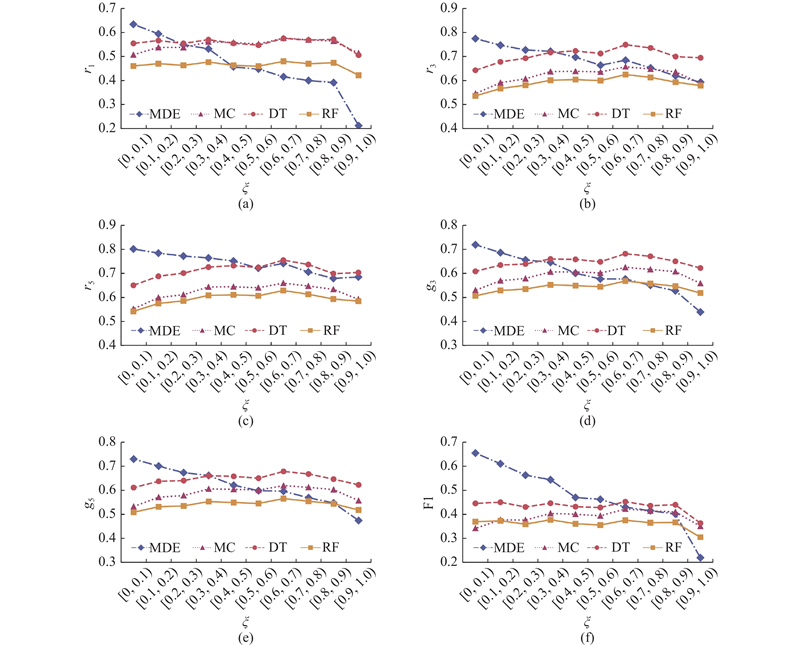
为了测试模型鲁棒性,对缺失率进行参数敏感性分析. MDE模型、MM模型、DT模型以及RF模型的精度指标随缺失率的变化情况如图11所示. 图中,精度指标包括r1(g1与r1的数值相等)、r3、r5、g3、g5、F1分数. 相较于基准模型,MDE模型在低缺失率情况下有较好的识别效果. 在高缺失率情况下,决策树模型的识别效果更好,原因是MDE模型具有处理高度缺失值的能力,能够灵活处理数据,自动忽略不相关特征. 虽然LBS数据覆盖范围广,定位精度高,但存在由于手机定位关闭、信号中断等原因导致的数据稀疏、信息缺失等问题. 本研究提出研究基于尾部缺失LBS数据的出行目的地识别方法. 在这样的情境之下,MDE模型具有最好的识别效果和应用价值. 以F1分数为例,当缺失率处于[0,0.6)时,MDE模型的F1分数远高于其他3种基准模型,验证了所提模型对于尾部轨迹数据缺失情况下的微观个体出行目的地识别问题具有良好的适应性;随着缺失率的增加,MDE模型在[0.6,1.0)的性能有所下降,可能的原因是随着数据缺失率的增加,距离真实目的地的距离增大,导致距离效应的效用有所下降,其余对比模型受该影响相对较低.
图 11
图 11 不同模型的缺失率敏感性分析
Fig.11 Sensitivity analysis of missing rate for different models
3.2. 数据集时间敏感性分析
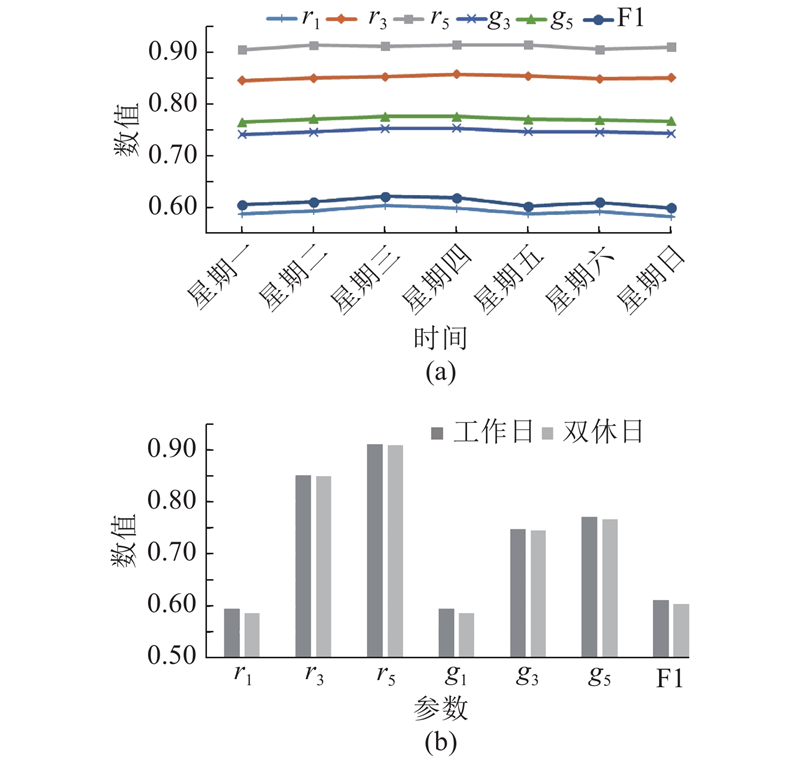
为了测试模型鲁棒性,对数据集的日期类别进行敏感性分析. MDE模型的各指标评估值随时间的变化情况如图12所示. 可以看出,MDE模型在周一至周日、工作日和非工作日的性能保持稳定,无明显变化,证明MED模型对于数据集的日期类别不敏感.
图 12
4. 结 语
针对位置服务数据缺失情况下的微观个体出行目的地识别问题,建立基于个体记忆效应和距离效应的出行目的地识别模型,并采用真实数据标定和检验模型. 结果表明所建模型的准确率、召回率、精确度和F1分数优于马尔可夫模型、决策树模型以及随机森林模型的对应指标,且所建模型具有较高的鲁棒性. 开展个体出行记忆效应模块和距离效应模块的消融实验,验证了综合考虑个体记忆效应和距离效应的必要性. 所建模型采用GeoHash网格编码方法提高了个体出行目的地的空间分辨率,利用个体历史出行信息简化模型结构,从个体出行行为机理角度出发,具有可解释性,实现部分个体出行轨迹观测数据缺失情况下的出行目的地识别,同时结构简单,易于标定参数,能够在出行识别等领域得到较好应用. 未来研究可以考虑更多个体出行影响因素,如出行时间、出行成本,开发准确性更高的识别模型. 同时,由于LBS数据自身缺乏真值的问题,未来考虑采用更精细化的数据进一步提升出行目的地识别准确性以及模型验证的合理性.
参考文献
Where to go next: a spatio-temporal gated network for next POI recommendation
[J].
A hybrid Markov-based model for human mobility prediction
[J].DOI:10.1016/j.neucom.2017.05.101 [本文引用: 1]
Universal predictability of mobility patterns in cities
[J].
Universal model of individual and population mobility on diverse spatial scales
[J].DOI:10.1038/s41467-017-01892-8 [本文引用: 2]
Unified underpinning of human mobility in the real world and cyberspace
[J].DOI:10.1088/1367-2630/18/5/053025 [本文引用: 1]
Modelling the scaling properties of human mobility
[J].DOI:10.1038/nphys1760 [本文引用: 1]
Understanding individual human mobility patterns
[J].DOI:10.1038/nature06958 [本文引用: 1]
The gravity model
[J].DOI:10.1146/annurev-economics-111809-125114 [本文引用: 1]
基于GeoHash的近邻查询位置隐私保护方法
[J].
Location privacy preserving nearest neighbor querying based on GeoHash
[J].
基于GeoHash和HDBSCAN的共享单车停车拥挤区域识别
[J].
Identification of crowded parking areas for shared bikes based on GeoHash and HDBSCAN
[J].
DP-BPR: destination prediction based on Bayesian personalized ranking
[J].DOI:10.1007/s11771-021-4617-x [本文引用: 2]
Evidence for a conserved quantity in human mobility
[J].DOI:10.1038/s41562-018-0364-x [本文引用: 1]
Identifying trip ends from raw GPS data with a hybrid spatio-temporal clustering algorithm and random forest model: a case study in Shanghai
[J].DOI:10.1080/03081060.2019.1675309 [本文引用: 1]
Model based comparison of discounted cumulative gain and average precision
[J].DOI:10.1016/j.jda.2012.10.002 [本文引用: 1]
基于JS散度和潜在特征提取的多块PCA故障监测
[J].
Multiblock PCA fault monitoring based on JS divergence and latent feature extraction
[J].
A universal model of commuting networks
[J].DOI:10.1371/journal.pone.0045985 [本文引用: 1]