(3) $ \begin{split} {\mathrm{ln}}\;&\left({L}_{1}\left(x;\alpha ,{k}_{1},{\theta }_{1},{k}_{2},{\theta }_{2}\right)\right)=\\ &\quad \sum _{i=1}^{n}\mathrm{ln}\;f\left({x}_{i};\alpha ,{k}_{1},{\theta }_{1},{k}_{2},{\theta }_{2}\right).\end{split} $
(4) $ \begin{split} {\mathrm{ln}}\;&\left({L}_{2}\left(y;\alpha ,{k}_{1},{\theta }_{1},{k}_{2},{\theta }_{2}\right)\right)=\\& \quad\sum _{j=1}^{m}\mathrm{ln}\;\left[1-F\left({y}_{j};\alpha ,{k}_{1},{\theta }_{1},{k}_{2},{\theta }_{2}\right)\right].\end{split} $
(5) $ \begin{split}\mathrm{m}\mathrm{a}\mathrm{x}\;&\left[{\mathrm{ln}}\;\left({L}_{1}\left(x;\alpha ,{k}_{1},{\theta }_{1},{k}_{2},{\theta }_{2}\right)\right)+\right.\\& \left.{\mathrm{ln}}\;\left({L}_{2}\left(y;\alpha ,{k}_{1},{\theta }_{1},{k}_{2},{\theta }_{2}\right)\right)\right].\end{split} $
[1]
YANG F, GU W, CASSIDY M, et al Achieving higher taxi outflows from a drop-off lane: a simulation-based study
[J]. Transportation Research Part C: Emerging Technologies , 2020 , 115 : 102623
DOI:10.1016/j.trc.2020.102623
[本文引用: 3]
[2]
CHEN Y, ZHANG N, WU H, et al. Calculation method of traffic capacity in airport curbside [C]// Proceedings of the 7th International Conference on Green Intelligent Transportation System and Safety . Singapore:Springer, 2018: 725−736.
[本文引用: 1]
[3]
刘淑敏, 孙莹莹 枢纽型机场陆侧交通系统后评价及优化研究: 以南京禄口国际机场为例
[J]. 交通与运输:学术版 , 2018 , (1 ): 42 - 45
LIU Shumin, SUN Yingying Study on post-evaluation and optimization of landside traffic system for airport: take Nanjing Lukou international airport as an example
[J]. Traffic and Transportation , 2018 , (1 ): 42 - 45
[4]
CHANG K Y. A simulation model for analyzing airport terminal roadway and traffic and curbside parking [D]. Colloge Park: University of Maryland, 2001.
[本文引用: 1]
[5]
赵林, 姜恒, 袁倩倩 深圳机场T3航站楼车道边规模分析
[J]. 交通标准化 , 2010 , (212 ): 205 - 207
[本文引用: 1]
ZHAO Lin, JIANG Heng, YUAN Qianqian Scale analysis for curbside at T3 airport terminal of Shenzhen
[J]. Transport Standardization , 2010 , (212 ): 205 - 207
[本文引用: 1]
[7]
杨方宜, 李铁柱 大型综合客运枢纽送站坪交通特性及通行能力
[J]. 浙江大学学报:工学版 , 2017 , 51 (11 ): 2207 - 2214
YANG Fangyi, LI Tiezhu Traffic characteristics and capacities of passenger drop-off area at large intermodal transportation terminals
[J]. Journal of Zhejiang University: Engineering Science , 2017 , 51 (11 ): 2207 - 2214
[8]
ASHFORD N, WRIGHT P, MUMAYIZ S. Airport engineering: planning, design, and development of 21st century airports [M]. Hobkin: John Wiley and Sons, 2011.
[本文引用: 1]
[9]
PASSOS L, KOKKINOGENIS Z, ROSSETTI R, et al. Multi-resolution simulation of taxi services on airport terminal's curbside [C]// International IEEE Conference on Intelligent Transportation Systems . The Hague: IEEE, 2013: 2361−2366.
[本文引用: 1]
[10]
HARRIS T, NOURINEJAD M, ROORDA M. A mesoscopic simulation model for airport curbside management [EB/OL]. [2023-02-01]. https://www.hindawi.com/journals/jat/2017/4950425/.
[11]
张晓丽. 基于元胞自动机的航站楼出发层车道边容量研究[D]. 西安: 长安大学, 2021.
[本文引用: 1]
ZHANG Xiaoli. Curbside capacity analysis departure floor based on cellular automata [D]. Xi'an: Changan University, 2021.
[本文引用: 1]
[12]
TRAIN K. Discrete choice models with simulation [M]. Cambridge: Cambridge University Press, 2002.
[本文引用: 1]
[13]
LUCE D. Individual choice behavior [M]. New York: John Wiley and Sons, 1959.
[本文引用: 1]
[14]
SOUZA F, LARRANAGA A, PALMA D, et al Modeling travel mode choice and characterizing freight transport in a Brazilian context
[J]. Transportation Letters , 2021 , 14 (9 ): 983 - 996
[本文引用: 1]
[15]
YAZICI M, KAMGA C, SINGHAL A Modeling taxi drivers' decisions for improving airport ground access: John F. Kennedy airport case
[J]. Transportation Research Part A: Policy and Practice , 2016 , 91 : 48 - 60
DOI:10.1016/j.tra.2016.06.004
[本文引用: 1]
[16]
YAO R, BEKHOR S Data-driven choice set generation and estimation of route choice models
[J]. Transportation Research Part C: Emerging Technologies , 2020 , 121 : 102832
DOI:10.1016/j.trc.2020.102832
[本文引用: 1]
[17]
WANG S, WANG Q, BAILEY N, et al Deep neural networks for choice analysis: a statistical learning theory perspective
[J]. Transportation Research Part B: Methodological , 2018 , 148 : 60 - 81
[本文引用: 1]
[18]
HASNINE S, HABIB K Modeling the dynamics between tour-based mode choices and tour-timing choices in daily activity scheduling
[J]. Transportation , 2020 , 47 : 2635 - 2669
DOI:10.1007/s11116-019-10036-4
[本文引用: 1]
[19]
NIRMALE S, PINJARI A, SHARMA A A discrete-continuous multi-vehicle anticipation model of driving behaviour in heterogeneous disordered traffic conditions
[J]. Transportation Research Part C: Emerging Technologies , 2021 , 128 : 103144
DOI:10.1016/j.trc.2021.103144
[本文引用: 1]
[20]
URATA J, XU Z, KE J Learning ride-sourcing drivers' customer-searching behavior: a dynamic discrete choice approach
[J]. Transportation Research Part C: Emerging Technologies , 2021 , 130 : 103293
DOI:10.1016/j.trc.2021.103293
[本文引用: 1]
[21]
RAMBHA T, NOZICK L, DAVIDSON R Modeling hurricane evacuation behavior using a dynamic discrete choice framework
[J]. Transportation Research Part B: Methodological , 2021 , 150 : 75 - 100
DOI:10.1016/j.trb.2021.06.003
[22]
ANTONINI G, BIERLAIRE M, WEBER M Discrete choice models of pedestrian walking behavior
[J]. Transportation Research Part B: Methodological , 2006 , 40 : 667 - 687
DOI:10.1016/j.trb.2005.09.006
[本文引用: 1]
[23]
HASSAN M, NAJMI A, RASHIDI T A two-stage recreational destination choice study incorporating fuzzy logic in discrete choice modelling
[J]. Transportation Research Part F: Traffic Psychology and Behaviour , 2019 , 67 : 123 - 141
DOI:10.1016/j.trf.2019.10.015
[本文引用: 1]
[24]
GUZMAN L, ARELLANA J, CAMARGO J A hybrid discrete choice model to understand the effect of public policy on fare evasion discouragement in Bogot´a's Bus Rapid Transit
[J]. Transportation Research Part A: Policy and Practice , 2021 , 151 : 140 - 153
DOI:10.1016/j.tra.2021.07.009
[本文引用: 1]
[27]
STROUGH J, MEHTA C, MCFALL J, et al Are older adults less subject to the sunk-cost fallacy than younger adults
[J]. Psychological Science , 2008 , 19 (7 ): 650 - 652
DOI:10.1111/j.1467-9280.2008.02138.x
[本文引用: 1]
[28]
FERNANDEZ P. The sunk cost fallacy and individual differences in health decisions [D]. EI Paso: The University of Texas, 2010.
[本文引用: 1]
[30]
GREENWOOD M. The natural duration of cancer [EB/OL]. [2023-02-01]. https://www.sciencedirect.com/science/article/abs/pii/S0140673601265386.
[本文引用: 1]
[31]
MADDALA G, WU S A comparative study of unit root tests with panel data and a new simple test
[J]. Oxford Bulletin of Economics and Statistics , 1999 , 61 (Supp.1 ): 631 - 652
[本文引用: 1]
Achieving higher taxi outflows from a drop-off lane: a simulation-based study
3
2020
... 在大型综合客运枢纽(如机场、高铁站),乘客通过公共汽车、出租车、私家车等交通工具到达指定的落客区,在落客区下车后进入候车大厅(站房).该区域出租车道经常采用单车道“先进先出”(first-in-first-out, FIFO)的运行模式,这种模式在中国大型高铁站较常见,例如南京南站、郑州东站、北京南站和广州南站等[1 ] . 在“先进先出”落客车道的出租车表现出其独特的运行特点:车队中的车辆都有落客需求,当车队的头车停车落客时,车队中所有车辆均必须停下来,但其中只有一部分车辆在停车等待一段时间后开始落客,而另一部分车辆则会选择继续等待,并在下次车队移动中寻找合适的落客位置. 如果每辆车都在期望停车位落客,则“先进先出”落客车道的车位有效利用率将会非常有限,这势必会造成枢纽落客区域的严重拥堵. ...
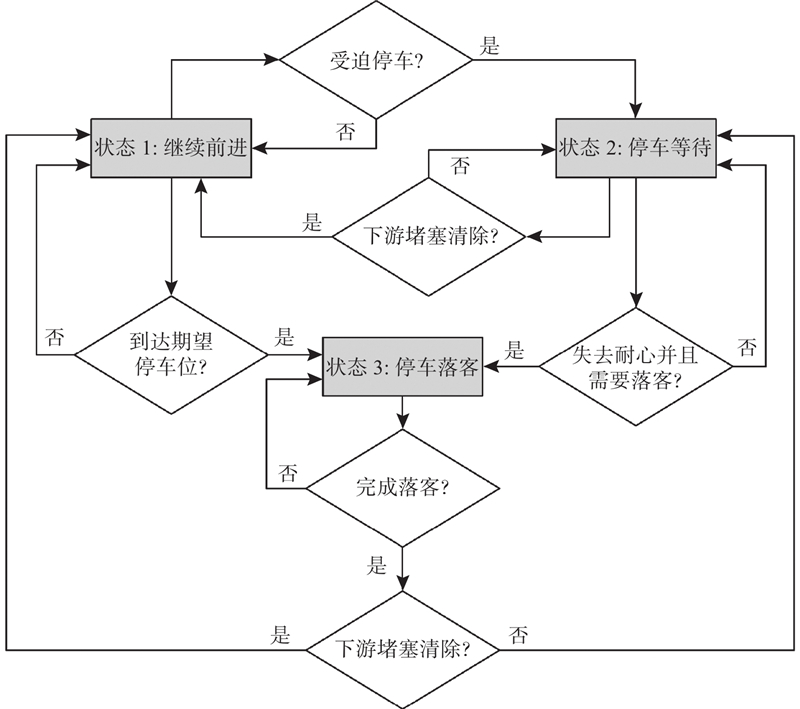
... 对于出租车落客车道,跟随车辆存在3个状态:移动、等待和落客. 当跟随车辆因下游车辆落客而被迫停车,它的状态从“移动”转换为“等待”,期望能够再次向前移动并到达其理想停车位. 如果车辆的停车时长超过等待耐性,它将会进行落客;如果车辆的停车时长未超过等待耐性,并能够继续向下游移动,车辆将会继续向期望停车位前进,或者再次受迫停车[1 ] . 上述出租车决策过程如图1 所示,该落客决策模型只保留了一些主要因素. 为了更好地理解出租车落客行为,对出租车道车辆停车行为分别从停车位置、停车时间和等待耐性3个方面进行详细分析,分析数据主要来自于文献[1 ]中的轨迹数据. ...
... 所示,该落客决策模型只保留了一些主要因素. 为了更好地理解出租车落客行为,对出租车道车辆停车行为分别从停车位置、停车时间和等待耐性3个方面进行详细分析,分析数据主要来自于文献[1 ]中的轨迹数据. ...
1
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
枢纽型机场陆侧交通系统后评价及优化研究: 以南京禄口国际机场为例
0
2018
枢纽型机场陆侧交通系统后评价及优化研究: 以南京禄口国际机场为例
0
2018
1
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
深圳机场T3航站楼车道边规模分析
1
2010
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
深圳机场T3航站楼车道边规模分析
1
2010
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
大型综合客运枢纽送站坪交通特性及通行能力
0
2017
大型综合客运枢纽送站坪交通特性及通行能力
0
2017
1
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
1
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
1
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
1
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
1
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
1
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
Modeling travel mode choice and characterizing freight transport in a Brazilian context
1
2021
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
Modeling taxi drivers' decisions for improving airport ground access: John F. Kennedy airport case
1
2016
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
Data-driven choice set generation and estimation of route choice models
1
2020
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
Deep neural networks for choice analysis: a statistical learning theory perspective
1
2018
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
Modeling the dynamics between tour-based mode choices and tour-timing choices in daily activity scheduling
1
2020
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
A discrete-continuous multi-vehicle anticipation model of driving behaviour in heterogeneous disordered traffic conditions
1
2021
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
Learning ride-sourcing drivers' customer-searching behavior: a dynamic discrete choice approach
1
2021
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
Modeling hurricane evacuation behavior using a dynamic discrete choice framework
0
2021
Discrete choice models of pedestrian walking behavior
1
2006
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
A two-stage recreational destination choice study incorporating fuzzy logic in discrete choice modelling
1
2019
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
A hybrid discrete choice model to understand the effect of public policy on fare evasion discouragement in Bogot′a's Bus Rapid Transit
1
2021
... 当前,对于大型综合客运枢纽落客区域的研究主要集中在多车道(即最内侧车道落客,其他车道通行),尽管多车道落客区域的相关研究非常丰富[2 -4 ] ,但这些研究中使用的方法和模型不能直接应用于“先进先出”落客车道. 该领域的一些早期研究依赖于经验方法和确定性模型[5 -8 ] ,忽略了现实复杂性,如随机需求、落客位置的选择和停留时间. 另一方面,通过仿真模型研究出租车落客行为可以包含更多真实的落客行为细节,例如车辆落客位置选择行为,但这些行为细节更多的是遵循统计分布,缺少对关键变量的机理分析[9 -11 ] . 为了理解送站坪出租车落客行为,须对个体选择行为进行分析建模. 在城市交通个体选择行为的研究中,离散选择Logit模型发挥着重要的作用,它是多重变量变量分析的方法之一. 目前为止最简单且使用最广的离散选择模型即为Logit模型[12 ] . 最初Logit公式是Luce[13 ] 根据不相关选项的独立性(independence from irrelevant alternatives,IIA)推导得出的. 随着Logit模型的发展,在基础Logit模型的基础上提出了更多的离散选择高阶段Logit模型,例如:混合Logit模型、混合选择模型(hybrid choice model)、动态Logit模型(dynamic Logit model). 其中一些模型已经广泛应用到交通行为分析中,大部分研究都是利用偏好数据来估计离散选择模型的,通过确定人的决策偏好来改善现有政策[14 -15 ] ;一些学者为了提高选择模型的预测精度和解释力,将统计学习理论框架引入到模型中[16 -17 ] ,但更多的做法是搭建混合模型框架,例如离散-连续选择框架[18 -19 ] 、动态离散选择框架[20 -22 ] 和分阶段选择框架[23 -24 ] 等. ...
大型综合客运枢纽送站坪的车辆延误
1
2018
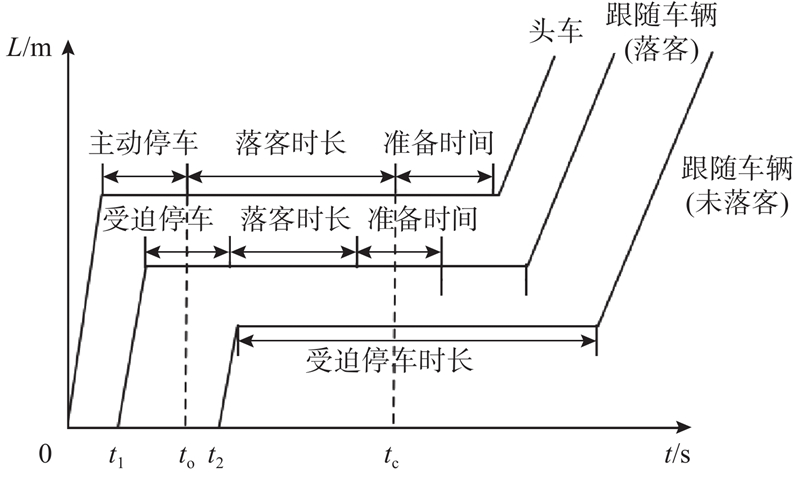
... 头车车门打开之前的主动停车时长和车门关闭之后的准备时间可通过 “停车数据”和“时间数据”处理得到,前者可以包含在头车的落客时长中,后者时长较短,经统计取值范围为1~2 s,可以采用均匀分布(取值1 s)来表示. 跟随车辆车门关闭之后的准备时间无法获取,但可以参照头车的准备时间. 经统计,车辆的落客时长分布服从负指数分布[25 ] ,其与车辆所处的位置、区域没有明显的相关性,在构建模型时可以忽略落客时长对落客决策的影响. 从如图1 所示的车辆落客决策模型可以看出,影响车辆落客决策的主要因素包括车辆停车位置及其期望停车位、受迫停车时长及其等待耐性,期望停车位置可以通过统计头车的落客位置得出,而等待耐性的分析则较复杂,其数据集包含2种类型,一种是受迫停车时长等于等待耐性的数据(受迫停车落客),另一种是受迫停车时长小于等待耐性的数据(受迫停车未落客),其对应分别如下: ...
大型综合客运枢纽送站坪的车辆延误
1
2018
... 头车车门打开之前的主动停车时长和车门关闭之后的准备时间可通过 “停车数据”和“时间数据”处理得到,前者可以包含在头车的落客时长中,后者时长较短,经统计取值范围为1~2 s,可以采用均匀分布(取值1 s)来表示. 跟随车辆车门关闭之后的准备时间无法获取,但可以参照头车的准备时间. 经统计,车辆的落客时长分布服从负指数分布[25 ] ,其与车辆所处的位置、区域没有明显的相关性,在构建模型时可以忽略落客时长对落客决策的影响. 从如图1 所示的车辆落客决策模型可以看出,影响车辆落客决策的主要因素包括车辆停车位置及其期望停车位、受迫停车时长及其等待耐性,期望停车位置可以通过统计头车的落客位置得出,而等待耐性的分析则较复杂,其数据集包含2种类型,一种是受迫停车时长等于等待耐性的数据(受迫停车落客),另一种是受迫停车时长小于等待耐性的数据(受迫停车未落客),其对应分别如下: ...
The psychology of sunk cost
1
1985
... 车辆的等待耐性分布通过分析车辆受迫停车时长获取,受迫停车行为是“沉没成本效应”的体现,沉没成本的影响导致车辆在落客决策中出现决策偏见,反映在单次受迫停车过程中,车辆在已经付出等待时间成本的情况下继续投入时间等待的倾向. 沉没成本效应是指决策者的决策行为因受沉没成本影响而产生的非理性决策现象,具体表现为决策者因顾及沉没成本而继续投入更多成本[26 -27 ] 或做出某一行为[28 ] . 在FIFO落客车道,车辆的等待耐性符合2类情况,一类是车辆受迫停车后愿意立即落客,另一类是受沉没成本影响下车辆愿意等待更长时间. ...
Are older adults less subject to the sunk-cost fallacy than younger adults
1
2008
... 车辆的等待耐性分布通过分析车辆受迫停车时长获取,受迫停车行为是“沉没成本效应”的体现,沉没成本的影响导致车辆在落客决策中出现决策偏见,反映在单次受迫停车过程中,车辆在已经付出等待时间成本的情况下继续投入时间等待的倾向. 沉没成本效应是指决策者的决策行为因受沉没成本影响而产生的非理性决策现象,具体表现为决策者因顾及沉没成本而继续投入更多成本[26 -27 ] 或做出某一行为[28 ] . 在FIFO落客车道,车辆的等待耐性符合2类情况,一类是车辆受迫停车后愿意立即落客,另一类是受沉没成本影响下车辆愿意等待更长时间. ...
1
... 车辆的等待耐性分布通过分析车辆受迫停车时长获取,受迫停车行为是“沉没成本效应”的体现,沉没成本的影响导致车辆在落客决策中出现决策偏见,反映在单次受迫停车过程中,车辆在已经付出等待时间成本的情况下继续投入时间等待的倾向. 沉没成本效应是指决策者的决策行为因受沉没成本影响而产生的非理性决策现象,具体表现为决策者因顾及沉没成本而继续投入更多成本[26 -27 ] 或做出某一行为[28 ] . 在FIFO落客车道,车辆的等待耐性符合2类情况,一类是车辆受迫停车后愿意立即落客,另一类是受沉没成本影响下车辆愿意等待更长时间. ...
Nonparametric estimation from incomplete observations
1
1958
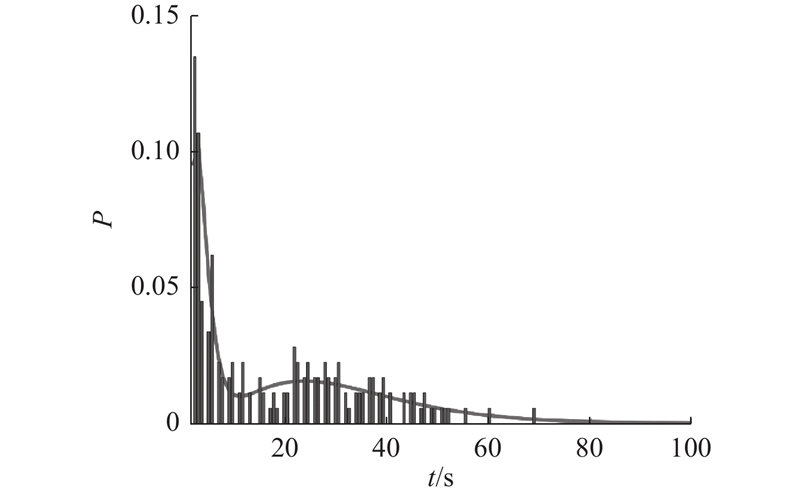
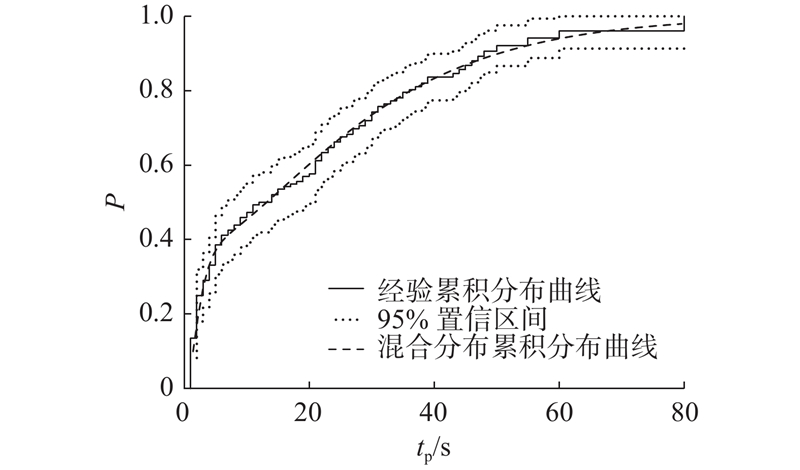
... 时间段1中区域1第1次受迫停车等待耐性的混合分布曲线如图3 所示.图中,P 为概率密度,即受迫停车事件随机发生的几率,t 表示受迫停车时长或等待耐性的统计值. 直方图为区域1第1次受迫停车出租车等待时长分布情况. 为了进一步验证模型的有效性,针对删失数据进行生存分析,采用非参数的Kaplan-Meier方法[29 ] 来估计经验累积分布(生存函数),将混合模型的累积分布函数与经验累积分布函数进行比较,并与通过Greenwood公式[30 ] 计算的95%上下限进行比较,结果如图4 所示. 图中,t p 表示等待耐性. 比较结果表明,混合模型的累积分布函数与经验累积分布函数较吻合,且始终位于95%上下限之间,说明拟合结果较好. 2个时间段数据集的估计都得到了类似的拟合优度. ...
1
... 时间段1中区域1第1次受迫停车等待耐性的混合分布曲线如图3 所示.图中,P 为概率密度,即受迫停车事件随机发生的几率,t 表示受迫停车时长或等待耐性的统计值. 直方图为区域1第1次受迫停车出租车等待时长分布情况. 为了进一步验证模型的有效性,针对删失数据进行生存分析,采用非参数的Kaplan-Meier方法[29 ] 来估计经验累积分布(生存函数),将混合模型的累积分布函数与经验累积分布函数进行比较,并与通过Greenwood公式[30 ] 计算的95%上下限进行比较,结果如图4 所示. 图中,t p 表示等待耐性. 比较结果表明,混合模型的累积分布函数与经验累积分布函数较吻合,且始终位于95%上下限之间,说明拟合结果较好. 2个时间段数据集的估计都得到了类似的拟合优度. ...
A comparative study of unit root tests with panel data and a new simple test
1
1999
... (b)平稳性检验:为了防止出现虚假回归的情况,首先对面板数据集中的单位根或平稳性进行检验. 对关键变量 “当前受迫停车时长是等待耐性的概率”、“行驶时间占比”进行LLC(Levin-Lin-Chu)检验,而近似分类变量的“车辆相对位置”和“当前停车位置是期望停车位的概率”进行Harris-Tzavalis检验[31 ] ,结果显示,所有变量都是平稳的,不存在单位根,无须进行协整检验. ...