基于应变影响线的桥梁模型修正试验

doi:10.3785/j.issn.1008-973X.2024.03.011

基于应变影响线的桥梁模型修正试验

周宇^,, 甘露一, 狄生奎, 贺文宇, 李宁波

1. 安徽建筑大学土木工程学院，安徽合肥 230601

2. 兰州交通大学土木工程学院，甘肃兰州 730070

3. 安徽建筑大学建筑健康监测与灾害预防技术国家地方联合工程实验室，安徽合肥 230601

4. 合肥市城市生命线工程安全运行监测中心，安徽合肥 230601

5. 合肥工业大学土木与水利工程学院，安徽合肥 230601

Bridge model modification experiment based on strain influence line

ZHOU Yu^,, GAN Luyi, DI Shengkui, HE Wenyu, LI Ningbo

1. College of Civil Engineering, Anhui Jianzhu University, Hefei 230601, China

2. School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China

3. National-local Joint Engineering Laboratory of Building Health Monitoring and Disaster Prevention Technology, Anhui Jianzhu University, Hefei 230601, China

4. Operation and Monitoring Center for Hefei Urban Safety and Security, Hefei 230601, China

5. College of Civil Engineering, Hefei University of Technology, Hefei 230601, China

收稿日期: 2023-01-6

基金资助:

国家自然科学基金资助项目 (51868045)；安徽省高校省级自然科学研究资助项目 (2022AH050248)；建筑健康监测与灾害预防国家地方联合工程实验室开放课题资助项目 (GG22KF002)；安徽省高校优秀拔尖人才培育资助项目 (gxgnfx2022021)；甘肃省建设科技资助项目 (JK2023-03)；企业委托技术开发课题资助项目 (HYB20220240, HYB20230001).

Received: 2023-01-6

Fund supported:

国家自然科学基金资助项目(51868045)；安徽省高校省级自然科学研究资助项目(2022AH050248)；建筑健康监测与灾害预防国家地方联合工程实验室开放课题资助项目(GG22KF002)；安徽省高校优秀拔尖人才培育资助项目(gxgnfx2022021)；甘肃省建设科技资助项目(JK2023-03)；企业委托技术开发课题资助项目(HYB20220240,HYB20230001).

作者简介 About authors

周宇（1989—），男，副教授，博士，从事桥梁结构损伤识别与健康评估研究.orcid.org/0000-0003-4743-241X.E-mail：yuzhou923@outlook.com , E-mail：yuzhou923@outlook.com

摘要

为了验证桥梁应变影响线用于模型修正的有效性，针对某三跨钢板组合连续梁桥在单辆重车移动加载下的应变时程响应进行研究. 联合实测应变影响线和计算影响线构建目标函数；以影响线形态控制点处的微应变试验值作为输入层参数，以有限元模型结构几何尺寸信息与材料特征值作为输出层参数，构建反向传播 (BP)神经网络进行自我学习；基于训练完毕的BP神经网络，对待修参数进行预测，开展桥梁模型修正研究. 结果表明，所提出的有限元模型修正方法能够减小真实结构不确定性带来的建模误差，修正后的优化模型比初始模型更加贴近真实结构，目标函数相对误差降低29%；可以采用基于BP神经网络的模型参数修正方法对有限元模型参数进行预测.

关键词： 桥梁工程 ; 模型修正 ; 应变影响线 ; 影响线识别 ; 前馈神经网络

Abstract

The investigation on a three-span steel plate composite continuous girder bridge was conducted to obtain the strain time response under the moving load of a single heavy vehicle, in order to verify the effectiveness of strain influence line for model modification. An objective function was constructed by measured and calculated strain influence lines. The back propagation (BP) neural network was constructed to do self-training, by taking the micro-strain test value at the control point of the influence line form as the input layer parameter, and the structural geometry information and material characteristic value of finite element model as the output layer parameters. The parameters to be modified were predicted and the bridge model modification was carried out, on the basis of the self-trained BP neural network. Results showed that the proposed finite element model modification method can reduce the modelling error caused by the uncertainty of the real structure, the revised optimization model was closer to the real structure than the initial model, and the relative error of the objective function was reduced by 29%. The model parameter modification method based on BP neural network can be used to predict the parameters of the finite element model.

Keywords： bridge engineering ; model modification ; strain influence line ; influence line identification ; feedforward neural network

PDF (1827KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

周宇, 甘露一, 狄生奎, 贺文宇, 李宁波. 基于应变影响线的桥梁模型修正试验. 浙江大学学报(工学版)[J], 2024, 58(3): 537-546 doi:10.3785/j.issn.1008-973X.2024.03.011

ZHOU Yu, GAN Luyi, DI Shengkui, HE Wenyu, LI Ningbo. Bridge model modification experiment based on strain influence line. Journal of Zhejiang University(Engineering Science)[J], 2024, 58(3): 537-546 doi:10.3785/j.issn.1008-973X.2024.03.011

得益于计算机软硬件的不断发展，有限元建模逐渐成为结构分析的常规手段，但即便是理想工程结构，其初始设计模型与既有实际工程间依然存在巨大偏差^[1]. 有限元建模很少考虑工程材料的离散型、施工误差的模糊性、截面尺寸的随机性^[2]，导致以往仅依据工程结构设计的几何尺寸与材料参数建模并不精确. 结构模型修正理论应运而生，并取得了可观的进展^[3].

有限元模型修正能够充分考虑工程实际，以真实结构客观存在的物理参数、几何特性为修正对象，使得修正后的模型更贴合实际，分析结果更具科学性. 模型修正基本思想是通过改变待修参数对目标函数开展最小化寻优研究，如何选择合适的寻优方法越来越受到学者们的重视^[4]. 马印平等^[5]以钢管混凝土组合桁架桥为工程背景，基于桥梁实测应变挠度响应构建模型修正目标函数，分析得到结构参数响应面方程，通过响应面开展目标参数寻优工作并以此开展结构模型修正研究. 郁胜等^[6]基于敏感性分析选取模型修正参数和特征量信息，依据模型分析不同参数水平下的特征量样本，构建参数样本与特征量样本间隐函数关系的径向响应面模型，进而展开模型修正研究. 上述研究采用优化算法对特征参数响应面函数求最优解，基于响应面的模型修正方法可有效、可靠地对目标函数开展寻优工作，但此类方法须构建较复杂的隐性函数关系式，存在计算量大、迭代次数多、耗时长等问题，从而引起优化结果不收敛并导致求解精度不稳定.

Liu等^[7]以模态频率为目标利用交叉模型交叉模态法(cross-model cross-mode，CMCM)对有限元模型参数开展修正研究. 王晓光等^[8]以结构自振频率为目标构造响应面函数，基于优化算法对某双塔双索面斜拉桥模型参数进行修正，继而获得更接近真实结构的有限元模型. 上述研究以结构模态参数为目标开展修正，结构模态频率能够反映桥梁整体刚度特性，但基于动力参数的模型修正可能存在频率信息量有限、振型识别精度低、受噪声影响较大等问题，故以频率参数为目标的修正方法存在一定误差^[9].

桥梁影响线可以通过单一测点输出桥梁截面刚度与结构边界特性^[10]，基于影响线的桥梁模型修正方法有望利用车辆移动快速加载与少量测点实现“轻量化”测试，从而获取丰富的桥梁截面与边界参数信息，其应用研究潜力巨大. 本研究选取连续梁桥应变影响线为目标参数，通过MATLAB构建2层前馈神经网络，建立有限元模型并生成30个样本数据代入展开神经网络训练，利用训练完善的神经网络预测桥梁在实测应变影响线下的模型结构参数，进而优化有限元模型使其截面刚度与边界特性更加逼近真实桥梁结构，为有限元模型结构的修正提供了新思路.

1. 模型修正方法的提出

有限元模型修正的中心思想是以理论计算与试验结果的误差为目标函数，多次调整修正模型物理几何参数，以减小数值模型与真实结构之间的分析偏差^[11]，提出采用反向传播(back propagation，BP)算法神经网络寻优的基于应变影响线的模型修正方法，该方法研究路线如图1所示.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

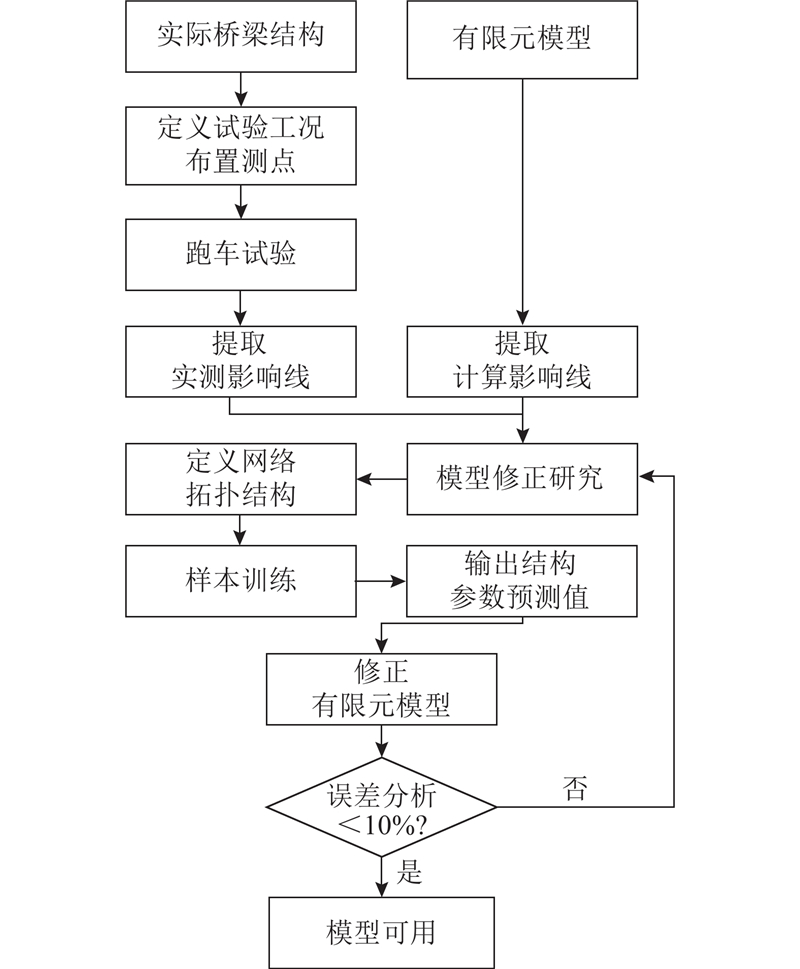
图 1 基于应变影响线的模型修正研究路线

Fig.1 Research route of model modification based on strain influence line

1.1. 目标函数

以桥梁应变影响线作为目标函数的特征参数，通过单辆重车最低怠速行驶过桥，来模拟荷载沿桥面各个位置连续静置加载，称为桥梁“准静态加载”实验^[12-13]，影响线类方法能克服结构动力测试模态数据存在的不完备问题，具有直观、经济、实用的优点^[14-15].

目标函数的建立旨在通过减小实测影响线和模型影响线间误差以修正模型，可采用误差公式定义目标函数. 其中绝对误差表达式为

(1)$ \sum {\left| {{\varepsilon _{_{\text{a}}}} - {\varepsilon _{\text{m}}}} \right|} . $

式中：$ {\varepsilon _{\text{a}}} $、$ {\varepsilon _{\text{m}}} $分别为应变影响线计算值与实测值.

百分比误差、相对误差表达式如下：

(2)$ {\sum {({\varepsilon _{\text{a}}} - {\varepsilon _{\text{m}}})} ^2}\bigg/{\sum {{\varepsilon _{\text{m}}}} ^2} \text{，} $

(3)$ \sum {\left| {{\varepsilon _{\text{a}}} - {\varepsilon _{\text{m}}}} \right|} \bigg/\sum {\left| {{\varepsilon _{\text{m}}}} \right|} . $

除了上述误差公式，进一步采用相关系数量化有限元模型和实际结构间的吻合程度：

(4)$ \frac{{\sum {({\varepsilon _{\rm{m}}} - {{\bar \varepsilon }_{\rm{m}}})({\varepsilon _{\rm{a}}} - {{\bar \varepsilon }_{\rm{a}}})} }}{{\sum {\sqrt {{{({\varepsilon _{\rm{m}}} - {{\bar \varepsilon }_{\rm{m}}})}^2}{{({\varepsilon _{\rm{a}}} - {{\bar \varepsilon }_{\rm{a}}})}^2}} } }} . $

式中：${{\bar \varepsilon }_{\rm{a}}}$、${{\bar \varepsilon }_{\rm{m}}}$分别为计算平均值与实测平均值.

1.2. 修正参数

修正参数可以分为矩阵参数与物理参数，其中矩阵参数为有限元模型中结构质量矩阵及刚度矩阵，矩阵参数型模型修正是通过直接修改有限元模型的矩阵参数，具有快速迭代的特点，但此类方法的子结构参数并无明确物理意义，甚至可能出现负刚度参数的异常情况^[16].

鉴于此，选取有限元模型中能够描述材料特性或几何性质的物理参数开展修正，对桥梁有限元模型各参数进行分析. 结合相关研究文献^[17-19]，考虑到钢梁与混凝土面板连接的剪力键影响，选取弹性模量E为待修正参数之一；试验桥梁支座处钢梁截面与跨中处钢梁截面存在尺寸差别，两截面在过渡区为线性变化的变截面，考虑到施工工艺的影响，选取钢梁顶板厚度、底板厚度及腹板厚度为待修正参数. 最终选取以下4个物理参数进行修正，即纵向主梁的弹性模量E、顶板厚度T₁、底板厚度T₂、腹板厚度T_w.

1.3. 修正方法

模型修正是典型的反向非线性问题，有限元模型修正是通过多次迭代调整物理参数与修正结果之间的表达关系，来实现对目标函数的最小化寻优^[20]. 神经网络是在物理机制上模拟人脑信息处理与传递，具有较好的学习能力与非线性映射能力^[21]. 采用BP神经网络开展模型修正研究可避免构建复杂的数学函数表达式，可以对任何一个闭区间内的连续函数进行逼近，完成m维到n维的映射，并通过样本数据的训练较好地学习系统的输入输出关系，具有研究价值^[22-24]. 因此，本研究通过构建带有反向传播算法的2层前馈神经网络，开展有限元模型修正方法研究.

2. 桥梁应变影响线测试与识别

考虑桥梁主梁截面抗弯刚度不确定，并在主梁两端引入竖向弹性支承与转动弹性约束的非理想边界，构建弹性支承约束主梁模型，用以模拟既有桥梁实际存在的结构模型参数不确定性，模型如图2所示. 图中，M_A、M_B为集中弯矩，P为外力，x'为外力P到点A的距离，l为长度，c为测点至梁端距离，D_C(x')为梁体C截面的位移，d_C(x')为主梁的弯曲效应，I为截面惯性矩，Λ(x)为截面抗弯的不确定系数.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2 两端带转动弹性约束的简支梁模型

Fig.2 Simple supported beam model with rotational elastic constraint at both ends

将虚拟集中弯矩M_A、M_B替代两端多余转动约束，建立点A、B的位移协调方程：

(5)$ {M_A}{\delta _{AA}}{\text+}{M_B}{\delta _{AB}}+{\varDelta _{AP}} = - {M_A}/{K_A} , $

(6)$ {M_A}{\delta _{BA}}{\text+}{M_B}{\delta _{BB}}+{\varDelta _{BP}} = - {M_B}/{K_B} . $

式中：δ_ij为柔度系数，表示在j处施加单位力，i处产生的转角；Δ_iP为协调方程自由项，表示在外力P作用下，i处产生的转角；K_i为i处转动约束刚度.

采用图乘法计算δ_ij、Δ_iP，并计算该模型的位移协调方程柔度系数与自由项，代入式(5)、(6)，可以得出

(7)$ {M_A}({x'}) = \frac{{{K_A}{K_B}({\delta _{BB}}{\varDelta _{AP}} - {\delta _{AB}}{\varDelta _{BP}})+{K_A}{\varDelta _{AP}}}}{{{K_A}{K_B}\delta _{AB}^2 - ({K_A}{\delta _{AA}}+1)({K_B}{\delta _{BB}}+1)}} , $

(8)$ {M_B}({x'}) = \frac{{{K_A}{K_B}({\delta _{AA}}{\varDelta _{BP}} - {\delta _{AB}}{\varDelta _{AP}})+{K_B}{\varDelta _{BP}}}}{{{K_A}{K_B}\delta _{AB}^2 - ({K_A}{\delta _{AA}}+1)({K_B}{\delta _{BB}}+1)}} . $

虚拟弯矩M_A、M_B分母处不含移动集中力的位置参数x'，而分子处参量x'的次数与Δ_iP一致，因此代入弹性约束内力，任意截面C处的弯矩影响线为

(9)$ {M_C}({x'}) = \left\{ {\begin{array}{*{20}{l}}{\dfrac{{l - c}}{l}{M_A} + \dfrac{c}{l}{M_B} + \dfrac{{P(l - c)x'}}{l},} & {x' \in [0,c);}\\{\dfrac{{l - c}}{l}{M_A} + \dfrac{c}{l}{M_B} + \dfrac{{P(l - x')c}}{l},} & {x' \in [c,l].}\end{array}} \right. $

进一步计算可得任意截面C处的应变影响线：

(10)$ {\varepsilon _C}({x'}) = \frac{{\sigma _C}({x'})} {E_C} = \frac{{{M_C}({x'})}}{{{W_C} {E_C}}} . $

式中：σ_C为点C的应力影响线，E_C为弹性模量，W_C为任意截面C的截面抵抗矩.

根据式（10）可知，桥梁应变影响线主要与结构跨度、材料弹性模量、截面惯性矩和桥梁边界约束刚度等因素有关，因此以应变影响线为目标参数开展模型修正研究可以全面地考虑桥梁截面几何尺寸、结构约束刚度、材料弹性模量等重要建模信息，使修正物理意义明确，修正计算结果科学、可靠.

2.1. 工程概况

以某钢板组合连续梁桥为试验对象，展开基于BP神经网络的桥梁应变影响线模型修正研究. 桥梁结构总长为105 m (35 m+35 m+35 m)，桥宽为12 m，正交布置. 桥梁上部结构采用工字形钢和混凝土面板组合梁，主桥钢结构采用Q345钢材，下部结构采用圆形墩柱式桥墩，采用C40抗硫混凝土，桥梁支座采用滑动摆支座. 桥面铺装采用胎体增强型防水涂层+60 mm中粒沥青铺装+40 mm细粒式沥青铺装. 桥梁几何尺寸如图3所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3 桥梁结构模型与截面尺寸信息

Fig.3 Bridge structural model and section information

2.2. 试验概况

为了更科学地开展桥梁有限元模型修正，为模型修正参数的选取提供可信数据支撑，现场结合设计图纸复核了桥梁截面主要几何尺寸信息.

试验加载车辆选取单辆两轴重车，车辆载重为37 t，加载车辆在桥面指定加载路径以最低怠速缓慢行进，由于荷载效率过大易导致荷载试验的安全事故，过小会导致结构响应不充分，故本次试验荷载效率设为0.2~0.5^[25]. 桥梁影响线测试试验选择桥梁中跨跨中截面布设表面式应变传感器，安装于主梁1#的梁底，采集设备采用DH3821应变测试分析系统，车辆采用最低怠速移动加载，车辆行进加载路线距桥梁中心线6.375 m，传感器采集频率设定为2 Hz，对桥梁中跨跨中测点在既定试验荷载下的应变影响线展开测试，测点布置图如图4所示.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4 试验桥梁应变影响线测试的测点布置及现场图

Fig.4 Monitoring points arrangment and site photo of strain influence line test of test bridge

2.3. 桥梁影响线的识别

采用单量重车移动驶过三跨钢板组合连续梁进行加载试验研究，试验测试提取桥梁中跨跨中应变时程响应，利用构造车辆信息矩阵剥离车辆多轴效应^[26]，进而将桥梁应变时程响应还原为单位集中荷载(1 kN)作用下的桥梁应变影响线$ {\varepsilon _{{C}}} $. 依据设计图纸与现场复核得到的桥梁结构尺寸信息，建立有限元初始模型，采用影响线加载定义移动荷载分析工况，为了精确对准实测影响线，加载步长选为403.846 mm，移动荷载分析工况共生成261个加载步.

以单位集中荷载模拟影响线加载，提取桥梁模型计算应变影响线，实测影响线与计算影响线对比如图5所示. 可以看出，通过移动车辆影响线加载试验测得桥梁跨中应变影响线符合三跨连续梁桥理论影响线的一般规律，左右波谷幅值基本相同，说明桥梁整体刚度分布均匀^[27]，曲线无明显突变，桥梁结构无明显损伤^[28]. 桥梁结构在单位荷载作用下中跨跨中的实测应变影响线最大值为0.1489×10⁻⁶，仅依据设计信息建立的有限元模型在同样加载工况下，桥梁计算应变影响线最大值为0.227×10⁻⁶，不难得知，实际桥梁结构相较理论设计模型更为安全，但正因为两者偏差较大，须对初始模型进一步展开有限元模型修正研究.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5 初始模型应变影响线与实测值的对比

Fig.5 Comparison of strain influence line of initial model with measured value

3. 桥梁应变影响线模型修正方法

3.1. BP神经网络原理及理论

BP神经网络是基于反向传播算法的多层前馈神经网络，其中隐含层节点可以表达为^[29]

(11)$ {y_i} = f({\rm{ne}}{{\rm{t}}_i}) = f\left(\sum\limits_j {{w_{ij}}{x_j} - {\theta _i}}\right) . $

式中：y_i为隐含层，x_j为输入层，w_ij为第1层权值，θ_i为第1层阈值. 输出层节点表达如下：

(12)$ {O_l} = f({\rm{ne}}{{\rm{t}}_l}) = f\left(\sum\limits_i {{T_{li}}{y_i} - {\theta _l}}\right) . $

式中：O_l为输出层，T_li为第2层权值，θ_l为第2层阈值. 将输出值与样本真值t_l代入误差公式：

(13)$ \begin{split} J =\;& \frac{1}{2}\sum\limits_l {{{({t_l} - {O_l})}^2}} = \\ \;& \frac{1}{2}\sum\limits_l \left( {t_l} - f\left(\sum\limits_i {{T_{li}}f\left(\sum\limits_j {{w_{ij}}{x_j} - {\theta _i}}\right) - {\theta _l} } \right)\right)^2 .\end{split} $

从输出层开始，计算误差后进行反向传播，计算权重修正值ΔT_li、Δw_ij：

(14)$ \Delta {T_{li}} = - \eta \frac{{\partial J}}{{\partial {T_{li}}}} = \eta {\delta _l}{y_i} \text{，} $

(15)$ \Delta {w_{ij}} = - {\eta '}\frac{{\partial J}}{{\partial {w_{ij}}}} = {\eta '}\delta _l'{x_j} . $

式中：$ \eta $、$ {\eta '} $为学习速率，会直接影响神经网络学习训练的权值变化，范围一般为(0,1.00)，本研究为了防止学习速率过大导致的网络训练过程不稳定问题，取$ \eta $=$ \eta' $=0.01^[30]；$ {\delta _l} $、$ \delta _i' $分别为输入层和隐含层的节点误差.

同理可得阈值的修正值Δθ_l及Δθ_i：

(16)$ \Delta {\theta _l} = - \eta \frac{{\partial J}}{{\partial {\theta _l}}} = \eta {\delta _l} \text{，} $

(17)$ \Delta {\theta _i} = - {\eta '}\frac{{\partial J}}{{\partial {\theta _i}}} = {\eta '}\delta _i' . $

3.2. 基于模型修正的神经网络拓扑结构

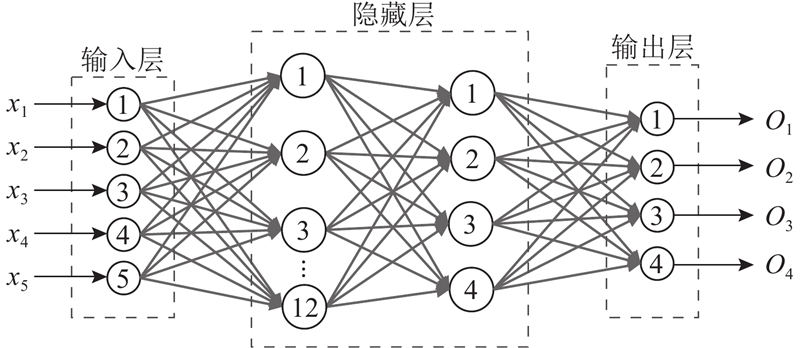
桥梁影响线理论本质为连续性函数曲线，鉴于观测手段的离散性，故提取影响线中5个形状控制点（3个跨中点及2个中跨1/4点）为输入层参数，将输入层设置5个节点. 输出层依据上述待修正参数的定义，设置4个节点.

由于输入层参数与输出层参数不是同一数量级，采用Min-Max归一化对数据进行处理：

(18)$ {\bar x} = \frac{{{x} - {x_{{\text{min}}}}}}{{{x_{{\text{max}}}} - {x_{{\text{min}}}}}} . $

式中：$\bar x $为参数归一化值，x为参数值，x_max和x_min分别为参数最大与最小值.

针对隐含层节点数，根据经验公式得到

(19)$ P = \sqrt {m+n} +a . $

式中：P为隐含层节点数，取P=12；m为输入层节点数；n为输出层节点数；a为[1，10]的常数.

依据所确定的各层节点数量，构建5-12-4-4的BP神经网络拓扑结构用于有限元模型修正，神经元间采用无反馈的前馈神经网络，网络节点传递函数采用tansig函数和pureline函数，反向传播算法采用列文伯格-马夸尔特算法(Levenberg-Marquardt，L-M)^[31]，神经网络拓扑结构如图6所示.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6 BP神经网络拓扑图

Fig.6 BP neural network topology

对初始有限元模型结构参数进行30 次随机缩放，提取对应结构参数下桥梁应变影响线，作为30 个神经网络样本集，如表1所示. 表中，下标p、q分别表中样本值、初始值. 为了验证网络模型的泛化能力，将上述30个样本集随机划分为训练集(70%)、测试集(15%)和验证集(15%)，进而将30 个样本集导入所建立的神经网络，对网络展开训练、测试以及验证.

表 1 神经网络样本参数表

Tab.1 Neural network sample parameter table

类别	E_p/E_q	T_1p/T_1q	T_2p/T_2q	T_wp/T_wq
初始值	1.00	1.00	1.00	1.00
样本1	1.05	1.10	1.05	1.10
样本2	1.05	1.10	1.20	1.15
样本3	1.05	1.20	1.20	1.30
样本4	1.05	1.25	1.25	1.25
样本5	1.05	1.30	1.20	1.15
样本6	1.10	1.00	1.00	1.00
样本7	1.10	1.05	1.05	1.05
样本8	1.10	1.20	1.15	1.25
样本9	1.10	1.20	1.20	1.30
样本10	1.10	1.30	1.30	1.15
样本11	1.15	1.20	1.10	1.20
样本12	1.15	1.20	1.25	1.30
样本13	1.15	1.25	1.15	1.15
样本14	1.15	1.25	1.20	1.20
样本15	1.15	1.25	1.20	1.30
样本16	1.20	1.15	1.15	1.20
样本17	1.20	1.25	1.15	1.25
样本18	1.20	1.25	1.20	1.30
样本19	1.20	1.30	1.25	1.30
样本20	1.20	1.30	1.30	1.30
样本21	1.25	1.15	1.25	1.35
样本22	1.25	1.20	1.20	1.25
样本23	1.25	1.20	1.25	1.30
样本24	1.25	1.30	1.30	1.25
样本25	1.25	1.35	1.35	1.30
样本26	1.29	1.15	1.25	1.20
样本27	1.29	1.20	1.30	1.25
样本28	1.29	1.25	1.25	1.30
样本29	1.29	1.30	1.35	1.20
样本30	1.29	1.35	1.35	1.30

新窗口打开| 下载CSV

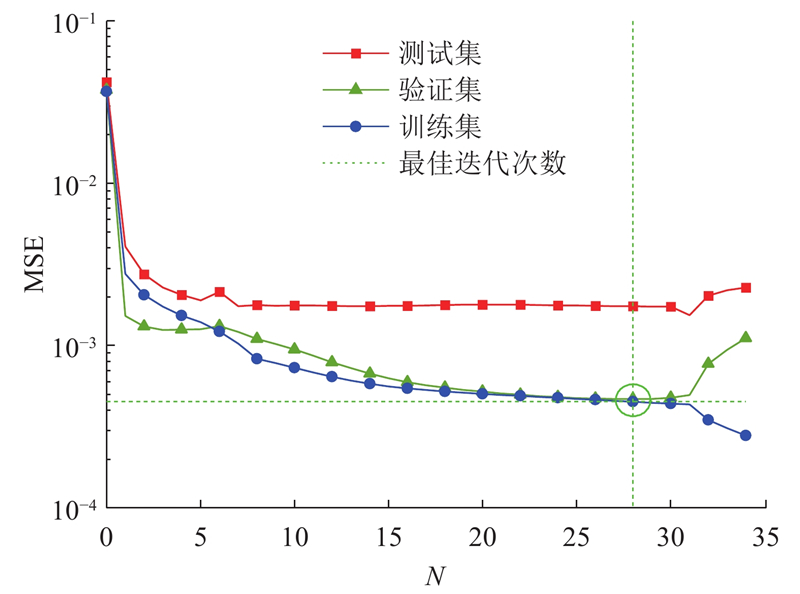
3.3. 模型修正网络训练结果

通过训练神经网络修正模型，并多次迭代L-M反向传播算法，结果如图7所示. 图中，N为迭代次数，MSE为不同迭代次数所对应的均方误差. 训练集、验证集、测试集和总集的回归系数分别为0.9673、0.9502、0.9315和0.9559，表明该神经网络有较强的拟合能力，可用于预测模型修正参数. 由图7可知，完成收敛的BP神经网络迭代次数N=34，其中最优迭代次数为28，此时均方误差MSE仅为4.69×10⁻⁴，满足计算误差要求.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7 最优迭代与误差分析

Fig.7 Optimal iteration and error analysis

3.4. 模型修正试验验证

提取桥梁实测应变影响线中5 个形状控制点，并作为输入参数导入训练后的BP神经网络，得到BP神经网络预测的结构物理参数，如表2所示. 可以看出，训练完毕的BP神经网络可以较好地对桥梁结构物理修正参数进行预测，修正后的结构弹性模量为290248 MPa，比初始值增大40%，是由于建模过程中尚未考虑混凝土面板与钢主梁间的剪力键作用. 修正后的结构顶板厚度为28.25 mm，底板厚度为36.41 mm，略薄于设计值，其中腹板厚度为20.39 mm，比设计值厚27%，是由于实际桥梁存在部分附属结构进而导致模型结构厚度产生微小的等效变化.

表 2 模型修正前后的参数取值

Tab.2 Parameter values before and after model modification

类别	E /MPa	T₁ /mm	T₂ /mm	T_w /mm
初始值	206 000	30.00	40.00	16.00
修正值	290 248	28.25	36.41	20.39

新窗口打开| 下载CSV

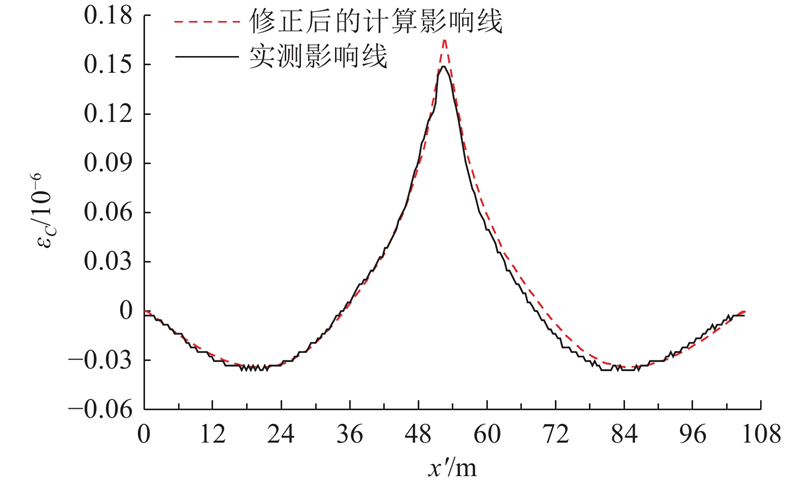
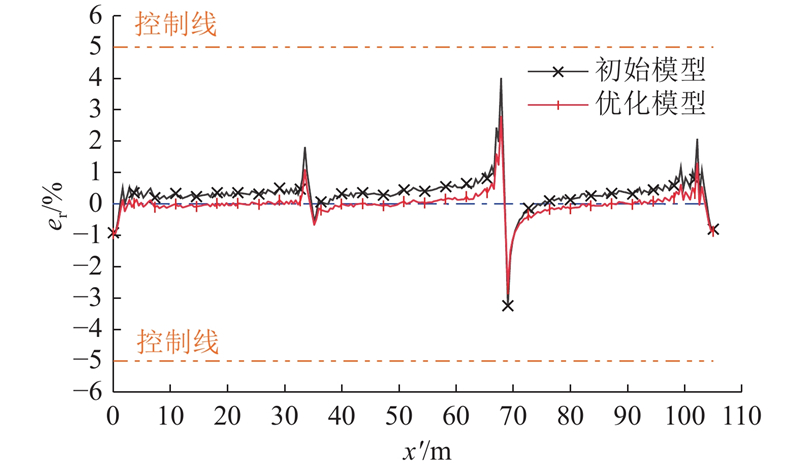
将网络预测得到的结构物理参数输入有限元模型，提取模型修正后的结构应变影响线，分析模型修正后与初始模型两者误差，如表3、图8、9所示. 表中，e_a、e_p、e_r分别为绝对误差、百分比误差、相对误差，R为相关系数. 由表3、图8可知，通过BP神经网络开展桥梁应变影响线模型修正可以较好地对桥梁结构有限元参数进行优化，模型修正后的结构应变影响线更加贴近结构实测影响线，其百分比误差下降至0.89%；相对误差下降至9.43%，误差均小于10%. 模型修正后的应变影响线较修正前，其数据相关系数由0.996 69提高至0.996 71. 由图9可知，模型修正前、后在各影响线加载步下的相对误差在连续梁桥支座附近出现极大值，是由于支座附近应变影响线系数绝对值小；相对误差均在±5%的控制线以内，相比于初始模型，优化模型相对误差绝对值更小，说明优化模型的应变影响线与实测应变影响线更吻合.

表 3 模型修正前后应变影响线误差对比

Tab.3 Comparison of strain influence line error before and after model modification

误差类别	e_a	e_p	e_r	R
修正前	3.34	16.49	38.00	0.996 69
修正后	0.83	0.89	9.43	0.996 71

新窗口打开| 下载CSV

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8 优化模型的应变影响线与实测值的对比

Fig.8 Comparison of strain influence line of modified model with measured value

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9 模型修正前后应变影响线相对误差对比

Fig.9 Comparison of relative errors of strain influence lines before and after model modification

桥梁影响线试验的本质是“拟静力”试验，可以全面、统一地反映桥梁结构截面抗弯刚度与支座边界条件，能够有效反映桥梁结构模型实际状态. 为了进一步分析基于BP神经网络的桥梁影响线模型修正方法对桥梁动力特性的影响，对模型修正后的桥梁优化模型开展自振频率分析，如图10所示. 图中，f为结构自振频率. M为频率阶数. 可以看出，模型修正后的结构自振频率相较于修正前均增加，且更加贴近桥梁实测频率，桥梁结构实测频率与计算频率误差从修正前的20%以内降低至10%以内，且一阶频率误差减小至1.89%，模型精度显著提升.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10 模型修正前后结构自振频率对比

Fig.10 Comparison of structural self-oscillation frequency before and after model modification

4. 结　论

(1)有限元模型的准确性将显著影响到分析结果，常规模拟难以确保所建模型精度，本研究提出基于BP神经网络的桥梁应变影响线模型修正方法，可有效减小桥梁结构目标函数及自振频率的相对误差. 研究表明，修正后的目标函数及频率误差均降低至0~10%，所提方法对静力特性及动力特性下的结构模型精度均存在显著提升.

(2)利用全局激励输出桥梁单一测点的影响线测试方法，可获取比常规静载试验更多的数据样本，实现桥梁“轻量化”测试. 基于应变影响线开展桥梁模型修正，可以更全面地评价修正前后模型误差，更完整地反映桥梁力学特性.

(3)采用BP神经网络开展桥梁模型修正研究，可有效避免构建复杂函数表达式，通过构建带有反向传播算法的2层前馈神经网络，能够快速有效地实现应变影响线误差目标最小化求优.

(4)研究提出的桥梁有限元模型修正方法，可为进一步开展结构抗震精细化模拟与真实损伤识别验证提供更为科学、精确的有限元结构模型.

(5)本研究以三跨连续梁为背景，仅研究了单车道加载下桥梁模型快速修正，多车道加载下的影响面模型修正研究仍具研究潜力. 另外，限于篇幅，本研究未对其他神经网络优化计算模型开展更为深入的研究对比.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

ZHOU L, WANG L, CHEN L, et al

Structural finite element model updating by using response surfaces and radial basis functions

[J]. Advances in Structural Engineering, 2016, 19 (9): 1446- 1462

DOI:10.1177/1369433216643876 [本文引用: 1]

[2]

周宇, 狄生奎, 项长生, 等

基于弹性约束支承梁转角影响线的梁结构损伤诊断

[J]. 浙江大学学报: 工学版, 2020, 54 (5): 879- 888