夹层组合梁具有可以充分利用组成材料的优点,在保证强度与刚度的基础上,节省材料、减轻重量,在正常使用状态和承载能力极限状态都能显示出其优势. 组合梁的连接件往往不足以保证各层之间实现完美连接(full-interaction),导致“部分作用(partial-interaction)”[1]的现象,即组合梁受力时各层之间将会产生层间的黏结滑移作用. 层间滑移的存在大大增加了组合梁计算分析的难度,国内外学者对此展开了广泛的研究.
Newmark[7]通过实验提出层间滑移与剪力之间的线性假设,基于Euler-Bernoulli梁理论建立钢-混凝土组合梁的控制方程,为部分作用组合梁的研究提供了值得借鉴的研究思路. 目前针对3层组合梁的研究较少,Chui等[8]给出了在均布荷载和集中力荷载作用下3层简支组合梁的解析解. Sousa等[9]研究基于Euler-Bernoulli梁和Timoshenko梁理论的多层组合梁的解析解. 在数值分析研究方面,Sousa[10]基于之前的解析方法提出新的有限元公式. Keo等[11]利用控制方程导出精确的刚度矩阵并提出精确有限元公式. Lin等[12]基于Timoshenko梁理论提出考虑独立截面转角和横向剪切变形的3层部分作用组合梁有限元分析方法.
本研究在Xu等[15]工作的基础上,采用Timoshenko梁理论,将高阶插值函数引入内部自由度以避免滑移/曲率锁定问题,并利用MATLAB编译有限元程序. 为了提高计算效率,推导并给出了3层组合梁的8×8刚度矩阵、质量矩阵以及几何刚度矩阵元素的显式表达式. 进行算例验证和应用,通过与文献和ABAQUS模拟结果对比分析,验证本研究提出的新型夹层组合梁有限元方法的准确性、收敛性和稳定性.
1. 理论模型
1.1. 组合梁结构与参数
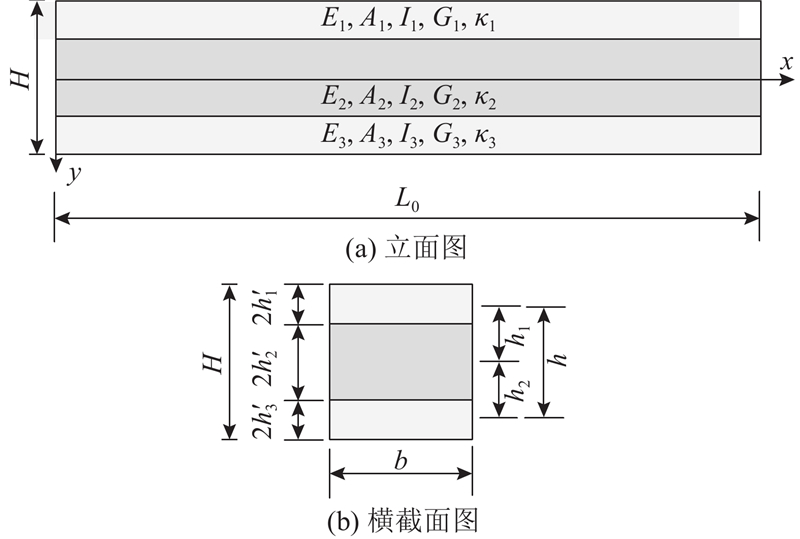
夹层组合梁剖面图如图1所示. 图中,Ei、Gi、Ii、Ai和κi
图 1
图 1 3层夹层组合梁及坐标系示意图
Fig.1 Three-layer sandwich composite beam and coordinate system
1.2. 理论推导
图 2
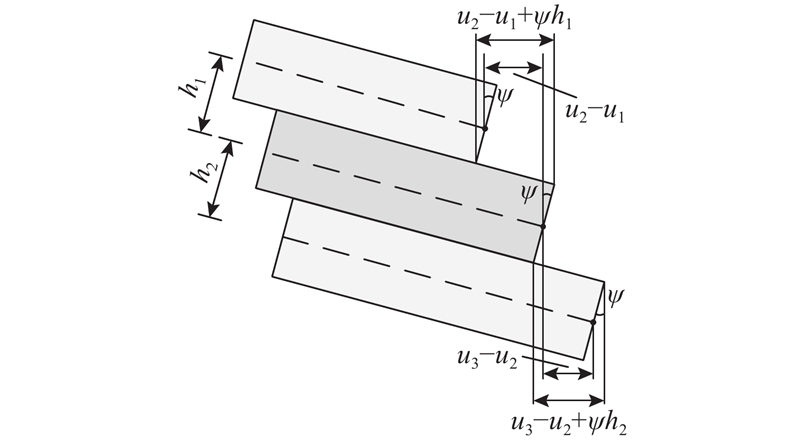
图 2 层间滑移、截面转角和轴向位移的几何关系
Fig.2 Geometrical relationship of interlayer slips, rotation angles and longitudinal displacements
式中:
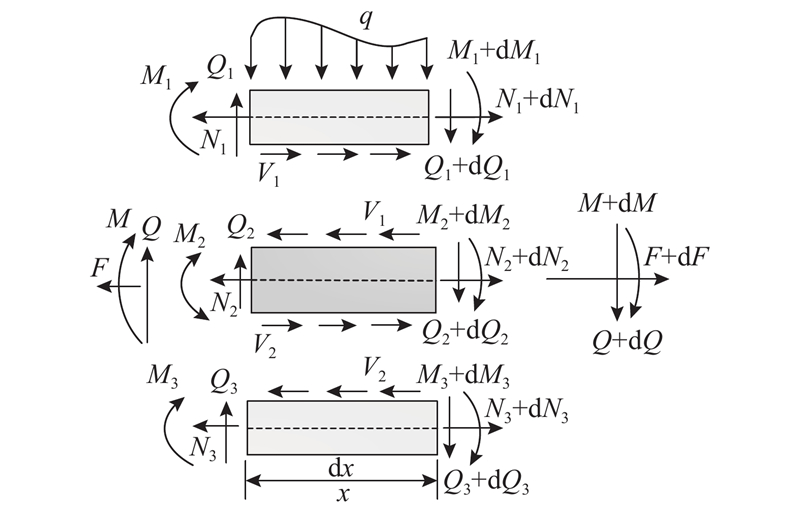
如图3所示为长度为dx的微小单元. 图中,M、Q、F分别表示整个横截面的弯矩、剪力和轴力,Ni、Mi和Qi(i=1,2,3) 为各层梁的轴力、弯矩和剪力,Vi为层间剪力,q、m分别表示作用在该单元上的均布载荷和弯矩.
图 3
根据单元在横截面上的平衡条件,可以得到
同时,根据x方向的平衡条件可以得到
整个单元横截面的弯矩可以表示为
各层间纵向剪力与连接件的抗剪刚度呈线性关系:
根据Timoshenko梁理论,内力与变形关系为
式中:
各层轴向力
1.3. 最小势能原理
为了推导夹层梁的有限元单元,首先须建立夹层梁的能量表达式:
式中:
式中:
2. 组合梁的有限元矩阵推导
2.1. 单元刚度矩阵推导
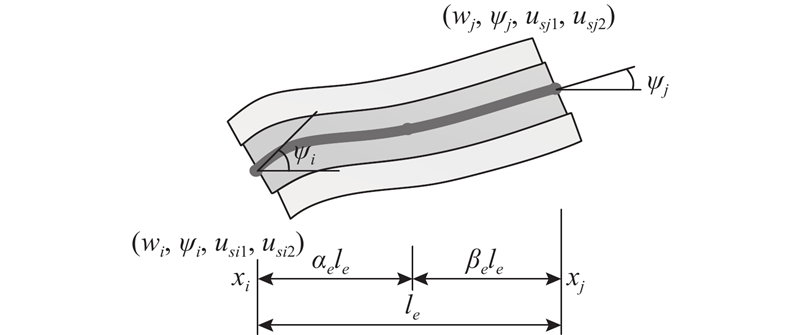
将组合梁沿轴向离散为若干个无穷小单元,如图4所示为其中第e个单元. 记单元节点位移为
图 4
式中:l为该单元的长度.
所假设位移的插值函数表达式如下:
式中:
将式(18)代入式(11),可以得到新的能量表达式:
式中:
为了消除内部的自由度,利用内部自由度应使单元的势能最小化的关系:
将式(19)重新表示为
进而可以得到内部自由度与单元节点上位移的关系:
式中:
利用式(22),位移表达式(18)可以重新表示为
式中:
将式(23)回代到能量方程(式(11))并进行变分可以得到8×8的对称单元刚度矩阵Ke,具体表达式如附录B所示.
广义载荷对应于外力做功表达式(式(15))中的线性项,即
将新的插值函数(式(23))代入式(24)得到广义载荷向量
组合梁的整体刚度矩阵和全局载荷向量表达式为
式中:N为单位数量.
可以得到组合梁的总势能为
采用最小势能原理可以得到
式中:
2.2. 动力有限元分析
组合梁的动力行为可以通过哈密顿原理获得[19]:
式中:T为动能,
对于自由振动频率
式中:符号“^”表示相应的模态形状函数. 基于哈密顿原理,可以得到自振频率的变分表达式:
式中:符号“st”表示驻值.
与自振频率分析类似,屈曲荷载
将式(23)代入式(31),沿单元长度进行积分得到不含内部自由度的第e个单元的能量方程,根据最小势能原理可以得到
式中:
类似于自振频率的分析,通过对式(32)进行变分可以得到单元的几何刚度矩阵:
式中:
3. 算例验证和应用
3.1. 文献[9]的算例
图 5
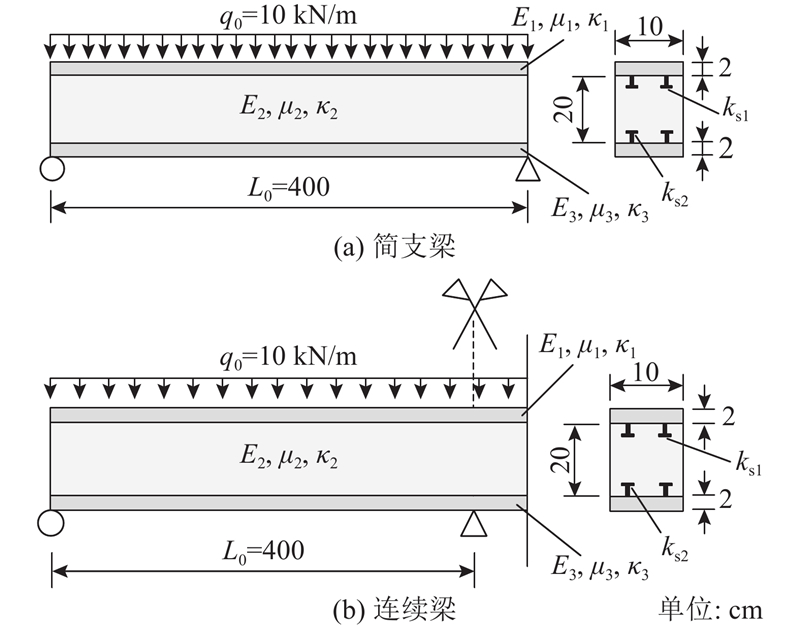
图 5 简支和连续3层钢-混组合梁算例
Fig.5 Simply supported and continuous three-layer steel-concrete composite beams
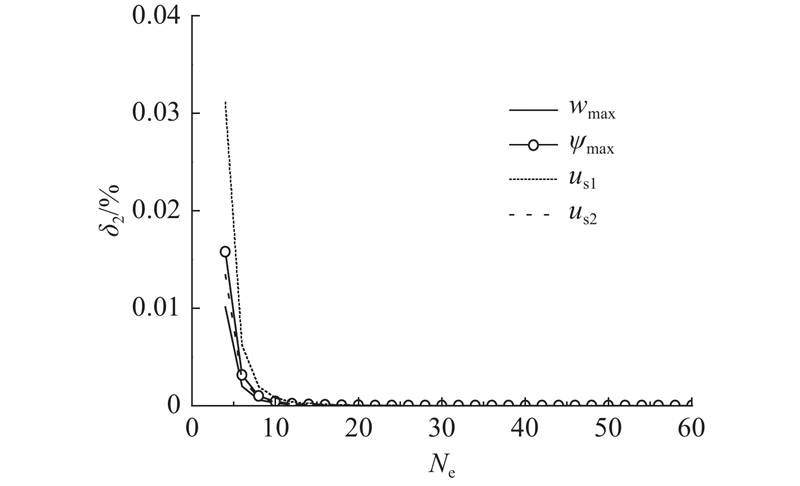
简支和连续2种不同边界条件下计算所得的层间最大滑移、最大挠度及连续梁跨间最大弯矩结果分别如表1、2所示. 表中,δ1为相对误差,δ1=[单元数为100时本研究结果−文献[9]结果)/文献[9]结果]×100%. 当单元数量为100时,计算所得相对误差均不超过0.1%,显示了本研究计算结果的准确性. 在使用100个组合结构单元时2个算例的计算时间分别仅为0.184 7、0.309 3 s(Intel Core i5-11400CPU @ 2.60 GHz),且对于独立转角假设的含三截面转角模型[12],计算时间分别为0.661 5、0.795 8 s,本研究方法分别节省了258%、157%的计算时间,表明本研究方法的计算效率高. 对于简支梁算例,计算结果相对误差随着单元数的增加而变化的情况如图6所示. 图中,Ne为单元数量;δ2为相对误差,δ2=[(不同单元数下计算结果−单元数为500时计算结果)/单元数为500时结果]×100%. 计算结果显示,采用本研究方法建立的有限元模型收敛速度快,在4个单元时最大相对误差为0.03%;当单元数大于22时,相对误差低于0.00005%.
表 1 简支边界条件下层间滑移与最大挠度计算结果对比
Tab.1
| 方法 | 单元数 | us1 /mm | us2 /mm | wmax /mm |
| 文献[9] | — | 0.778218480 | 1.00207365 | 10.91156269 |
| 本研究方法 | 4个单元 | 0.778460594 | 1.00220826 | 10.91915070 |
| 10个单元 | 0.778224788 | 1.00207715 | 10.91807360 | |
| 20个单元 | 0.778218881 | 1.00207388 | 10.91804750 | |
| 100个单元 | 0.778218487 | 1.00207366 | 10.91804580 | |
| δ1/% | 8.99×10−7 | 9.98×10−7 | 5.94×10−2 | |
表 2 连续边界条件下层间滑移与最大弯矩计算结果对比
Tab.2
| 方法 | 单元数 | us1 /mm | us2 /mm | Mmax /(kN·m) |
| 文献[9] | — | 0.427231210 | 0.56115713 | 18.80241423 |
| 本研究方法 | 4个单元 | 0.561469668 | 18.823051 | 18.823051 |
| 10个单元 | 0.561417252 | 18.812664 | 18.812664 | |
| 20个单元 | 0.561415993 | 18.812043 | 18.812043 | |
| 100个单元 | 0.561415910 | 18.811891 | 18.811891 | |
| δ1/% | 2.85×10−2 | 4.61×10−2 | 5.04×10−2 | |
图 6
图 6 简支边界条件下最大挠度、最大转角和层间滑移相对误差随单元数的变化
Fig.6 Variations of relative errors of maximum deflections, maximum rotation angles and interlayer slips with different element numbers under simply supported condition
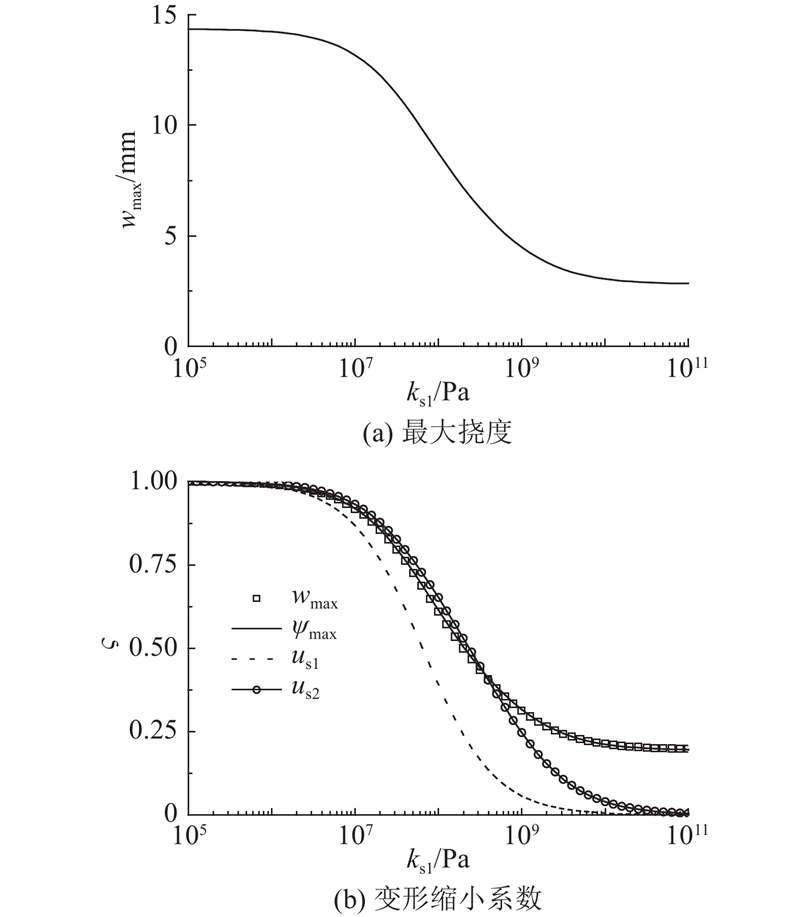
如图7(a)所示为简支边界时跨中最大挠度随层间抗剪刚度增大而变化的结果. 有限元模型中单元数为100,ks1由0.1 MPa增至100 GPa,ks2保持为ks1/8. 结果显示,当抗剪刚度较小时(ks1≤0.1 MPa),组合梁可以视为无抗剪刚度,跨中挠度超过14 mm;当抗剪刚度较大时(ks1≥100 GPa),组合梁可视为完美抗剪连接,跨中挠度为2.84 mm. 如图7(b)所示为变形缩减系数
图 7
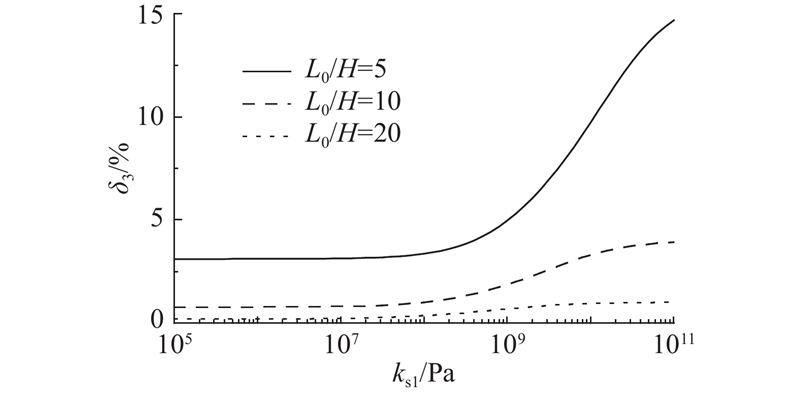
当简支梁模型跨高比L0/H=5、10和20时,采用Euler-Bernoulli梁(EB)与Timoshenko梁(TB)理论所得跨中挠度结果的相对误差随着抗剪刚度的变化如图8所示. 图中,δ3为相对误差,δ3=[(wmax,EB−wmax,TB)/wmax,TB]×100%,其中,wmax, EB、wmax, TB分别为EB、TB梁理论所得跨中挠度结果的最大值. 结果显示EB梁计算结果的相对误差随着抗剪刚度的增大而增大. 若以相对误差3%为界限,在低抗剪刚度(ks1=0.1 MPa)情况下,当L0/H=5时,EB梁计算结果不满足要求;当L0/H=10时,抗剪刚度超过6.3 GPa,EB梁计算结果误差将超限;对于L0/H=20的细长梁,EB梁计算结果相对误差不超过1%. 随着跨高比的减小,Euler-Bernoulli组合梁将不再适用,Timoshenko梁理论组合梁适用性更强.
图 8
图 8 最大挠度相对误差随抗剪刚度的变化
Fig.8 Variations of relative errors of maximum deflection with shear stiffness
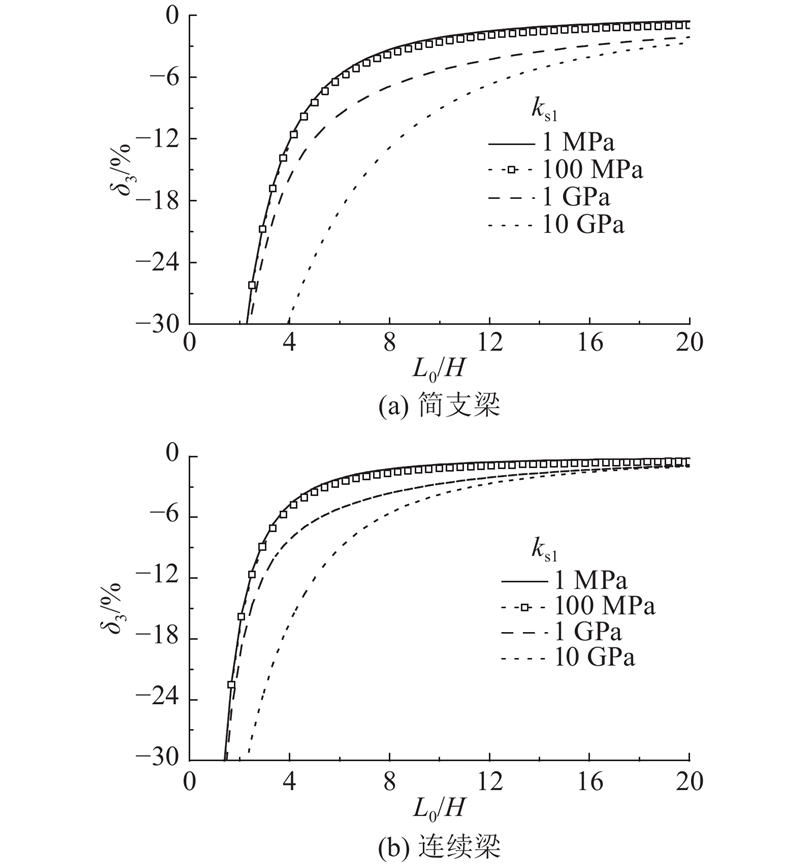
如图9所示为简支梁与连续梁模型4种不同抗剪刚度时,采用Euler-Bernoulli梁(EB)与Timoshenko梁(TB)理论所得跨中挠度结果的相对误差随着跨高比的变化. 结果显示简支梁与连续梁在跨高比较小时,EB梁与TB梁计算结果的相对误差较大. 若以3%幅值为界限,当ks1=1 MPa时,简支梁和连续梁的跨高比分别须大于5.4和8.8才可满足要求;当ks1=10 GPa时,简支梁和连续梁的跨高比则分别须大于11.7和18.8才可满足要求.
图 9
图 9 2种梁理论下跨中最大挠度的相对误差
Fig.9 Relative errors of maximum mid span deflection obtained by two different beam theories
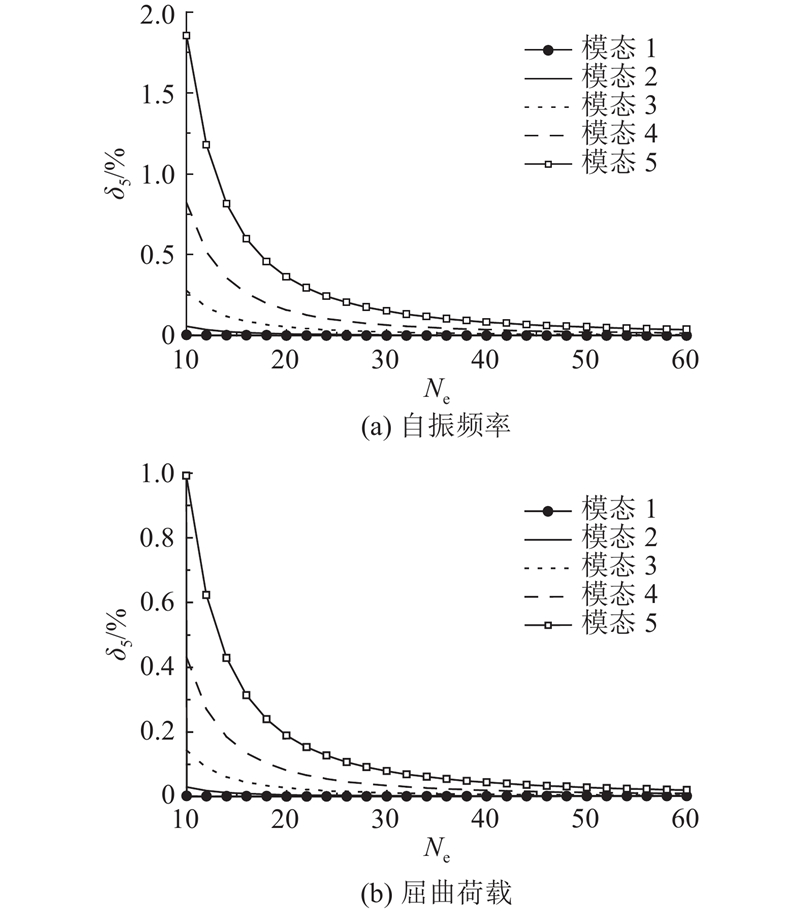
简支边界时自振频率与屈曲荷载的计算结果如表3所示,其中ABAQUS模拟时采用平面应力有限元模型,δ4为相对误差,δ4=[(本研究结果−ABAQUS结果)/ ABAQUS结果]×100%. 结果显示本研究方法结果可与ABAQUS数值模拟结果吻合. 第1阶自振频率与屈曲荷载的相对误差均小于1%;前4阶模态时相对误差均小于3%. 如图10所示为模态1~5的自振频率与屈曲荷载的相对误差δ5随单元数增加的变化,相对误差δ5=[计算结果−单元数为500时结果)/单元数为500时结果]×100%. 对于第1阶自振频率与屈曲荷载,4个单元时相对误差即小于0.06%. 随着自振和屈曲失稳模态阶数的提高,所需单元数量增加. 对于第5阶自振频率与屈曲荷载,为了保证相对误差小于0.5%所需的单元数量分别为16和18.
表 3 自振频率与屈曲荷载计算结果对比
Tab.3
| 阶次 | ω/Hz | δ4/% | Pcr/kN | δ4/% | ||
| ABAQUS | 本研究方法 | ABAQUS | 本研究方法 | |||
| 1 | 19.129 | 19.229 | 0.52 | 1865.4 | 1881.2 | 0.85 |
| 2 | 68.909 | 69.582 | 0.98 | 6104.5 | 6180.9 | 1.25 |
| 3 | 149.130 | 151.490 | 1.58 | 12885.0 | 13096.0 | 1.64 |
| 4 | 257.370 | 263.440 | 2.36 | 21986.0 | 22445.0 | 2.09 |
| 5 | 390.420 | 403.220 | 3.28 | 33085.0 | 33947.0 | 2.61 |
图 10
图 10 自振频率与屈曲荷载计算结果的相对误差
Fig.10 Relative errors of natural frequency and buckling load
3.2. 文献[11]的连续梁算例
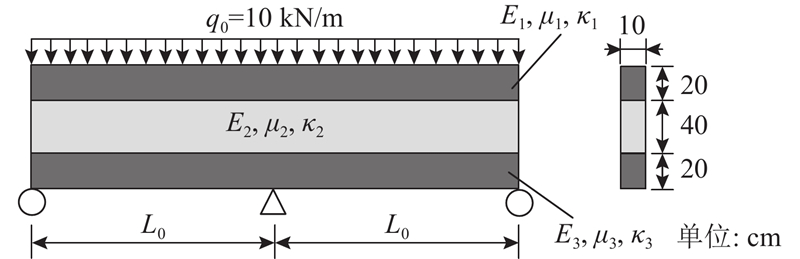
本节所分析的连续边界夹层组合梁如图11所示,横截面宽度为0.1 m,截面高度共为0.8 m,3层的厚度分别为0.2、0.4、0.2 m. 3层材料均相同,弹性模量E=8 GPa,泊松比μ=0.3,截面抗剪修正系数κ=5/6,上下层间抗剪刚度相同,ks1=ks2.
图 11
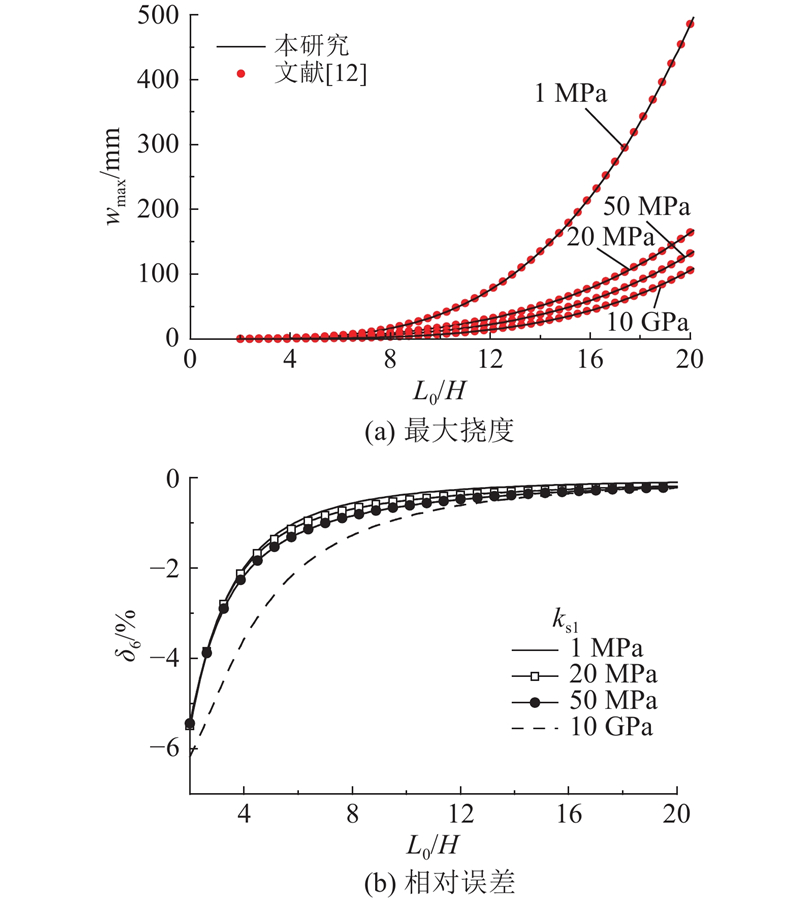
图 12
图 12 两跨连续夹层组合梁的最大挠度及相对误差
Fig.12 Maximum deflections and its errors of two-span continuous sandwich composite beam
4. 结 论
采用Timoshenko梁理论,引入含内部变量的高阶插值函数,推导3层组合梁的刚度矩阵、质量矩阵以及几何刚度矩阵元素的显式表达式. 利用MATLAB编译有限元程序,验证本研究方法的准确性和收敛性.
(1)通过算例分析表明,所提方法可以用于考虑界面滑移的夹层组合梁计算分析. 引入含内部变量高阶插值函数,避免了滑移锁定现象. 所提方法收敛速度快、所需单元少,简支梁静力算例中的单元数量取4时便有较高精度,相对误差仅为0.03%.
(2)当夹层梁跨高比相同时,Euler-Bernoulli梁的挠度计算结果相对于Timoshenko梁计算结果的误差随着抗剪刚度的增大而增大. 随着夹层梁跨高比的减小,采用基于Timoshenko梁理论的组合梁单元的必要性和优势逐渐凸显.
(3)相对于独立转角,假设的截面含多转角有限元模型,所推导的单元自由度更少,计算速度更快. 对于常规跨高比的各层材料性能没有较大突变的夹层梁,所提方法具有足够计算精度.
(4)所推导的3层组合梁的刚度矩阵、质量矩阵以及几何刚度矩阵元素的显式表达式具有计算效率高的优点,并可推广用于ABAQUS或ANSYS商业有限元软件程序中.
(5)本研究未考虑结合界面抗剪刚度的非线性力学行为,计算分析过程也未考虑材料非线性及几何非线性,相关问题值得进一步研究.
参考文献
Performance of shear connection in composite beams with profiled steel sheeting
[J].DOI:10.1016/j.jcsr.2005.11.004 [本文引用: 1]
Steel-concrete-steel sandwich composite structures-recent innovations
[J].DOI:10.1016/j.jcsr.2016.12.007 [本文引用: 1]
双钢板-混凝土组合防护结构受力机理研究综述
[J].
Review on mechanisms of double skin composite protective structures
[J].
基于Zig-zag理论的波形钢腹板梁自由振动分析
[J].
Free vibration analysis of concrete beams with corrugated steel webs based on Zig-zag theory
[J].
结构胶侧扭约束玻璃柱轴压承载力设计方法研究
[J].DOI:10.6052/j.issn.1000-4750.2020.04.0280 [本文引用: 1]
A study on the design method for axial compressive resistance of glass columns laterally and torsionally constrained by structural adhesive
[J].DOI:10.6052/j.issn.1000-4750.2020.04.0280 [本文引用: 1]
Tests and analysis of composite beams with incomplete interaction
[J].
Analysis of three-layer beams with non-identical layers and semi-rigid connections
[J].
Analytical and numerical analysis of multilayered beams with interlayer slip
[J].DOI:10.1016/j.engstruct.2010.02.015 [本文引用: 8]
Exact finite elements for multilayered composite beam-columns with partial interaction
[J].DOI:10.1016/j.compstruc.2013.04.008 [本文引用: 1]
Derivation of the exact stiffness matrix of shear-deformable multi-layered beam element in partial interaction
[J].DOI:10.1016/j.finel.2015.12.004 [本文引用: 2]
Static and dynamic analysis of three-layered partial-interaction composite structures
[J].DOI:10.1016/j.engstruct.2021.113581 [本文引用: 6]
Composite finite elements on dynamic and buckling responses of composite beams with independent rotations
[J].
Locking problems in the partial interaction analysis of multi-layered composite beams
[J].DOI:10.1016/j.engstruct.2008.04.006 [本文引用: 1]
Variational principle of partial-interaction composite beams using timoshenko's beam theory
[J].DOI:10.1016/j.ijmecsci.2012.04.012 [本文引用: 2]
Static, dynamic, and buckling analysis of partial interaction composite members using timoshenko's beam theory
[J].
Bending solutions of the timoshenko partial-interaction composite beams using euler-bernoulli solutions
[J].DOI:10.1061/(ASCE)EM.1943-7889.0000614 [本文引用: 1]
Variational principles and explicit finite-element formulations for the dynamic analysis of partial-interaction composite beams
[J].