分布式存储系统在云计算时代得到了广泛应用^[1]. 为了保证系统的持续可靠运转，须采用冗余策略来应对系统中的节点故障^[2]. “复制”策略操作简单，但存储效率较低；纠删码均衡了存储开销和纠错性能，但在修复过程中须重构原始文件，带来巨大的修复带宽开销^[3].

Gopalan等^[4]提出局部修复码(locally repairable codes, LRCs). 当一个数据节点发生故障时，系统会通过获取$ r\left( {r \ll k} \right) $个节点的数据在局部组内修复故障节点，而不再重构原始文件，带来了修复过程中带宽消耗与磁盘访问数量的减少，有效地提高了修复效率. 文献[4]证明$ \left( {n,k,r} \right) $局部修复码最小距离满足Singleton-型界，其中，n为码长，k为码字中信息位个数，r为局部性参数. Tamo等^[5]利用RS码和特殊的MDS码构造了一类最小距离最优局部修复码，但须在较大的有限域上编码，增加了实现的复杂性. Jin等^[6]利用有理函数域上的自同构群推广了RS码的构造，得到一类字母表大小与码长相当的最小距离最优局部修复码，但参数须满足$ \left( {r+1} \right)|n $. Luo等^[7]基于循环码和校验多项式构造了一类码长与字母表大小无关的局部修复码，但只有在最小距离$ d \in \left\{ {3,4} \right\} $时才能实现最小距离最优.

为了实现多故障节点修复，文献[8]提出具有$ \left( {r,t} \right) $局部性的局部修复码，不相交的t个修复集提高了系统的鲁棒性，同时支持数据的并行读取. 其中，t表示可用性参数. Jin等^[9]利用有理函数域上的自同构群构造了具有多个修复集的局部修复码，但码的最小距离没有达到上界且没有考虑码率. Hao等^[10]通过替换正则矩阵中特定行和列的方法，得到一类参数为$ \left( {r,t,\delta } \right) $的最小距离最优局部修复码，但字母表大小须满足$ q \geqslant r+\delta - 2 $，且码率较低. Ma等^[11]利用弱独立集构造出维度最优的二元线性局部修复码，但其参数须满足$ r \in \left\{ {2,3} \right\} $. Tan等^[12]利用线性代数和部分几何构造信息位具有$ \left( {r,t} \right) $局部性的局部修复码，其最小距离最优且码率较高，但当可用性较大时构造复杂度较高. Hao等^[13]研究LDPC码与局部修复码之间的关系，并构造3种信息位具有$ \left( {r,t} \right) $局部性的局部修复码，实现了最小距离最优. 其中，第1种基于射影平面的构造码率只有0.5，参数须满足$ r = t $；第2种删除仿射平面中特定点线的构造方法与第1种构造方法的性能相同；第3种基于阵列LDPC码的构造须对循环排列矩阵进行多次矩阵乘法运算，带来较大的计算开销.

针对上述问题，提出基于正交拉丁方的二元局部修复码构造方法，无须生成抽象几何图形和矩阵乘法运算，减小了构造复杂度. 根据正交拉丁方元素与矩阵位置的对应关系构造关联矩阵，得到一类具有全符号局部性的局部修复码，该码的码率和码长渐近边界条件；将关联矩阵级联一个单位矩阵，构造出一类信息位具有$ \left( {r,t = 2} \right) $局部性的单校验局部修复码，该码的最小距离和码率均满足边界条件，为最优局部修复码. 为了修复系统中的高故障率节点，利用正交拉丁方完备组构造一类具有高可用性的单校验局部修复码，可根据节点故障概率来选择可用性$ t $，提高系统的鲁棒性.

定义1　具有$ \left( {r,t} \right) $局部性的局部修复码^[8]. 在有限域$ {F_q} $中的$ {[n,k,d]_{{\text{ }}q}} $线性分组码，给定集合$ \left\{ {1,2,\cdots,n} \right\} $，$ {\boldsymbol{c}} = \left[{{\boldsymbol{c}}_1},{{\boldsymbol{c}}_2},\cdots,{{\boldsymbol{c}}_n}\right] $是一个码字，如果其中一个码元符号$ {{\boldsymbol{c}}_i} $具有局部性$ r $和可用性$ t $，那么须满足以下条件：

1）存在$ t $个子集，$ {R_1}(i),{\text{ }} \cdots ,{\text{ }}{R_{{\text{ }}t}}(i) \subset \left\{ {1,2,\cdots,n} \right\}\backslash \left\{ i \right\} $，满足$ \left| {{R_j}(i)} \right| \leqslant r $, $ j \in \left\{ {1,2,\cdots,t} \right\} $；

2）$ {R_j}(i) \cap {R_{{\text{ }}l}}(i) = \text{Ø} $，$ j \ne l $且$ j,l \in \left\{ {1,2, \cdots ,t} \right\} $；

3）$ {{\boldsymbol{c}}_i} \in {\mathrm{span}}\;\left( {{{{\boldsymbol{c}}_l}} } \right) $，其中$ l \in {R_j}\left( i \right),j \in \left\{ {1,2,\cdots,t} \right\} $，即向量$ {{\boldsymbol{c}}_i} $属于$ \left\{ {{{{\boldsymbol{c}}}_l}\left| {l \in {R_j}} \right.\left( i \right)} \right\} $张成的线性空间. 其中，称$ {R_j}(i) $为$ {{\boldsymbol{c}}_i} $的局部修复组.

对于$ \left( {n,k} \right) $局部修复码，若其所有符号都具有$ \left( {r,t} \right) $局部性，则称该码为具有全符号局部性的局部修复码(all symbol-locally repairable codes, AS-LRCs)；若只有信息位符号具有$ \left( {r,t} \right) $局部性，则称为具有信息符号局部性的局部修复码(information symbol-locally repairable codes, IS-LRCs)^[8].

Rawat等^[8]证明了当每个局部修复组中只包含一个校验符号时，信息位符号具有$ \left( {r,t} \right) $局部性LRCs的最小距离界为

(1)$ d \leqslant n - k - \left\lceil {\frac{{kt}}{r}} \right\rceil +t+1 . $

满足边界条件(式(1))的LRCs，称为最小距离最优的LRCs.

Tan等^[12]证明对于信息位符号具有$ \left( {r,t} \right) $局部性的$ {[n,k,d]_{{\text{ }}q}} $局部修复码，其最小距离满足

(2)$ d \geqslant t+1 . $

Tamo等^[14]提出具有$ \left( {r,t} \right) $局部性的LRCs码率边界为

(3)$ R \leqslant \frac{1}{{\prod _{i = 1}^t\left[1+{1}/{\left({ir}\right)}\right]}} . $

式中：R为码率.

Prakash等^[15]提出，当可用性$ t = 2 $时，$ (n,k,r,t = 2) $-LRCs的码率边界和码长边界为

(4)$ R \leqslant \frac{r}{{r+2}} \text{，} $

(5)$ n \geqslant k+\left\lceil {\frac{{2k}}{r}} \right\rceil . $

定义2　拉丁方^[16]. 设$ S = \left\{ {1,2, \cdots ,n} \right\} $为$ n $元集合，$ {\boldsymbol{L}} = {\left[ {{a_{i,{\text{ }}j}}} \right]_{n \times n}} $为集合$ S $上的$ n $阶方阵. 如果方阵$ {\boldsymbol{L}} $的每行每列都是集合$ S $中元素的一个全排列，则称$ {\boldsymbol{L}} $为$ S $上的一个$ n $阶拉丁方.

定义3　正交拉丁方^[16].设${{\boldsymbol{L}}_{{\text{ }}1}} = {\left[ {a_{i,j}^{(1)}} \right]_{n \times n}}$和${{\boldsymbol{L}}_{{\text{ }}2}} = {\left[ {a_{i,j}^{(2)}} \right]_{n \times n}}$为集合$ S = \left\{ {1,2, \cdots ,n} \right\} $上的2个$ n $阶拉丁方. 若它们叠合成的矩阵$ {\boldsymbol{C}} = {\left[ {(a_{i,j}^{\left( 1 \right)},a_{i,j}^{\left( 2 \right)})} \right]_{n \times n}} $中的$ {n^2} $个数对互不相同，其中$ i,j = 1,2, \cdots ,n $，则称拉丁方$ {{\boldsymbol{L}}_{{\text{ }}1}} $和$ {{\boldsymbol{L}}_{{\text{ }}2}} $正交，或$ {{\boldsymbol{L}}_{{\text{ }}1}} $和$ {{\boldsymbol{L}}_{{\text{ }}2}} $是一对$ n $阶正交拉丁方.

定理1^[16]　对于$ n $元集$ S $上的拉丁方，若$ n \ne 2,6 $，则必然存在一对$ n $阶正交拉丁方.

定义4　正交拉丁方组^[16]. 对于$ n $元集$ S $上的$ t\left( {t \geqslant 2} \right) $个拉丁方，若它们两两正交，则它们组成$ n $阶($ t $个)正交拉丁方组.

定理2^[16]　用$ N\left( n \right) $表示$ n $阶正交拉丁方组中拉丁方的最大个数，则$ N\left( n \right) \leqslant n - 1 $.

定义5　正交拉丁方完备组^[16]. 若$ n $阶正交拉丁方组中含有$ N\left( n \right) = n - 1 $个拉丁方，则称为$ n $阶正交拉丁方完备组.

定理3^[16]　若$ q $为素数，$ v $为正整数，$ p = {q^v} $为素数幂，且$ p \geqslant 3 $，则存在$ p $阶正交拉丁方完备组.

定义6　支撑集^[17]. 给定向量$ {\boldsymbol{v}} = \left[ {{v_1},{v_2}, \cdots ,{v_n}} \right] $，则它的支撑集为$ {\text{supp}}\left( {\boldsymbol{v}} \right) = \left\{ {i\left| {{v_i} \ne 0} \right.} \right\},\; {i = 1,2, \cdots ,n} $.

设集合$ \varOmega = \left\{ {1,2, \cdots ,{m^2}} \right\} $，矩阵$ {\boldsymbol{X}} $为由集合$ \varOmega $中$ {m^2} $个元素排列成的$ m $阶方阵，即

$ {\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} 1&2& \cdots &m \\ {m+1}&{m+2}& \cdots &{2m} \\ \vdots & \vdots & \quad & \vdots \\ {\left( {m - 1} \right)m+1}&{\left( {m - 1} \right)m+2}& \cdots &{{m^{{\text{ }}2}}} \end{array}} \right]. $

将方阵$ {\boldsymbol{X}} $与一对$ m $($ m \geqslant 3 $且$ m \ne 6 $)阶正交拉丁方叠合，若方阵$ {\boldsymbol{X}} $中的一些元素$ {\varOmega _j}\left( {\varOmega _j} \in \varOmega ,\right. \left.j = 1,2, \cdots, {m^2} \right) $对应一个拉丁方中的同一个字母，则这些元素构成一个子集$ B_i^h\left( {h = 1,2;{\text{ }}i = 1,2, \cdots ,m} \right) $，由一个拉丁方构造的子集组成集合$ {B^h} = \left\{ {B_i^h\left| i = 1,\right.}\right. \left.{\left.2, \cdots ,m \right.} \right\} $，集合$ B = {B^1} \cup {B^2} $，易得$ \left| {B_i^h} \right| = m $，$ \left| B \right| = 2m $.

将集合$ B $中的$ 2m $个大小为$ m $的子集$ B_i^h\left( {h = 1,2;}\right. \left.{i = 1,2, \cdots ,m} \right) $映射为矩阵的行，集合$ \varOmega $中的元素$ {\varOmega _j}\left( {{\varOmega _j} \in \varOmega } \right) $映射为矩阵的列，可以定义集合$ B $和集合$ \varOmega $的关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $，即

$ {{\boldsymbol{M}}_{2m \times {m^2}}} = \begin{array}{*{20}{c}}{{B^1}\left\{ {\begin{array}{*{20}{l}}{B_1^1}\\ \;\;\vdots \\{B_m^1}\end{array}} \right.}\\{\begin{array}{*{20}{l}} \;\\{{B^2}\left\{ {\begin{array}{*{20}{l}}{B_1^2}\\ \;\;\vdots \\{B_m^2}\end{array}} \right.}\end{array}}\end{array}\overbrace {\left[ {\begin{array}{*{20}{c}} * & * & \cdots & * & * \\ \vdots & \vdots & \quad & \vdots & \vdots \\ * & * & \cdots & * & * \\ \vdots & \vdots & \quad & \vdots & \vdots \\ * & * & \cdots & * & * \\ \vdots & \vdots & \quad & \vdots & \vdots \\ * & * & \cdots & * & * \end{array}} \right]}^\varOmega . $

其中*取0或1. $ {{\boldsymbol{M}}_{2m \times {m^2}}} = \left[ {{m_{k,j}}} \right] $的取值规则如下：

$ {m_{k,j}} = \left\{ \begin{array}{*{20}{c}} 1,\quad{\varOmega _j} \in B_i^h,\; 0 \leqslant k \leqslant 2m{\text{ , }}0 \leqslant j \leqslant {m^2}; \\ 0,\quad{\varOmega _j} \notin B_i^h,\; 0 \leqslant k \leqslant 2m{\text{ , }}0 \leqslant j \leqslant {m^2}. \\ \end{array} \right. $

由集合$ B $和$ \varOmega $的大小，易得关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $的行数为$ 2m $，列数为$ {m^2} $. 集合$ B $中每个子集$ B_i^h \subset \varOmega $，且$ \left| {B_i^h} \right| = m $，故关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $每行汉明重量为$ m $；集合$ \varOmega $中的每个元素$ {\varOmega _j}\left( {j = 1,2, \cdots, {m^2}} \right) $在集合$ {B^{ 1}} $和$ {B^{ 2}} $中分别只出现一次，故关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $每列汉明重量为2，因此关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $是$ \left( {2,m} \right) $-正则矩阵. 在集合$ {B^{ 1}} $和$ {B^{ 2}} $各自内部，任意2个$ m $-子集$ B_i^h、B_l^h\left( {1 \leqslant i,l \leqslant m,h = 1,2} \right) $不相交，即$ B_i^h \cap B_l^h = \text{Ø} $；从集合$ {B^{ 1}}、{B^{ 2}} $中分别选出一个$ m $-子集 $ B_i^1、 B_l^2\left( {1 \leqslant i,l \leqslant m} \right) $，由正交拉丁方的性质可知它们只相交于一个元素，即$ B_i^1 \cap B_l^2 = p\left( {p \in \varOmega } \right) $，因此，矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $中任意2个行向量的支撑集最多在1个符号位处相交. 用Tanner图表示关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $，由图中一系列边构成的一条封闭路径称为环，环的长度等于构成该环中边的个数，在给定的Tanner图中，最小的环长度称为围长(girth). 由于矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $中任意2个行向量的支撑集最多在1个符号位处相交，故其围长$ {\text{girth}} > 4 $.

定理4　将关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $作为校验矩阵$ {{\boldsymbol{H}}_1} $，可以构造参数为$ {n = {m^2}、k = {{\left( {m - 1} \right)}^2}、t = 2、r = m - 1} $的AS-LRCs，其中$ m \geqslant 3 $且$ m \ne 6 $.

证明　由关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $可知构造的局部修复码的码长$ n = {m^2} $，由于集合$ \varOmega $中的每个元素在集合$ {B^{ 1}} $和$ {B^{ 2}} $中分别只出现1次，在集合$ B $中共出现2次，故关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $中所有行向量构成了一个线性相关组，且其中不存在零向量. 用$ {{\boldsymbol{b}}_{{\text{ }}i}}\left( {1 \leqslant i \leqslant 2m} \right) $表示关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $的行向量，$ {{\boldsymbol{b}}_{{\text{ }}i}} \ne {\boldsymbol{0}} $，将所有行向量按分量相加得到零向量，即$ \sum\nolimits_{i = 0}^{2m} {{{\boldsymbol{b}}_{{\text{ }}i}}} = {\boldsymbol{0}} $. 随机删除1个行向量$ {{\boldsymbol{b}}_{{\text{ }}l}}\left( {l \in \left\{ {1,2, \cdots ,2m} \right\}} \right) $，根据正交拉丁方的正交性，剩余的行向量构成线性无关组. 因此关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $的秩为$ {\text{Rank}}\left( {{{\boldsymbol{M}}_{2m \times {m^2}}}} \right) = 2m - 1 $，局部修复码的维度为$ k = {m^2} - \left( {2m - 1} \right) = {\left( {m - 1} \right)^2} $. 关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $每列汉明重量为2，且每列“1”元素所在的行向量的支撑集只在该“1”元素坐标处相交，所以每个符号位具有2个不相交的局部修复组，即可用性$ t = 2 $. 关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $每行汉明重量为$ m $，当某个符号位丢失时须获得另外$ m - 1 $个符号位的信息才能恢复，故修复局部性$ r = m - 1 $.

例1　当$ m = 3 $时，$ \varOmega =\left\{1，2，\mathrm{\cdots}，\text{9}\right\} $，方阵$ {\boldsymbol{X}} $为

$ {\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} \begin{gathered} 1 \\ 4 \\ 7 \\ \end{gathered} &\begin{gathered} 2 \\ 5 \\ 8 \\ \end{gathered} &\begin{gathered} 3 \\ 6 \\ 9 \\ \end{gathered} \end{array}} \right]. $

2个3阶拉丁方如下：

$ {{\boldsymbol{L}}_{{\text{ }}1}} = \left[ {\begin{array}{*{20}{c}} A&B&C \\ B&C&A \\ C&A&B \end{array}} \right] \text{，} {{\boldsymbol{L}}_{{\text{ }}2}} = \left[ {\begin{array}{*{20}{c}} A&B&C \\ C&A&B \\ B&C&A \end{array}} \right]. $

集合如下：

$ {B^1} = \left\{ {B_1^1,B_2^1,B_3^1} \right\} = \big\{ {\left\{ {1,6,8} \right\},\left\{ {2,4,9} \right\},\left\{ {3,5,7} \right\}} \big\}, $

$ {B^2} = \left\{ {B_1^2,B_2^2,B_3^2} \right\} = \big\{ {\left\{ {1,5,9} \right\},\left\{ {2,6,7} \right\},\left\{ {3,4,8} \right\}} \big\}, $

$ \begin{split} B = \left\{ {{B^1},{B^2}} \right\} =& \big\{ \left\{ {1,6,8} \right\},\left\{ {2,4,9} \right\},\left\{ {3,5,7} \right\}, \big. \\ &\big.\left\{ {1,5,9} \right\},\left\{ {2,6,7} \right\},\left\{ {3,4,8} \right\} \big\}.\end{split} $

由集合$ B $和集合$ \varOmega $的映射关系易得关联矩阵：

$ {{\boldsymbol{M}}_{6 \times 9}} = \begin{array}{*{20}{c}} {{B^1}\left\{ \begin{gathered} B_1^1 \\ B_2^1 \\ B_3^1 \\ \end{gathered} \right.} \\ {{B^2}\left\{ \begin{gathered} B_1^2 \\ B_2^2 \\ B_3^2 \\ \end{gathered} \right.} \end{array}\mathop {\left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&1&0&1&0 \\ 0&1&0&1&0&0&0&0&1 \\ 0&0&1&0&1&0&1&0&0 \\ 1&0&0&0&1&0&0&0&1 \\ 0&1&0&0&0&1&1&0&0 \\ 0&0&1&1&0&0&0&1&0 \end{array}} \right]}\limits^{\begin{array}{*{20}{c}} 1&2&3&4&5&6&7&8&9 \end{array}}. $

将关联矩阵$ {{\boldsymbol{M}}_{6 \times 9}} $作为校验矩阵$ {{\boldsymbol{H}}_1} $，可以构造参数为$ n = 9、k = 4、t = 2、r = 2 $的AS-LRCs. 若码元符号$ {{\boldsymbol{c}}_1} $故障，其修复集为$ {R_1}\left( 1 \right) = \left\{ {6,8} \right\} $和$ {R_2}\left( 1 \right) = \left\{ {5,9} \right\} $，故$ {{\boldsymbol{c}}_1} = {{\boldsymbol{c}}_6} \oplus {{\boldsymbol{c}}_8} = {{\boldsymbol{c}}_5} \oplus {{\boldsymbol{c}}_9} $，其中$ \oplus $表示异或运算. 其他码元符号可以通过类似的方法进行修复.

定理5　定理4构造的AS-LRCs的最小距离为$ d = 4 $，且$ d \gt t+1 $.

证明　AS-LRCs的最小距离$ d = 4 $表明其校验矩阵$ {{\boldsymbol{H}}_1} $即关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $中任意3列线性无关，且存在4列线性相关.

首先证明关联矩阵中任意3列线性无关. 设$ {{{\boldsymbol{h}}}_{i}}\left( {1 \leqslant i \leqslant {m^2}} \right) $表示关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $的列向量，并将其按顺序分为$ m $组，每组包含$ m $个列向量，即第$ j \;$ 组中的列向量为$ \left\{ {{{\boldsymbol{h}}_{\left( {j - 1} \right)m+1}},{{\boldsymbol{h}}_{\left( {j - 1} \right)m+2}}, \cdots, {{\boldsymbol{h}}_{jm}}} \right\}\left( {1 \leqslant j \leqslant m} \right) $. 从$ {{\boldsymbol{h}}_i}\left( {1 \leqslant i \leqslant {m^2}} \right) $中任选3列，有以下3种情况：

1）若3列选自同一组，则对应于拉丁方同一行上的3个不同元素，由拉丁方的性质可知这3个元素处于不同的$ m $-子集中，故这3列必然线性无关，如例1中$ \left\{ {{{\boldsymbol{h}}_1},{{\boldsymbol{h}}_2},{{\boldsymbol{h}}_3}} \right\} $；

2）若3列中2列选自同一组，剩余1列选自其他组，同一组的2列必然线性无关，同组的2列相加可以得到一个汉明重量为4的列向量，而选自其他组的列向量汉明重量为2，因此这3列必然线性无关，如例1中$ \left\{ {{{\boldsymbol{h}}_1},{{\boldsymbol{h}}_2},{{\boldsymbol{h}}_4}} \right\} $；

3）若3列分别选自不同组，且对应于拉丁方中3个不同的元素，则与3列选自同一组的情况1)相同，3个列向量线性无关，如例1中$ \left\{ {{{\boldsymbol{h}}_1},{{\boldsymbol{h}}_4},{{\boldsymbol{h}}_7}} \right\} $；若选自不同组的3列对应于拉丁方中2个不同的元素，则对应于同一个元素的2列相加可以得到一个汉明重量为2的列向量，且2个“1”元素所在的2行所对应的$ m $-子集处于同一个$ {B^h}\left( {h = 1,2} \right) $中，而剩余1个列向量中“1”元素所在的2行所对应的$ m $-子集分别处于不同的$ {B^h}\left( {h = 1,2} \right) $中，故这3列必然线性无关，如例1中$ \left\{ {{{\boldsymbol{h}}_1},{{\boldsymbol{h}}_6},{{\boldsymbol{h}}_7}} \right\} $；若选自不同组的3列均对应于拉丁方中同一个元素，则3列所对应的集合$ \varOmega $中的元素所构成的子集$ \left\{ {{\varOmega _{{j_1}}},{\varOmega _{{j_2}}},{\varOmega _{{j_3}}}} \right\}\left( {1 \leqslant {j_1},{j_2},{j_3} \leqslant {m^2}} \right) $只能在$ {B^h}\left( {h = 1,2} \right) $中某个$ m $-子集出现一次，在另一个集合$ {B^h}\left( {h = 1,2} \right) $中，子集$ \left\{ {{\varOmega _{{j_1}}},{\varOmega _{{j_2}}},{\varOmega _{{j_3}}}} \right\} $中3个元素必处于3个不同的$ m $-子集中，故这3列必然线性无关，如例1中$ \left\{ {{{\boldsymbol{h}}_1},{{\boldsymbol{h}}_6},{{\boldsymbol{h}}_8}} \right\} $. 综上所述，关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $中任意3列线性无关，所以$ d \geqslant 4 $.

另一方面，从关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $中选择2个列向量$ \left\{ {{{\boldsymbol{h}}_{m1}},{{\boldsymbol{h}}_{m2}}} \right\}\left( {1 \leqslant m1,m2 \leqslant {m^2}} \right) $，使得它们的支撑集相交于一个坐标位$ i\left( {1 \leqslant i \leqslant 2m} \right) $，即$ {\text{supp}}\left( {{{\boldsymbol{h}}_{m1}}} \right) \cap {\text{supp}}\left( {{{\boldsymbol{h}}_{m2}}} \right) = \left\{ i \right\} $，则$ {{\boldsymbol{h}}_{m1}}、{{\boldsymbol{h}}_{m2}} $相加可以得到一个汉明重量为2的列向量，用$ {\boldsymbol{\alpha }} $表示，列向量$ {\boldsymbol{\alpha }} $中2个“1”元素位于同一个$ {B^h}\left( {h = 1,2} \right) $中，如例1中$ \left\{ {{{\boldsymbol{h}}_1},{{\boldsymbol{h}}_8}} \right\} $. 从关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $中任意选择一个“1”元素坐标位置与列向量$ {\boldsymbol{\alpha }} $中某个“1”元素坐标位置相同的列向量$ {\boldsymbol{\beta }} $，如例1中$ {{\boldsymbol{h}}_{5}} $. 将$ {\boldsymbol{\beta }} $与列向量$ {\boldsymbol{\alpha }} $相加，可以得到一个汉明重量为2的列向量$ {\boldsymbol{\gamma }} $，且列向量$ {\boldsymbol{\gamma }} $中2个“1”元素位于不同的$ {B^h}\left( {h = 1,2} \right) $中，则列向量$ {\boldsymbol{\gamma }} $必为关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $中的一列，如例1中$ {{\boldsymbol{h}}_{{\text{3}}}} $. 因此列向量$ \left\{ {{\boldsymbol{\gamma }},{\boldsymbol{\beta }}} \right\} $与选择的2个列向量$ \left\{ {{{\boldsymbol{h}}_{m1}},{{\boldsymbol{h}}_{m2}}} \right\} $线性相关，即关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}} $中存在4列线性相关，所以$ d \leqslant 4 $.

综上所述，定理4构造的AS-LRCs最小距离为$ d = 4 $，且满足$ d \gt t+1 = 2+1 = 3 $，得证.

如表1所示为几种典型的AS-LRCs在可用性$ t = 2 $时的参数. 表中，$ w $为任意正整数，$ m\left( m \geqslant 3,\right. \left. m \ne 6 \right) $为拉丁方的阶数. 可以发现，当可用性$ t = 2 $时，定理4构造的AS-LRCs最小距离最大，并且满足$ d \gt t+1 $.

由于不存在一对6阶的正交拉丁方，定理4无法构造局部性$ r = 5 $的AS-LRCs. 下面通过改变集合$ {B^2} = \left\{ {B_i^2\left| {i = 1,2, \cdots ,m} \right.} \right\} $的构造方法，可以得到任意局部性$ r \geqslant 2 $的AS-LRCs.

定理6　在$ m $阶方阵$ {\boldsymbol{X}} $上叠合一个$ m $阶标准型拉丁方，即该拉丁方第1行与第1列的元素均按顺序排列. 集合$ {B^1} = \left\{ {B_i^1\left| {i = 1,2, \cdots ,m} \right.} \right\} $仍然利用前面的方法构造，而集合$ {B^2} = \left\{ {B_i^2\left| {i = 1,2, \cdots ,m} \right.} \right\} $则利用标准型拉丁方每列元素在方阵$ {\boldsymbol{X}} $中对应的位置索引构造，集合$ B = {B^1} \cup {B^2} $. 将集合$ B $和集合$ \varOmega $的关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}^{\prime}} $作为校验矩阵$ {{\boldsymbol{H}}_1^{\prime}} $，可以构造参数为$ {n = {m^2}、 = {{\left( {m - 1} \right)}^2}、 t = 2、r = m - 1} $的AS-LRCs，其中$ m \geqslant 3 $.

可以证明定理6构造出来的AS-LRCs最小距离仍满足定理5.

例2　当$ m = 6 $时，$ \varOmega =\left\{1，2，\mathrm{\cdots}，\text{36}\right\} $，方阵$ {\boldsymbol{X}} $为

$ {\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 7&8&9&{10}&{11}&{12} \\ {13}&{14}&{15}&{16}&{17}&{18} \\ {19}&{20}&{21}&{22}&{23}&{24} \\ {25}&{26}&{27}&{28}&{29}&{30} \\ {31}&{32}&{33}&{34}&{35}&{36} \end{array}} \right]. $

6阶标准型拉丁方如下：

$ {{\boldsymbol{L}}_{{\text{ }}1}} = \left[ {\begin{array}{*{20}{c}} A&B&C&D&E&F \\ B&C&D&E&F&A \\ C&D&E&F&A&B \\ D&E&F&A&B&C \\ E&F&A&B&C&D \\ F&A&B&C&D&E \end{array}} \right]. $

集合如下：

$ \begin{split} {B^1} =& \left\{ {B_1^1,B_2^1,B_3^1,B_4^1,B_5^1,B_6^1} \right\} =\\ &\big\{ \left\{ {1,12,17,22,27,32} \right\},\left\{ {2,7,18,23,28,33} \right\}, \big. \\ &\left\{ {3,8,13,24,29,34} \right\},\left\{ {4,9,14,19,30,35} \right\}, \\ &\big.\left\{ {5,10,15,20,25,36} \right\},\left\{ {6,11,16,21,26,31} \right\} \big\},\end{split} $

$ \begin{split} {B^2} =& \left\{ {B_1^2,B_2^2,B_3^2,B_4^2,B_5^2,B_6^2} \right\} =\\& \big\{ \left\{ {1,7,13,19,25,31} \right\},\left\{ {2,8,14,20,26,32} \right\}, \big. \\ & \left\{ {3,9,15,21,27,33} \right\},\left\{ {4,10,16,22,28,34} \right\}, \\ & \big.\left\{ {5,11,17,23,29,35} \right\},\left\{ {6,12,18,24,30,36} \right\}\big\} ,\end{split} $

$ B = \left\{ {{B^1},{B^2}} \right\}. $

由集合$ B $和集合$ \varOmega $的映射关系得到关联矩阵$ {{\boldsymbol{M}}_{12 \times 36}} $，将其作为校验矩阵可以构造一个参数为$ n = 36、k = 25、t = 2、r = 5 $的AS-LRCs.

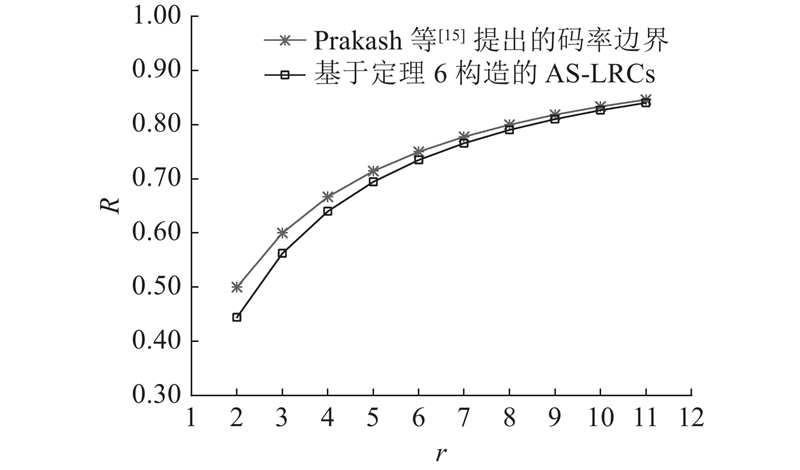
所构造的AS-LRCs码率为

$ R = \frac{k}{n} = \frac{{{{\left( {m - 1} \right)}^2}}}{{{m^2}}} = {\left( {\frac{{m - 1}}{m}} \right)^2} = {\left( {\frac{r}{{r+1}}} \right)^2}. $

如图1所示为定理6构造的AS-LRCs码率与 Prakash等^[15]提出的码率边界的比较. 图中，R为码率，R=k/n. 可以发现，随着局部性参数$ r $的增大，即拉丁方阶数$ m $的增大，AS-LRCs的码率将逐渐接近码率边界，即式(4)中的边界条件.

不过，由于

$ \begin{split} {\left( {\frac{r}{{r+1}}} \right)^2} =& {\left( {\frac{1}{{1+{1}/{r}}}} \right)^2} =\\&\frac{1}{{1+{2}/{r}+{1}/{{{r^2}}}}} \lt \frac{1}{{1+{2}/{r}}} = \frac{r}{{r+2}} \text{，}\end{split} $

定理6中的AS-LRCs码率始终小于边界条件(式(4)).

将码的参数代入码长边界（式(5)），可以得到

$ n \geqslant k+\left\lceil {\frac{{2k}}{r}} \right\rceil = {\left( {m - 1} \right)^2}+\left\lceil {\frac{{2{{\left( {m - 1} \right)}^2}}}{{m - 1}}} \right\rceil = {m^2} - 1. $

可以看出，定理6构造的AS-LRCs码长仅比最优码长界大1，能够更好地均衡系统的冗余.

定理7　在关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}^{\prime}} $右边级联一个$ 2m $阶单位矩阵$ {{\boldsymbol{I}}_{2m \times 2m}} $，构造校验矩阵$ {{\boldsymbol{H}}_2} $，即$ {{\boldsymbol{H}}_2} = [\left. {{{{\boldsymbol{M}}}_{2m \times {m^2}}^{\prime}}} \right|{{\boldsymbol{I}}_{2m \times 2m}}] $，则由校验矩阵$ {{\boldsymbol{H}}_2} $可以构造参数为$ n = 2m+{m^2}、k = {m^2}、t = 2、r = m $的单校验IS-LRCs，其中$ m \geqslant 3 $.

证明　由校验矩阵$ {{\boldsymbol{H}}_2} $可知构造的局部修复码的码长$ n = 2m+{m^2} $，且右边级联单位矩阵$ {{\boldsymbol{I}}_{2m \times 2m}} $使得校验矩阵$ {{\boldsymbol{H}}_2} $满秩，因此局部修复码的维度$ k = \left( {2m+{m^2}} \right) - 2m = {m^2} $. 矩阵$ {{\boldsymbol{H}}_2} $的前$ {m^2} $列对应信息位符号，后$ 2m $列对应校验位符号. 关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}^{\prime}} $中每列的汉明重量为2，且每列“1”元素所在行向量的支撑集只在该“1”元素坐标处相交，所以每个信息位具有2个不相交的局部修复组，即可用性$ t = 2 $. 同时，校验矩阵$ {{\boldsymbol{H}}_2} $每行的汉明重量为$ m+1 $，当某个信息位符号丢失时须获得另外$ m $个符号位的信息才能恢复，故修复局部性$ r = m $，且每个局部修复组中只有一个校验符号.

定理8　定理7构造的IS-LRCs的最小距离为$ d = 3 $，且最小距离最优.

证明　校验矩阵$ {{\boldsymbol{H}}_2} $的前$ {m^2} $列汉明重量均为2，后$ 2m $列为单位矩阵$ {{\boldsymbol{I}}_{2m \times 2m}} $. 从校验矩阵$ {{\boldsymbol{H}}_2} $的前$ {m^2} $列中任选一个列向量，表示为$ {\boldsymbol{\xi }} $，它是单位阵$ {{\boldsymbol{I}}_{2m \times 2m}} $中特定2列的线性组合，故矩阵$ {{\boldsymbol{H}}_2} $中存在3列线性相关，$ d \leqslant 3 $. 另一方面，从校验矩阵$ {{\boldsymbol{H}}_2} $中任选2个列向量$ \left\{ {{{\boldsymbol{h}}_{s1}},{{\boldsymbol{h}}_{s2}}} \right\} $，其中$ 1 \leqslant s1,s2 \leqslant 2m+{m^2} $，若2列都选自单位阵$ {{\boldsymbol{I}}_{2m \times 2m}} $，显然它们线性无关；若2列都选自关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}^{\prime}} $，类似于定理5可以证明它们线性无关；若其中一列选自单位阵$ {{\boldsymbol{I}}_{2m \times 2m}} $，另一列选自关联矩阵$ {{\boldsymbol{M}}_{2m \times {m^2}}^{\prime}} $，由于列重不同，它们必然线性无关. 因此，校验矩阵$ {{\boldsymbol{H}}_2} $中任意2列线性无关，从而 $ d \geqslant 3 $. 综上所述，定理7构造的IS-LRCs的最小距离为$ d = 3 $.

将参数$ {n = 2m+{m^2}、k = {m^2}、t = 2、r = m} $代入最小距离边界条件(式(1))，可得

$ \begin{split} d \leqslant & n - k - \left\lceil {\frac{{kt}}{r}} \right\rceil +t+1 = \\&2m+{m^2} - {m^2} - \left\lceil {\frac{{{m^2} \times 2}}{m}} \right\rceil +2+1 = 3,\end{split} $

满足边界条件(式(1))，所以定理7构造的IS-LRCs最小距离最优.

定理7构造的IS-LRCs码率为

$ R = \frac{k}{n} = \frac{{{m^2}}}{{2m+{m^2}}} = \frac{m}{{2+m}} = \frac{r}{{r+2}} \text{，} $

满足码率边界条件（式(4)），因此定理7构造的IS-LRCs码率最优.

此外，局部性$r$与维度$k$的比值为

$ \frac{r}{k} = \frac{m}{{{m^2}}} = \frac{1}{m}, $

即当系统发生单节点故障时，新生节点需要连接的帮助节点数仅为同参数下纠删码的$1/m$，能够有效降低修复过程中的磁盘I/O开销，加快修复效率.

3.1节构造的IS-LRCs的可用性参数仅局限于$ t = 2 $，对于存储系统中的高故障率节点，可能无法确保数据的可靠访问，须为其提供更高等级的保护. 利用正交拉丁方完备组构造可以灵活调节可用性参数的局部修复码.

故障率$ \tau $是指节点发生故障的频率，即单位时间内节点发生故障的次数^[20]. 通常用系统的平均无故障时间(mean time to failure, MTTF)来表示节点故障率，即

(6)$ \tau = 1 - {{\mathrm{exp}}\;\left({-\dfrac{{ 1}}{{{\text{MTTF}}}}}\right)} . $

式中：MTTF为系统从开始运行到发生故障的平均工作时间.

对第2章中的构造进行扩展，将方阵$ {\boldsymbol{X}} $与$ s $个$ m $阶相互正交拉丁方叠合，其中$ {2 \leqslant s \leqslant m - 1} $，$ m $为素数幂，且$ m \geqslant 3 $，$ s $的取值规则为

$ s = \left\{ \begin{array}{*{20}{c}} {\tau _{\max }} - 1,&{\tau _{\max }} < m; \\ m - 1,&{\tau _{\max }} \geqslant m. \\ \end{array} \right. $

式中：$ {\tau _{\max }} $为系统中信息位节点故障率的最大值，$ {\tau _{\max }} = \left\lceil {\max \;\left\{ {{\tau _i}} \right\}} \right\rceil ,\; {i = 1,2, \cdots, k} $.

若方阵$ {\boldsymbol{X}} $中的一些元素$ {\varOmega _j}\left( {{\varOmega _j} \in \varOmega,\; j = 1,2,} \right. \left.{\cdots,\; {m^2}} \right) $对应一个拉丁方中的同一个字母，则这些元素构成一个子集$ B_i^h\left( {h = 1,2, \cdots s;{\text{ }}i = 1,2, \cdots ,m} \right) $，由一个拉丁方构造的子集组成集合$ {B^h} = \left\{ B_i^h\left| {i = 1,}\right.\right. \left.\left.{2, \cdots ,m} \right. \right\} $，集合$ {B^c} = \left\{ {B_i^c\left| {i = 1,2, \cdots ,m} \right.} \right\} $由标准型拉丁方每列元素在方阵$ {\boldsymbol{X}} $中对应的位置索引构造，集合$ B = {B^1} \cup {B^2} \cup \cdots \cup {B^s} \cup {B^c} $，易得$ \left| {B_i^h} \right| = m $，|B|=$ ( {s+1} )m $.

将集合$ B $中的$ \left( {s+1} \right)m $个大小为$ m $的子集$ B_i^h\left( {h = 1,2, \cdots s,c;{\text{ }}i = 1,2, \cdots ,m} \right) $映射为矩阵的行，集合$ \varOmega $中的元素$ {\varOmega _j}\left( {{\varOmega _j} \in \varOmega } \right) $映射为矩阵的列，可以定义集合$ B $和集合$ \varOmega $的关联矩阵$ {{\boldsymbol{M}}_1} $如下：

$ {{\boldsymbol{M}}_1} = \left\{\begin{array}{*{20}{c}}{{B^1}\left\{ {\begin{array}{*{20}{l}}{B_1^1}\\ \;\;\vdots \\{B_m^1}\end{array}} \right.}\\{\begin{array}{*{20}{l}} \;\vdots \\{{B^c}\left\{ {\begin{array}{*{20}{l}}{B_1^c}\\ \;\;\vdots \\{B_m^c}\end{array}} \right.}\end{array}}\end{array}\overbrace {\left[ {\begin{array}{*{20}{c}} * & * & \cdots & * & * \\ \vdots & \vdots & \quad & \vdots & \vdots \\ * & * & \cdots & * & * \\ \vdots & \vdots & \quad & \vdots & \vdots \\ * & * & \cdots & * & * \\ \vdots & \vdots & \quad & \vdots & \vdots \\ * & * & \cdots & * & * \end{array}} \right]}^\varOmega\right.. $

其中，*取0或1，关联矩阵$ {{\boldsymbol{M}}_1} $是$ \left( {s+1,m} \right) $-正则矩阵.

${\boldsymbol{M}}_1=\left[m_{k,j}\right],\;m_{k,j} $取值规则如下：

$ {m_{k,j}} = \left\{ \begin{array}{l}1,\;{\varOmega _j} \in B_i^h;\\0,\;{\varOmega _j} \notin B_i^h.\end{array} \right. $

其中，$0 \leqslant k \leqslant \left( {s + 1} \right)m,\;0 \leqslant j \leqslant {m^2} $.

定理9　在关联矩阵$ {{\boldsymbol{M}}_1} $右边级联$ \left( {s+1} \right)m $阶单位矩阵$ {{\boldsymbol{I}}_{\left( {s+1} \right)m \times \left( {s+1} \right)m}} $，构造校验矩阵$ {{\boldsymbol{H}}_3} $，即$ {{\boldsymbol{H}}_3} = [\left. {{{\boldsymbol{M}}_1}} \right|{{\boldsymbol{I}}_{\left( {s+1} \right)m \times \left( {s+1} \right)m}}] $，其中$ m $为素数幂，且$ m \geqslant 3 $. 由校验矩阵$ {{\boldsymbol{H}}_3} $可构造参数为$ n = sm+m+{m^2}、 k = {m^2}、 t = s+1、r = m $的单校验IS-LRCs，且最小距离最优，$ d = s+2 = t+1 $.

证明　由校验矩阵$ {{\boldsymbol{H}}_3} $可知构造的局部修复码码长$ n = sm+m+{m^2} $，且右边级联单位矩阵使得校验矩阵$ {{\boldsymbol{H}}_3} $满秩，因此局部修复码的维度$ k = {m^2} $. 矩阵$ {{\boldsymbol{H}}_3} $的前$ {m^2} $列对应信息位，后$ \left( {s+1} \right)m $列对应校验位. 将关联矩阵$ {{\boldsymbol{M}}_1} $的行按顺序分为$ s+1 $组，每组包含$ m $个行向量，每组对应一个子集$ {B^h}\left( {h = 1,2, \cdots ,s,c} \right) $，集合$ \varOmega $中的每个元素在每个子集$ {B^h}\left( {h = 1,2, \cdots ,s,c} \right) $中出现一次，故关联矩阵$ {{\boldsymbol{M}}_1} $的列重为$ s+1 $，且每列“1”元素所在$ s+1 $行中任意2行的支撑集只在该“1”元素坐标处相交，所以每个信息位具有$ s+1 $个不相交的局部修复组，即可用性为$ t = s+1 $. 同时，校验矩阵$ {{\boldsymbol{H}}_3} $的行重为$ m+1 $，所以当某个信息位符号丢失时须获得其他$ m $个符号位的信息才能恢复，故修复局部性$ r = m $，且每个局部修复组中只有一个校验符号.

类似于定理8，可以证明校验矩阵$ {{\boldsymbol{H}}_3} $中任意$ s+1 $列线性无关，且存在$ s+2 $列线性相关，故最小距离为$ d = s+2 $. 此外，将码的参数代入式(1)得到

$ \begin{split} d \leqslant & n - k - \left\lceil {\frac{{kt}}{r}} \right\rceil +t+1 =sm+m+{m^2} - \\ &{m^2} - \left\lceil {\frac{{{m^2} \times \left( {s+1} \right)}}{m}} \right\rceil +s+2 = s+2 = t+1,\end{split} $

代入式(2)得到

$ d \geqslant s+2 = t+1, $

因此最小距离$ d = t+1 $，定理9构造的IS-LRCs最小距离最优.

例3　令$ m = 4 $，则$ \varOmega =\left\{1，2，\mathrm{\cdots}，\text{16}\right\} $，矩阵$ {\boldsymbol{X}} $为

$ {\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} 1&2&3&4 \\ 5&6&7&8 \\ 9&{10}&{11}&{12} \\ {13}&{14}&{15}&{16} \end{array}} \right]. $

假设系统中至少有一个信息节点在单位时间内的故障次数大于等于4，即$ {\tau _{\max }} \geqslant 4 $，则$ s = m - 1 = 3 $. 给出3个两两正交的4阶拉丁方:

$\begin{split} {{\boldsymbol{L}}_{{\text{ }}1}} =& \left[ {\begin{array}{*{20}{c}} A&B&C&D \\ B&A&D&C \\ C&D&A&B \\ D&C&B&A \end{array}} \right] \text{，} \\{{\boldsymbol{L}}_{{\text{ }}2}} =& \left[ {\begin{array}{*{20}{c}} A&B&C&D \\ C&D&A&B \\ D&C&B&A \\ B&A&D&C \end{array}} \right],\\{{\boldsymbol{L}}_{{\text{ }}3}} =& \left[ {\begin{array}{*{20}{c}} A&B&C&D \\ D&C&B&A \\ B&A&D&C \\ C&D&A&B \end{array}} \right].\end{split} $

集合如下：

$ \begin{split} {B^1} = \left\{ {B_1^1,B_2^1,B_3^1,B_4^1} \right\} = &\big\{ \left\{ {1,6,11,16} \right\},\left\{ {2,5,12,15} \right\}, \big. \\ &\big.\left\{ {3,8,9,14} \right\},\left\{ {4,7,10,13} \right\} \big\},\end{split} $

$ \begin{split} {B^2} = \left\{ {B_1^2,B_2^2,B_3^2,B_4^2} \right\} =& \big\{ \left\{ {1,7,12,14} \right\},\left\{ {2,8,11,13} \right\}, \big. \\ &\big.\left\{ {3,5,10,16} \right\},\left\{ {4,6,9,15} \right\} \big\},\end{split} $

$ \begin{split} {B^3} = \left\{ {B_1^3,B_2^3,B_3^3,B_4^3} \right\} = &\big\{ \left\{ {1,8,10,15} \right\},\left\{ {2,7,9,16} \right\}, \big. \\ &\big.\left\{ {3,6,12,13} \right\},\left\{ {4,5,11,14} \right\} \big\},\end{split} $

$\begin{split} &\begin{split} {B^c} =\left\{ {B_1^c,B_2^c,B_3^c,B_4^c} \right\} = &\big\{ \left\{ {1,5,9,13} \right\},\left\{ {2,6,10,14} \right\}, \big. \\ &\big.\left\{ {3,7,11,15} \right\},\left\{ {4,8,12,16} \right\} \big\},\end{split}\\&B = \left\{ {{B^1},{B^2},{B^3},{B^c}} \right\}.\end{split}$

由集合$ B $和集合$ \varOmega $的映射关系得到关联矩阵$ {{\boldsymbol{M}}_{16 \times 16}} $， 由$ {{\boldsymbol{H}}_3} = [\left. {{{\boldsymbol{M}}_{16 \times 16}}} \right|{{\boldsymbol{I}}_{16 \times 16}}] $可以得到参数为$ {n = 32、k = 16、t = 4、r = 4} $的IS-LRCs，且最小距离$ d = t+1 = 5 $.

假设系统中所有信息节点在单位时间内的故障次数均小于4，且最大故障率为3，即$ {\tau _{\max }} = 3 $，则$ s = {\tau _{\max }} - 1 = 2 $. 任意选择2个4阶正交拉丁方与集合$ {B^c} $构造关联矩阵$ {{\boldsymbol{M}}_{12 \times 16}} $，由$ {{\boldsymbol{H}}_3} = [\left. {{{\boldsymbol{M}}_{12 \times 16}}} \right| {{\boldsymbol{I}}_{12 \times 12}}] $可以得到参数为$ {n = 28、k = 16、t = 3、r = 4} $的IS-LRCs，且最小距离$ d = t+1 = 4 $.

定理9构造的IS-LRCs局部性$r$与维度$k$的比值为

$ \frac{r}{k} = \frac{m}{{{m^2}}} = \frac{1}{m}. $

在大规模分布式存储系统中，局部性$r$与维度$k$的比值将随着拉丁方阶数$m$的增大而显著减小，因此该IS-LRCs能够有效减小故障节点修复时间，提升修复效率.

进一步可以得到码率：

$ R = \frac{k}{n} = \frac{{{m^2}}}{{sm+m+{m^2}}} = \frac{m}{{s+1+m}} = \frac{r}{{r+t}}. $

又因为$ 2 \leqslant s \leqslant m - 1 $，故

$ R = \frac{m}{{s+1+m}} \geqslant \frac{m}{{2m}} = \frac{1}{2}, $

即定理9构造的IS-LRCs码率下界为0.5.

如表2所示为几种典型的基于校验矩阵构造的IS-LRCs与定理9构造的IS-LRCs的码率对比. 表中，参数$n、k$均用可用性$t$和局部性$r$表示，基于阵列LDPC码构造的IS-LRCs可用性$t$只能取偶数，$ v $为大于1的正整数.

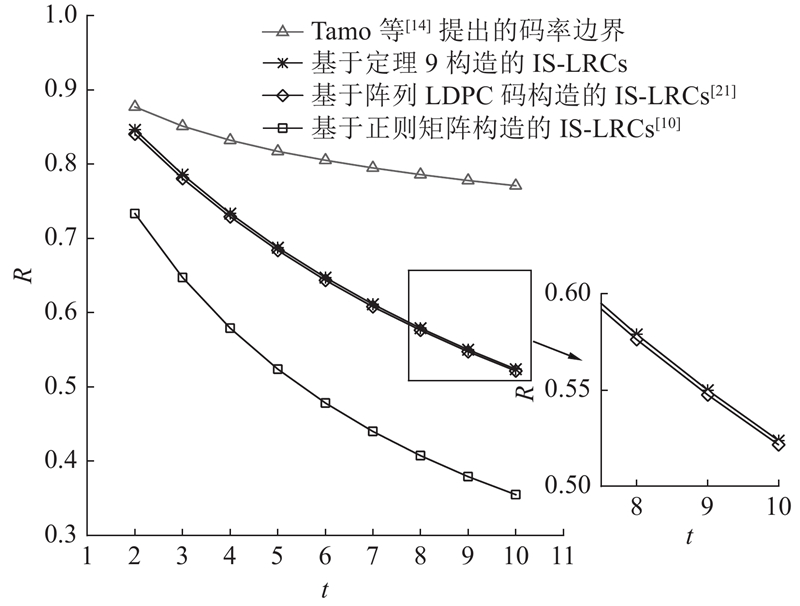
为了更加直观地对比几种方法构造出的局部修复码的码率，如图2所示给出了当局部性$r = 11$时，几种方法构造出的局部修复码码率与Tamo等^[14]提出的码率上界的比较. 可以看出，定理9构造的IS-LRCs码率始终大于基于阵列LDPC码和基于正则矩阵构造的IS-LRCs码率，当局部性$r$取其他值时，可以得到相同的结论. 随着可用性$ t $的增大，系统中存储的冗余数据增多，码率将缓慢减小，体现了可用性$ t $和码率$ R $这2个参数之间的均衡关系. 此外，Tamo等^[14]提出的码率上界适用于有限域$ {{{F}}_q} $上的二元及多元局部修复码，而定理9构造的是二元局部修复码，有限域的大小在一定程度上限制了码率的提高.

考虑到具有$ \left( {r,t} \right) $局部性的局部修复码不仅可以实现多故障节点的局部修复，还支持数据的并行读取，提出利用正交拉丁方构造二元局部修复码的方法，分别构造出全符号具有$ \left( {r,t = 2} \right) $局部性和信息位具有$ \left( {r,t = 2} \right) $局部性的局部修复码. 进一步考虑到系统中存在高故障率节点，利用正交拉丁方完备组构造一类扩展可用性的单校验局部修复码，提高了系统的可靠性. 理论分析表明，所构造的具有全符号局部性的局部修复码码率和码长渐近边界条件；信息位具有$ \left( {r,t = 2} \right) $局部性的单校验局部修复码的最小距离和码率均满足边界条件，为最优局部修复码；扩展可用性的单校验局部修复码最小距离最优，码率较高，始终大于等于0.5. 此外，所有的构造均基于二元有限域，即所有的编解码只涉及异或运算，大大提高了编解码速度，更加适用于实际的分布式存储系统.

本研究构造的局部修复码的参数与正交拉丁方的阶数相关，故正交拉丁方的存在性在一定程度上限制了参数的取值，构造参数能够更加灵活取值的局部修复码是未来值得研究的问题.