[2]
郑刚, 朱合华, 刘新荣, 等. 基坑工程与地下工程安全及环境影响控制 [J]. 土木工程学报, 2016, 49(6): 1-24.
[本文引用: 1]
ZHENG Gang, ZHU Hehua, LIU Xinrong, et al. Control of safety of deep excavations and underground engineering and its impact on surrounding environment [J]. China Civil Engineering Journal , 2016, 49(6): 1-24.
[本文引用: 1]
[3]
丁智, 王达, 王金艳, 等 浙江地区软弱土深基坑变形特点及预测分析
[J]. 岩土力学 , 2015 , 36 (Supple.1 ): 506 - 512
[本文引用: 1]
DING Zhi, WANG Da, WANG Jinyan, et al Deformation characteristics of Zhejiang soft soil deep foundation pits and their predictive analysis
[J]. Rock and Soil Mechanics , 2015 , 36 (Supple.1 ): 506 - 512
[本文引用: 1]
[4]
CHENG X S, ZHENG G, DIAO Y, et al Experimental study of the progressive collapse mechanism of excavations retained by cantilever piles
[J]. Canadian Geotechnical Journal , 2016 , 54 (4 ): 574 - 587
[5]
LI M G, ZHANG Z J, CHEN J J, et al Zoned and staged construction of an underground complex in Shanghai soft clay
[J]. Tunnelling and Underground Space Technology , 2017 , 67 : 187 - 200
DOI:10.1016/j.tust.2017.04.016
[本文引用: 1]
[6]
木林隆, 黄茂松 基于小应变特性的基坑开挖对邻近桩基影响分析方法
[J]. 岩土工程学报 , 2014 , 36 (Supple.2 ): 304 - 310
DOI:10.11779/CJGE2014S2054
[本文引用: 1]
MU Linlong, HUANG Maosong Small-strain behavior-based method for effect of excavations on adjacent pile foundations
[J]. Chinese Journal of Geotechnical Engineering , 2014 , 36 (Supple.2 ): 304 - 310
DOI:10.11779/CJGE2014S2054
[本文引用: 1]
[7]
PITTHAYA J, SITTISAK J, PORNKASEM J, et al Numerical analysis of lateral movements and strut forces in deep cement mixing walls with top-down construction in soft clay
[J]. Computers and Geotechnics , 2017 , 88 : 174 - 181
DOI:10.1016/j.compgeo.2017.03.018
[8]
SHI J W, ZHANG X, CHEN Y H, et al Numerical parametric study of countermeasures to alleviate basement excavation effects on an existing tunnel
[J]. Tunnelling and Underground Space Technology , 2018 , 2018 (72 ): 145 - 153
[本文引用: 1]
[9]
张雯超, 史培新, 刘维, 等 基于改进KNN与基坑参数对地连墙变形预测研究
[J]. 华中科技大学学报:自然科学版 , 2021 , 49 (9 ): 101 - 106
[本文引用: 1]
ZHANG Wenchao, SHI Peixin, LIU Wei, et al Research on deformation prediction of diaphragm wall based on improved KNN and parameters of subway deep excavation
[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition , 2021 , 49 (9 ): 101 - 106
[本文引用: 1]
[10]
洪宇超, 钱建固, 叶源新, 等 基于时空关联特征的CNN-LSTM模型在基坑工程变形预测中的应用
[J]. 岩土工程学报 , 2021 , 43 (Supple.2 ): 108 - 111
HONG Yuchao, QIAN Jiangu, YE Yuanxin, et al Application of CNN-LSTM model based on spatiotemporal correlation characteristics in deformation prediction of excavation engineering
[J]. Chinese Journal of Geotechnical Engineering , 2021 , 43 (Supple.2 ): 108 - 111
[11]
郭健, 陈健, 胡杨 基于小波智能模型的地铁车站基坑变形时序预测分析
[J]. 岩土力学 , 2020 , 41 (Supple.1 ): 299 - 304
[本文引用: 1]
GUO Jian, CHEN Jian, HU Yang Time series prediction for deformation of the metro foundation pit based on wavelet intelligence model
[J]. Rock and Soil Mechanics , 2020 , 41 (Supple.1 ): 299 - 304
[本文引用: 1]
[12]
OSMAN A S, BOLTON M D A new design method for retaining walls in clay
[J]. Canadian Geotechnical Journal , 2004 , 41 (3 ): 451 - 466
DOI:10.1139/t04-003
[本文引用: 3]
[13]
OSMAN A S, BOLTON M D Simple plasticity-based prediction of the undrained settlement of shallow circular foundations on clay
[J]. Géotechnique , 2005 , 55 (6 ): 435 - 447
[14]
OSMAN A S, BOLTON M D, MAIR R J Predicting 2D ground movements around tunnels in undrained clay
[J]. Géotechnique , 2006 , 56 (9 ): 597 - 604
[本文引用: 1]
[16]
KLAR A, OSMAN A S Load–displacement solutions for piles and shallow foundations based on deformation fields and energy conservation
[J]. Géotechnique , 2008 , 58 (7 ): 581 - 589
[本文引用: 1]
[17]
LAM S Y, BOLTON M D Energy conservation as a principle underlying mobilizable strength design for deep excavations
[J]. Journal of Geotechnical and Geoenvironmental Engineering , 2011 , 137 (11 ): 1062 - 1074
DOI:10.1061/(ASCE)GT.1943-5606.0000510
[本文引用: 7]
[18]
WANG L Z, LIU Y J, HONG Y, et al Predicting deformation of multipropped excavations in soft clay with a modified mobilizable strength design (MMSD) method
[J]. Computers and Geotechnics , 2018 , 104 : 54 - 68
DOI:10.1016/j.compgeo.2018.07.018
[本文引用: 4]
[19]
WANG L Z, LONG F Base stability analysis of braced deep excavation in undrained anisotropic clay with upper bound theory
[J]. Science China Technological Sciences , 2014 , 57 (9 ): 1865 - 1876
DOI:10.1007/s11431-014-5613-2
[本文引用: 2]
[20]
O'ROURKE T D. Base stability and ground movement prediction for excavations in soft clay [C] // Retaining Structures . London: Thomas Telford, 1993: 657-686.
[本文引用: 2]
[21]
TERZAGHI K. Theoretical soil mechanics [M]. New York: Wiley, 1943: 26-65.
[本文引用: 1]
[22]
黄茂松, 李弈杉, 唐震, 等 基于不排水强度的黏土基坑抗隆起稳定计算方法
[J]. 岩土工程学报 , 2020 , 42 (9 ): 1577 - 1585
DOI:10.11779/CJGE202009001
[本文引用: 2]
HUANG Maosong, LI Yishan, TANG Zhen, et al Analysis method for basal stability of braced excavations in clay based on undrained shear strength
[J]. Chinese Journal of Geotechnical Engineering , 2020 , 42 (9 ): 1577 - 1585
DOI:10.11779/CJGE202009001
[本文引用: 2]
[23]
HSIEH P G, OU C Y, LIU H T Basal heave analysis of excavations with consideration of anisotropic undrained strength of clay
[J]. Canadian Geotechnical Journal , 2008 , 45 (6 ): 788 - 799
DOI:10.1139/T08-006
[本文引用: 1]
[24]
王洪新 基坑的尺寸效应及考虑开挖宽度的抗隆起稳定安全系数计算方法
[J]. 岩土力学 , 2016 , 37 (Supple.2 ): 433 - 441
[本文引用: 1]
WANG Hongxin Size effect of foundation pits and calculation method of safety factor of heave-resistant stability considering excavation width
[J]. Rock and Soil Mechanics , 2016 , 37 (Supple.2 ): 433 - 441
[本文引用: 1]
[25]
周建, 蔡露, 罗凌晖, 等 各向异性软土基坑抗隆起稳定极限平衡分析
[J]. 岩土力学 , 2019 , 40 (12 ): 4848 - 4856
[本文引用: 1]
ZHOU Jian, CAI Lu, LUO Linghui, et al Limit equilibrium analysis on stability against basal heave of excavation in anisotropic soft clay
[J]. Rock and Soil Mechanics , 2019 , 40 (12 ): 4848 - 4856
[本文引用: 1]
[26]
HUANG M S, TANG Z, YUAN J Basal stability analysis of braced excavations with embedded walls in undrained clay using the upper bound theorem
[J]. Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research , 2018 , 79 : 231 - 241
[本文引用: 1]
[27]
HSIEH P G, OU C Y Shape of ground surface settlement profiles caused by excavation
[J]. Canadian Geotechnical Journal , 1998 , 35 (6 ): 1004 - 1017
DOI:10.1139/t98-056
[本文引用: 1]
[28]
KUNG G T, JUANG C H, HSIAO E C, et al Simplified model for wall deflection and ground-surface settlement caused by braced excavation in clays
[J]. Journal of Geotechnical and Geoenvironmental Engineering , 2007 , 133 (6 ): 731 - 747
DOI:10.1061/(ASCE)1090-0241(2007)133:6(731)
[本文引用: 1]
[29]
OU C Y, HSIEH P G A simplified method for predicting ground settlement profiles induced by excavation in soft clay
[J]. Computers and Geotechnics , 2011 , 38 (8 ): 987 - 997
DOI:10.1016/j.compgeo.2011.06.008
[本文引用: 4]
[30]
WANG Z W, CHARLES W, LIU G B Characteristics of wall deflections and ground surface settlements in Shanghai
[J]. Canadian Geotechnical Journal , 2005 , 42 (5 ): 1243 - 1254
DOI:10.1139/t05-056
[本文引用: 1]
[31]
徐中华. 上海地区支护结构与主体地下结构相结合的深基坑变形性状研究[D]. 上海: 上海交通大学, 2007.
XU Zhonghua. Deformation behavior of deep excavations supported by permanent structure in shanghai soft deposit [D]. Shanghai: Shanghai Jiao Tong University, 2007.
[32]
NG C, HONG Y, LIU G, et al Ground deformations and soil–structure interaction of a multi-propped excavation in Shanghai soft clays
[J]. Géotechnique , 2012 , 62 (10 ): 907 - 921
[本文引用: 1]
[33]
LI Q. Long-term settlement mechanisms of shield tunnels in Shanghai soft clay [D]. Hong Kong: Hong Kong University of Science and Technology, 2013.
[本文引用: 1]
软土地区基坑工程变形控制方法及工程应用
1
2022
... 在软土地区,深基坑开挖往往会引起较大的基坑围护结构和周边地层变形,对基坑周边的建(构)筑物、道路、地下管线及其他基础设施产生影响[1 ] . 尤其是对于一些变形要求高的建(构)筑物,例如古建筑、大型桥梁、地铁隧道等,基坑变形的控制要求可达mm级[2 ] ,因此开展软黏土基坑开挖的变形预测至关重要. ...
软土地区基坑工程变形控制方法及工程应用
1
2022
... 在软土地区,深基坑开挖往往会引起较大的基坑围护结构和周边地层变形,对基坑周边的建(构)筑物、道路、地下管线及其他基础设施产生影响[1 ] . 尤其是对于一些变形要求高的建(构)筑物,例如古建筑、大型桥梁、地铁隧道等,基坑变形的控制要求可达mm级[2 ] ,因此开展软黏土基坑开挖的变形预测至关重要. ...
1
... 在软土地区,深基坑开挖往往会引起较大的基坑围护结构和周边地层变形,对基坑周边的建(构)筑物、道路、地下管线及其他基础设施产生影响[1 ] . 尤其是对于一些变形要求高的建(构)筑物,例如古建筑、大型桥梁、地铁隧道等,基坑变形的控制要求可达mm级[2 ] ,因此开展软黏土基坑开挖的变形预测至关重要. ...
1
... 在软土地区,深基坑开挖往往会引起较大的基坑围护结构和周边地层变形,对基坑周边的建(构)筑物、道路、地下管线及其他基础设施产生影响[1 ] . 尤其是对于一些变形要求高的建(构)筑物,例如古建筑、大型桥梁、地铁隧道等,基坑变形的控制要求可达mm级[2 ] ,因此开展软黏土基坑开挖的变形预测至关重要. ...
浙江地区软弱土深基坑变形特点及预测分析
1
2015
... 预测基坑开挖引起围护结构变形的常用方法包括半经验法[3 -5 ] 、数值分析法[6 -8 ] 和算法分析法[9 -11 ] . 半经验法和算法分析法相似,都是根据大量已有数据总结变形趋势,进而预测变形. 这2种方法在实际使用时较方便,但建立不同地层区域的数据库很困难,数据库规模会限制预测精度. 数值分析法是基于各种土体本构模型实现变形预测,但本构模型较复杂且包含大量不易校准的参数,实际使用时很麻烦. ...
浙江地区软弱土深基坑变形特点及预测分析
1
2015
... 预测基坑开挖引起围护结构变形的常用方法包括半经验法[3 -5 ] 、数值分析法[6 -8 ] 和算法分析法[9 -11 ] . 半经验法和算法分析法相似,都是根据大量已有数据总结变形趋势,进而预测变形. 这2种方法在实际使用时较方便,但建立不同地层区域的数据库很困难,数据库规模会限制预测精度. 数值分析法是基于各种土体本构模型实现变形预测,但本构模型较复杂且包含大量不易校准的参数,实际使用时很麻烦. ...
Experimental study of the progressive collapse mechanism of excavations retained by cantilever piles
0
2016
Zoned and staged construction of an underground complex in Shanghai soft clay
1
2017
... 预测基坑开挖引起围护结构变形的常用方法包括半经验法[3 -5 ] 、数值分析法[6 -8 ] 和算法分析法[9 -11 ] . 半经验法和算法分析法相似,都是根据大量已有数据总结变形趋势,进而预测变形. 这2种方法在实际使用时较方便,但建立不同地层区域的数据库很困难,数据库规模会限制预测精度. 数值分析法是基于各种土体本构模型实现变形预测,但本构模型较复杂且包含大量不易校准的参数,实际使用时很麻烦. ...
基于小应变特性的基坑开挖对邻近桩基影响分析方法
1
2014
... 预测基坑开挖引起围护结构变形的常用方法包括半经验法[3 -5 ] 、数值分析法[6 -8 ] 和算法分析法[9 -11 ] . 半经验法和算法分析法相似,都是根据大量已有数据总结变形趋势,进而预测变形. 这2种方法在实际使用时较方便,但建立不同地层区域的数据库很困难,数据库规模会限制预测精度. 数值分析法是基于各种土体本构模型实现变形预测,但本构模型较复杂且包含大量不易校准的参数,实际使用时很麻烦. ...
基于小应变特性的基坑开挖对邻近桩基影响分析方法
1
2014
... 预测基坑开挖引起围护结构变形的常用方法包括半经验法[3 -5 ] 、数值分析法[6 -8 ] 和算法分析法[9 -11 ] . 半经验法和算法分析法相似,都是根据大量已有数据总结变形趋势,进而预测变形. 这2种方法在实际使用时较方便,但建立不同地层区域的数据库很困难,数据库规模会限制预测精度. 数值分析法是基于各种土体本构模型实现变形预测,但本构模型较复杂且包含大量不易校准的参数,实际使用时很麻烦. ...
Numerical analysis of lateral movements and strut forces in deep cement mixing walls with top-down construction in soft clay
0
2017
Numerical parametric study of countermeasures to alleviate basement excavation effects on an existing tunnel
1
2018
... 预测基坑开挖引起围护结构变形的常用方法包括半经验法[3 -5 ] 、数值分析法[6 -8 ] 和算法分析法[9 -11 ] . 半经验法和算法分析法相似,都是根据大量已有数据总结变形趋势,进而预测变形. 这2种方法在实际使用时较方便,但建立不同地层区域的数据库很困难,数据库规模会限制预测精度. 数值分析法是基于各种土体本构模型实现变形预测,但本构模型较复杂且包含大量不易校准的参数,实际使用时很麻烦. ...
基于改进KNN与基坑参数对地连墙变形预测研究
1
2021
... 预测基坑开挖引起围护结构变形的常用方法包括半经验法[3 -5 ] 、数值分析法[6 -8 ] 和算法分析法[9 -11 ] . 半经验法和算法分析法相似,都是根据大量已有数据总结变形趋势,进而预测变形. 这2种方法在实际使用时较方便,但建立不同地层区域的数据库很困难,数据库规模会限制预测精度. 数值分析法是基于各种土体本构模型实现变形预测,但本构模型较复杂且包含大量不易校准的参数,实际使用时很麻烦. ...
基于改进KNN与基坑参数对地连墙变形预测研究
1
2021
... 预测基坑开挖引起围护结构变形的常用方法包括半经验法[3 -5 ] 、数值分析法[6 -8 ] 和算法分析法[9 -11 ] . 半经验法和算法分析法相似,都是根据大量已有数据总结变形趋势,进而预测变形. 这2种方法在实际使用时较方便,但建立不同地层区域的数据库很困难,数据库规模会限制预测精度. 数值分析法是基于各种土体本构模型实现变形预测,但本构模型较复杂且包含大量不易校准的参数,实际使用时很麻烦. ...
基于时空关联特征的CNN-LSTM模型在基坑工程变形预测中的应用
0
2021
基于时空关联特征的CNN-LSTM模型在基坑工程变形预测中的应用
0
2021
基于小波智能模型的地铁车站基坑变形时序预测分析
1
2020
... 预测基坑开挖引起围护结构变形的常用方法包括半经验法[3 -5 ] 、数值分析法[6 -8 ] 和算法分析法[9 -11 ] . 半经验法和算法分析法相似,都是根据大量已有数据总结变形趋势,进而预测变形. 这2种方法在实际使用时较方便,但建立不同地层区域的数据库很困难,数据库规模会限制预测精度. 数值分析法是基于各种土体本构模型实现变形预测,但本构模型较复杂且包含大量不易校准的参数,实际使用时很麻烦. ...
基于小波智能模型的地铁车站基坑变形时序预测分析
1
2020
... 预测基坑开挖引起围护结构变形的常用方法包括半经验法[3 -5 ] 、数值分析法[6 -8 ] 和算法分析法[9 -11 ] . 半经验法和算法分析法相似,都是根据大量已有数据总结变形趋势,进而预测变形. 这2种方法在实际使用时较方便,但建立不同地层区域的数据库很困难,数据库规模会限制预测精度. 数值分析法是基于各种土体本构模型实现变形预测,但本构模型较复杂且包含大量不易校准的参数,实际使用时很麻烦. ...
A new design method for retaining walls in clay
3
2004
... 针对上述不足,Osman等[12 ] 在塑性变形机制和虚功原理的基础上提出动员强度设计(mobilizable strength design, MSD)方法,用于预测悬臂式挡土墙变形. 随后,MSD法不断发展[12 -14 ] ,成功应用于内支撑基坑施工引起的围护结构侧移和墙后地表沉降的计算[15 ] . Klar等[16 ] 使用能量守恒定律,进一步阐述了MSD法. Lam等[17 ] 在Osman等[15 ] 的基础上对宽基坑和窄基坑进行区分,讨论了分步开挖切应变增量和围护结构弹性变形能的影响. 在计算中考虑不同深度土体抗剪强度的差异,使之适用于分层地层的计算中. Wang等[18 -19 ] 没有延续Lam等[17 ] 有关分层地层的研究,而是修正了MSD法中的塑性变形机制,将该机制中三角函数形式的增量位移曲线改成更加符合实际的指数族函数形式,得到修正MSD法(modified mobilizable strength design, MMSD). 虽然利用MMSD法预测的墙体侧移的大小和形状都更接近实测值,但MMSD法变形机制不能很好地反映土体的真实变形情况. 该机制中的墙后影响区域随着开挖而减小,没有考虑分层地层和围护结构变形的影响,造成较大的误差. ...
... [12 -14 ],成功应用于内支撑基坑施工引起的围护结构侧移和墙后地表沉降的计算[15 ] . Klar等[16 ] 使用能量守恒定律,进一步阐述了MSD法. Lam等[17 ] 在Osman等[15 ] 的基础上对宽基坑和窄基坑进行区分,讨论了分步开挖切应变增量和围护结构弹性变形能的影响. 在计算中考虑不同深度土体抗剪强度的差异,使之适用于分层地层的计算中. Wang等[18 -19 ] 没有延续Lam等[17 ] 有关分层地层的研究,而是修正了MSD法中的塑性变形机制,将该机制中三角函数形式的增量位移曲线改成更加符合实际的指数族函数形式,得到修正MSD法(modified mobilizable strength design, MMSD). 虽然利用MMSD法预测的墙体侧移的大小和形状都更接近实测值,但MMSD法变形机制不能很好地反映土体的真实变形情况. 该机制中的墙后影响区域随着开挖而减小,没有考虑分层地层和围护结构变形的影响,造成较大的误差. ...
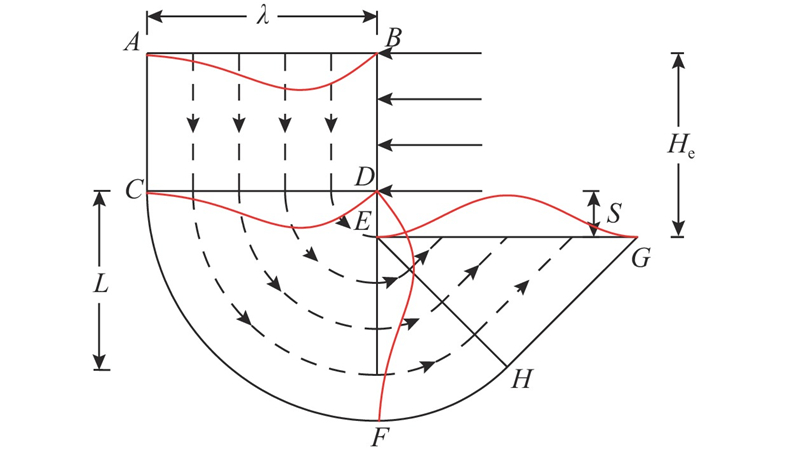
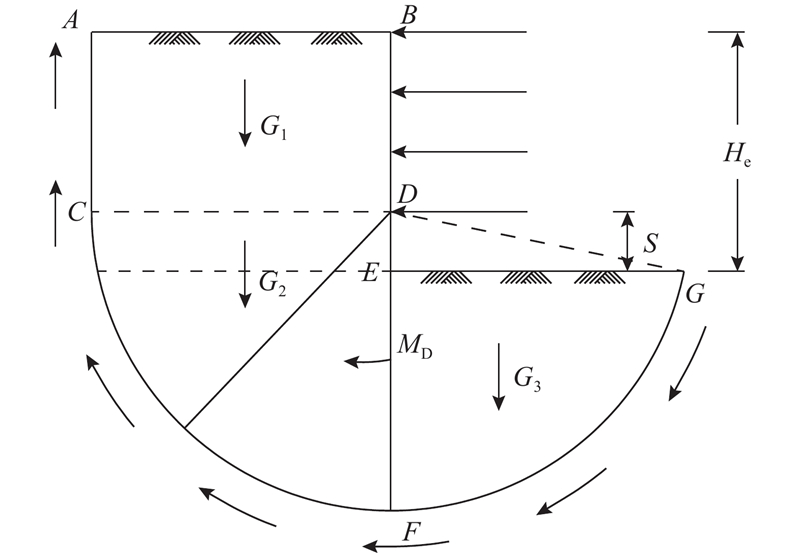
... 在MMSD法中,架设首道内支撑后的基坑塑性变形机制由位移场和增量位移曲线组成,墙体发生弯曲变形,最大侧移位于基坑底部. 在不排水剪切的条件下,位移场与文献[12 ]相同,如图2 所示. 图中,L 为最低一道支撑以下的围护结构长度,S 为最低一道支撑到坑底的距离,H e 为基坑开挖深度. 位移场包括4个剪切区,土体在各区边界处连续剪切,无相对滑动. 带虚线的箭头显示变形流向,沿着每一条线,增量位移都是常数. 该增量位移用指数族函数表示为 ...
Simple plasticity-based prediction of the undrained settlement of shallow circular foundations on clay
0
2005
Predicting 2D ground movements around tunnels in undrained clay
1
2006
... 针对上述不足,Osman等[12 ] 在塑性变形机制和虚功原理的基础上提出动员强度设计(mobilizable strength design, MSD)方法,用于预测悬臂式挡土墙变形. 随后,MSD法不断发展[12 -14 ] ,成功应用于内支撑基坑施工引起的围护结构侧移和墙后地表沉降的计算[15 ] . Klar等[16 ] 使用能量守恒定律,进一步阐述了MSD法. Lam等[17 ] 在Osman等[15 ] 的基础上对宽基坑和窄基坑进行区分,讨论了分步开挖切应变增量和围护结构弹性变形能的影响. 在计算中考虑不同深度土体抗剪强度的差异,使之适用于分层地层的计算中. Wang等[18 -19 ] 没有延续Lam等[17 ] 有关分层地层的研究,而是修正了MSD法中的塑性变形机制,将该机制中三角函数形式的增量位移曲线改成更加符合实际的指数族函数形式,得到修正MSD法(modified mobilizable strength design, MMSD). 虽然利用MMSD法预测的墙体侧移的大小和形状都更接近实测值,但MMSD法变形机制不能很好地反映土体的真实变形情况. 该机制中的墙后影响区域随着开挖而减小,没有考虑分层地层和围护结构变形的影响,造成较大的误差. ...
Ground movement predictions for braced excavations in undrained clay
5
2006
... 针对上述不足,Osman等[12 ] 在塑性变形机制和虚功原理的基础上提出动员强度设计(mobilizable strength design, MSD)方法,用于预测悬臂式挡土墙变形. 随后,MSD法不断发展[12 -14 ] ,成功应用于内支撑基坑施工引起的围护结构侧移和墙后地表沉降的计算[15 ] . Klar等[16 ] 使用能量守恒定律,进一步阐述了MSD法. Lam等[17 ] 在Osman等[15 ] 的基础上对宽基坑和窄基坑进行区分,讨论了分步开挖切应变增量和围护结构弹性变形能的影响. 在计算中考虑不同深度土体抗剪强度的差异,使之适用于分层地层的计算中. Wang等[18 -19 ] 没有延续Lam等[17 ] 有关分层地层的研究,而是修正了MSD法中的塑性变形机制,将该机制中三角函数形式的增量位移曲线改成更加符合实际的指数族函数形式,得到修正MSD法(modified mobilizable strength design, MMSD). 虽然利用MMSD法预测的墙体侧移的大小和形状都更接近实测值,但MMSD法变形机制不能很好地反映土体的真实变形情况. 该机制中的墙后影响区域随着开挖而减小,没有考虑分层地层和围护结构变形的影响,造成较大的误差. ...
... [15 ]的基础上对宽基坑和窄基坑进行区分,讨论了分步开挖切应变增量和围护结构弹性变形能的影响. 在计算中考虑不同深度土体抗剪强度的差异,使之适用于分层地层的计算中. Wang等[18 -19 ] 没有延续Lam等[17 ] 有关分层地层的研究,而是修正了MSD法中的塑性变形机制,将该机制中三角函数形式的增量位移曲线改成更加符合实际的指数族函数形式,得到修正MSD法(modified mobilizable strength design, MMSD). 虽然利用MMSD法预测的墙体侧移的大小和形状都更接近实测值,但MMSD法变形机制不能很好地反映土体的真实变形情况. 该机制中的墙后影响区域随着开挖而减小,没有考虑分层地层和围护结构变形的影响,造成较大的误差. ...
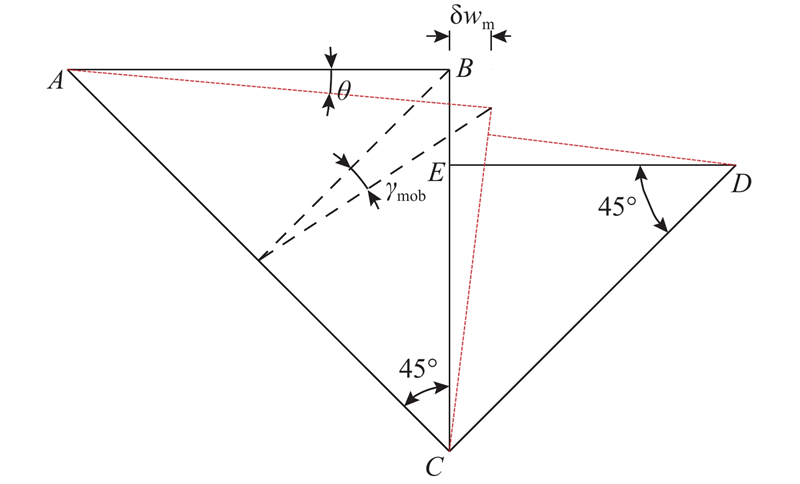
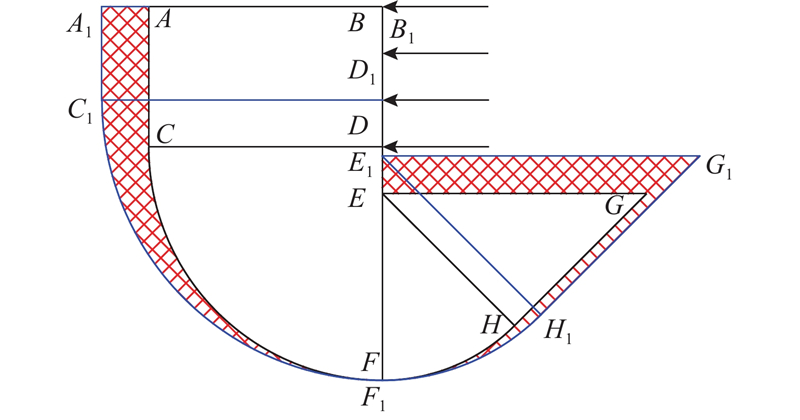
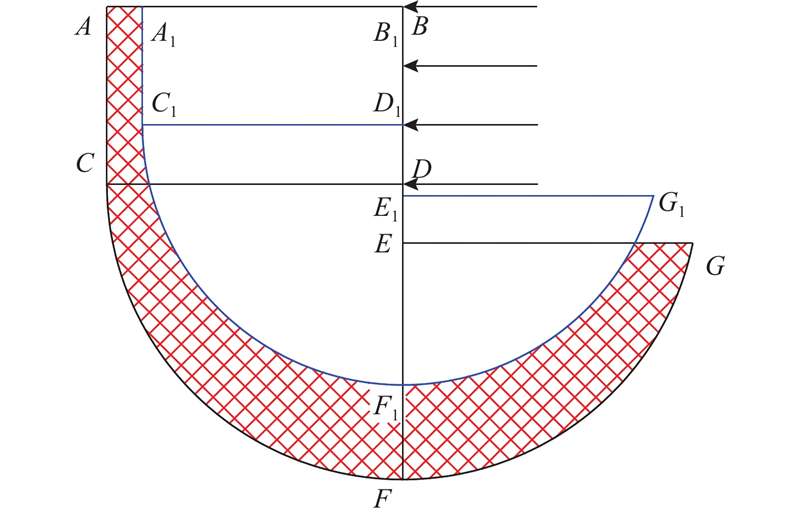
... 基坑塑性变形机制的确定是本文方法的关键. Osman等[15 ] 认为内撑式基坑围护结构侧移等于架设内支撑前悬臂变形与架设首道内支撑后分步开挖增量变形之和. 在架设内支撑前,基坑围护结构发生悬臂变形,变形机制如图1 所示,墙体不发生弯曲变形,最大侧移位于墙顶. 通过力和力矩平衡条件,可以算得围护结构的最大侧移. 图中,θ 为墙体偏转角,γ mob 为不排水切应变. ...
... 式中:y 为最低一道支撑以下任意点到D 点的距离; $ \mathrm{\delta }w $ y 处的墙体增量位移;$ {\mathrm{\delta }w}_{{\mathrm{m}}} $ $ \mathrm{\delta }w $ $ \lambda $ [20 ] ,整个位移场的尺寸取决于波长$ \lambda $ . Osman等[15 ] 认为$ \lambda $
... 确定基坑变形位移场的影响范围是基坑塑性变形机制的基础. 在Osman等[15 , 27 -28 ] 的研究中,将开挖深度作为预测开挖影响范围的唯一参数. 此外,大多数经验方法都是假定软土中开挖的沉降影响区约等于开挖深度的2倍. Ou等[29 ] 研究发现,前述方法不具备普遍性,无法兼顾不同基坑形状和土层特性. Ou等[29 ] 采用有限元参数研究结果和稳定机理,提出凹形沉降剖面的沉降影响区,在与实际案例的对比中验证良好. 本文在Ou等[29 ] 的研究成果基础上,提出与MMSD法相适配的位移场影响范围确定方法. ...
Load–displacement solutions for piles and shallow foundations based on deformation fields and energy conservation
1
2008
... 针对上述不足,Osman等[12 ] 在塑性变形机制和虚功原理的基础上提出动员强度设计(mobilizable strength design, MSD)方法,用于预测悬臂式挡土墙变形. 随后,MSD法不断发展[12 -14 ] ,成功应用于内支撑基坑施工引起的围护结构侧移和墙后地表沉降的计算[15 ] . Klar等[16 ] 使用能量守恒定律,进一步阐述了MSD法. Lam等[17 ] 在Osman等[15 ] 的基础上对宽基坑和窄基坑进行区分,讨论了分步开挖切应变增量和围护结构弹性变形能的影响. 在计算中考虑不同深度土体抗剪强度的差异,使之适用于分层地层的计算中. Wang等[18 -19 ] 没有延续Lam等[17 ] 有关分层地层的研究,而是修正了MSD法中的塑性变形机制,将该机制中三角函数形式的增量位移曲线改成更加符合实际的指数族函数形式,得到修正MSD法(modified mobilizable strength design, MMSD). 虽然利用MMSD法预测的墙体侧移的大小和形状都更接近实测值,但MMSD法变形机制不能很好地反映土体的真实变形情况. 该机制中的墙后影响区域随着开挖而减小,没有考虑分层地层和围护结构变形的影响,造成较大的误差. ...
Energy conservation as a principle underlying mobilizable strength design for deep excavations
7
2011
... 针对上述不足,Osman等[12 ] 在塑性变形机制和虚功原理的基础上提出动员强度设计(mobilizable strength design, MSD)方法,用于预测悬臂式挡土墙变形. 随后,MSD法不断发展[12 -14 ] ,成功应用于内支撑基坑施工引起的围护结构侧移和墙后地表沉降的计算[15 ] . Klar等[16 ] 使用能量守恒定律,进一步阐述了MSD法. Lam等[17 ] 在Osman等[15 ] 的基础上对宽基坑和窄基坑进行区分,讨论了分步开挖切应变增量和围护结构弹性变形能的影响. 在计算中考虑不同深度土体抗剪强度的差异,使之适用于分层地层的计算中. Wang等[18 -19 ] 没有延续Lam等[17 ] 有关分层地层的研究,而是修正了MSD法中的塑性变形机制,将该机制中三角函数形式的增量位移曲线改成更加符合实际的指数族函数形式,得到修正MSD法(modified mobilizable strength design, MMSD). 虽然利用MMSD法预测的墙体侧移的大小和形状都更接近实测值,但MMSD法变形机制不能很好地反映土体的真实变形情况. 该机制中的墙后影响区域随着开挖而减小,没有考虑分层地层和围护结构变形的影响,造成较大的误差. ...
... [17 ]有关分层地层的研究,而是修正了MSD法中的塑性变形机制,将该机制中三角函数形式的增量位移曲线改成更加符合实际的指数族函数形式,得到修正MSD法(modified mobilizable strength design, MMSD). 虽然利用MMSD法预测的墙体侧移的大小和形状都更接近实测值,但MMSD法变形机制不能很好地反映土体的真实变形情况. 该机制中的墙后影响区域随着开挖而减小,没有考虑分层地层和围护结构变形的影响,造成较大的误差. ...
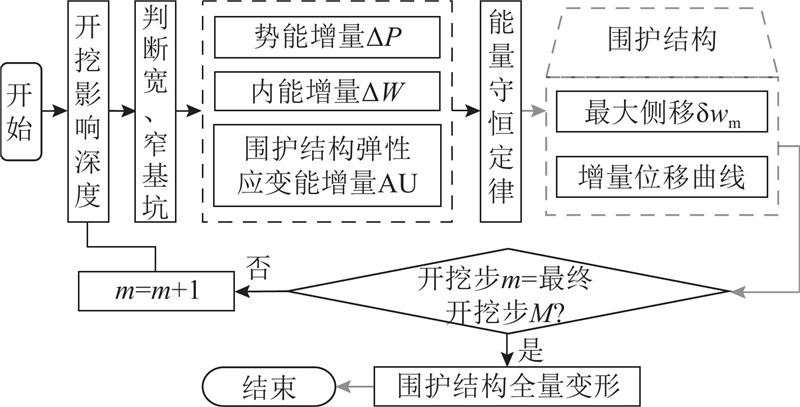
... 综上所述,为了更好地预测软土地区深基坑围护结构的变形,本文在Lam等[17 -19 ] 研究的基础上改进塑性变形机制. 基于圆弧滑动模式,提出新的位移场. 将增量位移曲线设置成指数族函数形式,通过基坑开挖主要影响深度来量化位移场尺寸. 改进后的MMSD法还能兼顾分层地层和围护结构弹性变形的影响. 将改进后的方法预测结果与上海软土地区的6个工程实例及MMSD法的预测结果进行对比验证. 研究成果可以为软土地区以柔性挡土墙和多道内支撑为支护结构的深基坑变形预测提供理论支撑. ...
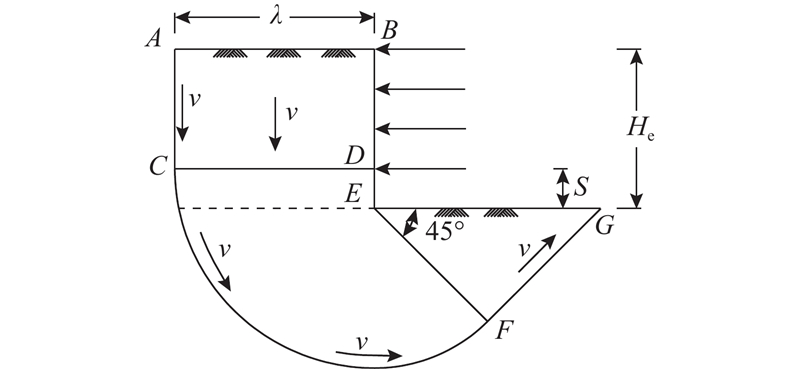
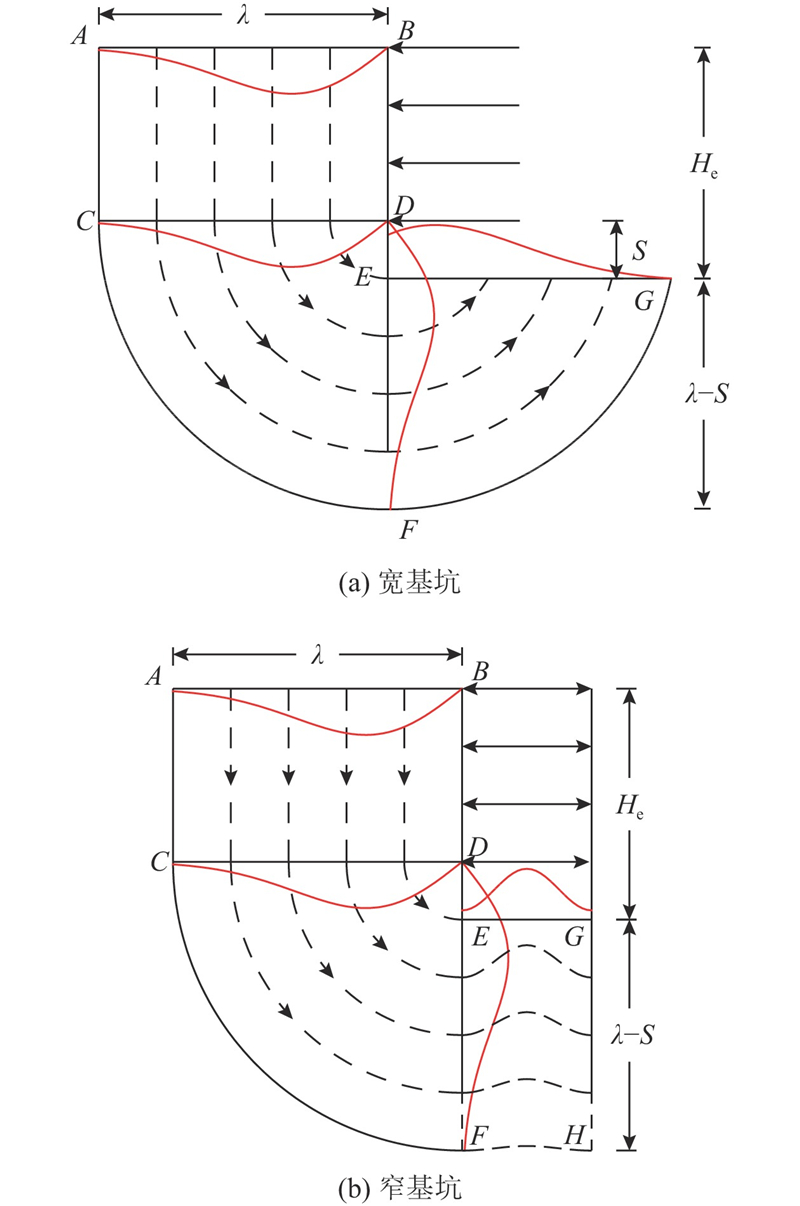
... 当基坑开挖宽度小于2倍三角形区域宽度时,坑底土体会同时受到两侧土体位移的影响,图2 中的变形机制不再适用. Lam等[17 ] 提出相应的窄基坑塑性变形机制,如图3 所示,窄基坑机制使用矩形区域EFGH 代替宽基坑机制中的三角形区域EGH ,在体现围护结构墙面-土体-墙面相互作用的同时,保证整个区域的体积应变为零,即满足不排水剪切条件. ...
... 3)将围护结构的弹性应变能纳入MMSD法计算体系. 围护结构墙体的强度远大于软土的强度,特别是当采取灌浆、土钉、锚杆支护等措施限制坑底土隆起的时候,墙后土体变形引起的土体内能增量相对较小,主要是结构系统本身的刚度限制了位移的增大[17 ] . ...
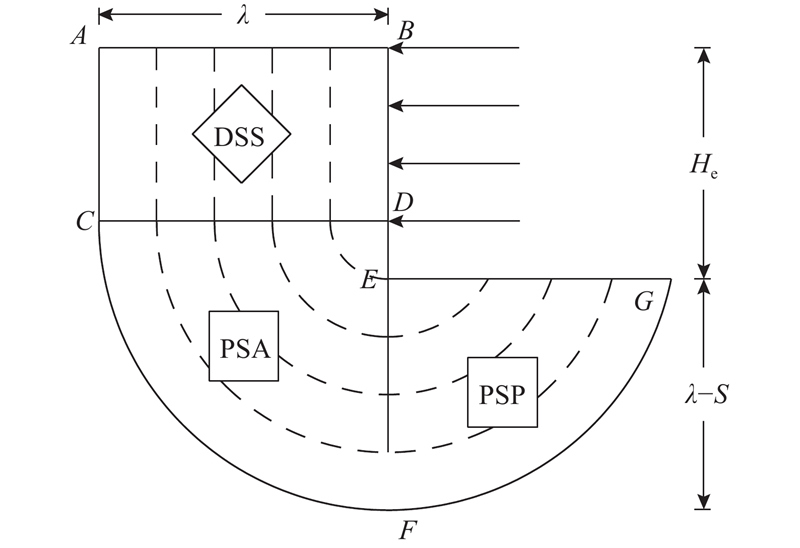
... 在软黏土中,不排水抗剪强度一般随深度和剪切方向的变化而变化. 如图11 所示为改进后宽基坑开挖塑性变形机制中各个剪切区域内的最大主应力方向以及各区域为了获得不排水抗剪强度的土体试验构型. 在矩形ABCD区域,假定土体垂直剪切,获得不排水抗剪强度的理想试验是简单直接剪切试验(direct simple shear test, DSS). 在扇形CDF区域和扇形EFG区域,剪切发生在与水平呈45°的方向上,这2个区域分别通过平面应变主动试验(plain-strain active, PSA)和平面应变被动试验(plain-strain passive, PSP)获取不排水抗剪强度[17 ] . 在一般的工程地质勘探报告上不会有如此详细的勘察数据,O`Rourke[20 ] 建议采用简单直接剪切试验结果近似代替PSA和PSP区域的不排水抗剪强度. ...
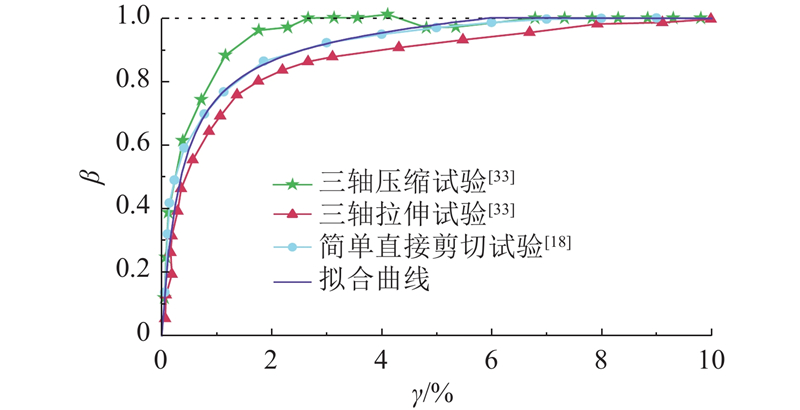
... 对于强度动员率$ \beta $ [17 ] . 本节的6个工程案例均来自上海地区,但每个工程案例都缺少详细的原位土体应力应变数据,因此采用上海地区已有的土体数据代替,如图12 所示. 图12 给出上海黏土强度动员率与动员切应变之间的关系,这些数据来自Li[33 ] 的不排水三轴试验和Wang等[18 ] 的简单直接剪切试验,试验土样均来自上海软土地区的基坑工程. 3条实测的黏土强度动员率曲线表现出非常相似的趋势,说明上海黏土有着良好的均匀性,因此采用这些数据对本文案例进行计算是可行的. 利用幂函数对实测数据进行拟合,可得强度动员率与动员切应变之间的关系: ...
Predicting deformation of multipropped excavations in soft clay with a modified mobilizable strength design (MMSD) method
4
2018
... 针对上述不足,Osman等[12 ] 在塑性变形机制和虚功原理的基础上提出动员强度设计(mobilizable strength design, MSD)方法,用于预测悬臂式挡土墙变形. 随后,MSD法不断发展[12 -14 ] ,成功应用于内支撑基坑施工引起的围护结构侧移和墙后地表沉降的计算[15 ] . Klar等[16 ] 使用能量守恒定律,进一步阐述了MSD法. Lam等[17 ] 在Osman等[15 ] 的基础上对宽基坑和窄基坑进行区分,讨论了分步开挖切应变增量和围护结构弹性变形能的影响. 在计算中考虑不同深度土体抗剪强度的差异,使之适用于分层地层的计算中. Wang等[18 -19 ] 没有延续Lam等[17 ] 有关分层地层的研究,而是修正了MSD法中的塑性变形机制,将该机制中三角函数形式的增量位移曲线改成更加符合实际的指数族函数形式,得到修正MSD法(modified mobilizable strength design, MMSD). 虽然利用MMSD法预测的墙体侧移的大小和形状都更接近实测值,但MMSD法变形机制不能很好地反映土体的真实变形情况. 该机制中的墙后影响区域随着开挖而减小,没有考虑分层地层和围护结构变形的影响,造成较大的误差. ...
... 在增量计算中,强度动员率$ \beta $ $ {c}_{{\mathrm{u}}} $ [18 ] 推荐的半经验公式确定. 综上所述,地面下的土体不排水抗剪强度可用下式表示: ...
... 对于强度动员率$ \beta $ [17 ] . 本节的6个工程案例均来自上海地区,但每个工程案例都缺少详细的原位土体应力应变数据,因此采用上海地区已有的土体数据代替,如图12 所示. 图12 给出上海黏土强度动员率与动员切应变之间的关系,这些数据来自Li[33 ] 的不排水三轴试验和Wang等[18 ] 的简单直接剪切试验,试验土样均来自上海软土地区的基坑工程. 3条实测的黏土强度动员率曲线表现出非常相似的趋势,说明上海黏土有着良好的均匀性,因此采用这些数据对本文案例进行计算是可行的. 利用幂函数对实测数据进行拟合,可得强度动员率与动员切应变之间的关系: ...
... 上海K0固结软土试样的归一化应力应变关系[18 ] ...
Base stability analysis of braced deep excavation in undrained anisotropic clay with upper bound theory
2
2014
... 针对上述不足,Osman等[12 ] 在塑性变形机制和虚功原理的基础上提出动员强度设计(mobilizable strength design, MSD)方法,用于预测悬臂式挡土墙变形. 随后,MSD法不断发展[12 -14 ] ,成功应用于内支撑基坑施工引起的围护结构侧移和墙后地表沉降的计算[15 ] . Klar等[16 ] 使用能量守恒定律,进一步阐述了MSD法. Lam等[17 ] 在Osman等[15 ] 的基础上对宽基坑和窄基坑进行区分,讨论了分步开挖切应变增量和围护结构弹性变形能的影响. 在计算中考虑不同深度土体抗剪强度的差异,使之适用于分层地层的计算中. Wang等[18 -19 ] 没有延续Lam等[17 ] 有关分层地层的研究,而是修正了MSD法中的塑性变形机制,将该机制中三角函数形式的增量位移曲线改成更加符合实际的指数族函数形式,得到修正MSD法(modified mobilizable strength design, MMSD). 虽然利用MMSD法预测的墙体侧移的大小和形状都更接近实测值,但MMSD法变形机制不能很好地反映土体的真实变形情况. 该机制中的墙后影响区域随着开挖而减小,没有考虑分层地层和围护结构变形的影响,造成较大的误差. ...
... 综上所述,为了更好地预测软土地区深基坑围护结构的变形,本文在Lam等[17 -19 ] 研究的基础上改进塑性变形机制. 基于圆弧滑动模式,提出新的位移场. 将增量位移曲线设置成指数族函数形式,通过基坑开挖主要影响深度来量化位移场尺寸. 改进后的MMSD法还能兼顾分层地层和围护结构弹性变形的影响. 将改进后的方法预测结果与上海软土地区的6个工程实例及MMSD法的预测结果进行对比验证. 研究成果可以为软土地区以柔性挡土墙和多道内支撑为支护结构的深基坑变形预测提供理论支撑. ...
2
... 式中:y 为最低一道支撑以下任意点到D 点的距离; $ \mathrm{\delta }w $ y 处的墙体增量位移;$ {\mathrm{\delta }w}_{{\mathrm{m}}} $ $ \mathrm{\delta }w $ $ \lambda $ [20 ] ,整个位移场的尺寸取决于波长$ \lambda $ . Osman等[15 ] 认为$ \lambda $
... 在软黏土中,不排水抗剪强度一般随深度和剪切方向的变化而变化. 如图11 所示为改进后宽基坑开挖塑性变形机制中各个剪切区域内的最大主应力方向以及各区域为了获得不排水抗剪强度的土体试验构型. 在矩形ABCD区域,假定土体垂直剪切,获得不排水抗剪强度的理想试验是简单直接剪切试验(direct simple shear test, DSS). 在扇形CDF区域和扇形EFG区域,剪切发生在与水平呈45°的方向上,这2个区域分别通过平面应变主动试验(plain-strain active, PSA)和平面应变被动试验(plain-strain passive, PSP)获取不排水抗剪强度[17 ] . 在一般的工程地质勘探报告上不会有如此详细的勘察数据,O`Rourke[20 ] 建议采用简单直接剪切试验结果近似代替PSA和PSP区域的不排水抗剪强度. ...
1
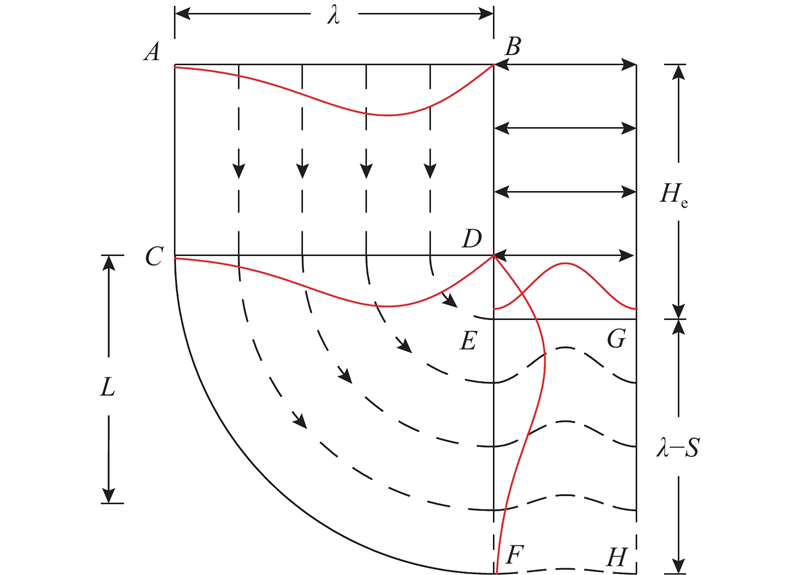
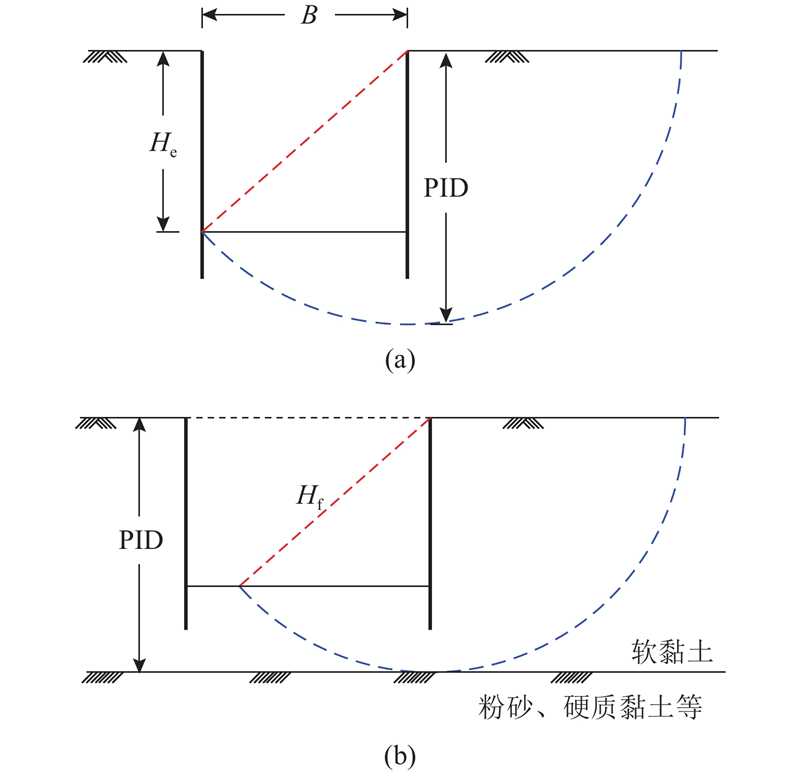
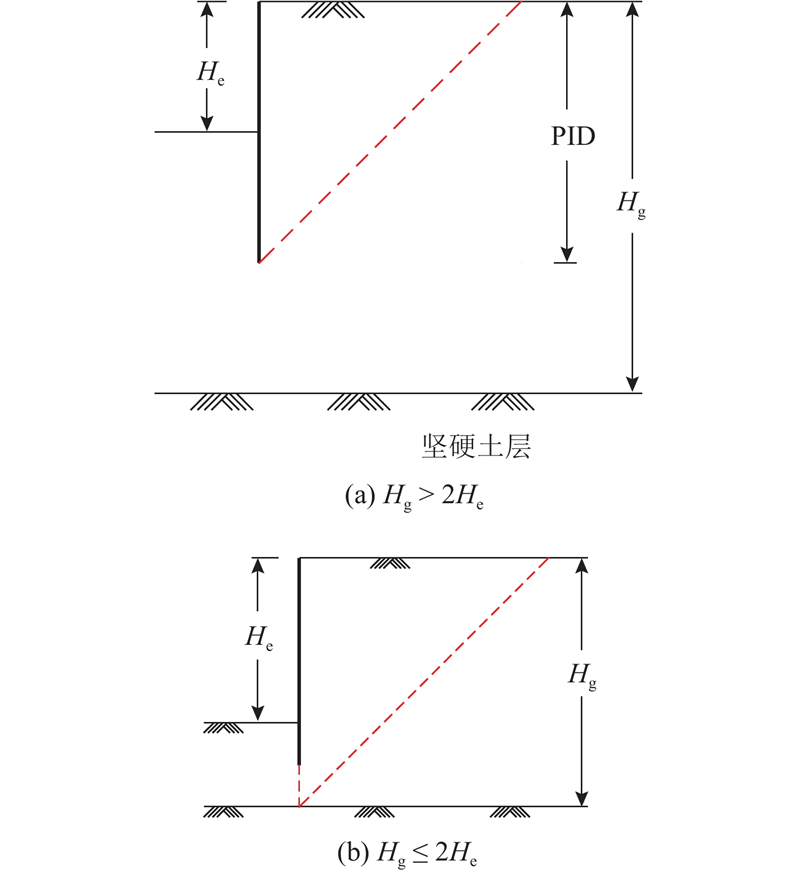
... MMSD法采用的塑性变形机制位移场建立在如图4 所示的Terzaghi模式[21 ] 的基础上,而该破坏模式被认为更加适用于宽浅的基坑[22 ] . 此外,MMSD法采用式(2)来确定整个位移场的尺寸,引入能量最小耗散原理,提高了$ 1.0 < \alpha < 2.0 $ $ \alpha $ $ 1.0 < \alpha < 2.0) $ $ \alpha $ 图5 所示,随着基坑开挖的进行,最低一道支撑以下的围护结构长度会减小,即L 减小,使得波长 $ \lambda $
基于不排水强度的黏土基坑抗隆起稳定计算方法
2
2020
... MMSD法采用的塑性变形机制位移场建立在如图4 所示的Terzaghi模式[21 ] 的基础上,而该破坏模式被认为更加适用于宽浅的基坑[22 ] . 此外,MMSD法采用式(2)来确定整个位移场的尺寸,引入能量最小耗散原理,提高了$ 1.0 < \alpha < 2.0 $ $ \alpha $ $ 1.0 < \alpha < 2.0) $ $ \alpha $ 图5 所示,随着基坑开挖的进行,最低一道支撑以下的围护结构长度会减小,即L 减小,使得波长 $ \lambda $
... 事实上,Terzaghi模式和圆弧滑动模式均属于地基隆起破坏上限分析的容许运动速度场,采用不同的模式进行上限分析. 当假设的模式更符合实际工程情况时,计算的上限解更准确. Hsieh等[23 ] 使用圆弧滑动法对软土地区基坑隆起进行分析,中国、日本规范采用基于圆弧滑动模式的极限平衡法. 近些年,王洪新等[24 -25 ] 从不同的角度出发,改进了圆弧滑动法,均取得了不错的效果;黄茂松等[22 ,26 ] 提出基于不排水强度的圆弧机构上限分析方法,通过实际工程验证,认为该方法能够更加合理地评价不排水软黏土基坑的抗隆起稳定性. ...
基于不排水强度的黏土基坑抗隆起稳定计算方法
2
2020
... MMSD法采用的塑性变形机制位移场建立在如图4 所示的Terzaghi模式[21 ] 的基础上,而该破坏模式被认为更加适用于宽浅的基坑[22 ] . 此外,MMSD法采用式(2)来确定整个位移场的尺寸,引入能量最小耗散原理,提高了$ 1.0 < \alpha < 2.0 $ $ \alpha $ $ 1.0 < \alpha < 2.0) $ $ \alpha $ 图5 所示,随着基坑开挖的进行,最低一道支撑以下的围护结构长度会减小,即L 减小,使得波长 $ \lambda $
... 事实上,Terzaghi模式和圆弧滑动模式均属于地基隆起破坏上限分析的容许运动速度场,采用不同的模式进行上限分析. 当假设的模式更符合实际工程情况时,计算的上限解更准确. Hsieh等[23 ] 使用圆弧滑动法对软土地区基坑隆起进行分析,中国、日本规范采用基于圆弧滑动模式的极限平衡法. 近些年,王洪新等[24 -25 ] 从不同的角度出发,改进了圆弧滑动法,均取得了不错的效果;黄茂松等[22 ,26 ] 提出基于不排水强度的圆弧机构上限分析方法,通过实际工程验证,认为该方法能够更加合理地评价不排水软黏土基坑的抗隆起稳定性. ...
Basal heave analysis of excavations with consideration of anisotropic undrained strength of clay
1
2008
... 事实上,Terzaghi模式和圆弧滑动模式均属于地基隆起破坏上限分析的容许运动速度场,采用不同的模式进行上限分析. 当假设的模式更符合实际工程情况时,计算的上限解更准确. Hsieh等[23 ] 使用圆弧滑动法对软土地区基坑隆起进行分析,中国、日本规范采用基于圆弧滑动模式的极限平衡法. 近些年,王洪新等[24 -25 ] 从不同的角度出发,改进了圆弧滑动法,均取得了不错的效果;黄茂松等[22 ,26 ] 提出基于不排水强度的圆弧机构上限分析方法,通过实际工程验证,认为该方法能够更加合理地评价不排水软黏土基坑的抗隆起稳定性. ...
基坑的尺寸效应及考虑开挖宽度的抗隆起稳定安全系数计算方法
1
2016
... 事实上,Terzaghi模式和圆弧滑动模式均属于地基隆起破坏上限分析的容许运动速度场,采用不同的模式进行上限分析. 当假设的模式更符合实际工程情况时,计算的上限解更准确. Hsieh等[23 ] 使用圆弧滑动法对软土地区基坑隆起进行分析,中国、日本规范采用基于圆弧滑动模式的极限平衡法. 近些年,王洪新等[24 -25 ] 从不同的角度出发,改进了圆弧滑动法,均取得了不错的效果;黄茂松等[22 ,26 ] 提出基于不排水强度的圆弧机构上限分析方法,通过实际工程验证,认为该方法能够更加合理地评价不排水软黏土基坑的抗隆起稳定性. ...
基坑的尺寸效应及考虑开挖宽度的抗隆起稳定安全系数计算方法
1
2016
... 事实上,Terzaghi模式和圆弧滑动模式均属于地基隆起破坏上限分析的容许运动速度场,采用不同的模式进行上限分析. 当假设的模式更符合实际工程情况时,计算的上限解更准确. Hsieh等[23 ] 使用圆弧滑动法对软土地区基坑隆起进行分析,中国、日本规范采用基于圆弧滑动模式的极限平衡法. 近些年,王洪新等[24 -25 ] 从不同的角度出发,改进了圆弧滑动法,均取得了不错的效果;黄茂松等[22 ,26 ] 提出基于不排水强度的圆弧机构上限分析方法,通过实际工程验证,认为该方法能够更加合理地评价不排水软黏土基坑的抗隆起稳定性. ...
各向异性软土基坑抗隆起稳定极限平衡分析
1
2019
... 事实上,Terzaghi模式和圆弧滑动模式均属于地基隆起破坏上限分析的容许运动速度场,采用不同的模式进行上限分析. 当假设的模式更符合实际工程情况时,计算的上限解更准确. Hsieh等[23 ] 使用圆弧滑动法对软土地区基坑隆起进行分析,中国、日本规范采用基于圆弧滑动模式的极限平衡法. 近些年,王洪新等[24 -25 ] 从不同的角度出发,改进了圆弧滑动法,均取得了不错的效果;黄茂松等[22 ,26 ] 提出基于不排水强度的圆弧机构上限分析方法,通过实际工程验证,认为该方法能够更加合理地评价不排水软黏土基坑的抗隆起稳定性. ...
各向异性软土基坑抗隆起稳定极限平衡分析
1
2019
... 事实上,Terzaghi模式和圆弧滑动模式均属于地基隆起破坏上限分析的容许运动速度场,采用不同的模式进行上限分析. 当假设的模式更符合实际工程情况时,计算的上限解更准确. Hsieh等[23 ] 使用圆弧滑动法对软土地区基坑隆起进行分析,中国、日本规范采用基于圆弧滑动模式的极限平衡法. 近些年,王洪新等[24 -25 ] 从不同的角度出发,改进了圆弧滑动法,均取得了不错的效果;黄茂松等[22 ,26 ] 提出基于不排水强度的圆弧机构上限分析方法,通过实际工程验证,认为该方法能够更加合理地评价不排水软黏土基坑的抗隆起稳定性. ...
Basal stability analysis of braced excavations with embedded walls in undrained clay using the upper bound theorem
1
2018
... 事实上,Terzaghi模式和圆弧滑动模式均属于地基隆起破坏上限分析的容许运动速度场,采用不同的模式进行上限分析. 当假设的模式更符合实际工程情况时,计算的上限解更准确. Hsieh等[23 ] 使用圆弧滑动法对软土地区基坑隆起进行分析,中国、日本规范采用基于圆弧滑动模式的极限平衡法. 近些年,王洪新等[24 -25 ] 从不同的角度出发,改进了圆弧滑动法,均取得了不错的效果;黄茂松等[22 ,26 ] 提出基于不排水强度的圆弧机构上限分析方法,通过实际工程验证,认为该方法能够更加合理地评价不排水软黏土基坑的抗隆起稳定性. ...
Shape of ground surface settlement profiles caused by excavation
1
1998
... 确定基坑变形位移场的影响范围是基坑塑性变形机制的基础. 在Osman等[15 , 27 -28 ] 的研究中,将开挖深度作为预测开挖影响范围的唯一参数. 此外,大多数经验方法都是假定软土中开挖的沉降影响区约等于开挖深度的2倍. Ou等[29 ] 研究发现,前述方法不具备普遍性,无法兼顾不同基坑形状和土层特性. Ou等[29 ] 采用有限元参数研究结果和稳定机理,提出凹形沉降剖面的沉降影响区,在与实际案例的对比中验证良好. 本文在Ou等[29 ] 的研究成果基础上,提出与MMSD法相适配的位移场影响范围确定方法. ...
Simplified model for wall deflection and ground-surface settlement caused by braced excavation in clays
1
2007
... 确定基坑变形位移场的影响范围是基坑塑性变形机制的基础. 在Osman等[15 , 27 -28 ] 的研究中,将开挖深度作为预测开挖影响范围的唯一参数. 此外,大多数经验方法都是假定软土中开挖的沉降影响区约等于开挖深度的2倍. Ou等[29 ] 研究发现,前述方法不具备普遍性,无法兼顾不同基坑形状和土层特性. Ou等[29 ] 采用有限元参数研究结果和稳定机理,提出凹形沉降剖面的沉降影响区,在与实际案例的对比中验证良好. 本文在Ou等[29 ] 的研究成果基础上,提出与MMSD法相适配的位移场影响范围确定方法. ...
A simplified method for predicting ground settlement profiles induced by excavation in soft clay
4
2011
... 确定基坑变形位移场的影响范围是基坑塑性变形机制的基础. 在Osman等[15 , 27 -28 ] 的研究中,将开挖深度作为预测开挖影响范围的唯一参数. 此外,大多数经验方法都是假定软土中开挖的沉降影响区约等于开挖深度的2倍. Ou等[29 ] 研究发现,前述方法不具备普遍性,无法兼顾不同基坑形状和土层特性. Ou等[29 ] 采用有限元参数研究结果和稳定机理,提出凹形沉降剖面的沉降影响区,在与实际案例的对比中验证良好. 本文在Ou等[29 ] 的研究成果基础上,提出与MMSD法相适配的位移场影响范围确定方法. ...
... [29 ]采用有限元参数研究结果和稳定机理,提出凹形沉降剖面的沉降影响区,在与实际案例的对比中验证良好. 本文在Ou等[29 ] 的研究成果基础上,提出与MMSD法相适配的位移场影响范围确定方法. ...
... [29 ]的研究成果基础上,提出与MMSD法相适配的位移场影响范围确定方法. ...
... 在确定了基坑开挖位移场和影响范围后,增量位移曲线随之变化. MMSD法对原MSD法中增量位移曲线的改进较合理,保留MMSD法中的增量位移曲线为指数族函数的形式,将围护墙增量位移最值点深度修正为$ \lambda /3 $ [29 ] . 以最低一道支撑端点为坐标原点,竖直向上为纵坐标方向,水平指向坑内为横坐标方向,修正后的增量位移曲线为 ...
Characteristics of wall deflections and ground surface settlements in Shanghai
1
2005
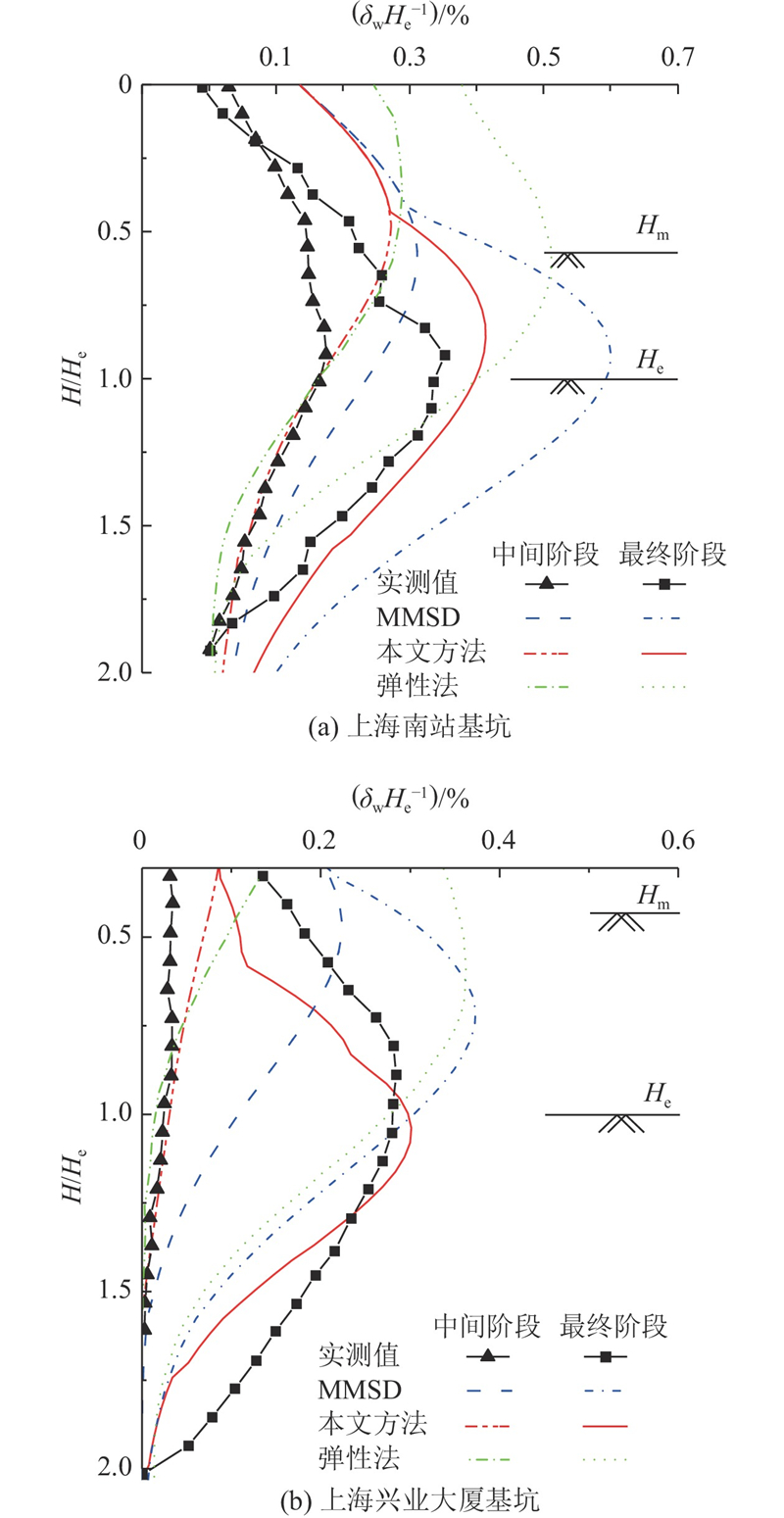
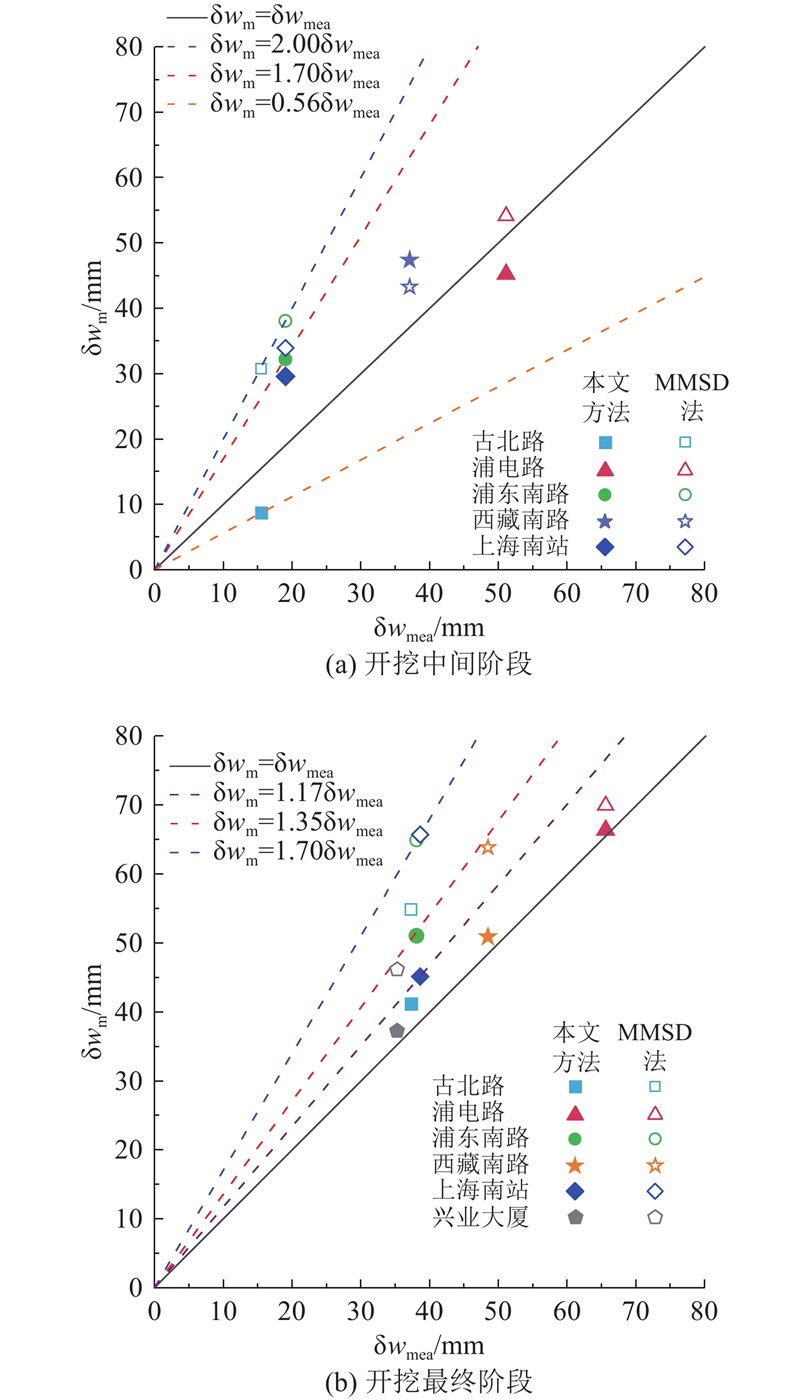
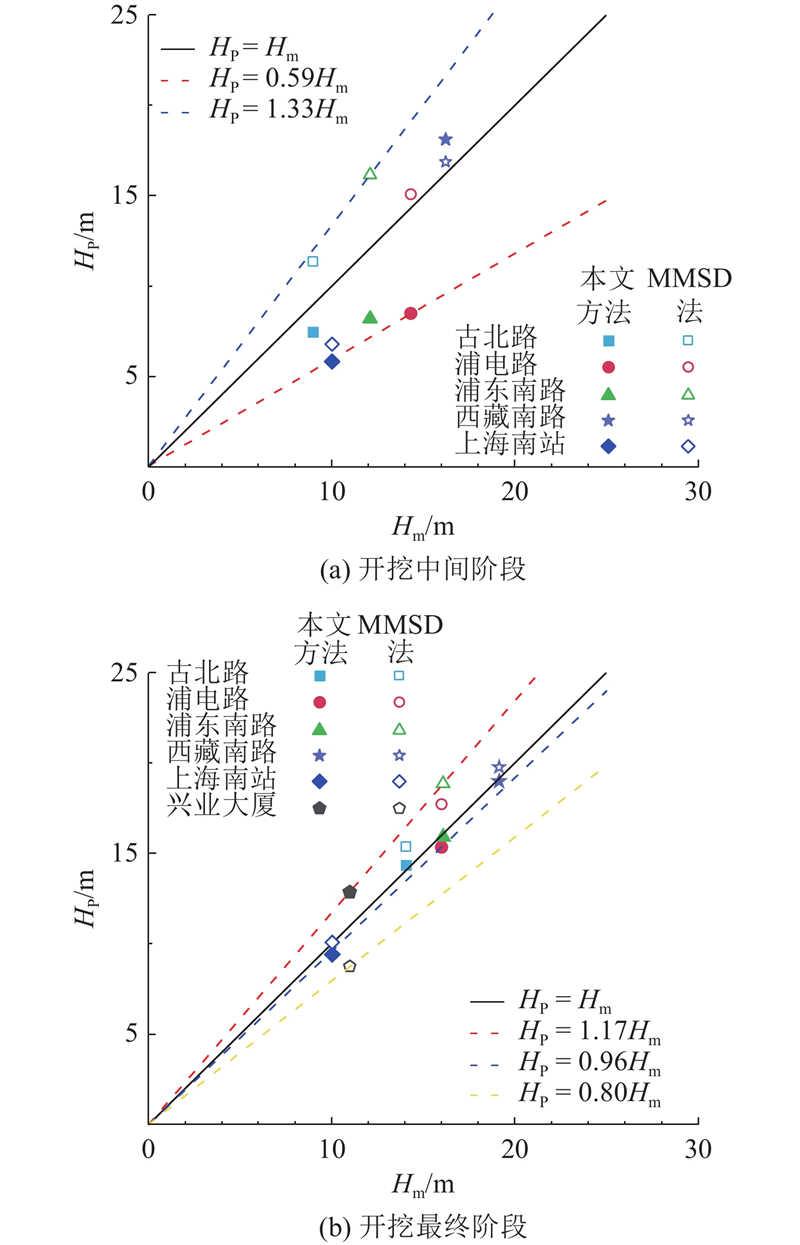
... 基坑开挖案例来自上海软黏土中6个有完整记录的深基坑工程[30 -32 ] ,对比MMSD法预测值、本文方法预测值及工程实测值,验证本文方法的准确性. ...
Ground deformations and soil–structure interaction of a multi-propped excavation in Shanghai soft clays
1
2012
... 基坑开挖案例来自上海软黏土中6个有完整记录的深基坑工程[30 -32 ] ,对比MMSD法预测值、本文方法预测值及工程实测值,验证本文方法的准确性. ...
1
... 对于强度动员率$ \beta $ [17 ] . 本节的6个工程案例均来自上海地区,但每个工程案例都缺少详细的原位土体应力应变数据,因此采用上海地区已有的土体数据代替,如图12 所示. 图12 给出上海黏土强度动员率与动员切应变之间的关系,这些数据来自Li[33 ] 的不排水三轴试验和Wang等[18 ] 的简单直接剪切试验,试验土样均来自上海软土地区的基坑工程. 3条实测的黏土强度动员率曲线表现出非常相似的趋势,说明上海黏土有着良好的均匀性,因此采用这些数据对本文案例进行计算是可行的. 利用幂函数对实测数据进行拟合,可得强度动员率与动员切应变之间的关系: ...