浙江大学学报(工学版)

浙江大学学报(工学版), 2024, 58(2): 399-412 doi: 10.3785/j.issn.1008-973X.2024.02.018

交通工程、土木工程

轻型组合桥梁负弯矩区接缝抗弯性能试验

邓舒文,, 邵旭东,, 晏班夫, 邱明红

1. 湖南农业大学 水利与土木工程学院，湖南 长沙 410125

2. 湖南大学 土木工程学院，湖南 长沙 410082

3. 广西大学 土木建筑工程学院，广西 南宁 530004

4. 香港大学 土木工程系，香港 999077

Experiment on flexure behavior of joint in negative moment area of lightweight composite bridge

DENG Shuwen,, SHAO Xudong,, YAN Banfu, QIU Minghong

1. College of Water Resources and Civil Engineering, Hunan Agricultural University, Changsha 410125, China

2. College of Civil Engineering, Hunan University, Changsha 410082, China

3. School of Civil Engineering and Architectural, Guangxi University, Nanning 530004, China

4. Department of Civil Engineering, University of Hong Kong, Hong Kong 999077, China

通讯作者: 邵旭东，男，教授. orcid.org/0000-0002-4092-0077. E-mail: shaoxd@hnu.edu.cn

收稿日期: 2023-02-23  

基金资助: 国家自然科学基金资助项目 (52108211)；湖南省自然科学基金资助项目 (2022JJ40186)；湖南省教育厅资助项目 (21B0188)

Received: 2023-02-23  

Fund supported: 国家自然科学基金资助项目(52108211)；湖南省自然科学基金资助项目(2022JJ40186)；湖南省教育厅资助项目(21B0188)

作者简介 About authors

邓舒文（1988—），女，博士后，从事超高性能混凝土桥梁结构的研究.orcid.org/0009-0008-5087-3834.E-mail：dengsw@hunau.edu.cn , E-mail：dengsw@hunau.edu.cn

摘要

对适用于轻型组合桥梁负弯矩区的T形横向接缝抗弯性能进行试验研究，对负弯矩加载接缝的全过程进行理论分析，对接缝设计参数进行讨论. 研究结果表明，随着荷载的增大，试件的主裂缝出现在连续浇筑的UHPC接缝界面和加载点下方的面板表面，试件中部未发现明显裂纹，UHPC接缝界面的可视初裂强度可以满足实桥设计荷载. 对试验梁进行分析，提出接缝最大裂缝宽度、考虑UHPC拉伸刚度效应的设计弯矩和挠度计算公式，获得每阶段承载力的计算式，预测结果与试验结果吻合良好. 通过参数讨论和计算可知，跨度L = 20~50 m的轻型组合桥梁T形接缝上部加长长度可以设置为0.1L.

关键词： 超高性能混凝土(UHPC) ; UHPC接缝 ; 抗弯性能试验 ; 裂缝宽度计算式 ; 挠度计算式 ; 极限承载力计算式

Abstract

Experimental research was conducted on the flexural performance of T-shaped transverse joints suitable for the negative bending moment area of lightweight composite bridges. A theoretical analysis of the entire process of applying negative bending moments was conducted, and the design parameters for the joint were discussed. Results show that the primary crack in the specimens appears at the interface of the continuously cast UHPC joint and the panel surface below the loading point as the load increases. No significant cracks were observed in the middle of the specimens, and the visual initial crack strength of the UHPC joint interface can meet the design loads of real bridges. An analysis of the test beam was conducted, and formulas for calculating the maximum crack width of the joint, the design bending moment considering the effect of UHPC tensile stiffness, and deflection were proposed. Formulas for calculating the bearing capacity at each stage were obtained, and the predicted results accorded well with the experimental results. Parameter discussions and calculations show that the upper extended length of T-shaped joint in lightweight composite bridges with spans ranging from 20 m to 50 m can be set to 0.1 times of spans.

Keywords： ultra high performance concrete (UHPC) ; UHPC joint ; bending resistance test ; calculation formula of crack width ; calculation formula of deflection ; calculation formula of ultimate bearing capacity

PDF (5099KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

邓舒文, 邵旭东, 晏班夫, 邱明红. 轻型组合桥梁负弯矩区接缝抗弯性能试验. 浙江大学学报(工学版)[J], 2024, 58(2): 399-412 doi:10.3785/j.issn.1008-973X.2024.02.018

DENG Shuwen, SHAO Xudong, YAN Banfu, QIU Minghong. Experiment on flexure behavior of joint in negative moment area of lightweight composite bridge. Journal of Zhejiang University(Engineering Science)[J], 2024, 58(2): 399-412 doi:10.3785/j.issn.1008-973X.2024.02.018

预制装配式桥梁结构是实现桥梁建筑工业化的重要途径[1]. 传统装配式桥梁结构饱受以下两大难题的困扰. 1）采用普通混凝土材料的桥梁结构在使用过程中极易开裂，从而导致废水内侵，引发耐久性难题[2-3]. 2）虽然梁体可在工厂内预制，但现场仍需进行焊接拼装、安装预应力、浇筑湿接缝等工序，现场施工时间长，给交通环境带来了极大的困扰. 上述问题严重降低了桥梁的营运效率，在我国重载交通量日益增大的情况下，解决上述问题的需求尤为迫切.

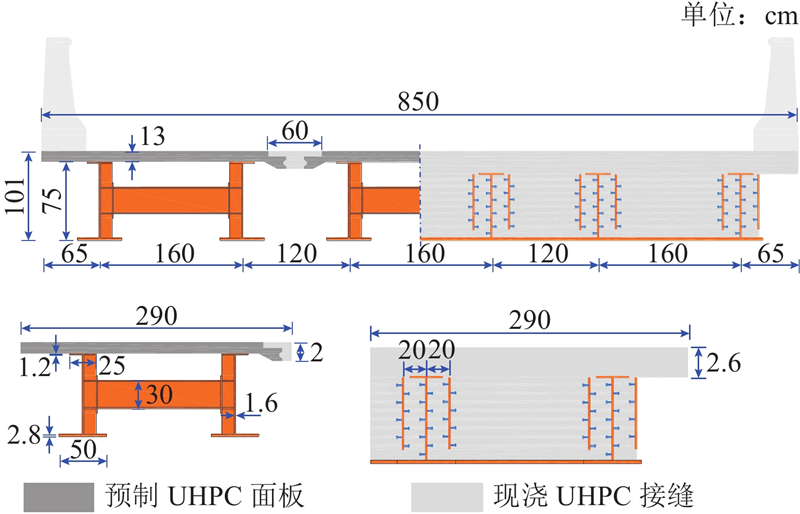
针对以上难题，将高强、高韧及高耐久的超高性能混凝土（ultra-high performance concrete，UHPC）引入中小跨径预制装配式桥梁建设中，形成新型的全预制钢-UHPC轻型组合桥梁结构（以下简称“轻型组合桥梁结构”）. 轻型组合桥梁由多个整体预制的钢-UHPC轻型组合梁单元沿纵横向拼接而成，施工过程主要包括：在工厂内制作轻型组合梁单元；拖运至施工现场吊装就位；铺设接缝连接钢筋（无须焊接和绑扎）；浇筑接缝处UHPC；完成施工.

与同等跨径和技术标准的传统预制装配式桥梁结构相比，轻型组合桥梁可以在初始造价基本持平（约3 900元/m2）的情况下，极大程度地降低结构自重（减少45%~65%）和梁体高度（减少19%~26%）[4]. 较轻的自重可以采用现有设备和技术，实现整跨运输和吊装；较低的梁高可以缩短引桥长度、降低桥墩高度，在高速公路跨线、多层城市高架的桥梁选型时拥有巨大的经济优势. 此外，轻型组合桥梁优异的耐久性能使得其后期维护费用将远低于传统方案. 从长远使用性能的角度考虑，轻型组合桥梁在经济性、施工性及耐久性方面具有明显优势.

对于预制装配式连续桥梁而言，负弯矩区接缝是结构的薄弱环节. 目前，有较多学者对UHPC作为接缝材料的可行性进行研究，主要包括大跨径钢桥面纵横接缝以及中小跨径桥梁面板间纵向接缝. 对于适用于大跨径钢桥面的接缝研究，通常考察不同接缝形式、底部异型钢板加强、焊接钢筋网等对接缝传力性能和传力效率的影响[5-14]. 对于中小跨径桥梁面板间纵向接缝的研究，通常考察不同接缝形式、界面处理方式、内部钢筋配置方法等对接缝抗裂性能和破坏模式的影响[15-25].

针对梁间负弯矩区的横向接缝的研究较少，特别是针对中小跨径钢-UHPC组合桥梁负弯矩区节点的设计研究目前暂未见到. 本文基于我国第一座中小跨径全预制钢UHPC轻型组合桥梁-麻浦停车区行车天桥，研究设置在桥墩顶部的T形梁间接缝，其抗弯性能试验、理论分析及参数讨论将在以下部分展示.

1. 工程背景

麻浦行车天桥为国内第一座中小跨径全预制钢-UHPC轻型组合桥梁（fully precast steel-UHPC lightweight composite bridge, SU-LWCB），位于广东省惠州市和清远市之间，如图1所示. 桥梁采用全预制钢-UHPC组合梁，总跨径为4 m×25 m，单幅横向布置三榀钢-UHPC轻型组合梁单元，全桥共计12榀. 每榀梁单元采用整体预制、整体运输、整体吊装就位. 桥梁的横截面如图2所示，组合梁单元高为101 cm，其中UHPC桥面板厚为13 cm，工字梁高为88 cm，二者通过剪力钉连接.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   麻浦行车天桥

Fig.1   Mapu Bridge overview


图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   麻浦行车天桥标准横断面

Fig.2   Cross section of Mapu Bridge


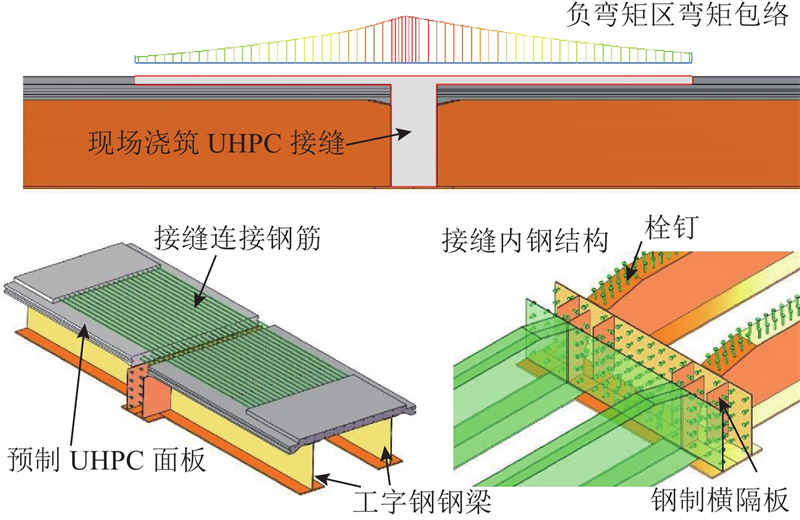
轻型组合桥梁两跨之间设计上部加长的T形横向接缝，如图3所示. 该设计可以将薄弱的、先后浇筑的界面移动至距离拉应力峰值较远处，显著降低接缝界面开裂的风险.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   现浇负弯矩区接缝结构的示意图

Fig.3   Schematic of cast-in-place joint in negative bending moment area


1.1. 技术经济对比

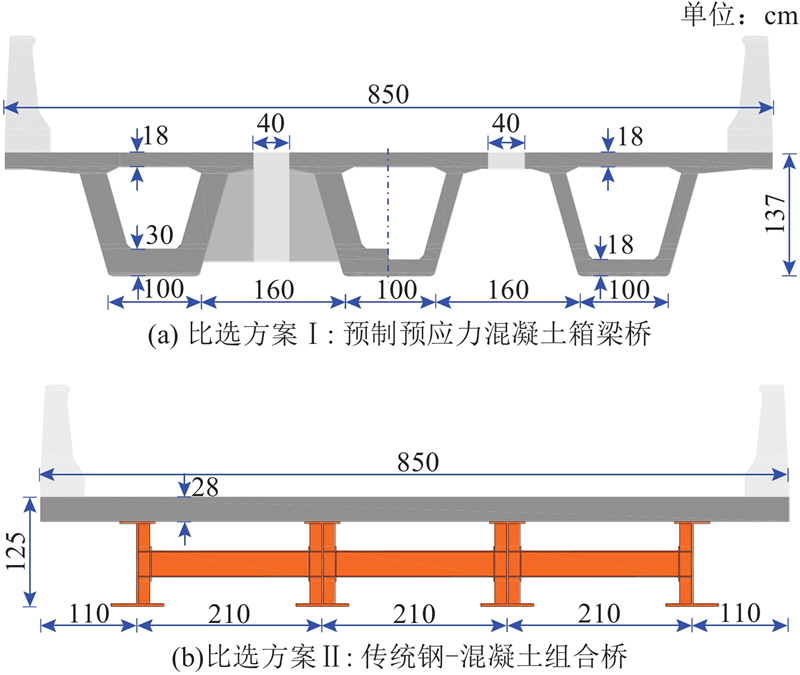
对相同跨度、相同技术标准的中小跨径装配式桥梁进行经济性能分析. 比较桥梁包括（I）预制预应力混凝土箱梁桥（见图4(a)）、（II）传统钢-混凝土组合桥（见图4(b)）和（III）SU-LWCB的现有设计（见图3）. 经济比较结果如表1所示[4]. 表中，V为单位面积上的材料体积，m为单位面积上的材料质量. 上部结构（下部结构）钢筋普通混凝土施工总价为3000（2200）元/m3，加固UHPC为9000元/m3，预应力筋为15000元/t，钢梁为10000元/t；桩基Φ1.5 m（Φ1.2 m）为5000（3300）元/m；运输和吊装为150元/t. 第Ⅰ种方案桩基采用204 mΦ1.5 m，价格是1200 元/m2；第Ⅱ种方案桩基采用204 mΦ1.2 m，价格是800元/m2；第Ⅲ种方案桩基采用204 mΦ1.2 m，价格是800元/m2.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   经济性能的比较方案

Fig.4   Comparison schemes of economic performance


表 1   不同桥梁方案的经济性能比较

Tab.1  Comparison of economic performance between different schemes

桥梁方案方案I方案II方案III
V/m3m/kg价格/
(元·m−2)		V/m3m/kg价格/
(元·m−2) 		V/m3m/kg价格/
(元·m−2)
上部结构C50或UHPC0.44—13200.28—8400.126—1130
预应力钢筋—18.3275——————
钢梁————1901900—1501500
铺装层0.11—200——————
运输吊装费—1200180—920140—50075
下部结构桥墩、盖梁和系梁0.23—505 0.18—400 0.18—400

新窗口打开| 下载CSV


从图2、4及表1可知，当采用相同跨径和技术标准时，三者梁高分别为1.37、1.25和1.01 m，SU-LWCB为其余二者的74%和81%；三者吊装质量分别为1 200、920和500 kg，SU-LWCB仅为其余二者的42%和54%；综合单价分别为3 680、4 080及3 905元，三者基本持平，考虑到UHPC的优异耐久性，当前设计的维护成本将低于传统设计，全寿命造价远低于传统方案. SU-LWCB上部结构轻盈，工厂化制造、装配化施工，现场作业量少，可以实现主梁一次成型、整体运输和整体吊装. UHPC超强的耐久性可以极大程度地降低后期维护费用，进而降低桥梁全寿命造价. 较低的梁体可以适应严苛的桥梁净空要求，整体架设的方案可以极大程度地减少对桥下现有交通的干扰，在高速公路跨线桥和城市桥梁方面具有广阔的应用前景，因此SU-LWCB方案拥有巨大的推广应用潜力.

1.2. 设计荷载计算

采用Midas Civil建立梁单元模型，获得麻浦行车天桥的设计荷载. 模型共计1 889个梁单元和2 270个节点，包含全部的梁段和约束. 其中钢筋、钢梁及UHPC面板均视为理想弹性，忽略UHPC面板及钢材之间的滑移作用，桥面铺装层仅作恒载考虑. 有限元模型按照实际约束的方式考虑，单个支点采用点约束形式施加于支座位置. 除桥梁自重外，施加的荷载包括二期恒载（铺装及护栏）、支座沉降、收缩徐变[26]、温度作用及汽车荷载作用.

计算中，UHPC和钢材均设置为理想线弹性材料. 其中，UHPC材料的弹性模量和泊松比分别为42.6 GPa和0.19，材料的徐变系数参考法国UHPC结构技术规程中建议的数据（未采用热养护的部分，徐变系数 ϕ = 0.8；采用温度高于90 ℃的热养护处理时，ϕ = 0.2）. 钢材参考规范[27]中的建议值206 GPa和0.3.

按照实际的施工过程，桥梁设计荷载的施加分为以下2个阶段. 第1阶段为简支梁阶段，即将单片的钢-UHPC轻型组合梁单元架设至施工位置，此时梁体仅承受自身的质量. 第2阶段为完成纵横向接缝、桥面铺装、桥梁护栏等工序，施加桥梁使用阶段荷载的阶段. 由此得到桥梁使用阶段的设计应力，如表2所示. 表中， “+”表示拉应力，“−”表示压应力.

表 2   桥梁使用阶段的设计应力

Tab.2  Design stress of bridge in service stage

项目应力/MPa位置
UHPC面板11.69墩顶
UHPC面板−20.75边跨跨中
UHPC面板5.28接缝界面
工字钢186.75边跨跨中下缘
工字钢−95.2墩顶钢板下缘

新窗口打开| 下载CSV


表2中，工字钢梁的最大设计应力为186.75 MPa，桥梁采用Q345钢材，根据规范[28]可知，屈服强度为345 MPa，因此工字钢梁的设计可以满足桥梁的使用需求. 对于UHPC材料而言，抗压强度一般大于120 MPa[29-30]，设计压应力计算值（−20.75 MPa）远小于UHPC的抗压强度. 表1中，最大拉应力设计值为11.69 MPa，大于常规UHPC材料的抗拉强度（6.67~7.91 MPa）[28]. 将UHPC应用在墩顶负弯矩区，需要进行验证和讨论.

2. 试验介绍

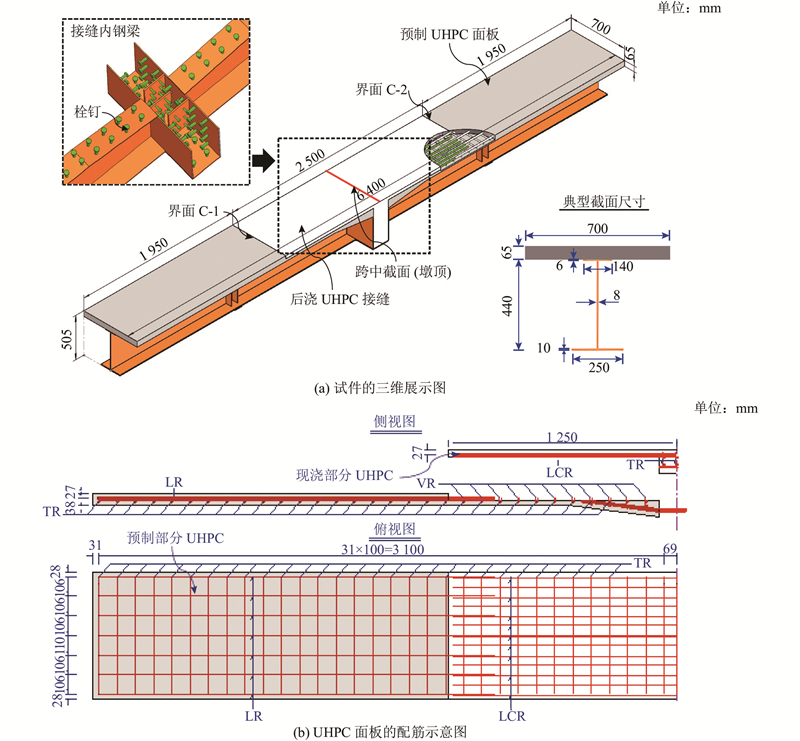
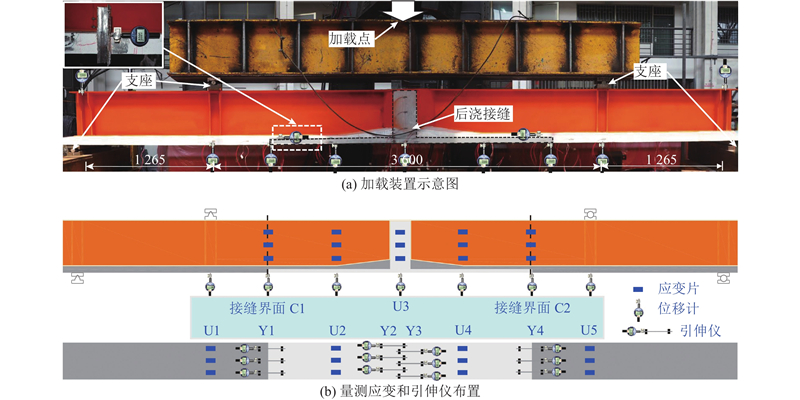
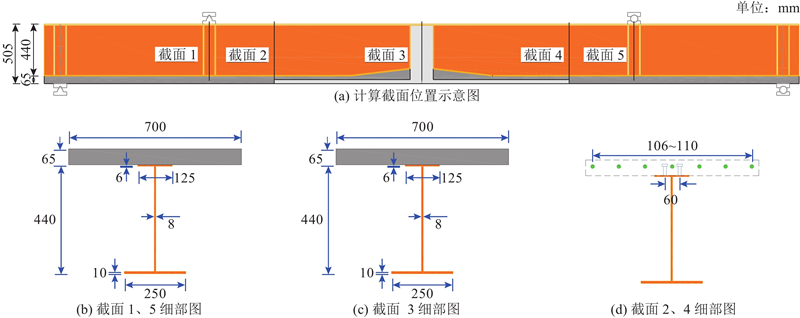
试验模型如图5所示. 试验梁设计为原桥横断面1/2尺寸的单T形模型，其中UHPC面板宽0.7 m，厚0.065 m，下部钢梁高0.44 m，截取两侧的预制钢-UHPC组合梁段及中间现浇接缝段3部分共6.4 m长试验段. 试验梁中先浇的UHPC面板内配置7根直径为16 mm的纵向钢筋，后浇接缝部分加密至13根，横向采用直径为12 mm的钢筋，间距为100 mm，如图5(b)所示，其中“LR”和“LCR”分别表示接头部分的纵向钢筋和纵向连接钢筋，它们的直径都是16 mm. “TR”为直径为12 mm的横向钢筋， “VR”是指直径为8 mm的竖向绑扎钢筋. 预制部分的纵向钢筋与现浇接缝部分的连接钢筋之间采用搭接，搭接重合段长度为225 mm. 钢结构部分采用Q345钢材焊接而成，桥面板与钢结构之间采用栓钉连接. 为了防止加载点局部失稳，试件在4个加载点处增设共计16块加劲钢板. 试件的制作流程如下. 1）制作工字钢梁. 2）安装混凝土浇筑模板，布置先浇部分UHPC面板内部钢筋. 3）浇筑预制部分UHPC，浇筑完毕后第26小时开始进行表面凿毛处理. 4）蒸汽养护预制部分UHPC件. 5）后浇T形接头钢筋的配置、浇筑及自然养护处理.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   轻型组合桥梁负弯矩区抗弯性能试验模型的示意图

Fig.5   Schematic of bending test model for negative moment region of lightweight composite bridge


本试验所用的材料主要包括钢纤维、硅灰、石英砂等. 钢纤维体积分数和类型略有不同：蒸汽养护的先浇UHPC面板内掺加体积分数为2.0%的直线型纤维，自然养护的后浇接缝段掺加体积分数为2.5%的混杂（1%直线型+1.5%端钩型）钢纤维. 先浇预制段UHPC浇注完毕后第26 h时，测定立方体试块（100 mm×100 mm×100 mm）的抗压强度为46.34 MPa，随后采用50 MPa高压水枪对预制段T形接缝处表面进行凿毛，经高压水枪凿毛后，试件预浇接缝部分的UHPC表面粗糙如图6所示. 第91 h时开始蒸养，蒸养过程中保持98 ℃高温48 h.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   先浇UHPC面板表面凿毛

Fig.6   Precast UHPC panel surface treatment


两次试件浇注时均同时浇注，力学性能测试用小试件，试件数量、尺寸及测试方法均参考规范[31]，抗压、抗折与弹性模量的测试结果如表3所示. 表中， fc为轴心抗压强度，fcf为抗折强度，E为弹性模量.

表 3   UHPC材料的力学性能

Tab.3  Mechanical property of UHPC materials

材料类型养护方案fc/MPafcf/MPaE/GPa
预制段UHPC蒸汽养护162.3828.7449.03
现浇段UHPC自然养护135.0132.1945.82

新窗口打开| 下载CSV


试件采用MTS控制加载，将试件翻转以施加负弯矩. 在正式试验开始前，开展预加载（0~20 kN），以保证试验装置正常工作，确定加载步长. 正式加载时，初期控制每步位移为0.4 mm，后期逐渐增至每步位移最大为2 mm，期间逐步记录试件的变形、应变及开裂情况. 试件加载及量测装置布置如图7所示.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   试验量测装置布置图示

Fig.7   Diagram of experimental measurement device


3. 试验结果与讨论

3.1. 荷载-位移变化

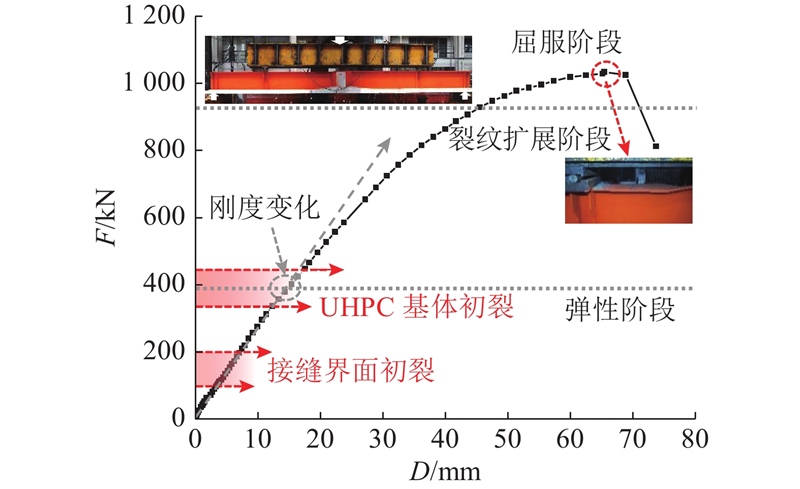
试件的荷载-跨中位移曲线可以分为以下3个主要的阶段（见图8）. 图中，F为荷载，D为跨中位移.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   试验梁的荷载-跨中位移曲线

Fig.8   Load-deflection curve of test beam mid-span


1）弹性阶段. 当荷载为143.5~196.6 kN时，该阶段内接缝界面处裂缝宽度达到名义开裂宽度0.05 mm，但此时曲线未见明显偏转. 当荷载达到336.5~424.5 kN时，先浇蒸养的UHPC面板裂缝宽度达到0.05 mm，在400 kN附近，荷载挠度曲线发生轻微偏转，表明此时结构刚度略微下降. 将该阶段定义为弹性阶段.

2）裂纹扩展阶段. 该阶段定义在424.5 kN~905 kN. 此时，接缝界面裂缝宽度超过0.05 mm，随荷载增加而不断增宽增长，最终形成通长裂缝. 面板其他部分的裂缝逐渐增多，裂缝间距逐渐缩小，基体加载点下方面板表面出现较大裂缝，荷载位移曲线略微偏转，暗示结构刚度略微下降.

3）屈服阶段. 当荷载达到950 kN时，荷载-跨中挠度曲线发生明显的偏转，表明试件的刚度显著下降. 当荷载达到1 033.9 kN时，结构变形迅速增加，但荷载无法继续施加，同时观测到试件加载点附近钢梁下翼缘屈曲，加载结束. 该阶段被定义为屈服阶段.

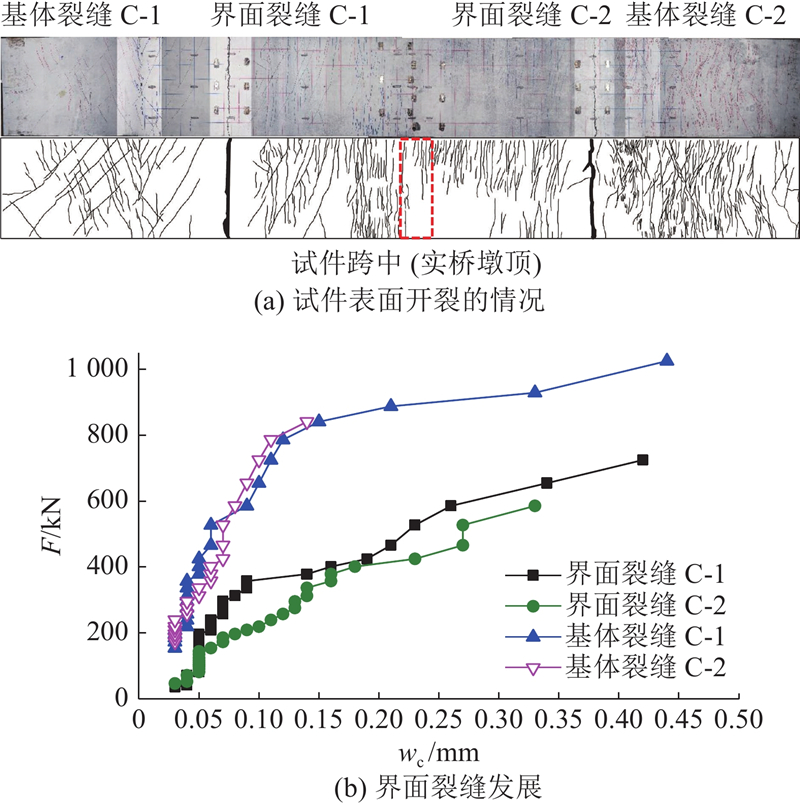
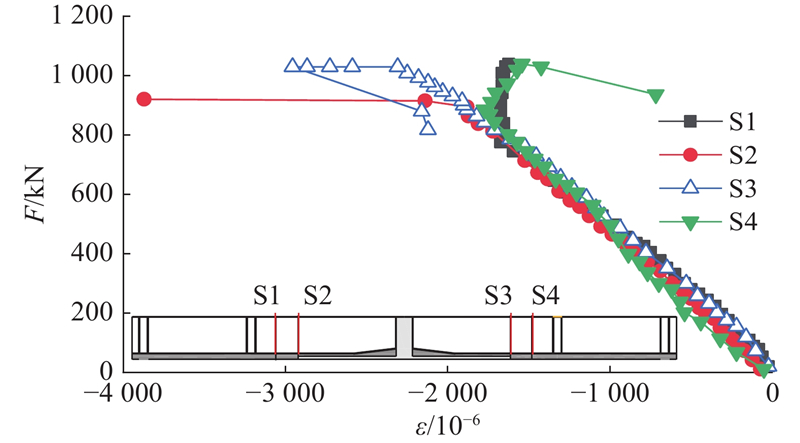
3.2. 裂缝宽度的变化

图9中，wc为裂缝宽度. 如图9所示，在试件加载过程中，随着荷载的施加，试件左、右两侧界面处分别在35.2 kN和46.7 kN时观测到第1条裂缝，定义为界面裂缝C-1和C-2. 随后裂缝宽度逐渐增长，直至81.2 kN，接缝界面裂缝宽度达到0.05 mm，左、右两侧界面裂缝分别在196.6 kN和143.5 kN时达到0.05 mm的最后一级. 当荷载达到153.8 kN和172.7 kN时，在UHPC基体上发现裂缝，此时裂缝宽度为0.03 mm. 当荷载增加至312.3 kN时，基体裂缝达到0.05 mm，位于加载点下方.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   试件接缝界面的裂缝发展

Fig.9   Crack development of specimen joint interface


随着荷载的继续增长，UHPC表面出现众多密集的细小裂缝，但主裂缝逐渐显现，即图9(a)所示的界面裂缝C-1和C-2，同时观测到加载点下方的UHPC预制面板部分出现较大裂缝，记为基体裂缝 C-1和C-2. 将这4条裂缝的宽度发展绘制于图9(b)，可见接缝界面处裂缝发展明显快于基体处，当基体处裂缝宽度小于0.1 mm时，裂缝宽度的扩展速度较缓慢.

如图10所示为3种不同基体的开裂特性. 如图10(a)所示为接缝界面处裂缝的情况. 可见，内钢纤维数量较少，呈乱向分布，纤维数量明显少于基体裂缝（见图10(b)）. 图10(b)中，基体裂缝中纤维相对较多，基本呈纵向分布特征，有利于抵抗拉力. 图10(c)中，在UHPC抗折试件破坏的裂缝中可以观察到更多的纤维，纤维具有显著的纵向分布特征. 由此可以看出：1）在接缝界面处，纤维相对较少且分布不规则，导致强度低于UHPC基体；2）UHPC基体内布置钢筋会使纤维分布不均匀，可能导致初始开裂强度低于素UHPC.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   不同基体上的裂缝形态

Fig.10   Crack patterns of different substrates


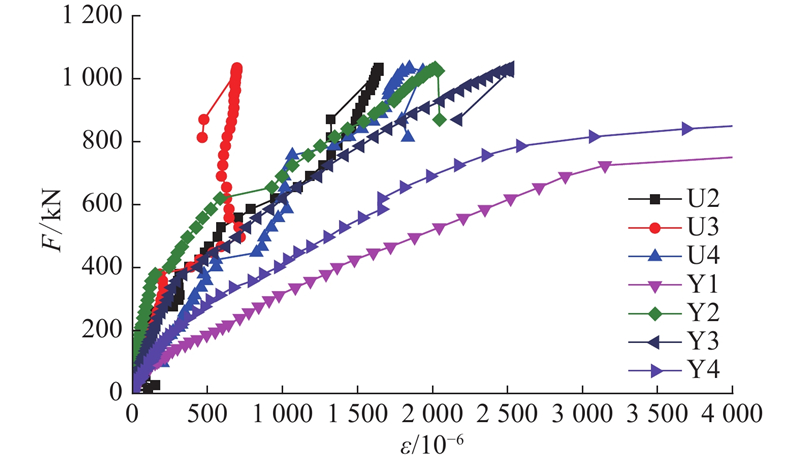
3.3. 应变发展

3.3.1. UHPC面板表面应变的变化

因UHPC表面分布有密集裂缝，无法展示所有应变片的测试结果，选择几个典型的截面应变平均值. 应变数值仅展示小于3×10−3的部分，将引伸仪测试的结果换算为应变一同展示.

如图11所示为UHPC表面应变的发展情况，其中应变截面位置可以参见图6. 图中，ε为应变. 从图11可见，接缝界面处（Y1、Y4）应变在同等荷载时大于基体处. 当接缝界面裂缝宽度达到0.05 mm时，应变为1.15×10−4~5.50×10−4（左侧界面C-1）、1.00×10−4~1.75×10−4（右侧界面C-2），远小于UHPC基体（7.65×10−4~1.267 ×10−3）[28]. 位于试件中部（对应实桥墩顶位置）的U3应变始终处于较小的状态.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   UHPC面板表面的应变发展

Fig.11   Strain development of UHPC


3.3.2. 钢结构表面应变的变化

钢结构部分的应变发展曲线如图12所示. 可见，所有测点均处于受压状态. 随着载荷的增加，曲线在782 kN处偏转. 由此可知，钢梁下翼缘在782 kN之前始终保持弹性状态，相应的应变为1.672×10−3~1.908×10−3. 根据规范[27]可知，Q345钢的屈服强度为345 MPa，弹性模量为206 GPa，那么对应的屈服应变为1.675×10−3. 由此可知，工字钢梁下翼缘在782 kN后逐渐屈服.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   钢结构的应变发展曲线

Fig.12   Strain development of steel girders


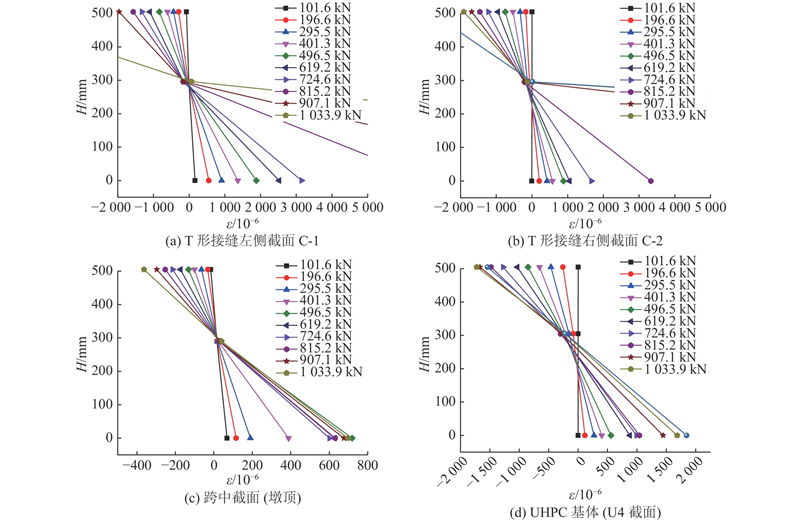
3.3.3. 应变沿高度方向的变化

取试件接缝左右两侧界面处、跨中截面处及UHPC基体处（U4截面），绘制应变沿试件高度方向的发展曲线，如图13所示. 图中，H为高度. 可见，当裂缝宽度小于0.05 mm时（接缝界面裂缝名义开裂荷载为143.5~196.6 kN，UHPC基体名义开裂荷载为336.6~424.5 kN），所有截面几乎均可以符合平截面假定. 这与Luo等[32-33]提出的“当UHPC的最大裂缝宽度达到0.05 mm时，试件仍处于裂纹扩展的早期阶段，当施加荷载达到极限荷载的76.7%~86%时，应变沿截面高度方向的分布仍大致符合平截面假定”这一结论基本相符. 墩顶和基体截面几乎加载全程均可以符合平截面假定.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   应变沿试件高度方向的发展曲线

Fig.13   Strain development curve along with height of specimen


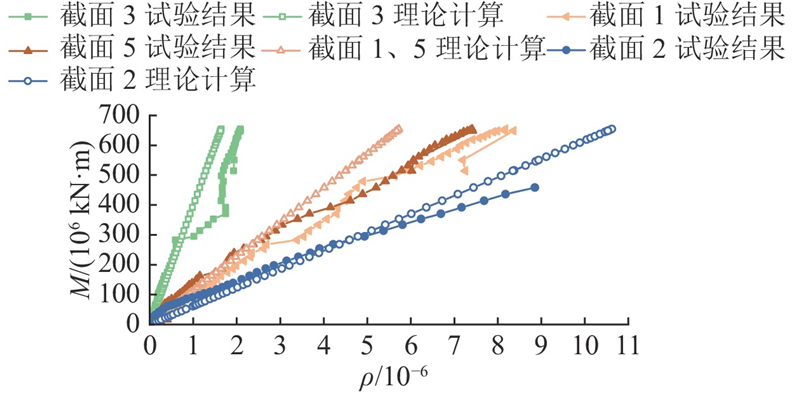
3.3.4. 特征截面弯矩-曲率分析

如图14所示为各截面的弯矩M-曲率ρ与理论值对比图. 可见，结构曲率随着弯矩的增大而逐渐增大，基体预制部分（图15中的截面1、3、5）的曲率增速明显慢于界面位置（截面2、4），其中试件中部（截面3）慢于常规基体（截面1、5），直至加载结束，基体中曲率最大为8.36×10−6.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   弯矩-曲率试验值与理论值的对比

Fig.14   Comparison between experimental and theoretical values of bending moment curvature


理论曲率采用理想弹性的计算方法，与试验值对比的结果表明，接缝界面处的刚度折减较严重. 采用开裂截面（仅计入钢筋与钢梁）进行理论计算，可以较好地拟合试验值. 跨中截面和基体截面分别用对应的实际截面进行理论值的计算，可以较好地拟合试验测试结果.

3.4. 名义开裂应力

名义开裂应力可以根据公式σ=Mdy/(αEI)进行计算，其中Md为施加的外力弯矩，y为截面中和轴到开裂表面的距离，αE=Es/EUHPC, I为截面抗弯惯性矩. 考虑到跨中裂缝宽度极小，计算采用极限荷载1033.9 kN. 计算截面如图15所示，结果见表4. 表中，Pcr为关键截面的开裂荷载，σcr为对应的名义开裂应力. 如表4所示，当裂纹宽度达到0.05 mm时，接缝界面的名义应力为5.40~7.39 MPa，平均值为6.4 MPa. 与表2中的设计应力（5.28 MPa）相比，试验结果可以满足设计要求.

图 15

新窗口打开| 下载原图ZIP| 生成PPT

图 15   计算截面的示意图

Fig.15   Schematic of calculation sections


表 4   关键截面的名义开裂应力

Tab.4  Nominal cracking stress of critical sections

截面编号Pcr/ kNσcr/ MPa
截面1 (UHPC基体)424.515.96
截面2 (接缝界面)196.67.39
截面3 (跨中，墩顶)1033.919.02
截面4 (接缝界面)143.55.40
截面5 (UHPC基体)336.512.66

新窗口打开| 下载CSV


4. 加载全过程分析

将3个阶段进行细分，如图16所示. 试件加载过程可以细分为以下5个阶段. 1）阶段1：UHPC基体在336.6 kN（点2）时达到可视裂缝宽度（可视裂缝宽度定义为0.05 mm），结构发生较明显的刚度变化. 该阶段包含界面达到可视裂缝宽度的荷载点1，但试件刚度未发生明显变化，此时荷载较小，因此将点1归并为阶段1. 2）阶段2：荷载达到782 kN（点3）时钢梁下翼缘屈服，此时结构刚度较阶段1略微下降，试件表面裂缝快速增多. 3）阶段3：当荷载达到815.2 kN（点4）时，UHPC基体达到极限拉应变（7.65×10−4[28]），该阶段非常短，几乎是钢梁下翼缘刚达到屈服强度时，UHPC面板达到极限. 4）阶段4：当荷载达到977.9 kN（点5）时，UHPC面板内钢筋达到屈服强度. 在该阶段，试件刚度迅速下降，主裂缝宽度迅速增大. 5）阶段5：当荷载达到极限时（1 033.9 kN，点6），挠度变大且荷载不再增长，结构屈服，此时两侧加载点附近钢梁下翼缘发生屈曲现象，试验终止.

图 16

新窗口打开| 下载原图ZIP| 生成PPT

图 16   试件加载过程的阶段细分图

Fig.16   Detailed diagram of test piece loading process


4.1. 阶段1：UHPC机体可视初裂

第1阶段定义为试验开始至UHPC基体出现可视裂缝. 在这一阶段中，接缝界面的裂缝宽度在点1达到0.05 mm.

1）接缝试件最大裂缝宽度的预测方法.

Luo等[32-33]对40块钢-UHPC组合板和8块钢-UHPC组合梁进行负弯矩测试. 探讨横向和纵向的开裂特性，基于《混凝土结构设计规范GB 50010—2010》[34]中裂缝宽度的计算公式，提出适用于钢-UHPC轻型组合桥面的裂缝宽度计算公式：

$ {w_{\max }} = {\alpha _{{\rm{cr}}}}\psi \frac{{{\sigma _{\rm{s}}}}}{{{E_{\rm{s}}}}}{l_{{\rm{cr}}}}, $

$ {\alpha _{{\rm{cr}}}}{\text{ = }}{\tau _{\rm{l}}}{\tau _{\rm{s}}}\beta {\alpha _{\rm{c}}}, $

$ {l_{{\rm{cr}}}} = 1.06{c_{\rm{s}}}+0.152\frac{{{d_{{\rm{eq}}}}}}{{{\rho _{{\rm{te}}}}}}, $

$ \psi = 1.1 - 0.12\frac{{{f_{{\rm{tk}}}}}}{{{\rho _{{\rm{te}}}}{\sigma _{\rm{s}}}}}, $

$ {w_{{\rm{s}}\max }} = {w_{\max }}\frac{{h - x}}{{h - x - c}}. $

式中：wmax为钢筋表面的最大裂缝宽度；αcr为构件特征受力系数；σs为UHPC面板内受拉钢筋应力；τl为长期作用的影响系数, 因UHPC材料经过蒸养后收缩为零，因此式（2）可以不考虑该影响；τs为最大裂缝宽度与评价裂缝宽度的比值，反映了裂缝宽度不均匀分布的影响，是一定荷载标准组合下裂缝宽度的不均匀性存在的扩大系数，规范GB 50010—2010中对于轴心受拉和偏心受拉构件建议取τs = 1.9；β为裂缝间距的影响系数，由于钢-UHPC 轻型组合桥面结构的横向和纵向受力特性分别为偏心受拉和轴心受拉，规范GB 50010—2010中规定对于偏心受拉构件和轴心受拉构件β取值分别为1.0和1.1；αc为裂缝间混凝土自身伸长对裂缝宽度的影响系数, 它与配筋率、截面形状和混凝土保护层厚度等因素有关，但在一般情况下，αc变化不大，对裂缝开展宽度的影响也不大，为了简化计算，规范GB 50010—2010中对于受弯、轴心受拉、偏心受力构件均取0.85；lcr为平均裂缝间距；cs为保护层厚度；ρte为有效截面配筋率；deq为纵向钢筋的有效钢筋直径；ftk为混凝土标准轴拉强度；wsmax为UHPC面板表面的最大裂缝宽度；h为组合截面的高度；x为组合截面中性轴至UHPC开裂表面的距离；c为钢筋形心到UHPC表面的距离.

Luo等[32-33]提出的公式适用于钢-UHPC轻型组合桥面结构，而本文提出的轻型组合桥梁略有不同.

对于UHPC基体，由于蒸养后UHPC的收缩徐变极低，因此Luo等[32-33]忽略了τl的影响. 本研究中的接缝由自然养护的后浇接缝与蒸汽养护的先浇UHPC面板组成，因此收缩徐变的特性与全桥面蒸养的钢-UHPC轻型组合桥面不同，该处τl取值参考规范规定的数值1.5.

Luo等 [32-33]指出，由于钢纤维的桥接作用，当计算钢-UHPC组合梁的钢筋应力时，应计入UHPC的抗拉强度. 对于本文连续浇筑的UHPC接缝的界面位置，根据裂缝开裂特征及特征截面曲率分析可知，采用开裂截面计算接缝界面处的钢筋应力更加合适. 预测值与试验值的对比如图17所示.

图 17

新窗口打开| 下载原图ZIP| 生成PPT

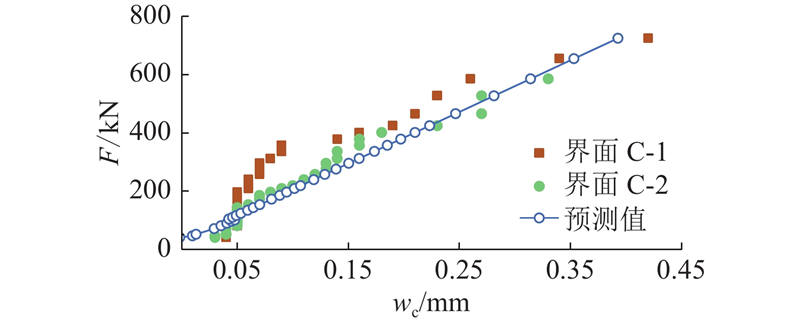
图 17   UHPC表面裂缝宽度理论与预测值的对比

Fig.17   Comparison between theoretical and predicted values of UHPC surface crack width


从图17可见，预测值与试验结果吻合较好. 预测初期与试验值相比略小，原因是式（1）~（5）在计算钢筋应力时忽略了接缝界面的抗拉强度，仅考虑了钢筋和梁组成的开裂截面.

从式（1）~（5）可以看出，裂纹宽度基本取决于钢筋应力. 文献[7, 35]的研究表明，提高配筋率、设置底部加强钢板以及底部为正交异性钢桥面板的方案均以不同形式提高了UHPC面板的受拉钢筋配筋率，降低了钢筋应力. 文献[7, 35]中所述的接缝开裂强度高于目前的接缝方案，提高界面处的配筋率可以有效地提高接缝界面的强度.

2）点2设计弯矩的简化计算方法.

该阶段基体裂缝宽度刚达到0.05 mm，根据文献[28]的研究可知，钢纤维体积分数为2%时的UHPC试件的可视初裂应变为196×10−6，因此可以定义εca = 196×10−6. 此时结构内力可以根据图18(a)~(d)进行计算，最终得到此时的承载力为

图 18

新窗口打开| 下载原图ZIP| 生成PPT

图 18   典型截面的内力计算示意图

Fig.18   Internal force calculation diagram of typical section


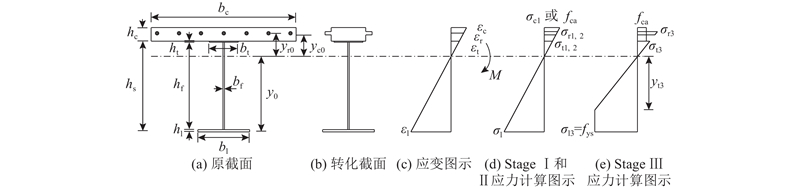
$ \begin{split} {M_1} = \;&\left( {{\sigma _{{\rm{c1}}}}+{\sigma _{{\rm{t1}}}}} \right){h_{\rm{c}}}{b_{\rm{c}}}{y_{{\rm{c0}}}}+{\sigma _{{\rm{r1}}}}{A_{\rm{r}}}{y_{{\rm{r0}}}} + \\ \;&{\sigma _{{\rm{t1}}}}{h_{\rm{t}}}{b_{\rm{t}}}\left( {{h_{\rm{s}}} - {y_{\rm{0}}} - {h_{\rm{t}}}/2} \right)+ \\ \;&\left[ {{\sigma _{{\rm{t1}}}}{{\left( {{h_{\rm{s}}} - {y_{\rm{0}}} - {h_{\rm{t}}}} \right)}^2}+{\sigma _{{\rm{l1}}}}{{\left( {{y_{\rm{0}}} - {h_{\rm{l}}}} \right)}^2}} \right]{b_{\rm{f}}}/3 + \\ \;&{\sigma _{{\rm{l1}}}}{h_{\rm{l}}}{b_{\rm{l}}}\left( {{y_{\rm{0}}} - {h_{\rm{l}}}/2} \right) .\end{split} $

式中：yr0和yc0分别为钢筋和UHPC面板到中性轴的距离，y0为中性轴高度，h、hc和hs分别为组合梁高度、面板厚度及工字钢梁高度，bc、bl、bf和bt分别为UHPC面板、工字钢梁上翼缘、腹板及下翼缘的宽度，σc1、σr1、σt1和σl1分别为UHPC上表面、钢筋及工字钢梁上、下翼缘的计算应力，Ar为纵向钢筋面积，Mc1、Mr1、Ms1分别为UHPC面板、钢筋及工字钢梁的计算弯矩，M1为阶段1的计算设计弯矩.

代入εca=196×10−6，经计算可知，点2的计算弯矩M1 =213.36 kN·m. 根据图17可知，当UHPC基体裂缝宽度达到0.05 mm时，对应的荷载为312.3~378.6 kN（197.53~239.46 kN·m）. 理论计算值在该范围内，说明计算是合理的. 点2的试验值为212.90 kN·m，与理论值完全一致.

3）考虑UHPC受拉刚化效应的钢-UHPC组合梁挠度计算方法[36].

对于传统受拉混凝土构件，考虑混凝土受拉刚化效应的挠度计算方法主要有以下几种：GB 50010—2010[34]采用刚度分析法，CEB-FIP[37]采用抗拉刚度修正法，ACI 318M—89[38]采用有效惯性矩法. ACI318M—89规定，当计算钢筋混凝土构件的挠度时，应使用截面的有效惯性矩：

$ {I_{{\rm{eff}}}} = {\left( {\frac{{{M_{{\rm{cr}}}}}}{M}} \right)^3}{I_0}+\left[ {1 - {{\left( {\frac{{{M_{{\rm{cr}}}}}}{M}} \right)}^3}} \right]{I_{{\rm{cr}}}} \leqslant {I_0}. $

式中：M为弹性理论计算得到的弯矩，Mcr为开裂弯矩，I0为原截面惯性矩，Icr为开裂截面惯性矩. 对于承受负弯矩的钢-UHPC轻型组合梁，开裂弯矩Mcr可以表示为UHPC面板初裂时对应的弯矩：

$ {M_{{\rm{cr}}}} = \frac{{{f_{{\rm{c}}{\text{t}}}}{I_0}{\alpha _{\rm{E}}}}}{{{y_{{\rm{cr}}}}}}. $

式中：fct为UHPC的初裂强度，αE=Es/Ec，ycr为开裂截面中工字钢梁底至中性轴的距离. 对于本文试验跨中挠度的计算，可以采用下式进行计算：

$ D = \frac{M}{{{E_{\rm{s}}}{I_{{\rm{eff}}}}}}\left( {3{L^2} - 4{a^2}} \right). $

式中：L为试验梁跨径，a为剪跨段长度.

根据课题组的前期研究成果[28]，钢纤维体积分数为2%的UHPC的初裂强度为6.67 MPa. 计算点2处的挠度D1=13.02 mm，该点的挠度试验值为12.32 mm，与计算值相近.

4.2. 阶段2：钢梁下缘屈服

第2阶段从点2开始，至点3结束. 在这一阶段，试件刚度略有下降，截面特性可按与第1阶段相同的截面进行计算，工字钢梁下翼缘在点3开始屈服. 计算假定下翼缘达到屈服强度，即σl = fys，fys为工字钢梁的屈服强度. 计算图如图18(a)~(c)、(e)所示，最终该点的承载能力计算结果为

$ \begin{split} {M_2}{\text{ = }}&{f_{{\rm{ca}}}}{h_{\rm{c}}}{b_{\rm{c}}}{y_{{\rm{c0}}}}+\frac{{{y_{{\rm{r}}0}}}}{{{y_0}}}{f_{{\rm{ys}}}}{A_{\rm{r}}}+ \\& \frac{{{h_{\rm{s}}} - {y_0}}}{{{y_0}}}{f_{{\rm{ys}}}}[ {A_{\rm{t}}}{y_{{\rm{t0}}}}+{b_{\rm{f}}}{\left( {{y_{{\rm{t0}}}} - {h_{\rm{t}}}/2} \right)^2}/3+\\&{b_{\rm{f}}}{\left( {{y_0} - {h_{\rm{l}}}}/2 \right)^2}/3+{A_{\rm{l}}}{y_{{\rm{l0}}}} ].\end{split} $

式中：fca为UHPC材料的弹性极限强度，fca= Ecaεca；At和Al分别为工字钢梁上、下翼缘的面积；yt0和yl0分别为中性轴至工字钢梁上、下翼缘的距离.

点3处的计算弯矩为M2 = 495.90 kN·m，对应的挠度可以采用式(16)进行计算，得到D2=35.03 mm. 根据工字钢梁下翼缘的荷载-应变曲线可知，下翼缘在782 kN(494.62 kN·m)处达到屈服强度，这与计算值完全吻合.

4.3. 阶段3：UHPC面板到达极限应变

第3阶段是从点3到点4. 在这一阶段，工字钢梁下翼缘达到屈服强度，先浇的UHPC面板在点4达到极限拉应变. 应力计算如图18(e)所示，计算钢梁腹板弹性受压部分的高度yt3，根据力矩平衡得到该点的承载力计算式M3：

$ \begin{split} {M_3}{\text{ = }}&{f_{{\rm{ca}}}}{h_{\rm{c}}}{b_{\rm{c}}}{y_{{\rm{c0}}}}+\frac{{y_{{\rm{r0}}}^2}}{{h - {y_0}}}{\varepsilon _{\lim }}{E_{\rm{s}}}{A_{\rm{r}}} + \\ &\frac{{{h_{\rm{s}}} - {y_0}}}{{h - {y_0}}}{\varepsilon _{\lim }}{E_{\rm{s}}}\left[ {{A_{\rm{t}}}{y_{{\rm{t0}}}}+\frac{1}{3}{b_{\rm{f}}}{{\left( {{h_{\rm{s}}} - {y_0} - {h_{\rm{t}}}} \right)}^2}} \right] + \\&\frac{1}{3}{f_{{\rm{ys}}}}{b_{\rm{f}}}{y_{{\rm{t3}}}}+\frac{1}{2}{f_{{\rm{ys}}}}{b_{\rm{f}}}\left[ {{{\left( {{y_0} - {h_{\rm{l}}}} \right)}^2} - y_{{\rm{t3}}}^2} \right]+{f_{{\rm{ys}}}}{A_{\rm{l}}}{y_{{\rm{l0}}}} .\end{split} $

根据文献[28]可知，当钢纤维体积分数为2%时，UHPC材料的极限拉应变为7.65×10−4. 点4的计算弯矩为M3=514.93 kN·m，对应挠度为D3 = 36.43 mm.

4.4. 阶段4：钢梁全截面屈服

第4阶段自点4开始，至点5结束. 在这一阶段，工字钢梁的上、下翼缘均达到屈服强度，腹板的一部分也达到屈服强度. UHPC面板内的钢筋在点5达到屈服强度，UHPC达到极限应变. 采用开裂截面（见图19(a)）进行计算. 计算图示如图19(c)所示. 在计算得到钢梁腹板弹性部分的高度后，可得该点的承载力：

图 19

新窗口打开| 下载原图ZIP| 生成PPT

图 19   典型截面的内力计算示意图

Fig.19   Internal force calculation diagram of typical section


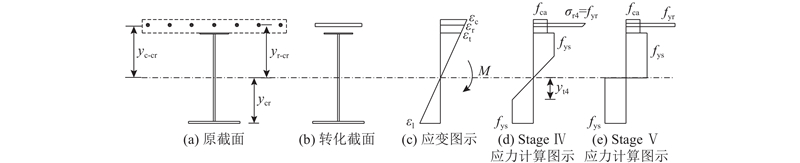
$ \begin{split} {M_4}{\text{ = }}&{f_{{\rm{ca}}}}{A_{\rm{c}}}{y_{{\rm{c}} - {\rm{cr}}}}+{f_{{\rm{yr}}}}{A_{\rm{c}}}{y_{{\rm{r}} - {\rm{cr}}}}+{f_{{\rm{ys}}}}{A_{\rm{t}}}{y_{{\rm{t}}{\text{ - }}{\rm{cr}}}}+ \\&{f_{{\rm{ys}}}}{b_{\rm{f}}}{y_{{\rm{t4}}}}\left( {\frac{1}{4}{h_{\rm{s}}} - \frac{1}{4}{y_{{\rm{cr}}}}+\frac{{11}}{{12}}{y_{{\rm{t4}}}}} \right)+ \\&\frac{1}{2}{f_{{\rm{ys}}}}{b_{\rm{f}}}\left( {{y_{{\rm{cr}}}} - {y_{{\rm{t4}}}} - {h_{\rm{l}}}} \right)\left( {{y_{{\rm{cr}}}}+{y_{{\rm{t4}}}}} \right)+{f_{{\rm{ys}}}}{A_{\rm{l}}}{y_{{\rm{l}}{\text{ - }}{\rm{cr}}}} .\end{split} $

式中：yr-cr、yc-cr、yt-cr及yl-cr分别为开裂截面中性轴至钢筋、UHPC面板、工字钢梁上翼缘及下翼缘中心的距离. 点5的计算弯矩M4 = 620.01 kN·m，对应挠度D4 = 44 mm.

4.5. 阶段5：承载能力极限

第5阶段自点5开始，至点6结束. 试件在点6处达到极限载荷. 计算图如图20(e)所示，随着荷载的增加，腹板弹性部分的高度yt逐渐减小，最后工字钢梁的全截面达到屈服. 本文的计算简化了这一过程，得到如图20(e)所示的计算图，极限承载力可以计算为

图 20

新窗口打开| 下载原图ZIP| 生成PPT

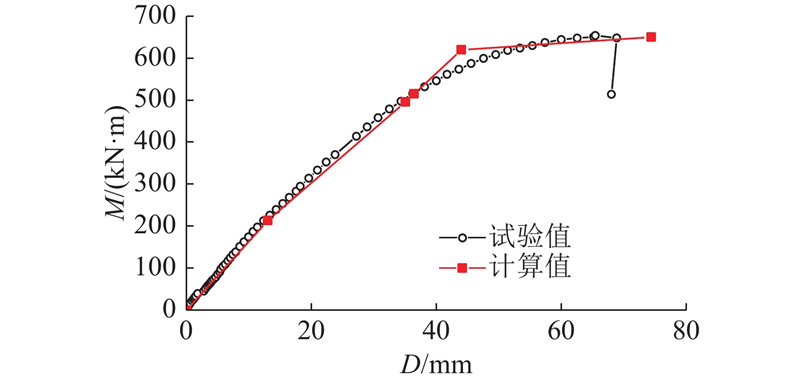
图 20   各阶段跨中位移计算值与试验结果的对比

Fig.20   Comparison of calculated values and test results of mid-span displacement


$ \begin{split} {M_{{\rm{u,ULS}}}} =& {f_{{\rm{ca}}}}{A_{\rm{c}}}{y_{{\rm{c}}{\text{-}}{\rm{cr}}}}+{f_{{\rm{yr}}}}{A_{\rm{r}}}{y_{{\rm{r}}{\text{-}}{\rm{cr}}}}+{f_{{\rm{yr}}}}\frac{{{y_{{\rm{s}}{\text{-}}{\rm{cr}}}}}}{{{y_{{\rm{r}}{\text{-}}{\rm{cr}}}}}}{A_{\rm{l}}}{y_{{\rm{l}}{\text{-}}{\rm{cr}}}} + \\ &\frac{1}{3}{f_{{\rm{yr}}}}{b_{\rm{f}}}\left( {\frac{{{y_{{\rm{s}}{\text{-}}{\rm{cr}}}}}}{{{y_{{\rm{r}}{\text{-}}{\rm{cr}}}}}}{y_{{\rm{ft}}}}^2+\frac{{{y_{{\rm{cr}}}}}}{{{y_{{\rm{r}}{\text{-}}{\rm{cr}}}}}}{y_{{\rm{fc}}}}^2} \right)+{f_{{\rm{yr}}}}\frac{{{y_{{\rm{cr}}}}}}{{{y_{{\rm{r}}{\text{-}}{\rm{cr}}}}}}{A_{\rm{t}}}{y_{{\rm{t}}{\text{-}}{\rm{cr}}}} . \end{split}$

式中：ys-cr为开裂截面钢梁形心至中性轴的距离，yft为腹板受拉部分形心至中性轴的距离，yfc为腹板受压部分形心至中性轴的距离. 可以得到点6的计算弯矩M5 = 650.07 kN·m，挠度D5 = 74.39 mm. 根据试验结果可知，试件的极限荷载和挠度分别为653.94 kN·m和65.43 mm. 与理论计算值相比略高，表明理论计算结果较保守.

将计算结果与试验结果进行比较，如图20所示. 图中，点2~4的计算结果与试验值吻合较好，点5、6的计算结果与试验结果略有不同，原因是这些方程简化了梁体实际的加载过程. 结构极限承载力和挠度的计算结果与试验结果相比略低，相对保守，误差是可以接受的.

5. 设计参数讨论

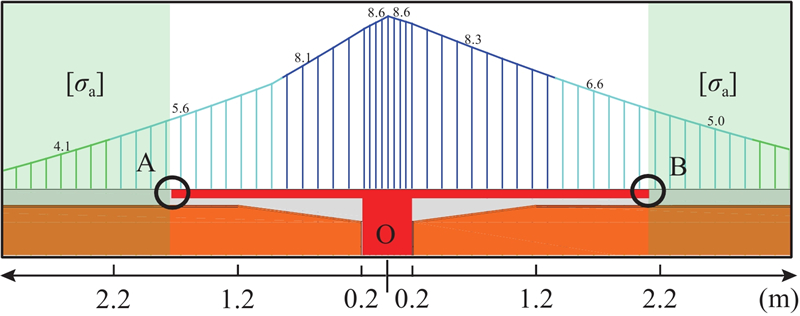
对25 m跨径麻浦行车天桥的横向接缝进行设计和试验. 结果表明，横向接缝可以满足工程使用的要求. T形横向接缝上部的长度为4.5 m (2.25 m×2)，长度根据应力包络图取值，见图21.

图 21

新窗口打开| 下载原图ZIP| 生成PPT

图 21   负弯矩区弯矩包络图

Fig.21   Bending moment envelope diagram in negative bending moment zone


根据试验结果可知，接缝界面处的可视初裂应力为5.4 MPa，对应图21中的点A和点B，AO与BO的长度分别为1.53 m和1.95 m，由此设置T形接缝界面距离墩顶支座中点2.25 m，约为0.089L（L为桥梁跨径，此处L = 25 m）.

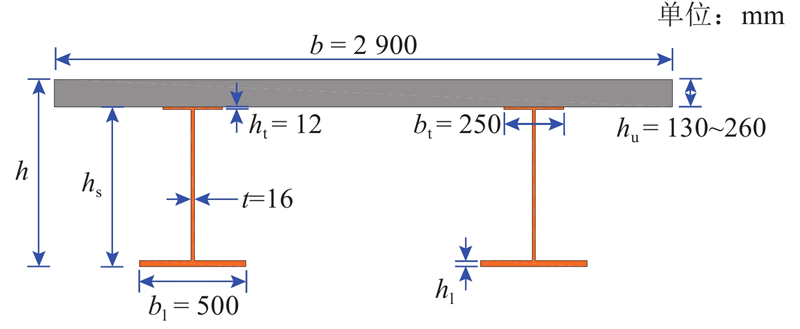
根据常规钢-混凝土组合梁的常见截面尺寸，设计3×L（L=20、30、40、50 m）跨径钢-UHPC组合梁截面，保持UHPC面板厚130~260 mm不变，仅增高工字钢梁高度和工字钢梁下翼缘厚度，4个截面的尺寸如图22所示. 建立有限元模型，采用同样的荷载计算不同跨度桥梁的荷载效应，根据计算结果确定T形接缝上的台阶长度，最终的计算结果如表5所示.

表 5   20~50 m钢-UHPC组合桥梁初步设计截面主尺寸

Tab.5  Main section dimensions of 20-50 m span SU-LWCBs preliminary design

L/mh/mhs/mhl/m单侧台阶长/m
200.880.75~0.620.0281.625
301.281.15~1.020.0282.92
401.931.80~1.670.0382.96
502.632.50~2.370.0383.51

新窗口打开| 下载CSV


图 22

新窗口打开| 下载原图ZIP| 生成PPT

图 22   20~50 m钢-UHPC组合桥梁初步设计截面

Fig.22   Preliminary design of 20–50 m span SU-LWCBs


从表5可见，当桥梁跨度为20~50 m时，T形接缝上延长部分的长度略有不同，分别为0.08L、0.1L和0.07L，但是它们都小于0.1L. 因此，设计值可以设置为0.1L.

6. 结　论

（1）试验结果表明，随着荷载的增大，试件的主裂缝出现在连续浇筑的UHPC接缝界面和加载点下方的面板表面，试件中部未发现明显裂纹. UHPC接缝界面的可视初裂强度为5.40~7.39 MPa，试件跨中开裂强度为19.02 MPa，均大于麻浦行车天桥使用阶段的设计荷载.

（2）提出试验梁加载过程关键阶段的简化计算方法，获得接缝最大裂缝宽度的计算式、考虑UHPC拉伸刚度效应的设计力矩和挠度公式、各阶段极限承载力的计算式. 计算结果与试验结果的比较表明，利用提出的方法，可以有效地预测负弯矩下钢-UHPC组合梁的性能.

（3）通过参数讨论和计算，跨度为20~50 m的SU-LWCB的T形接缝上部加长长度可以设置为0.1倍的桥梁跨度.

参考文献

张子飏, 邓开来, 徐腾飞

预制装配式混凝土桥梁结构2019年度研究进展

[J]. 土木与环境工程学报: 中英文, 2020, 42 (5): 183- 191

[本文引用: 1]

ZHANG Ziyang, DENG Kailai, XU Tengfei

State-of-the-art review of prefabricated concrete bridge structures in 2019

[J]. Journal of Civil and Environmental Engineering, 2020, 42 (5): 183- 191

[本文引用: 1]

董志强, 吴刚

FRP 筋增强混凝土结构耐久性能研究进展

[J]. 土木工程学报, 2019, 52 (10): 1- 19

[本文引用: 1]

DONG Zhiqiang, WU Gang

Research progress on durability of FRP bars reinforced concrete structures

[J]. China Civil Engineering Journal, 2019, 52 (10): 1- 19

[本文引用: 1]

王爱国, 郑毅, 张祖华, 等. 碱激发材料与普通硅酸盐水泥和混凝土的耐久性能比较[J], 工程(英文), 2020, 6(6): 695-706, 787-799.

[本文引用: 1]

WANG Aiguo , ZHENG Yi, ZHANG Zuhua, et al. The durability of alkali-activated materials in comparison with ordinary portland cements and concretes: a review [J]. Engineering, 2020, 6(6): 695-706, 787-799.

[本文引用: 1]

赵明, 何湘峰, 邱明红, 等

全预制钢-UHPC轻型组合梁在中小跨径桥梁中的设计与应用研究

[J]. 公路工程, 2019, 44 (5): 4

[本文引用: 2]

ZHAO Ming, HE Xiangfeng, QIU Minghong, et al

Research on design and application of fully prefabricated steel-UHPC lightweight composite girder in medium and small span girder bridge

[J]. Highway Engineering, 2019, 44 (5): 4

[本文引用: 2]

QI J, CHENG Z, WANG J, et al

Full-scale testing on the flexural behavior of an innovative dovetail UHPC joint of composite bridges

[J]. Structural Engineering and Mechanics, 2020, 75 (1): 49- 57

[本文引用: 1]

LU K, XU Q, LI W, et al

Fatigue performance of UHPC bridge deck system with field-cast dovetail joint

[J]. Engineering Structures, 2021, 237: 112108

DOI:10.1016/j.engstruct.2021.112108     

PAN W, FAN J, NIE J, et al

Experimental study on tensile behavior of wet joints in a prefabricated composite deck system composed of orthotropic steel deck and ultrathin reactive-powder concrete layer

[J]. Journal of Bridge Engineering, 2016, 21 (10): 04016064

DOI:10.1061/(ASCE)BE.1943-5592.0000935      [本文引用: 2]

邵旭东, 陈斌, 周绪红

钢-RPC轻型组合桥面结构湿接头弯曲试验

[J]. 中国公路学报, 2017, 30 (3): 210- 217

SHAO Xudong, CHEN Bin, ZHOU Xuhong

Experiment on bending behavior of wet joints in light-weighted composite deck system composed of steel and RPC layer

[J]. China Journal of Highway and Transport, 2017, 30 (3): 210- 217

HE S, MOSALLAM A S, FANG Z, et al

Structural evaluation of steel–concrete joint with UHPC grout in single cable–plane hybrid cable-stayed bridges

[J]. Journal of Bridge Engineering, 2019, 24 (4): 04019022

DOI:10.1061/(ASCE)BE.1943-5592.0001379     

JIA J, REN Z, BAI Y, et al

Tensile behavior of UHPC wet joints for precast bridge deck panels

[J]. Engineering Structures, 2023, 282: 115826

DOI:10.1016/j.engstruct.2023.115826     

XIAO J, GUO L, NIE J, et al. Flexural behavior of wet joints in steel-UHPC composite deck slabs under hogging moment [J]. Engineering Structures, 2022, 252: 113636.

QI J, BAO Y, WANG J, et al

Flexural behavior of an innovative dovetail UHPC joint in composite bridges under negative bending moment

[J]. Engineering Structures, 2019, 200: 109716

DOI:10.1016/j.engstruct.2019.109716     

DU L, QI J, CHENG Z, et al

Finite element modeling of UHPC slabs with dovetail joints and steel wire mesh using an innovative interfacial treating method

[J]. Structures, 2022, 37: 745- 755

DOI:10.1016/j.istruc.2022.01.057     

ZHAO C, WANG K, XU R, et al

Development of fully prefabricated steel-UHPC composite deck system

[J]. Journal of Structural Engineering, 2019, 145 (7): 04019051

DOI:10.1061/(ASCE)ST.1943-541X.0002338      [本文引用: 1]

CHITTY F, FREEMAN C, GARBER D

Joint design optimization for accelerated construction of slab beam bridges

[J]. Journal of Bridge Engineering, 2020, 25 (7): 04020029

DOI:10.1061/(ASCE)BE.1943-5592.0001561      [本文引用: 1]

ABOKIFA M, MOUSTAFA M

Experimental behavior of precast bridge deck systems with non-proprietary UHPC transverse field joints

[J]. Materials, 2021, 14 (22): 6964

DOI:10.3390/ma14226964     

DENG E, ZHANG Z, ZHANG C, et al

Experimental study on flexural behavior of UHPC wet joint in prefabricated multi-girder bridge

[J]. Engineering Structures, 2023, 275: 115314

DOI:10.1016/j.engstruct.2022.115314     

GRAYBEAL B. Design and construction of field-cast UHPC connections [R]. Washington, DC: Federal Highway Administration, 2014.

HE Z, MA Z, CHAPMAN C, et al

Longitudinal joints with accelerated construction features in decked bulb-tee girder bridges: strut-and-tie model and design guidelines

[J]. Journal of Bridge Engineering, 2012, 18 (5): 372- 379

JIANG H, HU Z, FENG J, et al

Flexural behavior of UHPC-filled longitudinal connections with non-contacting lap-spliced reinforcements for narrow joint width

[J]. Structures, 2022, 39: 620- 636

DOI:10.1016/j.istruc.2022.03.017     

QIU M, SHAO X, YAN B, et al. Flexural behavior of UHPC joints for precast UHPC deck slabs [J]. Engineering Structures, 2022, 251 (part A): 113422.

SHAH Y, HU Z, YIN B, et al

Flexural performance analysis of UHPC wet joint of prefabricated bridge deck

[J]. Arabian Journal for Science and Engineering, 2021, 46 (11): 11253- 11266

DOI:10.1007/s13369-021-05735-z     

ZHU Y, ZHANG Y, HUSSEIN H, et al

Flexural study on UHPC–steel composite beams with joints under negative bending moment

[J]. Journal of Bridge Engineering, 2020, 25 (10): 04020084

DOI:10.1061/(ASCE)BE.1943-5592.0001619     

TAN Y, LV L, ZHANG D, et al

Fatigue performance of a simply-supported T-beam UHPC bridge deck variable section joint structure

[J]. Engineering Structures, 2022, 269: 114758

DOI:10.1016/j.engstruct.2022.114758     

邵旭东, 胡伟业, 邱明红, 等. 组合梁负弯矩区UHPC接缝抗弯性能试验 [J]. 中国公路学报, 2021, 34(8): 246-260.

[本文引用: 1]

SHAO Xudong, HU Weiye, QIU Minghong, et al. Experiment on flexural behavior of UHPC joint in negative moment area of composite bridges [J]. China Journal of Highway and Transport, 2021, 34(8): 246-260.

[本文引用: 1]

AFGC-SETRA. National addition to Eurocode 2 — design of concrete structures: specific rules for ultra-high performance fibre-reinforced concrete (UHPFRC) [S]. Paris: French Standard Institute, 2016.

[本文引用: 1]

中交公路规划设计院有限公司. 公路钢结构桥梁设计规范 [M]. 北京: 人民交通出版社股份有限公司, 2015.

[本文引用: 2]

张哲, 邵旭东, 李文光, 等

超高性能混凝土轴拉性能试验

[J]. 中国公路学报, 2015, 28 (8): 50- 58

[本文引用: 7]

ZHANG Zhe, SHAO Xudong, LI Wenguang, et al

Axial tensile behavior test of ultra high performance concrete

[J]. China Journal of Highway and Transport, 2015, 28 (8): 50- 58

[本文引用: 7]

PIERRE R, MARCEL C

Composition of reactive powder concretes

[J]. Cement and Concrete Research, 1995, 25 (7): 1501- 1511

DOI:10.1016/0008-8846(95)00144-2      [本文引用: 1]

GRAYBEAL B, BRÜHWILER E, KIM B, et al

International perspective on UHPC in bridge engineering

[J]. Journal of Bridge Engineering, 2020, 25 (11): 04020094

DOI:10.1061/(ASCE)BE.1943-5592.0001630      [本文引用: 1]

中华人民共和国国家质量监督检验检疫总局. 活性粉末混凝土[S]. 北京: 中国标准出版社, 2015.

[本文引用: 1]

LUO J, SHAO X, FAN W, et al

Flexural cracking behavior and crack width predictions of composite (steel + UHPC) lightweight deck system

[J]. Engineering Structures, 2019, 194: 120- 137

DOI:10.1016/j.engstruct.2019.05.018      [本文引用: 5]

LUO J, SHAO X, CAO J, et al

Transverse bending behavior of the steel-UHPC lightweight composite deck: Orthogonal test and analysis

[J]. Journal of Constructional Steel Research, 2019, 162: 105708

DOI:10.1016/j.jcsr.2019.105708      [本文引用: 5]

中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010.

[本文引用: 2]

陈斌. 正交异性钢-UHPC轻型组合桥面结构湿接头抗弯性能研究与试验[D]. 长沙: 湖南大学, 2019.

[本文引用: 2]

CHEN Bin. Research and experiment on bending behavior of wet joints in lightweight composite deck system composed of orthotropic steel and UHPC layer [D]. Changsha: Hunan University, 2019.

[本文引用: 2]

张彦玲, 李运生, 樊健生

钢混凝土连续组合梁的刚度计算方法

[J]. 中南大学学报: 自然科学版, 2013, 44 (8): 3520- 3526

[本文引用: 1]

ZHANG Yanling, LI Yunsheng, FAN Jiansheng

Stiffness calculation method for steel-concrete continuous composite beams

[J]. Journal of Central South University: Science and Technology, 2013, 44 (8): 3520- 3526

[本文引用: 1]

Design of concrete structures: CEB-FIP-Model-Code 1990 [S]. London: British Standard Institution, 1993.

[本文引用: 1]

ACI Committee. Building code requirements for structural concrete (ACI 318-08) and commentary [S]. Michigan: ACI, 2008.

[本文引用: 1]

/

〈 〉