城市群是城市化进程中区域空间形态的高级形式，交通系统对城市群的快速发展具有支撑性作用^[1-2]. 近年来，城市群交通已初步形成多模式交通汇聚的格局，多模式互补成为城市群客运网络的重要特征之一. 在风险常态化的背景下，客运网络对灾害的承受能力较弱，系统遭到破坏后很难迅速恢复. 从现状来看，我国多模式客运网络组合效率、功能协作及应对突发事件的鲁棒性方面还存在短板^[3]. 因此，城市群的快速发展对多模式客运网络可靠运行提出了更高的要求，增强了城市群多模式客运网络的鲁棒性，降低灾害风险的冲击对维持城市群多模式客运网络的可持续运行具有重要意义.

国内外关于多模式客运网络鲁棒性的研究可以分为静态鲁棒性和动态鲁棒性2类. 前者认为交通站点是相对独立的，主要通过客运网络拓扑特征^[3-4]及可达性^[5-6]对鲁棒性进行测度. 后者认为一个节点失效会导致相邻节点失效，通过构建负载-容量模型或耦合映像格子模型，从级联失效角度对客运网络的鲁棒性进行测度^[7-9]，但这类研究大多关注客运网络耦合给鲁棒性带来的负面效应. 在模型构建方面，多数学者根据站点的地理位置构建复合网络模型，如公路-铁路^[7,10]复合网络和公交-地铁^[11-13]复合网络，但该方法忽略了不同交通模式运行特性的异质性.

客运网络间存在竞争和互补2种关系. 当研究多模式客运网络的鲁棒性时，互补关系比竞争关系更重要，因为客运网络间可以通过提供替代服务，增强鲁棒性^[11]. 部分学者将多模式客运网络间的互补关系对客运网络鲁棒性的积极影响描述为互补效应（complementary effect，CE），以公交-地铁^{[11-12, 14]}和高铁-航空双层网络^[15-18]为例，研究鲁棒性，证明了CE使客运网络在受到扰动时性能损失减小，提高了客运网络的鲁棒性. 为了分析不同客运网络间的互补强度差异，刘承良等^[19]构建城际交通互补度模型，结果表明，中国过半城市为铁路-公路“双轮驱动型”，公路和铁路之间的互补强度最高，高值区高度集聚于西部省份，但未考虑中断情景下客运网络的性能变化.

肖明辉等^{[11-12,14-19]}证明了是否考虑多模式客运网络间的CE对客运网络鲁棒性的影响，但关于CE如何在突发事件下影响客运网络的鲁棒性及影响程度大小的问题仍未得到解决，多数研究鲜有考虑不同客运网络运行服务的异质性. 本文从多种交通模式互补的视角，基于站点间的客运班次和出行时间数据建立鲁棒性测度指标，构建基于鲁棒性的动态互补强度模型，分析在应对突发事件时城市群多模式客运网络间的互补强度并量化CE对鲁棒性的提升程度. 以关中平原城市群为例，研究考虑互补效应的城市群多模式客运网络的鲁棒性，验证了模型的有效性.

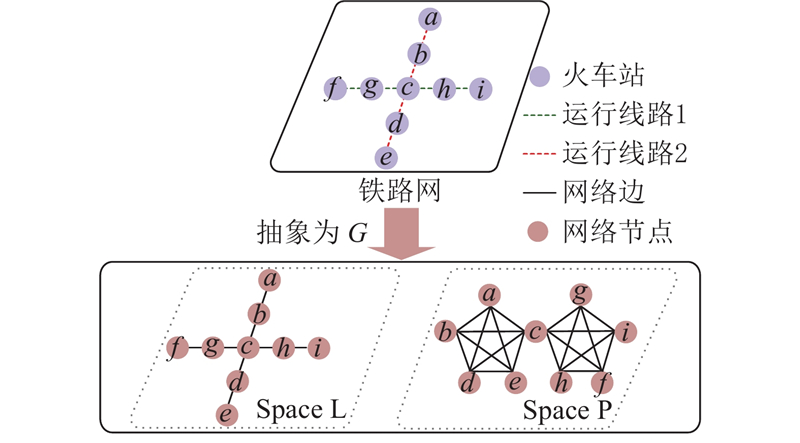
交通网络模型的构建方法包括Space P和Space L 2种方法. Space P方法中，网络节点对应实际站点，边对应站点之间的列车服务线路，若2个节点沿着同一服务线路，则无论它们是否相邻，对应的节点之间都存在边. Space L方法中，将实际站点视为网络节点，将列车服务线路视为边. 以铁路网为例，绘制Space L和Space P方法的示意图，如图1所示. 站点a至站点i为网络中的节点，黑色实线为网络中的边.

Space P建模方法从交通网络的服务特征突出了节点的连通性，适用于描述基于交通站点与服务之间关系的动态服务网络^[15]. 本文侧重于从交通网络服务特性的视角，研究城市群客运网络的鲁棒性，因此采用复杂网络的Space P建模方法. 以城市群内不同交通模式的所有长途客运站点为客运网络节点，根据不同交通模式站点之间是否存在直达班次、出行时间和列车频次，构建4种交通方式无向有权的客运网络G_S，分别为公路网G₁、铁路网G₂、航空网G₃和水运网G₄.

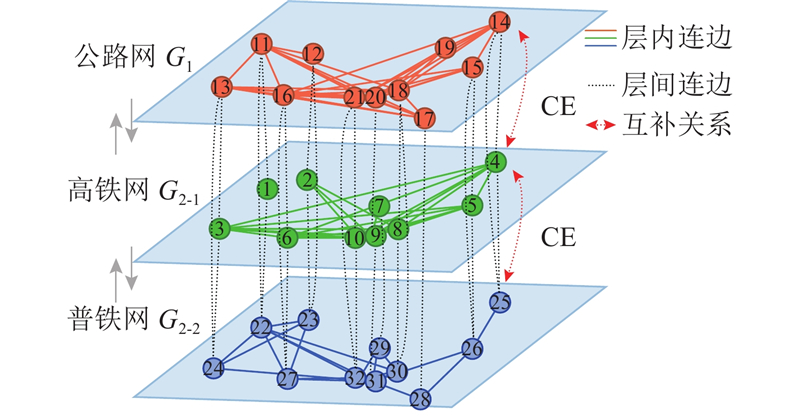
将客运网络抽象为图G=(N,E,W)，其中N为节点集合，E为连边集合，W为连边的权重集合. Space P方法将公路客运站、火车站、机场和港口分别定义为公路网、铁路网、航空网和水运网中的节点，若节点i和节点j存在车次联系，则节点i和节点j间存在一条连边，连边权重由节点间的出行时间和车站间日均客运班次决定. 多模式互补客运网络G_C拓扑模型由4个不同的客运网络复合而成，当公路客运站、火车站、高铁站、机场或港口位于同一个市时视为互补节点，互补节点内各交通方式的站点均互相连接，视为互补关系，互补关系对客运网络鲁棒性产生的影响为节点间的互补效应.

鲁棒性作为反映系统抗干扰能力的指标，被广泛应用于各种基础设施系统的安全性研究中，用于衡量系统在局部扰动下维持自身性能及连接状态的能力. 客运网络的重要功能是为乘客提供快速出行的服务，已有学者为了解决客运网络鲁棒性测度的问题，提出使用客运网络中OD对间的客流量和出行时间作为客运网络性能的计算指标，对客运网络鲁棒性进行测度. 参考文献[15, 20]，考虑客运网络的服务特性，选取城市群多模式客运网络中节点i和节点j间的客流量和出行时间，计算客运网络的性能P. 考虑到数据的可获得性，用航空、铁路和公路站点间的日均开行客运班次代替客流数据^[7,10]，将不同交通模式的日均开行客运班次统一定义为列车频次f_ij^[9,15]. 客运网络性能的计算公式如下所示：

(1)$ P = \frac{1}{{n(n - 1)}}\sum\limits_{i \ne j \in N}^{} {\frac{{{f_{ij}}}}{{{t_{ij}}}}} . $

式中：N为城市群多模式客运网络中的节点集合，n为节点总个数，f_ij为节点i和节点j之间的列车频次，t_ij为节点i和节点j之间的最短出行时间.

参考文献[16,20]的研究，城市群多模式客运网络的鲁棒性（robustness）可以通过计算中断情景下客运网络的相对性能R获得：

(2)$ R = 1 - \frac{{{P^{{\rm{no}}}} - {P^{{\rm{ab}}}}}}{{{P^{{\rm{no}}}}}} = \frac{{{P^{{\rm{ab}}}}}}{{{P^{{\rm{no}}}}}} . $

式中：P^ab和P^no分别为城市群多模式客运网络在正常运行状态和中断情景下的网络性能.

参考文献[3,8]的研究，假设城市群多模式客运网络中节点遭受攻击后立即失效，与其直接相连的所有连边随之失效. 在城市群多模式客运网络中，当一个客运网络的节点失效时，另一个或多个客运网络可以提供替代服务满足旅客出行需求. 当多个客运网络同时提供替代服务时，旅客根据目的地距离重新选择出行方式，不同交通方式提供替代服务时的客流量分流比例根据研究区域内各客运网络的年客运总量比例确定.

以公路网G₁和铁路网G₂为例，考虑G₁和G₂节点间的CE，当铁路网G₂中节点i失效时，一部分客流将会转移至公路模式，继续完成出行至节点j. 已有学者明确提出在客运网络中，两城市间的经济社会联系越紧密，客流引力就越强. 当解决多种交通模式互补的客流量转移比例问题时，提出应用引力模型计算城市间的引力^[15]，据此表示客流引力，引力模型的计算公式如下：

(3)$ {\theta _{ij}} = \frac{{\sqrt {{\mu _i}{\nu _i}} \sqrt {{\mu _j}{\nu _j}} }}{{k_{ij}^\lambda }} . $

式中：θ_ij为节点i和j所在城市之间的引力，它由2个城市的区域生产总值v_i、v_j、人口μ_i、μ_j及两者之间的距离k_ij决定，λ为距离的摩擦因数.

引力模型能够反映城市间的联系程度，对城市间的客流联系紧密度进行评估并量化不同城市对之间的客流引力差异. 该模型广泛应用在公路、铁路和航空等多种交通模式客运网络的相关研究中^[15,21]，与本文研究对象的适配度较高. 本文借鉴相关研究，应用引力模型计算城市间的客流引力. 根据引力归一化后的值确定客流量转移比例，用$ {{\bar \theta _{ij}}} $表示：

(4)$ {\overline \theta _{ij}} = \frac{{{\theta _{ij}}}}{{\max \; \left\{{\theta _{xy}},x \ne y \in N\right\}}} . $

转移的客流实际通过公路出行，但用铁路列车频次与转移比例的乘积表示，因此定义为间接列车需求指数. 归一化处理有助于消除不同OD对间引力的量纲差异，使得不同OD对间的引力具有可比性.

在城市群客运中不同区域的不同交通方式存在绝对优势出行距离^[22]，将公路、铁路和航空的绝对优势出行距离分别记为[x₁, x₂]、[x₂, x₃]和[x₃, x₄]. 用k_ij表示节点i和节点j所在城市间的地理距离，当铁路网G₂中节点i失效时，乘客选择出行方式到达目的地j有以下2种情景.

情景A：当k_ij≥x₂时，旅客有以下2种选择.

A₁：选择公路出行到达最近的公路客运站所在的城市o，在城市o中转选择铁路的方式继续到达目的地j，此时，

(5)$ \left. \begin{gathered} t_{ij}^{{G_2} \leftarrow {G_1}} = t_{io}^{{G_1}}+t_{oj}^{{G_2}}+t_{ij}^t, \\ f_{ij}^{{G_2} \leftarrow {G_1}} = f_{ij}^{{G_2}}{\overline \theta _{ij}}. \\ \end{gathered} \right\} $

A₂：选择公路方式直接到达目的地j，此时，

(6)$ \left. \begin{gathered} t_{ij}^{{G_2} \leftarrow {G_1}} = t_{ij}^{{G_1}}, \\ f_{ij}^{{G_2} \leftarrow {G_1}} = f_{ij}^{{G_2}}{\overline \theta _{ij}}. \\ \end{gathered} \right\} $

式中：$t_{ij}^{{G_2} \leftarrow {G_1}}$为当G₂中节点i失效时，考虑G₁中节点的互补效应时可以到达节点j的出行时间；$ t_{io}^{{G_1}} $为通过公路出行方式到达中转城市o所需的时间；$ t_{oj}^{{G_2}} $为通过铁路方式从中转城市o到目的地j所需的时间；$ t_{ij}^t $为中转时间，统一确定为0.5 h^[16]；$ f_{ij}^{{G_2}} $为G₂中节点i和节点j之间的列车频次；$ t_{ij}^{{G_1}} $为G₁中节点i和节点j的互补节点间的出行时间；$ f_{ij}^{{G_2} \leftarrow {G_1}} $为当G₂中节点i失效时，考虑G₂中节点的互补效应时可以到达节点j的列车频次. 当G₂中节点i失效时，即使考虑CE，旅客也无法到达节点j时$f_{ij}^{{G_2} \leftarrow {G_1}} = 0$，$t_{ij}^{{G_2} \leftarrow {G_1}} = \infty $. 由于构建的客运网络是无向的，同理可得节点j失效后考虑CE时可以到达节点i的列车频次和出行时间.

出行时间是本文计算客运网络性能的重要指标，因此在情景A中，假定旅客倾向于选择时间少的出行方式. 当$ {t}_{io}^{{G}_{1}}+{t}_{oj}^{{G}_{2}}+{t}_{ij}^{t}＜{t}_{ij}^{{G}_{1}} $时，旅客选择A₁；当$t_{io}^{{G_1}}+t_{oj}^{{G_2}}+t_{ij}^t \geqslant t_{ij}^{{G_1}}$时，旅客选择A_2.

情景B：当k_ij＜x₂时，旅客选择公路出行直达目的地，此时$ f_{ij}^{{G_2} \leftarrow {G_1}} $和$t_{ij}^{{G_2} \leftarrow {G_1}}$的计算同式(6).

互补强度是一个交通网络对另一个交通网络功能替代的比例^[17]. 根据对城市群多模式客运网络及互补效应的描述，考虑到节点失效情景下客运网络鲁棒性的变化，对城市群多模式客运网络节点间的互补强度进行量化^[5].

以公路网G₁和铁路网G₂为例，在G₁中节点失效的情景下，G₂对G₁的静态互补强度（static complementary strength，SCS）计算如下：

$ {\rm{SC}}{{\rm{S}}_{{G_2} \to {G_1}}} = \frac{{{n_{{G_2} \to {G_1}}}}}{{{n_{{G_1}}}}}. $

式中：${n_{{G_1}}}$为G₁中的节点个数，${n_{{G_2} \to {G_1}}}$为G₂中能为G₁提供互补作用的节点个数. SCS可以直观量化一个客运网络中能够为其他客运网络提供互补作用的节点个数，但无法反映在节点失效情景下客运网络间服务功能的互补作用. 以考虑CE时鲁棒性的变化情况刻画客运网络间服务功能的互补强度，据此量化不同客运网络间的动态互补强度（dynamic complementary strength，DSC）.

基于1.2节中构建的客运网络鲁棒性测度模型，在G₁中节点失效的情景下，不考虑CE时G₁的鲁棒性用${R_{{G_1}}}$表示，考虑CE时G₁的鲁棒性用${R_{{G_1}{G_2},{G_1}}}$表示，则G₂对G₁的动态互补强度${\rm{DC}}{{\rm{S}}_{{G_2} \to {G_1}}}$计算公式如下所示：

(8)$ {\rm{DC}}{{\rm{S}}_{{G_2} \to {G_1}}} = \frac{{{R_{{G_1}{G_2},{G_1}}} - {R_{{G_1}}}}}{{{R_{{G_1}}}}}. $

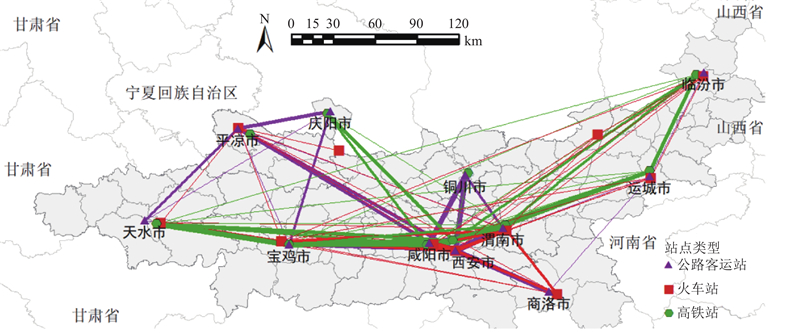
关中平原城市群地处我国内陆中心，是我国西部地区第二大城市群，横跨甘肃、山西、陕西3个省份，含11个地级市（平凉市、庆阳市、天水市、临汾市、运城市、宝鸡市、商洛市、铜川市、渭南市、西安市、咸阳市）的90个县级行政单元，是开创西部大开发格局、助力全国高质量发展的重要支撑. 关中平原城市群作为正在发展中的区域性城市群，是引领西北地区发展的重要增长极和内陆生态文明建设先行区. 随着城市群发展进程不断加快，关中平原城市群综合立体交通运输网基本形成，“米”字型高铁网加快构建，高速公路网规模不断扩大，已逐步形成多种交通模式汇聚的格局. 关中平原城市群组成城市和客运网络相对稀疏，交通系统鲁棒性面临网络和地理复合特性带来的独特挑战，多种交通模式间的衔接融合和优势互补仍显薄弱，具有城市群多模式客运网络鲁棒性研究的条件和需求.

关中平原城市群中交通站点的位置数据源于谷歌地图（http://www.gditu.net/）. 铁路客运包含高铁组列车G、D、C和普铁组列车Z、T、K，客运班次数据来自铁路12306官方网站（https://www.12306.cn）. 公路客运班次数据来自携程官方网站（https://www.ctrip.com）. 铁路和公路客运列车频次均以2022年12月24日至2023年1月9日的日客运班次平均值表示，地区生产总值（GDP）和人口数来源于各城市的2022年统计公报.

关中平原城市群内城际出行以公路和铁路为主，航空和水运承担的运输比例较小. 通过客运网络服务特性，对关中平原城市群多模式客运网络的鲁棒性进行测度，在铁路客运中，普速铁路（普铁）和高速铁路（高铁）速度、运力和价格等方面存在差异，这导致两者的服务特性差异较大. 将铁路细分为普速铁路和高速铁路^[8]，将同一城市内相同交通模式的客运站点进行合并，选取客流量最大的站点为代表. 本文的主要目的是研究城市群不同客运网络间的CE及CE对客运网络鲁棒性的影响，因此基本假设是城市中某种交通模式失效，且与城际出行时间相比，城市内不同模式间的换乘时间可以忽略不计^[16].

最终选择公路客运站11个、高铁站10个、普铁站11个，分别构建公路网G₁、高铁网G_2-1和普铁网G_2-2，以2.1节中的11个地级市顺序对G_2-1、G_2-2和G₁中的节点进行编号. 使用ArcGIS软件绘制关中平原城市群多模式客运网络拓扑图，如图2所示. 图中，线条宽度表示连边权重，宽度越大，表示连边权重越大. 根据互补关系，建立29条层间连接边，构建关中平原城市群多模式互补网络G_C，客运网络及层间节点的互补关系如图3所示.

根据关中平原城市群客运网络拓扑结构，借助Gephi软件计算网络密度、平均路径长度和平均聚类系数3个指标. 对关中平原城市群G_C、G₁、G_2-1和G_2-2的结构指标进行测度，结果如表1所示.

从表1可知，关中平原城市群多模式互补客运网络G_C的网络密度为0.206，城市对间建立相互关系的数量不足总数的1/4，说明关中平原城市群地区网络整体处于弱连接状态，城市间交通联系有待进一步加强. 平均路径长度反映了网络的连通性，G_C的平均路径长度为2.126，参照对比侯兰功等^[10]的研究可知，成渝城市群和长江中游城市群客运网络平均路径长度为1.4~1.7，可见关中平原城市群互补客运网络的整体连通性较弱.

从单个客运网络来看，高铁网G_2-1和普铁网G_2-2的连通性较高，公路网G₁的连通性较弱. 平均聚类系数反映了交通网络集聚程度，平均聚类系数越大，则交通网络节点受到攻击后节点间的离散程度越高，网络的鲁棒性越差^[10]. 关中平原城市群中高铁网G_2-1的平均聚类系数为0.805，在3个客运网络中最高，高铁网的集聚效应最显著，鲁棒性最弱.

对城市群多模式客运网络的鲁棒性进行测度，须以客运网络的性能指标计算为基础. 依据1.2节构建的客运网络性能测度指标，计算得到城市群多模式客运网络正常运行时的公路网性能P^no(G₁) = 1.447，高铁网性能P^no(G_2-1) = 6.219，普铁网性能P^no(G_2-2) = 2.839. 选择合适的攻击策略对交通网络鲁棒性的测度至关重要. 按照攻击对象的类别，攻击策略可以分为攻击节点和攻击边. 攻击节点会在删除节点的同时，删除与点相连的边，而攻击边仅会导致某条线路失效. 由于城市群多模式互补客运网络本身是多种客运网络复合的结果，某条线路失效，节点之间仍可通过其他方式到达，对城市群多模式互补客运网络鲁棒性的影响较小. 选取攻击节点的策略研究城市群多模式客运网络的鲁棒性，应用MATLAB软件依次对3个客运网络节点进行攻击. 结果按照鲁棒性从小到大进行排序，如表2所示.

从表2可知，当西安、咸阳和渭南3个城市的客运站点失效时，在G₁、G_2-1和G_2-2鲁棒性值排序中均位居前列，此时，客运网络维持正常运行状态性能的能力最差. 在西安市3种客运站点失效后，所在客运网络的鲁棒性均为最小值. 这是因为在关中平原城市群，西安作为核心城市，是连接山西省和甘肃省的重要中间点，一旦节点失效，G₁、G_2-1和G_2-2的连接关系就会被极大程度地削弱，客运网络处于大面积崩溃的状态. 当咸阳和渭南2个城市的客运站点失效时，所在客运网络的鲁棒性最小值分别为0.470和0.633，表明除西安外，这2个城市也在关中平原城市群中承担了一定的区域客流组织功能. 基于以上分析，部分客运站点失效对关中平原城市群客运网络鲁棒性的影响较大，这导致关中平原城市群路网的容错能力较差，当节点受到攻击后有较少路径保障网络正常运行. 由此可见，关中平原城市群城际出行网络形成了以西安为主中心、咸阳和渭南为次级中心的客运网络格局. 除G_2-1中的独立站点平凉南站外，对G₁、G_2-1和G_2-2网络性能影响最小的节点分别为临汾北汽车站、铜川东站和长庆桥站，节点失效后网络性能变化极小，鲁棒性接近于1. 这说明在客运网络服务特性方面，客运网络中各节点在城市群中的重要性差距较大. 分析表2可知，不考虑CE时，公路网、高铁网和普铁网站点失效时的鲁棒性平均值分别为0.787、0.800和0.818，可见在关中平原城市群中，普铁网应对突发事件时的鲁棒性最强，公路网应对突发事件时的鲁棒性最弱.

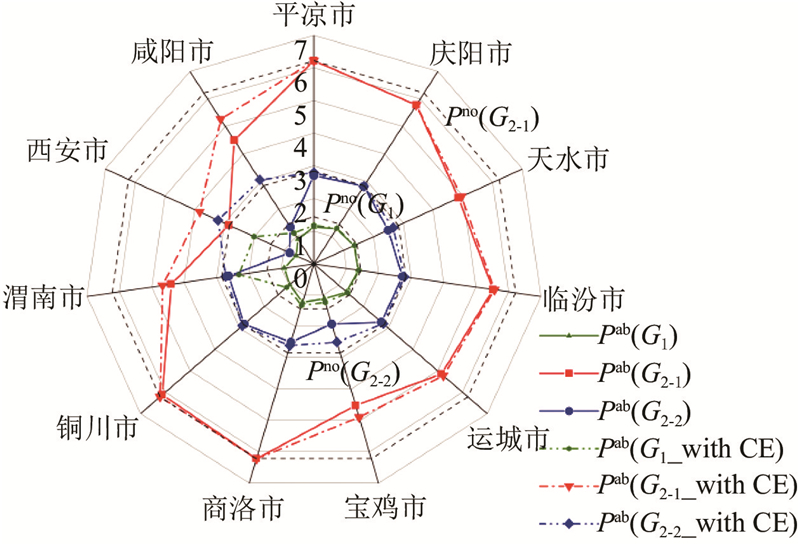
当原出行方式的站点失效时，旅客将根据目的地的距离重新选择出行方式，项昀等^[22]研究证明在关中平原城市群中公路和铁路的绝对优势出行距离分别为[8,163]和[164,1 575] km. 为了研究CE对关中平原城市群多模式客运网络性能的影响，计算得到在单个节点失效情景下是否考虑CE时客运网络的性能，如图4所示. 图中，P^no(G₁)、P^no(G_2-1)和P^no(G_2-2)分别为公路网、高铁网和普铁网在正常运行情况下的客运网络性能值，P^ab(G₁)、P^ab(G_2-1)和P^ab(G_2-2)分别为公路网、高铁网和普铁网在节点失效时不考虑CE时的客运网络性能值， P^ab(G₁_with CE)、P^ab(G_2-1_with CE)和P^ab(G_2-2_with CE)分别为公路网、高铁网和普铁网在节点失效时考虑CE时的客运网络性能值. 在考虑CE时，须计算间接列车需求指数${\overline \theta _{ij}} $，其中引力模型中距离摩擦因数λ的取值为2^[21].

从图4可知，当关中平原城市群多模式客运网络中的节点失效时，考虑CE时的客运网络性能值始终高于不考虑CE时的性能值，CE使得在应对突发事件时客运网络性能损失值显著下降. 在西安汽车站、西安北站和西安站失效后，考虑CE时，G₁、G_2-1和G_2-2的网络性能提升值最高，分别为50.2%、26.5%和44.5%. 仿真结果验证了CE使得G₁、G_2-1和G_2-2的网络性能均有明显提升，表明在节点失效情景下不同客运网络合作的必要性. 根据仿真结果计算可知，当考虑CE时，公路网、高铁网和普铁网单个节点失效后，鲁棒性平均值分别为0.872、0.920和0.943，可见在关中平原城市群中，无论是否考虑CE，普铁网应对突发事件时的鲁棒性最强，公路网应对突发事件时的鲁棒性最弱.

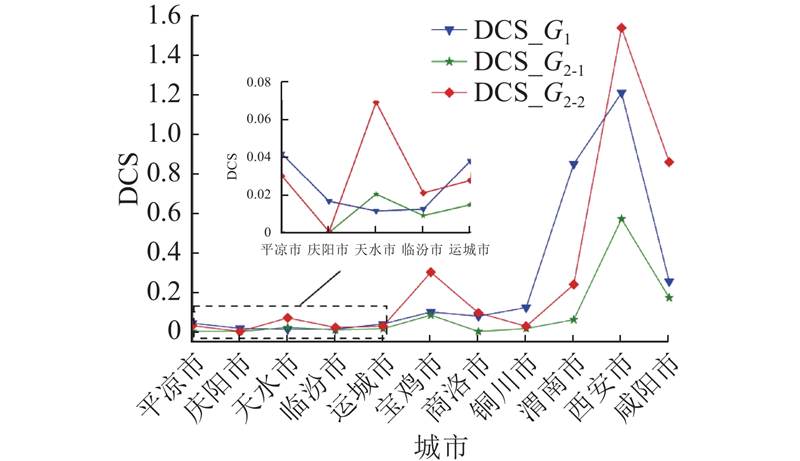
根据建立的动态互补强度模型，计算关中平原城市群每个站点的互补强度，如图5所示. 图中，DCS_ G₁为G₁中节点失效后G_2-1和G_2-2对G₁的动态互补强度，DCS_ G_2-1为G_2-1中节点失效后G₁和G_2-2对G_2-1的动态互补强度，DCS_ G_2-2为G_2-2中节点失效后G₁和G_2-1对G_2-2的动态互补强度.

从图5可知，关中平原城市群中互补强度较大的交通站点均位于中心城市西安、渭南和咸阳. G₁、G_2-1和G_2-2中西安市的各类客运站点在考虑CE时互补强度最大，分别为1.212、0.569和1.543. 这是因为关中平原城市群是以西安市为中心的单核城市群，当一种交通模式失效而互补客运网络中的节点全部正常运行时，可提供的替代路径最多，对客运网络鲁棒性的提升最大.

与关中平原城市群多模式客运网络中单个节点失效时客运网络性能的下降排序相同，互补强度紧随其后的是咸阳和渭南，但在G_2-2中商洛站的DCS为0.104，略高于渭南站0.095. 这说明关中平原城市群多模式客运网络节点失效对网络性能影响较小的节点，在互补作用下也能给客运网络性能带来较大的提升.

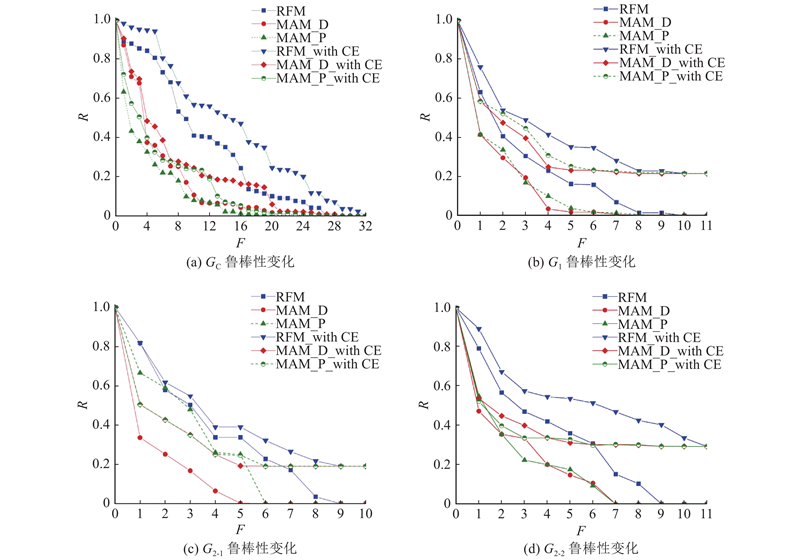
自然灾害、人为破坏和公共卫生事件等突发事件可能导致城市群多模式客运网络中多个节点同时失效，以往研究大多使用随机攻击（RFM）和蓄意攻击（MAM）2种攻击方式模拟各种突发事件^[8,15]，因此采用RFM和MAM 2种方式，模拟突发事件下多个节点同时失效对关中平原城市群客运网络鲁棒性的影响. 在RFM中，节点选择是随机的；在MAM中，节点选择根据其在交通网络中的重要性决定. 在交通网络中，节点度值越大，节点越重要^[23]；删除节点后网络性能变化幅度越大，节点越重要^[24]. 选择节点度值D和受到攻击时的网络性能P下降值作为重要性的评判标准，对应的攻击策略分别为MAM_D和MAM_P，仿真结果如图6所示. 图中，F为节点失效个数，R为鲁棒性，RFM_with CE、MAM_D_with CE和MAM_P_with CE分别表示考虑CE时的RFM、MAM_D和MAM_P攻击策略.

对比随机攻击和蓄意攻击下的关中平原城市群多模式客运网络鲁棒性可知，客运网络节点失效时在随机攻击下有较强的鲁棒性，但蓄意攻击相比于随机攻击能够显著降低城市群多模式客运网络的鲁棒性，更早使客运网络趋于崩溃状态.当图6(b)~(d)中节点失效的比例为60%时，G₁、G_2-1和G_2-2在MAM中几乎失去了所有的性能，网络鲁棒性接近于0；在RFM中保留了至少30%的性能. 考虑CE时，在MAM和RFM中大多数节点失效时，G₁、G_2-1和G_2-2可以保持一定的性能水平. 即使关中平原城市群某个客运网络的所有站点都被蓄意攻击，互补客运网络仍然可以提供补充服务，以保持该客运网络正常运行时性能值的19%以上. 这是因为在客运网络中，节点一旦失效，网络中的许多节点将无法到达. 当考虑CE时，其他客运网络提供了旅客到达目的地的替代路径，此时关中平原城市群客运网络均具有较强的鲁棒性. 从图6(a)可知，无论采取何种攻击策略，当考虑CE时，关中平原城市群多模式互补客运网络G_C的鲁棒性有所提高. 当G_C中节点全部失效时，没有节点可以在异常的情况下提供补充服务，G_C的鲁棒性为0，G₁、G_2-1和G_2-2均处于崩溃状态.

从图5(b)~(d)可知，当G₁、G_2-1和G_2-2中的节点全部失效时，考虑CE时，鲁棒性值分别为0.215、0.190和0.294，这说明分别能够保持初始性能的21.5%、19%和29.4%. 由此可见，在关中平原城市群中普铁网和公路网在节点中断后其他模式客运网络提供的互补效应较强，高铁网最弱. 这是因为从客运网络服务特性的角度选取列车频次和出行时间作为性能计算指标，而高速铁路出行速度快、耗时少，城市群内列车频次较多，当高铁站点失效时，即使有其他出行模式可以提供替代服务，客流量损失也相对较大. 仿真结果表明，面对城市群中多模式交通汇聚的现状，当考虑客运网络的鲁棒性时，应该从系统的角度考虑其他客运网络的CE以及节点之间的相互依赖性.

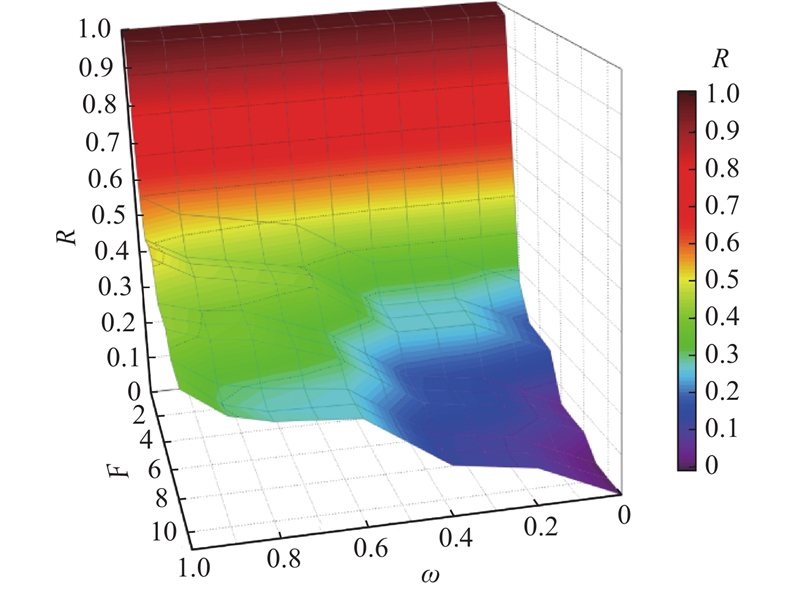
从以上分析可知，G_2-2在互补作用下的鲁棒性提升程度最高，说明客运网络节点失效后，G₁和G_2-1对G_2-2的CE强度最大. 选取普铁网G_2-2为例，研究客运网络鲁棒性随互补客运网络中失效节点个数变化的情况. 当不考虑CE时G_2-2中节点度值和失效后性能损失值前50%的节点失效后，G_2-2鲁棒性几乎为0，其余节点失效对G_2-2鲁棒性无显著影响. 为了得到客运网络间相互影响更显著的结论，选择RFM随机攻击的方式，对G₁、G_2-1和G_2-2进行攻击. 用ω表示互补客运网络G₁和G_2-1中正常运行的站点比例，ω = 0.8表示互补客运网络中80%的站点处于正常状态，20%的站点已经失效. 仿真结果如图7所示.

从图7可知，ω的取值不同对G_2-2节点失效时的鲁棒性有不同的影响. 当G_2-2中的失效节点个数一定时，随着ω的增大，普铁网G_2-2的鲁棒性随之增强. 随着关中平原城市群中的G_2-2节点失效个数增加，为了保持较高的鲁棒性水平，对互补客运网络中正常运行节点的比例要求增高. 这是因为随着ω的提升，当面对节点失效的突发情况时，旅客完成出行的可替代路径增多，对旅客出行的影响降低，客运网络的鲁棒性随之增强.

引入子网敏感度，研究关中平原城市群各客运网络和互补客运网络之间的关系. 子网敏感度是指某一种交通方式站点失效后对互补客运网络的服务功能影响程度^[25]，本文中G_s（s = 1, 2-1, 2-2，分别表示公路网、高铁网和普铁网）的敏感度测度指标M_s计算公式如下：

(9)$ {M_s} = 1 - \frac{{P_{}^{{\rm{ab}}}({{{G}}_{{\rm{C}} - s}})}}{{P_{}^{{\rm{no}}}({G_{\rm{C}}})}}. $

式中：P^no(G_C)为关中平原城市群多模式互补客运网络G_C正常运行状态的性能值，P^ab(G_C-s)为G_s中节点失效后G_C的性能值.

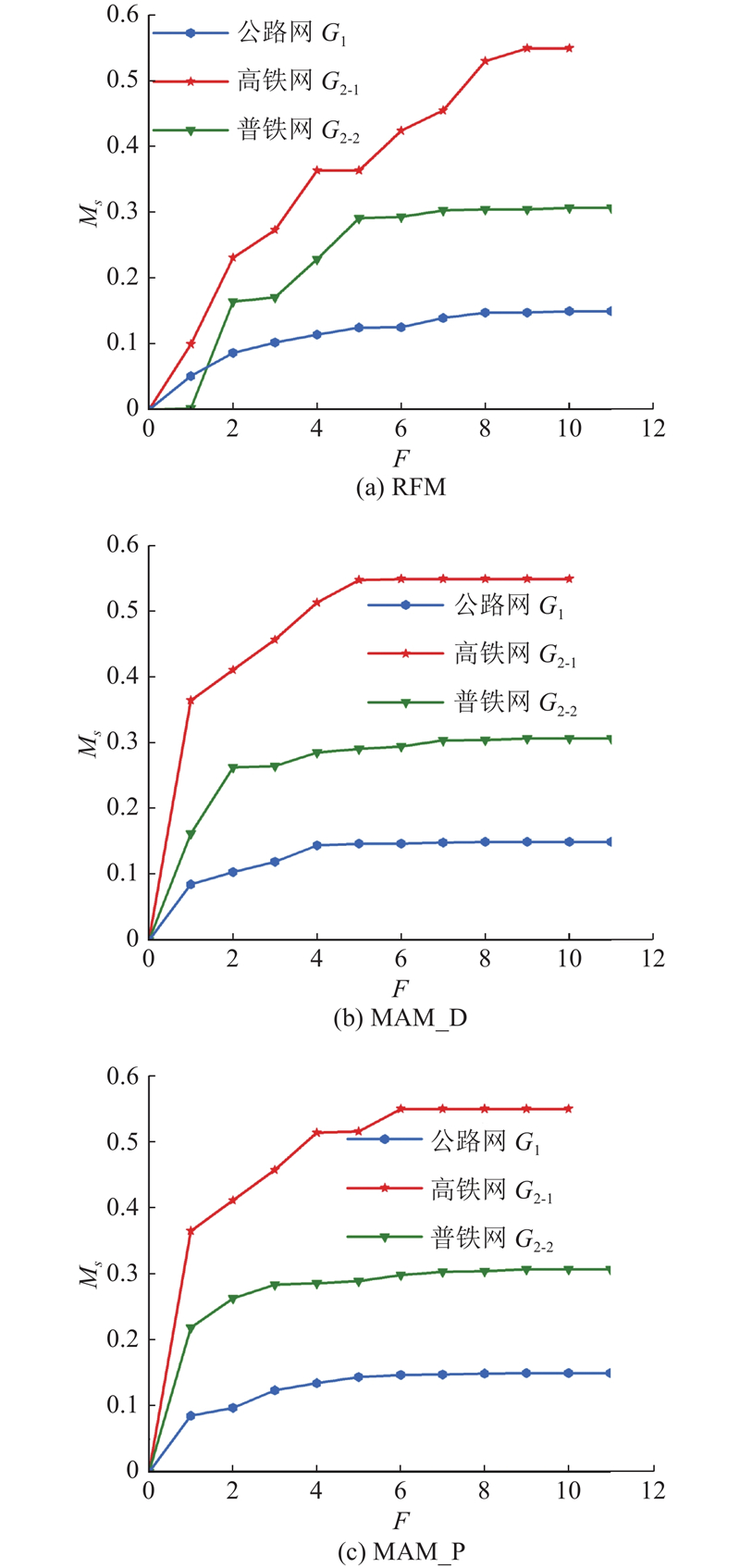
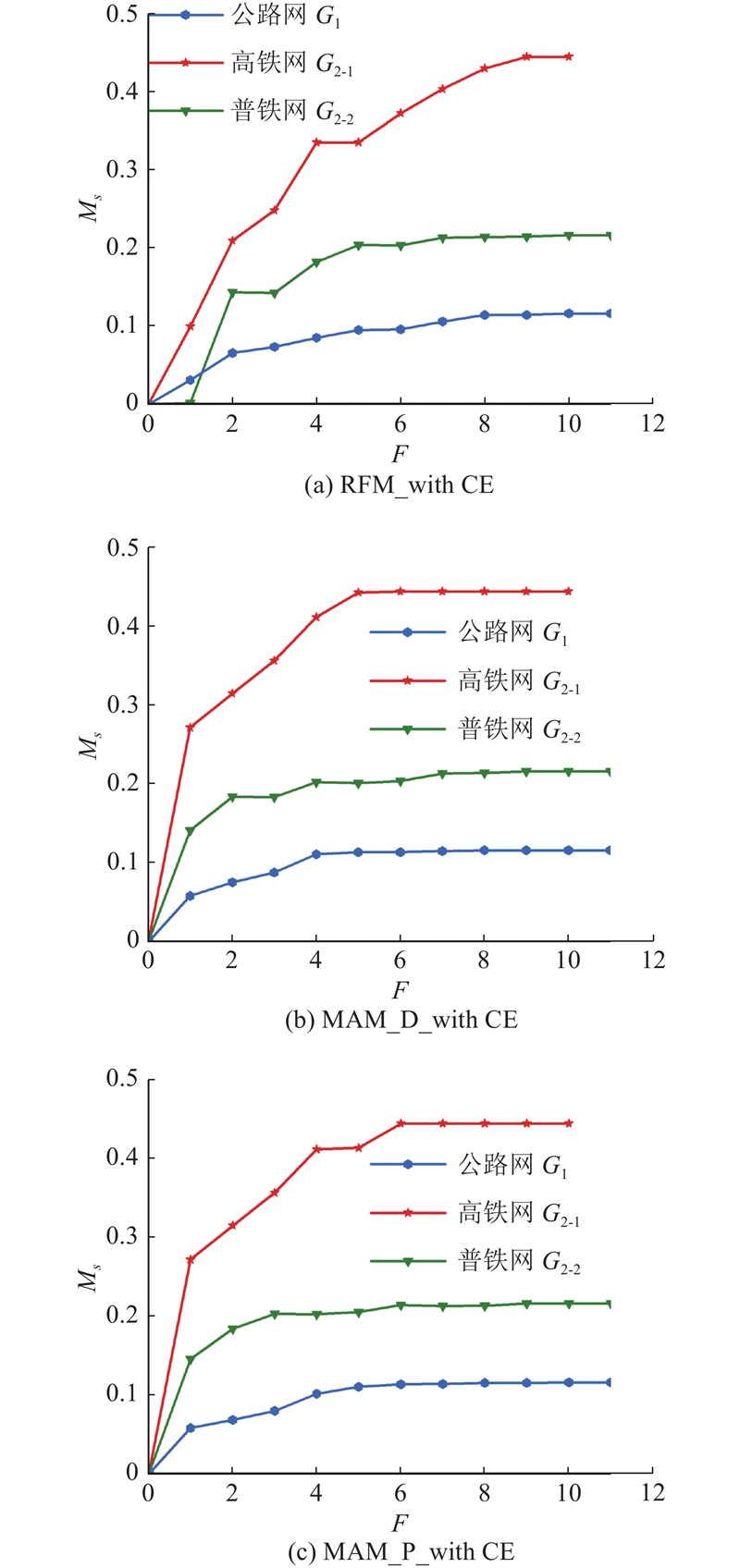
如图8(a)~(c)所示为不考虑CE时客运网络在不同攻击策略下的敏感度变化曲线，如图9(a)~(c)所示为考虑CE时客运网络在不同攻击策略下的敏感度变化曲线. 从图8、9可知，无论在何种攻击策略下，关中平原城市群G₁、G_2-1和G_2-2节点失效对多模式互补客运网络性能影响的敏感度从大到小趋势为：高铁网、普铁网、公路网. 这是因为在城际出行中，当考虑交通服务特性时，高铁具有速度快和效率高的绝对优势，在关中平原城市群中出行频次多，出行时间短，一旦站点失效，对城市群多模式客运网络中的旅客出行影响最大. 相对于铁路出行，公路出行的速度和效率都较低，在关中平原城市群中公路网的网络密度最小，城市间通过公路出行的联系最少；因此，公路站点失效对城市群互补客运网络的敏感度最微弱.

当考虑CE时，关中平原城市群高铁网、普铁网和公路网的敏感度分别从0.550、0.307和0.150下降至0.445、0.217和0.117，下降比例分别为19.1%、29.3%和22.0%，可见CE虽然对子网敏感度排序无影响，但在CE影响下，G₁、G_2-1和G_2-2的敏感度都有不同程度的下降. 由此可见，关中平原城市群多模式客运网络间互相衔接，可以减小单个客运网络节点失效对互补客运网络性能的影响程度，提高整个交通系统的运行效率和鲁棒性.

（1）考虑客运网络的服务特性时，城市群多模式客运网络鲁棒性呈现出差异性和互补性，互补效应对客运网络鲁棒性的影响程度存在空间差异. 无论是否考虑CE，普铁网应对突发事件时的鲁棒性最强，公路网应对突发事件时的鲁棒性最弱. 互补强度较大的交通站点均位于中心城市，但非中心城市的交通站点失效后，城市群多模式客运网络的鲁棒性有明显提升.

（2）城市群多模式客运网络对随机攻击策略有较好的容忍性，在蓄意攻击策略下鲁棒性较差. 当考虑CE时，城市群多模式互补客运网络及单个客运网络的鲁棒性均有明显提升. 多个节点同时失效时，考虑CE时公路网、高铁网和普铁网的鲁棒性提升值分别为0.215、0.190和0.294. 当分析城市群不同客运网络间如何相互影响时，用ω表示公路网和高铁网中正常运行的站点比例，当普铁网节点失效个数不变时，鲁棒性随ω的增大而增强.

（3）CE对城市群中不同客运网络敏感度大小的排序无显著影响，但当考虑CE时，子网敏感度均有不同程度的下降. 无论采取何种攻击策略，当节点失效数量相同时，城市群单个客运网络对多模式互补客运网络性能影响的敏感度从大到小总体趋势为：高铁网、普铁网、公路网. 当考虑CE时，高铁网、普铁网和公路网的敏感度分别下降了19.1%、29.3%和22.0%.

从城市群多模式客运网络互补的视角，提出鲁棒性测度模型，可以有效测度鲁棒性及CE对鲁棒性的提升程度，有利于制定针对性的交通规划策略，以确保城市群交通系统高效运行. 本文仅从空间维度分析城市群多模式客运网络的鲁棒性，客运网络鲁棒性及CE是否会随突发事件发生时间变化，须在今后的研究中进一步分析.