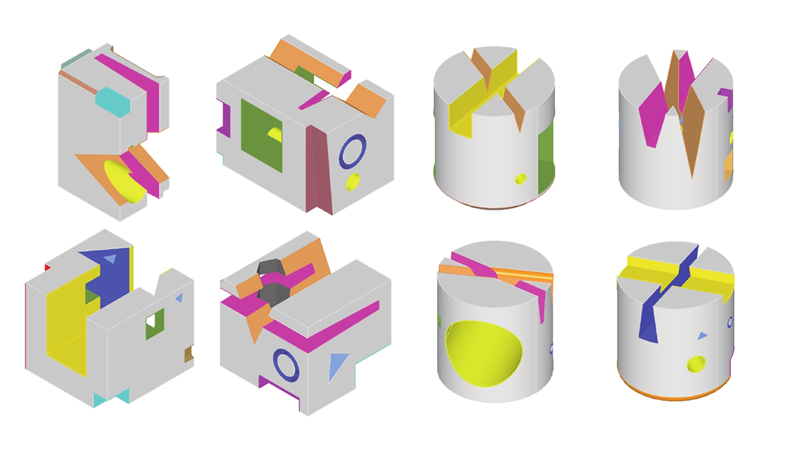
深度学习特征识别方法输入数据的类型可以大致分为体素、多视图、点云、图. Zhang等[7]将深度学习应用到加工特征识别中,提出三维卷积神经网络FeatureNet,通过binvox网格体素库将边界表示模型转化为体素模型,对网络进行训练,以学习加工特征的形状与分布. 在多视图神经网络的启发下,Shi等[8]提出基于多截面视图表示的特征识别深度学习框架MsvNet. MsvNet使用三维模型的截面视图作为神经网络的输入,通过神经网络组合不同视图获得的信息以用于识别. 与二维图像相比,三维点云能够获得更多的空间信息. Ma等[9]通过模型转换和特征采样,构建用于学习三维点云数据的样本库. 基于PointNet[10]对单特征模型进行识别,对点云噪声表现出较好的鲁棒性. 高玉龙[11]提出基于加工面点云深度学习的加工特征识别方法,通过对点云进行随机破坏来模拟特征相交造成的边界破坏. Yao等[12]提出基于层次神经网络的加工特征识别方法,该方法基于聚类和面片重组的多特征分割技术,将复杂的多特征点云模型分割为单特征点云模型进行识别.
基于体素的方法随着体素分辨率的增加,计算复杂度呈3次方增长,导致计算成本高昂. 与基于体素的方法相比,利用基于多视图的方法提高了计算效率与对相交特征的识别能力. 这类方法使用二维图像来表示三维模型,可能会导致几何和拓扑信息的丢失. 这类方法通过预测加工特征的长方体包围盒来粗略定位加工特征,无法精确确定加工特征面. 基于点云的方法在识别复杂零件的加工特征时,往往需要密集的采样点,零件模型的点云表示难以保留拓扑结构信息.
与上述离散化表示方法相比,三维模型的边界表示具有更高的准确性与适用性,能够反映模型的拓扑结构,然而很少有神经网络能够直接读取边界表示模型的信息. 为了解决该问题,Cao等[13]将边界表示模型转化为属性邻接图,通过图神经网络对特征进行识别,这是首次将深度学习应用于三维模型的图表示. 该方法使用平面方程的系数作为节点特征来描述几何形状,无法处理含有曲面的模型.
本文针对复杂结构零部件中相交特征难以识别、无法精确确定加工特征面的问题,基于压缩激励网络和图注意力网络构建神经网络模型,提出零部件加工特征识别网络,在多加工特征零件模型上验证了本文方法的有效性.
1. 基于属性邻接图的零件模型表征
1.1. 属性邻接图的理论基础
1.1.1. 边的凹凸性
三维实体模型中的边是2个相邻面的相交边界,边的凹凸性在一定程度上反映了2个面之间的几何特征. 边的凹凸性定义如下:当边的两相邻面外侧(面法向量的方向)夹角小于180°时,该边为凹边;当边的两相邻面外侧夹角大于180°时,该边为凸边;当边的两相邻面外侧夹角等于180°时,该边为切边.
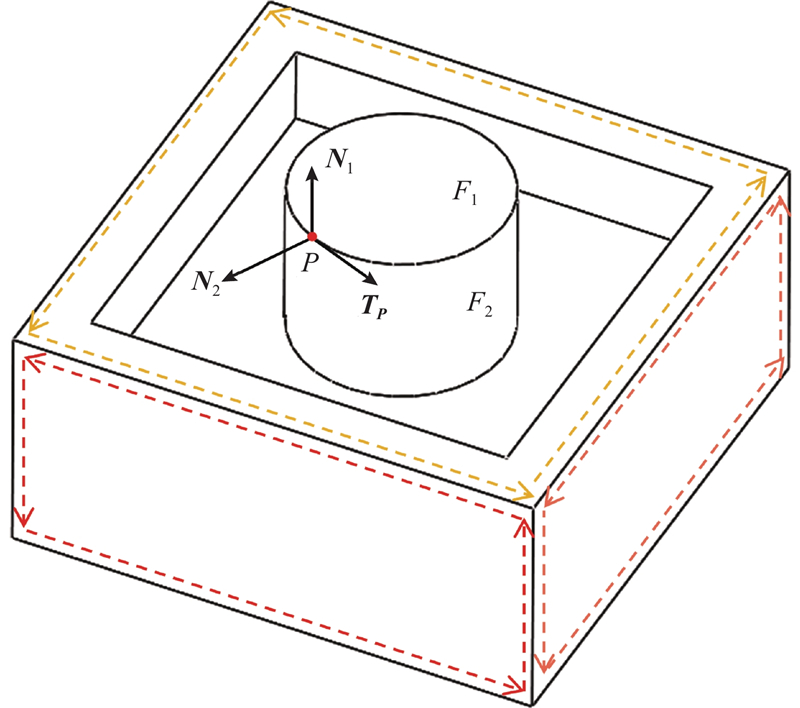
当边的2个相邻面之中的任意一个不是平面时,无法通过直接计算面法向量夹角的方法来判断边的凹凸性,因为非平面的法向量可能随面内位置的变动而变化. 采用如下方法来判断边的凹凸性:假设面Fi与面Fj的公共边为E,公共边E上的任意一点为P,面Fi与面Fj在点P的法向量分别为Ni与Nj,则判断边E凹凸性的具体步骤如下.
1)判断边E和点P在面Fi中的方向,其定义为当沿着边E的方向前进时面Fi始终在其左侧,点P的方向为P在其所处位置的切线方向,记为TP,如图1所示. 图中,虚线为边在各面中的方向.
图 1
2)计算面法向量Ni与Nj的矢量积V,
3)计算TP与V的数量积CE. 若CE < 0,则边E为凹边;若CE > 0,则边E为凸边;若CE = 0,则边E为切边,面Fi与面Fj光滑连接.
1.1.2. 节点与邻接边的属性定义
通过对零部件模型的面与边进行采样,构建其特征矩阵作为属性邻接图节点与邻接边的属性,具体的定义方式如下.
1)节点的属性定义.
a) 节点序号:使用唯一的整数来表示属性邻接图中的一个节点,标识零件模型中对应的面.
b) 面采样点的坐标:使用浮点型变量,标识面上采样点的x、y、z坐标.
面采样点法向量:使用浮点型变量,标识面上采样点的法向量Nx、Ny、Nz.
面的凹凸性:使用浮点型变量,标识面上采样点的高斯曲率K.
2)邻接边的属性定义.
a) 邻接边序号:使用唯一的整数来表示属性邻接图中的一条邻接边,标识零件模型中对应的公共边.
b) 邻接边的起点和终点:使用2个整型变量分别存储邻接边的起始节点序号和终止节点序号,由机械零件模型构建成的属性邻接图本质上是无向图,因此零件模型中的一条公共边对应属性邻接图中的2条有向邻接边,它们的方向相反,这2条有向邻接边对应边界表示模型拓扑结构环中的2条有向边.
c)边采样点的坐标:使用浮点型变量,标识边上采样点的x、y、z坐标.
d) 边采样点切向量:使用浮点型变量,标识面上采样点的法向量Tx、Ty、Tz.
e) 邻接边的凹凸性:使用浮点型变量,标识公共边上采样点的凹凸性.
1.2. 属性邻接图的构建
1.2.1. 边与面的采样算法
为了更好地反映曲线曲率变化明显处的几何特征,满足后续使用的神经网络结构对输入数据尺寸的一致性要求,提出如下的曲线采样算法,具体流程如下.
1)判断模型边的类型,当边为直线时,直接使用等参数采样获得n个采样点返回. 当边为非直线类型时,对曲线进行密集的等参数采样,将采样点数设置为曲线弧长的10倍.
2)计算曲线上相邻点之间的距离,对距离进行累加并归一化,得到曲线的累计距离分布. 计算曲线在各点处的曲率,对曲率进行累加并归一化,得到曲线上的累计曲率分布. 将累计距离分布和累计曲率分布相加并归一化,得到混合分布.
3)生成n个在[0, 1.0]上均匀分布的采样点p,根据混合分布找到离p最近的点的索引,得到索引集合p_index,去除p_index中重复的索引.
4)若p_index中的索引数小于n,则需要添加更多的采样点.
a) 计算每个区间的长度,其中区间由2个相邻的索引p_index[i−1]和p_index[i]之间的点组成.
b) 计算每个区间的平均曲率,找到平均曲率最大的区间. 在该区间内进一步细分采样,得到新的采样点的索引.
c) 将新的索引添加到索引集合p_index中,对索引集合进行排序.
d) 重复步骤a)~c),直至p_index中的索引数等于n.
5)根据p_index中的索引,返回曲线上对应的n个采样点.
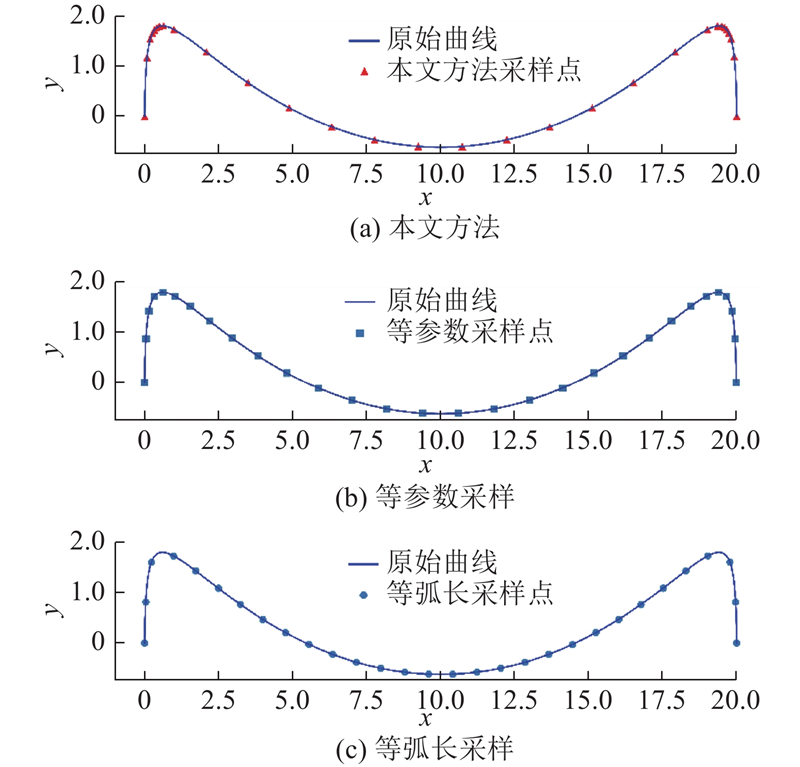
在n = 30的情况下,上述曲线采样算法与等参数采样、等弧长采样在同一段曲线上的采样结果如图2所示. 可以看出,本文方法在曲线曲率变化明显的位置采样密集,在曲线平坦的位置会设置一定数量的采样点.
图 2
为了使不同曲面上的采样点数一致,尽可能表征曲面的形状,使用边缘样本交叉积曲面采样算法[14]. 利用下式依次计算曲面在节点方向上的边际累积面积:
式中:
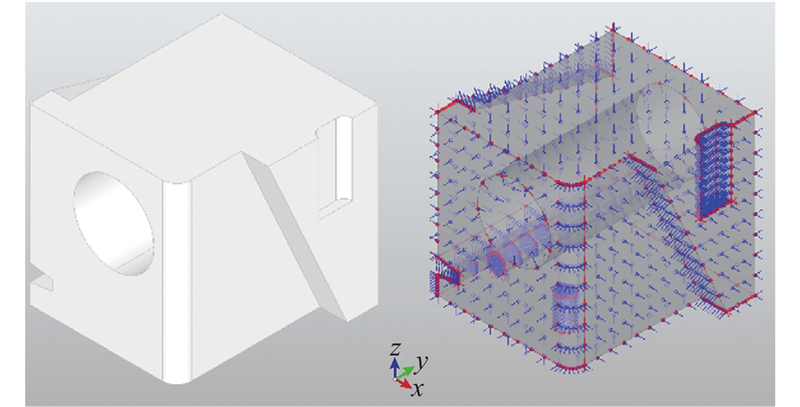
如图3所示为零件模型及对应的采样点分布. 图中,面上的采样点和边上的采样点均用点表示出来. 在采样点处边的切向量方向与面的法向量方向均使用短线表示.
图 3
1.2.2. 点采样曲面高斯曲率的计算
面的凹凸性通常根据曲面在某一位置处高斯曲率的正、负来判断,胡盼旺[15]通过计算曲面上某点处的法向量与曲率圆的位置关系来判断高斯曲率的正负性. 对于凹凸性随位置而变化的自由曲面,利用该方法无法判断整体的凹凸性,因此直接计算曲面上各采样点处的高斯曲率.
Meyer等[16]基于三角网格模型提出Voronoi曲率估算方法,通过一簇三角网格来线性逼近光滑曲面,将网格顶点处的度量定义为该顶点邻域的空间平均值. 在局部有限体积区域内,由高斯-博涅定理可得
式中:
利用边缘样本交叉积曲面采样算法对曲面进行采样,获得曲面的点集模型. 与三角形网格模型相比,点集模型不标识某点pi的邻接点集合N(pi),因此使用K近邻算法确定邻接点集合N(pi). Pauly等[17]证明密集的点采样可以替代三角形网格的连通性信息,不会显著降低简化曲面的质量.
直接使用线性扫描计算可知,K近邻中2点之间的距离的时间复杂度为O(n2). 为了提高搜索效率,使用基于k-d树的K近邻算法.
k-d树是空间分区数据结构,用于组织k维空间中的点,k-d树本质上是二叉搜索树,其中每个节点均为k维点. k-d树搜索可以在时间复杂度为O(log2 n)的情况下找出距离输入点pi最近的k个点,具体步骤如下.
1)从根节点开始,递归地向下访问树,直至到达叶子节点.
2)将该叶子节点视为当前最近点,计算该叶子节点与输入点pi的欧氏距离dmin.
3)从叶子节点开始进行回溯,对遍历到的当前点开展如下操作.
a) 计算当前点到输入点pi的距离dcur, 若dcur < dmin,则将当前点作为当前最近点.
b) 检查以输入点pi为球心、dmin为半径的超球体是否与另一子树节点相交. 若相交,则从另一子树节点开始向下搜索;若不相交,则继续向上进行回溯.
4)当回溯至根节点时,当前最近点为距离输入点pi最近的点,将其添加至近邻点集合中. 重复步骤1)~3) K次,即可完成搜索.
通过基于k-d树的K近邻算法获取点pi的近邻点集合N(pi),分别计算点pi与其近邻点形成的夹角之和与点pi处的Voronoi区域面积AM,代入式(6),可以计算得到该点处的高斯曲率.
1.2.3. 属性邻接图的构建算法
在对节点与邻接边属性定义的基础上,属性邻接图构建算法的具体步骤如下.
1)使用NetworkX开源库构建没有节点与邻接边的空图,读取零件边界表示模型与标签文件,对零件模型进行解析.依次遍历模型中的所有面、边与点,构建Map类,将面、边、顶点对象的哈希值映射至整型索引.
2)遍历零件模型中的所有面,对于面Fi,将面对象与其序号作为节点参数添加至步骤1)的空图中. 遍历零件模型中的所有边,对于边Ej,将边对象、边序号与相邻面序号作为邻接边参数添加至图中,完成邻接图表达结构的创建.
3)创建节点属性列表,遍历图中的节点,依次计算节点面对象上采样点的坐标、法向量与凹凸性,合并后添加至节点属性列表中. 创建邻接边属性列表,遍历图中的邻接边,依次计算边对象上采样点的坐标、切向量与凹凸性,合并后添加至邻接边属性列表. 完成零件模型属性邻接图的构建.
假设构建的属性邻接图中节点个数为num_nodes,邻接边条数为num_edges,曲面在各方向上的采样点数均为m,曲线上的采样点数为n,则节点面的特征矩阵尺寸为[num_nodes,m,m,7],邻接边的特征矩阵尺寸为[num_edges,n,7].
2. 基于双层注意力机制的加工特征识别网络
2.1. 加工特征识别网络架构的设计
构建的加工特征识别网络整体架构如图4所示,网络整体上可以分为基于压缩激励网络的特征提取部分与基于图注意力网络的节点分割部分. 节点与邻接边的特征矩阵分别经过对应的特征提取网络. 压缩激励网络部分的输出,作为图注意力网络的输入,在图注意力网络中使用节点级与邻接边级的双层注意力机制,在学习节点嵌入的同时学习边的嵌入,在每个注意力层进行更新. 将学习到的节点嵌入经过多层感知机与Softmax函数,输出每个节点所属各加工特征类别的概率.
图 4
2.2. 基于压缩激励网络的特征提取
图 5
表 1 节点特征提取网络的参数
Tab.1
| 节点特征提取网络各层 | 输入特征尺寸 | 输出特征尺寸 |
| Conv2d(7,64,3,1,1) | (Nv,7,10,10) | (Nv,64,10,10) |
| SE(16) | (Nv,64,10,10) | (Nv,64,10,10) |
| Conv2d(64,128,3,1,2) | (Nv,64,10,10) | (Nv,128,5,5) |
| SE(16) | (Nv,128,5,5) | (Nv,128,5,5) |
| Conv2d(128,256,3,1,2) | (Nv,128,5,5) | (Nv,256,3,3) |
| SE(16) | (Nv,256,3,3) | (Nv,256,3,3) |
| MixPool | (Nv,256,3,3) | (Nv,256,1,1) |
| Reshape | (Nv,256,1,1) | (Nv,256) |
| Linear | (Nv,256) | (Nv,64) |
在每一层卷积运算后,均开展了批量规范化处理. 即对所有批次中同一个信道的数据进行规范化处理,使得每一层神经网络的特征能够保持相同的分布.
表 2 边特征提取网络的参数
Tab.2
| 边特征提取网络各层 | 输入特征尺寸 | 输出特征尺寸 |
| Conv1d(7,64,3,1,1) | (Ne,7,10) | (Ne,64,10) |
| SE(16) | (Ne,64,10) | (Ne,64,10) |
| Conv1d(64,128,3,1,2) | (Ne,64,10) | (Ne,128,5) |
| SE(16) | (Ne,128,5) | (Ne,128,5) |
| Conv1d(128,256,3,1,2) | (Ne,128,5) | (Ne,256,3) |
| SE(16) | (Ne,256,3) | (Ne,256,3) |
| MixPool | (Ne,256,3) | (Ne,256,1) |
| Reshape | (Ne,256,1) | (Ne,256) |
| Linear | (Ne,256) | (Ne,64) |
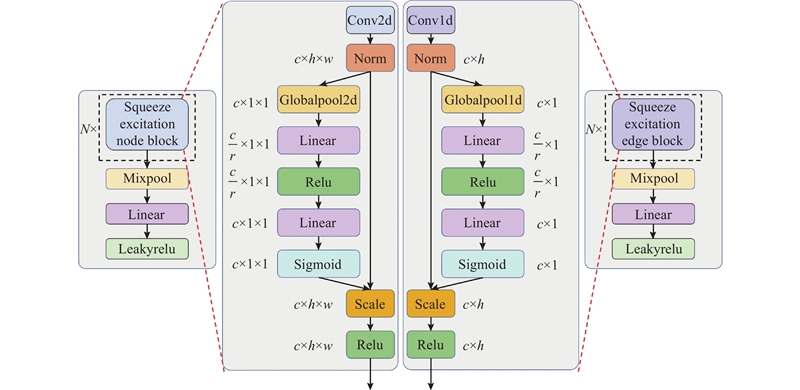
规范化后的特征进入压缩激励层,在该层中会执行压缩和激励2步操作. 压缩操作通过全局平均池化将全局的空间特征编码为信道描述器,生成信道维度特征响应的全局分布描述. 在压缩操作后的激励操作用来获取信道之间的相关性,为了提升泛化能力及降低模型复杂度,使用2个线性层分别进行降维与升维,将各信道的激活值与原始特征相乘,得到压缩激励层的输出.
在经过压缩激励层后,使用混合自适应池化对特征矩阵进行降维处理,去除冗余信息. 混合池化将平均池化与最大池化相结合,可以表示为
在使用的混合池化中,
在卷积网络预处理部分的最后,通过一组线性变换将每个节点与每条邻接边的特征转换为64维特征向量,通过LeakyRelu函数进行激活. 处理后的节点与邻接边特征矩阵与图结构信息一并传入图注意力网络中,学习节点与邻接边嵌入.
2.3. 基于图注意力网络的节点分割
2.3.1. 节点注意力模块
图注意力网络部分使用2级节点注意力模块,单个模块的构造如图6所示. 为了提高注意力机制的泛化能力,每个模块中均使用多头注意力层.
图 6
在每个单头注意力层需要生成目标节点与每个邻域节点之间的注意力系数. 注意力系数不仅包括2个节点的特征,还包括连接它们的边的特征. 假设当前为第l级节点注意力模块,邻域节点vj与边eij对节点vi的相对重要性εij可以表示为
式中:Wn、We分别为对输入节点特征与输入边特征进行线性转换的可学习权重矩阵;a为共享的自注意力机制,在本文中为单层前馈网络. 利用Softmax函数对εij进行归一化,得到注意力系数αij.
聚合的节点特征中不仅包含目标节点vi一阶邻域的节点特征,还包括目标节点vi本身的特征,这意味着式(9)中会出现自环eii的特征xii. 由零件模型构建成的属性邻接图中通常不会出现自环,也没有自环特征xii. 为了解决该问题,特征矩阵在输入模型之前,每个节点均添加一个自环,自环特征xii计算为所有与节点vi相连的边特征的平均值,可以表示为
在得到每个邻域节点的注意力系数αij后,通过对这些邻域节点特征进行加权求和,得到第k个单头注意力层的输出特征
在多头注意力机制下,可以对各单头的输出进行多维拼接或者取平均,在2级节点注意力模块中均对单头输出的特征进行拼接. 拼接后的特征经过由2层全连接层组成的多层感知机后,即为单个节点注意力模块的输出.
从式(12)可以看出,生成新的节点特征时只聚合了节点特征,边的特征仅在权重计算这一过程中起作用. 这样设计的原因在于后续生成边特征时,将节点特征作为其中一部分,若在每次迭代节点特征时将边特征合并进去,则可能会使整个网络变得更加混乱.
2.3.2. 边注意力模块
图注意力网络部分使用了2级边注意力模块,在每个边注意力模块中通过融合节点特征来生成新的边特征,因此需要学习边上节点相对于边的注意力系数.
边上的节点vp对于边eij的归一化注意力系数可以表示为
在得到每个边上节点的注意力系数βijp后,对这些节点特征进行加权求和,再与边特征xij相加,可得第k个单头注意力层的边输出特征
每一级节点注意力模块输出的节点特征在传递给下一级模块的同时,也会传递到最后一级的合并层中进行拼接. 拼接后的特征经过由3层线性层组成的多层感知机与Softmax后,输出归一化概率. 该概率为面节点属于不同加工特征标签的概率,其中最大概率确定为该面节点所属的加工特征.
3. 实验结果与分析
3.1. 实验设置
图 7
图 8
图 9
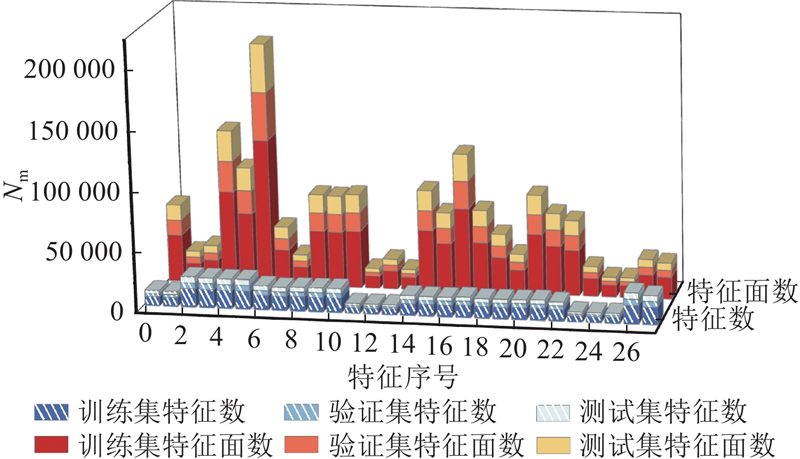
图 9 多加工特征数据集特征与特征面分布
Fig.9 Feature and feature surface distribution of multi-machining feature dataset
由于PointNet与DGCNN均为基于点云的深度学习模型,将上述3种数据集中的零件模型转化为具有固定数量的点云数据. 对零件模型进行三角剖分转化为三角网格模型,以每个三角形的表面积为权重,在每个三角形内进行均匀采样,以生成固定数量的点,同时需要存储零件模型面与点云中单个点之间的映射,以方便比较不同网络模型在每个面上的识别结果. 数据集中的每个零件模型均被转化为含有2 048个点的点云数据.
3.2. 加工特征识别
为了对不同模型的加工特征识别效果进行评价,选取准确率、平均类准确率与交并比3种指标. 准确率是正确分类的样本数占总样本数的比例,可以计算为
式中:N为类别数,TPi为第
平均类准确率是指所有类别准确率的平均值,计算公式为
交并比IoU是指预测结果和真实结果的交集与并集的比值,可以量化预测结果与真实结果之间的重叠度.
在本文方法与UV-Net上计算每个模型面的识别结果,在PointNet与DGCNN 2种基于点云的模型上分别计算每个模型面与每个点的识别结果.
图 10
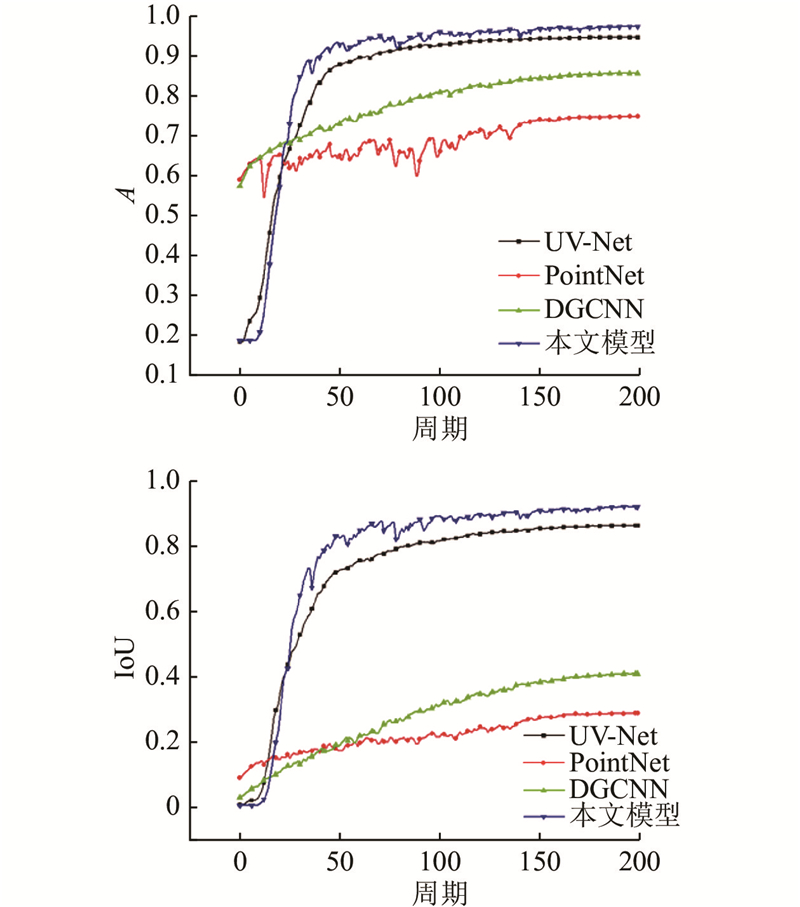
图 10 多加工特征数据集验证集的准确率与交并比曲线
Fig.10 Accuracy and IoU curves of multi-machining feature validation set
表 3 多加工特征数据集的不同模型实验结果比较
Tab.3
| 模型 | A | Apc | IoU | |||||
| 基于面 | 基于点 | 基于面 | 基于点 | 基于面 | 基于点 | |||
| 本文 模型 | 97.35 | — | 95.15 | — | 92.16 | — | ||
| PointNet | 38.85 | 75.52 | 32.04 | 35.49 | 20.45 | 27.53 | ||
| UV-Net | 94.65 | — | 91.25 | — | 86.31 | — | ||
| DGCNN | 51.44 | 85.65 | 46.06 | 54.08 | 31.99 | 40.95 | ||
图 11
3.3. 消融实验
为了验证输入特征及加工特征识别网络中各部分组件对最终识别效果的影响,设置如下3种参数状态与完整网络进行对比.
去除邻接边特征:该组设置去除了输入特征中的邻接边特征,只保留了节点特征,还去除了压缩激励网络中的边特征提取部分与图注意力网络中的边特征部分.
去除图注意力网络结构:该组设置去除了图注意力网络部分,将其替换为同等参数的多层感知机.
只保留零件拓扑结构特征:该组设置中去除了压缩激励特征提取部分,将图中的节点和边特征设置为从正态分布中随机采样的噪声,使得网络仅使用零件的拓扑结构特征来进行特征识别.
利用上述4种模型,在多加工特征数据集上进行消融实验,实验结果如表4所示. 与完整网络模型相比,去除邻接边特征的模型在3种指标上略有下降,表明邻接边特征对特定特征模式的识别效果的贡献更明显. 去除图注意力网络的模型的3种指标均显著下降,相较于多层感知机,图注意力网络能够更好地捕捉特征组合的内在模式,减少图中噪声信息的干扰. 只保留拓扑结构的网络模型对加工特征的识别效果较差,与传统子图同构方法难以识别复杂特征的局限性相符合.
表 4 消融实验不同参数结果的比较
Tab.4
| 模型 | A | Apc | IoU |
| 完整网络模型 | 97.35 | 95.15 | 92.16 |
| 去除邻接边特征 | 96.36 | 93.46 | 89.60 |
| 去除图注意力网络 | 85.71 | 86.65 | 78.52 |
| 只保留拓扑结构 | 40.25 | 27.11 | 17.12 |
消融实验的结果可以进一步说明本文方法的优势. 本文方法利用了零件模型的面特征与边特征,结合了零件模型的拓扑结构,应用图注意力网络对特征信息进行更好地捕捉. 这3个方面有机地结合在一起,形成高效、准确的加工特征识别框架,表现出优异的识别效果和泛化能力.
4. 结 语
本文提出基于双层注意力机制的加工特征识别网络,通过压缩激励模块提取节点与邻接边的特征,提取后的特征经过节点级与邻接边级的双层注意力网络后输出每个节点对应的加工特征. 本文方法在多加工特征零件数据集上与其他3种特征识别方法进行实验对比,在3种指标上均取得了最优结果. 通过消融实验,研究各部分组件对特征识别效果的影响. 利用本文所提的加工特征识别方法,可以部分地解决相交特征的识别问题,但对于存在面合并的相交特征,尚未能解决公用面的特征归属问题,需要在下一阶段的研究工作中继续探索.
参考文献
Spatial reasoning for the automatic recognition of machinable features in solid models
[J].DOI:10.1109/34.250845 [本文引用: 1]
A hint-based machining feature recognition system for 2.5 D parts
[J].DOI:10.1080/00207540600919373 [本文引用: 1]
Manufacturing feature recognition method based on graph and minimum non-intersection feature volume suppression
[J].
Recognition of maximal features by volume decomposition
[J].DOI:10.1016/S0010-4485(01)00080-X [本文引用: 1]
Featurenet: machining feature recognition based on 3d convolution neural network
[J].DOI:10.1016/j.cad.2018.03.006 [本文引用: 1]
A novel learning-based feature recognition method using multiple sectional view representation
[J].
A machining feature recognition approach based on hierarchical neural network for multi-feature point cloud models
[J].DOI:10.1007/s10845-022-01939-8 [本文引用: 1]
Curvature based sampling of curves and surfaces
[J].
Dynamic graph CNN for learning on point clouds
[J].