目前大部分研究的重点集中在如何实现更优性能的光开关单元和光开关阵列,光学器件的瞬态响应性能大都利用波形发生设备进行验证,对与光芯片配合的电学模块关注相对较少. 实际上,与硅光器件紧密结合的电学驱动模块作为光互连系统中不可缺少的组件,影响着系统的通信速率和可靠性,有着巨大的价值和潜力. 在光交换系统的研究中,光电片上集成是未来发展的主要趋势[11-14],但受到复杂度高、成本昂贵和工艺难度大的限制. 板级驱动电路具有低成本、可靠性高、便于维护等优势,目前仍然是光互连系统中电学模块的主流解决方案. Jiang等[15]制作驱动电路并实现了6 ns的阵列切换时间,但仍无法完全满足高速光交换系统的需求,提示该领域还有一定的提升空间.
随着光通信技术的发展和光开关性能的提升,驱动电路需要不断地提高性能和可靠性,以实现更高效、更实用的系统. 另一方面,从电路设计的角度来说,光开关单元作为负载,很大程度上影响着电路系统的功耗、稳定性、阻抗匹配等关键因素,所以建立完整、准确的光开关单元电学模型对电学模块的分析、仿真和设计有着重大意义.
本文提出并验证了光开关单元的等效电学模型,利用该模型能够定量地描述光开关单元的瞬态特性,将光开关单元工作复杂的物理过程简化为电学模型分析. 将该模型作为负载,针对光开关阵列设计高速驱动控制电路,结合仿真探究电压尖峰对光开关单元瞬态响应的影响. 实测结果表明,驱动电路输出高速切换的可调电压信号,避免了光信号响应速度受电信号切换速度限制的问题. 光开关阵列达到ns级的开关时间,驱动电路配合光开关阵列实现了较先进的高速光交换系统.
1. 光开关单元及其等效电学模型
1.1. 光开关单元的基本结构和工作原理
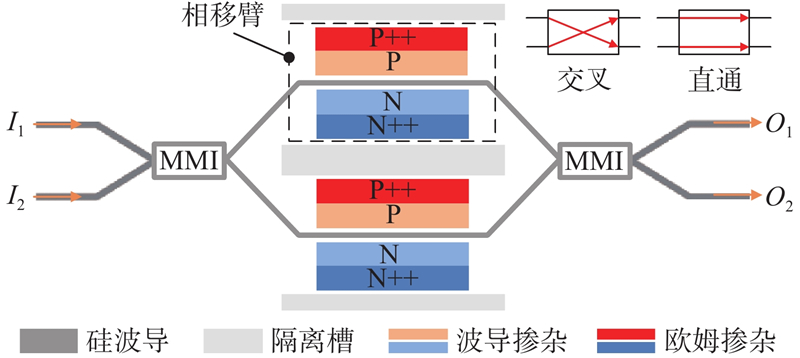
光开关单元的基本结构如图1所示,由2×2多模干涉耦合器(multimode interference coupler,MMI)和相移臂组成. 多模干涉耦合器具有带宽大、工艺容差大的优点,是光开关设计中耦合分束部分的理想选择[16]. 为了提升器件的响应速度,目前高速电光开关相移臂设计的主流方案采用正偏PIN结的结构,利用该结构能够实现较高的调制效率[17]. 如图1所示为相移臂的物理结构. 在硅波导两侧,P型和N型波导掺杂区域与本征半导体接触构成PIN结,接触界面形成空间电荷区,电荷动态平衡并产生自建电场,克服自建电场所需的电压称为PIN结的开启电压. P++与N++是与金属电极连接的欧姆掺杂区域,能够减小金属与半导体之间的接触电阻[18].
图 1
为了减小器件的开关功耗,光开关单元设计为双臂相位调制并加入光学相位预偏置,采用推挽(push-pull)驱动方式,即在光开关一端相对于基准电压分别施加正、负电压来调整2个相移臂的状态. 光开关单元在该驱动方式下,相移臂只要移相π/2,即可实现状态切换[21].
1.2. 光开关单元等效电学模型的提出及验证
光开关单元状态切换是通过驱动相移臂,改变两臂的有效折射率实现的. 通过建立等效电学模型,可以定量地描述光开关单元的电学特性,将光开关单元工作复杂的物理过程简化为电学模型分析. 光开关单元作为驱动电路的负载,影响电路系统的功耗、稳定性、阻抗匹配等关键指标. 需要建立完整、准确的光开关单元电学模型,以便于仿真和系统设计.
图 2
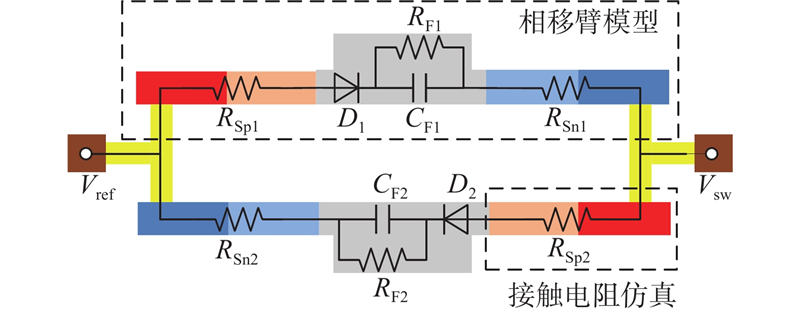
图 2 光开关单元等效电学模型的示意图
Fig.2 Schematic diagram of equivalent electrical model of photonic switch cell
该模型中参数的数值由光开关单元的结构参数和工作条件共同决定. 根据所设计光开关单元的尺寸参数和掺杂浓度,在软件Silvaco下的组件DeckBuild中建立如图2所示的相移臂模型. 通过仿真得到工作电压下PIN结等效电容CF = 35 pF. 对P++欧姆掺杂区域和P波导掺杂区域进行直流仿真,得到接触电阻RSp = 13 Ω. 同样地,可以得到RSn = 10 Ω,RS = 23 Ω.
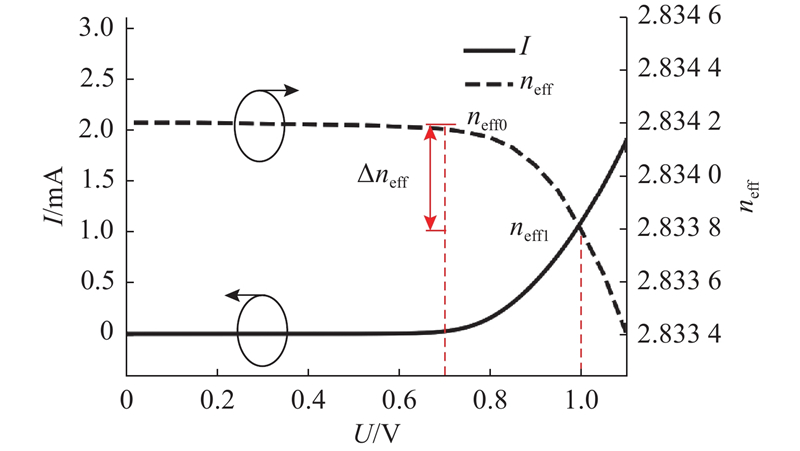
施加工作电压驱动光开关状态切换,推挽驱动方式下,仅有一个相移臂中的PIN结导通,另一相移臂中的PIN结截止,故单个相移臂电学响应的仿真结果能够表征光开关单元的性能. 设置激励信号,对光开关单元的直流特性和瞬态特性进行仿真. 如图3所示为光开关单元伏安特性的仿真结果,电压扫描范围为0~1.1 V. 图中,U为电压,I为电流,neff为有效折射率. 光开关单元的开启电压为0.7 V,开启后光开关单元电流与电压呈指数关系,neff随电压的增大而减小. 相移臂相位差变化量Δφ与有效折射率变化量Δneff的关系为
图 3
图 3 光开关单元伏安特性的仿真结果
Fig.3 Simulation results of volt-ampere characteristics of photonic switch cell
式中:λ为真空下光的波长,L为相移臂的长度. 光开关状态切换所需的Δφ为π/2,PIN结未导通时相移臂的有效折射率记为neff0. 根据所设计的相移臂长度并结合式(1),能够计算出光开关状态切换所需的有效折射率变化量Δneff,得到状态切换完成后的有效折射率neff1,对应的工作电压为1 V,工作电流约为1.1 mA.
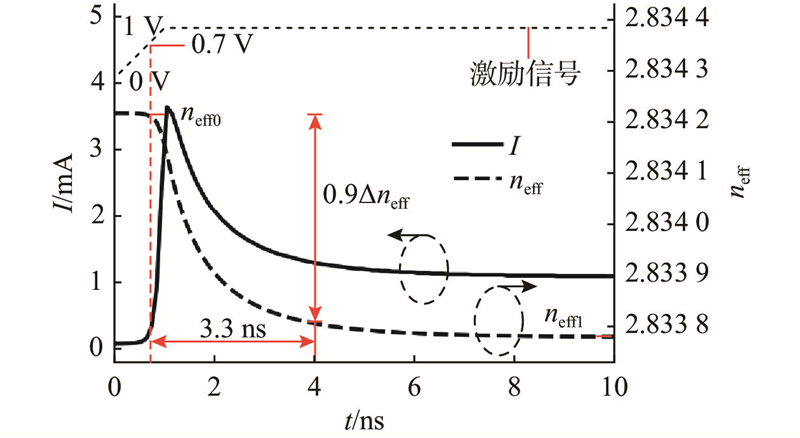
等效电容CF表征的PIN结电容很大程度上决定了光开关单元的切换时间[22]. DeckBuild中无法仿真内部PIN结电容的电压响应情况,但能够得到相移臂整体的电流响应情况,光开关单元切换过程中二者能够对应,故用相移臂电流作为表征参数来分析光开关单元的瞬态特性. 瞬态仿真使用的激励信号的上升时间为1 ns,高、低电平分别为0 V和1 V的方波. 如图4所示为光开关切换过程中相移臂的电流和有效折射率的变化情况. 在激励信号电压大于开启电压0.7 V后,光开关单元开始状态切换. 由于PIN结电容的存在,相移臂电流迅速产生跳变并逐步恢复至稳态,有效折射率由PIN结未导通时的neff0逐步变化为工作电压下的稳定值neff1,光开关切换完成. 对于有效折射率变化量Δneff取90%的变化范围,近似得到光开关单元切换时间的仿真结果为3.3 ns.
图 4
图 4 光开关切换过程中相移臂电流和有效折射率的变化
Fig.4 Variation of phase shifter current and effective refractive index during photonic switch cell switching
在软件ADS(advanced design system)中建立等效电学模型,将该模型的电学仿真结果与光开关单元的仿真结果进行比较,评价模型的有效性. 根据光开关单元仿真的开启电压,等效电学模型中二极管D的开启电压取0.7 V. 在关注的工作范围内,忽略RF随驱动电压的变化,将RF设为固定阻值,以简化分析. 根据光开关单元1 V工作电压下对应的电流,结合仿真确定RF的取值为200 Ω,以保证稳态工作时等效电学模型与光开关单元的直流特性一致.
使用与光开关单元瞬态仿真相同的激励信号仿真等效电学模型,如图5所示为等效电学模型和光开关单元瞬态响应过程中回路电流的对比. 可知,二者表现出一致的瞬态特性,能够验证提出模型的有效性.
图 5
图 5 等效电学模型和光开关单元的瞬态特性对比
Fig.5 Comparison of transient characteristics between equivalent electrical model and photonic switch cell
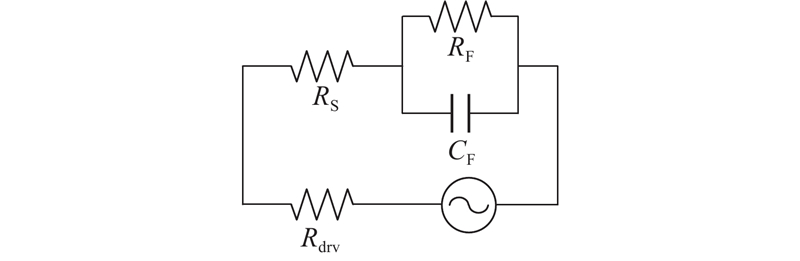
利用该模型,能够指导光开关的分析与设计. 在光开关切换过程中,相移臂电流变化与等效电容CF上的电压变化相对应,CF的电压变化不存在跳变,更易于分析和计算. 分析等效电学模型的瞬态响应,在模型中的二极管导通后,CF开始充电,故略去二极管模型,以简化分析. 此时信号源驱动单个相移臂的电路图如图6所示. 图中,Rdrv为信号源的内阻.
图 6
图 6 等效电学模型的瞬态响应分析
Fig.6 Transient response analysis of equivalent electrical model
此时,图6中系统的时间常数τ为
切换时间与
2. 电路设计
2.1. 电路方案的设计及仿真
根据光开关单元的特性,驱动电路在保证驱动能力和输出电压精度的前提下,还需要能够实现驱动电压的快速切换,以满足光开关ns级开关时间的要求. 若电信号的切换时间过长,光开关单元受电信号的限制,则无法充分发挥光学器件的性能. 根据光开关单元瞬态响应的结果,驱动电路要求实现1 ns以下的切换时间. 控制信号要求能够同时控制光开关阵列中所有光开关单元的状态.
结合图7所示的系统框图,对光开关阵列高速驱动控制电路的方案进行说明:数模转换器(DAC)输出Cross态和Bar态下的工作电压,接入运算放大器进行功率放大保证驱动能力,输出信号分别为Vcross和Vbar. 在推挽驱动方式下,光开关一端接入预设的基准电压Vref,模拟开关器件分别选通2个工作电压,输出信号Vsw接入光开关的另一端,光开关两端施加的电压为Vsw与Vref的差值. 光开关阵列工作时,上位机与现场可编程逻辑门阵列 (field programmable gate array,FPGA)采用通用异步收发器(universal asynchronous receiver transmitter,UART)方式通信,FPGA向模拟开关发送逻辑信号,控制光开关状态的切换.
图 7
图 7 光开关阵列高速驱动控制电路的系统框图
Fig.7 System block diagram of high-speed driving control circuit for photonic switch matrix
在提出的电路方案中,DAC器件须满足0.01 V的最小精度,以保证光开关工作电压的准确性. 为了满足驱动电压快速切换的要求,与模拟开关器件配合的运算放大器须具备高压摆率和高增益带宽积的特性. 此类高速运放的输出电阻在较高的工作频率下都接近于零,使得图6所示电路的系统时间常数尽可能小. 模拟开关器件考虑尽量短的切换时间,所选取器件的切换时间仅为0.5 ns,但只能在正电压下工作. 为了配合模拟开关器件,将基准电压设置为正电压,此时光开关单元一端接入正基准电压,另一端在2个工作电压间切换,能够满足推挽驱动下正、负电压的需求.
在光开关单元负载被上拉和下拉的过程中,基准电压受输出电流的影响,会产生偏移. 若光开关阵列共用一个基准电压平面,当光开关阵列处于不同的工作状态时,流经基准电压平面的电流各不相同,则将导致基准电压平面产生不同的偏移量,使得光开关单元两端的电压无法保持稳定的数值. 为了保证基准电压的稳定可控,对于各个光开关单元建立独立的驱动回路,此时回路中的参考电压平面只流过单个光开关单元极小的工作电流. 各个光开关单元的基准电压通过高速运算放大器输出得到,高速性能可以使得基准电压在切换过程中快速达到稳态,较小的输出电阻和工作电流使得基准电压产生的偏移量可以忽略不计.
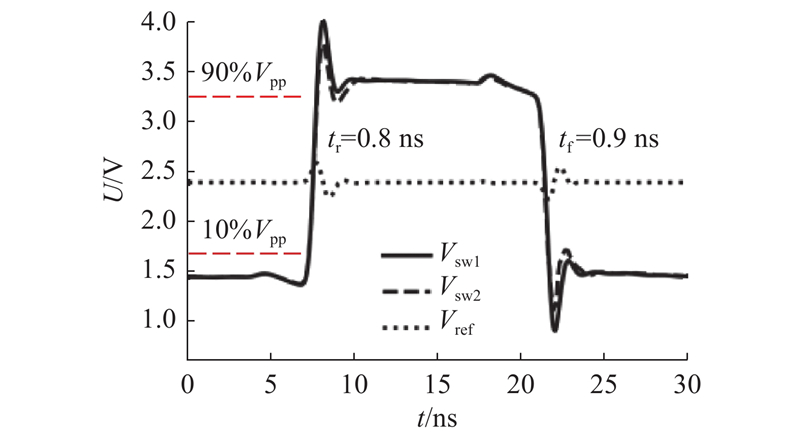
通过仿真,对设计的电路方案进行验证. 在Spice软件中调用所选取的器件,将等效电学模型作为负载接入电路,设置激励信号控制模拟开关切换,得到如图8所示的电路瞬态响应仿真结果. 仿真结果表明,在驱动电压切换的过程中,基准电压Vref产生微小的抖动后迅速恢复至稳态,能够保证负载两端电压快速达到稳定状态. 驱动信号的上升、下降时间分别为0.8、0.9 ns,受运放的特性参数和负载的影响,驱动信号存在过冲. 从原理上进行分析可知, 运放输出的电压尖峰与频率特性(零极点)、开环增益及增益带宽积相关[23]. 光开关单元的等效电容及线路、引脚产生的寄生电容,与产生的寄生电感作用,会对电压尖峰产生影响. 在实际的电路设计中,通过修改运放的反馈电阻Rf和增益电阻Rg,改变运放的电学特性. 图8中驱动信号Vsw1对应的运放反馈电阻Rf1和增益电阻Rg1相等,驱动信号Vsw2对应的运放反馈电阻Rf2和增益电阻Rg2均为2倍的Rf1,两运放电压增益均设置为2,与Vsw1相比,Vsw2产生的电压尖峰峰值较小. 结合仿真结果,能够对电压尖峰作出较准确的判断.
图 8
图 8 等效电路模型作为负载的电路瞬态响应仿真结果
Fig.8 Simulation results of transient response when equivalent electrical model act as load
2.2. 电压尖峰对光开关单元瞬态响应的影响
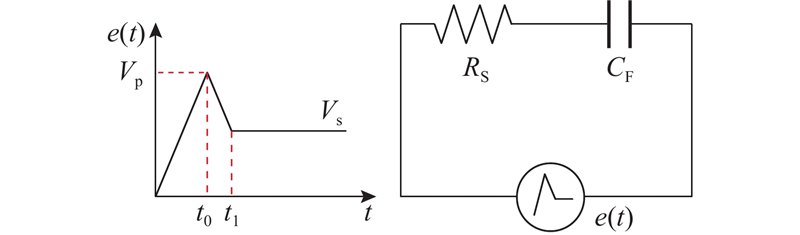
光开关单元两端施加的电压是驱动信号Vsw与基准电压Vref的差值,在到达稳态前存在电压尖峰. 为了探究电压尖峰对光开关瞬态响应的影响,分析CF两端电压UC在图9所示的信号e(t)激励下的响应情况. 由于上升、下降过程中的信号波形对称性较高,仅分析上升过程中的电压情况. 设定激励信号e(t) 2段斜坡信号的斜率绝对值为k,2段斜坡信号转换的时间为t0,对应的电压为Vp,t1时电压到达稳定值Vs,可得
图 9
图 9 斜坡信号及其激励下的电容电压响应分析
Fig.9 Ramp signal excitation and analysis of voltage response of capacitor under excitation
利用拉普拉斯变换法求解,第1段斜坡信号激励下UC的象函数F(s)为
可得UC的时域表达式为
同理,可得第2段斜坡信号激励下UC的时域表达式为
对于2段斜坡信号模拟的尖峰信号,理想情况下第2段斜坡电压到达稳定值时UC刚好同时到达稳定值,即UC最快达到稳定状态的时间与第2段斜坡电压到达稳定值的时间一致. 令t1时刻的UC等于UC的稳定值,即
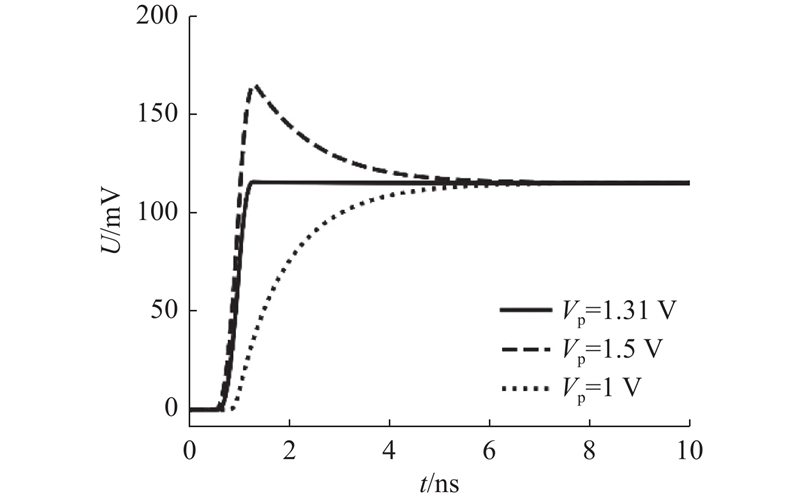
对于给定的t0,通过上述推导能够近似得到Vp的最优解. 在ADS中利用等效电学模型进行仿真验证,设置激励信号的t0 = 1 ns,Vs = 1 V,Vp分别取1.31、1.5和1 V,与计算得到的激励信号最优解、电路瞬态响应仿真结果及不存在尖峰的激励信号对应,CF两端电压UC的响应情况如图10所示.
图 10
图 10 不同激励信号下的电容电压响应情况
Fig.10 Voltage response of capacitor under different excitation signals
在Deckbuild中验证电压尖峰对光开关单元瞬态响应的影响. 分别设置激励信号与等效电学模型仿真的激励信号对应,光开关单元瞬态响应有效折射率的仿真结果如图11所示. 光开关单元切换的稳定时间与电学模型仿真UC的稳定时间较一致.
图 11
图 11 不同激励信号下光开关单元的有效折射率变化
Fig.11 Variation of effective refractive index of photonic switch cell under different excitation signals
对于同一个光开关单元,施加不同的激励信号能够影响其工作性能. 与不存在尖峰直接到达稳定电压的激励信号相比,一定程度的电压尖峰能够加速光开关等效电容的充电过程,缩短切换时间;若尖峰峰值电压过大,使得光开关等效电容被充电至高于稳定值,产生了不必要的电压恢复时间,则会对光开关单元的瞬态响应性能产生负面影响. 对于实际电路中驱动信号边沿产生的电压尖峰,在光开关等效电容被充电至稳定值前,不规则的电压尖峰只决定光开关等效电容充电速度的快慢,不会对光开关切换过程的稳定性产生影响.
3. 实验结果
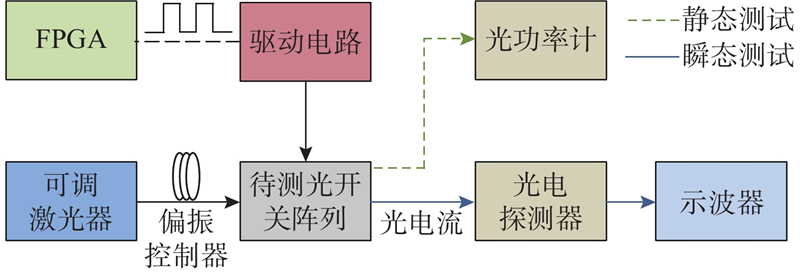
器件制作在新加坡AMF公司完成,通过测试验证光开关单元的性能. 将光芯片封装在电路板上,通过金丝引线的方式和电路板连接,再进行光纤阵列封装. 封装完成后的系统模块如图12所示.
图 12
图 12 驱动电路及光开关阵列的芯片封装
Fig.12 Driving circuits and chip packaging for photonic switch matrix
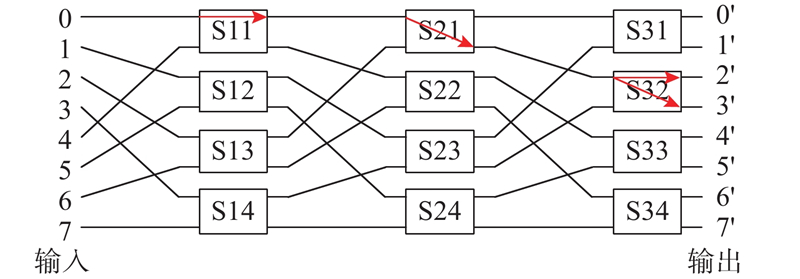
如图13所示为本次流片的8×8光开关阵列的示意图,采用了Omega网络拓扑结构[24],将光开关阵列中的光开关分为3级,S11~S14、S21~S24、S31~S34分别为第1、第2、第3级光开关. 通过控制各个光开关单元的工作状态,能够实现8输入8输出通道的光路传输和交换. 对于大容量光开关阵列,光电处理与传输的随机性变得极为敏感和关键. 为了验证系统性能,须考察不同路径下的工作情况. 测试单个光开关切换及阵列中所有光开关切换2种极端情况:设置前2级光开关工作状态,使得从端口0输入的光分别从第3级的4个光开关输出,每次仅控制第3级光开关切换,此时阵列中仅有1个光开关切换;测试阵列中所有光开关同时切换的情况,控制所有光开关同时在Cross和Bar状态之间切换.
图 13
以从端口0输入的光通过控制光开关S32,在端口2′输出和端口3′输出之间切换为例,2条测试光路在图13中用箭头标出. 2条光路中的光开关S11和光开关S21分别工作在Bar态和Cross态,只要改变光开关S32的工作状态,就能实现输出端口间的切换.
图 14
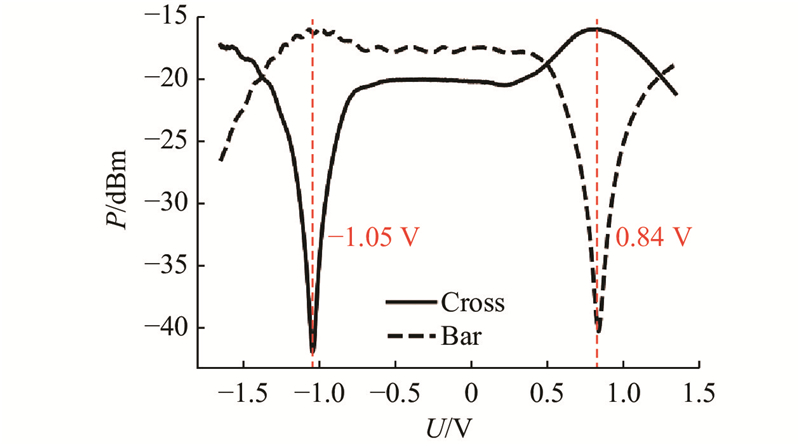
如图15所示为光开关单元S32的静态测试结果,通过最优的消光比确定光开关Cross状态和Bar状态的工作电压分别为−1.05 V和0.84 V. 图中,P为光开关单元的功率. 由于芯片制作过程中存在工艺误差,导致光开关单元2个相移臂的初始相位差偏移原始设计,使得调节到Cross态和Bar态的相移量不等于初始设计值π/2,造成工作电压不完全对称,与设计的±1 V工作电压略有偏差. 将驱动电路的基准电压设定为2.4 V,实际施加在光开关另一端的电压分别为1.35和3.24 V.
图 15
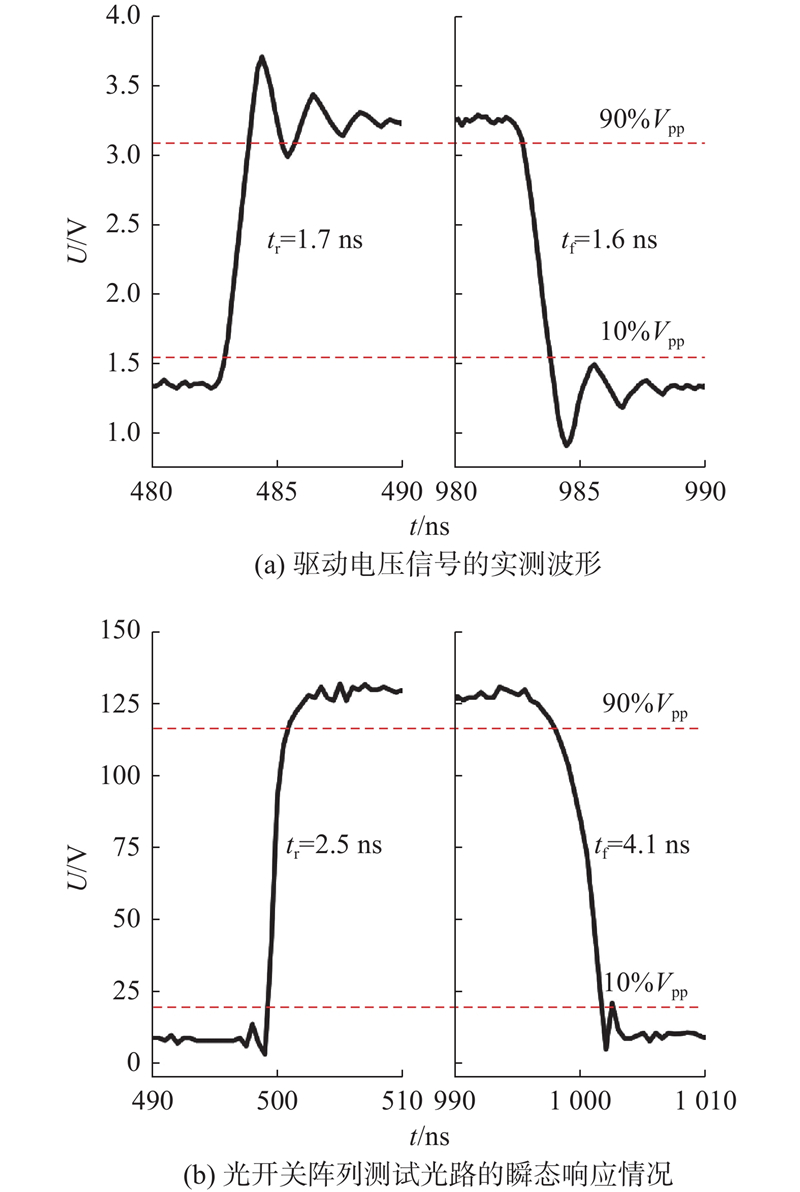
图16给出瞬态测试实时示波器的测试结果,得到光开关单元S32上施加的驱动电压信号上升、下降时间为1.7、1.6 ns,略慢于理想的仿真结果. 由于受限的带宽和阻抗不完全匹配,驱动信号边沿产生了振铃现象,但振铃信号未对光开关切换过程的稳定性产生影响,与2.2节的分析一致.
图 16
由于光电探测器需要一定的转换时间,造成光路瞬态响应的输出波形略慢于驱动电信号的输出波形. 监测输出端口2′的光功率变化,得到测试光路切换的上升、下降时间为2.5、4.1 ns. 利用载流子色散效应的电光开关,响应时间主要与光开关单元的PIN结电容相关. 当驱动电压增大时,载流子注入增强导致波导中的载流子浓度增大,而扩散电容正相关于载流子浓度,故2种状态下工作电压的偏差导致阵列光路切换的上升、下降时间存在一定的差异. 从图16可知,光开关单元对施加的电压信号有很强的敏感性,电路中产生的系统噪声使得光开关两端的驱动电压信号在稳态下存在一定的抖动,造成了光开关阵列输出光功率的轻微抖动.
如表1所示为依据测试方案得到的光开关阵列在不同路径下的工作情况,给出对应路径下执行切换的光开关单元、光路的输入输出端口以及切换的上升时间tr、下降时间tf,可得光开关阵列的切换时间为2.1~5.9 ns.
表 1 光开关阵列在不同路径下的工作情况
Tab.1
| 切换单元 | 光路传输情况 | tr, tf / ns | 切换单元 | 光路传输情况 | tr, tf / ns | |
| S31 | 0→0'/1' | 2.8, 3.1 | 所有单元 | 0→0'/7' | 3.1, 3.3 | |
| 1→1'/0' | 2.7, 2.3 | 1→1'/6' | 2.9, 2.4 | |||
| S32 | 0→2'/3' | 2.5, 4.1 | 2→2'/5' | 2.9, 4.8 | ||
| 3→3'/2' | 3.8, 2.4 | 3→3'/4' | 4.2, 2.5 | |||
| S33 | 0→4'/5' | 2.2, 4.6 | 4→4'/3' | 2.6, 4.7 | ||
| 5→5'/4' | 4.5, 2.1 | 5→5'/2' | 4.8, 2.6 | |||
| S34 | 0→6'/7' | 5.3, 2.4 | 6→6'/1' | 5.9, 2.4 | ||
| 7→7'/6' | 2.2, 4.3 | 7→7'/0' | 2.1, 4.7 |
4. 结 语
本文提出正偏PIN结相移臂结构光开关单元的等效电学模型. 该模型较好地体现了光开关单元的瞬态特性,能够用于电路分析和系统设计. 利用该模型,能够定量描述光开关单元的瞬态响应,从电学模型分析角度为光开关设计提供了思路. 基于该模型,针对光开关阵列设计高速驱动控制电路,结合仿真探究电压尖峰对光开关单元瞬态响应的影响. 测试结果表明,设计的驱动电路能够在推挽驱动方式下实现光开关驱动信号的高速切换,施加在光开关单元上的电学信号切换时间为1.7、1.6 ns,避免了光信号响应速度受电信号切换速度限制的问题,能够在系统应用中获得较理想的光开关器件性能. 由上位机通过FPGA发送控制指令,能够实现光开关阵列不同状态之间的快速切换,切换时间为2.1~5.9 ns. 通过实验,验证了所设计的驱动电路是简单、成熟、低成本的方案,该电路设计配合光开关阵列,实现了较先进的高速光交换系统.
参考文献
Review of silicon photonics technology and platform development
[J].
Monolithic III-nitride photonic circuit towards on-chip optical interconnection
[J].
Optical interconnection networks for high-performance computing systems
[J].
Nanosecond optical switching and control system for data center networks
[J].
High performance ridge type PLZT optical switch with offset upper electrode
[J].
Large-scale broadband digital silicon photonic switches with vertical adiabatic couplers
[J].
Monolithic silicon integration of scaled photonic switch fabrics, CMOS logic, and device driver circuits
[J].
Nanosecond photonic switch architectures demonstrated in an all-digital monolithic platform
[J].
General self-imaging properties in N×N multimode interference couplers including phase relations
[J].
25-Gb/s broadband silicon modulator with 0.31-V·cm VπL based on forward-biased PIN diodes embedded with passive equalizer
[J].
Electrooptical effects in silicon
[J].
Broadband hitless silicon electro-optic switch for on-chip optical networks
[J].
32×32 silicon electro-optic switch with built-in monitors and balanced-status units
[J].
Compact PIN-diode-based silicon modulator using side-wall grating waveguide
[J].
Relationship between frequency response and settling time of operational amplifiers
[J].
Equivalent permutation capabilities between time-division optical Omega networks and non-optical extra-stage Omega networks
[J].