近年来, 动态点云的压缩方法主要分为以下2种类型. 1)基于视频的点云压缩 (video based point cloud compression, VPCC), 即将点云投影到二维平面上, 利用视频压缩的方法进行处理. 2)考虑动态点云的运动信息, 利用帧间冗余信息直接进行压缩. VPCC是MPEG团队提出的基于视频流的动态点云压缩标准, VPCC将输入点云经过分块, 投影到立体空间的6个方向的平面, 将各个二维平面的信息填充到同一个二维图像中, 对图像进行压缩. Kathariya等[1 ] 在VPCC的基础上, 对分块重新分组的步骤进行改进, 提出自适应分组方法, 将相似程度高的相邻帧分配到相同的组中. Thanou等[2 ] 用一组序列图来存储转换后的空间序列点云信息, 用图顶点的信息表示点云的几何与属性信息,利用谱图小波变换,在相邻帧点云之间进行特征对应,计算相邻帧之间的残差信息,消除时间冗余. De Queiroz等[3 ] 采用分块的方式, 将单帧的点云分成多个小的体素块, 每个小块内单独处理,利用率失真决定每个小块的具体划分方式. Kammerl等[4 ] 利用八叉树结构压缩动态点云, 通过异或方式将点云的运动信息编码到连续八叉树的特定结构中, 利用八叉树的特性压缩时间冗余. Sun等[5 ] 引入新的投影方式, 通过球面投影将动态点云投影为图像进行压缩. 近年来,出现了一些利用深度学习进行动态点云压缩的方式. Biswas等[6 ] 提出新颖的条件熵模型来建模八叉树符号概率, 兼顾了粗粒度的几何信息以及上下文的几何与密度信息, 用于处理连续的雷达点云序列. Yu等[7 ] 基于曲率估计和分层策略, 提出动态几何压缩方法, 能够有效地平衡压缩质量和压缩时间. Fan等[8 ] 将运动向量映射到高维特征空间, 在特征空间进行多尺度的运动融合,设计三维自适应权重插值方法用于运动补偿, 实现了端到端的动态点云压缩. 除了传统方法之外,现有的基于深度学习的动态点云压缩方法只能处理体素化点云, 利用本文方法可以压缩原始的动态点云.
式中:${{G}}( \cdot )$ $\odot $ $ {{\boldsymbol{f}}_{{{{\mathrm{mv}}}}}} \in {{\bf{R}}^{c \times N}} $ $c 、N $ ${{\boldsymbol{\mu }}_s} = [ {\mu _{s,0}},{\text{ }}{\mu _{s,1}},{\text{ }} \cdots {\text{, }}{\mu _{s,c - 1}}] $ ${{{\mu}} _{s,i}} \in \bf{R}$ s 为增益向量在增益矩阵中的索引. 所有增益向量组成增益矩阵$ {\boldsymbol{\mu }}\in {\bf{R}}^{c\times n} $ n 为增益向量的个数. 类似地,逆增益单元由逆增益矩阵${\boldsymbol{\mu }}' \in {{\bf{R}}^{c \times n}}$ $ {{\boldsymbol{\mu }}'_s} = [ {\mu '_{s,0}},{\text{ }}{\mu '_{s,1}},{\text{ }} \cdots ,{\text{ }}{\mu '_{s,c - 1}}] $ ${\mu '_{s,i}} \in \bf{R}$ ${\text{IG}}( \cdot )$ [18 ] , 对运动向量进行上采样. 子点卷积模块是对输入进行分组, 再分别进行卷积并扩展维度, 将各个组合并, 达到上采样的目的. 在经过解码端后,可以得到最终重构的运动向量信息, 用于下一阶段的运动补偿模块.
运动补偿模块利用上一帧的坐标信息和运动向量,对当前帧进行补偿. 在图像领域也有类似的运动补偿模块, 图像领域利用光流和前一帧的图像信息进行融合. 本文的运动补偿思想借鉴了DVC[19 ] 中的视频运动补偿框架. 在视频压缩框架中, 网络中处理的是$ N\times c\times H\times W $ $ N\times c $ 图3 所示, 网络的输入为前一帧的空间中连续的坐标信息${P_{t - 1}}$ ${\bar P_t}$ ${P_t}$ $N \times 3$ $N \times 3$ . 将前一帧直接加上运动向量mv , 得到偏移后的前一帧, 称为变形帧(warpframe). 利用直接算术相加得到的warpframe与当前帧${P_t}$ ${P_{t - 1}}$ f $N \times 6$ . 将f 图3 的虚线部分所示,通过一维卷积操作将f [20 ] 组归一化函数,对输出进行标准化操作, 得到最终的预测帧坐标信息.
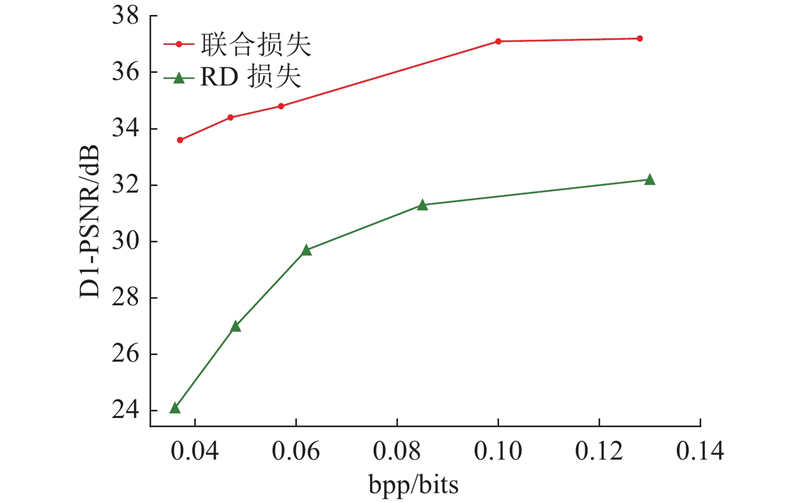
在训练阶段, 从训练集中的点云片段中选取第1帧为前一帧, 从该片段后续的3帧中随机选取一帧作为当前帧, 将前一帧到当前帧的运动向量作为场景流的真实标签. 在运动压缩网络和残差压缩网络的下采样模块中, 编码端的下采样率和解码端的上采样率分别设置为[1/4,1/2,1/2]、[2,2,4], 整个压缩网络的特征通道的大小设置为16. 在联合损失函数中, RD损失的系数$\alpha $ $\beta $ $\lambda = \{ 10,50,100,500,1\;000, 4\;000\} $ . 网络使用的梯度方向传播模块是Adam优化器[24 ] , 优化器的学习率设置为0.001, 网络的batch size大小是16, 总共训练100个轮次.
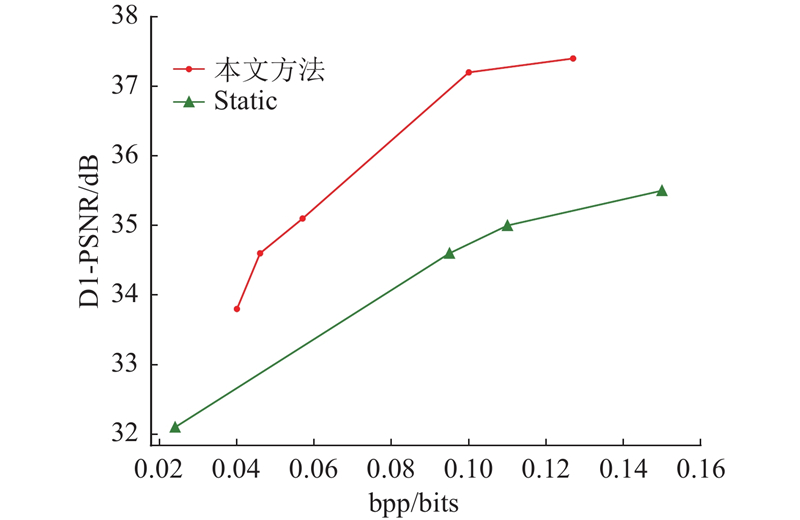
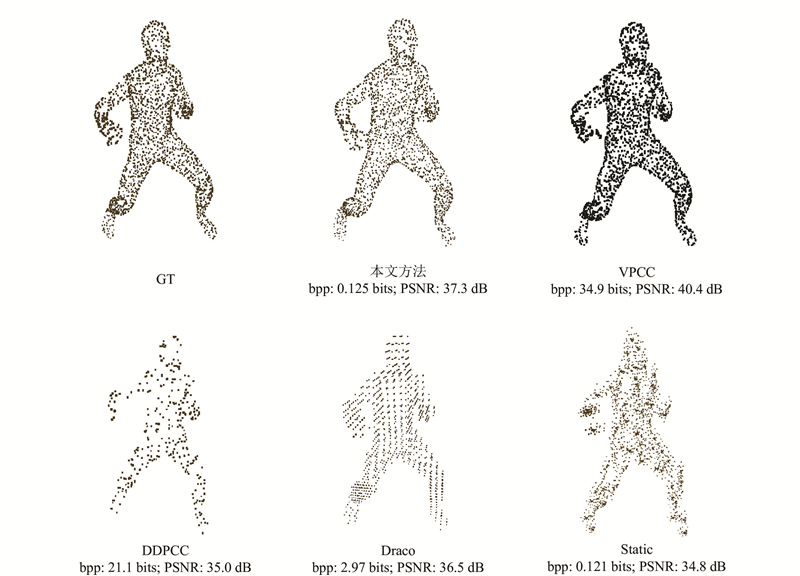
由于本文方法和Draco、VPCC、DDPCC方法压缩所需的比特率存在较大的差异, 导致RD曲线的可视化效果很差. 选取各种方法对应的最优重构结果, 制作表格进行对比, 如表1 所示. 表中,t e 、t d 分别为编码时间和解码时间. 其中, Draco采用传统的静态压缩方法, 但由于传统压缩方法在优化点云空间关联方面的局限性,无法自适应地学习到数据中的冗余, 导致编码时的冗余信息偏大. 为了达到与深度学习相近的解码结果, 所需的编码位数是本文方法的几十倍以上. 与VPCC和DDPCC方法相比, 这2种方法所需的bpp比本文方法高2个数量级以上, 这可能是由于VPCC和DPPCC都是用于压缩体素化稠密动态点云的方法, 对于点数较少的点云数据集, 体素化会产生大量的空体素,需要额外的位数表示占位信息, 导致编码时需要使用更多的比特位保存额外信息,用于后续的解码过程. VPCC是传统的压缩方法. 与基于深度学习的DDPCC压缩方法相比, 本文结果所需的bpp非常小, PSNR有5%左右的提升. 如图5 所示为可视化结果, 从AMASS数据集中随机选取一帧的重构结果, 对各种方法的结果都进行可视化. 可以看出, 与静态方法Static、Draco及DDPCC的结果相比, 本文方法的重构结果与原始点云的点分布更加相近, 可视化效果更好. Static的重构结果具有明显的噪声点, Draco对大量的点进行量化, 将点的位置都量化到某一区域, 视觉效果中的点分布在集中的多层平面上. 与VPCC方法相比, 虽然本文方法的PSNR指标差于VPCC, 但是对应的bpp明显小于VPCC, 意味着压缩所需的带宽明显优于VPCC. 此外, VPCC重构后的点都是一个一个的局部点形成的小平面, 重构后的点数是原始点云的数十倍, 约为3万个点, 相比而言, 本文方法重构后不仅点数没有增加, 而且不会出现VPCC中顶点局部聚集的现象. 本文方法更接近于原始点云的空间分布.
[1]
KATHARIYA B, LI L, LI Z, et al. Lossless dynamic point cloud geometry compression with inter compensation and traveling salesman prediction [C]// Data Compression Conference . Boston: IEEE, 2018: 414.
[本文引用: 1]
[2]
THANOU D, CHOU P A, FROSSARD P Graph-based compression of dynamic 3D point cloud sequences
[J]. IEEE Transactions on Image Processing 2016 , 25 (4 ): 1765 - 1778
DOI:10.1109/TIP.2016.2529506
[本文引用: 1]
[3]
DE QUEIROZ R L, CHOU P A Motion-compensated compression of dynamic voxelized point clouds
[J]. IEEE Transactions on Image Processing 2017 , 26 (8 ): 3886 - 3895
DOI:10.1109/TIP.2017.2707807
[本文引用: 1]
[4]
KAMMERL J, BLODOW N, RUSU R B, et al. Real-time compression of point cloud streams [C]// IEEE International Conference on Robotics and Automation . [S. l.]: IEEE, 2012: 778-785.
[本文引用: 1]
[5]
SUN X, MA H, SUN Y, et al A novel point cloud compression algorithm based on clustering
[J]. IEEE Robotics and Automation Letters 2019 , 4 (2 ): 2132 - 2139
DOI:10.1109/LRA.2019.2900747
[本文引用: 1]
[6]
BISWAS S, LIU J, WONG K, et al Muscle: multi sweep compression of lidar using deep entropy models
[J]. Advances in Neural Information Processing Systems 2020 , 33 (2 ): 22170 - 22181
[本文引用: 1]
[7]
YU S, SUN S, YAN W, et al A method based on curvature and hierarchical strategy for dynamic point cloud compression in augmented and virtual reality system
[J]. Sensors 2022 , 22 (3 ): 1262
DOI:10.3390/s22031262
[本文引用: 1]
[8]
FAN T, GAO L, XU Y, et al. D-DPCC: deep dynamic point cloud compression via 3D motion prediction [C]// Proceedings of the 31st International Joint Conference on Artificial Intelligence . Vienna: [s. n.], 2022: 898-904.
[本文引用: 2]
[9]
GEORGE T, SEAN M, SUNG J, et al. Variable rate image compression with recurrent neural networks [C]// International Conference on Learning Representations . Puerto Rico: [s. n.], 2016.
[本文引用: 1]
[10]
CHEN T, MA Z. Variable bitrate image compression with quality scaling factors [C]// IEEE International Conference on Acoustics, Speech and Signal Processing . Barcelona: IEEE, 2020: 2163-2167.
[本文引用: 1]
[11]
YANG F, HERRANZ L, WEIJER J, et al. Variable rate deep image compression with modulated autoencoder [J]. IEEE Signal Processing Letters , 2020, 27: 331-335.
[本文引用: 1]
[12]
CUI Z, WANG J, GAO S, et al. Asymmetric gained deep image compression with continuous rate adaptation [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Baltimore: IEEE, 2021: 10532-10541.
[本文引用: 2]
[13]
MUZADDID M A, BEKSI W J. Variable rate compression for raw 3D point clouds [C]// International Conference on Robotics and Automation . Philadelphia: [s. n.], 2022: 8748-8755.
[本文引用: 1]
[14]
QI C R, YI L, SU H, et al. Pointnet++: deep hierarchical feature learning on point sets in a metric space [C]// Advances in Neural Information Processing Systems . Long Beach: [s. n.], 2017: 30.
[本文引用: 2]
[15]
WU W, WANG Z Y, LI Z, et al. Pointpwc-net: cost volume on point clouds for (self-) supervised scene flow estimation [C]// 16th European Conference on Computer Vision. Glasgow: Springer, 2020.
[本文引用: 1]
[16]
WU W, QI Z, FUXIN L. Pointconv: deep convolutional networks on 3d point clouds [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2019: 9621-9630.
[本文引用: 1]
[17]
ENGEL N, BELAGIANNIS V, DIETMAYER K Point transformer
[J]. IEEE Access 2021 , 9 (1 ): 134826 - 134840
[本文引用: 1]
[18]
HE Y, REN X, TANG D, et al. Density-preserving deep point cloud compression [C] // Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . New Orleans: IEEE, 2022: 2333-2342.
[本文引用: 1]
[19]
LU G, OUYANG W, XU D, et al. Dvc: an end-to-end deep video compression framework [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2019: 11006-11015.
[本文引用: 1]
[20]
WU Y, HE K. Group normalization [C]// Proceedings of the European Conference on Computer Vision . Munich: [s. n.], 2018: 3-19.
[本文引用: 1]
[21]
HUANG L, WANG S, WONG K, et al. Octsqueeze: octree-structured entropy model for lidar compression [C] // Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 1313-1323.
[本文引用: 1]
[22]
MAHMOOD N, GHORBANI N, TROJE N F, et al. AMASS: archive of motion capture as surface shapes [C]// Proceedings of the IEEE/CVF International Conference on Computer Vision . Seoul: IEEE, 2019: 5442-5451.
[本文引用: 1]
[23]
SEBASTIAN S, MARIUS P, VITTORIO B, et al Emerging mpeg standards for point cloud compression
[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems 2019 , 9 (1 ): 133 - 148
DOI:10.1109/JETCAS.2018.2885981
[本文引用: 1]
[24]
ZHANG Z. Improved Adam optimizer for deep neural networks [C]// IEEE/ACM 26th International Symposium on Quality of Service . Banff: IEEE, 2018: 1-2.
[本文引用: 1]
[25]
ZHANG J, LIU G, DING D, et al. Transformer and upsampling-based point cloud compression [C]// ACM MM Workshops on Advances in Point Cloud Compression, Processing and Analysis. Lisbon: ACM, 2022: 33-39.
[本文引用: 1]
[26]
Google. Draco 3D data compression [EB/OL]. [2023-08-01]. https://github.com/google/draco.
[本文引用: 1]
[27]
JANG E S, PREDA M, MAMMOU K, et al Video-based point-cloud-compression standard in MPEG: from evidence collection to committee draft standards in a nutshell
[J]. IEEE Signal Processing Magazine 2019 , 36 (3 ): 118 - 123
DOI:10.1109/MSP.2019.2900721
[本文引用: 1]
1
... 近年来, 动态点云的压缩方法主要分为以下2种类型. 1)基于视频的点云压缩 (video based point cloud compression, VPCC), 即将点云投影到二维平面上, 利用视频压缩的方法进行处理. 2)考虑动态点云的运动信息, 利用帧间冗余信息直接进行压缩. VPCC是MPEG团队提出的基于视频流的动态点云压缩标准, VPCC将输入点云经过分块, 投影到立体空间的6个方向的平面, 将各个二维平面的信息填充到同一个二维图像中, 对图像进行压缩. Kathariya等[1 ] 在VPCC的基础上, 对分块重新分组的步骤进行改进, 提出自适应分组方法, 将相似程度高的相邻帧分配到相同的组中. Thanou等[2 ] 用一组序列图来存储转换后的空间序列点云信息, 用图顶点的信息表示点云的几何与属性信息,利用谱图小波变换,在相邻帧点云之间进行特征对应,计算相邻帧之间的残差信息,消除时间冗余. De Queiroz等[3 ] 采用分块的方式, 将单帧的点云分成多个小的体素块, 每个小块内单独处理,利用率失真决定每个小块的具体划分方式. Kammerl等[4 ] 利用八叉树结构压缩动态点云, 通过异或方式将点云的运动信息编码到连续八叉树的特定结构中, 利用八叉树的特性压缩时间冗余. Sun等[5 ] 引入新的投影方式, 通过球面投影将动态点云投影为图像进行压缩. 近年来,出现了一些利用深度学习进行动态点云压缩的方式. Biswas等[6 ] 提出新颖的条件熵模型来建模八叉树符号概率, 兼顾了粗粒度的几何信息以及上下文的几何与密度信息, 用于处理连续的雷达点云序列. Yu等[7 ] 基于曲率估计和分层策略, 提出动态几何压缩方法, 能够有效地平衡压缩质量和压缩时间. Fan等[8 ] 将运动向量映射到高维特征空间, 在特征空间进行多尺度的运动融合,设计三维自适应权重插值方法用于运动补偿, 实现了端到端的动态点云压缩. 除了传统方法之外,现有的基于深度学习的动态点云压缩方法只能处理体素化点云, 利用本文方法可以压缩原始的动态点云. ...
Graph-based compression of dynamic 3D point cloud sequences
1
2016
... 近年来, 动态点云的压缩方法主要分为以下2种类型. 1)基于视频的点云压缩 (video based point cloud compression, VPCC), 即将点云投影到二维平面上, 利用视频压缩的方法进行处理. 2)考虑动态点云的运动信息, 利用帧间冗余信息直接进行压缩. VPCC是MPEG团队提出的基于视频流的动态点云压缩标准, VPCC将输入点云经过分块, 投影到立体空间的6个方向的平面, 将各个二维平面的信息填充到同一个二维图像中, 对图像进行压缩. Kathariya等[1 ] 在VPCC的基础上, 对分块重新分组的步骤进行改进, 提出自适应分组方法, 将相似程度高的相邻帧分配到相同的组中. Thanou等[2 ] 用一组序列图来存储转换后的空间序列点云信息, 用图顶点的信息表示点云的几何与属性信息,利用谱图小波变换,在相邻帧点云之间进行特征对应,计算相邻帧之间的残差信息,消除时间冗余. De Queiroz等[3 ] 采用分块的方式, 将单帧的点云分成多个小的体素块, 每个小块内单独处理,利用率失真决定每个小块的具体划分方式. Kammerl等[4 ] 利用八叉树结构压缩动态点云, 通过异或方式将点云的运动信息编码到连续八叉树的特定结构中, 利用八叉树的特性压缩时间冗余. Sun等[5 ] 引入新的投影方式, 通过球面投影将动态点云投影为图像进行压缩. 近年来,出现了一些利用深度学习进行动态点云压缩的方式. Biswas等[6 ] 提出新颖的条件熵模型来建模八叉树符号概率, 兼顾了粗粒度的几何信息以及上下文的几何与密度信息, 用于处理连续的雷达点云序列. Yu等[7 ] 基于曲率估计和分层策略, 提出动态几何压缩方法, 能够有效地平衡压缩质量和压缩时间. Fan等[8 ] 将运动向量映射到高维特征空间, 在特征空间进行多尺度的运动融合,设计三维自适应权重插值方法用于运动补偿, 实现了端到端的动态点云压缩. 除了传统方法之外,现有的基于深度学习的动态点云压缩方法只能处理体素化点云, 利用本文方法可以压缩原始的动态点云. ...
Motion-compensated compression of dynamic voxelized point clouds
1
2017
... 近年来, 动态点云的压缩方法主要分为以下2种类型. 1)基于视频的点云压缩 (video based point cloud compression, VPCC), 即将点云投影到二维平面上, 利用视频压缩的方法进行处理. 2)考虑动态点云的运动信息, 利用帧间冗余信息直接进行压缩. VPCC是MPEG团队提出的基于视频流的动态点云压缩标准, VPCC将输入点云经过分块, 投影到立体空间的6个方向的平面, 将各个二维平面的信息填充到同一个二维图像中, 对图像进行压缩. Kathariya等[1 ] 在VPCC的基础上, 对分块重新分组的步骤进行改进, 提出自适应分组方法, 将相似程度高的相邻帧分配到相同的组中. Thanou等[2 ] 用一组序列图来存储转换后的空间序列点云信息, 用图顶点的信息表示点云的几何与属性信息,利用谱图小波变换,在相邻帧点云之间进行特征对应,计算相邻帧之间的残差信息,消除时间冗余. De Queiroz等[3 ] 采用分块的方式, 将单帧的点云分成多个小的体素块, 每个小块内单独处理,利用率失真决定每个小块的具体划分方式. Kammerl等[4 ] 利用八叉树结构压缩动态点云, 通过异或方式将点云的运动信息编码到连续八叉树的特定结构中, 利用八叉树的特性压缩时间冗余. Sun等[5 ] 引入新的投影方式, 通过球面投影将动态点云投影为图像进行压缩. 近年来,出现了一些利用深度学习进行动态点云压缩的方式. Biswas等[6 ] 提出新颖的条件熵模型来建模八叉树符号概率, 兼顾了粗粒度的几何信息以及上下文的几何与密度信息, 用于处理连续的雷达点云序列. Yu等[7 ] 基于曲率估计和分层策略, 提出动态几何压缩方法, 能够有效地平衡压缩质量和压缩时间. Fan等[8 ] 将运动向量映射到高维特征空间, 在特征空间进行多尺度的运动融合,设计三维自适应权重插值方法用于运动补偿, 实现了端到端的动态点云压缩. 除了传统方法之外,现有的基于深度学习的动态点云压缩方法只能处理体素化点云, 利用本文方法可以压缩原始的动态点云. ...
1
... 近年来, 动态点云的压缩方法主要分为以下2种类型. 1)基于视频的点云压缩 (video based point cloud compression, VPCC), 即将点云投影到二维平面上, 利用视频压缩的方法进行处理. 2)考虑动态点云的运动信息, 利用帧间冗余信息直接进行压缩. VPCC是MPEG团队提出的基于视频流的动态点云压缩标准, VPCC将输入点云经过分块, 投影到立体空间的6个方向的平面, 将各个二维平面的信息填充到同一个二维图像中, 对图像进行压缩. Kathariya等[1 ] 在VPCC的基础上, 对分块重新分组的步骤进行改进, 提出自适应分组方法, 将相似程度高的相邻帧分配到相同的组中. Thanou等[2 ] 用一组序列图来存储转换后的空间序列点云信息, 用图顶点的信息表示点云的几何与属性信息,利用谱图小波变换,在相邻帧点云之间进行特征对应,计算相邻帧之间的残差信息,消除时间冗余. De Queiroz等[3 ] 采用分块的方式, 将单帧的点云分成多个小的体素块, 每个小块内单独处理,利用率失真决定每个小块的具体划分方式. Kammerl等[4 ] 利用八叉树结构压缩动态点云, 通过异或方式将点云的运动信息编码到连续八叉树的特定结构中, 利用八叉树的特性压缩时间冗余. Sun等[5 ] 引入新的投影方式, 通过球面投影将动态点云投影为图像进行压缩. 近年来,出现了一些利用深度学习进行动态点云压缩的方式. Biswas等[6 ] 提出新颖的条件熵模型来建模八叉树符号概率, 兼顾了粗粒度的几何信息以及上下文的几何与密度信息, 用于处理连续的雷达点云序列. Yu等[7 ] 基于曲率估计和分层策略, 提出动态几何压缩方法, 能够有效地平衡压缩质量和压缩时间. Fan等[8 ] 将运动向量映射到高维特征空间, 在特征空间进行多尺度的运动融合,设计三维自适应权重插值方法用于运动补偿, 实现了端到端的动态点云压缩. 除了传统方法之外,现有的基于深度学习的动态点云压缩方法只能处理体素化点云, 利用本文方法可以压缩原始的动态点云. ...
A novel point cloud compression algorithm based on clustering
1
2019
... 近年来, 动态点云的压缩方法主要分为以下2种类型. 1)基于视频的点云压缩 (video based point cloud compression, VPCC), 即将点云投影到二维平面上, 利用视频压缩的方法进行处理. 2)考虑动态点云的运动信息, 利用帧间冗余信息直接进行压缩. VPCC是MPEG团队提出的基于视频流的动态点云压缩标准, VPCC将输入点云经过分块, 投影到立体空间的6个方向的平面, 将各个二维平面的信息填充到同一个二维图像中, 对图像进行压缩. Kathariya等[1 ] 在VPCC的基础上, 对分块重新分组的步骤进行改进, 提出自适应分组方法, 将相似程度高的相邻帧分配到相同的组中. Thanou等[2 ] 用一组序列图来存储转换后的空间序列点云信息, 用图顶点的信息表示点云的几何与属性信息,利用谱图小波变换,在相邻帧点云之间进行特征对应,计算相邻帧之间的残差信息,消除时间冗余. De Queiroz等[3 ] 采用分块的方式, 将单帧的点云分成多个小的体素块, 每个小块内单独处理,利用率失真决定每个小块的具体划分方式. Kammerl等[4 ] 利用八叉树结构压缩动态点云, 通过异或方式将点云的运动信息编码到连续八叉树的特定结构中, 利用八叉树的特性压缩时间冗余. Sun等[5 ] 引入新的投影方式, 通过球面投影将动态点云投影为图像进行压缩. 近年来,出现了一些利用深度学习进行动态点云压缩的方式. Biswas等[6 ] 提出新颖的条件熵模型来建模八叉树符号概率, 兼顾了粗粒度的几何信息以及上下文的几何与密度信息, 用于处理连续的雷达点云序列. Yu等[7 ] 基于曲率估计和分层策略, 提出动态几何压缩方法, 能够有效地平衡压缩质量和压缩时间. Fan等[8 ] 将运动向量映射到高维特征空间, 在特征空间进行多尺度的运动融合,设计三维自适应权重插值方法用于运动补偿, 实现了端到端的动态点云压缩. 除了传统方法之外,现有的基于深度学习的动态点云压缩方法只能处理体素化点云, 利用本文方法可以压缩原始的动态点云. ...
Muscle: multi sweep compression of lidar using deep entropy models
1
2020
... 近年来, 动态点云的压缩方法主要分为以下2种类型. 1)基于视频的点云压缩 (video based point cloud compression, VPCC), 即将点云投影到二维平面上, 利用视频压缩的方法进行处理. 2)考虑动态点云的运动信息, 利用帧间冗余信息直接进行压缩. VPCC是MPEG团队提出的基于视频流的动态点云压缩标准, VPCC将输入点云经过分块, 投影到立体空间的6个方向的平面, 将各个二维平面的信息填充到同一个二维图像中, 对图像进行压缩. Kathariya等[1 ] 在VPCC的基础上, 对分块重新分组的步骤进行改进, 提出自适应分组方法, 将相似程度高的相邻帧分配到相同的组中. Thanou等[2 ] 用一组序列图来存储转换后的空间序列点云信息, 用图顶点的信息表示点云的几何与属性信息,利用谱图小波变换,在相邻帧点云之间进行特征对应,计算相邻帧之间的残差信息,消除时间冗余. De Queiroz等[3 ] 采用分块的方式, 将单帧的点云分成多个小的体素块, 每个小块内单独处理,利用率失真决定每个小块的具体划分方式. Kammerl等[4 ] 利用八叉树结构压缩动态点云, 通过异或方式将点云的运动信息编码到连续八叉树的特定结构中, 利用八叉树的特性压缩时间冗余. Sun等[5 ] 引入新的投影方式, 通过球面投影将动态点云投影为图像进行压缩. 近年来,出现了一些利用深度学习进行动态点云压缩的方式. Biswas等[6 ] 提出新颖的条件熵模型来建模八叉树符号概率, 兼顾了粗粒度的几何信息以及上下文的几何与密度信息, 用于处理连续的雷达点云序列. Yu等[7 ] 基于曲率估计和分层策略, 提出动态几何压缩方法, 能够有效地平衡压缩质量和压缩时间. Fan等[8 ] 将运动向量映射到高维特征空间, 在特征空间进行多尺度的运动融合,设计三维自适应权重插值方法用于运动补偿, 实现了端到端的动态点云压缩. 除了传统方法之外,现有的基于深度学习的动态点云压缩方法只能处理体素化点云, 利用本文方法可以压缩原始的动态点云. ...
A method based on curvature and hierarchical strategy for dynamic point cloud compression in augmented and virtual reality system
1
2022
... 近年来, 动态点云的压缩方法主要分为以下2种类型. 1)基于视频的点云压缩 (video based point cloud compression, VPCC), 即将点云投影到二维平面上, 利用视频压缩的方法进行处理. 2)考虑动态点云的运动信息, 利用帧间冗余信息直接进行压缩. VPCC是MPEG团队提出的基于视频流的动态点云压缩标准, VPCC将输入点云经过分块, 投影到立体空间的6个方向的平面, 将各个二维平面的信息填充到同一个二维图像中, 对图像进行压缩. Kathariya等[1 ] 在VPCC的基础上, 对分块重新分组的步骤进行改进, 提出自适应分组方法, 将相似程度高的相邻帧分配到相同的组中. Thanou等[2 ] 用一组序列图来存储转换后的空间序列点云信息, 用图顶点的信息表示点云的几何与属性信息,利用谱图小波变换,在相邻帧点云之间进行特征对应,计算相邻帧之间的残差信息,消除时间冗余. De Queiroz等[3 ] 采用分块的方式, 将单帧的点云分成多个小的体素块, 每个小块内单独处理,利用率失真决定每个小块的具体划分方式. Kammerl等[4 ] 利用八叉树结构压缩动态点云, 通过异或方式将点云的运动信息编码到连续八叉树的特定结构中, 利用八叉树的特性压缩时间冗余. Sun等[5 ] 引入新的投影方式, 通过球面投影将动态点云投影为图像进行压缩. 近年来,出现了一些利用深度学习进行动态点云压缩的方式. Biswas等[6 ] 提出新颖的条件熵模型来建模八叉树符号概率, 兼顾了粗粒度的几何信息以及上下文的几何与密度信息, 用于处理连续的雷达点云序列. Yu等[7 ] 基于曲率估计和分层策略, 提出动态几何压缩方法, 能够有效地平衡压缩质量和压缩时间. Fan等[8 ] 将运动向量映射到高维特征空间, 在特征空间进行多尺度的运动融合,设计三维自适应权重插值方法用于运动补偿, 实现了端到端的动态点云压缩. 除了传统方法之外,现有的基于深度学习的动态点云压缩方法只能处理体素化点云, 利用本文方法可以压缩原始的动态点云. ...
2
... 近年来, 动态点云的压缩方法主要分为以下2种类型. 1)基于视频的点云压缩 (video based point cloud compression, VPCC), 即将点云投影到二维平面上, 利用视频压缩的方法进行处理. 2)考虑动态点云的运动信息, 利用帧间冗余信息直接进行压缩. VPCC是MPEG团队提出的基于视频流的动态点云压缩标准, VPCC将输入点云经过分块, 投影到立体空间的6个方向的平面, 将各个二维平面的信息填充到同一个二维图像中, 对图像进行压缩. Kathariya等[1 ] 在VPCC的基础上, 对分块重新分组的步骤进行改进, 提出自适应分组方法, 将相似程度高的相邻帧分配到相同的组中. Thanou等[2 ] 用一组序列图来存储转换后的空间序列点云信息, 用图顶点的信息表示点云的几何与属性信息,利用谱图小波变换,在相邻帧点云之间进行特征对应,计算相邻帧之间的残差信息,消除时间冗余. De Queiroz等[3 ] 采用分块的方式, 将单帧的点云分成多个小的体素块, 每个小块内单独处理,利用率失真决定每个小块的具体划分方式. Kammerl等[4 ] 利用八叉树结构压缩动态点云, 通过异或方式将点云的运动信息编码到连续八叉树的特定结构中, 利用八叉树的特性压缩时间冗余. Sun等[5 ] 引入新的投影方式, 通过球面投影将动态点云投影为图像进行压缩. 近年来,出现了一些利用深度学习进行动态点云压缩的方式. Biswas等[6 ] 提出新颖的条件熵模型来建模八叉树符号概率, 兼顾了粗粒度的几何信息以及上下文的几何与密度信息, 用于处理连续的雷达点云序列. Yu等[7 ] 基于曲率估计和分层策略, 提出动态几何压缩方法, 能够有效地平衡压缩质量和压缩时间. Fan等[8 ] 将运动向量映射到高维特征空间, 在特征空间进行多尺度的运动融合,设计三维自适应权重插值方法用于运动补偿, 实现了端到端的动态点云压缩. 除了传统方法之外,现有的基于深度学习的动态点云压缩方法只能处理体素化点云, 利用本文方法可以压缩原始的动态点云. ...
... 为了验证本文方法的有效性,选取静态点云压缩的方法Static [25 ] 、Draco点云压缩库 [26 ] 、MPEG组织的VPCC压缩标准 [27 ] 及最新的动态点云压缩方法D-DPCC [8 ] 作为对比, 开展实验结果分析. Static方法是基于深度学习的静态点云压缩方法, Draco是传统的静态压缩方法, 二者均将点云序列的每帧独立压缩的结果作为实验结果进行比较. VPCC是MPEG组织提出的动态点云压缩标准,是一种传统方法, D-DPCC是基于深度学习的动态点云方法. 这2种压缩方法常用来压缩体素化点云序列. ...
1
... 基于深度学习的可变速率压缩方法最早来自于图像压缩领域. 在早期的图像压缩方法中, George等[9 ] 采用循环神经网络实现图像压缩的可变速率控制. 由于网络框架构造比较复杂,后续的许多图像压缩工作提出了改进方法. Chen等[10 ] 提出将缩放因子嵌入到自动编码器框架中的方法, 通过缩放因子控制压缩率的变化. Yang等[11 ] 提出基于可调制网络的可调制编码器, 将额外的可调制网络与自动编码器融合, 可调制网络能够通过反向传播,自动学习到类似于缩放因子的缩放调节网络. 最近, Cui等[12 ] 提出新的基于增益和对称高斯混合模型的可变图像压缩方法, 该方法通过增益单元实现连续可调的图像压缩结果,验证了通道的冗余度和增益单元的即插即用特性, 使得增益单元能够兼容其他图像压缩方法. ...
1
... 基于深度学习的可变速率压缩方法最早来自于图像压缩领域. 在早期的图像压缩方法中, George等[9 ] 采用循环神经网络实现图像压缩的可变速率控制. 由于网络框架构造比较复杂,后续的许多图像压缩工作提出了改进方法. Chen等[10 ] 提出将缩放因子嵌入到自动编码器框架中的方法, 通过缩放因子控制压缩率的变化. Yang等[11 ] 提出基于可调制网络的可调制编码器, 将额外的可调制网络与自动编码器融合, 可调制网络能够通过反向传播,自动学习到类似于缩放因子的缩放调节网络. 最近, Cui等[12 ] 提出新的基于增益和对称高斯混合模型的可变图像压缩方法, 该方法通过增益单元实现连续可调的图像压缩结果,验证了通道的冗余度和增益单元的即插即用特性, 使得增益单元能够兼容其他图像压缩方法. ...
1
... 基于深度学习的可变速率压缩方法最早来自于图像压缩领域. 在早期的图像压缩方法中, George等[9 ] 采用循环神经网络实现图像压缩的可变速率控制. 由于网络框架构造比较复杂,后续的许多图像压缩工作提出了改进方法. Chen等[10 ] 提出将缩放因子嵌入到自动编码器框架中的方法, 通过缩放因子控制压缩率的变化. Yang等[11 ] 提出基于可调制网络的可调制编码器, 将额外的可调制网络与自动编码器融合, 可调制网络能够通过反向传播,自动学习到类似于缩放因子的缩放调节网络. 最近, Cui等[12 ] 提出新的基于增益和对称高斯混合模型的可变图像压缩方法, 该方法通过增益单元实现连续可调的图像压缩结果,验证了通道的冗余度和增益单元的即插即用特性, 使得增益单元能够兼容其他图像压缩方法. ...
2
... 基于深度学习的可变速率压缩方法最早来自于图像压缩领域. 在早期的图像压缩方法中, George等[9 ] 采用循环神经网络实现图像压缩的可变速率控制. 由于网络框架构造比较复杂,后续的许多图像压缩工作提出了改进方法. Chen等[10 ] 提出将缩放因子嵌入到自动编码器框架中的方法, 通过缩放因子控制压缩率的变化. Yang等[11 ] 提出基于可调制网络的可调制编码器, 将额外的可调制网络与自动编码器融合, 可调制网络能够通过反向传播,自动学习到类似于缩放因子的缩放调节网络. 最近, Cui等[12 ] 提出新的基于增益和对称高斯混合模型的可变图像压缩方法, 该方法通过增益单元实现连续可调的图像压缩结果,验证了通道的冗余度和增益单元的即插即用特性, 使得增益单元能够兼容其他图像压缩方法. ...
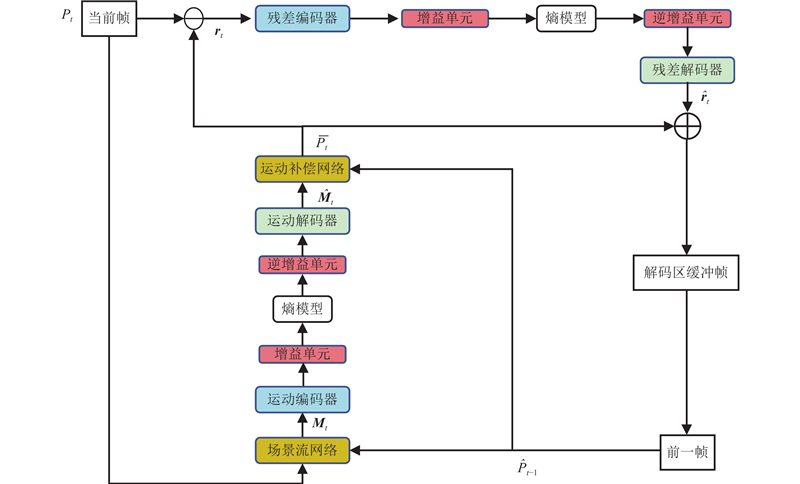
... 受文献[12 ]的启发, 在压缩运动向量$ {{\boldsymbol{M}}_{{t}}} $ $ {{\boldsymbol{r}}_{{t}}} $
1
... 在点云压缩领域, 大部分现有的点云压缩方法通过训练多个模型来得到不同压缩率, 基于深度学习的可变速率点云压缩很少涉及. Muzaddia等[13 ] 提出可变比特率的静态点云压缩方法, 利用PointNet++[14 ] 网络中的特征提取模块作为编码器, 全连接层作为解码器, 引入权重熵损失函数, 通过裁剪向量的通道控制可变比特率. 这种裁剪方式导致解码端的重构精度下降. 目前,基于深度学习的可变速率动态点云压缩工作未见报道. 本文的任务是压缩动态点云,借鉴了增益单元的思想, 通过消除特征向量在不同通道上的冗余, 减少信息损失. ...
2
... 在点云压缩领域, 大部分现有的点云压缩方法通过训练多个模型来得到不同压缩率, 基于深度学习的可变速率点云压缩很少涉及. Muzaddia等[13 ] 提出可变比特率的静态点云压缩方法, 利用PointNet++[14 ] 网络中的特征提取模块作为编码器, 全连接层作为解码器, 引入权重熵损失函数, 通过裁剪向量的通道控制可变比特率. 这种裁剪方式导致解码端的重构精度下降. 目前,基于深度学习的可变速率动态点云压缩工作未见报道. 本文的任务是压缩动态点云,借鉴了增益单元的思想, 通过消除特征向量在不同通道上的冗余, 减少信息损失. ...
... 在运动压缩部分, 对运动向量进行压缩编码. 其中的运动向量编码解码网络是多尺度的特征提取网络, 将运动向量$ {{\boldsymbol{M}}}_{t} $ [14 ] 中的特征提取模块和注意力模块[17 ] 进行特征提取, 得到中间层的运动向量高维特征$ {{\boldsymbol{f}}_{{{{\mathrm{mv}}}}}} $ . 对 $ {{\boldsymbol{f}}}_{{\mathrm{mv}}} $
1
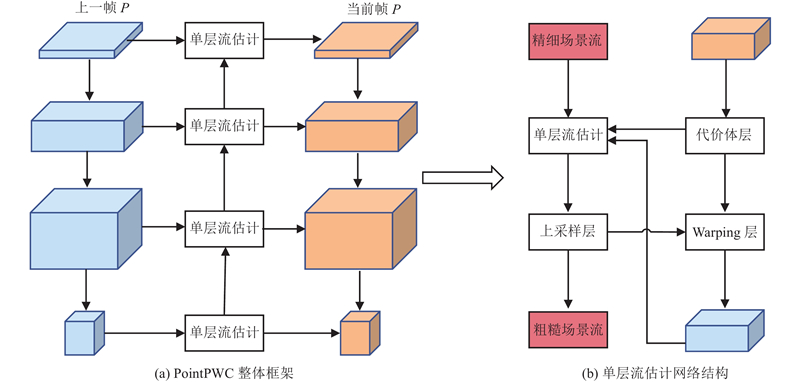
... 运动估计模块通过场景流网络,根据输入的前一帧点云和当前帧点云的坐标信息, 预测前一帧到当前帧的运动向量. 网络的设计以PointPWC-Net[15 ] 为基础, 整个网络的输入是相邻的2帧点云, 2帧点云不断通过下采样和特征提取操作, 获取输入点云的多尺度特征表示.下采样阶段采用最远点下采样算法进行下采样, 利用PointConv[16 ] 进行特征提取,得到不同尺度下的点云特征.在场景流估计网络中,通过对下一层进行上采样,逐步提升感受野,与上一层提取的点云特征进行拼接,实现粗粒度场景流到细粒度场景流的转换. 中间每一层网络结构相同, 用于估计每一层的运动信息, 其中代价立方体(cost volume, CV)的计算公式如下: ...
1
... 运动估计模块通过场景流网络,根据输入的前一帧点云和当前帧点云的坐标信息, 预测前一帧到当前帧的运动向量. 网络的设计以PointPWC-Net[15 ] 为基础, 整个网络的输入是相邻的2帧点云, 2帧点云不断通过下采样和特征提取操作, 获取输入点云的多尺度特征表示.下采样阶段采用最远点下采样算法进行下采样, 利用PointConv[16 ] 进行特征提取,得到不同尺度下的点云特征.在场景流估计网络中,通过对下一层进行上采样,逐步提升感受野,与上一层提取的点云特征进行拼接,实现粗粒度场景流到细粒度场景流的转换. 中间每一层网络结构相同, 用于估计每一层的运动信息, 其中代价立方体(cost volume, CV)的计算公式如下: ...
Point transformer
1
2021
... 在运动压缩部分, 对运动向量进行压缩编码. 其中的运动向量编码解码网络是多尺度的特征提取网络, 将运动向量$ {{\boldsymbol{M}}}_{t} $ [14 ] 中的特征提取模块和注意力模块[17 ] 进行特征提取, 得到中间层的运动向量高维特征$ {{\boldsymbol{f}}_{{{{\mathrm{mv}}}}}} $ . 对 $ {{\boldsymbol{f}}}_{{\mathrm{mv}}} $
1
... 式中:${{G}}( \cdot )$ $\odot $ $ {{\boldsymbol{f}}_{{{{\mathrm{mv}}}}}} \in {{\bf{R}}^{c \times N}} $ $c 、N $ ${{\boldsymbol{\mu }}_s} = [ {\mu _{s,0}},{\text{ }}{\mu _{s,1}},{\text{ }} \cdots {\text{, }}{\mu _{s,c - 1}}] $ ${{{\mu}} _{s,i}} \in \bf{R}$ s 为增益向量在增益矩阵中的索引. 所有增益向量组成增益矩阵$ {\boldsymbol{\mu }}\in {\bf{R}}^{c\times n} $ n 为增益向量的个数. 类似地,逆增益单元由逆增益矩阵${\boldsymbol{\mu }}' \in {{\bf{R}}^{c \times n}}$ $ {{\boldsymbol{\mu }}'_s} = [ {\mu '_{s,0}},{\text{ }}{\mu '_{s,1}},{\text{ }} \cdots ,{\text{ }}{\mu '_{s,c - 1}}] $ ${\mu '_{s,i}} \in \bf{R}$ ${\text{IG}}( \cdot )$ [18 ] , 对运动向量进行上采样. 子点卷积模块是对输入进行分组, 再分别进行卷积并扩展维度, 将各个组合并, 达到上采样的目的. 在经过解码端后,可以得到最终重构的运动向量信息, 用于下一阶段的运动补偿模块. ...
1
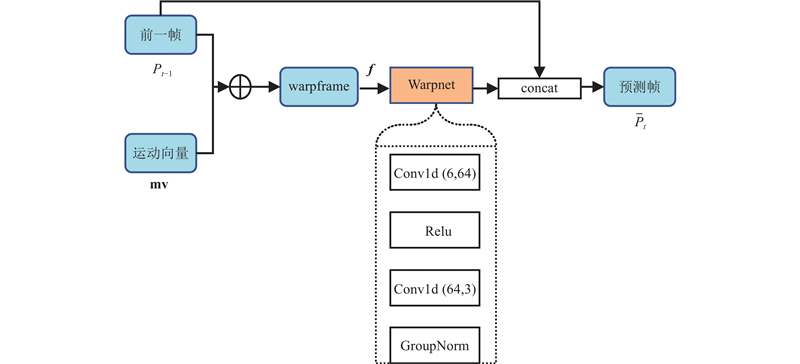
... 运动补偿模块利用上一帧的坐标信息和运动向量,对当前帧进行补偿. 在图像领域也有类似的运动补偿模块, 图像领域利用光流和前一帧的图像信息进行融合. 本文的运动补偿思想借鉴了DVC[19 ] 中的视频运动补偿框架. 在视频压缩框架中, 网络中处理的是$ N\times c\times H\times W $ $ N\times c $ 图3 所示, 网络的输入为前一帧的空间中连续的坐标信息${P_{t - 1}}$ ${\bar P_t}$ ${P_t}$ $N \times 3$ $N \times 3$ . 将前一帧直接加上运动向量mv , 得到偏移后的前一帧, 称为变形帧(warpframe). 利用直接算术相加得到的warpframe与当前帧${P_t}$ ${P_{t - 1}}$ f $N \times 6$ . 将f 图3 的虚线部分所示,通过一维卷积操作将f [20 ] 组归一化函数,对输出进行标准化操作, 得到最终的预测帧坐标信息. ...
1
... 运动补偿模块利用上一帧的坐标信息和运动向量,对当前帧进行补偿. 在图像领域也有类似的运动补偿模块, 图像领域利用光流和前一帧的图像信息进行融合. 本文的运动补偿思想借鉴了DVC[19 ] 中的视频运动补偿框架. 在视频压缩框架中, 网络中处理的是$ N\times c\times H\times W $ $ N\times c $ 图3 所示, 网络的输入为前一帧的空间中连续的坐标信息${P_{t - 1}}$ ${\bar P_t}$ ${P_t}$ $N \times 3$ $N \times 3$ . 将前一帧直接加上运动向量mv , 得到偏移后的前一帧, 称为变形帧(warpframe). 利用直接算术相加得到的warpframe与当前帧${P_t}$ ${P_{t - 1}}$ f $N \times 6$ . 将f 图3 的虚线部分所示,通过一维卷积操作将f [20 ] 组归一化函数,对输出进行标准化操作, 得到最终的预测帧坐标信息. ...
1
... 式中:D 为当前帧$P$ $\hat P$ [21 ] , 用于衡量重构后的点云和真实点云之间的差距,计算的是点级别之间的平均距离;R 为比特率损失,包含运动向量部分和残差2部分的比特率损失;$R_{{\mathrm{mv}}} $ $R_{{{\mathrm{residual}} }} $
1
... 选用AMASS[22 ] 数据集作为预处理的原始数据集. AMASS数据集是三维人体动作捕捉数据集, 经过SMPL模板进行标准化处理, 将现有的基于光学标记的人体运动捕捉的数据集标准化集成到一起, 包括CMU、MPI-HDM05、MPIPose、KIT、BioMotion Lab、TCD和ACCAD等数据集中的样本. AMASS具有丰富的运动数据和长时间的运动序列, 总共包含300多个不同的人体对象, 有超过10 000个不同的动作序列.仅选取AMASS动态网格中的顶点,计算顶点的运动向量作为标签, 得到原始的动态点云数据集, 将它用于网络的训练和验证. 为了检验本文方法的有效性,对来自MPEG中的8i Voxelized Full Bodies(8iVFB)[23 ] 标准人体数据集使用最远点采样算法,从每帧点云中采样出2 048个点,将这类数据集作为测试集. ...
Emerging mpeg standards for point cloud compression
1
2019
... 选用AMASS[22 ] 数据集作为预处理的原始数据集. AMASS数据集是三维人体动作捕捉数据集, 经过SMPL模板进行标准化处理, 将现有的基于光学标记的人体运动捕捉的数据集标准化集成到一起, 包括CMU、MPI-HDM05、MPIPose、KIT、BioMotion Lab、TCD和ACCAD等数据集中的样本. AMASS具有丰富的运动数据和长时间的运动序列, 总共包含300多个不同的人体对象, 有超过10 000个不同的动作序列.仅选取AMASS动态网格中的顶点,计算顶点的运动向量作为标签, 得到原始的动态点云数据集, 将它用于网络的训练和验证. 为了检验本文方法的有效性,对来自MPEG中的8i Voxelized Full Bodies(8iVFB)[23 ] 标准人体数据集使用最远点采样算法,从每帧点云中采样出2 048个点,将这类数据集作为测试集. ...
1
... 在训练阶段, 从训练集中的点云片段中选取第1帧为前一帧, 从该片段后续的3帧中随机选取一帧作为当前帧, 将前一帧到当前帧的运动向量作为场景流的真实标签. 在运动压缩网络和残差压缩网络的下采样模块中, 编码端的下采样率和解码端的上采样率分别设置为[1/4,1/2,1/2]、[2,2,4], 整个压缩网络的特征通道的大小设置为16. 在联合损失函数中, RD损失的系数$\alpha $ $\beta $ $\lambda = \{ 10,50,100,500,1\;000, 4\;000\} $ . 网络使用的梯度方向传播模块是Adam优化器[24 ] , 优化器的学习率设置为0.001, 网络的batch size大小是16, 总共训练100个轮次. ...
1
... 为了验证本文方法的有效性,选取静态点云压缩的方法Static [25 ] 、Draco点云压缩库 [26 ] 、MPEG组织的VPCC压缩标准 [27 ] 及最新的动态点云压缩方法D-DPCC [8 ] 作为对比, 开展实验结果分析. Static方法是基于深度学习的静态点云压缩方法, Draco是传统的静态压缩方法, 二者均将点云序列的每帧独立压缩的结果作为实验结果进行比较. VPCC是MPEG组织提出的动态点云压缩标准,是一种传统方法, D-DPCC是基于深度学习的动态点云方法. 这2种压缩方法常用来压缩体素化点云序列. ...
1
... 为了验证本文方法的有效性,选取静态点云压缩的方法Static [25 ] 、Draco点云压缩库 [26 ] 、MPEG组织的VPCC压缩标准 [27 ] 及最新的动态点云压缩方法D-DPCC [8 ] 作为对比, 开展实验结果分析. Static方法是基于深度学习的静态点云压缩方法, Draco是传统的静态压缩方法, 二者均将点云序列的每帧独立压缩的结果作为实验结果进行比较. VPCC是MPEG组织提出的动态点云压缩标准,是一种传统方法, D-DPCC是基于深度学习的动态点云方法. 这2种压缩方法常用来压缩体素化点云序列. ...
Video-based point-cloud-compression standard in MPEG: from evidence collection to committee draft standards in a nutshell
1
2019
... 为了验证本文方法的有效性,选取静态点云压缩的方法Static [25 ] 、Draco点云压缩库 [26 ] 、MPEG组织的VPCC压缩标准 [27 ] 及最新的动态点云压缩方法D-DPCC [8 ] 作为对比, 开展实验结果分析. Static方法是基于深度学习的静态点云压缩方法, Draco是传统的静态压缩方法, 二者均将点云序列的每帧独立压缩的结果作为实验结果进行比较. VPCC是MPEG组织提出的动态点云压缩标准,是一种传统方法, D-DPCC是基于深度学习的动态点云方法. 这2种压缩方法常用来压缩体素化点云序列. ...