应急工作站点选址优化问题常被建模为覆盖问题,通过优化应急救援设施的布设位置和数量,以覆盖更多、更重要的路段和节点[4-7]. Guo等[5]提出协作覆盖模型,研究多交通方式联运网络中应急救援设施的选址策略. 交通网络恢复决策优化问题常被建模为选择问题或排程问题[8],通过确定待修复路段的集合和修复时序,提升路网抗灾能力. 其中,应急救援设施的排程调度优化得到了广泛的研究和讨论[8-9]. Li等[8]在恢复决策建模中综合选择问题与排程问题,获得应急恢复阶段路段恢复持续时间不确定情况下的待修复路段集合及修复时序. Maya-Duque等[10-12]研究应急救援设施排程调度和路径决策综合优化问题,考虑受损路段可达性对路网恢复决策的影响. Maya-Duque等[10-11]提出考虑路径决策的路网恢复优化模型,研究假设应急救援设施仅能够修复路网中可达的受损路段.
除了由恢复工作组和恢复设备组成的应急救援设施,灾后恢复工作的高效开展还需要后勤保障资源的支持,包括水泥、钢材和燃油等消耗性资源[13]. 2008—2011年,汶川地震灾区的水泥和钢铁供应量分别为12 300万t和1 080万t[14]. Yan等[13]研究后勤保障资源的最优调度问题,以最小化车辆运营成本和后勤保障资源调度成本为优化目标. Li等[15]构建应急救援设施和后勤保障资源的综合调度优化模型,定性建模了两者相互协作关系对路网恢复的影响. 然而,应急救援设施和后勤保障资源在耗尽性、恢复作用和运输方式上有显著差异. 应急救援设施是非消耗性资源,决定了路网恢复的速度;后勤保障资源是消耗性资源,影响路网恢复程度[16]. 为了尽可能降低运输成本,在最短时间内覆盖更多的受损路段,应急救援设施在完成一条路段的恢复后会直接前往下一条受损路段进行工作[17]. 后勤保障资源所需的数量巨大,不能一次性跟随应急救援设施全部运往受损路段,而是需要单独从应急工作站点运往受损路段[15].
综上所述,道路交通网络多阶段抗灾决策优化依赖于后勤保障资源和应急救援设施的相互协作. 当前的研究大多集中在应急救援设施多阶段优化模型的构建上,忽略了后勤保障资源的多阶段优化. Hackl等[16]研究考虑灾后恢复阶段2类资源的综合建模,但是未能有效地刻画两者的特点,也未能定量建模两者对路段恢复的影响和相互协作关系. 本文提出混合整数3层规划模型. 上层模型用于确定应急工作站点的灾前选址布设. 中层模型通过计算应急救援设施路径流和后勤保障资源路径流,获得不同时间步下的路网恢复状况. 下层模型用于获得不同时间步下的用户出行情况. 基于贵州省区域高速公路网络,验证了本文模型的有效性和优越性.
1. 研究方法
1.1. 模型构建
1.1.1. 基本假设
1)重大灾害后受损路段无法双向通行,采用无向网络
1.1.2. 优化目标
重大灾害下的路网抗灾成本包括灾前应急工作站点布设成本和灾后路网恢复成本[16-17]. 灾后恢复成本包括与灾后恢复决策相关的直接成本和与用户出行相关的间接成本. 其中,直接成本主要指与灾后恢复决策相关的各项开支,如路段重建和费用物资运输费用[16]. 间接成本为与用户出行相关的费用. 本文的优化对象为受损路网恢复到灾前状态的全恢复过程,恢复决策无法降低包括路段重建在内的固定费用,而合理的物资调配路径规划可以有效地降低物资运输成本. 与后勤保障资源相比,路网恢复所需的应急救援设施数量小得多. 由于应急救援设施无须返回应急工作站点,直接前往下一受损路段进行作业,运输路径的长度相对更小. 应急救援设施的运输成本相对很小,甚至可以忽略不计. 选取后勤保障资源运输成本
式中:
重大灾害后,路网中存在大量的不连通OD,恢复路网连通性是路网恢复决策的首要任务,以保障应急救援和灾后重建工作的顺利进行. 选取未满足出行需求惩罚成本
式中:
除了大量的不连通OD,路段受损也会造成交通拥堵和出行绕行,导致连通OD出行成本的增加. 为了更好地评估重大灾害对人们出行的影响,选取连通OD出行阻抗增加惩罚成本
式中:
1.1.3. 决策优化模型
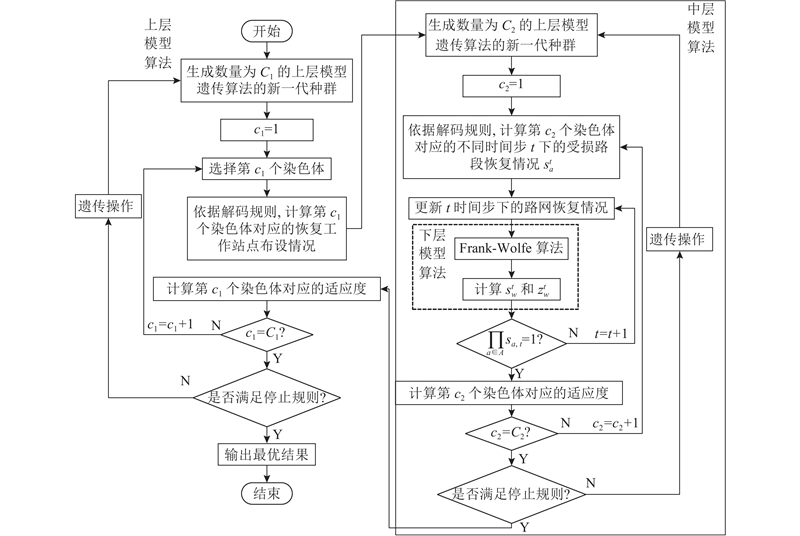
建立的道路网络多阶段抗灾能力优化模型为混合整数3层规划模型,其中上层模型为应急工作站点布设决策优化问题,中层模型为最小费用流问题[19],下层模型为用户均衡配流模型. 模型的作用机制如下:上层模型决策变量输入到中层模型,决定灾前各节点的应急救援设施布设数量和后勤保障资源存放能力,影响灾后各时间步的应急救援设施流和后勤保障资源流. 根据中层模型,计算获得不同时间步下各受损路段的恢复情况,传递到下层模型. 基于不同时间步下的路网运营状态,下层模型通过求解用户均衡配流模型,计算得到各时间步下所有OD的行程时间阻抗和运营状态,并传递回中层模型. 利用中层模型计算得到灾后路网加权总恢复成本,并输入到上层模型,以便上层模型计算出优化目标路网抗灾成本.
上层模型如下:
式中:
式(4)为上层模型目标函数,最小化路网恢复成本与工作站点布设成本之和. 式(5)为应急工作站点的布设数量约束.
中层模型如下:
式中:
式(7)为中层模型的目标函数,旨在最小化灾后总加权恢复成本,其中加权系数
下层模型:
式中:
1.1.4. 模型分析
现有道路交通网络多阶段综合优化问题多关注应急救援设施的布设和调度优化问题,忽略了后勤保障资源的多阶段优化. 尽管有研究考虑了后勤保障资源与应急救援设施的综合优化,但未能区分两者间的特点差异和定量建模两者间的相互协作关系. 通过构建不同的流量守恒约束,区分两者在耗尽性和运输方式上的差异. 式(8)、(10)约束后勤保障资源只能从应急工作站点分发,且数量会因路段的恢复而减少,而式(12)~(14)保障应急救援设施能够在完成一条路段的恢复工作后直接抵达下一条受损路段,且数量不会发生变化. 模型通过式(11)、(16)和(20)区分了两者恢复作用的差异,后勤保障资源决定了路段恢复程度,应急救援设施决定了路段恢复速度. 基于“瓶颈效应”的思想,该模型通过式(20)定量建模了两者间的相互协作关系.
1.2. 算法设计
图 1
1.2.1. 染色体编码
上层遗传算法采用二进制编码方法,对应急工作站点的选址进行编码. 染色体的长度为路网中的节点数目,每一位依次用于判断路网中的相应节点是否被选为工作站点. 其中,数字“1”表示选择该站点为工作站点,数字“0”则相反. 例如,“001100”表示在染色体第3位和第4位对应节点布设应急救援设施和后勤保障资源. 下层遗传算法使用基于优先度的整数编码方法. 染色体的长度为路网中受损路段的数目,每一位表示受损路段的恢复优先级,优先级越高的路段越被优先分配应急救援设施和后勤保障资源,如“1432576”表示染色体第1位所对应的路段将优先被分配应急救援设施和后勤保障资源. 下一节将详细描述下层遗传算法的解码过程,具体流程如图2所示.
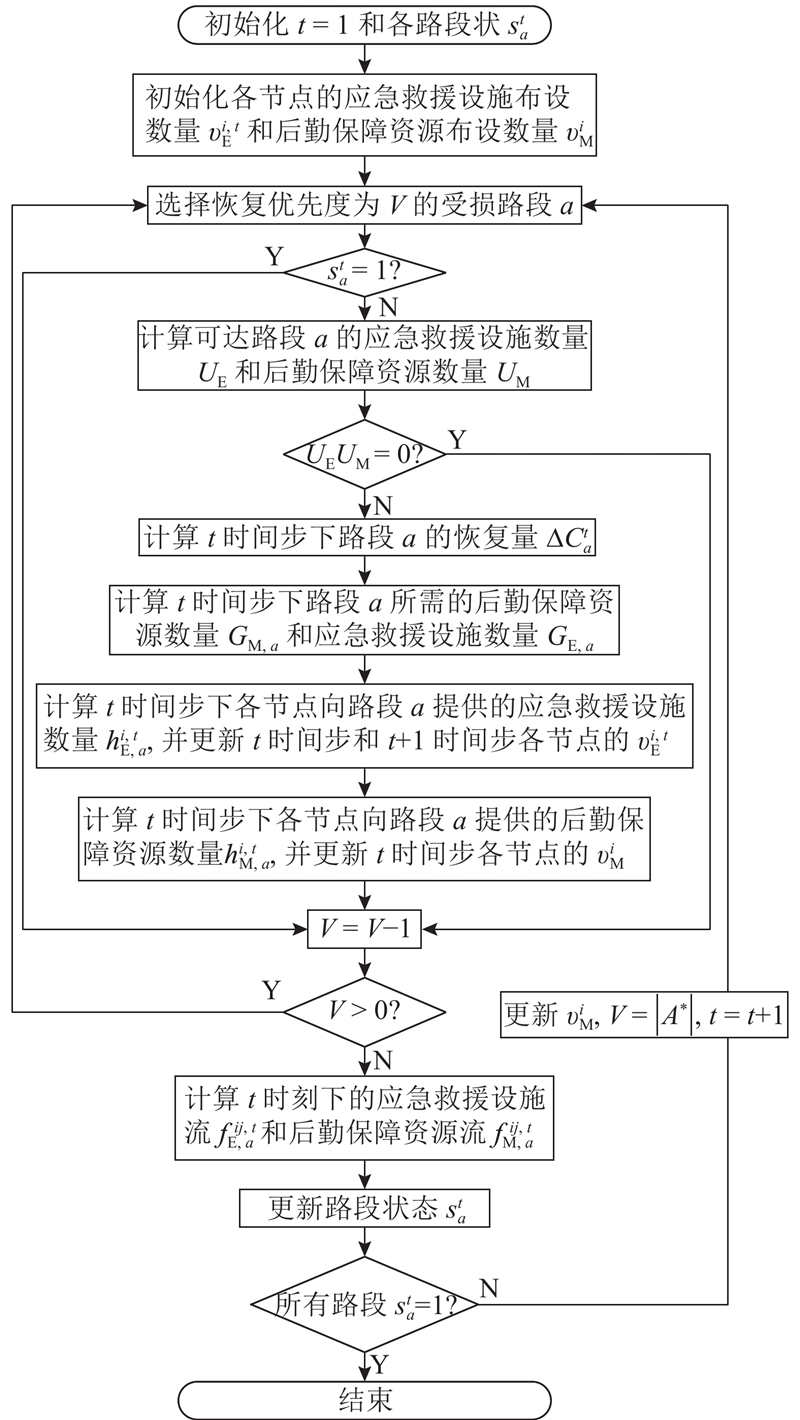
图 2
图 2 下层遗传算法解码过程的流程图
Fig.2 Flowchart of decoding process for lower-level genetic algorithm
1.2.2. 中层模型的遗传算法解码过程
1)设定初始时间步,
2)基于Dijkstra算法,生成
3)判断优先级为
4)判断优先级为
5)判断优先级为
6)确定受损路段
7)记
记所需的应急救援设施数量为
8)确定
9)确定
10)
11)依据全有全无分配原则,计算
12)基于
2. 研究数据
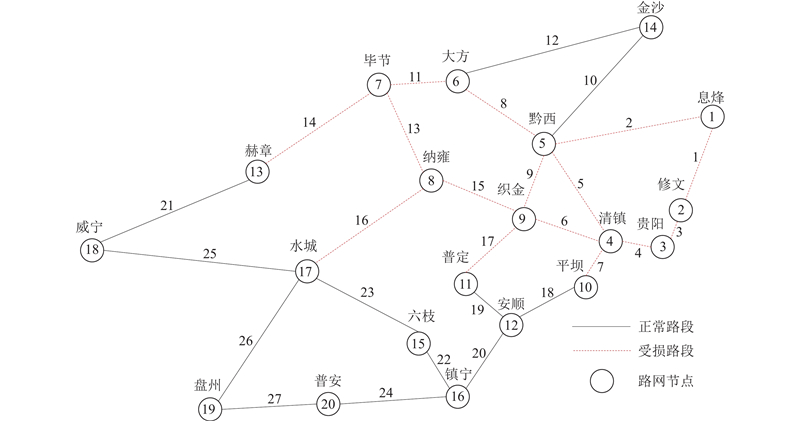
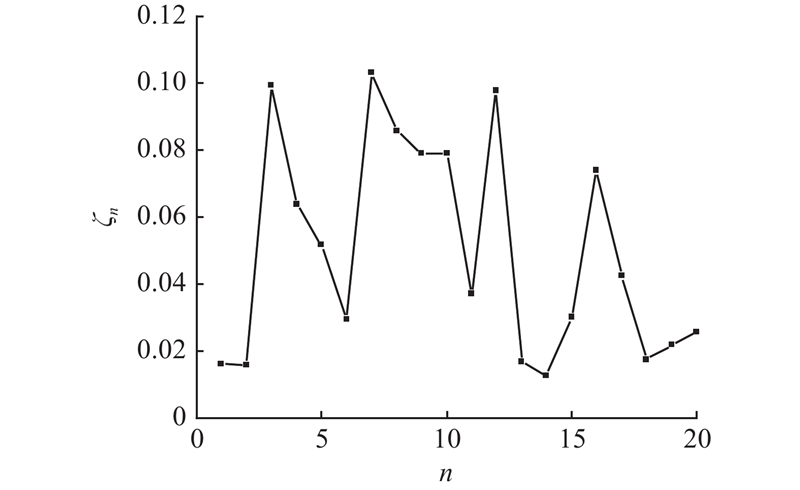
为了验证上述模型和算法的有效性,基于贵州省2020年7月24日高速公路门架数据,以毕节市、六盘水市、安顺市和贵阳市内部分区县组成的区域高速公路网为研究对象,构建无向拓扑网络. 如图3所示,以县(区)为网络节点,其中地级市管辖范围内的区被划为一个节点,如贵阳市的白云区、云岩区和观山湖区等均归为节点3. 研究区域内有20个节点、27条路段、380对OD. 各路段的参数如表1所示. 各节点的加权客流介数ζn如图4所示. 图中,n为节点编号. 加权客流介数为最短路经过该节点的OD客流量之和与路网总客流的比值,用于表示各节点重要程度[21]. 假设重大自然灾害导致路网中15条路段受到不同程度的损害,各受损路段的受损程度如表2所示. 通过穷举出15条受损路段所有连通情况下的路网状态,获得恢复过程中不同路网状态下的未满足出行需求、用户出行阻抗增量以及后勤保障资源运输成本,计算得到最佳的目标函数加权因子
图 3
表 1 贵州省区域高速公路网的路段参数
Tab.1
| | | | | | | | | | | | |
| 1 | 33 | 4 200 | 40 | 10 | 62 | 4 200 | 89 | 19 | 18 | 4 200 | 23 |
| 2 | 65 | 4 200 | 104 | 11 | 23 | 4 200 | 32 | 20 | 46 | 4 200 | 52 |
| 3 | 25 | 4 200 | 32 | 12 | 76 | 4 200 | 95 | 21 | 45 | 4 200 | 61 |
| 4 | 22 | 4 200 | 28 | 13 | 56 | 4 200 | 70 | 22 | 29 | 4 200 | 39 |
| 5 | 50 | 4 200 | 69 | 14 | 56 | 4 200 | 74 | 23 | 61 | 4 200 | 79 |
| 6 | 76 | 4 200 | 92 | 15 | 45 | 4 200 | 56 | 24 | 81 | 4 200 | 106 |
| 7 | 20 | 4 200 | 26 | 16 | 59 | 4 200 | 71 | 25 | 61 | 4 200 | 74 |
| 8 | 42 | 4 200 | 54 | 17 | 44 | 4 200 | 61 | 26 | 85 | 4 200 | 108 |
| 9 | 34 | 4 200 | 47 | 18 | 28 | 4 200 | 33 | 27 | 45 | 4 200 | 60 |
图 4
表 2 受损路段的参数
Tab.2
| | | | | | | ||
| 1 | 100 | 6 | 100 | 13 | 100 | ||
| 2 | 50 | 7 | 75 | 14 | 25 | ||
| 3 | 25 | 8 | 25 | 15 | 50 | ||
| 4 | 75 | 9 | 75 | 16 | 25 | ||
| 5 | 100 | 11 | 75 | 17 | 50 |
3. 案例分析
3.1. 灾前工作站点布设决策的分析
表 3 不同预算下的灾前工作站点选址决策
Tab.3
| B | 站点选址 | ||
| 最优决策P | 决策P1 | 决策P2 | |
| 1 | 11 | 11 | 9 |
| 2 | 10,17 | 10,11 | 4,8 |
| 3 | 4,7,11 | 4,11,17 | 3,5,8 |
| 4 | 4,7,8,11 | 4,10,13,17 | 3,5,7,9 |
| 5 | 3,4,7,8,9 | 4,7,10,11,17 | 3,5,7,8,9 |
图 5
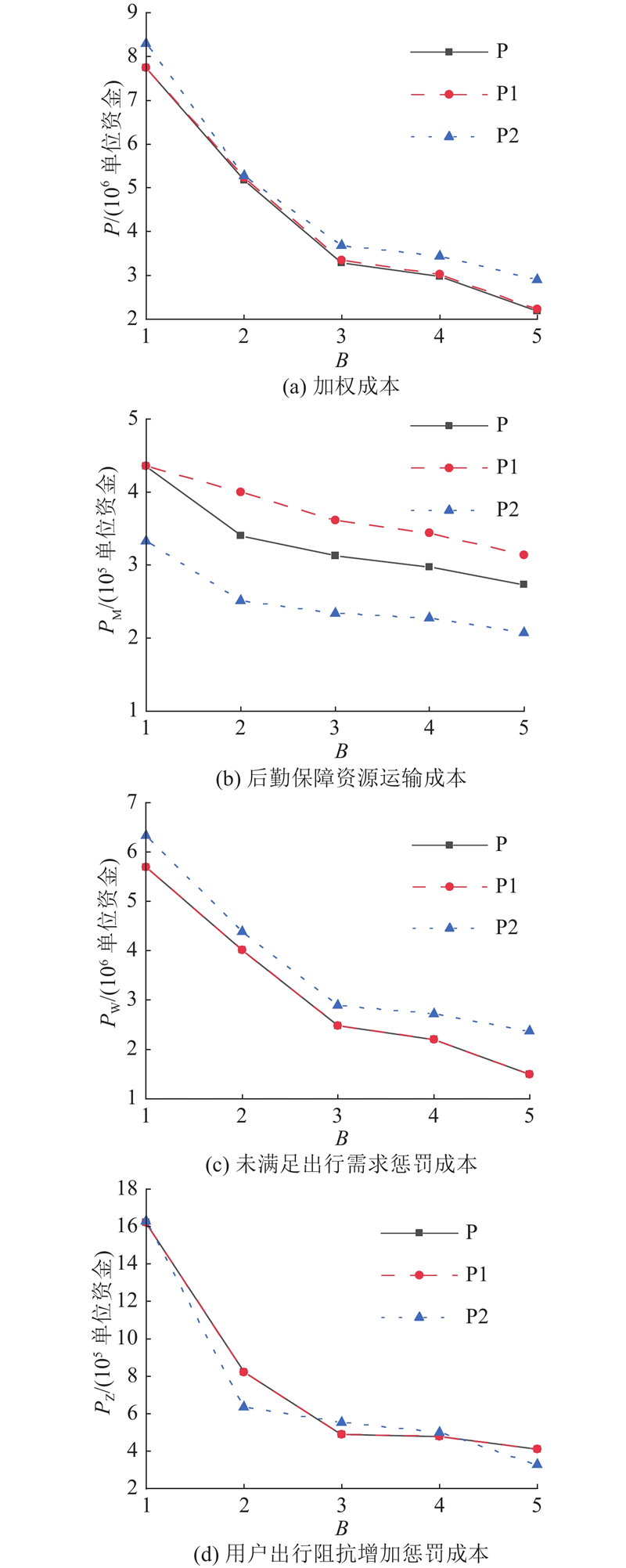
图 5 不同预算下不同灾前布设方案的灾后路网恢复效果
Fig.5 Post-disaster road network recovery effects of different pre-disaster deployment decisions under different budgets
如图5所示,对比最优决策P和决策P1可知,两者对灾后路网恢复效果影响的差异主要体现在后勤保障资源运输成本. 5种预算下考虑后勤保障资源的灾前布设决策可以平均降低10.96%的
图 6
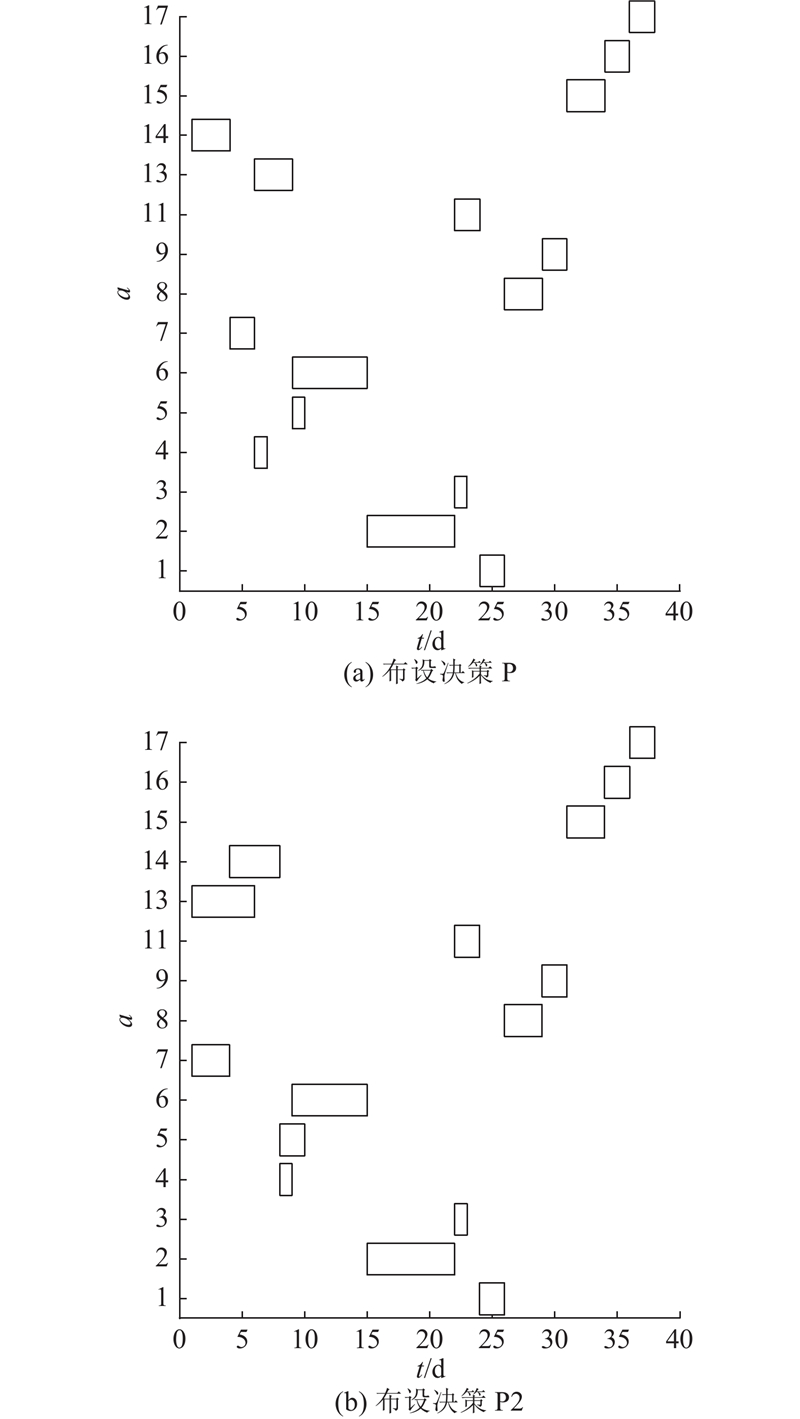
图 6 B = 2下灾前布设决策P和决策P2对应的灾后路网恢复排程甘特图
Fig.6 Post-disaster road network recovery effects of pre-disaster deployment decision P and decision P2 under budget B = 2
如图5所示,与决策P2相比,5种预算下最优决策P分别平均降低了11.51%和17.73%的
3.2. 灾后受损路段恢复决策的分析
为了分析后勤保障资源与应急救援设施的相互协作关系对灾后路网恢复效果的影响,对比分析
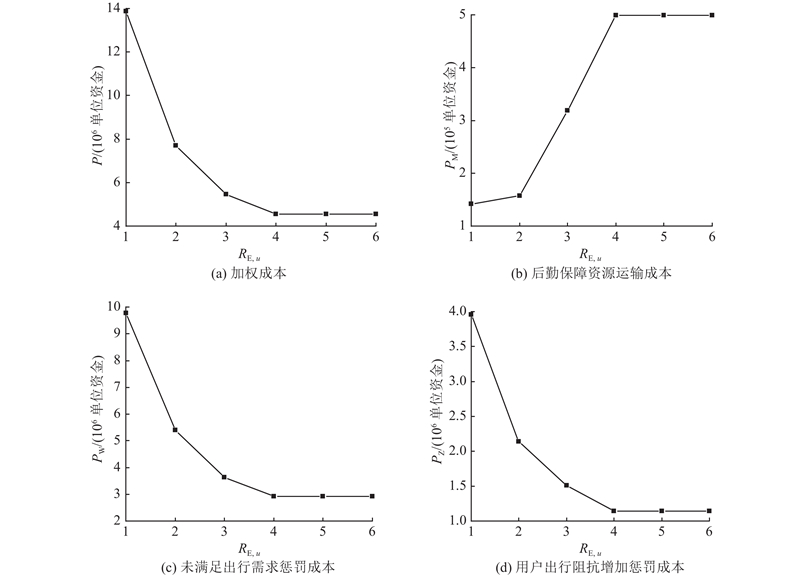
如图7所示,设定每个工作站点的
图 7
图 7
B = 2下不同
Fig.7
Post-disaster road network recovery effect of optimal recovery decision under different
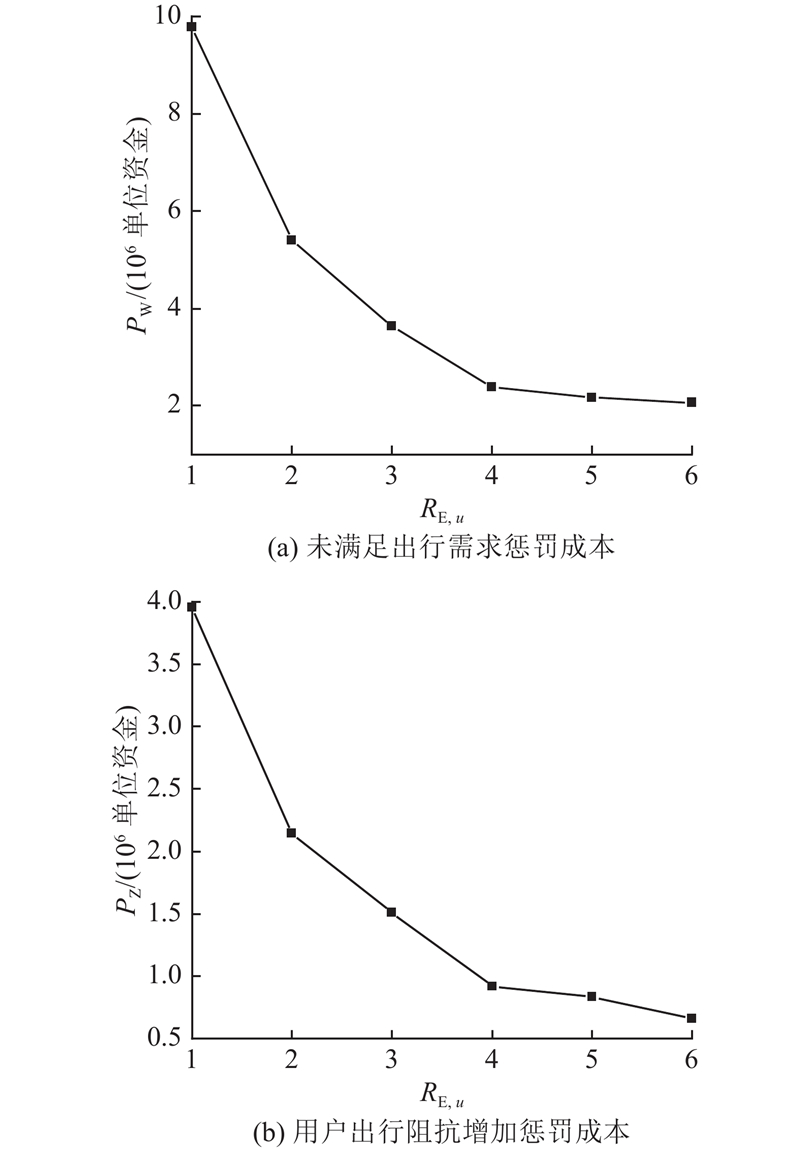
图 8
图 8
B = 2下不同
Fig.8
Post-disaster road network recovery effect of optimal recovery decision under different
图 9
图 9
B = 2下不同
Fig.9
Post-disaster road network recovery effects of recovery decisions without considering logistical support resources for different
对比图7(b)、8(b)可知,保持
4. 结 论
(1)利用构建的路网抗灾能力决策优化模型,可以有效地降低路网灾害应对成本. 较未考虑后勤保障资源的灾前布设决策,该模型通过优化后勤保障资源的运输路径,有效降低了后勤保障资源的运输成本. 与未考虑灾后恢复过程的灾前布设决策相比,该模型能够保证网络中关键节点的快速连通,有效降低了未满足出行需求的惩罚成本.
(2)后勤保障资源和应急救援设施共同决定灾后路网恢复过程. 当其中一项所能恢复的路段容量超过另一项时,增加其数量将无法改善路网的恢复效果. 忽略两者间的协作关系,将会高估应急救援设施布设数量的增加对恢复效果的影响. 在路网恢复过程中,需要确保后勤保障资源和应急救援设施数量的相互匹配,以提高路网恢复效率,避免资源浪费.
(3)后勤保障资源和应急救援设施数量的变化会对后勤保障资源运输成本产生相反的影响,随着应急救援设施数量的增大而增大,随着后勤保障资源数量的增大而减小. 在实际应用中,需要准确认识和辨析后勤保障资源和应急救援设施数量变化对路网恢复效果的影响.
(4)为了降低模型求解的复杂度,仅考虑一种类型的应急工作站点. 考虑到不同路段的受损程度、初始容量、恢复优先程度等不同,它们对在其周围布设的应急救援设施和后勤保障资源的需求有差异. 下一步将研究考虑多种类型灾前应急工作站点的道路交通网络多阶段抗灾能力优化问题.
参考文献
Use of OR in earthquake operations management: a review of the literature and roadmap for future research
[J].DOI:10.1016/j.ijdrr.2021.102539 [本文引用: 1]
A decomposition-based heuristic for a multicrew coordinated road restoration problem
[J].DOI:10.1016/j.trd.2021.102854 [本文引用: 1]
Routing multiple work teams to minimize latency in post-disaster road network restoration
[J].DOI:10.1016/j.ejor.2021.07.048 [本文引用: 1]
Covering models and optimization techniques for emergency response facility location and planning: a review
[J].DOI:10.1007/s00186-011-0363-4 [本文引用: 1]
A method to improve the resilience of multimodal transport network: location selection strategy of emergency rescue facilities
[J].DOI:10.1016/j.cie.2021.107678 [本文引用: 1]
Increasing the resilience level of a vulnerable rail network: the strategy of location and allocation of emergency relief trains
[J].
Multi-objective optimization of rescue station selection for emergency logistics management
[J].DOI:10.1016/j.ssci.2019.07.011 [本文引用: 1]
Resilience-based transportation network recovery strategy during emergency recovery phase under uncertainty
[J].DOI:10.1016/j.ress.2019.03.052 [本文引用: 3]
Optimal restoration schedules of transportation network considering resilience
[J].DOI:10.1080/15732479.2020.1801764 [本文引用: 2]
Network repair crew scheduling and routing for emergency relief distribution problem
[J].DOI:10.1016/j.ejor.2015.06.026 [本文引用: 3]
A branch-and-benders-cut algorithm for the crew scheduling and routing problem in road restoration
[J].DOI:10.1016/j.ejor.2018.11.004 [本文引用: 1]
Assessment of post-earthquake resilience of highway–bridge networks by considering downtime due to interaction of parallel restoration actions
[J].DOI:10.1080/15732479.2021.1961826 [本文引用: 1]
Optimal scheduling of logistical support for an emergency roadway repair work schedule
[J].DOI:10.1080/0305215X.2011.628389 [本文引用: 2]
Resourcing for a resilient post-disaster reconstruction environment
[J].DOI:10.1108/17595901011026481 [本文引用: 1]
A new model for road network repair after natural disasters: integrating logistics support scheduling with repair crew scheduling and routing activities
[J].DOI:10.1016/j.cie.2020.106506 [本文引用: 2]
Determination of near-optimal restoration programs for transportation networks following natural hazard events using simulated annealing
[J].DOI:10.1111/mice.12346 [本文引用: 4]
Integrating location and network restoration decisions in relief networks under uncertainty
[J].DOI:10.1016/j.ejor.2019.06.012 [本文引用: 2]
Resilience of traffic networks: from perturbation to recovery via a dynamic restricted equilibrium model
[J].DOI:10.1016/j.ress.2016.07.020 [本文引用: 1]
求解最小费用最大流问题的信念传播算法
[J].DOI:10.19734/j.issn.1001-3695.2020.10.0357 [本文引用: 1]
Belief propagation algorithm for solving minimum cost maximum flow problem
[J].DOI:10.19734/j.issn.1001-3695.2020.10.0357 [本文引用: 1]
城市轨道交通网络关键站点识别方法对比与分析
[J].
Comparison and analysis of identification methods for critical stations in urban rail transit networks
[J].
On the distribution approach to location problems
[J].DOI:10.1016/S0360-8352(00)00025-5 [本文引用: 1]