1. 相关工作
当前,区块链Kad网络性能方面的研究主要集中在通过改变网络结构以提高数据传输效率. Yu等[3]将K桶均匀划分成多个区域,每个分区存储不同的节点信息. Liang[4]为网络中所有节点都添加了本地缓存以扩大存储空间. 此外,部分研究探讨了加快节点定位速率的方法. Zhang等[5] 提出Kadabra协议,该协议创造了可以根据网络的异质性进行动态调整的路由表,减少了网络查找的延迟. 网络结构的改变容易损害网络的安全性,为了增强网络抵御攻击的能力,Eisenbarth等[6]分析以太坊的网络特性,提出检测和废除可疑节点的架构,以抵御Sybil攻击. 类似地,Xu等[7] 设计基于随机森林分类算法的日蚀攻击检测模型,能以较高的准确率检测出以太坊网络中的恶意节点.
小世界现象源于Milgram [8]设计的小世界实验,他通过实验证明只需不到6个人就可以将一封信从奥马哈市的志愿者寄送给波士顿的一位居民. Watts等[9]通过对规则网络的每条边进行随机化重连,构建WS小世界模型. 通过实验发现,该模型的网络性能优于结构化网络,但是可能出现孤立节点. Watts等[10]对其加以改进,提出NW小世界模型,将随机化重连改为随机化加边,保证了网络的连通性. Kleignberg系统地研究小世界理论,给出建立小世界网络的具体方法. 通过该方法,Zou等[11-12]将小世界理论应用于Can和Chord这2种P2P网络,提升了网络性能. 近年来,一些学者尝试将小世界理论引入区块链网络中. Serena等[13] 使用分布式账本网络分析器,研究比特币和以太坊网络的交易图,检测到这些交易图都有小世界特征. Wang等[14] 利用以太坊网络分析仪探测以太坊的P2P网络,发现该网络具有无标度网络的特征且存在一定的小世界效应.
2. 基于小世界理论的Kademila网络模型
2.1. 方案介绍
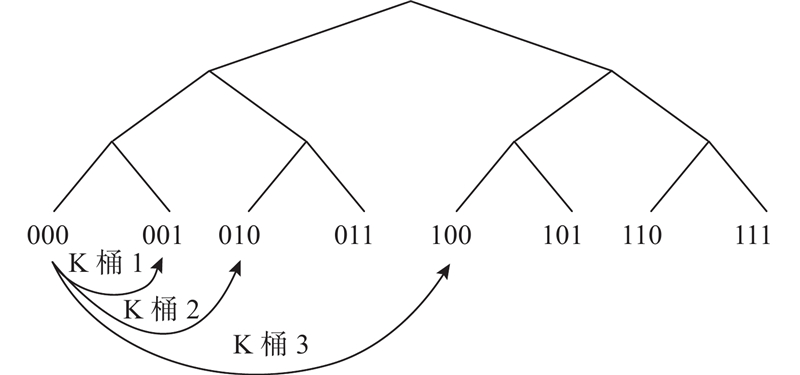
Kad网络是基于二叉树结构的P2P网络,其中每个节点被映射为二叉树的叶子节点. 这些节点维护一组被称为K桶的信息存储结构,K桶数量等于节点ID的位数. 每个K桶存储的节点信息与节点间的逻辑距离相对应,此处的逻辑距离指2个节点ID的异或值. 每个节点都可以计算自身与目的节点的逻辑距离,通过不断地迭代查询,获取目的节点的地址信息. 通常情况下,每个K桶中能存储的节点数量不超过k个. 当Kad网络的节点ID是3 bits时,设k = 1,整个网络空间的结构如图1所示.
图 1
在该网络中,假设每个K桶都存储与本节点逻辑距离最近的k个节点. 以节点000作为广播消息的起点,节点000的K桶1、2、3分别存储节点001、节点010、节点100. 这3个节点连接的节点依次是(节点000、节点011、节点101)、(节点011、节点000、节点110)、(节点101、节点110、节点000). 当该网络经历2个传输层级即传播两跳时(将同一层级内多次消息传输只看作一跳),全网仍有节点111未收到消息. 这是因为存在冗余,如节点001和节点100都保存了节点101的地址信息. 冗余保证了网络的连通性,也增强了网络的健壮性和安全性. 在区块链网络中,适量的冗余是必需的.
在保证网络存在冗余的前提下,为了减少网络传输的层级,可以让节点000额外存储节点111的信息. 此时消息只要传播两跳就可以发送到全网. 一个节点的地址信息包含节点ID、IP地址、端口号等内容,大小只有几十字节. 扩容一个节点需要花费的代价很小,但是网络性能提升很多. 该方法的效果良好,主要是因为扩容了适当的节点. 考虑到实际网络结构的复杂性,需要探索准确且便捷的节点选择方式,因此在Kad网络中引入小世界理论.
本文的主要思想源于Kleignberg建立的K模型. 该模型的实现方式是使所有节点以
式中:a、b、c为网络中的任意3个节点,
图 2
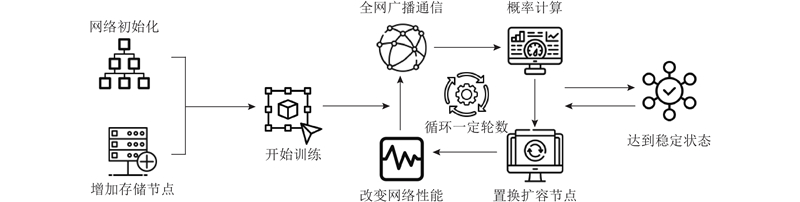
首先将区块链Kad网络初始化,并为每个节点扩容,使它们额外存储相同数量的节点信息. 之后训练网络. 具体来说,让全网每个节点都能广泛地通信,便于它们收集到其他节点的地址信息,按照概率公式进行计算,通过计算结果判断是否置换扩容节点,每一次改变都会影响网络性能,这个过程会反复进行多轮. 在网络状态稳定后停止训练,从而构建出小世界网络.
由于网络中节点数量的动态变化,网络性能可能会受到影响. 当网络性能下降到一定程度时,必须重新训练网络,以使性能恢复到最佳状态. 为了确定重新训练的时机,可以在最后一次训练结束后测量并记录网络的平均广播跳数,将其设定为阈值. 在网络正常运行期间,需要定期测量网络的平均广播跳数. 若一天内多次测量值均超过阈值的10%,则判断网络性能严重下降,需要重新训练. 选择10%作为阈值的原因如下:相比于普通Kad网络,该模型的性能提升最多只有30%. 若平均广播跳数下降超过10%,意味着算法的改进效果十分有限,需要重新投入训练. 时间窗口设定为1天,以确保性能下降不是由短期的网络波动所引起的. 在重新训练时,可以选择网络交易数量较少的时刻,例如全网负荷不到50%时,这样可以减少对网络正常操作的干扰. 小世界Kad方法的一大优势是无论网络的初始状态如何,利用该模型均能改善网络的通信性能. 在重新训练后,网络性能必然得到提升. 通过以上方法,该模型能够及时识别网络性能下降的情况并采取相应的措施,以保持网络的高性能状态.
本方案的核心理念是让网络中大部分节点与距离自身较近的节点保持连接,只有少数节点与远距离节点建立连接. 这种方式使得整个网络空间呈现出短链多、长链少的特点,符合K模型的核心特征.
2.2. 推导证明
假设Kad网络中存在N个节点,若所有节点按照概率公式置换扩容节点,则这个过程的状态转移仅依赖于当前状态,是马尔科夫过程.因为它的时间和状态都离散,可以被视为马尔科夫链. 为了便于理解和研究,将任意2个节点间的距离视作一种状态,因而节点a的状态空间可以被表示成
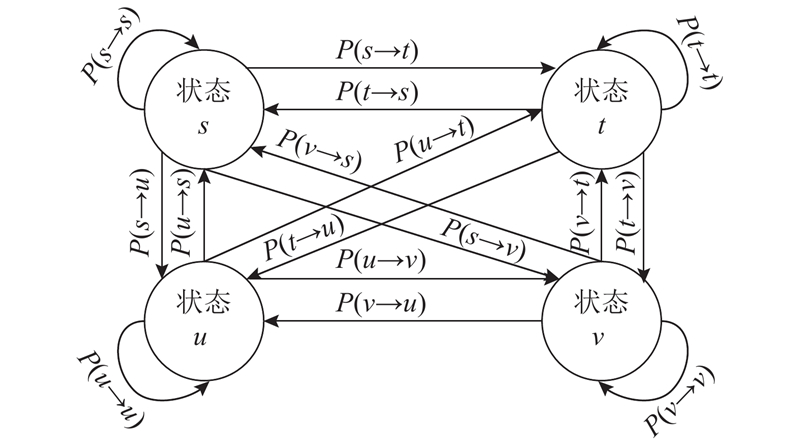
为了简洁地说明情况,如图3所示,展现了节点a仅有4个状态时的状态转换示例.
图 3
根据马尔科夫定理可知,若马尔科夫链的状态数量有限,状态转移过程不存在周期且转移矩阵元素全部为正数,则该链具有遍历性和不可约性,它的平稳分布存在且唯一,等于它的极限分布. 假设这条马尔科夫链的平稳分布是
式中:
网络中任意一节点经过有限步数的节点置换,会趋于稳定的状态,这与节点的起始状态无关,所以网络初始化阶段可以随机分配存储节点. 在马尔科夫链达到稳态后,状态的转出和转入会达到平衡,此时从稳定状态j到状态s的转出概率等于从状态s到状态j的转入概率(
从式(2)可知,平稳分布
C为任意大于0的常数,方程的一个解为
节点状态表示节点之间的距离,任意2个状态的运算结果必为一确定常数,所以式(4)是常系数方程. 设状态空间A中存在n个状态,可将这些状态依次代入式(4),得到n元方程组. 该方程组只存在一个解,即式(6). 这个结果与该马尔科夫链中平稳分布等于极限分布相符. 式(6)说明网络中每个节点连接其他节点的概率分布与它们之间的距离呈反比,与本方案的思想一致.
在普通的Kad网络中,节点间的距离一般指2个节点ID的异或值即逻辑距离,但是这种距离没有考虑路由跳数的影响. 路由跳数反映了节点传输信息需要经过的中间节点数量. 在小世界网络的相关研究中,通常将路由跳数认定为节点间的距离[15]. 为了平衡逻辑距离和路由跳数的影响,增强算法的优化效果,提出实际距离
式中:
当计算置换概率时,节点间的逻辑距离可以通过对节点ID进行异或运算取得,路由跳数通过发送消息测量. 为了获取准确的跳数,减少重复传输,可以在每条消息中增加传输路径信息. 该信息包含发送节点的节点ID、地址信息以及中间节点和目的节点与发送节点的逻辑距离集合. 存储逻辑距离是因为在大多数区块链网络中节点ID长度远大于逻辑距离,例如在以太坊中逻辑距离的字节大小是4,节点ID的字节大小是32. 在目的节点收到消息后,可以将传输路径中中间节点数量最少的消息转发回发送节点,以便发送节点获取自身与目的节点之间的广播路由跳数.
2.3. 时间分析
虽然在经过一定轮数的训练后,小世界Kad网络能够趋于稳定状态,但是本模型要求所有节点在每一轮训练过程中广播自身的地址信息,以便其他节点能够计算概率并进行置换. 这导致状态变化过程非常复杂,无法使用马尔科夫链的相关理论推导得到本文算法准确的时间复杂度.目前,Wright[16]证明了大小为n的马尔科夫链最多需要
根据时间复杂度的分析可知,随着节点数量和维度的增长,算法达到稳定状态需要的时间会显著增加.节点数量无法改变,而维度可以调整,然而维度改变会影响网络性能,本研究最主要的目的是提升Kad网络的传输性能,而不是使模型达到完全稳定的状态. 由后续实验可知,当其他条件相同时,增加维度能够一定程度上改善算法的优化效果. 通过实验发现,该模型在训练前期性能提升很快,但是十几轮后性能改变幅度很小,因此可以在每一轮训练后测量网络的平均广播跳数. 若连续3轮跳数的下降比例不到1%,则判定该模型训练成功. 利用该策略,可以在合理的时间内获得性能相对良好的模型,减少模型的训练成本.
该模型的训练时间为
式中:N为节点总数,
区块链作为动态的开放环境,式(8)的各项参数均会动态变化. 以以太坊作为示例,提供所有参数的估计值,评估该方案的时间效率. 以太坊的数据传输速率为20 Mb/s,节点数量约为104,大多数节点能够在6跳内将消息广播至全网. 在训练过程中,每次传输消息的数据量不到100字节,其中发送节点ID、IP地址和端口号等信息大小约为54字节,发送节点与其他节点的逻辑距离集合大小约为24字节. 考虑到性能提升幅度在训练十几轮后变得较小,可以将训练轮数设定为30. 根据所设定的参数,预计在以太坊上,该模型的理论训练时间约为9 s,耗时很少. 该模型具有极高的时间效率. 对于其他应用Kad网络的区块链项目,它们的训练时间与以太坊接近.
2.4. 算法描述
该算法的具体步骤如算法1所示.
算法1 small world Kademlia
输入:网络节点数量N,K桶数量bc,每桶存储的最多节点数量kc,增加节点数量sc,训练轮数E.
输出:小世界Kad网络结构
1.function build origin kad network
2. create N nodes in network
3. for node
4. create bc buckets
5. for bucket
6. add random nodes until full or kc
7. end
8. end
9.function add sc nodes
10. for node
11. create (bc + 1)th bucket
12. add random sc nodes in the bucket
13. end
14.function replace nodes by training
15. for
16. for
17. broadcast message to all nodes;
18. receive message
19. compute real distance
20. compute probability
21. decide whether change or not
22. perform operation
23. end
24. end
3. 性能分析
3.1. 实验环境
该方法的实验环境如下:操作系统为Windows 11教育版64位,CPU为13th Gen Intel(R) Core(TM) i5-13600K 3.50 GHz,内存大小为64 GB,利用Java语言来编写代码,开发工具是VScode.
在实验过程中,对模型的效果进行初步验证,通过对照实验确定主要的参数值. 将该方案的优化算法与其他算法进行比较,综合评估该模型在消息广播、节点定位和网络安全性方面的表现.
3.2. 方法验证
创建包含128个虚拟节点的Kad网络,其中节点的ID使用7位二进制数表示,因此K桶数为7,k设置为4,每个节点保存了23个节点的地址信息. 对每个节点扩容,使它们额外存储4个节点的信息. 根据概率公式训练网络,记录实验结果. 共进行10组实验,分别以0~9设置Java随机数生成器的初始值,即通过不同的随机数种子Aseed对网络进行初始化,以确保网络的初始状态不同. 通过这些操作,展现了该算法在不同初始状态的网络下的应用效果,实验结果如图4所示.
图 4
图 4 不同初始状态时算法的平均广播跳数
Fig.4 Average broadcast hop count of algorithm in different initial states
图4中,E为训练轮数;Bhop为平均广播跳数,即所有节点进行全网广播时需要经历的平均传输层级. 平均广播跳数越小,表示网络的通信速率越快,网络性能越好,这意味着区块链上处理交易的速度会更快. 由于各节点全网广播所经历的传输层级不完全相同,平均广播跳数可能为小数. 实验结果显示,改造后的网络在经过一定轮数的训练后,性能得到提升并且状态逐渐趋于稳定. 无论网络的初始情况如何,该方案均能够对网络进行有效的优化,证明该算法具有收敛性和鲁棒性.
3.3. 参数确定
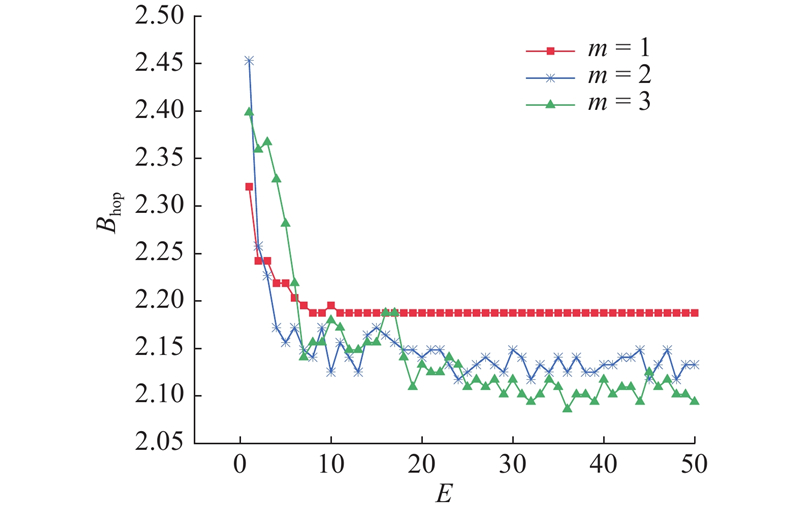
该算法需要确定的2个重要参数分别是维度以及逻辑距离与路由跳数的比例,它们会影响算法的优化效果. 实验采用之前创建的网络,Aseed设为0. 维度对算法性能的影响如图5所示.
图 5
图 5 不同维度时算法的平均广播跳数
Fig.5 Average broadcast hop count of algorithm in differen dimensions
从图5可以看出,当维度增加时,节点向全网广播消息所需的平均跳数有所减少,网络性能得到提升. 相较于维度从1变为2时显著的性能差异,当维度从2增加到3时,网络性能只有微小的改变. 当维度为1时,算法只须训练10轮左右就能达到稳定状态,比其他维度快很多,但是训练速度快的代价是网络性能较差. 即使在所有维度的训练轮数均设定为10的情况下,维度为2和3时的性能也优于维度为1时的性能.
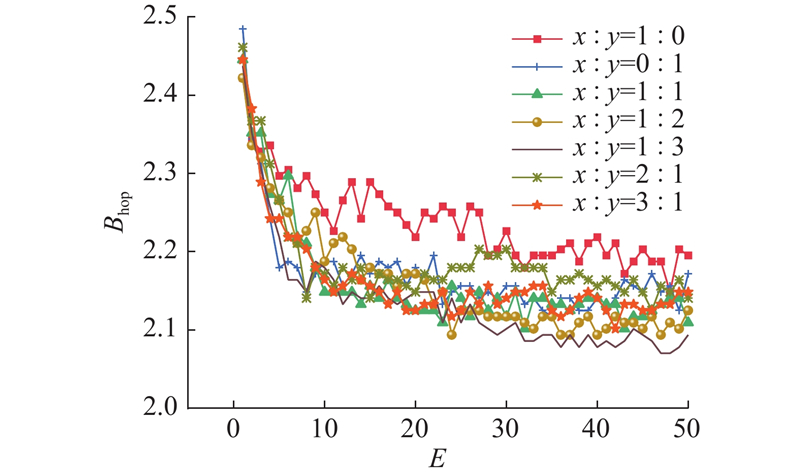
如图6所示为逻辑距离与路由跳数比例的变化对算法性能的影响.
图 6
图 6 不同比例时算法的平均广播跳数
Fig.6 Average broadcast hop count of algorithm in differen proportions
实验结果表明,当逻辑距离与路由跳数任意一个系数比例为0时,平均广播跳数较多,优化效果较差. 这说明逻辑距离与路由跳数都在算法中发挥着重要作用,不能忽视其中任何一个. 随着路由跳数占比的增加,算法性能略有提升,当比例为1∶3时,性能相对最佳.
3.4. 方案对比
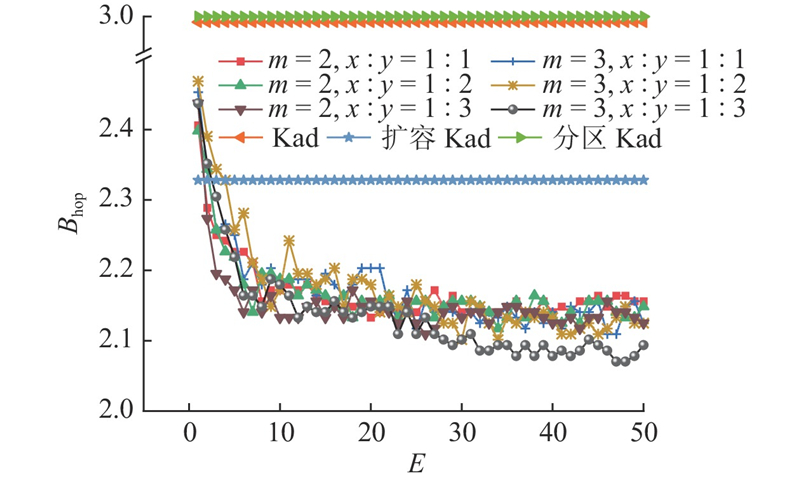
图 7
图 7 不同参数组合时提出模型与其他模型的对比
Fig.7 Comparison between proposed model and other models in different parameter combinations
如图7所示,经过训练后,该模型在不同维度和比例组合下均取得显著的性能提升,优于其他模型. 当维度为3,比例为1∶3时,模型性能达到最佳水平,因此在后续实验中采用该参数组合.
之前实验中的节点总数都是128,后续实验将网络的节点数量细分为5部分,分别为128、 256、512、1 024、2 048. 魏战争等[18]通常认为0~200个节点的网络是小型网络,200~1 000个节点的网络是中型网络,1 000个节点以上的网络是大型网络. 后续实验涵盖了小、中、大3种类型的网络,以全方位地探究小世界Kad网络的性能表现.
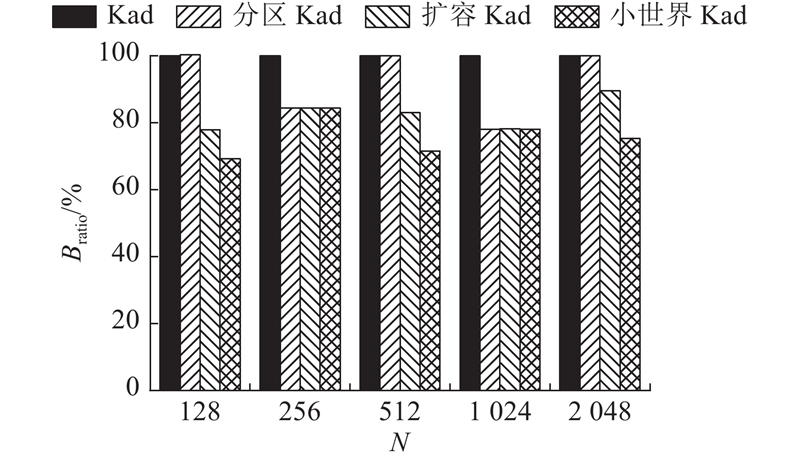
在Kad协议中,k的选取需要考虑系统性能和网络负载的平衡. 例如BitTorrent中k被设定为8,以太坊的k为16. 为了更好地呈现实验结果,针对小型、中型和大型3种规模的网络设置不同的k,分别是4、8和16. 当进行4类Kad协议的对比实验时,原始Kad和分区Kad中每个节点保存相同数量的节点信息,扩容Kad和小世界Kad中的节点需要额外存储k个节点. 在不同节点总数的网络中,原始Kad和分区Kad中每个节点存储的节点数量分别为23、47、55、111和127. 扩容Kad和小世界Kad将其分别扩大到27、55、63、127和143. 虽然小世界Kad的存储成本增加了12.6%~17.4%,但是额外消耗的存储空间不到1 kB,对比实验的结果如图8所示.
图 8
图8中,N为节点总数;Bratio为各优化模型与原始Kad的平均广播跳数的比值,即广播跳数优化比例. Bratio越小,表示网络广播速率越快,因此原始Kad的优化比例保持不变,全部是100%. 这能直观地展示各方案的优化效果. 与原始Kad相比,本模型的平均广播跳数减少了15.7%~30.8%,均高于它增加的存储消耗. 小世界Kad的性能提升水平在节点总数为128、512、2 048时明显优于其他方案,在另外2种情况下与其他优化方案相同.
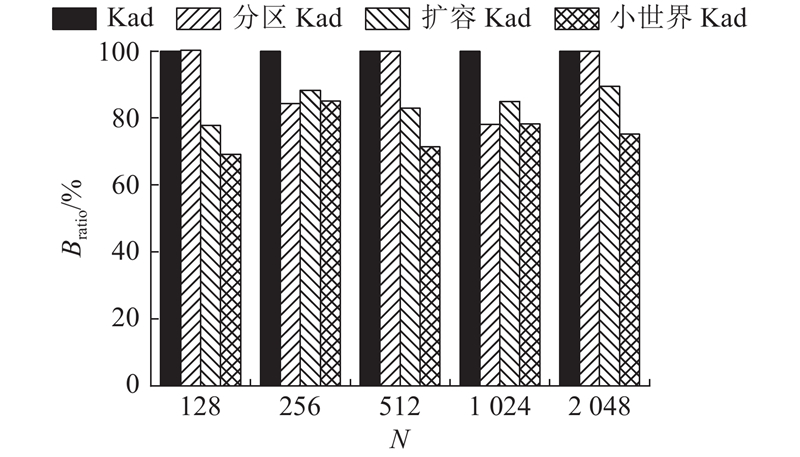
当网络节点总数为256和1 024时,扩容Kad和小世界Kad实现了相同的优化效果. 在增加了k个节点的存储容量后,这2种网络的性能均达到最佳状态;因此,可以适当减少额外补充的节点数量以降低存储开销,且尽可能保证优化效果不受影响. 经过多次测试发现,在256和1 024个节点的小世界Kad网络中,只需要每个节点额外多连接k/4个节点,即分别多存储2个和4个节点的地址信息,就能够将全网广播的平均跳数降低到接近最佳值,如图9所示.
图 9
图 9 调整后的平均广播跳数优化比例
Fig.9 Optimization ratio of average broadcast hop count after adjusting
图9中,网络节点总数为128、512、2 048时的存储成本与性能提升水平均与图8相同. 当节点总数为256和1 024时,小世界Kad较原始Kad额外花费的存储代价仅为4%左右,平均广播跳数分别下降了15.0%和21.8%. 小世界Kad的优化作用强于扩容Kad,与分区Kad几乎等同. 这表明小世界Kad具有很好的灵活性,可以根据需要调整网络中额外存储的节点数量,从而以更小的存储开销换取较多的性能提升. 分区Kad的优化效果会受到节点总数与k的影响,当节点总数为128、512、2 048时没有发挥作用,性能甚至比原始Kad更差. 相比之下,采用小世界Kad的所有网络都实现了性能优化,这说明小世界Kad具备更加广泛的适用性,能够应对不同场景下的网络优化需求. 由于调整效果良好,在后续的实验中,本方案将保持这个配置,即在节点总数为256和1 024时,每个节点只额外存储k/4个节点的地址信息,其余情况下存储k个.
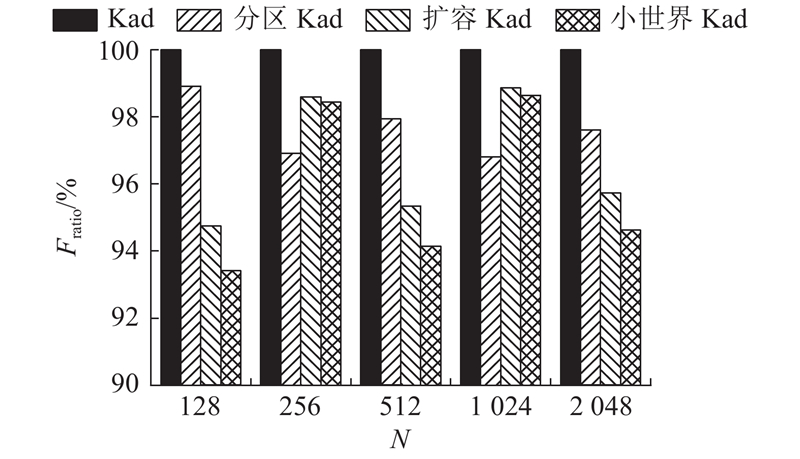
图10中,Fratio为各模型相对于原始Kad的平均查找跳数优化比例.小世界Kad的查找跳数较原始Kad下降了1.4%~6.6%.优化效果只在节点总数为256和 1 024时差于分区Kad,在其他情况下,都是表现最好的.
图 10
3.5. 安全性评估
双花攻击是指用户恶意利用区块链的交易确认机制,通过在网络中重复花费同一笔资产来获得不当利益的攻击行为. 双花攻击的本质是利用交易未被确认的时间窗口进行多次消费,而小世界Kad可以提升全网广播交易消息的速度,从而缩短时间窗口,降低发生双花攻击的风险.
DDoS攻击通过控制大量傀儡机,对一个或多个目标节点发送大量请求,使目标节点无法正常工作. 在小世界Kad网络中,向目标节点发送消息,需要事先保存该节点的地址信息,然而这些信息如果被存储在小世界桶(按照概率公式存储节点地址信息的空间结构)中,那么有可能会被置换,导致攻击不能顺利实施.
Sybil攻击是指攻击者通过将单个节点伪造成多个虚假节点以操纵网络的攻击方式. 为了实现这种攻击,虚假节点的地址信息必须被网络中的其他节点所保存,而在小世界Kad网络中,每个节点会定期更换扩容的节点信息,这增大了发动Sybil攻击的难度.
日蚀攻击的基本原理类似于Sybil攻击,但是前者更加着重于攻击单个节点. 日蚀攻击的主要目的是覆盖目标节点与网络的全部连接,使目标节点被隔离在网络之外. 以太坊曾经饱受日蚀攻击的困扰. 为了抵御日蚀攻击,以太坊在Geth v1.8.1版本上作了改进,将网络中每个节点存储的K桶数从256削减为17,只保留距离最远的17个K桶[23]. 这虽然增强了网络的安全性,但是导致了传输性能的下降.
旧版本的以太坊难以抵御日蚀攻击,是因为网络中的节点ID由公钥生成,不受IP限制,用户可以通过密钥生成算法大量制造. Kad网络的高度结构化导致其缺乏弹性,每个节点的i 号K桶都只存储与自身逻辑距离为
与这2个方案相比,小世界Kad按照概率存储扩容节点,引入了一定的随机性,安全性更强. 概率置换公式中的实际距离由逻辑距离和路由跳数共同决定,而虚假节点无法改变自身与目标节点的路由跳数,这由网络的整体情况决定,因此小世界桶中的节点可信度很高. 小世界桶中保存的节点信息会根据概率公式被多次置换,即使在某一时刻小世界桶中存储了虚假节点,它们也很可能会在下一时刻被换掉,不会长期存在. 攻击者几乎不可能使虚假节点完全占据小世界桶,导致目标节点被网络隔离. 当攻击者发动50%的日蚀攻击,即覆盖目标节点50%的对外连接时,需要花费的成本即创造的虚假节点数量如图11所示.
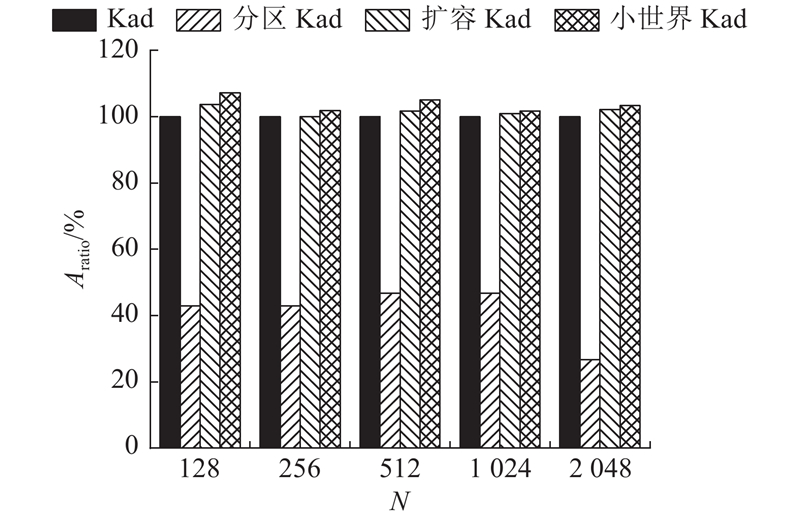
图 11
图 11 发动50%的日蚀攻击的虚假节点数量优化比例
Fig.11 Optimization ratio of number of false nodes of launching 50% eclipse attack
图11中,Aratio为各模型与原始Kad中虚假节点数量的比例,比例越大表明该模型抵御日蚀攻击的能力越强,比例越小表明该模型越容易受到日蚀攻击的侵害. 当攻击者对小世界Kad发动50%的日蚀攻击时,承担的成本最大,相较于原始Kad增加了1.7%~7.1%. 对于分区Kad,攻击者花费的代价最小,需要生成的节点数仅为原始Kad的26.7%~46.7%.
4. 结 语
为了提升区块链网络的可扩展性和安全性,本文提出在区块链Kademlia网络上构建小世界网络的方法. 该方法以节点间距离与连接概率成反比的方式置换扩容节点,提高了网络的传输性能. 具体而言,平均广播跳数减少了15.0%~30.8%,平均查找跳数减少了1.4%~6.6%. 该方法引入一定的随机性,增强了网络抵御各种攻击的能力,如攻击者发动 50%的日蚀攻击的成本增加了1.7%~7.1%,几乎不可能实现100%的日蚀攻击. 尽管该方法增加了3.6%~17.4%的存储成本,但是额外消耗的空间不到1 kB,代价很小. 在后续的研究中,会考虑现实环境对网络的影响,将物理层面上节点的距离、网络带宽和CPU运行速度等因素纳入概率公式,使得该方法能够更好地应用于实际的网络拓扑.
参考文献
Fine-grained, secure and efficient data provenance on blockchain systems
[J].DOI:10.14778/3329772.3329775 [本文引用: 1]
A scalable blockchain network model with transmission paths and neighbor node subareas
[J].DOI:10.1007/s00607-021-00913-1 [本文引用: 2]
Ethereum’s peer-to-peer network monitoring and sybil attack prevention
[J].DOI:10.1007/s10922-022-09676-2 [本文引用: 1]
Am I eclipsed? a smart detector of eclipse attacks for Ethereum
[J].DOI:10.1016/j.cose.2019.101604 [本文引用: 1]
Collective dynamics of ‘small-world’ networks
[J].
Identity and search in social networks
[J].DOI:10.1126/science.1070120 [本文引用: 1]
Cryptocurrencies activity as a complex network: analysis of transactions graphs
[J].DOI:10.1007/s12083-021-01220-4 [本文引用: 1]
Ethna: analyzing the underlying peer-to-peer network of ethereum blockchain
[J].DOI:10.1109/TNSE.2021.3078181 [本文引用: 1]
Statistical complexity of the power method for Markov chains
[J].DOI:10.1016/0885-064X(89)90001-0 [本文引用: 1]
中型网络中交换机连接技术的探讨
[J].DOI:10.3969/j.issn.1673-1328.2010.18.070 [本文引用: 1]
Discussion on switch connection technology in medium-sized network
[J].DOI:10.3969/j.issn.1673-1328.2010.18.070 [本文引用: 1]
DDoS attacks and defense mechanisms: classification and state-of-the-art
[J].DOI:10.1016/j.comnet.2003.10.003 [本文引用: 1]
Low-resource eclipse attacks on Ethereum’s peer-to-peer network
[J].